Abstract
The two-parameter logistic (2PL) item response model is likely the most frequently applied item response model for analyzing dichotomous data. Linking errors quantify the variability in means or standard deviations due to the choice of items. Previous research presented analytical work for linking errors in the one-parameter logistic model. In this article, we present linking errors for the 2PL model using the general theory of M-estimation. Linking errors are derived in the case of log-mean-mean linking for linking two groups. The performance of the newly proposed formulas is evaluated in a simulation study. Furthermore, the linking error estimation in the 2PL model is also treated in more complex settings, such as chain linking, trend estimation, fixed item parameter calibration, and concurrent calibration.
1. Introduction
Item response theory (IRT) models [1,2] are an important class of multivariate statistical models for analyzing dichotomous random variables used to model testing data from educational or psychological applications. Of particular relevance is the application of item response models in educational large-scale assessments [3], such as the programme for international student assessment (PISA; [4]) study.
In this article, we only investigate unidimensional IRT models. Let be the vector of I dichotomous random variables (also referred to as items). A unidimensional item response model [5] is a statistical model for the probability distribution for , where
where is the density of the normal distribution with mean and standard deviation . The vector contains the distribution parameters. The vector contains all estimated item parameters of item response functions .
The one-parameter logistic (1PL) model (also referred to as the Rasch model; [6]) employs the item response function , where denotes the logistic distribution function, and is the item difficulty of item i. In this case, . The two-parameter logistic (2PL) model [7] additionally includes the item discrimination (i.e., ), and the item response function is given by .
Note that distribution parameters and item parameters cannot be simultaneously identified. In applications such as PISA in which a country mean and a country standard deviation , item parameters are often fixed at values that are used for all countries. In this situation, and can be identified. If sample data for N persons are available, unknown model parameters in (1) can be estimated by (marginal) maximum likelihood (ML) using an expectation maximization algorithm [8,9].
In practice, data-generating item parameters differ from assumed fixed item parameters . This property is also referred to as differential item functioning (DIF; [10,11]). DIF effects are defined as deviations . The occurrence of DIF causes additional variability in the estimated (country) mean and standard deviation [12,13]. The estimated distribution parameters depend on the choice of selected items, even in infinite sample sizes of persons. This variability is quantified in the linking error [14,15,16,17,18,19].
There exist simple formulas for linking errors based on variance components for the 1PL model [15,17]. For more complex models, resampling techniques [20,21] such as jackknife [15,17] or the (balanced) half sampling [18] of items can be employed. In this article, we provide closed formulas for the linking error for the 2PL model in various applications based on the M-estimation theory. The proposed formulas have the advantage of avoiding computationally more demanding resampling approaches for computing linking errors.
The rest of this article is structured as follows. The foundation of the M-estimation theory for the application of the computation of the linking error in the 2PL model is presented in Section 2. The specialization of M-estimation to log-mean-mean linking is treated in Section 3. The performance of the newly proposed linking errors is investigated in a simulation study in Section 4. Section 5 provides a further analytical treatment of the linking error in the 2PL model to more complex applications. Finally, this article closes with a discussion in Section 6.
2. Linking Error and M-Estimation
In this section, we discuss the computation of the linking error in the 2PL model for two groups. We do this in a general setting of M-estimation theory [22,23,24] because our treatment will apply to many of the recently discussed linking methods. However, we focus on log-mean-mean linking in this article as an important example in Section 3 and Section 4.
Assume that the 2PL model holds in two groups or two time points. The goal is to determine the mean and the standard deviation of the second group, while the first group is assumed to have a mean of 0 and a standard deviation of 1. The DIF effects and for logarithmized item discriminations and item difficulties follow
It is assumed that and are independently and identically distributed with zero means and variances , , and the covariance is defined as .
In the first step of the linking approach, the 2PL model is separately estimated in each of the two groups. Because the ability for the first group has zero mean and a standard deviation of 1, the identified item parameters and equal the data-generating item parameters and , respectively, (). In the second group, we fix the mean to 0 and the standard deviation to 1 and obtain identified parameters
In the second step of the linking approach, identified item parameters and are used in determining the mean and the standard deviation in the second group. Note that we assume that identified item parameters are known. Hence, we implicitly have infinite sample sizes of persons. In practice, we estimate item parameters from finite sample sizes. Appropriate adjustments are discussed in Section 5.8.
A general estimating equation of the type
is employed for determining the parameter or with as the distribution parameters of interest. M-estimation theory provides the asymptotic variance in an estimate . Because linking errors refer to the uncertainty regarding item choice, this asymptotic variance can be used to compute the linking error.
In the two-group 2PL case, we have two unknown distribution parameters (or ) and . Hence, involves two equations for two unknowns that must be solved. The two M-estimation equations of the linking approaches can be generally written as
M-estimation theory provides the asymptotic variance (for ) for the estimate with the sandwich formula [22]
The matrix is denoted as the bread matrix, while the matrix is referred to as the meat matrix. The latter matrix is given by
where denotes a covariance matrix. The bread matrix is given as
The two matrices in Equations (7) and (8) require the computation of expected values and variances of random variables. If these were unavailable or the quantities could not be algebraically determined, sample-based versions of the bread and the meat matrix are frequently used [23]. The meat matrix can be estimated based on sample data using (7)
An empirical version of is given by
If and are used for computing the variance matrix for (i.e., ), the estimate is denoted as the expected sandwich (ESW) estimate. The observed sandwich (OSW) estimate is obtained by using and in the formula of the variance matrix (i.e., ). Finally, a bias-corrected observed sandwich (BOSW) is obtained by using (see [25,26,27]).
We want to emphasize that M-estimation theory is not restricted to applications of linking approaches for two groups and two distribution parameters. The parameter can be of any finite dimensionality and could, for example, involve unknown parameters for linking G groups.
M-estimation theory was applied in the investigation of DIF and linking in [28,29,30]. The simultaneous treatment of standard errors and linking errors in IRT models relying on M-estimation was presented in [18,31] (see also [32]).
3. Linking Error of Log-Mean-Mean Linking
We now apply the M-estimation of computing linking errors to log-mean-mean linking [33,34] for linking two groups in the 2PL model. The logarithm of the standard deviation is estimated by
It can be shown that is an unbiased and consistent estimate for s [34]. Moreover, is obtained by computing .
An estimate of the group mean is obtained using
We can reformulate (11) and (12) as M-estimators
using . Now, we determine the linking errors for and in log-mean-mean linking using the sandwich formula (6) of M-estimation. First, we compute the variance matrix of . We obtain using and
Hence, it follows that
Now, we compute derivatives of with respect to s and and obtain the bread matrix as
The inverse of the bread matrix can be determined as
Formulas (18) and (19) involve unknown parameters , , , and that must be estimated. The quantities and can be replaced with their sample estimates to estimate unknown variances and covariances in the and matrices. We obtain the expected sandwich estimator (ESW) using Equation (6) by
The observed sandwich (OSW) estimate uses empirical moments in the estimation. First, the bread matrix is estimated by
The meat matrix is estimated by
Finally, we use a bias-corrected variant of the observed sandwich estimator [27] as
Linking errors can be obtained as square roots of the diagonal elements of the variance matrices . The linking error for based on the ESW estimate is given by
By utilizing the delta method, we can obtain the linking error for as
Finally, the linking error for can be estimated by
In the absence of a nonuniform DIF, we have , and the linking error for the 1PL model is obtained from (27)
Interestingly, the presence of a nonuniform DIF () introduces additional uncertainty in computing the group mean. However, there is only an effect of a nonuniform DIF if the average item difficulty does not match the group mean (i.e., ). In typical applications, the third term in (27) will be much more important than the second term . Hence, a nonuniform DIF particularly plays an important role if uniform and nonuniform DIF effects are strongly correlated.
4. Simulation Study
4.1. Method
In this simulation study, we investigate the performance of different linking error estimates for the log-mean-mean linking approach in the 2PL model. In particular, we compare the jackknife linking error (JK) with linking errors obtained by the empirical sandwich (ESW), observed sandwich (OSW), and the bias-corrected observed sandwich (BOSW) estimates. The formulas for the sandwich estimates are presented in Section 3. The jackknife linking error estimate is computed by repeating the linking procedure when omitting the ith item for . Let or be the distribution parameter of interest and be the corresponding estimate. Let be the estimated parameter if item i was removed from the linking procedure. Then, the jackknife linking error is defined as (see [15])
For identification, the first group had a zero mean and a standard deviation of the ability variable . For the second group, we defined and in the simulation. Item parameters for 10 items are presented in Table 1. In the simulation, we used , or 80 items. For item numbers as multiples of 10, we duplicated the item parameters of the 10 items presented in Table 1 accordingly. The standard deviation of uniform DIF effects was chosen as or 0.50. The standard deviation of nonuniform DIF effects was chosen as or 0.25. The first condition mimics the case of the practical absence of nonuniform DIF effects. The correlation of DIF effects between and was set at 0.3 in all simulation conditions (i.e., ). Finally, we chose three types of distributions for DIF effects . We specified them as a bivariate normal copula model and chose different marginal distributions. First, we chose the normal distribution (i.e., denoted as “Normal”) as a marginal distribution appropriately scaled by and . Second, we chose a scaled t distribution with four degrees of freedom (i.e., denoted as “”) with an appropriate scaling factor to match the desired standard deviation of DIF effects. Third, we use the distribution function F of a normal mixture model (i.e., denoted as “Normal Mixture”) of the type
where and . This distribution can be interpreted as a contaminated distribution that includes a few outlying DIF effects in with proportion . Such a distribution is often employed in robust statistics [35]. For a prespecified DIF effect , we obtain from (30) the determining equation .

Table 1.
Simulation Study: Used item parameters of the 2PL model.
To disentangle standard errors due to the sampling of persons from linking errors due to item choice, we assumed no sampling error for identified parameters and . That is, identified item parameters for the second group only vary across replications in the simulation study because different DIF effects and were simulated in each replication. It seems reasonable in the simulation study in the comparison of the different M-estimation approaches with a jackknife to exclude the effects of sampling errors because these are just another source of uncertainty in distribution parameter estimates.
In each of the cells of the simulation, 40,000 replications were conducted. We assessed coverage rates at the 95% confidence level based on the normal distribution for distribution parameter estimates. The linking error computation for the estimated standard deviation utilized the delta method.
The R software [36] was used for simulation and analysis. We used the qmixnorm function from the R package KScorrect [37] for determining quantiles in the data simulation of DIF effects. Because analytical solutions are not available to compute a quantile function for the normal mixture model, the qmixnorm function approximates the quantile function using a spline function calculated from cumulative density functions for the specified mixture distribution [37]. Quantiles for probabilities near zero or one are approximated by taking a randomly generated sample.
4.2. Results
In Table 2, the coverage rates for the estimated mean are presented as a function of the standard deviation of the DIF effects, the number of items, and the type of distribution for the DIF effects. It turned out that there were no substantial differences in the performance of the different linking error methods with respect to the distribution types of the DIF effects. The jackknife and the ESW estimates were very similar. The OSW estimate did not reach the desired coverage rates in a short test (i.e., ) but improved in longer tests. Moreover, the BOSW slightly improved the OSW estimate but still was inferior to the ESW estimate.

Table 2.
Simulation Study: Coverage rates for estimated mean as a function of the standard deviation of DIF effects for a () and b (), number of items (I), and the type of distribution for DIF effects.
In Table 3, the coverage rates for the estimated standard deviation are presented as a function of the standard deviation of the DIF effects, the number of items, and the type of distribution for the DIF effects. The OSW and BOSW had particular issues in the coverage rates with very small nonuniform DIF effects. These issues also remained in the longer tests. However, the estimated standard deviations of the nonuniform DIF effects turned out to be unbiased and can be detectable in such situations to indicate that linking errors for would be tiny in this situation. Hence, the practical absence of nonuniform DIF effects using the simulation condition might not be very realistic, and future studies could investigate the performance using .

Table 3.
Simulation Study: Coverage rates for estimated standard deviation as a function of the standard deviation of DIF effects for a () and b (), number of items (I), and the type of distribution for DIF effects.
Overall, the findings of this simulation study indicate that the sandwich estimates (in particular the ESW) are as effective as the jackknife estimates for linking errors.
5. Further Applications of the Linking Error in the 2PL Model
In this section, several applications of the linking error computations in the 2PL model are presented. In Section 5.1, the M-estimation theory is applied to linking approaches other than the log-mean-mean linking. Section 5.2 discusses the computation of the linking errors if the items are nested within testlets. The linking errors for chain linking and trend estimation are discussed in Section 5.3 and Section 5.4, respectively. In Section 5.5, the linking error under a fixed item parameter calibration is derived. Section 5.6 presents the linking error in the 2PL model for a concurrent calibration. Section 5.7 investigates the computation of the linking errors of derived parameters. Finally, Section 5.8 focuses on the computation of the total error and sampling error corrections in the linking error estimation.
5.1. Different Linking Methods
We now illustrate how the sandwich estimates in the M-estimation theory from Section 2 can be used for other linking approaches.
5.1.1. Robust Log-Mean-Mean Linking
Log-mean-mean linking involves two steps that compute the mean for determining the logarithm of the standard deviation and the mean . A few outlying items might introduce bias in the estimated distribution parameters [18]; robust estimators for the location measures can be preferred. In this case, the estimating functions for are given by
using a robust function that fulfills the property for (see [29,30]). For example, if the median was used, would be the sign function . A differentiable approximation of this function is given by for and . The observed sandwich formula can be easily applied to obtain linking errors for a wide class of robust linking approaches.
5.1.2. Haebara Linking
Haebara (HAE) linking [38] aligns item response functions instead of directly aligning item parameters. The linking function in HAE linking is given as
where is a weighting function. By defining the difference
we can rewrite (33) as
The estimating equations for and can be determined by
Again, linking errors can be easily obtained using the observed sandwich (OSW) formula.
5.2. Linking Error with Testlets
In educational large-scale assessment studies such as PISA, several items frequently share a common item stimulus. In this situation, items are nested within testlets [39,40,41]. It was demonstrated that DIF effects are also pronounced at the testlet level and not only at the item level [17,42]. This additional source of uncertainty should be included in the computation of linking errors to avoid negatively biased linking error estimates.
We illustrate how to apply the theory of M-estimation in the case of testlets. The linking error for and in log-mean-mean linking is derived. Let there be H testlets, and there are items within each testlet h. It holds that . The data-generating model for DIF effects in the 2PL model in Equation (2) is adapted to include DIF effects at the item and the testlet level. DIF effects for logarithmized item discriminations now include two terms referring to testlets (i.e., h) and items within testlets (i.e., item i nested within testlet h). We assume
Note that item parameters now possess an item index i and a testlet index h in (38). Again, it is assumed that the DIF effects are independently distributed across items, and we define , , , , , and .
The estimating equations in log-mean-mean linking are the same. However, they must include the testlet structure of items. The estimating Equations (13) and (14) are rearranged as
The essential change in the computation of the sandwich variance in the testlet case is that the variance matrix (i.e., the meat matrix) requires the computation of the variance that is carried out at each testlet h instead of each individual item i (see [27]). To indicate the dependency from the testlet structure, it is more appropriate to label the meat matrix because testlets are independent units, not items. The entry involving the variance in DIF effects in item discriminations in the meat matrix can be computed as
The other variance and the covariance can be derived similarly. Consequently, the meat matrix is given by
The bread matrix only involves the expected value of the derivatives of the estimating equations. Hence, this matrix remains unchanged in a testlet structure [27].
The unknown variance and covariance components in (42) can be replaced by sample estimates. Then, an expected sandwich variance estimate can be obtained. A sample estimate of the meat matrix can be obtained by replacing the population variance in (41) with an empirical variance. Like in the case of independent items, the observed sandwich variance estimate can be modified to obtain a bias-corrected variant. In the testlet case, one should use correction factor instead of .
5.3. Linking Error in Chain Linking
In this subsection, we discuss the computation of the linking error in chain linking [33,43,44] in log-mean-mean linking. Figure 1 illustrates the test design in the chain linking. The items are administered at three time points, T1, T2, and T3 (or in three groups). The goal is to determine the distribution parameters at T3. The distribution parameters of the ability variable at T3 can be compared with those at T1 by carrying out the linking step T1↔T2 and T2↔T3. The set of all items is denoted as and is partitioned into three distinct sets, , , and . The set contains items that were administered at all three time points. Items in and are administered at T1 and T2 and T2 and T3, respectively. We fix the distribution parameters at the first time point T1 to a mean of 0 and a standard deviation of 1. The mean of at T2 is denoted by and the standard deviation by . The mean of at T3 is denoted by and the standard deviation by .
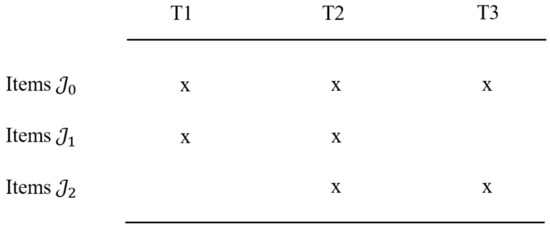
Figure 1.
Illustration of chain linking at three time points: T1, T2, and T3.
We assume that the 2PL model holds at the three time points. For longitudinal data, DIF is referred to as item parameter drift (IPD; [45,46]). The data-generating model involves IPD effects for item discriminations and for item intercepts ().
All IPD effects are allowed to be correlated within each item i but are uncorrelated across items.
In chain linking, the 2PL model is separately estimated for the three time points. The identified item parameters are given as , and
In the first linking step T1↔T2, the mean and the standard deviation are determined in log-mean-mean linking. In the second linking step T1↔T2, linking constants and are derived that refer to the linear transformation .
In the chain linking approach, the unknown parameters are collected in the vector . The parameters of interest are computed as a derived parameter given by
Let be the number of items in the sets for . We define and for . The two successive linking steps are formulated as a joint linking problem involving four estimating equations
where includes all identified item parameters and design variables for item i. The first two estimating equations in (46) refer to log-mean-mean linking of the step T1↔T2, while the last two refer to step T2↔T3. In Equation (46), dummy indicators are used that take the value of one if item i is contained in or for . Note that for and .
We can now compute the meat matrix
Moreover, we can determine the expected value of the bread matrix as
The inverse of can be computed as
Using the matrices and , the variance matrix of can be computed using the sandwich formula (6).
We now explicitly derive linking errors for and . First, the standard deviation at T3 is given as . We derive the variance by applying the delta method to the nonlinear transformation h and using the variance matrix . The first-order partial derivatives of h are given by
Hence, the linking error of the estimated standard deviation can be determined as
The algebraic derivation for the linking error formula was somewhat more intricate, which is why the R package rSymPy package [47] as a wrapper to the SymPy computer algebra system [48] was used. The square of the linking error for (i.e., the quantity ) is computed using (56)
The linking error for the estimated mean can be determined as a derived parameter using the transformation . The first-order partial derivatives of h are given by
The linking error for can be computed by using (56)
In chain linking in the 1PL model, the linking error for substantially simplifies by setting , (see also [49])
Note that all DIF effects referring to item discriminations vanish in this case.
5.4. Linking Error for Trend Estimates in Educational Large-Scale Assessment Studies
We now turn to the important application of linking errors for trend estimates [13,15,50,51] in educational LSA studies such as PISA [16,52]. The main goal is to compute a linking error for a trend estimate in country means or country standard deviations between two successive assessments. Again, we rely on the 2PL model and use log-mean-mean linking for the derivation of the linking errors. Previous research derived closed formulas for linking errors in the 1PL model [17]. It was stated in official PISA publications that there does not exist a simple generalization to the 2PL model [52]. However, this section provides a closed formula for the 2PL model.
Figure 2 illustrates the problem of trend estimation in LSA studies. The label “NAT” refers to a nation (i.e., a country) c. The label “INT” refers to the international metric that is defined as a pooled sample comprising all students of participating countries in the LSA study. A trend estimate for a country between two LSA assessments can involve means and standard deviations at T1 and T2 (i.e., it compares NAT2 and NAT1). The first linking step NAT1↔INT1 maps country-specific results onto an international metric at T1. This step allows a cross-sectional comparison of countries on an international reference metric. The second linking step INT1↔INT2 links results of two LSA studies at T1 and T2 at the international metric. The third linking step NAT2↔INT2 maps country-specific results to the international metric at T2.
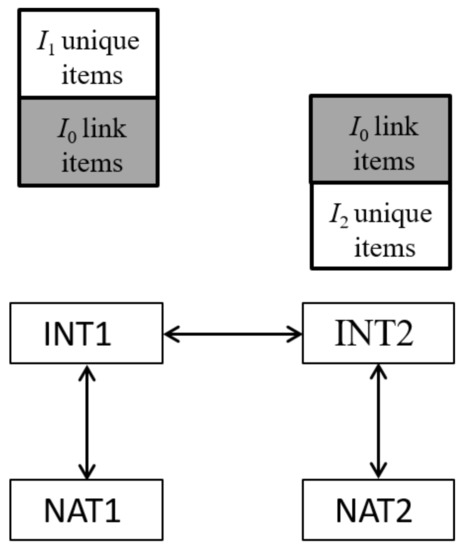
Figure 2.
Trend estimation for country means and standard deviations at two time points in an international large-scale assessment study.
The set of administered items typically differs across assessments [53]. There are link items that are administered at both time points. A set of unique items is only administered at T1, while a set of unique items is only administered at T2. For identification reasons, we assume that the ability variable has zero mean and a standard deviation of one at T1. Then, we can identify the mean and the standard deviation of country c at T1. Furthermore, we assume that the mean at the international metric at T2 is and the standard deviation is . We can also identify the mean and the standard deviation of country c at T2.
The first linking step NAT1↔INT1 in log-mean-mean linking estimates and . The second linking step INT1↔INT2 estimates and . The third linking step NAT2↔INT2 estimates linking constants and to put the results of country c at the international metric at T2.
The country mean and standard deviation of country c at T2 are derived functions of the estimated linking parameters
The linking constants for the link INT2↔NAT2 are recomputed using (61) as
The main idea is to apply the M-estimation theory and the sandwich formula for deriving linking errors for trend estimates. The three-step linking procedure can also be written as a simultaneous estimation problem involving six estimating equations for the vector of unknown linking parameters . The trend estimate in means is given as
The trend estimate in standard deviations is given as
The source of linking errors in trend estimates is the presence of DIF effects. We now present a data-generating model for DIF effects in item parameters in the 2PL model. Let and for be item discriminations and item difficulties for country c. These item parameters are referred to as national item parameters [17]. International item parameters that result from item response models at the international metric that involves students from all countries are denoted by and . We use the same random effects model as in [17] for item difficulties
The variance component refers to item parameter drift (IPD; [54]). The variance is referred to as cross-sectional country DIF, and the variance refers to time-point-specific country DIF. All DIF effects are uncorrelated with each other.
We now extend the random effects model in [17] to item discriminations
All DIF effects for logarithmized item discriminations are uncorrelated, but DIF effects e and f can be correlated for the same type of heterogeneity (i.e., , , and ).
Identified national item parameters are given as and for . Moreover, for international item parameters, it holds that and at T1, and and .
We now apply the M-estimation theory to the estimation of linking errors. The three log-mean-mean linking steps can be formalized as the following six estimating equations:
The estimating equations in (67) define an estimate of the parameter of interest . We now use the sandwich formula to derive the asymptotic variance of by means of the sandwich Formula (6).
The entries of the meat matrix in the sandwich formula are denoted by
The non-zero entries in are given as
Moreover, we can determine the bread matrix as
The inverse of can be computed as
We now derive the linking error of the trend estimate in standard deviations that is a nonlinear function of
The first-order partial derivatives of h are given by
Using (56), we can determine the square of the linking error by using computer algebra software [47,48] as
We now compute the linking error for the trend estimate in the mean in the 2PL model. The country mean difference can be computed as
The first-order partial derivatives are given as
The linking error for the trend estimate in means is given by
5.5. Linking Error in Fixed Item Parameter Calibration
In this subsection, linking errors for the estimated mean and the estimated standard deviations under fixed item parameter calibration (FIPC) are derived. It is assumed that one uses fixed item parameters and , but the true item parameters and have DIF effects and follow the data-generating model (2).
The FIPC is typically applied using marginal maximum likelihood estimation [55]. However, we derive the linking error for a diagonally weighted least squares (DWLS) estimation that approximates the former estimation method [56]. The DWLS minimizes the weighted sums of the differences between the estimated and model-implied item thresholds as well as the tetrachoric correlations. For the simplicity of exposition in this subsection, we assume that there are only DIF effects in item difficulties (i.e., uniform DIF). Hence, we can assume that the standard deviation can be estimated without bias.
The item-specific weights in the DWLS estimation are precision weights that are defined as the inverse of the variance in thresholds . When omitting a factor that involves the sample size, precision weights are determined by
Equation (80) is displayed in Figure 3. It can be seen that extreme thresholds are downweighted.
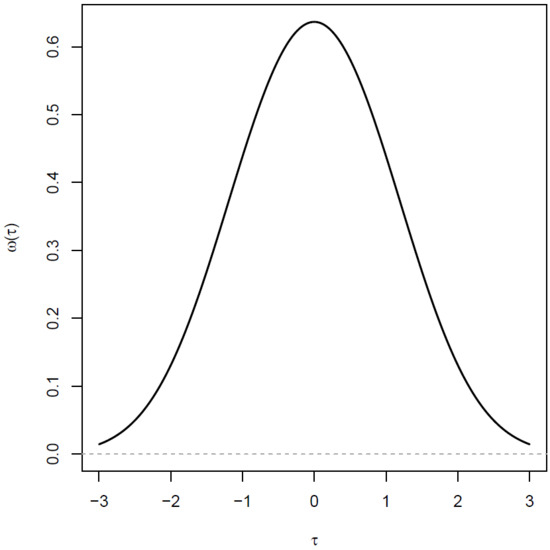
Figure 3.
Precision weights as a function of the threshold (see Equation (80)).
The optimization function for in DWLS is given by
where is the identified threshold of item i and is the model-implied threshold. Now, define , where is the logistic variance that is the byproduct of using the logistic instead of the probit link function in the 2PL model. Then, (81) can be rewritten as
where (C is an appropriate scaling constant) and . Note that for a data-generating true mean .
Hence, one can determine the linking error as the variance in the second term on the right-hand side in (83). We then obtain the linking error in fixed item parameter calibration
By the Cauchy–Schwarz inequality, it holds that
Hence, we get from (84) by using (85)
Hence, the linking error has a lower bound in which all item-specific weights were set equal to one. This case corresponds to the linking error in the Rasch model obtained for mean-mean linking [15,17]
This linking error is also obtained in FIPC of the 1PL model using unweighted least squares (ULS) estimation.
Interestingly, the finding in (86) illustrates that using incorrect item parameters in the FIPC in the presence of DIF effects results in a precision loss. Hence, the maximum likelihood estimation can only achieve the most efficient estimates under correctly specified models. Because it is almost always expected that there are some intentionally unmodeled DIF effects in real datasets, the dominance of the maximum likelihood estimation in LSA practice can be questioned.
5.6. Linking Error in Concurrent Calibration
In this subsection, we derive the linking error for the estimation of the 2PL model in two groups. The mean and the standard deviation of the ability variable are fixed to 0 and 1, respectively. The mean and the standard deviation of the second group are estimated.
Like in Section 5.5, we assume that there are only DIF effects in item difficulties and no DIF effects in item discriminations. We assume that can be estimated without bias and derive the linking error under concurrent calibration using DWLS. DIF effects with zero means follow . The identified parameters are given by and . The estimation of the vector of common item difficulties and the mean is conducted using a weighted square loss of differences in estimated and model-implied item thresholds. By simplifying the setting while assuming known item discriminations and standard deviation, the optimization function is given by
where weights are allowed to be group specific (). The estimating equations for and are given as
Equation (91) can be further simplified to
By defining , we obtain from (92)
Hence, we obtain the linking error for
where . Again, one can conclude . Hence, using the linking error that does not take item-specific weights into account provides a lower bound of the true linking error.
If the weights and would be equal across both groups, we obtain the same linking error like under fixed item parameter calibration.
5.7. Linking Error for Derived Parameters
In previous sections of this paper, we derived the linking error for and for different applications of the 2PL model. Sometimes, other distribution parameters might be estimated. In this subsection, we assume that the ability variable is approximately normally distributed and derive the linking error for nonlinear functions h of and . Let be a nonlinear function of the mean and the standard deviation . Let denote the variance matrix of regarding item choice (i.e., quantifying linking errors). The linking error estimate is given as
We now illustrate the computation in two examples.
5.7.1. Proportions
First, we are interested in computing the probability p
The partial derivatives of h are given as
where Hence, we can determine the linking error of using (95) as
where , , and are estimated linking variances and covariances.
5.7.2. Percentiles
Second, the linking error of the pth percentile should be computed. The pth percentile is defined by
Hence, we can solve (100) for and obtain
where is the pth percentile for the standard normal distribution.
5.8. Computation of Total Error and Sampling Error Correction for Linking Error Estimates
In practical applications, the sampling error due to the sampling of persons must also be taken into account to quantify the uncertainty in the and estimates. The total error () is given by (see [18,19])
A critical issue might be that estimated linking errors also include a portion of variability that can be attributed to the sampling error of persons. We illustrate an analytical bias correction method for the case of log-mean-mean linking. The issue in the sandwich estimate is the variance matrix (i.e., the meat matrix) (see (15) for the computation). The identified item parameters also include a sampling error variance that can be estimated by fitting an item response model. Let be the variance of due to person sampling (i.e., . Then, we can determine a corresponding entry in the meat matrix by modifying (15) into
In the derivation of (105), we relied on the property that item parameters of different items are approximately uncorrelated in sufficiently long tests [57]. The other entries in can be similarly determined. By defining and , Equations (16) and (17) can be modified to
Hence, the originally obtained meat matrix can be removed from sampling error contributions by defining a bias-corrected estimate
This approach was implemented in the simplified setting in the 1PL model [17].
We now show how to generalize the bias-corrected estimate of the meat matrix . We can rewrite the estimate from Equation (9) as
where . The estimate includes the sampling error, and the sampling variance is denoted as
The estimating function in (109) can be viewed as a function . Denote by the matrix of partial derivatives with respect to . We can now apply a Taylor expansion and obtain
Using , we can obtain a bias-corrected estimate of the bread matrix as
6. Discussion
In this article, we have shown that the sandwich formula from the M-estimation theory can be successfully employed for computing the linking error in the 2PL model in a variety of situations. It was shown in a simulation study for the log-mean-mean linking of two groups that the expected sandwich estimate of the linking error produced satisfactory coverage rates. Interestingly, it had a comparable performance to the jackknife linking error in the 2PL model.
As with any simulation study, some limitations of our study can be stated. More comprehensive studies could involve a different range of standard deviations of the DIF effects, different test lengths, or other linking approaches. It might be interesting to compare the performance of the M-estimation approach with the jackknife linking error for the more complex linking problems of chain linking and trend estimation.
In the simulation study, we only considered uncertainty in distribution parameters due to DIF effects (i.e., linking errors). In practical applications, there will also be a sampling of persons, and the simultaneous assessment of sampling errors and linking errors would be an exciting extension of this study.
In most of the applications involving instruments with cognitive and noncognitive items, linking errors are not reported even if linking approaches were utilized [43,58,59]. There might be two reasons why this is the case. First, simulation studies typically presuppose that the IRT model perfectly fits the data. That is, the DIF is absent, and the IRT model is correctly specified. Second, items could be treated as fixed, and the model misspecification is taken for granted but is not included in the uncertainty quantification of the linking approach. In our view, linking errors provide additional information about the impact of heterogeneous item functioning on parameters of interest and should, therefore, (almost always) be additionally reported. In general, we do not think that the presence of DIF or IPD threatens the validity of group differences or trend estimates.
It should be emphasized that our proposed linking error for the trend estimates in the 2PL model differs from a newly proposed linking error estimate since PISA 2015 [4]. The latter relies on a recalibration approach of the item response data from the first time point [34,60]. The new PISA linking error rather assesses the extent of the assumed noninvariant item parameters across the two PISA studies instead of quantifying the variability due to heterogeneous item functioning.
The derived linking errors rely on the assumption that item parameters are identified. In LSA studies such as PISA, balanced incomplete block designs are employed in which only a subset of items is administered to each student [61]. If item parameters can be identified in such test designs, linking error formulas would not change because country means and standard deviations are based on all the items administered in the test, irrespective of the proportion of items administered to each student.
As argued by an anonymous reviewer, the computation of linking errors relies on the assumption of a representative item sample from an item population. Notably, the identification of item parameters in the joint maximum likelihood estimation also requires asymptotic regimes regarding the sample size and the number of items [62,63,64] but does not require that items are a random sample from an item population. However, the main difference in the computation of linking errors is that linking errors reflect the variability in the distribution parameter estimates due to the DIF. Infinite item samples are not required for model identification; they are only used as a statistical tool for justifying the statistical inference with respect to modeled or unmodeled DIF.
Finally, we assumed that DIF effects had zero means throughout this paper. However, this assumption is not essential in deriving linking errors because the M-estimation theory does not require that estimated parameters converge to true parameters. The M-estimation theory will nevertheless provide the asymptotic variance in a potentially biased estimator. However, DIF effects could also result in a mean that is different from zero. For example, Ref. [28] assumes that the median of the DIF effects equals zero. In this case, log-mean-mean linking in the 2PL model could be replaced by an alternative robust linking method in which the mean is substituted with the median. Notably, the choice of an adequate estimating function to provide unbiased distribution parameters depending on the distribution of DIF effects is a different topic though [18].
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 1PL | one-parameter logistic |
| 2PL | two-parameter logistic |
| DIF | differential item functioning |
| DWLS | diagonally weighted least squares |
| FIPC | fixed item parameter calibration |
| IPD | item parameter drift |
| IRT | item response theory |
| JK | jackknife |
| LE | linking error |
| LSA | large-scale assessment studies |
| PIRLS | progress in international reading literacy study |
| PISA | programme for international student assessment |
| ULS | unweighted least squares |
References
- Chen, Y.; Li, X.; Liu, J.; Ying, Z. Item response theory—A statistical framework for educational and psychological measurement. arXiv 2021, arXiv:2108.08604. [Google Scholar] [CrossRef]
- van der Linden, W.J. Unidimensional logistic response models. In Handbook of Item Response Theory, Volume 1: Models; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 11–30. [Google Scholar]
- Rutkowski, L.; von Davier, M.; Rutkowski, D. (Eds.) A Handbook of International Large-Scale Assessment: Background, Technical Issues, and Methods of Data Analysis; Chapman Hall: London, UK; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar] [CrossRef]
- OECD. PISA 2018. Technical Report; OECD: Paris, France, 2020. [Google Scholar]
- Yen, W.M.; Fitzpatrick, A.R. Item response theory. In Educational Measurement; Brennan, R.L., Ed.; Praeger Publishers: Westport, CT, USA, 2006; pp. 111–154. [Google Scholar]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Danish Institute for Educational Research: Copenhagen, Denmark, 1960. [Google Scholar]
- Birnbaum, A. Some latent trait models and their use in inferring an examinee’s ability. In Statistical Theories of Mental Test Scores; Lord, F.M., Novick, M.R., Eds.; MIT Press: Reading, MA, USA, 1968; pp. 397–479. [Google Scholar]
- Aitkin, M. Expectation maximization algorithm and extensions. In Handbook of Item Response Theory, Vol. 2: Statistical Tools; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 217–236. [Google Scholar] [CrossRef]
- Bock, R.D.; Aitkin, M. Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika 1981, 46, 443–459. [Google Scholar] [CrossRef]
- Holland, P.W.; Wainer, H. (Eds.) Differential Item Functioning: Theory and Practice; Lawrence Erlbaum: Hillsdale, NJ, USA, 1993. [Google Scholar] [CrossRef]
- Penfield, R.D.; Camilli, G. Differential item functioning and item bias. In Handbook of Statistics, Vol. 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 125–167. [Google Scholar] [CrossRef]
- Joo, S.; Ali, U.; Robin, F.; Shin, H.J. Impact of differential item functioning on group score reporting in the context of large-scale assessments. Large-Scale Assess. Educ. 2022, 10, 18. [Google Scholar] [CrossRef]
- Sachse, K.A.; Roppelt, A.; Haag, N. A comparison of linking methods for estimating national trends in international comparative large-scale assessments in the presence of cross-national DIF. J. Educ. Meas. 2016, 53, 152–171. [Google Scholar] [CrossRef]
- Battauz, M. Multiple equating of separate IRT calibrations. Psychometrika 2017, 82, 610–636. [Google Scholar] [CrossRef]
- Monseur, C.; Berezner, A. The computation of equating errors in international surveys in education. J. Appl. Meas. 2007, 8, 323–335. [Google Scholar]
- OECD. PISA 2012. Technical Report; OECD: Paris, France, 2014; Available online: https://bit.ly/2YLG24g (accessed on 3 December 2022).
- Robitzsch, A.; Lüdtke, O. Linking errors in international large-scale assessments: Calculation of standard errors for trend estimation. Assess. Educ. 2019, 26, 444–465. [Google Scholar] [CrossRef]
- Robitzsch, A. Robust and nonrobust linking of two groups for the Rasch model with balanced and unbalanced random DIF: A comparative simulation study and the simultaneous assessment of standard errors and linking errors with resampling techniques. Symmetry 2021, 13, 2198. [Google Scholar] [CrossRef]
- Wu, M. Measurement, sampling, and equating errors in large-scale assessments. Educ. Meas. 2010, 29, 15–27. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar] [CrossRef]
- Kolenikov, S. Resampling variance estimation for complex survey data. Stata J. 2010, 10, 165–199. [Google Scholar] [CrossRef]
- Boos, D.D.; Stefanski, L.A. Essential Statistical Inference; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Stefanski, L.A.; Boos, D.D. The calculus of M-estimation. Am. Stat. 2002, 56, 29–38. [Google Scholar] [CrossRef]
- Zeileis, A. Object-oriented computation of sandwich estimators. J. Stat. Softw. 2006, 16, 1–16. [Google Scholar] [CrossRef]
- Fay, M.P.; Graubard, B.I. Small-sample adjustments for Wald-type tests using sandwich estimators. Biometrics 2001, 57, 1198–1206. [Google Scholar] [CrossRef]
- Li, P.; Redden, D.T. Small sample performance of bias-corrected sandwich estimators for cluster-randomized trials with binary outcomes. Stat. Med. 2015, 34, 281–296. [Google Scholar] [CrossRef]
- Zeileis, A.; Köll, S.; Graham, N. Various versatile variances: An object-oriented implementation of clustered covariances in R. J. Stat. Softw. 2020, 95, 1–36. [Google Scholar] [CrossRef]
- Chen, Y.; Li, C.; Xu, G. DIF statistical inference and detection without knowing anchoring items. arXiv 2021, arXiv:2110.11112. [Google Scholar] [CrossRef]
- Halpin, P.F. Differential item functioning via robust scaling. arXiv 2022, arXiv:2207.04598. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.; Liu, H. Testing differential item functioning without predefined anchor items using robust regression. J. Educ. Behav. Stat. 2022, 47, 666–692. [Google Scholar] [CrossRef]
- Robitzsch, A. Lp loss functions in invariance alignment and Haberman linking with few or many groups. Stats 2020, 3, 246–283. [Google Scholar] [CrossRef]
- Hunter, J.E. Probabilistic foundations for coefficients of generalizability. Psychometrika 1968, 33, 1–18. [Google Scholar] [CrossRef]
- Kolen, M.J.; Brennan, R.L. Test Equating, Scaling, and Linking; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Robitzsch, A. A comparison of linking methods for two groups for the two-parameter logistic item response model in the presence and absence of random differential item functioning. Foundations 2021, 1, 116–144. [Google Scholar] [CrossRef]
- Maronna, R.A.; Martin, R.D.; Yohai, V.J. Robust Statistics: Theory and Methods; Wiley: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 11 January 2022).
- Novack-Gottshall, P.; Wang, S.C. KScorrect: Lilliefors-Corrected Kolmogorov-Smirnov Goodness-of-Fit Tests; R Package Version 1.4-0. 2019. Available online: https://CRAN.R-project.org/package=KScorrect (accessed on 3 July 2019).
- Haebara, T. Equating logistic ability scales by a weighted least squares method. Jpn. Psychol. Res. 1980, 22, 144–149. [Google Scholar] [CrossRef]
- Bradlow, E.T.; Wainer, H.; Wang, X. A Bayesian random effects model for testlets. Psychometrika 1999, 64, 153–168. [Google Scholar] [CrossRef]
- Sireci, S.G.; Thissen, D.; Wainer, H. On the reliability of testlet-based tests. J. Educ. Meas. 1991, 28, 237–247. [Google Scholar] [CrossRef]
- Wainer, H.; Bradlow, E.T.; Wang, X. Testlet Response Theory and Its Applications; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Monseur, C.; Sibberns, H.; Hastedt, D. Linking errors in trend estimation for international surveys in education. IERI Monogr. Ser. 2008, 1, 113–122. [Google Scholar]
- Battauz, M. IRT test equating in complex linkage plans. Psychometrika 2013, 78, 464–480. [Google Scholar] [CrossRef]
- Battauz, M. Factors affecting the variability of IRT equating coefficients. Stat. Neerl. 2015, 69, 85–101. [Google Scholar] [CrossRef]
- Arce-Ferrer, A.J.; Bulut, O. Investigating separate and concurrent approaches for item parameter drift in 3PL item response theory equating. Int. J. Test. 2017, 17, 1–22. [Google Scholar] [CrossRef]
- Taherbhai, H.; Seo, D. The philosophical aspects of IRT equating: Modeling drift to evaluate cohort growth in large-scale assessments. Educ. Meas. 2013, 32, 2–14. [Google Scholar] [CrossRef]
- Grothendieck, G. rSymPy: R Interface to SymPy Computer Algebra System. R Package Version 0.2-1.2. 2010. Available online: https://CRAN.R-project.org/package=rSymPy (accessed on 31 July 2010).
- Meurer, A.; Smith, C.P.; Paprocki, M.; Čertík, O.; Kirpichev, S.B.; Rocklin, M.; Kumar, A.; Ivanov, S.; Moore, J.K.; Singh, S.; et al. SymPy: Symbolic computing in Python. PeerJ Comput. Sci. 2017, 3, e103. [Google Scholar] [CrossRef]
- Fischer, L.; Gnambs, T.; Rohm, T.; Carstensen, C.H. Longitudinal linking of Rasch-model-scaled competence tests in large-scale assessments: A comparison and evaluation of different linking methods and anchoring designs based on two tests on mathematical competence administered in grades 5 and 7. Psych. Test Assess. Model. 2019, 61, 37–64. [Google Scholar]
- Sachse, K.A.; Haag, N. Standard errors for national trends in international large-scale assessments in the case of cross-national differential item functioning. Appl. Meas. Educ. 2017, 30, 102–116. [Google Scholar] [CrossRef]
- Sachse, K.A.; Mahler, N.; Pohl, S. When nonresponse mechanisms change: Effects on trends and group comparisons in international large-scale assessments. Educ. Psychol. Meas. 2019, 79, 699–726. [Google Scholar] [CrossRef]
- OECD. PISA 2015. Technical Report; OECD: Paris, France, 2017; Available online: https://bit.ly/32buWnZ (accessed on 3 December 2022).
- Weeks, J.; von Davier, M.; Yamamoto, K. Design considerations for the program for international student assessment. In A Handbook of International Large-Scale Assessment: Background, Technical Issues, and Methods of Data Analysis; Rutkowski, L., von Davier, M., Rutkowski, D., Eds.; Chapman Hall: London, UK; CRC Press: Boca Raton, FL, USA, 2013; pp. 259–276. [Google Scholar] [CrossRef]
- Kang, H.A.; Lu, Y.; Chang, H.H. IRT item parameter scaling for developing new item pools. Appl. Meas. Educ. 2017, 30, 1–15. [Google Scholar] [CrossRef]
- König, C.; Khorramdel, L.; Yamamoto, K.; Frey, A. The benefits of fixed item parameter calibration for parameter accuracy in small sample situations in large-scale assessments. Educ. Meas. 2021, 40, 17–27. [Google Scholar] [CrossRef]
- Cai, L.; Moustaki, I. Estimation methods in latent variable models for categorical outcome variables. In The Wiley Handbook of Psychometric Testing: A Multidisciplinary Reference on Survey, Scale and Test; Irwing, P., Booth, T., Hughes, D.J., Eds.; Wiley: New York, NY, USA, 2018; pp. 253–277. [Google Scholar] [CrossRef]
- Yuan, K.H.; Cheng, Y.; Patton, J. Information matrices and standard errors for MLEs of item parameters in IRT. Psychometrika 2014, 79, 232–254. [Google Scholar] [CrossRef]
- González, J.; Wiberg, M. Applying Test Equating Methods. Using R; Springer: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Jewsbury, P.A. Error Variance in Common Population Linking Bridge Studies; (Research Report No. RR-19-42); Educational Testing Service: Princeton, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Martin, M.O.; Mullis, I.V.S.; Foy, P.; Brossman, B.; Stanco, G.M. Estimating linking error in PIRLS. IERI Monogr. Ser. 2012, 5, 35–47. Available online: https://bit.ly/2Vx3el8 (accessed on 3 December 2022).
- Frey, A.; Hartig, J.; Rupp, A.A. An NCME instructional module on booklet designs in large-scale assessments of student achievement: Theory and practice. Educ. Meas. 2009, 28, 39–53. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Zhang, S. Joint maximum likelihood estimation for high-dimensional exploratory item factor analysis. Psychometrika 2019, 84, 124–146. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Zhang, S. Structured latent factor analysis for large-scale data: Identifiability, estimability, and their implications. J. Am. Stat. Assoc. 2020, 115, 1756–1770. [Google Scholar] [CrossRef]
- Haberman, S.J. Maximum likelihood estimates in exponential response models. Ann. Stat. 1977, 5, 815–841. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).