Computational Electromagnetics: A Miscellany

Abstract

The paper presents a miscellany of unorthodox and, in some cases, paradoxical or controversial items related to computational and applied electromagnetics. The topics include a definition of the magnetic source field via a line integral, losses in electric power transmission vs. losses in photonics, homogenization of periodic electromagnetic structures, spurious modes, models of plasmonic media, and more. It is hoped that this assortment of subjects will be of interest to a broad audience of scientists and engineers.

1. Introduction

Computational electromagnetics has been a very active research area for six decades. The computational capabilities over this time have grown by leaps and bounds due to the development of various discretization techniques, system solvers, as well as advances in software and Moore’s-law-driven hardware.

In some cases, this research has led to unexpected or counterintuitive conclusions and occasionally to misconceptions. The paper presents an assortment of issues of this kind in the hope that they will be of interest to a wide audience of readers in the field of computational electromagnetics and related areas of physics, engineering and applied mathematics. A condensed summary of some of these issues appears in [1] (Chapter 10); here this material is extended and expanded significantly. While the selection of topics for this paper is subjective, all of them are directly related to current research in computational and applied electromagnetics. Among these topics are efficient computation of magnetic “source fields” as line integrals rather than volume integrals, effective parameters of metamaterials, a rigorous definition of electric polarization, physically valid boundary conditions for plasmonic media, spurious modes, and more.

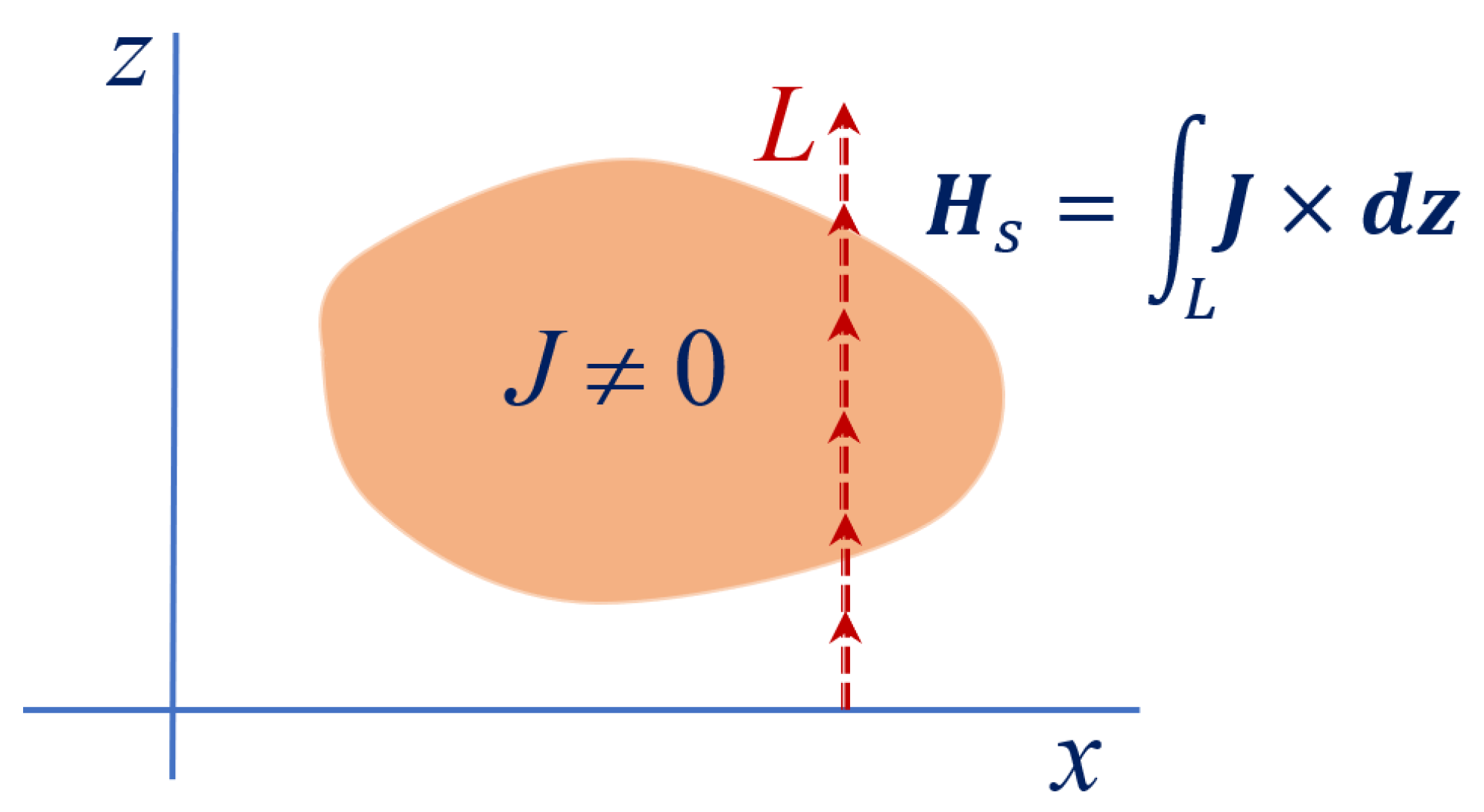
2. The Magnetostatic “Source Field” and the Biot–Savart Law

The governing curl equation for the magnetic field is

$$\nabla \times \mathbf{H}=\alpha \mathbf{J},\alpha =\left\{\begin{array}{cc}1,\hfill & \mathrm{SI}\hfill \\ \frac{4\pi }{c},\hfill & \mathrm{Gaussian}\hfill \end{array}\right.$$

(1)

In magnetostatics, $\mathbf{J}$ is the density of known excitation currents; beyond statics, $\mathbf{J}$ may include eddy currents and displacement currents. For the purposes of this section, a distinction between these types of currents does not need to be made, and $\mathbf{J}$ is considered as the total current density regardless of its nature.

As is the case for any linear equation with a nonzero right hand side, one can split the $\mathbf{H}$ field up into a particular one and a homogeneous one, $\mathbf{H}={\mathbf{H}}_s+{\mathbf{H}}_h$. Any particular solution ${\mathbf{H}}_s$ is known as a source field, which, by definition, satisfies Equation (1) but does not need to be subject to any other constraints (such as divergence or boundary conditions). The homogeneous part ${\mathbf{H}}_h$ is, also by definition, curl-free. Therefore, if the computational domain is simply connected, then

$${\mathbf{H}}_h=-\nabla u$$

(2)

where u is the magnetic scalar potential. Hence,

$$\mathbf{H}={\mathbf{H}}_s+{\mathbf{H}}_h={\mathbf{H}}_s-\nabla u$$

(3)

(For complications arising in multiply-connected domains, see [2,3,4,5].)

For a given constitutive relationship $\mathbf{B}=\mathcal{B}\left(\mathbf{H}\right)$ (linear or nonlinear), the zero-divergence condition for the $\mathbf{B}$ field, along with (3), yields

$$\nabla ·\mathcal{B}({\mathbf{H}}_s-\nabla u)=0$$

(4)

In particular, if $\mathbf{B}=\mu \mathbf{H}$ (where for brevity dependence on position is not explicitly indicated), then the following equation for the magnetic scalar potential ensues:

$$\nabla ·\mu \nabla u=\nabla ·\mu {\mathbf{H}}_s$$

(5)

The magnetic scalar potential formulation and Equations (4) and (5) are known very well [2,4,5,6,7,8,9,10]. The subject of this section is not these equations per se but rather an efficient way of computing the source field ${\mathbf{H}}_s$. The standard expression for it is the Biot–Savart law:

$${\mathbf{H}}_{\mathrm{Biot}}\left(\mathbf{r}\right)=\frac{\alpha }{4\pi }{\int }_{{\mathbb{R}}^3}\frac{\mathbf{J}\left({\mathbf{r}}^{\prime }\right)\times (\mathbf{r}-{\mathbf{r}}^{\prime })}{|\mathbf{r}-{\mathbf{r}}^{\prime }{|}^3}d{\mathbf{r}}^{\prime }$$

(6)

In magnetostatics, integration reduces to the region occupied by the excitation currents.

It is well known that ${\mathbf{H}}_{\mathrm{Biot}}$ is the magnetic field produced by currents in free space. However, in the presence of magnetic materials the Biot–Savart field (6) no longer corresponds to the actual field and is arguably no better than any other source field. At the same time, expression (6) is computationally expensive because it involves, in general, volume integration. In the case of line or surface currents the domain of integration reduces to one or two dimensions, respectively, and the cost of integration is lower. Additionally, clever ways to reduce the dimensionality of integration exist in special cases of uniform current distributions [11,12,13].

What is known less widely is that the source field can always be expressed as a line integral easily computable in many practical cases [7,8,9,14]. As a bonus, this field has a zero component in at least one coordinate direction, which entails additional computational advantages.

To wit, for a given current density distribution $\mathbf{J}\left(\mathbf{r}\right)$, we set out to define a two-component source field

$${\mathbf{H}}_s=H_{sx}\widehat{x}+H_{sy}\widehat{y};\nabla \times {\mathbf{H}}_s=\mathbf{J}$$

(7)

Component-wise, this curl condition reads

$${\partial }_x{H}_{sy}-{\partial }_y{H}_{sx}=J_z$$

(8)

$$-{\partial }_z{H}_{sy}=J_x$$

(9)

$${\partial }_z{H}_{sx}=J_y$$

(10)

Let the current density distribution $\mathbf{J}\left(\mathbf{r}\right)$ occupy a finite region, as is always the case in practical problems. Without any loss of generality, let us assume that this region is located in the upper half-space $z>0$. Then, from (9) and (10), respectively, we derive

$$H_{sy}(x,y,z)=-{\int }_{(x,y,0)}^{(x,y,z)}{J}_{x}dz$$

(11)

$$H_{sx}(x,y,z)={\int }_{(x,y,0)}^{(x,y,z)}{J}_{y}dz$$

(12)

or, in more compact form,

$${\mathbf{H}}_s(x,y,z)={\int }_L\mathbf{J}\times \mathbf{dz}$$

(13)

where L is a straight path from point $(x,y,0)$ to $(x,y,z)$ for arbitrary x, y, z. A 2D rendition of this integration is shown in Figure 1.

It is straightforward to verify that (8) also holds with this definition of ${\mathbf{H}}_s$:

$${\partial }_x{H}_{sy}-{\partial }_y{H}_{sx}=-{\int }_{(x,y,0)}^{(x,y,z)}{\partial }_x{J}_{x}dz-{\int }_{(x,y,0)}^{(x,y,z)}{\partial }_y{J}_{y}dz$$

$$\stackrel{\nabla ·\mathbf{J}=0}{=}{\int }_{(x,y,0)}^{(x,y,z)}{\partial }_z{J}_{z}dz=J_z(x,y,z)-J_z(x,y,0)=J_z(x,y,z)$$

(14)

With regard to the last transformation, note that $J_z(x,y,0)=0$ by assumption.

Naturally, (13) generalizes to

$${\mathbf{H}}_s={\int }_L\mathbf{J}\times \mathbf{dl}$$

(15)

where $\mathbf{dl}$ is any fixed direction in space, as long as the starting plane of that integration ($l=0$) is current-free.

For a general orthogonal coordinate system $(q_1,q_2,q_3)$, one may also seek ${\mathbf{H}}_s$ in the two-component form [14]

$${\mathbf{H}}_s=H_{s1}{\widehat{q}}_1+H_{s2}{\widehat{q}}_2(H_{s3}=0)$$

(16)

Then we have component-wise conditions generalizing (8)–(10):

$${\partial }_{q1}\left(h_2{H}_{s2}\right)-{\partial }_{q2}\left(h_1{H}_{s1}\right)=h_1{h}_2{J}_3$$

(17)

$$-{\partial }_{q3}\left(h_2{H}_{s2}\right)=h_2{h}_3{J}_1$$

(18)

$${\partial }_{q3}\left(h_1{H}_{s1}\right)=h_3{h}_1{J}_2$$

(19)

where $h_{1,2,3}$ are the Lamé coefficients. Therefore, from the last two equations,

$$h_2{H}_{s2}(q_1,q_2,q_3)=-{\int }_{(q_1,q_2,0)}^{(q_1,q_2,q_3)}{h}_2{h}_3{J}_{1}d{q}_3$$

(20)

$$h_1{H}_{s1}(q_1,q_2,q_3)={\int }_{(q_1,q_2,0)}^{(q_1,q_2,q_3)}{h}_3{h}_1{J}_{2}d{q}_3$$

(21)

Verifying (17):

$${\partial }_{q1}\left(h_2{H}_{s2}\right)-{\partial }_{q2}\left(h_1{H}_{s1}\right)=-{\int }_{(q_1,q_2,0)}^{(q_1,q_2,q_3)}{\partial }_{q1}\left(h_2{h}_3{J}_1\right)d{q}_3-{\int }_{(q_1,q_2,0)}^{(q_1,q_2,q_3)}{\partial }_{q2}\left(h_3{h}_1{J}_2\right)d{q}_3$$

$$\stackrel{\nabla ·\mathbf{J}=0}{=}{\int }_{(q_1,q_2,0)}^{(q_1,q_2,q_3)}{\partial }_{q3}\left(h_1{h}_2{J}_3\right)d{q}_3=h_1{h}_2{J}_3$$

(22)

where the zero-divergence condition for $\mathbf{J}$ was used, viz.:

$$h_1{h}_2{h}_3\nabla ·\mathbf{J}(q_1,q_2,q_3)={\partial }_{q1}\left(h_2{h}_3{J}_1\right)+{\partial }_{q2}\left(h_3{h}_1{J}_2\right)+{\partial }_{q3}\left(h_1{h}_2{J}_3\right)=0$$

(23)

As a common example, in the cylindrical system $q_1=z$, $q_2=r$, $q_3=\varphi$, the Lamé coefficients are $h_1=h_2=1$, $h_3=r$, and Equations (20) and (21) become

$$H_{sr}(z,r,\varphi )=-{\int }_{(z,r,0)}^{(z,r,\varphi )}r{J}_{z}d\varphi$$

(24)

$$H_{sz}(z,r,\varphi )={\int }_{(z,r,0)}^{(z,r,\varphi )}r{J}_{r}d\varphi$$

(25)

or more compactly

$${\mathbf{H}}_s(z,r,\varphi )={\int }_{(z,r,0)}^{(z,r,\varphi )}r\mathbf{J}\times \widehat{\varphi }d\varphi$$

(26)

where $\widehat{\varphi }$ is the unit vector in the angular direction. Expressions in the cylindrical system are quite useful in applications to rotating electrical machines [7,8,9,14].

It is interesting to note a discrete analog of analytical two-component fields. In FEM with edge elements, magnetic fields are defined via their circulations along the edges of triangular (in 2D), tetrahedral (in 3D) or other elements. There exists the so-called “tree /co-tree” gauge ([15] and §4.1 of [16]), defined as follows.

Let an FE mesh be considered as a graph, with element nodes as vertices. Pick an arbitrary node and generate a tree in the graph, with this node as the root. The edges not in the tree form a co-tree. The discrete curl on each finite element can be defined via the total circulation of the field around that element in the 2D case or around each face of any element in 3D. To obtain any prescribed set of values of the discrete curl over all faces, it suffices to define the source field only on the edges of the co-tree and set the circulations of the magnetic field to zero on the edges of the tree [15,16].

One final note is that Equation (15), when written in the spherical system with $\mathbf{dl}\equiv \mathbf{dr}$, is a particular case of the Poincaré gauge [17,18].

3. Good or Poor Conductors for Low Loss? (Part 1)

Let us first recall that in a lossy material with a scalar dielectric permittivity ${ϵ}^{\prime }$ and conductivity $\sigma$, the Maxwell curl $\mathbf{H}$ equation is, in the SI system,

$$\nabla \times \mathbf{H}=\mathbf{J}+{\partial }_t\mathbf{D}=\sigma \mathbf{E}+{\partial }_t\left({ϵ}^{\prime }\mathbf{E}\right)$$

(27)

In the frequency domain, under the $exp(-i\omega t)$ phasor convention, the right-hand side gets expressed in terms of the complex permittivity $ϵ=ϵ\left(\omega \right)={ϵ}^{\prime }\left(\omega \right)+i{ϵ}^{″}\left(\omega \right)$:

$$\nabla \times \mathbf{H}=-i\omega ϵ\mathbf{E},ϵ={ϵ}^{\prime }+i{ϵ}^{″},{ϵ}^{″}\stackrel{\mathrm{def}}{=}\frac{\sigma }{\omega }$$

(28)

(frequency dependence of $ϵ$ is not explicitly indicated for brevity).

It is common knowledge that electric power transmission and consumption relies on good conductors (such as copper or aluminum)—that is, materials with a high conductivity, $\sigma \gg \omega {ϵ}^{\prime }$, or equivalently

$$|{ϵ}^{″}|\gg {ϵ}^{\prime }\left(\mathrm{power}\mathrm{applications}\right)$$

(29)

The absolute value for $|{ϵ}^{″}|$ is used because the sign of $\mathrm{Im}ϵ$ depends on the $exp(\pm i\omega t)$ phasor convention. The ratio $|{ϵ}^{″}|/{ϵ}^{\prime }$ is the standard loss tangent.

Highly conductive materials in electric power applications minimize losses. This observation appears obvious and unremarkable, until a comparison is drawn with applications in optics and photonics, where the use of good conductors (e.g., gold or silver) leads to higher losses. The desirable relation therefore is

$$|{ϵ}^{″}|\ll {ϵ}^{\prime }\left(\mathrm{optics}\mathrm{and}\mathrm{photonics}\right)$$

(30)

In the area of plasmonics in particular, it is usually desirable to reduce losses and use materials with a small imaginary part of the dielectric permittivity [19].

Thus the low-loss conditions in optical vs. traditional electrical applications are diametrically opposite, and a natural question is: Why?

The first inclination may be to appeal to frequency differences, but conditions (29) and (30) are frequency independent. I invite the reader to find a more credible explanation. For my own take on this, see Section 9.

4. Topics in Homogenization

4.1. Introduction

Analysis of heterostructures with fine-scale features is greatly simplified if these structures can be accurately represented by a homogeneous effective medium. This means that scattered fields or reaction fields of the homogenized sample are approximately the same as those of the original heterostructure. Effective medium theories (EMT) were first developed in the 19th and early 20th century [20,21,22,23,24,25] and were advanced significantly in the middle of the 20th century [26,27,28]; for contemporary reviews, see §9.3 in [1,29,30].

With the advent of photonic crystals and metamaterials in the 1990s and in the early 2000s, homogenization theories needed to be enhanced further. The main reason is that, in contrast with natural materials, in metamaterials the lattice cell size can form an appreciable fraction of the free-space wavelength, in which case the homogenization theories developed earlier are not accurate anymore. This is a non-asymptotic case: the lattice cell size is not assumed to tend to zero.

In the spirit of this paper, I focus on some unorthodox aspects of these theories; for a detailed analysis or review of EMT, the interested reader is referred to the references cited.

One issue, which (somewhat surprisingly) turns out to be critical, is the role of boundary conditions for finite samples in addition to field behavior in the bulk. Another counter-intuitive aspect is that in periodic structures there is no transition to bulk behavior when the geometric dimensions of the sample increase and reach a certain threshold—even one lattice layer already exhibits characteristics indistinguishable from those in the bulk.

In eddy current problems typical for electrical machinery, there is a curious case of “effective medium transformation”: the eddy current problem in laminated magnetic cores turns, upon homogenization, into a magneto-quasistatic one; eddy currents just cannot be rendered on the coarse scale.

The last issue addressed in this Section is homogenization of periodic structures lacking mirror symmetry. At first glance, such structures cannot be accurately homogenized because the homogeneous sample is, perforce, geometrically symmetric. However, it turns out that the asymmetry can be adequately represented if the effective material parameters include magnetoelectric coupling.

4.2. Boundary Conditions in Effective Medium Theory

It is usually assumed that effective parameters of periodic electromagnetic structures can be derived from the dispersion relations alone–that is, from the behavior of Bloch waves in the bulk. The following argument demonstrates, however, that this assumption cannot be correct. Indeed, the Maxwell equation

$$\nabla \times \mathbf{H}=\left[\frac{1}{c}\right]{\partial }_t\mathbf{D}$$

(31)

(where the factor in the brackets applies in the Gaussian system but not in SI) is obviously invariant with respect to the rescaling

$${\mathbf{H}}^{\prime }=\xi \mathbf{H};{\mathbf{D}}^{\prime }=\xi \mathbf{D}$$

(32)

where $\xi$ is an arbitrary factor. Suppose now that the $\mathbf{E}$ and $\mathbf{B}$ fields are fixed (these fields are arguably more physical than $\mathbf{H}$ and $\mathbf{D}$, since they are directly related to forces acting on charges). Then transformation (32) results in the following rescaling of the material parameters:

$${\mu }^{\prime }=\mu /\xi ;{ϵ}^{\prime }=\xi ϵ$$

(33)

and Maxwell’s equations hold. Hence the bulk behavior alone does not determine the material parameters uniquely. What fixes these parameters are the boundary conditions, which couple the tangential components of the $\mathbf{H}$ field in the material and air. For further details, see §9.3 in [1,31,32]. This conclusion is not yet recognized as widely as it should be, as boundary effects are difficult to analyze and, moreover, do not play a significant role in the classical limit of a vanishingly small lattice cell size. Hence, it is tempting to sweep these effects under the rug. The relevant analyses do exist [33,34,35,36,37], but more work needs to be done. In particular, boundary effects play a critical role in the still emerging area of topological photonics [38,39,40,41,42,43,44,45].

4.3. One Layer Is “Bulk”

Suppose that one starts with just a single layer of lattice cells, periodic and infinite in two directions. Let the number of layers, and thus the thickness of the sample, be gradually increased. Intuitively, one would expect that when the thickness has reached a certain threshold, the effective material properties of the structure will exhibit transition to their bulk values. However, it turns out that for periodic structures such a transition does not take place; in some sense, one layer is already “bulk” [46]. This can be explained as follows.

Fields can be described as a superposition of Bloch waves in periodic heterostructures and of plane waves in homogeneous ones. Therefore, if Bloch waves and plane waves can be put into a one-to-one correspondence, then the fields outside the periodic and homogenized structures will be indistinguishable. The number of layers is thus irrelevant because Bloch waves do not depend on it. This one-to-one correspondence is established if the wave vectors and boundary impedances of the Bloch and plane waves are the same, which is possible to achieve exactly for a fixed angle of incidence and approximately for a range of angles. A detailed analysis can be found in [46].

4.4. Effective Medium Transformation

In standard effective medium theories, the type of the problem under consideration does not change upon homogenization. For example, a stationary heat transfer problem in a heterogeneous structure is, upon homogenization, still a heat transfer problem, with some effective parameters. Likewise, a wave problem remains a wave problem in an effective medium, and so on.

However, there is a peculiar case where homogenization changes qualitatively the character of the problem, both mathematical and physical. This has to do with eddy currents in stratified structures, typical for various types of electrical machines. To reduce induced currents and losses, magnetic cores are usually laminated: thin conducting magnetic sheets are coated with a thin layer of insulation, so that eddy currents are confined to the laminated sheets and cannot run across the whole magnetic core. As shown in [47], this eddy current problem becomes, under typical assumptions, mathematically a magneto-quasistatic one with a complex magnetic permeability. Here is a brief explanation of why this happens.

Consider cylindrical geometry typical for electric machines. The stratified structure is assumed to be infinite in the longitudinal (z) direction. Under this assumption, homogenization leads to fields and currents that cannot depend on z and do not have z-components. Then from the $\nabla \times \mathbf{H}=\mathbf{J}$ equation in the cylindrical system (displacement currents are neglected in the eddy current problem), one has

$$J_z=0;J_r=r^{-1}{\partial }_{\varphi }{H}_z-{\partial }_z{H}_{\varphi }=0-0=0;J_{\varphi }={\partial }_z{H}_r-{\partial }_r{H}_z=0-0=0$$

(34)

This shows that in this setup eddy currents cannot be represented on the coarse scale, and the character of the problem has indeed changed qualitatively: eddy current equations have turned into magneto-quasistatic ones [47].

4.5. Homogenization and Symmetry Breaking

Consider a periodic structure lacking mirror symmetry; a prototypical example is a layered medium composed of two alternating layers with different widths and/or different material properties. One manifestation of this asymmetry is that the phase of the reflection coefficient depends on which side the sample is illuminated from [48,49]. Since such a structure is to be replaced with a uniform medium upon homogenization, it appears that there is no way to preserve this intrinsic symmetry breaking (ISB) [49] (in contrast with extrinsic symmetry breaking (ESB), which may occur if the external media on the two sides of the structure are different).

One way to account for ISB is via an additional artificial layer introduced on the boundary of the sample [50]; however, such a layer is extrinsic to the sample and works only for one-sided illumination.

Propitiously, the homogenization procedure of [31,32] automatically accounts for ISB via an effective material tensor with magnetoelectric coupling terms. This tensor is independent of the illumination conditions, accounts for anisotropy and magnetic effects, and does not require additional artificial layers, nonlocality of material response or other amendments. The technical details can be found in [49].

5. “Spurious Modes”

As a model problem, consider electromagnetic resonances in a cavity $\Omega$ with perfectly conductive walls. The electric field is described by the well-known curl-curl equation:

$$\nabla \times {\mu }^{-1}\nabla \times \mathbf{E}-{\alpha }^2ϵ\mathbf{E}=0,\alpha =\left\{\begin{array}{cc}\omega ,\hfill & \mathrm{SI}\hfill \\ k,\hfill & \mathrm{Gaussian}\hfill \end{array}\right.$$

(35)

where $k=\omega /c$ is the wavenumber. The tangential component of the electrical field on the domain boundary is zero:

$$\widehat{\mathbf{n}}\times \mathbf{E}=0\mathrm{on}\partial \Omega$$

(36)

where $\widehat{\mathbf{n}}$ is the unit normal to the boundary.

The weak formulation of this problem adopted in finite element analysis reads:

$$({\mu }^{-1}\nabla \times \mathbf{E},\nabla \times {\mathbf{E}}^{\prime })-{\alpha }^2(ϵ\mathbf{E},{\mathbf{E}}^{\prime })=0,\mathbf{E},\forall {\mathbf{E}}^{\prime }\in H_0(\mathrm{curl},\Omega )$$

(37)

where ${\mathbf{E}}^{\prime }$ is a test function and $H_0(\mathrm{curl},\Omega )$ is the subspace of functions that belong to $H(\mathrm{curl},\Omega )$ and have zero tangential traces on the boundary $\partial \Omega$ (for a rigorous functional-analytic definition of these spaces, see e.g., [51]).

In the 1970s—early 1980s, traditional nodal elements were applied to (37). Unexpectedly, nodal FEM produced nonphysical solutions, which became known as “spurious modes” [52]. A typical feature of these modes was a nonzero divergence of the $\mathbf{D}$ field throughout, which of course is incorrect for the actual electrical field in homogeneous subdomains. This was indeed surprising because nodal FEM had proved to be reliable in many other problems—magnetostatics, eddy currents, etc.

For a long time, the source of the parasitic modes was not clear, but it was also discovered that FEM with edge elements did not produce such modes. This led to the following misconception: the “spurious modes” are presumably absent in edge element analysis because the lowest order element-wise basis functions in the Nédélec–Whitney edge elements [10] are divergence-free; as a side note, it was also stated that these elements could not be applied to fields with nonzero divergence [53].

If such statements were true, then first order nodal elements would be perfect for the Laplace equation (because the Laplacian of a linear function is exactly zero) and could not be applied at all to, say, a general Poisson equation. What matters in the weak formulation is what happens not only inside the element but at the inter-element boundaries as well. For spurious modes, the divergence-free property of edge elements is in fact irrelevant [54].

A sensible explanation was given in 1990 by Bossavit [55]. The following is a condensed version of that (see [55,56] for details).

For the zero-divergence condition to hold in a weak sense, one needs the test field to be a gradient, ${\mathbf{E}}^{\prime }=\nabla u^{\prime }$. Then the $\nabla \times {\mathbf{E}}^{\prime }$ term in the weak formulation (37) vanishes and one arrives at the weak form of the zero-divergence condition for the $\mathbf{D}$ field:

$$(ϵ\mathbf{E},\nabla u^{\prime })=0,$$

(38)

For this condition to hold on the discrete level, the space of test functions has to contain a sufficiently rich—in some sense—subspace of gradients. It can be shown that this is not true for traditional nodal elements [56] but is true for edge elements.

Arguments along these lines are convincing but do not constitute a complete theory of spectral convergence. Such theories are quite sophisticated and revolve around the so-called “discrete compactness” condition [54,57,58,59].

Curiously, spurious modes of analytical rather than numerical nature exist in periodic structures; see Figure 1 in [60], Appendix A in [60].

6. TE and TM Modes

In contrast with the other sections, this one is concerned with the nomenclature rather than principles. However, terminological confusion can be unpleasant and detrimental to scientific discourse. Transverse Electric (TE) and Transverse Magnetic (TM) modes are a case in point.

In waveguide theory, the TE and TM modes are defined unambiguously as having no electric field or no magnetic field, respectively, along the axis of the guide. Unfortunately, when translated to wave propagation, this terminology becomes much less clear. What exactly are the electric or magnetic field “transverse” to? This is not just a question of semantics.

Table 1. Definitions of the TE mode differ. Table adapted by permission from Springer Table 8.1 in [1] ©2020.

One-Component E, Two-Component H	One-Component H, Two-Component E
[48,61,62,63,64]	[65,66,67] and p. 179 in [68]

and

Table 2. A few representative quotes on TE/TM modes. Table adapted by permission from Springer Table 8.2 in [1] ©2020.

One-Component E, Two-Component H

One-Component H, Two-Component E

“Transmission of s- (TE-) polarized light through the metal-dielectric structure…” [64] “TE-polarized … waves … have the component of the electric field parallel to the layers ($E=E_y$)” [62] [The primary variables are] “electric field $e_x$ for TE modes and magnetic field $h_x$ for TM modes, respectively.” [61]

“…consider a TE-polarized electromagnetic wave, with nonvanishing $H_z$, $E_x$, and $E_y$ components” [65] “the magnetic field along z (TE fields) or the electric field along z (TM fields) p. 179 in [68] “… The TM mode in which the electric field is parallel to the axis of the holes, and the TE mode in which it is perpendicular.” [66] “The polarization of the incident wave is TM in the first band and TE in the second band (E parallel and perpendicular to the rods, respectively)” [67]

[1] show that different researchers attribute opposite meanings to the TE/TM designations.

The TE/TM terminology is ubiquitous in the literature, and it would be counterproductive to argue against its use. However, because of the ambiguities noted above, it would be highly desirable to state clearly in each research paper which components of which fields are zero and which are not.

7. Electric Polarization

Most textbooks define polarization as the “dipole moment per unit volume”. However, simple examples and critical analysis show that this definition is flawed. Indeed, imagine a chain of alternating charges $+q$, $-q$, $+q$, $-q$, … as a toy model of an ionic crystal (Figure 1 in [30,69]). Clearly, the “dipole moment per unit volume” cannot be unambiguously defined and will depend on whether the chain is partitioned into the “+ –” set of dipoles or, alternatively, into the “– +” set. The standard definition is even more dubious for realistic continuous electron charge distributions which cannot be partitioned meaningfully into individual dipoles—e.g., Figure 3 in [70], Figure 2 in [71], Figure 5 in [72], Figure 5 in [73]. The textbook definition is narrowly applicable only in the case of well-defined and well-separated dipoles.

These issues are discussed thoroughly, and with a reference to the “the modern theory of polarization” (MTP) [71,74,75,76], in [77], where the following approach is advocated.

Let polarization be treated as a characteristic not of a single state of a physical medium but of an adiabatic transition from one state (“unperturbed”) to another one (“perturbed”). The charge continuity equation, which must hold during this transition, is

$$\nabla ·\mathbf{j}=-{\partial }_{\lambda }\rho$$

(39)

where $\mathbf{j}=\mathbf{j}\left(\lambda \right)$ is the current density as a function of an adiabatic parameter $\lambda \in [0,1]$ ($\lambda =0$ in the initial state and $\lambda =1$ in the final state). This leads to the following constructive definition of polarization [77]:

$$\mathbf{p}\left(\mathbf{r}\right)\equiv \mathbf{p}(\mathbf{r},\lambda =1)={\int }_0^1\mathbf{j}(\mathbf{r},\lambda )d\lambda$$

(40)

Polarization so defined satisfies the classical condition

$$\nabla ·\mathbf{p}\left(\mathbf{r}\right)=-\delta \rho \left(\mathbf{r}\right)$$

(41)

Definition (40) is general: the charge distribution can be finite or infinite; periodic or nonperiodic; discrete or continuous; molecular-scale, microscale or macroscale; electrically neutral or (counter-intuitively) non-neutral; corresponding to spontaneous polarization (as, e.g., in ferroelectrics) or to polarization induced by external electric fields, at any temperature. There is no need to group charges into “molecules” of any kind or to partition a continuous charge distribution into a set of dipoles. Note that even if the charge density distribution $\rho \left(\mathbf{r}\right)$ is not neutral, the perturbation $\delta \rho \left(\mathbf{r}\right)$ is.

Analysis of fields and polarization in natural materials involves two scales: fine (molecular) and coarse (macroscopic). More generally, one may consider coarse-graining a fine-scale distribution by convolving it with a smooth integration kernel (e.g., a sharp Gaussian). Since convolution commutes with differential operators, relationships such as (41) are preserved after coarse-graining. However, adjustments may need to be made at the boundaries of a finite charge distribution or material sample [77].

As a simple illustrative example, suppose that a charged microparticle of dust is displaced in space over a small segment $0\le x\le a$. Then, according to the proposed definition of polarization $\mathbf{p}\left(\mathbf{r}\right)$,

$$\mathbf{p}\left(\mathbf{r}\right)=q{\Pi }_{0\le x\le a}\left(\mathbf{r}\right)\delta \left(y\right)\delta \left(z\right)\widehat{x}$$

(42)

where q is the charge of the particle, ${\Pi }_{[0,a]}$ is the characteristic function of the segment (equal to 1 within $[0,a]$ and zero elsewhere); the $\delta$s are the Dirac delta functions. This polarization can be used to compute the change in the far field due to the displacement [77]. Furthermore, if there is a cloud of charged microparticles, each being randomly or non-randomly displaced by a small amount, then by coarse-graining the $\mathbf{p}\left(\mathbf{r}\right)$ one would obtain a large-scale counterpart of dielectric polarization $\mathbf{P}\left(\mathbf{r}\right)$ [77].

8. Boundary Conditions for Induced Currents

Induced currents are a feature of all non-static electromagnetic phenomena in conducting media. At power frequencies, eddy currents are ubiquitous in electrical machinery; at optical frequencies, the induced currents are often detrimental in conductors and lossy dielectrics, although in some practical cases these losses can be put to good use [78,79].

It is typical to assume that at the boundary of a conducting region (e.g., a metal particle) the normal component $J_n$ of the current density is zero because, intuitively, the current cannot cross the surface. However, this justification is not accurate. In fact, the divergence condition for the current density is

$$\nabla ·\mathbf{J}=-{\partial }_t\rho$$

(43)

where $\rho$ is the volume charge density.

At the boundary of the conducting region, this divergence condition becomes

$$J_n=-{\partial }_t{\rho }_S$$

(44)

where ${\rho }_S$ is the surface charge density, which does not have to be zero. An intuitive physical picture is that of electrons bouncing back and forth between the walls of a conducting domain, leading to repeated accumulation and depletion of charges on this or that side of the boundary.

As an important case, let us consider the popular hydrodynamic model of electron flow in plasmonic structures. This model comes in several flavors; in one version, the equation for the “hydrodynamic” current density ${\mathbf{J}}_{\mathrm{HD}}$ in the frequency domain is, according to [80] and using the notation of that paper,

$${\beta }^2\nabla (\nabla ·{\mathbf{J}}_{\mathrm{HD}}(\mathbf{r},\omega ))+\omega (\omega +i\gamma ){\mathbf{J}}_{\mathrm{HD}}(\mathbf{r},\omega )=i\omega {\omega }_p^2{ϵ}_0\mathbf{E}(\mathbf{r},\omega )$$

(45)

where ${\omega }_p=e{n}_0^{\frac{1}{2}}{\left({ϵ}_0{m}_e\right)}^{-\frac{1}{2}}$ is the plasma frequency of the free electron gas, $\beta$ is a parameter related to the Fermi velocity, $n_0$ is the equilibrium density of the electron gas, $m_e$ is the effective electron mass, $\gamma$ is the damping constant (inverse of the collision time). This equation describes the hydrodynamic current driven by an electric field $\mathbf{E}$.

This hydrodynamic equation is coupled with the Maxwell electric field equation, written in the SI system of units:

$$\nabla \times {\mu }_0^{-1}\nabla \times \mathbf{E}(\mathbf{r},\omega )-{\omega }^2ϵ\mathbf{E}(\mathbf{r},\omega )=i\omega {\mathbf{J}}_{\mathrm{HD}}(\mathbf{r},\omega )$$

(46)

This model is cited here for reference; the goal of this section is to draw attention to the $J_n=0$ condition imposed e.g., in p. 5892 in [80,81]; quote: “...in order to confine the electron fluid to the nanoparticle, we impose the so-called slip boundary condition, i.e., the normal component of the current density vanishes at the particle’s surface” p. 1165 in [81].

Admirably, Miano et al. have developed a physically consistent model with a correct boundary condition for $\mathbf{J}$ and presented a finite element/boundary integral numerical solution [82,83].

The role surface charges ultimately play in conducting structures depends on the strength of the capacitive effects. For large structures such as stator cores of electrical machines with their typical geometric and physical parameters, the capacitive effects were found to be very weak [84]. However, for small particles and other micro- or nanoscale structures, the situation may very well be different.

9. Good or Poor Conductors for Low Loss? (Part 2)

Let us return to the paradox of Section 3: why are low losses associated with good conductors in some cases and poor ones in other cases? That is, how can the opposite conditions $|{ϵ}^{″}|\gg {ϵ}^{\prime }$ and $|{ϵ}^{″}|\ll {ϵ}^{\prime }$ be reconciled?

Let us start with the following analogy. There are two different but equivalent expressions for power dissipation P in a resistor R:

$$P=I^{2}R$$

(47)

$$P=\frac{V^2}{R}$$

(48)

with the standard notation for voltage V and current I. If one maintains a fixed value of the current, (47) shows that low loss corresponds to low resistance. On the other hand, if a fixed value of voltage is maintained, (48) shows that low loss corresponds to high resistance. (In electric machine design, cases analogous to these two are sometimes called “current driven” and “voltage driven,” respectively.)

To understand the relevance of this analogy to the topic of this section, let us examine two model problems. In the first one, an electromagnetic wave impinges on a slab of a lossy material and propagates through that slab; normal incidence is assumed for simplicity. This setup is sketched in Figure 2a; the $\mathbf{E}$ field is in the z direction (along the slab).

The voltage V across a given section $[z_{+},z_{-}]$ of the slab is

$$V={\int }_{z_{+}}^{z_{-}}Edz$$

(49)

The loss P in that section is due to the current density

$$\mathbf{J}=\sigma \mathbf{E}$$

(50)

and is equal to

$$P={\int }_{z_{+}}^{z_{-}}dz{\int }_S\sigma E^{2}dS\sim E^{2}l\sigma S\sim {\left(El\right)}^2\frac{\sigma S}{l}\sim \frac{V^2}{r};l\equiv |z_{-}-z_{+}|$$

(51)

Here S and $r=l/\left(\sigma S\right)$ are the cross-section and static resistance of the slab, respectively. The ‘∼’ sign indicates estimates, accurate for wavelengths much longer than the geometric dimensions of the slab, when the field variation across the slab can be neglected. However, the main conclusion holds in any event: the losses are lower for lower conductivity (higher resistance). Figure 2b is a qualitative representation of losses in the slab via an equivalent circuit. As a side note, the magnetic field $\mathbf{H}$ is related to losses only in a roundabout way, via its connection to $\mathbf{E}$ in Maxwell’s equations, so there is no need to consider $\mathbf{H}$ in this qualitative analysis.

In the second problem, a power line with some resistance r connects a generator V to a resistive load R (Figure 3). The losses in the line are

$$P_{\mathrm{line}}=I^{2}r=\frac{V^2}{{(R+r)}^2}r$$

(52)

In this case, lower losses correspond to lower resistance r (under the natural assumption $r<R$). This conclusion would be even more obvious if the generator acted as a current source rather than a voltage source.

The qualitative analysis above explains why lower conductivity leads to lower losses in optics/photonics but to higher losses in power transmission.

10. Discussion and Conclusions

Even though computational electromagnetics is quite a mature area already, this paper highlights a few unconventional or counter-intuitive ideas. First, it is shown that the source field in magnetostatic or eddy current problems can be represented via a line integral as an alternative to the Biot–Savart law. The line integral has several advantages: it is much more efficient computationally and, as a bonus, produces a “source field” with a zero component along one of the coordinate directions. A loose discrete analogy of that is the so-called tree/co-tree gauge in finite element analysis with edge elements.

A paradox arises with regard to applications of conducting materials in electric power transmission on the one hand and optics and photonics on the other. In electrical engineering, good conductors (materials with a high conductivity, such as copper or aluminum) are expected to have low losses. The opposite is true in optics and photonics, where dielectrics with zero or negligible conductivity are employed. Why is there such a qualitative difference between traditional areas of electrical engineering and optics/photonics? The answer given in this paper lies in the different type of excitation in those two cases. Electric power transmission can be qualitatively characterized as “current-driven”, while wave transmission in photonics can be schematically viewed as “voltage-driven”. In the first instance, the lower the resistance (the higher the conductivity), the lower the losses; in the second case, the opposite is true.

Another subject reviewed in this paper is effective medium theory for periodic electromagnetic heterostructures. Attention is drawn to several unorthodox aspects of homogenization. The first one is that boundary conditions are as important for homogenization theory of metamaterials as is the bulk behavior of waves. The second aspect is that for periodic structures there is no salient transition to bulk properties when the thickness of the sample is gradually increased. That is, one lattice layer is, in a sense, already “bulk”. Third, structures lacking mirror symmetry can be accurately homogenized if the effective parameters include magnetoelectric coupling. Finally, mentioned in the section on homogenization is “effective medium transformation”—a special case of stratified magnetic structures such as laminated cores of electrical machines. In that case, under a few natural assumptions, the qualitative physical nature of the problem changes upon homogenization. Namely, if the fields in the fine-scale (stratified) structure are governed by Maxwell’s equations in the eddy current approximation, fields in the homogenized structure are governed by magneto-quasistatic equations with complex magnetic permeability.

Yet another issue summarized in the paper is the so-called spurious (nonphysical) modes, which manifest themselves in the nodal FEM electromagnetic eigenvalue problems such as cavity resonances. The source of this problem and some misconceptions in its analysis are outlined. Spurious Bloch modes in periodic media are mentioned in passing.

A short note is related to the use of the terms TE and TM modes. Even though this nomenclature is natural to electrical engineers, it turns out that in the literature there is no uniformity with regard to its use: different authors attribute opposite meanings to the TE and TM terms.

The notion of electric polarization turns out, upon closer inspection, to be much more subtle than the standard textbooks would lead one to believe. The classical definition as the “dipole moment per unit volume” does not stand up to scrutiny. Instead, electric polarization can be properly defined as a function of not just one state but of a transition between two nearby states. This definition is quite general and applies to any charge distributions—microscopic or macroscopic, periodic or non-periodic, electrically neutral or not, etc. The analysis outlined in the paper is in the framework of classical electrodynamics, but references are given to the “modern theory of polarization”, which is quantum-mechanical.

Finally, attention is drawn to the fact that the correct boundary condition for currents induced in conducting materials is not the zero normal component of these currents at the boundary. Clearly, in classical electrodynamics currents cannot “go through” the boundary and escape; however, they may certainly lead to accumulation or depletion of surface charges on the boundary. For large-scale objects, such as conducting parts of electric machines, these capacitive effects appear to be negligible; however, this may not be the case in nano-plasmonics—for example, in the popular hydrodynamic models of the electron gas.

It is hoped that the cases considered in this paper will stimulate further discussion and a fresh look at various problems of computational electromagnetics. Even in this mature area, there are unsolved problems and out-of-the-box ideas.