Abstract
There is an ongoing demand for data on population health, for reasons of resource allocation, future planning and crucially to address inequalities in health between people and between populations. Although there are regular sources of data at coarse spatial scales, such as countries or large sub-national units such as states, there is often a lack of good quality health data at the local level. One method to develop reliable estimates of population health outcomes is spatial microsimulation, an approach that has its roots in economic studies. Here, we share a review of this method for estimating health in populations, explaining the different approaches available and examples where the method is applied successfully for creating both static and dynamic populations. Recent notable advances in the method that allow uncertainty to be represented are highlighted, along with the evolving approaches to validation that are an ongoing challenge in small-area estimation. The summary serves as a primer for academics new to the area of research as well as an overview for non-academic researchers who consider using these models for policy evaluations.
1. Introduction
The aim of this review is to extend earlier reviews of spatial microsimulation first as a method [1] and then within the application area of estimation models for health [2]. Here, we combine the approaches used in these previous reviews to explore, in more detail, the subset of applications within spatial microsimulation that provide a specific focus on health outcomes and behaviours in populations.
At a time when population health globally is under threat from known health epidemics such as obesity and mental health as well as contagious diseases such as COVID-19, there remain longstanding challenges in public health from non-communicable disease and associated health behaviours. In order to consider the appropriate public health responses to poor health in populations, the spatial distribution of health outcomes and behaviours is required to identify where more action is needed to reduce health inequalities and what the impact of these interventions is likely to be. This is true in most settings across the global north and south, where adequate support for health is the responsibility of local governments. Further, it is in the interest of local and national governments to support positive behaviours influencing health outcomes such as diet, physical activity, smoking cessation; high blood pressure, linked to each of these outcomes, costs the National Health Service (NHS) GBP 2 billion annually [3]. Even where data on the national prevalence of an outcome, such as type two diabetes, are known, there are often poor quality or non-existent data on health at the local level where decisions on resource distribution are made. One approach to estimating population health in these small areas is spatial microsimulation, an approach that uses existing data to recreate individual-level populations, the focus of this review.
The United Kingdom has the benefit of a National Health Service where all residents have access to primary and secondary healthcare. What may be surprising is the difficulty in collecting up-to-date and comprehensive data on the health of individuals living in the UK; not all people have visited a GP recently and the data held on individuals may be difficult to access for researchers and policymakers due to patient confidentiality. To better understand the health of residents there are national and local surveys such as the Health Surveys for England, Scotland, Wales and Northern Ireland which run annually and collect detailed data on the health and health-related behaviours of people living in private homes in each nation (see https://www.data-archive.ac.uk/, accessed on 25 May 2021). At the aggregate national or regional level, these surveys provide a snapshot of the health of the population across a range of demographic characteristics. These data can form the basis of local-level estimates to support decision making, either at one point in time or forecasting into the future to predict demand on health and social care services as the population ages or experiences ill-health due to non-/communicable disease.
In this review we will begin with an overview of population estimation models, then describe spatial microsimulation modelling development including static and dynamic models. We will outline the most common algorithms used to support spatial microsimulation of health outcomes and behaviours, highlighting recent advances in this method which are overcoming historic challenges in the use of spatial microsimulation. The review will provide researchers who are new to the area of spatial microsimulation with a strong grounding in the background of this approach to small-area estimation specifically for health outcomes and health behaviours, while also supporting public health academics who want to gain a deeper understanding of the strengths and benefits of this method.
2. Materials and Methods
Microsimulation is the process by which an individual-level population is constructed from a Census and enriched with other data, typically from surveys. Adding geographical attributes to this population is referred to as spatial microsimulation.
To identify the peer-reviewed literature on spatial microsimulation for health research, a comprehensive review was undertaken within the medical and social science literature. We first searched the PubMed database, which includes medical and public health literature, for the terms “spatial microsimulation” AND “health” for 1975–2021. We repeated this search in Science Direct, a database that captures a wider literature including the social sciences. Known authors in the field were searched individually to identify manuscripts not included in the original results.
This review will also describe the different approaches to spatial microsimulation for public health outcomes and behaviours, building on a wider literature that includes previous reviews [1,4,5] and further methodological developments identified in the literature [6,7,8,9]. In particular, we will discuss the range of approaches, defined by Tanton [5] and O’Donoghue et al. [10] as synthetic reconstruction and reweighting broadly, bringing in examples where this process is applied to health outcomes. The review then outlines the shift towards dynamic models and notes the improved techniques to express uncertainty in the estimates [8] and the increasing availability of software and code, enhancing the reproducibility of spatial microsimulation.
3. Results
3.1. Search Results
The PubMed search returned 21 articles from 2006 to 2021 and the same search criteria on ScienceDirect returned 46 articles from 2000 to 2021, of which 37 were research articles and there were two duplicates, reducing the total to 35. Following filtering based on titles and abstracts, there was a total of 21 articles that used spatial microsimulation to model health outcomes or behaviours in people; many of the other fourteen publications were about methodological innovation [4,8]. We then added a further three articles identified through hand searches of key authors (Figure 1).
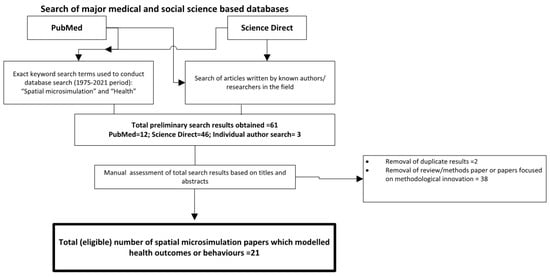
Figure 1.
Diagram of results from the systematic searches.
What is evident from the 24 research articles is the focus on a narrow range of outcomes, with diet and weight status the most common topics [11,12,13,14] and smoking [15,16,17] also appearing frequently. The reasons for this focus may be due to the importance of the health outcomes or behaviours for public health policy due to the associated increased morbidity and mortality in populations. Other health behaviours or conditions identified in the review included problem gambling [18], mental health and alcohol consumption [19] and combinations of health outcomes [20,21,22,23]. Dental health [24], diabetes [25] and mortality [26] are more recent topics that were modelled. Spatial microsimulation for resource allocation, with the example of maternity services in England [27], or estimating the impacts of policies on health [28] were more unusual applications of this method for public health interests. Overall, there are numerous applications for models of local population health behaviours or outcomes, with the main rationale for these models being support for national and local decision-making around the prioritisation of areas for interventions and funding.
As we will discuss in the following sections, there are dominant trends in the methods used in spatial microsimulation for health-related outcomes and behaviours, and in the types of modelled outputs: one point in time static models, or those that project ahead further to predict population health outcomes (dynamic). We will highlight new developments in spatial microsimulation that improve the utility of the method for wider adoption outside of academic research and online tools to facilitate modelling.
3.2. Review of Methods
Spatial microsimulation sits within a group of methods to support small-area estimation, which includes statistical techniques and spatial microsimulation [8]. Statistical approaches include Bayesian methods [29,30] and multilevel modelling [31,32]. Both of these have been used extensively in public health applications. Many of the health-focused spatial microsimulation models were developed at or in collaboration with the University of Leeds in the UK and the SimBritain model by Ballas and colleagues; see [11,16,17,19,22,33,34].
Microsimulation belongs to a category of individual-based models, though depending on the model, the results may be expressed as prevalence in a population within areas [11,16,17,35]. Other principle methods include cellular automata (CA) and agent-based modelling (ABM). All of these put the individual at the centre of the simulation and their ready ability to capture and simulate individual behaviour and movement have made them an attractive research tool within the social sciences. However, whilst there is somewhat of a blurring within the definition of these approaches, it is important to note that CA and ABM are distinct from microsimulation. CA is typically applied to simulating units of land in urban development models, whilst ABMs are used to explore behaviours and interactions within populations [36].
The origins of these models are in non-spatial microsimulation in the 1950s (see Orcutt 1957 reproduced in 2007 [37]). Over the last two decades, a division has appeared between probabilistic approaches, which return slightly different results each time [21,38], and deterministic methods, which provide the same estimates if all input variables remain constant [11,12,17,19,20,22,33,34,39,40]. Synthetic reconstruction, such as the use of Monte Carlo sampling to add additional population characteristics to simulated populations in areas, appears much less frequently [14].
The probabilistic methods include combinatorial optimisation (using simulated annealing most often) and the deterministic methods frequently employ an Iterative Proportional Fitting (IPF) method. In both approaches, there are two datasets required: a known population distribution in each small area such as Census data and a dataset that includes the outcome(s) of interest, for example, a health survey. This is often referred to in the literature as microdata [41]. The variables used to link the two datasets, population distributions and microdata, are referred to as constraint variables. For both approaches to provide meaningful outputs, the constraint variables need to be associated with the outcome of interest [7]. For example, in the case of constructing a type two diabetes model, the following characteristics associated with the disease would be included: age, sex, ethnicity and some indicator of relative socioeconomic status. The expressed benefit of deterministic approaches has been described as more appropriate for policy analysis, where the impact of policy changes may be more evident if inputs are changed to the models, as described by Ballas and colleagues [11].
3.2.1. Combinatorial Optimisation
Two methods are typically employed to allocate individuals to areas in static spatial microsimulation: deterministic reweighting and combinatorial optimisation [10]. Deterministic reweighting methods like IPF typically compute decimal weights for each person and area combination, leading to fractions of people (decimals) being allocated to areas; this approach will be described further in the following section.
Combinatorial optimisation, in contrast, allocates entire individuals to areas and seeks out the optimal fit for populations within areas as defined by a dataset [41]. Combinatorial optimisation methods work by using a random allocation of individuals from the microdata into each area in turn. As each person is assigned a place in an area, the goodness-of-fit for the new population of the area is recalculated. Simulated annealing is one such technique to generate new populations within areas that have the characteristics of interest, such as smoking, diabetes status, level of physical activity. This technique chooses an optimal configuration from the microdata population constrained by known area-level population counts from the Census (typically age–sex–ethnicity distributions). This microdata population could also be another source of sufficiently detailed complete data on a population such as a school pupil census or registers from a doctor’s surgery.
People are randomly selected from the microdata and considered for inclusion in the population of an area if they improve the goodness of fit of the population against constraint tables [5]. These steps of aggregation of data and evaluation of fit against known data are repeated. If the fit is improved with the addition of a “new” individual, then they replace an “old” individual in that area. In this process, each person has a weight of either one if they are chosen to reside in an area or zero if they are not selected to be included in an area’s estimated population. The estimated or synthetic population is a realistic approximation of the known population based on the selected constraints. The new synthetic population has these new attributes of interest attached to them as well as the core demographic constraint data. Outputs can be counts of people with a given attribute or represented as prevalence within a population. This also allows for cross-tabulated data for the estimated values, as the synthetic population is based on “whole” individuals.
3.2.2. Deterministic Reweighting
Deterministic reweighting follows a similar process, however, outputs may only be expressed as prevalence estimates due to the use of decimals in the weighting process. This algorithm is described in detail elsewhere [33,41]. The main difference is that individuals from the microdata (survey) dataset are given a weight or probability of living in an area based on the known population distribution of the constraint variables. The algorithm creates a new weight for each person from the microdata to live in each small area for every constraint, iterating through this reweighting process until a predefined level of agreement between the known distribution of constraint variables in an area and the estimated distribution of these variables is reached. Some variations of this algorithm attempt to smooth the population distribution towards the mean, which requires an additional step of cluster analysis prior to implementing the reweighting algorithm [7]. The cluster analysis on key predictive population characteristics for the health outcome of interest improves the accuracy of modelled estimates for unknown outcomes.
With both the combinatorial optimisation and deterministic reweighting approaches to spatial microsimulation one consideration is the microdata. These populations will be replicated many times over to represent the population of interest if the microdata includes a sample of perhaps 15,000 individuals to synthetically generate the population of an entire nation of millions. When this is the situation, each person from the microdata may have a very small weight or probability of living in an area that has a population of 1500–7000 individuals depending on the scale. The decimal weights for all 15,000 people in the microdata are summed for each area to provide the numerator in a fraction that calculates the population prevalence of an outcome in a small area population. With combinatorial optimization, the resulting synthetic population may be based on fewer individuals from the microdata in each small area, certainly not exceeding the known population. Combinatorial optimisation works well at recreating populations of “real” people. An earlier analysis of methods concluded that deterministic reweighting performed slightly better for estimating health outcomes compared to other methods [9].
3.3. Static and Dynamic Models
The models discussed in this review are predominantly static spatial microsimulation models that is they model the health of a population at one point in time by bringing together a microdata set and a population dataset. While this can be very useful where little is known about the current health of populations in small areas, in other situations there will be more interest in future modelling or testing policy scenarios. For these purposes, dynamic spatial microsimulation models are needed. This section will briefly describe the static spatial microsimulation models before discussing the few available dynamic spatial microsimulation models available.
3.3.1. Static Spatial Microsimulation Models
The majority of spatial microsimulation models are static; the aim of these models is to create a reliably estimated population dataset for one time point [9,11,12,15,16,17,19,20,21,22,33,34,35,38,39,40,42]. The simplicity of these models with regards to temporal specificity allows users to explore research questions termed “what-if” scenario modelling. Because only a very few variables are changed to model a potential change in policy and thus a change in health, the consideration for change over time in a population or individual is not included. They can be used to monitor health outcomes in small areas, or estimate demand for services, as seen in work by Tomintz and colleagues [17,27].
Output from some spatial microsimulation models that provide individual-level data can be linked to other models, such as agent-based models. There are very few published examples of spatial microsimulation being used to create a population that can be turned into agents (see Wu et al., 2008 for one example [43]), likely limited by computational power. However, this could be a valuable option for health policy research—agents with detailed health attributes—for applications that require interaction and explore “nudges” for behaviour change.
3.3.2. Dynamic Spatial Microsimulation
Dynamic models simulate changes in people and their circumstances over time. The early dynamic model developed by Orcutt (1961) [44] became DYNASIM (The Dynamic Simulation of Income Model [45], a model for prediction into the future and policy analysis. Following this example, a number of dynamic microsimulation models were created for a range of applications. Li and O’Donoghue [46] published a review including 61 dynamic models developed between 1977 and 2013 with social or economic applications.
Dynamic models start with a population that has a number of individual characteristics. These populations are created through similar methods to those described previously or may be individuals from survey datasets. The population is allowed to age and develop over time, and individuals may move between different states in the model (such as changing marital status from single to married). Parameters and assumptions of changes to status (known as transition probabilities) allow the researchers to test different interventions and observe the outcomes on the status of individuals. These changes in status, or transition probabilities, are often based on known longitudinal data where available.
Developing the demographic basis of a dynamic model is described in detail by Ballas et al. [33]. The SMILE (Simulation Model for the Irish Local Economy) model begins with a static population from a spatial microsimulation (IPF) with the characteristics of age, sex, marital status, employment and geographic location (District Electoral Division). Demographic characteristics of births, deaths and internal migration are estimated for this starting population and used to project them forward in time. A random number between 0 and 1 is assigned to each person and mortality is calculated based on their characteristics and a vital statistics table. A person with a 50% chance of survival from the vital statistics would survive if their random number is between 0 and 0.5 but would die if the random number was 0.51 or greater. Migration is similarly estimated based on probability. Individuals move to new locations based on population size. The resulting populations for small areas are projected with these characteristics in mind and the results are then compared with aggregate data at a larger spatial scale, with absolute percentage error calculated as a means of validation.
The newer dynamic spatial microsimulation models are increasingly complex in terms of the characteristics modelled. They follow a process like SMILE with movement between areas for internal migration and changes in status, or transition, for attributes such as marital status, employment and health. A model based in the US is the Future Elderly Model, which explores the demographic transition by modelling several health outcomes (stroke, cancer, diabetes) for those age 50 years and over. The scenario modelling considers different interventions for health care as well as the cost of health outcomes in the population [47]. In the UK, another model is MOSES [48], with outputs suitable for spatial analysis, and in Sweden, there is SVERIGE [49], which draws upon detailed datasets for their relatively smaller population. Here, additional characteristics such as education and income are modelled alongside employment and migration within the country at a fine spatial scale using a 100m grid, all informed by longitudinal microdata.
SPENSER (Synthetic Population Estimation and Scenario Projection Model) is a compilation of software packages to model future population change and movement using dynamic microsimulation [50]. SPENSER can provide customised populations for unique research questions by linking to a range of datasets including the UK Census and any of the national health surveys. SPENSER has the capacity to model individuals within households and includes a variety of options for validation. One application of the SPENSER model is in the Systems science In the Public Health and Health Economics Research (SIPHER) project. In the SIPHER project, SPENSER has created synthetic populations with attributes to simulate the impacts of a number of interventions including mental health impacts [51].
This research with dynamic spatial microsimulation is timely, as funding for expensive traditional research approaches such as clinical trials is pressurised, and many public health research questions do not lend themselves to a standard randomised control trial approach. The building of a synthetic population on which to “test” interventions to improve health can save funding bodies millions of pounds as well as the ethical concerns of running trials on human participants. In contrast, a reliable computer model informed by real-world observations may quickly test several policy scenarios and model the impacts on health. Examples of this include taxation on unhealthy food and subsidies on healthier options, see Blakely et al., 2020 [52].
3.4. Challenges with Spatial Microsimulation
Modelled estimates, whether they are for applications in transportation [53], demography [50] or health, need to include some indication of accuracy. In 2000, this was explored by Voas and Williamson [54], and to date, this is a frequently cited publication for the appropriate methods of assessing the accuracy of outputs from spatial microsimulation models. Often, this is a combination of internal model validation using total absolute error (TAE) and external validation against some related outcome, such as hospitalisation records (see [29]) or where possible, known data for the same outcome to provide more confidence in the application of the model for other health outcomes (see [16]). Additionally, the estimates at a smaller level may be aggregated up to a higher level of geography where the distribution of health outcomes is known [12,19].
The validation of models, for spatial microsimulation or another method of estimating outcomes in individuals or populations where a phenomenon is unknown, is an inherent weakness in terms of the estimated outcomes being used with confidence. As these models are used to inform policy decisions and resource allocation, there needs to be ease of communicating the uncertainty around estimates. Whitworth and colleagues [6,8] made substantial gains in this area of research. By using outputs from multilevel regression for the constraint variables in an IPF reweighting model, they were able to provide credible intervals around the estimated data within small areas. In a similar vein, pattern-orientated modelling (POM) could offer an alternative method of validation by examining multiple points at different spatial scales [55]. Although typically used with ABMs, POM could allow a more robust identification and validation of processes and uncertainty within the model input and output. Previously there was no capacity to indicate the uncertainty around estimates from spatial microsimulation outputs, hindering their adoption more widely. With the move towards an expectation to provide not just the estimated values but also a measure of uncertainty around them, the use of spatial microsimulation is likely to increase.
A further barrier to the adoption of spatial microsimulation models, and perhaps a stronger explanation for the relatively low evidence of application in many settings, is the previous requirement to create software capable of developing the estimates. In contrast, the multilevel approaches to small-area estimation may be used by anyone with access to appropriate software including MLWin. For Bayesian methods, there have long been options including winbugs. Spatial microsimulation software is often bespoke and created by a person for one main project using Java, which was the situation with SimBritain [33] and several related models [11,16,17,19,20]. As free open source software including R has gained popularity, there is more opportunity to develop a spatial microsimulation model that can be coded more easily. A free online platform for spatial microsimulation was available, SimSalud [56], which offered the option of either combinatorial optimisation or deterministic reweighting. The user simply uploaded data in a predefined format with a wizard-based graphical user interface. At the time of writing, this website is no longer live. Other similar options include Lovelace’s free R code and book for spatial microsimulation on GitHub [57] and the Flexible Modelling Framework developed at the University of Leeds [42]. As code sharing becomes more common, which is indeed expected with the publication of research, the ability of more academics and policymakers to use spatial microsimulation models will increase.
4. Discussion
We present an overview of the applications of spatial microsimulation to address public health. Notably, the majority of papers included focus on non-communicable disease (NCD) and behaviours, while communicable disease or vector-borne disease is largely absent. This may be explained by considering the alternative options for modelling population health as behaviours, such as agent-based modelling mentioned previously. ABM allows users to model interactions between agents and with the environment, which are particularly relevant for communicable disease modelling, while far fewer ABMs have sought to model NCDs [36]. In contrast, NCDs such as type 2 diabetes typically develop over a longer time period and population movement is less relevant.
The differing approaches to spatial microsimulation, such as probabilistic and deterministic methods, each offer unique values to the modeler. With the more common deterministic methods, there is the possibility to test out the changes in health in populations in response to a stimulus such as new food tax policies, if there are some data to show how the new policy may impact diet choices. Because the health of the estimated populations would otherwise remain the same without amended inputs, any estimated changes in behaviour from the policy would be evident in the difference between outputs from the “baseline” model and the “post-policy” model. If, however, probabilistic methods like combinatorial optimisation are applied, the models will need to be run many more times to reach conclusions about the health impacts of policy, but the randomness inherent in the model may offer a better representation of human behaviour.
The ability to explore uncertainty in spatial microsimulation is a relatively new and valuable feature—this will allow more confidence in the use of estimated values for planning for public health activities in local areas, as strategists are familiar with confidence/credible intervals. The next important phase of research is to improve communication of the methods that provide these estimates, as a clear representation of the process followed will further support the adoption of these estimates for intervention or policy planning. This will be more feasible with the availability of model code on resources such as Github and the push for greater reproducibility in academic publications.
5. Conclusions
Spatial microsimulation offers the option to estimate attributes of a population living within an area. For those working in public health or researching health geographies, this is a valuable tool; often in research, the question remains whether observed differences in health at coarse population levels occur due to differences between the composition of populations, or the context they live within [58,59]. Understanding which aspect may be driving differences in health is crucial to devise acceptable and impactful policy actions. However, many datasets are limited by a lack of spatial detail and the data are only available for relatively large populations. To develop meaningful interventions that support population health, smaller-scale data are required. These allow for better identification of neighbourhoods that may need additional resources, such as screening for type 2 diabetes [60,61] when the early identification of this disease will lead to better outcomes for the population and individuals.
Microsimulation and spatial microsimulation in particular have a historic application in creating synthetic populations to help answer these types of research questions. Here, we outlined the main applications, methods and areas of development for spatial microsimulation in health. The shifting focus to dynamic models of population health and linking together spatial microsimulation with other approaches that allow behaviours to emerge over time including agent-based models is an exciting area for further development. The main challenge will be in researchers’ abilities to communicate the methods clearly to non-experts to encourage the adoption of these techniques and to explain the limitations associated with each method. Further barriers include demonstrating uncertainty, and by extension confidence in the results, and the inability to use the models outside of specialised groups due to lack of software resources. Both of these limitations are being reduced through new projects such as SPENSER.
Overall, this is an exciting time in the evolution of spatial microsimulation models. Computational power is increasing, and new forms of data are constantly emerging that provide more insight into human behaviour and decision-making. Policymakers are increasingly comfortable with advanced methods of geocomputation where adequate explanations for the data, methods and results are documented. As we look to model interventions ahead of implementation to save the cost of expensive trials, dynamic spatial microsimulation provides an excellent opportunity to support public health at multiple scales across a range of topics.
Author Contributions
Conceptualization, D.M.S.; writing—Original draft preparation, D.M.S., A.H.; writing—Review and editing, D.M.S., A.H., M.C. All authors have read and agreed to the published version of the manuscript.
Funding
M.C. is funded by the ESRC South Coast Doctoral Training Programme (ES/P000673/1).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tanton, R. Spatial Microsimulation: Developments and Potential Future Directions. Int. J. Microsimul. 2017, 11, 143–161. [Google Scholar] [CrossRef]
- Schofield, D.J.; Zeppel, M.J.B.; Tan, O.; Lymer, S.; Cunich, M.M.; Shrestha, R.N. A Brief, Global History of Microsimulation Models in Health: Past Applications, Lessons Learned and Future Directions. Int. J. Microsimul. 2017, 11, 97–142. [Google Scholar] [CrossRef]
- Department of Health. New Figures Show that High Blood Pressure Cost the NHS Billions Each Year. 2016. Available online: https://www.gov./government/news/new-figures-show-high-blood-pressure-costs-nhs-billions-each-year (accessed on 25 May 2021).
- Rahman, A. Estimating small area health-related characteristics of populations: A methodological review. Geospat. Health 2017, 12, 495. [Google Scholar] [CrossRef]
- Tanton, R. A Review of Spatial Microsimulation Methods. Int. J. Microsimul. 2013, 7, 4–25. [Google Scholar] [CrossRef]
- Moretti, A.; Whitworth, A. Estimating the Uncertainty of a Small Area Estimator Based on a Microsimulation Approach. Sociol. Methods Res. 2021. [Google Scholar] [CrossRef]
- Smith, D.M.; Clarke, G.P.; Harland, K. Improving the Synthetic Data Generation Process in Spatial Microsimulation Models. Environ. Plan. A Econ. Space 2009, 41, 1251–1268. [Google Scholar] [CrossRef]
- Whitworth, A.; Carter, E.; Ballas, D.; Moon, G. Estimating uncertainty in spatial microsimulation approaches to small area estimation: A new approach to solving an old problem. Comput. Environ. Urban. Syst. 2017, 63, 50–57. [Google Scholar] [CrossRef]
- Harland, K.; Heppenstall, A.; Smith, D.; Birkin, M. Creating Realistic Synthetic Populations at Varying Spatial Scales: A Comparative Critique of Population Synthesis Techniques. J. Artif. Soc. Soc. Simul. 2012, 15, 1. [Google Scholar] [CrossRef]
- O’Donoghue, C.; Morrissey, K.; Lennon, J. Spatial Microsimulation Modelling: A Review of Applications and Methodo-logical Choices. Int. J. Microsimul. 2014, 7, 26–75. [Google Scholar] [CrossRef]
- Edwards, K.L.; Clarke, G.P. The design and validation of a spatial microsimulation model of obesogenic environments for children in Leeds, UK: SimObesity. Soc. Sci. Med. 2009, 69, 1127–1134. [Google Scholar] [CrossRef]
- James, W.H.M.; Lomax, N.; Birkin, M. Local level estimates of food, drink and tobacco expenditure for Great Britain. Sci. Data 2019, 6, 56. [Google Scholar] [CrossRef]
- Koh, K.; Grady, S.C.; Darden, J.T.; Vojnovic, I. Adult obesity prevalence at the county level in the United States, 2000–2010: Downscaling public health survey data using a spatial microsimulation approach. Spat. Spatio Temporal Epidemiol. 2018, 26, 153–164. [Google Scholar] [CrossRef] [PubMed]
- Philips, I.; Clarke, G.; Watling, D. A fine grained hybrid spatial microsimulation technique for generating detailed syn-thetic individuals from multiple data sources: An application to walking and cycling. Int. J. of Microsimul. 2017, 10, 167–200. [Google Scholar] [CrossRef]
- Hermes, K.; Poulsen, M. Small area estimates of smoking prevalence in London. Testing the effect of input data. Health Place 2012, 18, 630–638. [Google Scholar] [CrossRef]
- Smith, D.M.; Pearce, J.R.; Harland, K. Can a deterministic spatial microsimulation model provide reliable small-area estimates of health behaviours? An example of smoking prevalence in New Zealand. Health Place 2011, 17, 618–624. [Google Scholar] [CrossRef] [PubMed]
- Tomintz, M.N.; Clarke, G.P.; Rigby, J.E. The geography of smoking in Leeds: Estimating individual smoking rates and the implications for the location of stop smoking services. Area 2008, 40, 341–353. [Google Scholar] [CrossRef]
- Markham, F.; Young, M.; Doran, B. Improving spatial microsimulation estimates of health outcomes by including geo-graphic indicators of health behaviour: The example of problem gambling. Health Place 2017, 46, 29–36. [Google Scholar] [CrossRef]
- Riva, M.; Smith, D.M. Generating small-area prevalence of psychological distress and alcohol consumption: Validation of a spatial microsimulation method. Soc. Psychiatry Psychiatr. Epidemiol. 2011, 47, 745–755. [Google Scholar] [CrossRef]
- Campbell, M.; Ballas, D. SimAlba: A Spatial Microsimulation Approach to the Analysis of Health Inequalities. Front. Public Health 2016, 4. [Google Scholar] [CrossRef]
- Clark, S.D.; Birkin, M.; Heppenstall, A. Sub regional estimates of morbidities in the English elderly population. Health Place 2014, 27, 176–185. [Google Scholar] [CrossRef]
- Ballas, D.; Clarke, G.; Dorling, D.; Rigby, J.; Wheeler, B. Using geographical information systems and spatial microsimulation for the analysis of health inequalities. Health Inform. J. 2006, 12, 65–79. [Google Scholar] [CrossRef] [PubMed]
- Basra, K.; Fabian, M.P.; Holberger, R.R.; French, R.; Levy, J.I. Community-Engaged Modeling of Geographic and Demographic Patterns of Multiple Public Health Risk Factors. Int. J. Environ. Res. Public Health 2017, 14, 730. [Google Scholar] [CrossRef]
- Broomhead, T.; Ballas, D.; Baker, S.R. Application of geographic information systems and simulation modelling to dental public health: Where next? Community Dent. Oral Epidemiol. 2018, 47, 1–11. [Google Scholar] [CrossRef]
- Crespo, R.; Alvarez, C.; Hernandez, I.; García, C. A spatially explicit analysis of chronic diseases in small areas: A case study of diabetes in Santiago, Chile. Int. J. Health Geogr. 2020, 19, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Marvuglia, A.; Koppelaar, R.; Rugani, B. The effect of green roofs on the reduction of mortality due to heatwaves: Results from the application of a spatial microsimulation model to four European cities. Ecol. Model. 2020, 438, 109351. [Google Scholar] [CrossRef]
- Tomintz, M.N.; Clarke, G.P.; Rigby, J.E.; Green, J.M. Optimising the location of antenatal classes. Midwifery 2013, 29, 33–43. [Google Scholar] [CrossRef]
- Symonds, P.; Hutchinson, E.; Ibbetson, A.; Taylor, J.; Milner, J.; Chalabi, Z.; Davies, M.; Wilkinson, P. MicroEnv: A microsimulation model for quantifying the impacts of environmental policies on population health and health inequalities. Sci. Total. Environ. 2019, 697, 134105. [Google Scholar] [CrossRef]
- Congdon, P. Estimating diabetes prevalence by small area in England. J. Public Health 2006, 28, 71–81. [Google Scholar] [CrossRef][Green Version]
- Utazi, C.E.; Thorley, J.; Alegana, V.A.; Ferrari, M.J.; Nilsen, K.; Takahashi, S.; Metcalf, C.; Lessler, J.; Tatem, A.J. A spatial regression model for the disaggregation of areal unit based data to high-resolution grids with application to vaccination coverage mapping. Stat. Methods Med. Res. 2019, 28, 3226–3241. [Google Scholar] [CrossRef]
- Moon, G.; Quarendon, G.; Barnard, S.; Twigg, L.; Blyth, B. Fat nation: Deciphering the distinctive geographies of obesity in England. Soc. Sci. Med. 2007, 65, 20–31. [Google Scholar] [CrossRef]
- Taylor, J.; Moon, G.; Twigg, L. Using geocoded survey data to improve the accuracy of multilevel small area synthetic estimates. Soc. Sci. Res. 2016, 56, 108–116. [Google Scholar] [CrossRef]
- Ballas, D.; Clarke, G.; Dorling, D.; Eyre, H.; Thomas, B.; Rossiter, D. SimBritain: A spatial microsimulation approach to population dynamics. Popul. Space Place 2005, 11, 13–34. [Google Scholar] [CrossRef]
- Morrissey, K.; Clarke, G.; Ballas, D.; Hynes, S.; O’Donoghue, C. Examining access to GP services in rural Ireland using microsimulation analysis. Area 2008, 40, 354–364. [Google Scholar] [CrossRef]
- Tomintz, M.; Kosar, B.; Clarke, G. smokeSALUD: Exploring the effect of demographic change on the smoking prevalence at municipality level in Austria. Int. J. Health Geogr. 2016, 15, 1–14. [Google Scholar] [CrossRef]
- Heppenstall, A.; Malleson, N.; Crooks, A. “Space, the Final Frontier”: How Good are Agent-Based Models at Simulating Indi-viduals and Space in Cities? Systems 2016, 4, 9. [Google Scholar] [CrossRef]
- Orcutt, G.H. A new type of socio-economic system. Int. J. Microsimul. 2007, 1, 3–9. [Google Scholar] [CrossRef]
- Cataife, G. Small area estimation of obesity prevalence and dietary patterns: A model applied to Rio de Janeiro city, Brazil. Health Place 2014, 26, 47–52. [Google Scholar] [CrossRef] [PubMed]
- Campbell, M.; Ballas, D. A spatial microsimulation approach to economic policy analysis in Scotland. Reg. Sci. Policy Pract. 2013, 5, 263–288. [Google Scholar] [CrossRef]
- Smith, D.; Vogel, C.; Campbell, M.; Alwan, N.; Moon, G. Adult diet in England: Where is more support needed to achieve dietary recommendations? PLoS ONE 2020, in press. [Google Scholar] [CrossRef]
- Lovelace, R.; Dumont, M. Spatial Microsimulation with R; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Flexible Modelling Framework 2012. Available online: https://github.com/MassAtLeeds/FMF/releases (accessed on 25 May 2021).
- Wu, B.; Birkin, M.; Rees, P. A spatial microsimulation model with student agents. Comput. Environ. Urban. Syst. 2008, 32, 440–453. [Google Scholar] [CrossRef]
- Orcutt, G.H. Microanalysis of Socioeconomic Systems: A Simulation Study; Harper: New York, NY, USA, 1961. [Google Scholar]
- Urban Institute. The Dynamic Simulation of Income Model. DYNASIM3 A Brief. Overview. 2015. Available online: https://www.urban.org/sites/default/files/publication/67366/2000391-The-Dynamic-Simulation-of-Income-Model-DYNASIM-%20An-Overview.pdf (accessed on 25 May 2021).
- Li, J.; O’Donoghue, C. A survey of dynamic microsimulation models: Uses, model structure and methodology. Int. J. Microsimul. 2012, 6, 3–55. [Google Scholar] [CrossRef]
- Goldman, D.P.; Orszag, P.R. The Growing Gap in Life Expectancy: Using the Future Elderly Model to Estimate Implications for Social Security and Medicare. Am. Econ. Rev. 2014, 104, 230–233. [Google Scholar] [CrossRef]
- Birkin, M.; Wu, B.; Rees, P. Moses: Dynamic Spatial Microsimulation with Demographic Interactions. In New Frontiers in Microsimulation Modelling; Routledge: London, UK, 2017; pp. 53–77. [Google Scholar]
- Rephann, T.J.; Holm, E. Economic-Demographic Effects of Immigration: Results from a Dynamic Spatial Microsimulation Model. Int. Reg. Sci. Rev. 2004, 27, 379–410. [Google Scholar] [CrossRef]
- Lomax, N.; Smith, A. Microsimulation for demography. Aust. Popul. Stud. 2017, 1, 73–85. [Google Scholar] [CrossRef]
- Lomax, N. Digital Twins and Microsimulation in SIPHER. 2019. Available online: https://sipher.ac.uk/wp-content/uploads/2019/11/Digital-Twins-and-Microsimulation-Dr-Nik-Lomax.pdf (accessed on 25 May 2021).
- Blakely, T.; Cleghorn, C.; Mizdrak, A.; Waterlander, W.; Nghiem, N.; Swinburn, B.; Wilson, N.; Ni Mhurchu, C. The effect of food taxes and subsidies on population health and health costs: A modelling study. Lancet Public Health 2020, 5, e404–e413. [Google Scholar] [CrossRef]
- Lovelace, R.; Ballas, D.; Watson, M. A spatial microsimulation approach for the analysis of commuter patterns: From individual to regional levels. J. Transp. Geogr. 2014, 34, 282–296. [Google Scholar] [CrossRef]
- Voas, D.; Williamson, P. An evaluation of the combinatorial optimisation approach to the creation of synthetic microdata. Int. J. Popul. Geogr. 2000, 6, 349–366. [Google Scholar] [CrossRef]
- Grimm, V.; Revilla, E.; Berger, U.; Jeltsch, F.; Mooij, W.M.; Railsback, S.F.; Thulke, H.; Weiner, J.; Wiegand, T.; de Angelis, D.L. Pattern-Oriented Modeling of Agent-Based Complex Systems: Lessons from Ecology. Science 2005, 310, 987–991. [Google Scholar] [CrossRef] [PubMed]
- Tomintz, M.N.; Kosar, B.; García-Barrios, V.M. simSALUD: Design and Implementation of an Open-source Wizard based Spatial Microsimulation Framework. Int. J. Microsimul. 2016, 10, 118–143. [Google Scholar] [CrossRef]
- Lovelace, R. Robin Lovelace on Github. 2021. Available online: https://github.com/Robinlovelace (accessed on 25 May 2021).
- MacIntyre, S.; Maciver, S.; Sooman, A. Area, Class and Health: Should we be Focusing on Places or People? J. Soc. Policy 1993, 22, 213–234. [Google Scholar] [CrossRef]
- Cummins, S.; MacIntyre, S. Food environments and obesity—Neighbourhood or nation? Int. J. Epidemiol. 2005, 35, 100–104. [Google Scholar] [CrossRef] [PubMed]
- Noble, D.; Smith, D.; Mathur, R.; Robson, J.; Greenhalgh, T. Feasibility study of geospatial mapping of chronic disease risk to inform public health commissioning. BMJ Open 2012, 2, e000711. [Google Scholar] [CrossRef] [PubMed]
- Mathur, R.; Noble, D.; Smith, D.; Greenhalgh, T.; Robson, J. Quantifying the risk of type 2 diabetes in East London using the QDScore: A cross-sectional analysis. Br. J. Gen. Pract. 2012, 62, e663–e670. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).