On Some New Neighborhood Degree-Based Indices for Some Oxide and Silicate Networks

Abstract

Topological indices are numeric quantities that describes the topology of molecular structure in mathematical chemistry. An important area of applied mathematics is the chemical reaction network theory. Real-world problems can be modeled using this theory. Due to its worldwide applications, chemical networks have attracted researchers since their foundation. In this report, some silicate and oxide networks are studied, and exact expressions of some newly-developed neighborhood degree-based topological indices named as the neighborhood Zagreb index ($M_N$), the neighborhood version of the forgotten topological index ($F_N$), the modified neighborhood version of the forgotten topological index ($F_N^{\ast }$), the neighborhood version of the second Zagreb index ($M_2^{\ast }$), and neighborhood version of the hyper Zagreb index ($H{M}_N$) are obtained for the aforementioned networks. In addition, a comparison among all the indices is shown graphically.

1. Introduction

Networks connect nodes that are somehow interconnected. Numerous personal computers connected together form a network. Cell phone users create a network. The networking process involves examining the best way to implement a network. Cheminformatics is a new area of research in which chemistry, mathematics, and information science are combined. That is how it caught the attention of researchers around the world. In this paper, we consider different silicate and oxide networks. The most abundant minerals in the Earth’s crust are silicates. In most frequently-found silicates, including almost all silicate minerals found in the crust of the Earth, each silicon atom comprises the center of a tetrahedron (Figure 1), the corners of which are occupied by oxygen atoms, connected to it by single covalent bonds according to the octet rule. Silicates are obtained by fusing metal oxides or metal carbonates from sand. We can get various silicate structures by combining different tetrahedron silicates. Similarly, silicate networks are built by different silicate structures. The oxide networks are obtained by removing silicon atoms from the center of tetrahedra. Here, we also consider the copper (II) oxide (cupric oxide) network. Copper has enormous applications in medical science. It plays an important role in the synthesis and stabilization of skin proteins, and it also has potent biocidal properties [1]. The copper (II) oxide (cupric oxide) forms an inorganic chemical compound $CuO$. This mineral is important in animals and plants. Copper (II) oxide is utilized in mineral and vitamin supplements as a copper source and is regarded as safe.

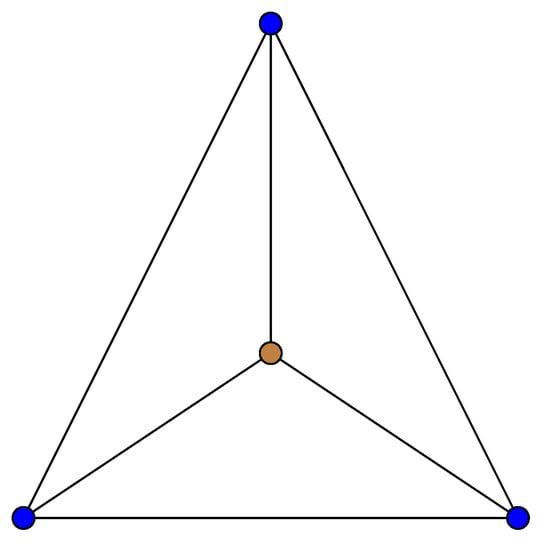
Figure 1. Silicate tetrahedra ($Si{O}_4$).

Molecular graphs are pictorial models of chemical compounds, assigning atoms as nodes and chemical bonds as edges. Throughout this report, we consider only molecular graphs [2,3,4]. We consider $V\left(G\right)$ and $E\left(G\right)$ as vertex and edge sets, respectively, for a graph G. The degree of a vertex $u\in V\left(G\right)$, denoted by $d_G\left(u\right)$, is the number of edges that are incident to u in G. We say that a node u is a neighbor of another node v if u is adjacent to v in G. Here, ${\delta }_G\left(v\right)$ represents the totality of degrees of all neighbors of v in G, i.e.,

$$\begin{array}{c}\hfill {\delta }_G\left(v\right)={\displaystyle \sum _{u\in N_G\left(v\right)}}{d}_G\left(u\right),\end{array}$$

where $N_G\left(v\right)=\{u\in V\left(G\right):uv\in E\left(G\right)\}$. Graph theory creates a link between mathematics and chemistry by a useful tool named the topological index. A topological index is a real number associated with a graph obtained by certain rules such that two isomorphic graphs have the same topological index. It characterizes the topology of molecular structure. Topological indices play a vital role in the quantitative structure–property relationship (QSPR) and the quantitative structure–activity relationship (QSAR) models to predict different physico-chemical properties and bioactivity that help in drug discovery. Its applications in various fields such as nano-science, biotechnology, etc., are also remarkable. That is why it has attracted researchers’ attention worldwide. The journey of topological indices started when chemist Harold Wiener introduced the Wiener index [5] in 1947. Several topological indices have been introduced over the past decades based on the vertex degree. Inspired by the works [6,7,8], we designed some new degree-based topological indices [9,10] having nice correlations with entropy and the acentric factor. Their mean isomer degeneracy is also remarkable. These indices are defined as follows.

The neighborhood Zagreb index is denoted by $M_N\left(G\right)$ and is defined as:

$$\begin{array}{c}\hfill M_N\left(G\right)={\displaystyle \sum _{v\in V\left(G\right)}}{\delta }_G{\left(v\right)}^2.\end{array}$$

The neighborhood version of the forgotten topological index is denoted by $F_N\left(G\right)$ and is defined as:

$$\begin{array}{c}\hfill F_N\left(G\right)={\displaystyle \sum _{v\in V\left(G\right)}}{\delta }_G{\left(v\right)}^3.\end{array}$$

The modified neighborhood version of the forgotten topological index is denoted by $F_N^{\ast }\left(G\right)$ and is defined as:

$$\begin{array}{c}\hfill F_N^{\ast }\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2].\end{array}$$

The neighborhood version of the second Zagreb index is denoted by $M_2^{\ast }\left(G\right)$ and is defined by:

$$\begin{array}{c}\hfill M_2^{\ast }\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}}\left[{\delta }_G\left(u\right){\delta }_G\left(v\right)\right].\end{array}$$

The neighborhood version of the hyper Zagreb index is denoted by $H{M}_N\left(G\right)$ and is defined by:

$$\begin{array}{c}\hfill H{M}_N\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}}{[{\delta }_G\left(u\right)+{\delta }_G\left(v\right)]}^2.\end{array}$$

In [11,12,13,14,15,16,17,18,19], topological indices for different chemically important graphs were discussed. Baig et al. [20] derived topological indices for some silicate and oxide networks. Javaid et al. [21] discussed the topological properties of rhombus-type silicate and oxide networks. In [22], topological indices for the copper (II) oxide network were obtained. For further work related to this field, readers are referred to [23,24,25,26]. Motivated by those works, in this paper, we obtain some exact expressions of five novel indices described above for some silicate and oxide networks and compare the results graphically.

This paper is organized as follows. In the next section, the motivation behind this work is described. The usefulness of these indices is illustrated here. The computation of the topological indices for different silicate and oxide networks using vertex and edge partition procedures is presented in Section 3. The graphical representation of the results is shown here using MATLAB (9.2, The MathWorks, Inc., Natick, MA, USA) and Maple (2015.1, Maplesoft, Waterloo, ON Canada) software. We conclude this report with a comparative study of the indices for different networks under consideration.

2. Motivation

In order to determine the usefulness of a topological index to predict the physico-chemical behavior of a chemical compound, the correlation coefficient $\left(r\right)$ between the physico-chemical properties and topological indices is calculated. In QSPR/QSAR analysis, the topological indices for which $r^2$ exceeds 0.8 are very useful. In [9,10], it was shown that the $r^2$ values of five topological indices $M_N,F_N,F_N^{\ast },M_2^{\ast }$, and $H{M}_N$ have excellent correlations with entropy and the acentric factor for octane isomers. The $r^2$ values of those indices with entropy are 0.989, 0.88, 0.868, 0.926, and 0.879, respectively. The $r^2$ values of those indices with the acentric factor are 0.907, 0.989, 0.952, 0.819, and 0.961, respectively. Linear correlations of these indices with entropy and the acentric factor are depicted in Figure 2. The above-mentioned indices are therefore effective in QSPR/QSAR analysis with high statistical accuracy. Furthermore, their mean isomer degeneracy is also remarkable in comparison with other degree-based topological indices [9,10], which provides assurance of their good isomer discrimination ability. Calculating these indices for distinct chemically-important networks and composite graphs is therefore worthwhile. Here, we consider some oxide and silicate networks.

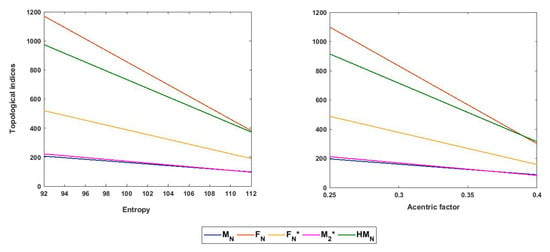
Figure 2. Linear fitting of five topological indices with entropy and the acentric factor.

3. Computation of Topological Indices

In this section, we first discuss the vertex and edge partition of the networks, and then, using that partition, we obtain five topological indices discussed in the previous section for the networks. Here, we consider dominating silicate $\left(DSL\right(n\left)\right)$ and oxide $\left(DOX\right(n)$)) networks, regular triangulene silicate $\left(RTSL\right(n\left)\right)$ and oxide $\left(RTOX\right(n)$) networks, rhombus silicate ($RHSL\left(n\right)$) and oxide ($RHOX\left(n\right)$) networks, and the copper (II) oxide ($CuO$) network. The construction procedures of these networks are discussed in detail in [21,22,26]. The first three types of networks can be constructed from a honeycomb network $HC\left(n\right)$ of dimension n (number of hexagonal layers) [26]. The structure of $HC\left(3\right)$ is shown in Figure 3. To create the vertex and edge partitions, we consider the following notations.

$$\begin{array}{c}\hfill V_i=\{u\in V\left(G\right):{\delta }_G\left(u\right)=i\},\end{array}$$

$$\begin{array}{c}\hfill E_{(p,q)}=\{uv\in E\left(G\right):{\delta }_G\left(u\right)=p,{\delta }_G\left(v\right)=q\}.\end{array}$$

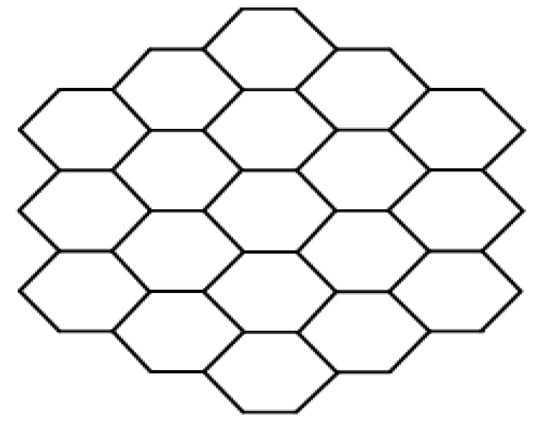
Figure 3. Honeycomb network $HC\left(3\right)$ of dimension three.

By $|V_i|$ and $|E_{(p,q)}|$, we mean the cardinality of the sets $V_i$ and $E_{(p,q)}$, respectively.

3.1. Dominating Silicate $\left(DSL\right(n\left)\right)$ and Oxide $\left(DOX\right(n)$)) Networks

In this subsection, we obtain the five aforementioned indices for dominating silicate ($DSL\left(n\right)$) and oxide ($DOX\left(n\right)$) networks. The structures of $DSL\left(3\right)$ and $DOX\left(3\right)$ are depicted in Figure 4 and Figure 5, respectively. Dominating silicate networks have $45n^2-39n+12$ nodes and $108n^2-108n+36$ edges [20,26]. Dominating oxide networks admit $27n^2-21n+6$ nodes and $54n^2-54n+18$ edges [20,26]. Vertex and edge partitions for dominating silicate networks are as follows.

$$V\left(DSL\left(n\right)\right)=V_{15}\cup V_{18}\cup V_{24}\cup V_{27}\cup V_{30},$$

(1)

$$\begin{array}{c}E\left(DSL\left(n\right)\right)=E_{(15,15)}\cup E_{(15,24)}\cup E_{(15,27)}\cup E_{(18,27)}\cup E_{(18,30)}\cup E_{(24,24)}\\ \cup E_{(24,27)}\cup E_{(27,30)}\cup E_{(30,30)}\end{array}$$

(2)

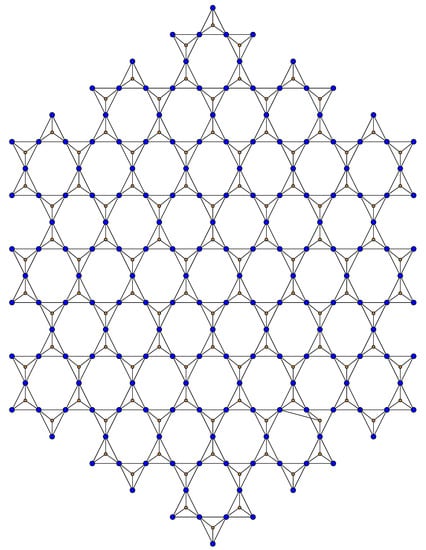
Figure 4. Dominating silicate network ($DSL\left(3\right)$).

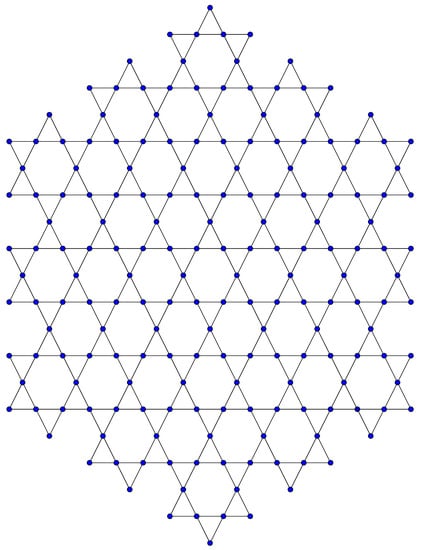
Figure 5. Dominating oxide network ($DOX\left(3\right)$).

Vertex and edge partitions for dominating oxide networks are as follows.

$$V\left(DOX\left(n\right)\right)=V_8\cup V_{12}\cup V_{14}\cup V_{16},$$

(3)

$$E\left(DOX\left(n\right)\right)=E_{(8,12)}\cup E_{(8,14)}\cup E_{(12,12)}\cup E_{(12,14)}\cup E_{(14,16)}\cup E_{(16,16)}.$$

(4)

Theorem 1.

The neighborhood Zagreb index ($M_N$) of the dominating silicate $\left(DSL\right(n\left)\right)$ and oxide $\left(DOX\right(n)$)) networks for $n\ge 2$ is given by:

(i) 

$M_N\left(DSL\left(n\right)\right)=\mathrm{30,132}{n}^2-\mathrm{38,016}n+\mathrm{14,040},$

(ii) 

$M_N\left(DOX\left(n\right)\right)=6912n^2-9072n+3408.$

Proof. 

The general formula of the neighborhood Zagreb index is given by:

$$\begin{array}{c}\hfill M_N\left(G\right)={\displaystyle \sum _{v\in V\left(G\right)}}{\delta }_G{\left(v\right)}^2.\end{array}$$

(i)

Let $G\cong DSL\left(n\right)$. Now, applying vertex partition (1) on the definition of the neighborhood Zagreb index, we get:

$$\begin{array}{cc}{M}_N\left(G\right)\hfill & & ={\displaystyle \sum _{v\in V_{15}}}{\delta }_G{\left(v\right)}^2+{\displaystyle \sum _{v\in V_{18}}}{\delta }_G{\left(v\right)}^2+{\displaystyle \sum _{v\in V_{24}}}{\delta }_G{\left(v\right)}^2+{\displaystyle \sum _{v\in V_{27}}}{\delta }_G{\left(v\right)}^2+{\displaystyle \sum _{v\in V_{30}}}{\delta }_G{\left(v\right)}^2.\hfill \end{array}$$

Using Table 1, we obtain:

$$\begin{array}{ccc}\hfill M_N\left(G\right)& \hfill =& |V_{15}|\left({15}^2\right)+|V_{18}|\left({18}^2\right)+|V_{24}|\left({24}^2\right)+|V_{27}|\left({27}^2\right)+\left|V_{30}\right|\left({30}^2\right)\hfill \\ \hfill & \hfill =& (24n-12)\left({15}^2\right)+(18n^2-30n+12)\left({18}^2\right)+\left(6n\right)\left({24}^2\right)\hfill \\ \hfill & \hfill & +12(n-1)\left({27}^2\right)+(27n^2-51n+24)\left({30}^2\right)\hfill \\ \hfill & \hfill =& \mathrm{30,132}{n}^2-\mathrm{38,016}n+\mathrm{14,040}.\hfill \end{array}$$

Table 1. Vertex partition of dominating silicate networks ($DSL\left(n\right)$) with dimension n.

${\mathit{V}}_{\mathit{i}}$	${\mathit{V}}_{15}$	${\mathit{V}}_{18}$	${\mathit{V}}_{24}$	${\mathit{V}}_{27}$	${\mathit{V}}_{30}$
$|V_i|$	$24n-12$	$18n^2-30n+12$	$6n$	$12(n-1)$	$27n^2-51n+24$

(ii)

Let $G\cong DOX\left(n\right)$. Now, using vertex partition (3) and Table 2 on the definition of the neighborhood Zagreb index, we obtain:

$$\begin{array}{ccc}\hfill M_N\left(G\right)& \hfill =& |V_8|\left(8^2\right)+|V_{12}|\left({12}^2\right)+|V_{14}|\left({14}^2\right)+\left|V_{16}\right|\left({16}^2\right)\hfill \\ \hfill & \hfill =& (12n-6)\left(8^2\right)+\left(6n\right)\left({12}^2\right)+12(n-1)\left({14}^2\right)\hfill \\ \hfill & \hfill & +(27n^2-51n+24)\left({16}^2\right).\hfill \end{array}$$

Table 2. Vertex partition of dominating oxide networks ($DOX\left(n\right)$) with dimension n.

${\mathit{V}}_{\mathit{i}}$	${\mathit{V}}_8$	${\mathit{V}}_{12}$	${\mathit{V}}_{14}$	${\mathit{V}}_{16}$
$|V_i|$	$12n-6$	$6n$	$12(n-1)$	$27n^2-51n+24$

After simplifying and arranging the terms, the required result can be obtained easily.

Hence the proof. ☐

Theorem 2.

The neighborhood versions of the forgotten topological index ($F_N$) of the dominating silicate $\left(DSL\right(n\left)\right)$ and oxide $\left(DOX\right(n)$)) networks for $n\ge 2$ are given by:

(i) 

$F_N\left(DSL\left(n\right)\right)=\mathrm{833,976}{n}^2-\mathrm{1,151,820}n+\mathrm{441,288},$

(ii) 

$F_N\left(DOX\left(n\right)\right)=\mathrm{110,592}{n}^2-\mathrm{159,456}n+\mathrm{62,304}.$

Proof. 

The general formulation of the neighborhood version of the forgotten topological index is given by:

$$\begin{array}{c}\hfill F_N\left(G\right)={\displaystyle \sum _{v\in V\left(G\right)}}{\delta }_G{\left(v\right)}^3.\end{array}$$

(i)

Let $G\cong DSL\left(n\right)$. Using vertex partition (1) and Table 1 on the above formula, we have:

$$\begin{array}{ccc}\hfill F_N\left(G\right)& \hfill =& (24n-12)\left({15}^3\right)+(18n^2-30n+12)\left({18}^3\right)+\left(6n\right)\left({24}^3\right)+\hfill \\ \hfill & \hfill & 12(n-1)\left({27}^3\right)+(27n^2-51n+24)\left({30}^3\right)\hfill \\ \hfill & \hfill =& \mathrm{8,33,976}{n}^2-\mathrm{11,51,820}n+\mathrm{4,41,288}.\hfill \end{array}$$

(ii)

Let $G\cong DOX\left(n\right)$. Using vertex partition (3) and Table 2, the general formula of the $F_N$ index gives the following computation.

$$\begin{array}{ccc}\hfill F_N\left(G\right)& =\hfill & (12n-6)\left(8^3\right)+\left(6n\right)\left({12}^3\right)+12(n-1)\left({14}^3\right)+\hfill \\ \hfill & \hfill & +(27n^2-51n+24)\left({16}^3\right)\hfill \\ \hfill & =\hfill & \mathrm{1,10,592}{n}^2-\mathrm{1,59,456}n+\mathrm{62,304}.\hfill \end{array}$$

Hence the proof. ☐

Theorem 3.

The modified neighborhood versions of the forgotten topological index ($F_N^{\ast }$) of the dominating silicate $\left(DSL\right(n\left)\right)$ and oxide $\left(DOX\right(n)$)) networks for $n\ge 2$ are given by:

(i) 

$F_N^{\ast }\left(DSL\left(n\right)\right)=\mathrm{163,296}{n}^2-\mathrm{215,136}n+\mathrm{80,676},$

(ii) 

$F_N^{\ast }\left(DOX\left(n\right)\right)=\mathrm{27,648}{n}^2-\mathrm{37,824}n+\mathrm{14,400}.$

Proof. 

The general formula of the modified neighborhood version of the forgotten topological index is given by:

$$\begin{array}{c}\hfill F_N^{\ast }\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2].\end{array}$$

(i)

Let G be the dominating silicate network with dimension n. Then, applying edge partition (2) on the definition of the $F_N^{\ast }$ index, we have:

$$\begin{array}{ccc}\hfill F_N^{\ast }\left(G\right)& =\hfill & {\displaystyle \sum _{uv\in E\left(G\right)}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2]\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{uv\in E_{(15,15)}}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2]+{\displaystyle \sum _{uv\in E_{(15,24)}}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2]\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{uv\in E_{(15,27)}}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2]+{\displaystyle \sum _{uv\in E_{(18,27)}}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2]\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{uv\in E_{(18,30)}}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2]+{\displaystyle \sum _{uv\in E_{(24,24)}}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2]\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{uv\in E_{(24,27)}}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2]+{\displaystyle \sum _{uv\in E_{(27,30)}}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2]\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{uv\in E_{(30,30)}}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2.\hfill \end{array}$$

Using Table 3, we can obtain:

$$\begin{array}{ccc}\hfill F_N^{\ast }\left(G\right)& =& |E_{(15,15)}|({15}^2+{15}^2)+|E_{(15,24)}|({15}^2+{24}^2)+\left|E_{(15,27)}\right|({15}^2+{27}^2)\hfill \\ \hfill & \hfill & +|E_{(18,27)}|({18}^2+{27}^2)+|E_{(18,30)}|({18}^2+{30}^2)+\left|E_{(24,24)}\right|({24}^2+{24}^2)\hfill \\ \hfill & \hfill & +|E_{(24,27)}|({24}^2+{27}^2)+|E_{(27,30)}|({27}^2+{30}^2)+\left|E_{(30,30)}\right|({30}^2+{30}^2)\hfill \\ \hfill & =\hfill & 6(2n-1)({15}^2+{15}^2)+\left(24n\right)({15}^2+{24}^2)+24(n-1)({15}^2+{27}^2)\hfill \\ \hfill & \hfill & +12(n-1)|({18}^2+{27}^2)+(54n^2-102n+48)({18}^2+{30}^2)\hfill \\ \hfill & \hfill & +\left(6\right)({24}^2+{24}^2)+12(n-1)({24}^2+{27}^2)+24(n-1)({27}^2+{30}^2)\hfill \\ \hfill & \hfill & +(54n^2-114n+60)({30}^2+{30}^2).\hfill \end{array}$$

Table 3. Edge partition of dominating silicate networks ($DSL\left(n\right)$) with dimension n.

${\mathit{E}}_{(\mathit{p},\mathit{q})}$	${\mathit{E}}_{\left(\mathrm{15,15}\right)}$	${\mathit{E}}_{\left(\mathrm{15,24}\right)}$	${\mathit{E}}_{\left(\mathrm{15,27}\right)}$	${\mathit{E}}_{\left(\mathrm{18,27}\right)}$	${\mathit{E}}_{\left(\mathrm{18,30}\right)}$	${\mathit{E}}_{\left(\mathrm{24,24}\right)}$	${\mathit{E}}_{\left(\mathrm{24,27}\right)}$	${\mathit{E}}_{\left(\mathrm{27,30}\right)}$	${\mathit{E}}_{\left(\mathrm{30,30}\right)}$
$|E_{(p,q)}|$	$6(2n-1)$	$24n$	$24(n-1)$	$12(n-1)$	$54n^2-102n+48$	6	$12(n-1)$	$24(n-1)$	$54n^2-114n+60$

After simplification, the desired result is clear.

(ii)

Let G be the dominating silicate network with dimension n.

Now, applying the vertex partition (4) and Table 4 on the definition of the $F_N^{\ast }$ index, we have:

$$\begin{array}{ccc}\hfill F_N^{\ast }\left(G\right)& =\hfill & |E_{(8,12)}|(8^2+{12}^2)+|E_{(8,14)}|(8^2+{14}^2)+\left|E_{(12,12)}\right|({12}^2+{12}^2)\hfill \\ \hfill & \hfill & +|E_{(12,14)}|({12}^2+{14}^2)+|E_{(14,16)}|({14}^2+{16}^2)+\left|E_{(16,16)}\right|({16}^2+{16}^2)\hfill \\ \hfill & =\hfill & \left(12n\right)(8^2+{12}^2)+12(n-1)(8^2+{14}^2)+\left(6\right)({12}^2+{12}^2)\hfill \\ \hfill & \hfill & +12(n-1)({12}^2+{14}^2)+24(n-1)({14}^2+{16}^2)\hfill \\ \hfill & \hfill & +(54n^2-114n+60)({16}^2+{16}^2)\hfill \\ \hfill & =\hfill & \mathrm{27,648}{n}^2-\mathrm{37,824}n+\mathrm{14,400}.\hfill \end{array}$$

Table 4. Edge partition of dominating oxide networks ($DOX\left(n\right)$) with dimension n.

${\mathit{E}}_{(\mathit{p},\mathit{q})}$	${\mathit{E}}_{\left(\mathrm{8,12}\right)}$	${\mathit{E}}_{\left(\mathrm{8,14}\right)}$	${\mathit{E}}_{\left(\mathrm{12,12}\right)}$	${\mathit{E}}_{\left(\mathrm{12,14}\right)}$	${\mathit{E}}_{\left(\mathrm{14,16}\right)}$	${\mathit{E}}_{\left(\mathrm{16,16}\right)}$
$|E_{(p,q)}|$	$12n$	$12(n-1)$	6	$12(n-1)$	$24(n-1)$	$54n^2-114n+60$

Hence the theorem. ☐

Theorem 4.

The neighborhood versions of the second Zagreb index ($M_2^{\ast }$) of the dominating silicate $\left(DSL\right(n\left)\right)$ and oxide $\left(DOX\right(n)$)) networks for $n\ge 2$ are given by:

(i) 

$M_2^{\ast }\left(DSL\left(n\right)\right)=\mathrm{77,760}{n}^2-\mathrm{103,572}n+\mathrm{39,258},$

(ii) 

$M_2^{\ast }\left(DOX\left(n\right)\right)=\mathrm{13,824}{n}^2-\mathrm{19,296}n+7488.$

Proof. 

The general formula of the neighborhood version of the second Zagreb index is given by:

$$\begin{array}{c}\hfill M_2^{\ast }\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}}\left[{\delta }_G\left(u\right){\delta }_G\left(v\right)\right].\end{array}$$

(i)

Let $G\cong DSL\left(n\right)$. Now, applying the edge partition (2) and Table 3 on the definition of the neighborhood version of the second Zagreb index, we get the desired result as follows.

$$\begin{array}{lll}\hfill M_2^{\ast }\left(G\right)& \hfill =& 6(2n-1)\left(15.15\right)+24n\left(15.24\right)+24(n-1)\left(15.27\right)+12(n-1)\left(18.27\right)\hfill \\ \hfill & \hfill & +(54n^2-102n+48)\left(18.30\right)+6\left(24.24\right)+12(n-1)\left(24.27\right)\hfill \\ \hfill & \hfill & +24(n-1)\left(27.30\right)+(54n^2-114n+60)\left(30.30\right)\hfill \\ \hfill & \hfill =& \mathrm{77,760}{n}^2-\mathrm{103,572}n+\mathrm{39,258}.\hfill \end{array}$$

(ii)

Let $G\cong DOX\left(n\right)$. Applying the edge partition (4) and Table 4 on the definition of the neighborhood version of the second Zagreb index, we get the desired result as follows.

$$\begin{array}{ccc}\hfill M_2^{\ast }\left(G\right)& =\hfill & 12n\left(8.12\right)+12(n-1)\left(8.14\right)+6\left(12.12\right)+12(n-1)\left(12.14\right)\hfill \\ \hfill & \hfill & +24(n-1)\left(14.16\right)+(54n^2-114n+60)\left(16.16\right)\hfill \\ \hfill & =\hfill & \mathrm{13,824}{n}^2-\mathrm{19,296}n+7488.\hfill \end{array}$$

Hence the proof. ☐

Theorem 5.

The neighborhood versions of the hyper Zagreb index ($H{M}_N$) of the dominating silicate $\left(DSL\right(n\left)\right)$ and oxide $\left(DOX\right(n)$)) networks for $n\ge 2$ are given by:

(i) 

$H{M}_N\left(DSL\left(n\right)\right)=\mathrm{318,816}{n}^2-\mathrm{422,280}n+\mathrm{159,192},$

(ii) 

$H{M}_N\left(DOX\left(n\right)\right)=\mathrm{55,296}{n}^2-\mathrm{76,416}n+\mathrm{29,376}.$

Proof. 

(i)

Let $G\cong DSL\left(n\right)$. Now, applying edge partition (2) and Table 3 on the definition of the $H{M}_N$ index, we get the following computation.

$$\begin{array}{ccc}\hfill H{M}_N\left(G\right)& =\hfill & {\displaystyle \sum _{uv\in E\left(G\right)}}{[{\delta }_G\left(u\right)+{\delta }_G\left(v\right)]}^2\hfill \\ \hfill & =\hfill & 6(2n-1){(15+15)}^2+\left(24n\right){(15+24)}^2+24(n-1){(15+27)}^2\hfill \\ \hfill & \hfill & +12(n-1)({(18+27)}^2+(54n^2-102n+48){(18+30)}^2\hfill \\ \hfill & \hfill & +6{(24+24)}^2+12(n-1){(24+27)}^2+24(n-1){(27+30)}^2\hfill \\ \hfill & \hfill & +(54n^2-114n+60){(30+30)}^2\hfill \\ \hfill & =\hfill & \mathrm{318,816}{n}^2-\mathrm{422,280}n+\mathrm{159,192}.\hfill \end{array}$$

(ii)

Let $G\cong DOX\left(n\right)$. Now, applying edge partition (4) and Table 4 on the definition of the $H{M}_N$ index, we get the following computation.

$$\begin{array}{ccc}\hfill H{M}_N\left(G\right)& =\hfill & {\displaystyle \sum _{uv\in E\left(G\right)}}{[{\delta }_G\left(u\right)+{\delta }_G\left(v\right)]}^2\hfill \\ \hfill & =\hfill & \left(12n\right){(8+12)}^2+12(n-1){(8+14)}^2+6{(12+12)}^2\hfill \\ \hfill & \hfill & +12(n-1)({(12+14)}^2+24(n-1){(14+16)}^2\hfill \\ \hfill & \hfill & +(54n^2-114n+60){(16+16)}^2\hfill \\ \hfill & =\hfill & \mathrm{55,296}{n}^2-\mathrm{76,416}n+\mathrm{29,376}.\hfill \end{array}$$

Hence the theorem. ☐

Five topological indices for $DSL\left(n\right)$ and $DOX\left(n\right)$ are shown graphically in Figure 6.

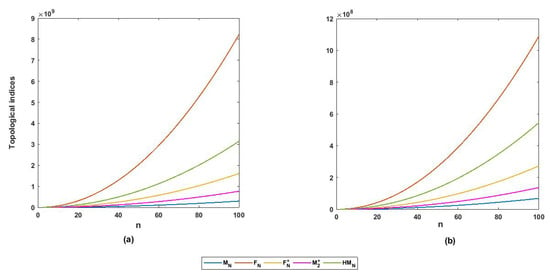
Figure 6. Different topological indices for dominating (a) silicate and (b) oxide networks.

3.2. Regular Triangulene Silicate $\left(RTSL\right(n\left)\right)$ and Oxide $\left(RTOX\right(n)$) Networks

In this subsection, we obtain the five aforementioned indices for regular triangulene silicate ($RTSL\left(n\right)$) and oxide ($RTOX\left(n\right)$) networks. The structures of $RTSL\left(5\right)$ and $RTOX\left(5\right)$ are shown in Figure 7 and Figure 8, respectively. Using the method described in [26], it can be said that regular triangulene silicate networks have $\frac{5n^2+15n+2}{2}$ nodes and $3n^2+31n-28$ edges. The regular triangulene oxide network admits $\frac{3n^2+9n+2}{2}$ nodes and $3n^2+6n$ edges [23,26]. Vertex and edge partitions for the regular triangulene silicate network are as follows.

$$V\left(RTSL\left(n\right)\right)=V_{12}\cup V_{15}\cup V_{18}\cup V_{24}\cup V_{27}\cup V_{30},$$

(5)

$$\begin{array}{c}E\left(RTSL\left(n\right)\right)=E_{(12,12)}\cup E_{(12,15)}\cup E_{(12,24)}\cup E_{(15,15)}\cup E_{(15,24)}\cup E_{(15,27)}\cup E_{(18,24)}\\ \cup E_{(18,27)}\cup E_{(18,30)}\cup E_{(24,24)}\cup E_{(24,27)}\cup E_{(27,27)}\cup E_{(27,30)}\cup E_{(30,30)}.\end{array}$$

(6)

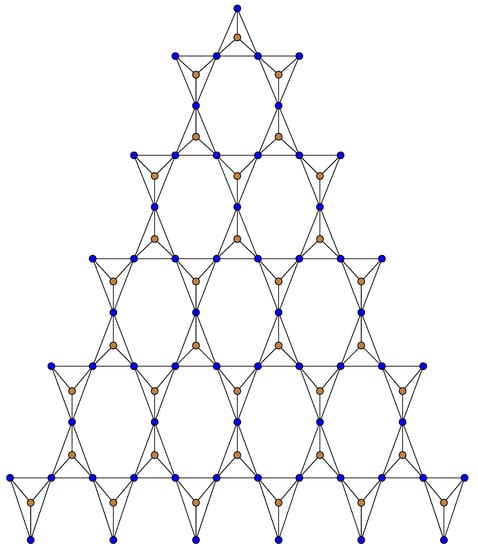
Figure 7. Regular triangulene silicate network ($RTSL\left(5\right)$).

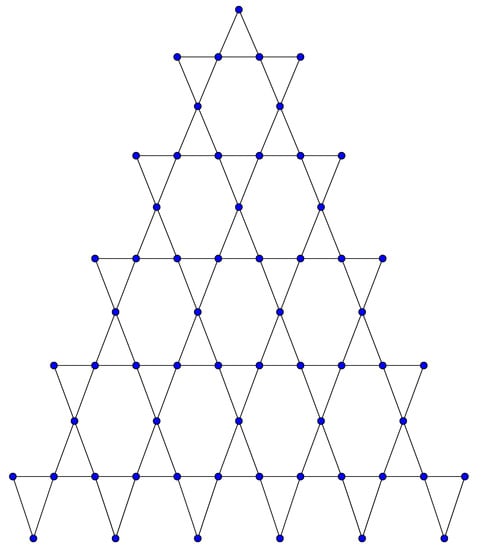
Figure 8. Regular triangulene oxide network ($RTOX\left(5\right)$).

Vertex and edge partitions for the regular triangulene oxide network are as follows.

$$V\left(RTOX\left(n\right)\right)=V_6\cup V_8\cup V_{12}\cup V_{14}\cup V_{16},$$

(7)

$$E\left(RTOX\left(n\right)\right)=E_{(6,6)}\cup E_{(6,12)}\cup E_{(8,12)}\cup E_{(8,14)}\cup E_{(12,12)}\cup E_{(12,14)}\cup E_{(14,14)}\cup E_{(14,16)}\cup E_{(16,16)}.$$

(8)

Theorem 6.

The neighborhood Zagreb index ($M_N$) of the regular triangulene silicate $\left(RTSL\right(n\left)\right)$ and oxide $\left(RTOX\right(n)$)) networks for $n\ge 2$ is given by:

(i) 

$M_N\left(RTSL\left(n\right)\right)=1674n^2+1674n-702,$

(ii) 

$M_N\left(RTOX\left(n\right)\right)=384n^2+216n-208.$

Proof. 

The general formula of the neighborhood Zagreb index is given by:

$$\begin{array}{c}\hfill M_N\left(G\right)={\displaystyle \sum _{v\in V\left(G\right)}}{\delta }_G{\left(v\right)}^2.\end{array}$$

(i)

Let $G\cong RTSL\left(n\right)$. Now, apply vertex partition (5) and Table 5 on the definition of the neighborhood Zagreb index, we get:

$$\begin{array}{ccc}\hfill M_N\left(G\right)& =\hfill & |V_{12}|\left({12}^2\right)+|V_{15}|\left({15}^2\right)+|V_{18}|\left({18}^2\right)+\left|V_{24}\right|\left({24}^2\right)\hfill \\ \hfill & \hfill & +|V_{27}|\left({27}^2\right)+\left|V_{30}\right|\left({30}^2\right)\hfill \\ \hfill & =\hfill & \left(4\right)\left({12}^2\right)+(6n-2)\left({15}^2\right)+\left(n^2\right)\left({18}^2\right)+\left(4\right)\left({24}^2\right)+(6n-8)\left({27}^2\right)\hfill \\ \hfill & \hfill & +\left(\frac{3n^2-9n+6}{2}\right)\left({30}^2\right).\hfill \end{array}$$

Table 5. Vertex partition of regular triangulene silicate networks ($RTSL\left(n\right)$) with dimension n.

${\mathit{V}}_{\mathit{i}}$	${\mathit{V}}_{12}$	${\mathit{V}}_{15}$	${\mathit{V}}_{18}$	${\mathit{V}}_{24}$	${\mathit{V}}_{27}$	${\mathit{V}}_{30}$
$|V_i|$	4	$6n-2$	$n^2$	4	$6n-8$	$\frac{3n^2-9n+6}{2}$

After simplification, the desired result can be obtained easily.

(ii)

Let $G\cong RTOX\left(n\right)$. Now, using vertex partition (7) and Table 6 on the definition of the neighborhood Zagreb index, we obtain:

$$\begin{array}{ccc}\hfill M_N\left(G\right)& =\hfill & |V_6|\left(6^2\right)+|V_8|\left(8^2\right)+|V_{12}|\left({12}^2\right)+|V_{14}|\left({14}^2\right)+\left|V_{16}\right|\left({16}^2\right)\hfill \\ \hfill & =\hfill & \left(4\right)\left(6^2\right)+(3n-2)\left(8^2\right)+\left(4\right)\left({12}^2\right)+(6n-8)\left({14}^2\right)\hfill \\ \hfill & \hfill & +\left(\frac{3n^2-9n+6}{2}\right)\left({16}^2\right).\hfill \end{array}$$

Table 6. Vertex partition of regular triangulene oxide networks ($RTOX\left(n\right)$) with dimension n.

${\mathit{V}}_{\mathit{i}}$	${\mathit{V}}_6$	${\mathit{V}}_8$	${\mathit{V}}_{12}$	${\mathit{V}}_{14}$	${\mathit{V}}_{16}$
$|V_i|$	4	$3n-2$	4	$6n-8$	$\frac{3n^2-9n+6}{2}$

After simplifying and arranging the terms, the required result can be obtained easily.

Hence the proof. ☐

Theorem 7.

The neighborhood version of the forgotten topological index ($F_N$) of the regular triangulene silicate $\left(RTSL\right(n\left)\right)$ and oxide $\left(RTOX\right(n)$)) networks for $n\ge 2$ is given by:

(i) 

$F_N\left(RTSL\left(n\right)\right)=\mathrm{46,332}{n}^2+\mathrm{16,848}n+\mathrm{113,994},$

(ii) 

$F_N\left(RTOX\left(n\right)\right)=6144n^2-432n-2912.$

Proof. 

The general formulation of the neighborhood version of the forgotten topological index is given by:

$$\begin{array}{c}\hfill F_N\left(G\right)={\displaystyle \sum _{v\in V\left(G\right)}}{\delta }_G{\left(v\right)}^3.\end{array}$$

(i)

Let G be a regular triangulene silicate network having dimension n. Using vertex partition (5) and Table 5 on the above formula, we have:

$$\begin{array}{ccc}\hfill F_N\left(G\right)& =\hfill & \left(4\right)\left({12}^3\right)+(6n-2)\left({15}^3\right)+\left(n^2\right)\left({18}^3\right)+\left(4\right)\left({24}^3\right)+\hfill \\ \hfill & \hfill & (6n-8)\left({27}^3\right)+\left(\frac{3n^2-9n+6}{2}\right)\left({30}^3\right)\hfill \\ \hfill & =\hfill & \mathrm{46,332}{n}^2+\mathrm{16,848}n+\mathrm{113,994}.\hfill \end{array}$$

(ii)

Let G be a regular triangulene oxide network having dimension n. Using vertex partition (7) and Table 6, the general formula of the $F_N$ index gives the following computation.

$$\begin{array}{ccc}\hfill F_N\left(G\right)& =\hfill & \left(4\right)\left(6^3\right)+(3n-2)\left(8^3\right)+\left(4\right)\left({12}^3\right)+(6n-8)\left({14}^3\right)\hfill \\ \hfill & \hfill & +\left(\frac{3n^2-9n+6}{2}\right)\left({16}^3\right)\hfill \\ \hfill & =\hfill & 6144n^2-432n-2912.\hfill \end{array}$$

Hence the proof. ☐

Theorem 8.

The modified neighborhood version of the forgotten topological index ($F_N^{\ast }$) of the regular triangulene silicate $\left(RTSL\right(n\left)\right)$ and oxide $\left(RTOX\right(n)$)) networks for $n\ge 2$ is given by:

(i) 

$F_N^{\ast }\left(RTSL\left(n\right)\right)=5400n^2+\mathrm{28,278}n-\mathrm{38,394},$

(ii) 

$F_N^{\ast }\left(RTOX\left(n\right)\right)=1536n^2+480n-864.$

Proof. 

The general formula of the modified neighborhood version of the forgotten topological index is given by:

$$\begin{array}{c}\hfill F_N^{\ast }\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2].\end{array}$$

(i)

Let $G\cong RTSL\left(n\right)$. Then, applying edge partition (6) and Table 7 on the definition of the $F_N^{\ast }$ index, we have:

$$\begin{array}{ccc}\hfill F_N^{\ast }\left(G\right)& =\hfill & \left(2\right)({12}^2+{12}^2)+\left(4\right)({12}^2+{15}^2)+\left(4\right)({12}^2+{24}^2)+(3n-2)({15}^2\hfill \\ \hfill & \hfill & +{15}^2)+\left(10\right)({15}^2+{24}^2)+(12n-16)({15}^2+{27}^2)+\left(2\right)({18}^2+\hfill \\ \hfill & \hfill & {24}^2)+(6n-8)({18}^2+{27}^2)+(10n-24)({18}^2+{30}^2)+\left(1\right)({24}^2\hfill \\ \hfill & \hfill & +{24}^2)+\left(6\right)({24}^2+{27}^2)+(6n-7)({27}^2+{27}^2)+(6n-12)({27}^2+\hfill \\ \hfill & \hfill & {30}^2{)+3(n-2)}^2({30}^2+{30}^2).\hfill \end{array}$$

Table 7. Edge partition of regular triangulene silicate networks ($RTSL\left(n\right)$) with dimension n.

${\mathit{E}}_{(\mathit{p},\mathit{q})}$	${\mathit{E}}_{\left(\mathrm{12,12}\right)}$	${\mathit{E}}_{\left(\mathrm{12,15}\right)}$	${\mathit{E}}_{\left(\mathrm{12,24}\right)}$	${\mathit{E}}_{\left(\mathrm{15,15}\right)}$	${\mathit{E}}_{\left(\mathrm{15,24}\right)}$	${\mathit{E}}_{\left(\mathrm{15,27}\right)}$	${\mathit{E}}_{\left(\mathrm{18,24}\right)}$	${\mathit{E}}_{\left(\mathrm{18,27}\right)}$	${\mathit{E}}_{\left(\mathrm{18,30}\right)}$	${\mathit{E}}_{\left(\mathrm{24,24}\right)}$	${\mathit{E}}_{\left(\mathrm{24,27}\right)}$	${\mathit{E}}_{\left(\mathrm{27,27}\right)}$	${\mathit{E}}_{\left(\mathrm{27,30}\right)}$	${\mathit{E}}_{\left(\mathrm{30,30}\right)}$
$|E_{(p,q)}|$	2	4	4	$3n-2$	10	$12n-16$	2	$6n-8$	$10n-24$	1	6	$6n-7$	$6n-12$	$3{(n-2)}^2$

After simplification and arranging the terms, we can get the desired result.

(ii)

Let $G\cong RTOX\left(n\right)$. Now, applying the edge partition (8) and Table 8 on the definition of the $F_N^{\ast }$ index, we have:

$$\begin{array}{ccc}\hfill F_N^{\ast }\left(G\right)& =\hfill & |E_{(6,6)}|(6^2+6^2)+|E_{(6,12)}|(6^2+{12}^2)+\left|E_{(8,12)}\right|(8^2+{12}^2)\hfill \\ \hfill & \hfill & +|E_{(8,14)}|(8^2+{14}^2)+|E_{(12,12)}|({12}^2+{12}^2)+\left|E_{(12,14)}\right|({12}^2+{14}^2)\hfill \\ \hfill & \hfill & +|E_{(14,14)}|({14}^2+{14}^2)+|E_{(14,16)}|({14}^2+{16}^2)+\left|E_{(16,16)}\right|({16}^2+{16}^2)\hfill \\ \hfill & =\hfill & \left(2\right)(6^2+6^2)+\left(4\right)(6^2+{12}^2)+\left(4\right)(8^2+{12}^2)+(6n-8)(8^2+{14}^2)\hfill \\ \hfill & \hfill & \left(1\right)({12}^2+{12}^2)+\left(6\right)({12}^2+{14}^2)+(6n-9)({14}^2+{14}^2)\hfill \\ \hfill & \hfill & +(6n-12)({14}^2+{16}^2)+(3n^2-12n+12)({16}^2+{16}^2)\hfill \\ \hfill & =\hfill & 1536n^2+480n-864.\hfill \end{array}$$

Table 8. Edge partition of regular triangulene oxide networks ($RTOX\left(n\right)$) with dimension n.

${\mathit{E}}_{(\mathit{p},\mathit{q})}$	${\mathit{E}}_{\left(\mathrm{6,6}\right)}$	${\mathit{E}}_{\left(\mathrm{6,12}\right)}$	${\mathit{E}}_{\left(\mathrm{8,12}\right)}$	${\mathit{E}}_{\left(\mathrm{8,14}\right)}$	${\mathit{E}}_{\left(\mathrm{12,12}\right)}$	${\mathit{E}}_{\left(\mathrm{12,14}\right)}$	${\mathit{E}}_{\left(\mathrm{14,14}\right)}$	${\mathit{E}}_{\left(\mathrm{14,16}\right)}$	${\mathit{E}}_{\left(\mathrm{16,16}\right)}$
$|E_{(p,q)}|$	2	4	4	$6n-8$	1	6	$6n-9$	$6n-12$	$3n^2-12n+12$

Hence the theorem. ☐

Theorem 9.

The neighborhood version of the second Zagreb index ($M_2^{\ast }$) of the regular triangulene silicate $\left(RTSL\right(n\left)\right)$ and oxide $\left(RTOX\right(n)$)) networks for $n\ge 2$ is given by:

(i) 

$M_2^{\ast }\left(RTSL\left(n\right)\right)=2700n^2+\mathrm{12,285}n-\mathrm{16,713},$

(ii) 

$M_2^{\ast }\left(RTOX\left(n\right)\right)=768n^2+120n-380.$

Proof. 

The general formula of the neighborhood version of the second Zagreb index is given by:

$$\begin{array}{c}\hfill M_2^{\ast }\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}}\left[{\delta }_G\left(u\right){\delta }_G\left(v\right)\right].\end{array}$$

(i)

Let G be the regular triangulene silicate network having dimension n. Applying the edge partition (6) and Table 7 on the definition of the neighborhood version of the second Zagreb index, we get the desired result as follows.

$$\begin{array}{ccc}\hfill M_2^{\ast }\left(G\right)& =\hfill & 2\left(12.12\right)+4\left(12.15\right)+4\left(12.24\right)+(3n-2)\left(15.15\right)+10\left(15.24\right)\hfill \\ \hfill & \hfill & +(12n-16)\left(15.27\right)+2\left(18.24\right)+(6n-8)\left(18.27\right)+(10n\hfill \\ \hfill & \hfill & -24\left)\right(18.30)+1(24.24)+6(24.27)+(6n-7\left)\right(27.27)\hfill \\ \hfill & \hfill & +(6n-12)\left(27.30\right)+3{(n-2)}^2\left(30.30\right)\hfill \\ \hfill & =\hfill & 2700n^2+\mathrm{12,285}n-\mathrm{16,713}.\hfill \end{array}$$

(ii)

Let G be a regular triangulene oxide network having dimension n. Applying the edge partition (8) and Table 8, on the definition of the neighborhood version of the second Zagreb index, we get the desired result as follows.

$$\begin{array}{ccc}\hfill M_2^{\ast }\left(G\right)& =\hfill & 2\left(6.6\right)+4\left(6.12\right)+4\left(8.12\right)+2(3n-4)\left(8.14\right)+1\left(12.12\right)+6\left(12.14\right)\hfill \\ \hfill & \hfill & +3(2n-3)\left(14.14\right)+6(n-2)\left(14.16\right)+3(n^2-4n+4)\left(16.16\right)\hfill \\ \hfill & =\hfill & 768n^2+120n-380.\hfill \end{array}$$

Hence the proof. ☐

Theorem 10.

The neighborhood version of the hyper Zagreb index ($H{M}_N$) of the regular triangulene silicate $\left(RTSL\right(n\left)\right)$ and oxide $\left(RTOX\right(n)$)) networks for $n\ge 2$ is given by:

(i) 

$H{M}_N\left(RTSL\left(n\right)\right)=\mathrm{10,800}{n}^2+\mathrm{52,848}n-\mathrm{71,820},$

(ii) 

$H{M}_N\left(RTOX\left(n\right)\right)=3072n^2+720n-1624.$

Proof. 

The general formula of the neighborhood version of the hyper Zagreb index is given by:

$$\begin{array}{c}\hfill H{M}_N\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}}{[{\delta }_G\left(u\right)+{\delta }_G\left(v\right)]}^2.\end{array}$$

(i)

Let $G\cong RTSL\left(n\right)$. Now, applying edge partition (6) and Table 7 on the definition of the $H{M}_N$ index, we get the following computation.

$$\begin{array}{ccc}\hfill H{M}_N\left(G\right)& =\hfill & 2{(12+12)}^2+4{(12+15)}^2+4{(12+24)}^2+(3n-2){(15+15)}^2\hfill \\ \hfill & \hfill & +10{(15+24)}^2+(12n-16){(15+27)}^2{+2((18+24)}^2\hfill \\ \hfill & \hfill & +(6n-8){(18+27)}^2+(10n-24){(18+30)}^2+1(24+\hfill \\ \hfill & \hfill & {24)}^2+6{(24+27)}^2+(6n-7){(27+27)}^2+(6n-\hfill \\ \hfill & \hfill & {12)(27+30)}^2+3{(n-2)}^2{(30+30)}^2\hfill \\ \hfill & =\hfill & \mathrm{10,800}{n}^2+\mathrm{52,848}n-\mathrm{71,820}.\hfill \end{array}$$

(ii)

Let $G\cong RTOX\left(n\right)$. Now, applying edge partition (8) and Table 8 on the definition of the $H{M}_N$ index, we get the following computation.

$$\begin{array}{ccc}\hfill H{M}_N\left(G\right)& =\hfill & 2{(6+6)}^2+4{(6+12)}^2+4{(8+12)}^2+(6n-8){(8+14)}^2\hfill \\ \hfill & \hfill & +1{(12+12)}^2+6{(12+14)}^2+(6n-12){(14+16)}^2\hfill \\ \hfill & \hfill & +(3n^2-12n+12){(16+16)}^2\hfill \\ \hfill & =\hfill & 3072n^2+720n-1624.\hfill \end{array}$$

Hence the theorem. ☐

Five topological indices for $RTSL\left(n\right)$ and $RTOX\left(n\right)$ are shown graphically in the Figure 9.

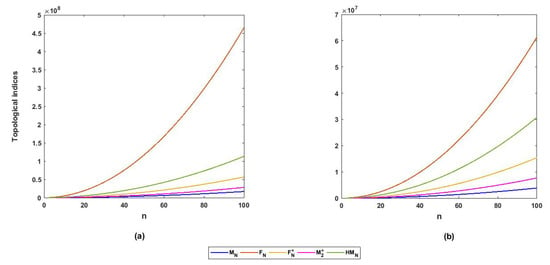
Figure 9. Different topological indices for regular triangulene (a) silicate and (b) oxide networks.

3.3. Rhombus Silicate ($RHSL\left(n\right)$) and Oxide ($RHOX\left(n\right)$) Networks

In this subsection, we obtain the five aforementioned indices for rhombus silicate ($RHSL\left(n\right)$) and oxide ($RHOX\left(n\right)$) networks. The structures of $RHSL\left(3\right)$ and $RHOX\left(3\right)$ are shown in Figure 10 and Figure 11, respectively. For a rhombus silicate network ($RHSL\left(n\right)$) having dimension n, the number of nodes and edges is $5n^2+2n$ and $12n^2$, respectively [21]. For a rhombus oxide network ($RHOX\left(n\right)$) having dimension n, the number of nodes and edges is $3n^2+2n$ and $6n^2$, respectively [21,26]. The vertex and edge partitions of the rhombus silicate network are as follows.

$$V\left(RHSL\left(n\right)\right)=V_{12}\cup V_{15}\cup V_{18}\cup V_{24}\cup V_{27}\cup V_{30},$$

(9)

$$\begin{array}{c}E\left(RHSL\left(n\right)\right)=E_{(12,12)}\cup E_{(12,24)}\cup E_{(15,24)}\cup E_{(18,24)}\cup E_{(24,27)}\cup E_{(15,15)}\cup E_{(18,27)}\\ \cup E_{(27,27)}\cup E_{(15,27)}\cup E_{(27,30)}\cup E_{(18,30)}\cup E_{(30,30)}.\end{array}$$

(10)

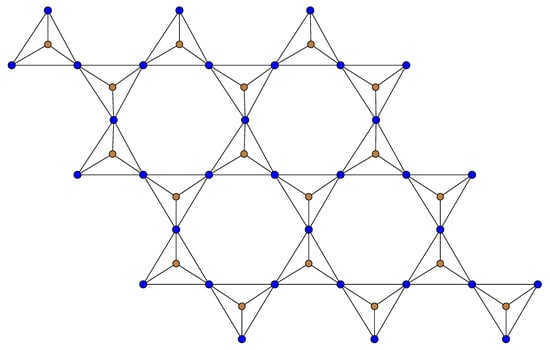
Figure 10. Rhombus-type silicate network ($RHSL\left(3\right)$).

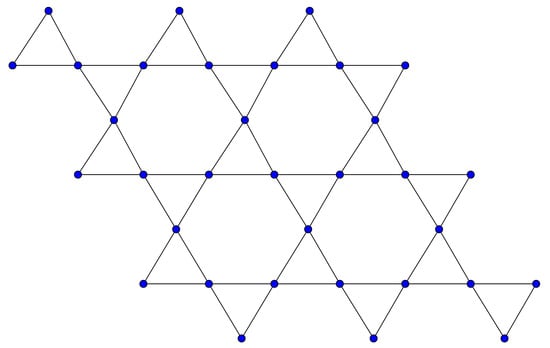
Figure 11. Rhombus-type oxide network ($RHOX\left(3\right)$).

The vertex and edge partitions of the rhombus oxide network are as follows.

$$V\left(RHOX\left(n\right)\right)=V_6\cup V_8\cup V_{12}\cup V_{14}\cup V_{16},$$

(11)

$$E\left(RHOX\left(n\right)\right)=E_{(6,6)}\cup E_{(6,12)}\cup E_{(8,12)}\cup E_{(8,14)}\cup E_{(12,14)}\cup E_{(14,14)}\cup E_{(14,16)}\cup E_{(16,16)}.$$

(12)

Theorem 11.

The neighborhood Zagreb index ($M_N$) of the rhombus silicate $\left(RHSL\right(n\left)\right)$ and oxide $\left(RHOX\right(n)$)) networks for $n\ge 2$ is given by:

(i) 

$M_N\left(RHSL\left(n\right)\right)=1548n^2+3636n-4932,$

(ii) 

$M_N\left(RHOX\left(n\right)\right)=768n^2-736n+2048.$

Proof. 

(i)

Let $G\cong RHSL\left(n\right)$. Now, applying vertex partition (9) and Table 9 on the definition of the neighborhood Zagreb index, we obtain:

$$\begin{array}{ccc}\hfill M_N\left(G\right)& =\hfill & |V_{12}|\left({12}^2\right)+|V_{15}|\left({15}^2\right)+|V_{18}|\left({18}^2\right)+|V_{24}|\left({24}^2\right)+|V_{27}|\left({27}^2\right)+\left|V_{30}\right|\left({30}^2\right)\hfill \\ \hfill & =\hfill & 6\left({12}^2\right)+8(n-1)\left({15}^2\right)+2{(n-1)}^2\left({18}^2\right)+\left(4\right)\left({24}^2\right)\hfill \\ \hfill & \hfill & +(8n-12)\left({27}^2\right)+(n-2)(n-1)\left({30}^2\right)\hfill \\ \hfill & =\hfill & 768n^2-736n+2048.\hfill \end{array}$$

Table 9. Vertex partition of rhombus silicate networks ($RHSL\left(n\right)$) with dimension n.

${\mathit{V}}_{\mathit{i}}$	${\mathit{V}}_{12}$	${\mathit{V}}_{15}$	${\mathit{V}}_{18}$	${\mathit{V}}_{24}$	${\mathit{V}}_{27}$	${\mathit{V}}_{30}$
$|V_i|$	6	$8(n-1)$	$2{(n-1)}^2$	4	$8n-12$	$(n-2)(n-1)$

(ii)

Let $G\cong RHOX\left(n\right)$. Now, using vertex partition (11) and Table 10 on the definition of the neighborhood Zagreb index, we obtain:

$$\begin{array}{ccc}\hfill M_N\left(G\right)& =\hfill & |V_6|\left(6^2\right)+|V_8|\left(8^2\right)+|V_{12}|\left({12}^2\right)+|V_{14}|\left({14}^2\right)+\left|V_{16}\right|\left({16}^2\right)\hfill \\ \hfill & =\hfill & 4\left(6^2\right)+4(n-1)\left(8^2\right)+4\left({12}^2\right)+(8n-12)\left({14}^2\right)\hfill \\ \hfill & \hfill & +(3n^2-10n+8)\left({16}^2\right).\hfill \end{array}$$

Table 10. Vertex partition of rhombus oxide networks ($RHOX\left(n\right)$) with dimension n.

${\mathit{V}}_{\mathit{i}}$	${\mathit{V}}_6$	${\mathit{V}}_8$	${\mathit{V}}_{12}$	${\mathit{V}}_{14}$	${\mathit{V}}_{16}$
$|V_i|$	4	$4(n-1)$	4	$8n-12$	$3n^2-10n+8$

After simplifying and arranging the terms, the required result can be obtained easily.

Hence the proof. ☐

Theorem 12.

The neighborhood version of the forgotten topological index ($F_N$) of the rhombus silicate $\left(RHSL\right(n\left)\right)$ and oxide $\left(RHOX\right(n)$)) networks for $n\ge 2$ is given by:

(i) 

$F_N\left(RHSL\left(n\right)\right)=\mathrm{38,664}{n}^2+\mathrm{80,136}n-\mathrm{131,868},$

(ii) 

$F_N\left(RHOX\left(n\right)\right)=\mathrm{12,288}{n}^2-\mathrm{16,960}n+5568.$

Proof. 

(i)

Let $G\cong RHSL\left(n\right)$. Using vertex partition (9) and Table 9 on the above formula, we have:

$$\begin{array}{ccc}\hfill F_N\left(G\right)& =\hfill & 6\left({12}^3\right)+8(n-1)\left({15}^3\right)+2{(n-1)}^2\left({18}^3\right)+\left(4\right)\left({24}^3\right)\hfill \\ \hfill & \hfill & +(8n-12)\left({27}^3\right)+(n-2)(n-1)\left({30}^3\right).\hfill \end{array}$$

After simplification and arranging the terms, the required result is obtained.

(ii)

Let $G\cong RHOX\left(n\right)$. Using vertex partition (11) and Table 10, the general formula of the $F_N$ index gives the following computation.

$$\begin{array}{ccc}\hfill F_N\left(G\right)& =\hfill & 4\left(6^3\right)+4(n-1)\left(8^3\right)+4\left({12}^3\right)+(8n-12)\left({14}^3\right)\hfill \\ \hfill & \hfill & +(3n^2-10n+8)\left({16}^3\right).\hfill \\ \hfill & =\hfill & 768n^2-736n+2048.\hfill \end{array}$$

Hence the proof. ☐

Theorem 13.

The modified neighborhood version of the forgotten topological index ($F_N^{\ast }$) of the rhombus silicate $\left(RHSL\right(n\left)\right)$ and oxide $\left(RHOX\right(n)$)) networks for $n\ge 2$ is given by:

(i) 

$F_N^{\ast }\left(RHSL\left(n\right)\right)=\mathrm{18,144}{n}^2-\mathrm{17,496}n+5472,$

(ii) 

$F_N^{\ast }\left(RHOX\left(n\right)\right)=3072n^2-3456n+712.$

Proof. 

The general formula of the modified neighborhood version of the forgotten topological index is given by:

$$\begin{array}{c}\hfill F_N^{\ast }\left(G\right)={\displaystyle \sum _{uv\in E\left(G\right)}}[{\delta }_G{\left(u\right)}^2+{\delta }_G{\left(v\right)}^2].\end{array}$$

(i)

Let $G\cong RHSL\left(n\right)$. Then, applying vertex partition (10) and Table 11 on the definition of the $F_N^{\ast }$ index, we have:

$$\begin{array}{ccc}\hfill F_N^{\ast }\left(G\right)& =\hfill & 6({12}^2+{12}^2)+6({12}^2+{24}^2)+8({15}^2+{24}^2)+2({18}^2+{24}^2)\hfill \\ \hfill & \hfill & +8({24}^2+{27}^2)+4(n-1)({15}^2+{15}^2)+4(2n-3)({18}^2+{27}^2)\hfill \\ \hfill & \hfill & +8(n-2)+2({27}^2+{27}^2)+8(2n-3)({15}^2+{27}^2)\hfill \\ \hfill & \hfill & +8(n-2)({27}^2+{30}^2)+2(n-2)(3n-4)({18}^2+{30}^2)\hfill \\ \hfill & \hfill & +6{(n-2)}^2({30}^2+{30}^2)\hfill \\ \hfill & =\hfill & \mathrm{18,144}{n}^2-\mathrm{17,496}n+5472.\hfill \end{array}$$

Table 11. Edge partition of rhombus silicate networks ($RHSL\left(n\right)$) with dimension n.

${\mathit{E}}_{(\mathit{p},\mathit{q})}$	${\mathit{E}}_{\left(\mathrm{12,12}\right)}$	${\mathit{E}}_{\left(\mathrm{12,24}\right)}$	${\mathit{E}}_{\left(\mathrm{15,24}\right)}$	${\mathit{E}}_{\left(\mathrm{15,27}\right)}$	${\mathit{E}}_{\left(\mathrm{18,24}\right)}$	${\mathit{E}}_{\left(\mathrm{18,27}\right)}$	${\mathit{E}}_{\left(\mathrm{24,27}\right)}$	${\mathit{E}}_{\left(\mathrm{15,15}\right)}$	${\mathit{E}}_{\left(\mathrm{27,27}\right)}$	${\mathit{E}}_{\left(\mathrm{27,30}\right)}$	${\mathit{E}}_{\left(\mathrm{18,30}\right)}$	${\mathit{E}}_{\left(\mathrm{30,30}\right)}$
$|E_{(p,q)}|$	6	6	8	$8(2n-3)$	2	$4(2n-3)$	8	$4(n-1)$	$8(n-2)+2$	$8(n-2)$	$2(n-2)(3n-4)$	$6{(n-2)}^2$

(ii)

Let $G\cong RHOX\left(n\right)$. Now, applying the vertex partition (12) and the Table 12 on the definition of the $F_N^{\ast }$ index, we have:

$$\begin{array}{ccc}\hfill F_N^{\ast }\left(G\right)& =\hfill & 2(6^2+6^2)+4(6^2+{12}^2)+4(8^2+{12}^2)+4(2n-3)(8^2+{14}^2)\hfill \\ \hfill & \hfill & +8({12}^2+{14}^2)+2(4n-7)({14}^2+{14}^2)+8(n-2)({14}^2+{16}^2)\hfill \\ \hfill & \hfill & +6{(n-2)}^2({16}^2+{16}^2)\hfill \\ \hfill & =\hfill & 3072n^2-3456n+712.\hfill \end{array}$$

Table 12. Edge partition of rhombus oxide networks ($RHOX\left(n\right)$) with dimension n.

${\mathit{E}}_{(\mathit{p},\mathit{q})}$	${\mathit{E}}_{\left(\mathrm{6,6}\right)}$	${\mathit{E}}_{\left(\mathrm{6,12}\right)}$	${\mathit{E}}_{\left(\mathrm{8,12}\right)}$	${\mathit{E}}_{\left(\mathrm{8,14}\right)}$	${\mathit{E}}_{\left(\mathrm{12,14}\right)}$	${\mathit{E}}_{\left(\mathrm{14,14}\right)}$	${\mathit{E}}_{\left(\mathrm{14,16}\right)}$	${\mathit{E}}_{\left(\mathrm{16,16}\right)}$
$|E_{(p,q)}|$	2	4	4	$4(2n-3)$	8	$2(4n-7)$	$8(n-2)$	$6{(n-2)}^2$

Hence the theorem. ☐

Theorem 14.

The neighborhood versions of the second Zagreb index ($M_2^{\ast }$) of the rhombus silicate $\left(RHSL\right(n\left)\right)$ and oxide $\left(RHOX\right(n)$)) networks for $n\ge 2$ are given by:

(i) 

$M_2^{\ast }\left(RHSL\left(n\right)\right)=8640n^2-8820n+2142,$

(ii) 

$M_2^{\ast }\left(RHOX\left(n\right)\right)=1536n^2-1888n-784.$

Proof. 

(i)

Let G be the rhombus-type silicate network having dimension n. Applying the edge partition (10) and Table 11,on the definition of the neighborhood version of the second Zagreb index, we get the desired result as follows.

$$\begin{array}{ccc}\hfill M_2^{\ast }\left(G\right)& =& 6\left(12.12\right)+6\left(12.24\right)+8\left(15.24\right)+2\left(18.24\right)+8\left(24.27\right)+4(n-1)\left(15.15\right)\hfill \\ \hfill & \hfill & +4(2n-3)\left(18.27\right)+\left(\right(n-2)+2)\left(27.27\right)+8(2n-3)\left(15.27\right)\hfill \\ \hfill & \hfill & +8(n-2)\left(27.30\right)+2(n-2)(3n-4)\left(18.30\right)+6{(n-2)}^2\left(30.30\right)\hfill \\ \hfill & \hfill =& 8640n^2-8820n+2142.\hfill \end{array}$$

(ii)

Let G be the rhombus-type oxide network having dimension n. Applying the edge partition (12) and Table 12 on the definition of the neighborhood version of the second Zagreb index, we get the desired result as follows.

$$\begin{array}{ccc}\hfill M_2^{\ast }\left(G\right)& =& 2\left(6.6\right)+4\left(6.12\right)+4\left(8.12\right)+4(2n-3)\left(8.14\right)\hfill \\ \hfill & \hfill & +8\left(12.14\right)+2(4n-7)\left(14.14\right)+8(n-2)\left(14.16\right)+6{(n-2)}^2\left(16.16\right)\hfill \\ \hfill & \hfill =& 1536n^2-1888n-784.\hfill \end{array}$$

 ☐

Theorem 15.

The neighborhood versions of the hyper Zagreb index ($H{M}_N$) of the rhombus silicate $\left(RHSL\right(n\left)\right)$ and oxide $\left(RHOX\right(n)$)) networks for $n\ge 2$ are given by:

(i) 

$H{M}_N\left(RHSL\left(n\right)\right)=\mathrm{35,424}{n}^2-\mathrm{35,136}n+7956,$

(ii) 

$H{M}_N\left(RHOX\left(n\right)\right)=6144n^2-7232n+1984.$

Proof. 

(i)

Let $G\cong RHSL\left(n\right)$. Now, applying edge partition (10) and Table 11, on the definition of the $H{M}_N$ index, we get the following computation.

$$\begin{array}{ccc}\hfill H{M}_N\left(G\right)& =\hfill & 6{(12+12)}^2+6{(12+24)}^2+(4n-4){(15+15)}^2+8{(15+24)}^2\hfill \\ \hfill & \hfill & +(16n-24){(15+27)}^2+2{(18+24)}^2+(8n-12){(18+27)}^2\hfill \\ \hfill & \hfill & +2(n-2)(3n-4){(18+30)}^2+(8n-14){(27+27)}^2\hfill \\ \hfill & \hfill & +(8n-16){(27+30)}^2+6{(n-2)}^2{(30+30)}^2\hfill \\ \hfill & =\hfill & \mathrm{35,424}{n}^2-\mathrm{35,136}n+7956.\hfill \end{array}$$

(ii)

Let $G\cong RHOX\left(n\right)$. Now, applying edge partition (12) and Table 12 on the definition of the $H{M}_N$ index, we get the following computation.

$$\begin{array}{ccc}\hfill H{M}_N\left(G\right)& =\hfill & 2{(6+6)}^2+4{(6+12)}^2+4{(8+12)}^2+(8n-12){(8+14)}^2\hfill \\ \hfill & \hfill & +8{(12+14)}^2+(8n-14){(14+14)}^2+(8n-16){(14+16)}^2\hfill \\ \hfill & \hfill & +6{(n-2)}^2{(16+16)}^2\hfill \\ \hfill & =\hfill & 6144n^2-7232n+1984.\hfill \end{array}$$

Hence the theorem. ☐

The five topological indices for $RHSL\left(n\right)$ and $RHOX\left(n\right)$ are shown graphically in Figure 12.

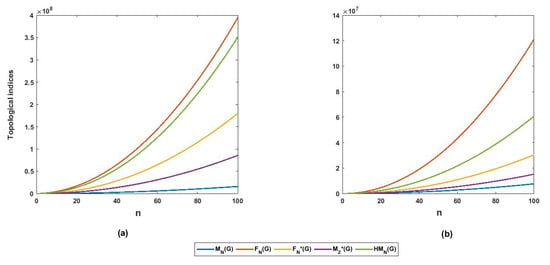
Figure 12. Different topological indices for rhombus-type (a) silicate and (b) oxide network.

3.4. Copper (II) Oxide

We obtain topological indices for copper (II) oxide ($CuO$) here. Its molecular graph is depicted in Figure 13. In the $CuO$ structure, the octagons are linked to each other in columns and rows. The connection between two octagons is achieved by creating one $C_4$ bond between two octagons. It contains $4mn+3n+m$ nodes and $6mn+2n$ edges, where m and n represent the number of octagons in rows and columns, respectively [22]. The vertex and edge partitions of the copper oxide network are as follows.

$$V\left(CuO\right)=V_4\cup V_5\cup V_6\cup V_{10}\cup V_{12},$$

(13)

$$E\left(CuO\right)=E_{(4,4)}\cup E_{(4,5)}\cup E_{(4,6)}\cup E_{(5,6)}\cup E_{(6,6)}\cup E_{(6,10)}\cup E_{(10,10)}\cup E_{(10,12)}.$$

(14)

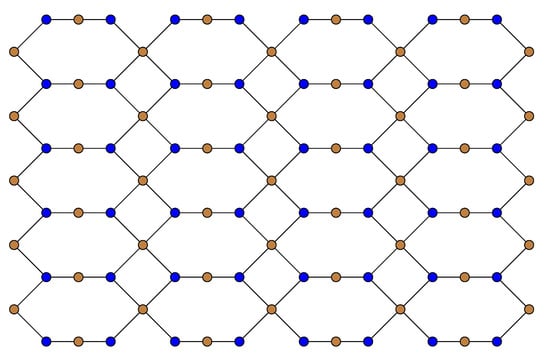
Figure 13. Copper oxide ($CuO$) network with five rows and four columns.

Theorem 16.

The neighborhood Zagreb index ($M_N$) of copper oxide ($CuO$) for $m,n>2$ is given by:

$$\begin{array}{c}\hfill M_N\left(CuO\right)=380mn-200m-148n+92.\end{array}$$

Proof. 

The general formula of the neighborhood Zagreb index is given by:

$$\begin{array}{c}\hfill M_N\left(G\right)={\displaystyle \sum _{v\in V\left(G\right)}}{\delta }_G{\left(v\right)}^2.\end{array}$$

Let G be a copper oxide network having m rows and n columns. Now, applying vertex partition (13) and Table 13 on the definition of the neighborhood Zagreb index, we get:

$$\begin{array}{ccc}\hfill M_N\left(G\right)& =& |V_4|\left(4^2\right)+|V_5|\left(5^2\right)+|V_6|\left(6^2\right)+|V_{10}|\left({10}^2\right)+\left|V_{12}\right|\left({12}^2\right)\hfill \\ \hfill & \hfill =& (2n+4)\left(4^2\right)+4\left(5^2\right)+(mn+4m+3n-10)\left(6^2\right)+(2mn-2m)\left({10}^2\right)\hfill \\ \hfill & \hfill & +(mn-m-2n+2)\left({12}^2\right)\hfill \\ \hfill & \hfill =& 380mn-200m-148n+92.\hfill \end{array}$$

Table 13. Vertex partition of copper oxide ($CuO$) with m rows and n columns.

${\mathit{V}}_{\mathit{i}}$	${\mathit{V}}_4$	${\mathit{V}}_5$	${\mathit{V}}_6$	${\mathit{V}}_{10}$	${\mathit{V}}_{12}$
$|V_i|$	$2n+4$	4	$mn+4m+3n-10$	$2mn-2m$	$mn-m-2n+2$

Hence the proof. ☐

Theorem 17.

The neighborhood version of the forgotten topological index ($F_N$) of copper oxide ($CuO$) for $m,n>2$ is given by:

$$\begin{array}{c}\hfill F_N\left(CuO\right)=3944mn-2864m-2680n+2052.\end{array}$$

Proof. 

Applying vertex partition (13) and Table 13 on the definition of the neighborhood version of the forgotten topological index, the required result can be obtained easily like the previous proof. ☐

Theorem 18.

The modified neighborhood version of the forgotten topological index ($F_N^{\ast }$) of copper oxide ($CuO$) for $m,n>2$ is given by:

$$\begin{array}{c}\hfill F_N^{\ast }\left(CuO\right)=1248mn-816m-672n+508.\end{array}$$

Proof. 

Let G be a copper oxide network with m rows and n columns. Now, by the edge partition (14) and Table 14, we have from the general formulation of $F_N^{\ast }$ the following.

$$\begin{array}{ccc}\hfill F_N^{\ast }\left(G\right)& \hfill =& |E_{\left(\mathrm{4,4}\right)}|(4^2+4^2)+|E_{\left(\mathrm{4,5}\right)}|(4^2+5^2)+|E_{\left(\mathrm{4,6}\right)}|(4^2+6^2)+|E_{\left(\mathrm{5,6}\right)}\left|\right(5^2\hfill \\ \hfill & \hfill & +6^2)+|E_{\left(\mathrm{6,6}\right)}|(6^2+6^2)+\left|E_{(6,10)}\right|(6^2+{10}^2)\hfill \\ \hfill & \hfill & +|E_{\left(\mathrm{10,10}\right)}|({10}^2+{10}^2)+\left|E_{(10,12)}\right|({10}^2+{12}^2)\hfill \\ \hfill & \hfill =& \left(4\right)(4^2+4^2)+\left(4\right)(4^2+5^2)+(4n-4)(4^2+6^2)+\left(4\right)(5^2+6^2)\hfill \\ \hfill & \hfill & +(6m-10)(6^2+6^2)+(2mn-2m+2n-2)(6^2+{10}^2)\hfill \\ \hfill & \hfill & +(4n-4)({10}^2+{10}^2)+(4mn-4m-8n+8)({10}^2+{12}^2).\hfill \end{array}$$

Table 14. Edge partition of copper oxide ($CuO$) with m rows and n columns.

${\mathit{E}}_{(\mathit{p},\mathit{q})}$	${\mathit{E}}_{\left(\mathrm{4,4}\right)}$	${\mathit{E}}_{\left(\mathrm{4,5}\right)}$	${\mathit{E}}_{\left(\mathrm{4,6}\right)}$	${\mathit{E}}_{\left(\mathrm{5,6}\right)}$	${\mathit{E}}_{\left(\mathrm{6,6}\right)}$	${\mathit{E}}_{\left(\mathrm{6,10}\right)}$	${\mathit{E}}_{\left(\mathrm{10,10}\right)}$	${\mathit{E}}_{\left(\mathrm{10,12}\right)}$
$|E_{(p,q)}|$	4	4	$4n-4$	4	$6m-10$	$2mn-2m+2n-2$	$4n-4$	$4mn-4m-8n+8$

The required result is obvious after simplification. ☐

Theorem 19.

The neighborhood version of the second Zagreb index ($M_2^{\ast }$) of copper oxide ($CuO$) for $m,n>2$ is given by:

$$\begin{array}{c}\hfill M_2^{\ast }\left(CuO\right)=600mn-384m-344n+248.\end{array}$$

Proof. 

Applying edge partition (14) and Table 14 on the the general formula of the $M_2^{\ast }$ index, the required result can be obtained easily like the previous proof. ☐

Theorem 20.

The neighborhood version of the hyper Zagreb index ($H{M}_N$) of copper oxide ($CuO$) for $m,n>2$ is given by:

$$\begin{array}{c}\hfill H{M}_N\left(CuO\right)=2448mn-1584m-1360n+984.\end{array}$$

Proof. 

Applying edge partition (14) and Table 14 on the the general formula of the $M_2^{\ast }$ index, the required result follows in the same way as before. ☐

The five topological indices for $CuO$ are depicted graphically in Figure 14, Figure 15 and Figure 16.

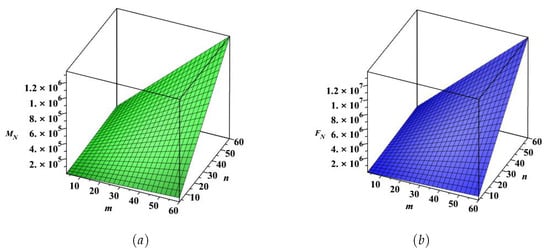
Figure 14. (a) The $M_N$ index and (b) the $F_N$ index of the copper oxide network.

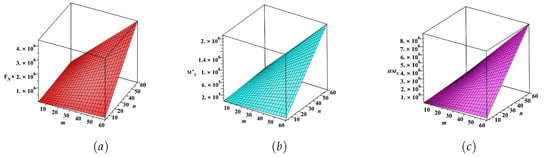
Figure 15. (a) The $F_N^{\ast }$ index, (b) the $M_2^{\ast }$ index, and (c) the $H{M}_N$ index of the copper oxide network.

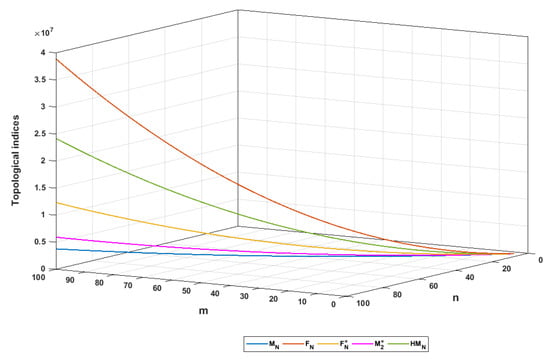
Figure 16. Different topological indices for the copper oxide network.

4. Remarks and Conclusions

In this work, we derived some explicit expressions of five topological indices, namely the neighborhood Zagreb index ($M_N$), the neighborhood version of the forgotten topological index ($F_N$), the modified neighborhood version of the forgotten topological index ($F_N^{\ast }$), the neighborhood version of the second Zagreb index ($M_2^{\ast }$), and the neighborhood version of the hyper Zagreb index ($H{M}_N$), for dominating silicate ($DSL\left(n\right)$) and oxide ($DOX\left(n\right)$) networks, regular triangulene silicate ($RTSL\left(n\right)$) and oxide ($RTOX\left(n\right)$) networks, rhombus-shaped silicate ($RHSL\left(n\right)$) and oxide ($RHOX\left(n\right)$) networks, and the copper oxide ($CuO$) network. Furthermore, we made a comparison graphically among all indices for the above-mentioned networks. The comparison was made in Figure 6, Figure 9, Figure 12, and Figure 16. The aforementioned indices were very close at the initial stage of the given domain and then grew. Among the five topological indices, the neighborhood version of the forgotten topological index ($F_N$) had the most dominating power in comparison with the other indices. The neighborhood Zagreb index $\left(M_N\right)$ grew more slowly than the other indices. The nature of the neighborhood version of the second Zagreb index ($M_2^{\ast }$) was close to the $F_N$ index. In comparison to other networks, the $H{M}_N$ index was close to the $F_N$ index in $RTSL\left(n\right)$. In $RTSL\left(n\right)$, the gap between the $F_n$ and $H{M}_N$ indices was more than the other networks. From the vertical axis, it was clear that the indices for different networks grew in the following order:

$$\begin{array}{c}\hfill CuO<RTOX\left(n\right)<RHOX\left(n\right)<RHSL\left(n\right)<RTSL\left(n\right)<DOX\left(n\right)<DSL\left(n\right),\end{array}$$

where in each case, the indices had the following order:

$$\begin{array}{c}\hfill M_N<M_2^{\ast }<F_N^{\ast }<H{M}_N<F_N,\end{array}$$

i.e., all the indices behaved differently in each network discussed above. This work will help researchers working in network science understand the topology of the aforementioned networks. In the future, we would like to obtain these indices for some other chemical networks, trees, dendrimers, etc.