CFD Simulation of the Interaction Between a Macrobubble and a Dilute Dispersion of Oil Droplets in Quiescent Water
Abstract
1. Introduction
2. CFD Model Formulation
2.1. Governing Equations
2.2. Volume of Fluid Model
2.3. Discrete Phase Model
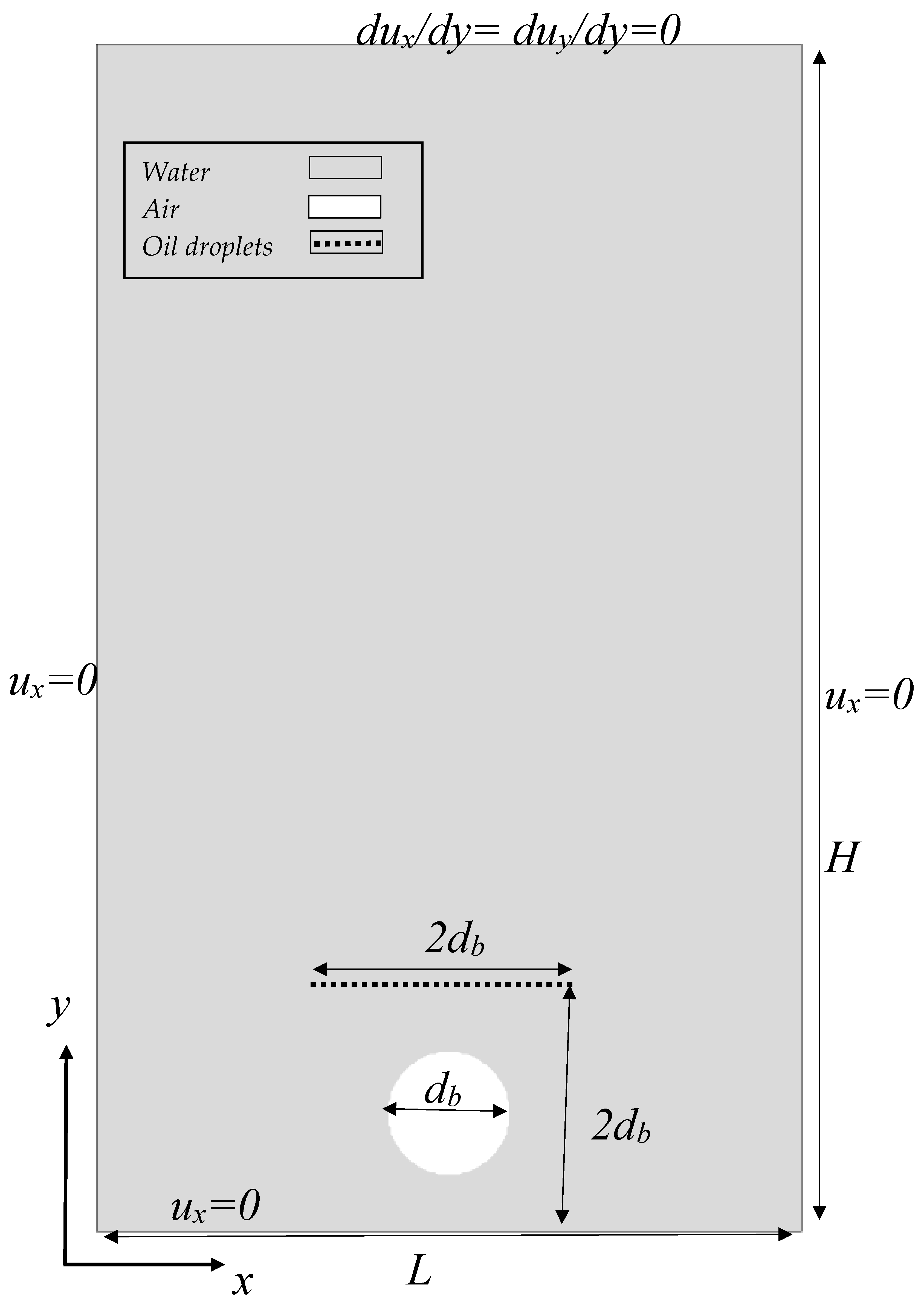
3. Numerical Solution
4. Results and Discussion
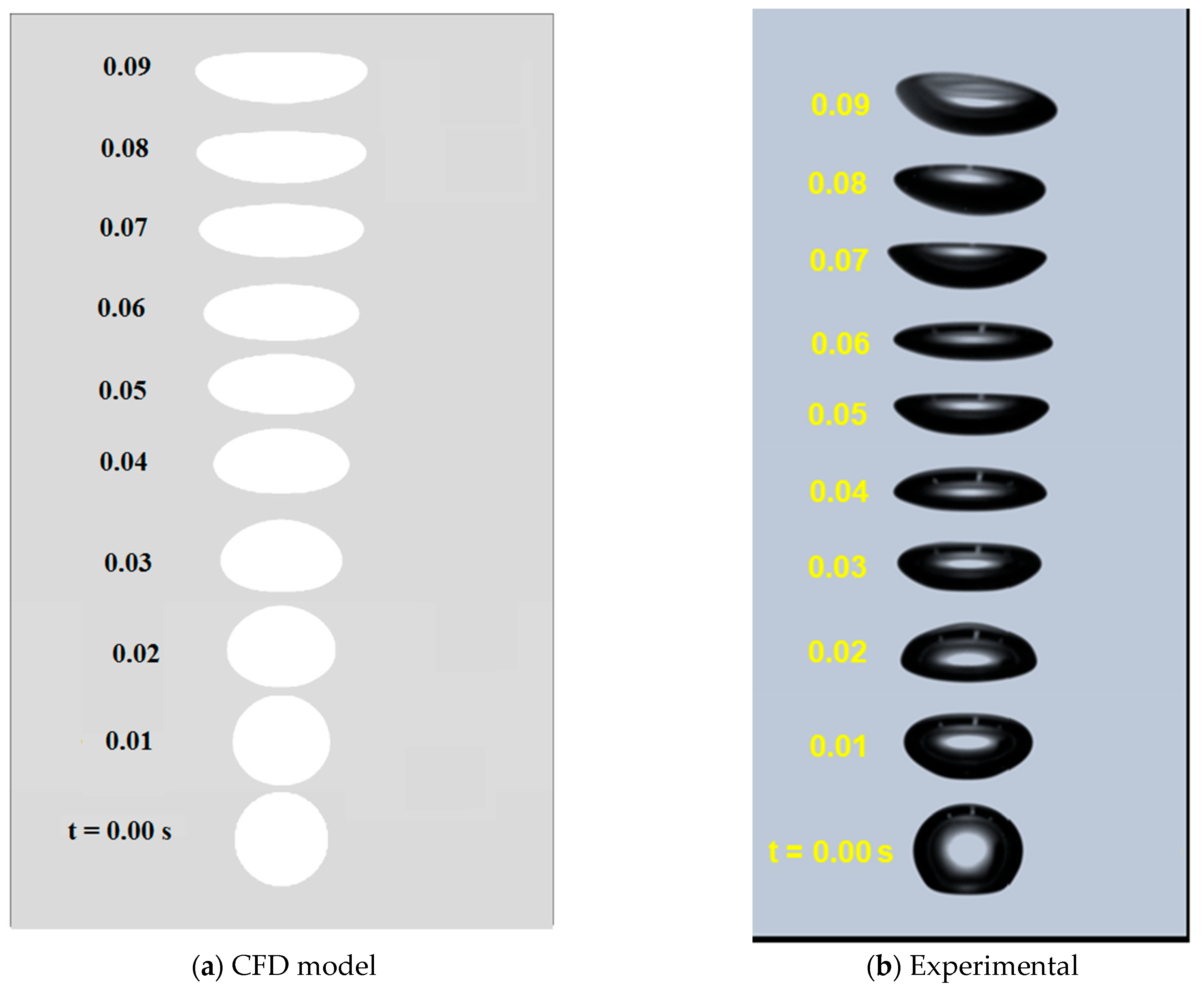
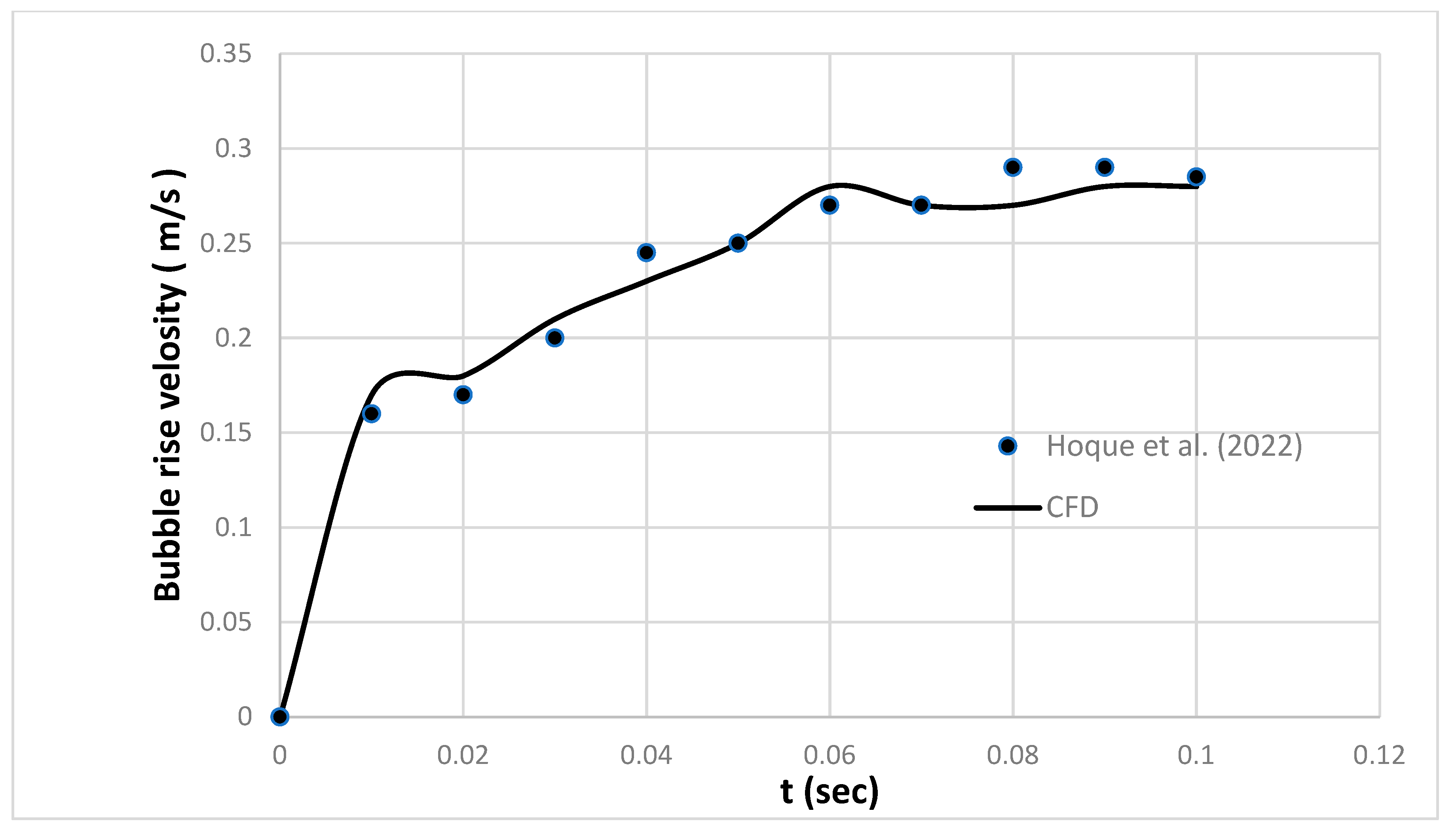
4.1. Model Validation
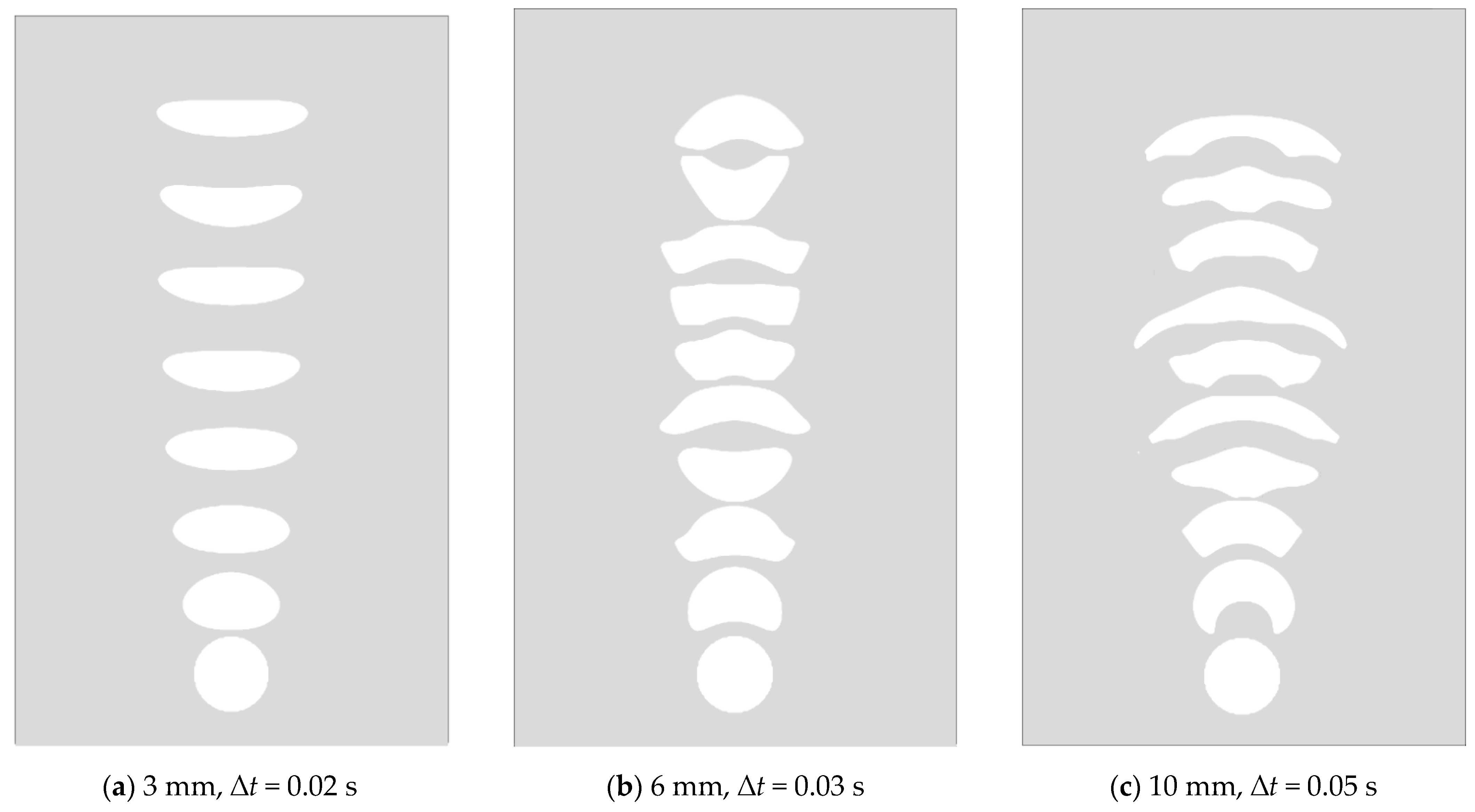
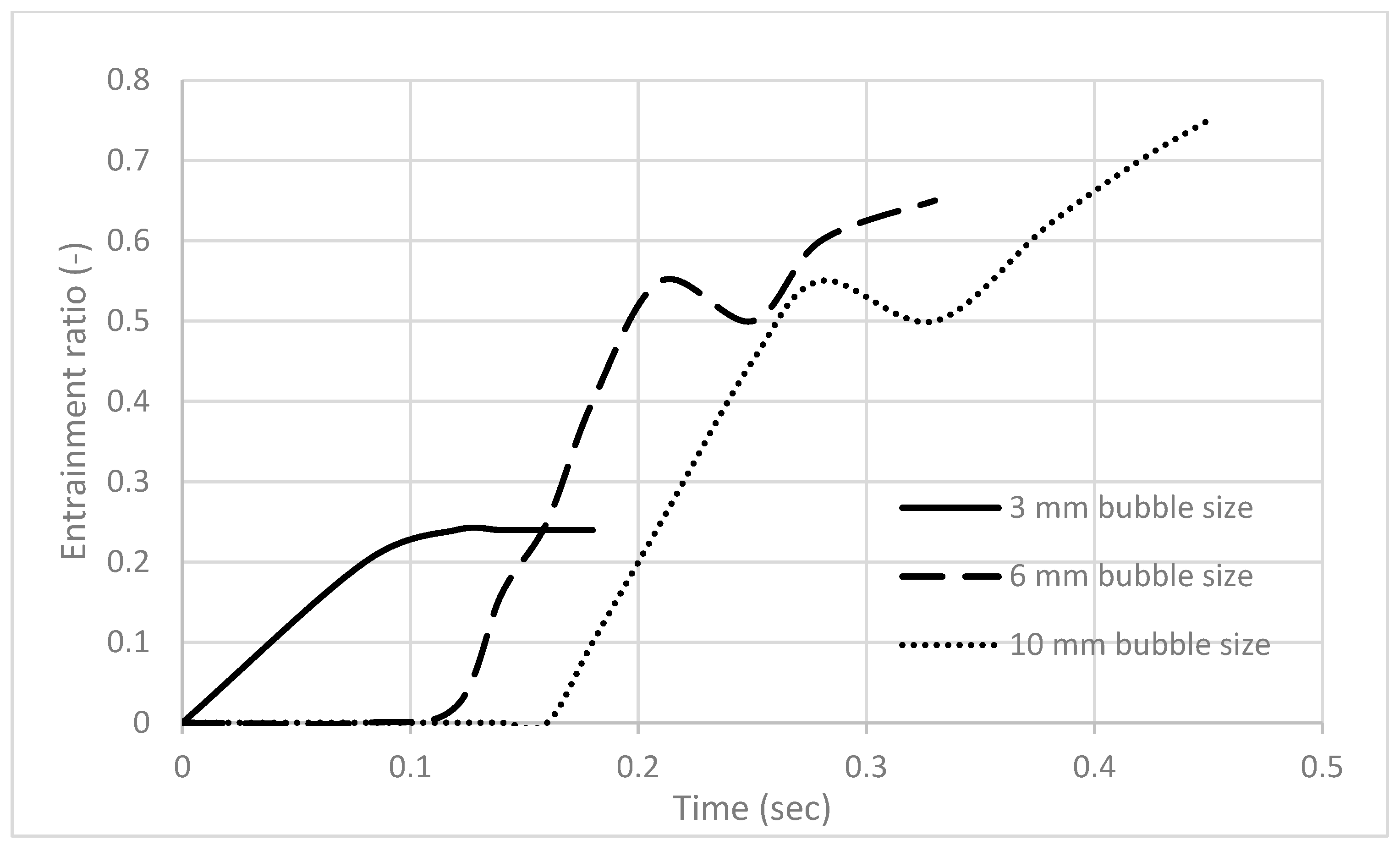
4.2. Bubble Dynamics
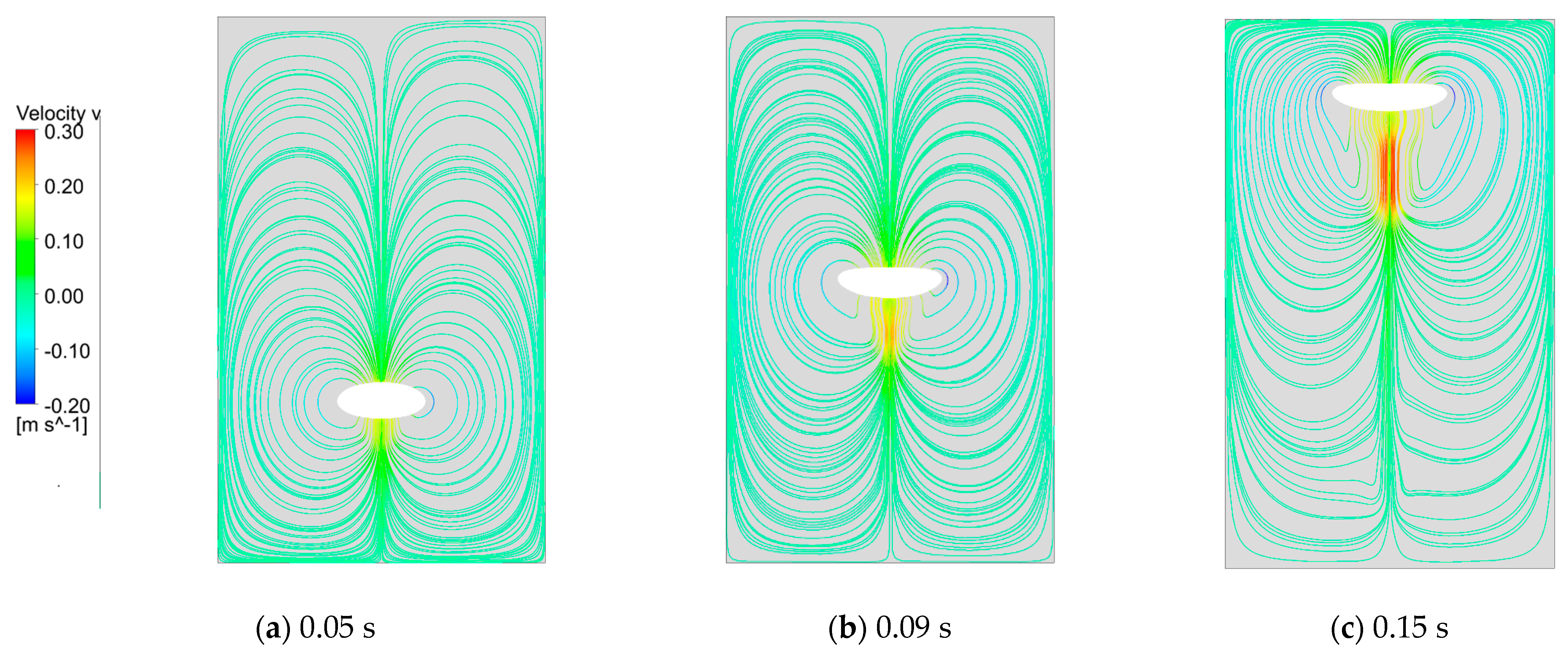
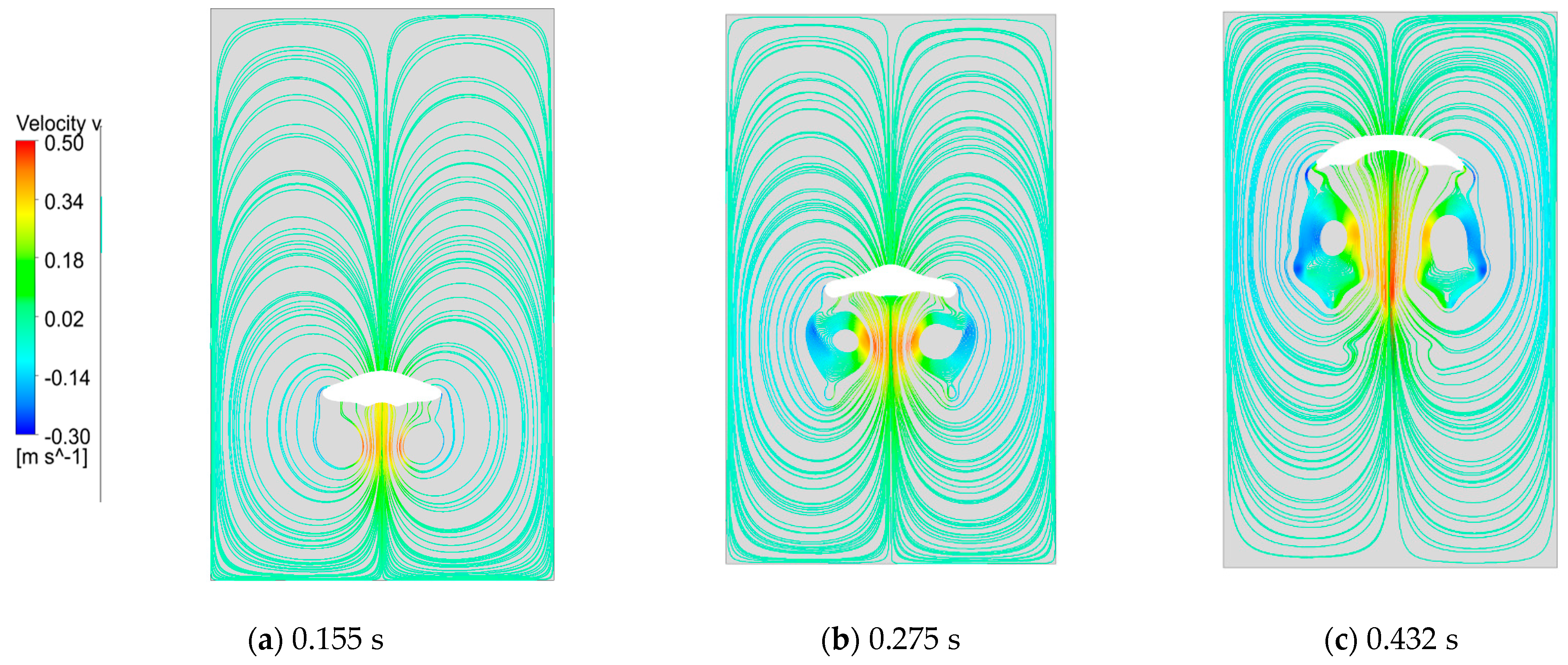
4.3. Hydrodynamic Flow Field
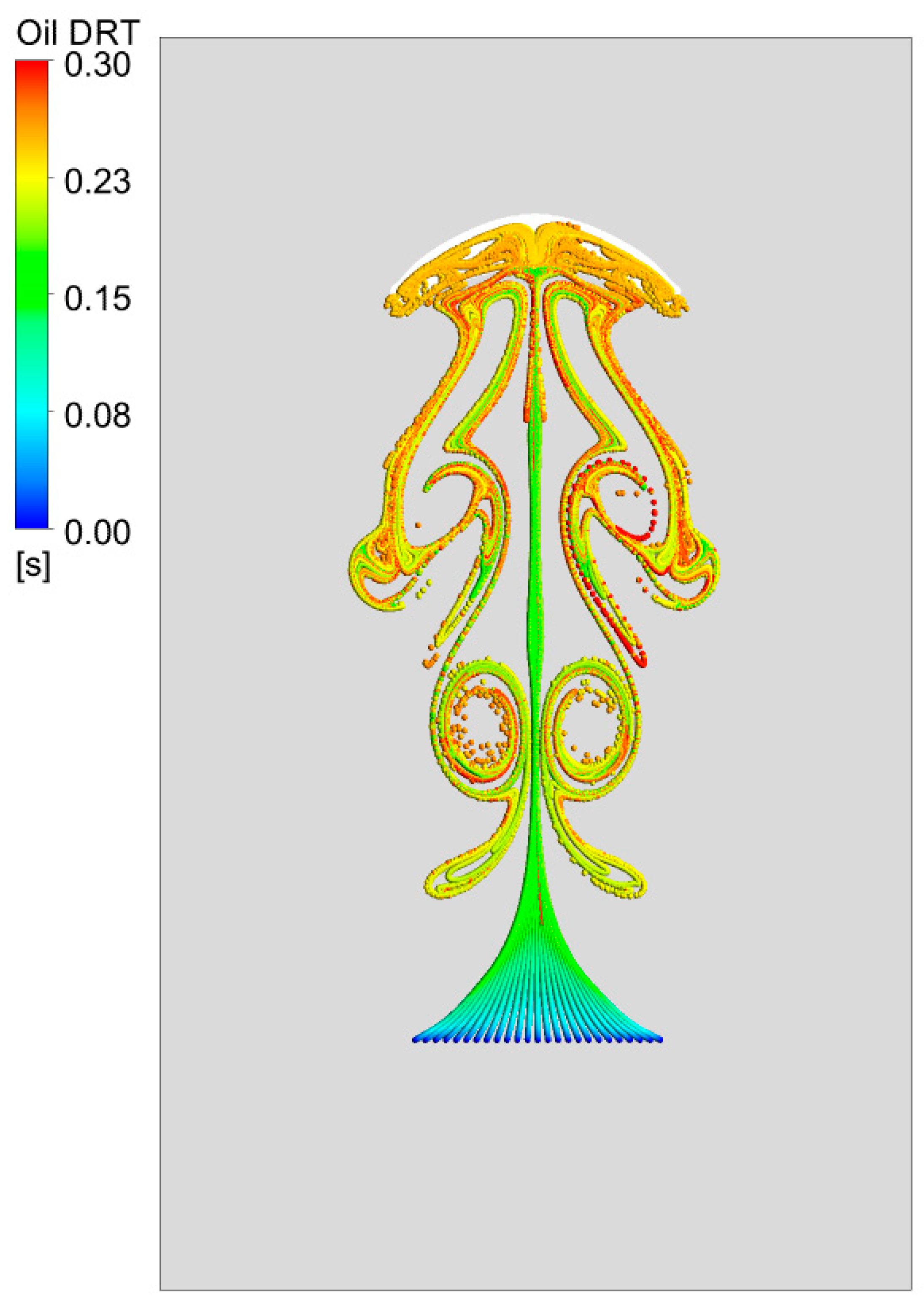
4.4. Oil Droplet Dynamics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| a1–a3 | constants |
| CD | droplet-liquid drag force coefficient |
| db | bubble diameter (mm) |
| dd | droplet diameter (µm) |
| Eo | Eötvös number |
| phase interaction forces from bubbles and droplets (N) | |
| Fb | bubble–liquid interface coupling interaction force (N) |
| Fd | droplet–liquid interface coupling interaction force (N) |
| FD | drag force (N) |
| surface tension force | |
| gravitational acceleration vector (m/s2) | |
| M | Morton number |
| normal unit vector | |
| p | pressure (pa) |
| r | bubble radius (mm) |
| Re | Reynolds number |
| droplet Stokes number | |
| t | time (s) |
| t* | dimensionless time (-) |
| velocity vector (m/s) | |
| ub | gas bubble rise velocity (m/s) |
| ug | superficial gas velocity (m/s) |
| Greek Letters | |
| volume fraction scalar | |
| viscosity (Pa.s) | |
| density (kg/m3) | |
| surface tension force (N/m) | |
| free surface curvature | |
| Subscripts | |
| b | bubble index |
| d | droplet index |
| g | gas index |
| l | liquid index |
References
- Fakhru’L-Razi, A.; Pendashteh, A.; Abdullah, L.C.; Biak, D.R.A.; Madaeni, S.S.; Abidin, Z.Z. Review of technologies for oil and gas produced water treatment. J. Hazard. Mater. 2009, 170, 530–551. [Google Scholar] [CrossRef]
- Dudek, M.; Kancir, E.; Øye, G. Influence of the Crude Oil and Water Compositions on the Quality of Synthetic Produced Water. Energy Fuels 2017, 31, 3708–3716. [Google Scholar] [CrossRef]
- Amakiri, K.T.; Canon, A.R.; Molinari, M.; Angelis-Dimakis, A. Review of oilfield produced water treatment technologies. Chemosphere 2022, 298, 134064. [Google Scholar] [CrossRef] [PubMed]
- Piccioli, M.; Aanesen, S.V.; Zhao, H.; Dudek, M.; Øye, G. Gas Flotation of Petroleum Produced Water: A Review on Status, Fundamental Aspects, and Perspectives. Energy Fuels 2020, 34, 15579–15592. [Google Scholar] [CrossRef]
- Shen, W.; Mukherjee, D.; Koirala, N.; Hu, G.; Lee, K.; Zhao, M.; Li, J. Microbubble and Nanobubble-Based Gas Flotation for Oily Wastewater Treatment: A review. Environ. Rev. 2022, 30, 359–379. [Google Scholar] [CrossRef]
- Li, X.B.; Liu, J.T.; Wang, Y.T.; Wang, C.Y.; Zhou, X.H. Separation of oil from wastewater by column flotation. J. China Univ. Min. Technol. 2007, 1, 546–551. [Google Scholar] [CrossRef]
- Moosai, R.; Dawe, R.A. Oily Wastewater Cleanup by Gas Flotation. West Indian. J. Eng. 2002, 25, 25–41. [Google Scholar]
- Huang, Q.; Long, X. Analysis of the influencing factors on oil removal efficiency in large-scale flotation tanks: Experimental observation and numerical simulation. Energies 2020, 13, 927. [Google Scholar] [CrossRef]
- Rubio, J.; Souza, M.L.; Smith, R.W. Overview of flotation as a wastewater treatment technique. Miner. Eng. 2002, 15, 139–155. [Google Scholar] [CrossRef]
- Owens, N.; Lee, D.W. The Use of Micro-Bubble Flotation Technology in Secondary & Tertiary Produced Water Treatment a Technical Comparison with Other Separation Technologies. In Proceedings of the TUV NEL, 5th Produced Water Workshop, Aberdeen, Scotland, 30–31 May 2007; pp. 1–19. [Google Scholar]
- Edzwald, J.K. Dissolved air flotation and me. Water Res. 2010, 44, 2077–2106. [Google Scholar] [CrossRef] [PubMed]
- Hassanzadeh, A.; Safari, M.; Hoang, D.H.; Khoshdast, H.; Albijanic, B.; Kowalczuk, P.B. Technological assessments on recent developments in fine and coarse particle flotation systems. Miner. Eng. 2022, 180, 107509. [Google Scholar] [CrossRef]
- Van Le, T.; Imai, T.; Higuchi, T.; Yamamoto, K.; Sekine, M.; Doi, R.; Vo, H.T.; Wei, J. Performance of tiny microbubbles enhanced with “normal cyclone bubbles” in separation of fine oil-in-water emulsions. Chem. Eng. Sci. 2013, 94, 1–6. [Google Scholar]
- Khuntia, S.; Majumder, S.K.; Ghosh, P. Microbubble-aided water and wastewater purification: A review. Rev. Chem. Eng. 2012, 28, 191–221. [Google Scholar] [CrossRef]
- Lim, M.W.; Lau, E.V.; Poh, P.E. Micro-bubbles interactions and its application in flotation technology for the recovery of high-density oil from contaminated sands. J. Petrol. Sci. Eng. 2018, 161, 29–37. [Google Scholar] [CrossRef]
- Federle, M.E.; Das, A.; Mathai, V.; Zenit, R. The interaction of an oil droplet and a gas bubble rising in a quiescent fluid. Int. J. Multiph. Flow 2023, 171, 104682. [Google Scholar] [CrossRef]
- Oliveira, R.C.G.; Gonzalez, G.; Oliveira, J.F. Interfacial studies on dissolved gas flotation of oil droplets for water purification. Colloids Surf. 1999, 154, 127–135. [Google Scholar] [CrossRef]
- Rawlins, C.H. Flotation of Fine Oil Droplets in Petroleum Production Circuits. In Mineral Processing Plant Design; Society for Mining, Metallurgy, and Exploration and The Minerals, Metals, and Materials Society: Tucson, AZ, USA, 2009. [Google Scholar]
- Yan, S.; Yang, X.; Bai, Z.; Xu, X.; Wang, H. Drop attachment behavior of oil droplet-gas bubble interactions during flotation. Chem. Eng. Sci. 2020, 223, 115740. [Google Scholar] [CrossRef]
- Moosai, R.; Dawe, R.A. Gas attachment of oil droplets for gas flotation for oily wastewater cleanup. Sep. Purif. Tech. 2003, 33, 303–314. [Google Scholar] [CrossRef]
- Rawlins, C. Hank Mechanisms for Flotation of Fine Oil Droplets; SME Annual Meeting & Exhibit: Littleton, CO, USA, 2011; pp. 1–11. [Google Scholar]
- Dudek, M. Produced Water Quality and Microfluidic Methods for Studying Drop-Drop and Drop-Bubble Interactions in Produced Water. Ph.D. Thesis, Norwegian University of Science and Technology NTNU, Trondheim, Norway, 2018. [Google Scholar]
- Saththasivam, J.; Loganathan, K.; Sarp, S. An overview of oil–water separation using gas flotation systems. Chemosphere 2016, 144, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Räbiger, N. Hydrodynamics and Mass Transfer in Loop-Reactors with Three-Phase Flow-an Overview with New Perspective. In Proceedings of the 2nd International Symposium on Multiscale Multiphase Process Engineering, Hamburg, Germany, 24–27 September 2014. [Google Scholar]
- Ralston, J.; Dukhin, S.S.; Mishchuk, N.N. Wetting film stability and flotation kinetics. Adv. Colloid Interface Sci. 2002, 95, 145–236. [Google Scholar] [CrossRef]
- Federle, M.; Zenit, R. Physical conditions for droplet–bubble coalescence in flotation. Int. J. Multiph. Flow 2024, 179, 104933. [Google Scholar] [CrossRef]
- Miettinen, T.; Ralston, J.; Fornasiero, D. The limits of fine particle flotation. Miner. Eng. 2010, 23, 420–437. [Google Scholar] [CrossRef]
- Chen, H.; Li, Y.; Xiong, Y.; Wei, H.; Saxén, H.; Yu, Y. Effect of particle holdup on bubble formation in suspension medium by VOF–DPM simulation. Granul. Matter 2022, 24, 120. [Google Scholar] [CrossRef]
- Cai, X.; Chen, J.; Liu, M.; Ji, Y.; Ding, G.; Zhang, L. CFD simulation of oil-water separation characteristics in a compact flotation unit by population balance modeling. J. Dispers. Sci. Technol. 2017, 38, 1435–1447. [Google Scholar] [CrossRef]
- Xu, Y.G.; Ersson, M.; Jonsson, P.G. A numerical study about the influence of a bubble wake flow on the removal of inclusions. ISIJ Int. 2016, 56, 1982–1988. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, X.; Pan, W.; Jian-liang, X. Numerical simulation of wake structure and particle entrainment behavior during a single bubble ascent in liquid-solid system. Chem. Eng. Sci. 2022, 253, 117573. [Google Scholar] [CrossRef]
- Hua, J.; Stene, J.F.; Lin, P. Numerical simulation of 3D bubbles rising in viscous liquids using a front tracking method. J. Comput. Phys. 2008, 227, 3358–3382. [Google Scholar] [CrossRef]
- Zhang, A.; Guo, Z.; Wang, Q. Three-dimensional numerical simulation of bubble rising in viscous liquids: A conservative phase-field lattice-Boltzmann study. Phys. Fluids 2019, 31, 063106. [Google Scholar] [CrossRef]
- Akhtar, A.; Pareek, V.; Tade, M. CFD simulations for continuous flow of bubbles through gas-liquid columns: Application of VOF method. Chem. Prod. Process Model. 2007, 2, 9. [Google Scholar] [CrossRef]
- Inguva, V.; Schulz, A.; Kenig, E. On methods to reduce spurious currents within VOF solver frameworks. Part 1: A review of the static bubble/droplet. Chem. Prod. Process Model. 2020, 17, 121–135. [Google Scholar] [CrossRef]
- Pourtousi, M.; Ganesan, P.; Kazemzadeh, A.; Sandaran, S.C.; Sahu, J.N. Methane bubble formation and dynamics in a rectangular bubble column: A CFD study. Chemom. Intell. Lab. Syst. 2015, 147, 111–120. [Google Scholar] [CrossRef]
- Xia, Y.K. CFD Simulation of Fine Particle Gravity Separation in Hindered-settling Bed Separators. Chem. Prod. Process. Model. 2007, 2, 1–21. [Google Scholar] [CrossRef]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Pan, W.T.; Chen, X.L.; Dai, G.C.; Wang, F.C. Enhanced Effect of Bubble Deformation on Internal Particle Transport. Ind. Eng. Chem. Res. 2020, 59, 905–918. [Google Scholar] [CrossRef]
- Yang, X.; Xi, T.; Qin, Y.; Zhang, H.; Wang, Y. Computational Fluid Dynamics–Discrete Phase Method Simulations in Process Engineering: A Review of Recent Progress. Appl. Sci. 2024, 14, 3856. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS Fluent Theory Guide, Release 15.0, November 2013. Available online: http://www.ansys.com/ (accessed on 14 May 2025).
- Elghobashi, S. Particle-laden turbulent flows: Direct simulation and closure models. Appl. Sci. Res. 1991, 48, 301–314. [Google Scholar] [CrossRef]
- Saleh, S.N. CFD Simulations of a co-current spray dryer. World Acad. Sci. Technol. 2010, 62, 772–777. [Google Scholar]
- Hua, J.; Lou, J. Numerical simulation of bubble rising in viscous liquids. J. Comput. Phys. 2007, 222, 769–795. [Google Scholar] [CrossRef]
- Smolianski, A.; Haario, H.; Luukka, P. Vortex shedding behind a rising bubble and two-bubble coalescence: A numerical approach. Appl. Math. Model. 2005, 29, 615–632. [Google Scholar] [CrossRef]
- Hoque, M.M.; Moreno-Atanasio, R.; Doroodchi, E.; Joshi, J.; Evans, G.M.; Mitra, S. 20 Dynamics of a single bubble rising in a quiescent medium. Exp. Therm. Fluid Sci. 2022, 132, 110546. [Google Scholar] [CrossRef]
- Bhaga, D.; Weber, M.E. Bubbles in viscous liquids, shapes, wakes and velocities. J. Fluid Mech. 1981, 105, 61–85. [Google Scholar] [CrossRef]
- Krishna, R.; Van Baten, J.M. Rise characteristics of gas bubbles in a 2D rectangular column: VOF simulations vs experiments. Int. Commun. Heat Mass Transf. 1999, 26, 965–974. [Google Scholar] [CrossRef]
- Abbassi, W.; Besbes, S.; Elhajem, M.; Aissia, H.; Ben Champagne, J.Y. Numerical simulation of free ascension and coaxial coalescence of air bubbles using the volume of fluid method (VOF). Comput. Fluids 2018, 161, 47–59. [Google Scholar] [CrossRef]
- Grace, J.R.; Wairegi, T.; Nguyen, T.H. Shapes and velocities of single drops and bubbles moving freely through immiscible liquids. Trans. Inst. Chem. Eng. 1976, 54, 167. [Google Scholar]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: London, UK, 1978. [Google Scholar]
- Kracht, W.; Finch, J.A. Effect of frother on initial bubble shape and velocity. Int. J. Miner. Process. 2010, 94, 115–120. [Google Scholar] [CrossRef]
- Chakraborty, I.; Biswas, G.; Ghoshdastidar, P.S. A coupled level-set and volume of- fluid method for the buoyant rise of gas bubbles in liquids. Int. J. Heat Mass Transf. 2013, 58, 240–259. [Google Scholar] [CrossRef]
- Kulkarni, A.A.; Joshi, J.B. Bubble formation and bubble rise velocity in gas-liquid systems: A review. Ind. Eng. Chem. Res. 2005, 44, 5873–5931. [Google Scholar] [CrossRef]
- Ziegenhein, T.; Lucas, D. Observations on bubble shapes in bubble columns under different flow conditions. Exp. Therm. Fluid Sci. 2017, 85, 248–256. [Google Scholar] [CrossRef]
- Sharaf, D.M.; Premlata, A.R.; Tripathi, M.K.; Karri, B.; Sahu, K.C. Shapes and paths of an air bubble rising in quiescent liquids. Phys Fluids 2017, 29, 122104. [Google Scholar] [CrossRef]
- Meehan, R.O.; Donnelly, B.; Nolan, K.; Persoons, T.; Murray, D.B. Flow structures and dynamics in the wakes of sliding bubbles. Int. J. Multiph. Flow. 2016, 84, 145–154. [Google Scholar] [CrossRef]
- Krishna, R. A scale up strategy for a commercial scale bubble column slurry reactor for Fischer Tropsch synthesis. Oil Gas Sci. Technol. 2000, 55, 359–393. [Google Scholar] [CrossRef][Green Version]
- Dai, J.; Sterling, J.D.; Nadim, A. Numerical Simulation of Air Bubbles Rising in Water Using an Axisymmetric VOF method. In Proceedings of the 2nd International Conference on Computational Methods in Multiphase Flow, Santa Fe, NM, SAD, 3–5 November 2003; pp. 343–351. [Google Scholar]
- Krishna, R.; Van Baten, J.M. Simulating the Rise Characteristics of Gas Bubbles in Liquids Using CFD. Chem. Eng. Technol. 2001, 24, 427–430. [Google Scholar] [CrossRef]
- Cao, Y.; Macián-Juan, R. The wobbling motion of single and two inline bubbles rising in quiescent liquid. Phys. Fluids 2021, 33, 073305. [Google Scholar] [CrossRef]
- Kitano, K.; Fan, L.-S. Near-Wake Structure of a Single Gas Bubble in a Two-Dimensional Liquid-Solid Fluidized Bed: Solids Holdup. Chem. Eng. Sci. 1988, 43, 1355–1361. [Google Scholar] [CrossRef]





| Parameter | |
|---|---|
| Liquid | Water |
| Gas | Air |
| Oil | Cyclohexane |
| Liquid density, kg/m3 | 998 |
| Gas density, kg/cm3 | 1.225 |
| Oil density, kg/m3 | 779 |
| Liquid viscosity, 10−3 Pa.s | 1.003 |
| Gas viscosity, 10−3 Pa.s | 0.018 |
| Oil viscosity, 10−3 Pa.s | 0.883 |
| Water–air interfacial tension, 10−3 N.m−1 | 72 |
| Oil–air interfacial tension, 10−3 N.m−1 | 24.4 |
| Oil–water interfacial tension, 10−3 N.m−1 | 26.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saleh, S.N.; Barghi, S. CFD Simulation of the Interaction Between a Macrobubble and a Dilute Dispersion of Oil Droplets in Quiescent Water. Clean Technol. 2025, 7, 65. https://doi.org/10.3390/cleantechnol7030065
Saleh SN, Barghi S. CFD Simulation of the Interaction Between a Macrobubble and a Dilute Dispersion of Oil Droplets in Quiescent Water. Clean Technologies. 2025; 7(3):65. https://doi.org/10.3390/cleantechnol7030065
Chicago/Turabian StyleSaleh, Saad N., and Shahzad Barghi. 2025. "CFD Simulation of the Interaction Between a Macrobubble and a Dilute Dispersion of Oil Droplets in Quiescent Water" Clean Technologies 7, no. 3: 65. https://doi.org/10.3390/cleantechnol7030065
APA StyleSaleh, S. N., & Barghi, S. (2025). CFD Simulation of the Interaction Between a Macrobubble and a Dilute Dispersion of Oil Droplets in Quiescent Water. Clean Technologies, 7(3), 65. https://doi.org/10.3390/cleantechnol7030065







