Mathematical Modeling of Particle Terminal Velocity for Improved Design of Clarifiers, Thickeners and Flotation Devices for Wastewater Treatment
Abstract
1. Introduction
2. Materials and Methods
2.1. Dimensional Analysis
2.2. Experimental Data
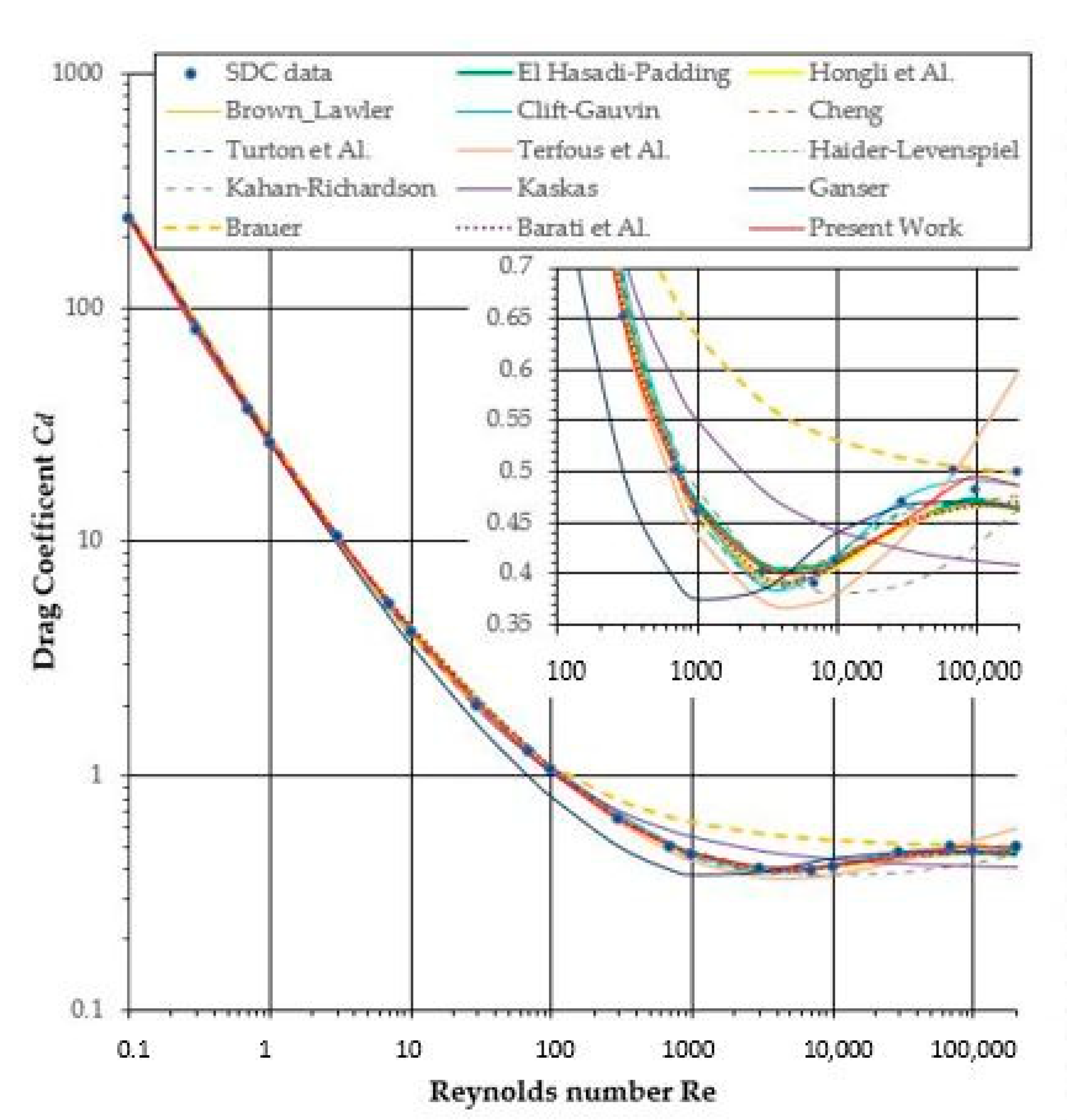
3. Results and Discussion
3.1. Formulas and
3.2. Formula
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SDC | Standard drag curve |
| RD | Relative difference |
| MRD | Mean relative difference |
| HRD | Highest relative difference |
| SD | Standard deviation |
References
- Ganguly, U.P. On the prediction of terminal settling velocity of solids in-solid systems. Int. J. Miner. Process. 1990, 29, 235–247. [Google Scholar] [CrossRef]
- Tsakalakis, K.G.; Stamboltzis, G.A. Prediction of the settling velocity of irregularly shaped particles. Miner. Eng. 2001, 14, 349–357. [Google Scholar] [CrossRef]
- Goossens, W.R.A. Review of the empirical correlations for the drag coefficient of rigid spheres. Powder Technol. 2019, 352, 350–359. [Google Scholar] [CrossRef]
- El Hasadi, Y.M.F.; Padding, J.T. Do logarithmic terms exist in the drag coefficient of a single sphere at high Reynolds numbers? Chem. Eng. Sci. 2023, 265, 118195. [Google Scholar] [CrossRef]
- Kynch, G.J. A theory of sedimentation. Trans. Faraday Soc. 1952, 48, 166–176. [Google Scholar] [CrossRef]
- Richardson, J.F.; Zaki, W.N. Sedimentation and fluidization: Part I. Trans. Inst. Chem. Eng. 1954, 32, S82–S100. [Google Scholar]
- Chang, D.; Lee, T.; Jang, Y.; Kim, M.; Lee, S. Non colloidal sedimentation compared with Kynch theory. Powder Technol. 1997, 92, 81–87. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, J. Demarcation on a new conventional circulating fluidization regime in liquid-solids fluidization via experimental and numerical studies. Chem. Eng. J. 2021, 412, 128578. [Google Scholar] [CrossRef]
- Reguła, T.; Frączek, J.; Fitas, J. A Model of Transport of Particulate Biomass in a Stream of Fluid. Processes 2021, 9, 5. [Google Scholar] [CrossRef]
- do Nascimento, O.L.; Reay, D.A.; Zivkovic, V. Solid Circulating Velocity Measurement in a Liquid–Solid Micro-Circulating Fluidised Bed. Processes 2020, 8, 1159. [Google Scholar] [CrossRef]
- Alghamdi, Y.A.; Peng, Z.; Luo, C.; Almutairi, Z.; Moghtaderi, B.; Doroodchi, E. Systematic Study of Pressure Fluctuation in the Riser of a Dual Inter-Connected Circulating Fluidized Bed: Using Single and Binary Particle Species. Processes 2019, 7, 890. [Google Scholar] [CrossRef]
- Lucena-Thomas, J.P.D.; Boonprasirt, P.; Luetchford, K.; De Bank, P.; Ellis, M. Bed expansion properties of tissue engineering particles in a fluidised bed bioreactor. Biochem. Eng. J. 2020, 160, 107632. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, L.; Chang, H.; Zhang, Q. A review of drag coefficient models in gas-liquid two-phase flow. ChemBioEng Rev. 2023, 10, 311–325. [Google Scholar] [CrossRef]
- Maiti, S.B.; Bar, N.; Das, S.K. Terminal settling velocity of solids in the pseudoplastic non-Newtonian liquid system—Experiment and ANN modeling. Chem. Eng. J. Adv. 2021, 7, 100136. [Google Scholar] [CrossRef]
- Trofa, M.; D’Avino, G. Sedimentation of Fractal Aggregates in Shear-Thinning Fluids. Appl. Sci. 2020, 10, 3267. [Google Scholar] [CrossRef]
- Ma, X.; Ji, G.; Li, Z.; Ju, G. An Improved Model for Predicting the Drag Coefficient and Terminal Settling Velocity of Natural Sands in Newtonian Fluid. Processes 2022, 10, 1579. [Google Scholar] [CrossRef]
- Moruzzi, R.B.; Campos, L.C.; Sharifi, S.; Grava da Silva, P.; Gregory, J. Nonintrusive investigation of large Al-kaolin fractal aggregates with slow settling velocities. Water Res. 2020, 185, 116287. [Google Scholar] [CrossRef]
- Nikolaev, A.A. The Physical Characterization and Terminal Velocities of Aluminium, Iron and Plastic Bottle Caps in a Water Environment. Recycling 2022, 7, 28. [Google Scholar] [CrossRef]
- Jang, S.; Lim, K.-S.S.; Ko, J.; Kim, K.; Lee, G.; Cho, S.-J.; Ahn, K.-D.; Lee, Y.-H. Revision of WDM7 Microphysics Scheme and Evaluation for Precipitating Convection over the Korean Peninsula. Remote Sens. 2021, 13, 3860. [Google Scholar] [CrossRef]
- Naves, J.; Anta, J.; Suárez, J.; Puertas, J. Development and Calibration of a New Dripper-Based Rainfall Simulator for Large-Scale Sediment Wash-Off Studies. Water 2020, 12, 152. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Nakagawa, H.; Kawaike, K.; Prajapati, R. Evaluating the rainfall erosivity (R-factor) from daily rainfall data: An application for assessing climate change impact on soil loss in Westrapti River basin, Nepal. Model. Earth Syst. Environ. 2020, 6, 1741–1762. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Chai, Z.; Min, F.; Jiang, X.; Zhu, K.; Dai, J. New model for predicting terminal settling velocity and drag coefficient of the Oncomelania. Front. Environ. Sci. 2022, 10, 1051392. [Google Scholar] [CrossRef]
- Takemi, T.; Poulidis, A.P.; Iguchi, M. High–Resolution Modeling of Airflows and Particle Deposition over Complex Terrain at Sakurajima Volcano. Atmosphere 2021, 12, 325. [Google Scholar] [CrossRef]
- Kalman, H. Role of Reynolds and Archimedes numbers in particle-fluid flows. Rev. Chem. Eng. 2020, 38, 149–165. [Google Scholar] [CrossRef]
- Goossens, W.R.A. Classification of fluidized particles by Archimedes number. Powder Technol. 1998, 98, 48–53. [Google Scholar] [CrossRef]
- Loncin, M.; Merson, R.L. Food Engineering: Principles and Selected Application, 1st ed.; Accademic Press: New York, NY, USA, 1979; pp. 94–97. [Google Scholar]
- Mafart, P.; Belliard, E. Genie Industriel Alimentaire, 2nd ed.; Lavoisier: Paris, France, 2004; Volume 2, p. 81. [Google Scholar]
- Khan, A.R.; Richardson, J.F. The resistance to motion of a solid sphere in a fluid. Chem. Eng. Commun. 1987, 62, 135–150. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Nguyen, A.V.; Stechemesser, H.; Zobel, G.; Schulze, H.J. An improved formula for terminal velocity of rigid spheres. Int. J. Miner. Process. 1997, 50, 53–61. [Google Scholar] [CrossRef]
- Brown, P.P.; Lawler, D.F. Sphere Drag and Settling Velocity Revisited. J. Environ. Eng. ASCE 2003, 129, 222–231. [Google Scholar] [CrossRef]
- Lapple, C.E.; Shepherd, C.B. Calculation of particle trajectories. Ind. Eng. Chem. 1940, 32, 605–617. [Google Scholar] [CrossRef]
- Perry, R.H.; Green, D.W. Chemical Engineers’ Handbook, 6th ed.; McGraw-Hill: Singapore, 1984; Chapter 5; p. 67. [Google Scholar]
- Molerus, O. Fluid mechanics in term of eigen parameter. Part 1: Fundamentals. Chem. Eng. Sci. 2000, 55, 1171–1177. [Google Scholar] [CrossRef]
- Gomez, C.O.; Maldonado, M. Modelling Bubble Flow Hydrodynamics: Drift-Flux and Molerus Models. Minerals 2022, 12, 1502. [Google Scholar] [CrossRef]
- Kalman, H.; Matana, E. Terminal velocity and drag coefficient for spherical particles. Powder Technol. 2022, 396, 181–190. [Google Scholar] [CrossRef]
- Stokes, G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Phillosophical Soc. 1851, 9, 38–39. [Google Scholar]
- Hongli, Y.; Minqiang, F.; Airong, L.; Lianping, D. General formulas for drag coefficient and settling velocity of sphere based on theoretical law. Int. J. Min. Sci. Technol. 2015, 25, 219–223. [Google Scholar] [CrossRef]
- Clift, R.; Gauvin, W.H. Motion of entrained particles in gas streams. Proc. Chem. 1970, 70, 14. [Google Scholar] [CrossRef]
- Cheng, N.-S. Comparison of formulas for drag coefficient and settling velocity of spherical particles. Powder Technol. 2009, 189, 395–398. [Google Scholar] [CrossRef]
- Terfous, A.; Hazzab, A.; Ghenaim, A. Predicting the drag coefficient and settling velocity of spherical particles. Powder Technol. 2013, 239, 12–20. [Google Scholar] [CrossRef]
- Turton, R.; Levenspiel, O. A short note on the drag correlation for spheres. Powder Technol. 1996, 47, 83–86. [Google Scholar] [CrossRef]
- Kaskas, A.A. Schwarmgeschwindigkeit in Mehrkornsuspensionen am Beispiel der Sedimentation. Ph.D. Dissertation, TU Berlin, Berlin, Germany, 1970. [Google Scholar]
- Ganser, G.H. A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Brauer, H. Momentum, mass, and heat-transfer through boundary surface of spherical-particles. Chem. Ing. Tech. 1973, 45, 1099–1103. [Google Scholar] [CrossRef]
- Barati, R.; Neyshabouri, S.A.A.S.; Ahmadi, G. Development of empirical models with high accuracy for estimation of drag coefficient of flow around a smooth sphere: An evolutionary approach. Powder Technol. 2014, 257, 11–19. [Google Scholar] [CrossRef]
- Friso, D. A new mathematical model for food thermal process prediction. Model. Simul. Eng. 2013, 569473, 21. [Google Scholar] [CrossRef]
- Friso, D. Energy saving with total energy system for cold storage in Italy: Mathematical modeling and simulation, exergetic and economic analysis. Appl. Math. Sci. 2014, 8, 6529–6546. [Google Scholar] [CrossRef]

| Variables | Symbol | Dimension |
|---|---|---|
| Diameter of the particle | D [m] | L |
| Terminal velocity | v [m s−1] | L T−1 |
| Acceleration (gravity or centrifugal) | a [m s−2] | L T−2 |
| Fluid density | ρf [kg m−3] | M L−3 |
| Particle density—fluid density | (ρp − ρf) [kg m−3] | M L−3 |
| Viscosity | μ [kg m−1 s−1] | M L−1 T−1 |
| Cd Value from Standard Drag Curve (SDC) | Reynolds Number Re | Archimedes Number Ar |
|---|---|---|
| 240 | 0.1 | 1.8 |
| 80 | 0.3 | 5.4 |
| 36.5 | 0.7 | 13.4 |
| 26.5 | 1 | 19.9 |
| 10.4 | 3 | 70.2 |
| 5.4 | 7 | 198.5 |
| 4.1 | 10 | 307.5 |
| 2.0 | 30 | 1350 |
| 1.27 | 70 | 4667 |
| 1.07 | 100 | 8025 |
| 0.65 | 300 | 43,875 |
| 0.50 | 700 | 183,750 |
| 0.46 | 1000 | 345,000 |
| 0.40 | 3000 | 2,700,000 |
| 0.39 | 7000 | 14,332,500 |
| 0.41 | 10,000 | 3075 × 104 |
| 0.47 | 30,000 | 31,725 × 104 |
| 0.50 | 70,000 | 18,375 × 105 |
| 0.48 | 100,000 | 36 × 108 |
| 0.498 | 200,000 | 149.4 × 108 |
| Cd Value from Equation (15) | Cd Value from Standard Drag Curve (SDC) | Relative Difference (RD) (%) | Reynolds Number Re | Archimedes Number Ar |
|---|---|---|---|---|
| 240.27 | 240 | 0.11 | 0.1 | 1.8 |
| 80.55 | 80 | 0.68 | 0.3 | 5.4 |
| 36.12 | 36.5 | −1.05 | 0.7 | 13.4 |
| 26.23 | 26.5 | −1.01 | 1 | 19.9 |
| 10.40 | 10.4 | 0.03 | 3 | 70.2 |
| 5.41 | 5.4 | 0.15 | 7 | 198.5 |
| 4.22 | 4.1 | 2.86 | 10 | 307.5 |
| 2.03 | 2.0 | 1.57 | 30 | 1350 |
| 1.24 | 1.27 | −2.18 | 70 | 4667 |
| 1.03 | 1.07 | −3.31 | 100 | 8025 |
| 0.655 | 0.65 | 0.72 | 300 | 43,875 |
| 0.504 | 0.50 | 0.85 | 700 | 183,750 |
| 0.464 | 0.46 | 0.96 | 1000 | 345,000 |
| 0.401 | 0.40 | 0.14 | 3000 | 2,700,000 |
| 0.397 | 0.39 | 1.88 | 7000 | 14,332,500 |
| 0.406 | 0.41 | −1.03 | 10,000 | 3075 × 104 |
| 0.456 | 0.47 | −3.03 | 30,000 | 31,725 × 104 |
| 0.495 | 0.50 | −1.02 | 70,000 | 18,375 × 105 |
| 0.502 | 0.48 | 4.68 | 100,000 | 36 × 108 |
| 0.490 | 0.498 | −1.58 | 200,000 | 149.4 × 108 |
| Authors | Year | Formula | Ar Range |
|---|---|---|---|
| Khan–Richardson [28] | 1987 | 1.8 ÷ 353,250 | |
| Haider–Levenspiel [29] | 1989 | 1.8 ÷ 149.4·108 | |
| Nguyen et al. [30] | 1997 | 1.8 ÷ 353,250 | |
| Brown–Lawler, their Equation (37) in [31] | 2003 | 1.8 ÷ 27·105 |
| Authors | Year | Mean Relative Difference (MRD) (%) | Standard Deviation (SD) (%) | Ar Range | Re Range |
|---|---|---|---|---|---|
| Khan–Richardson [28] | 1987 | 2.24 | 1.90 | 1.8 ≤ Ar ≤ 353,250 | 0.1 ≤ Re ≤ 1000 |
| Haider–Levenspiel [29] | 1989 | 12.34 | 8.08 | 1.8 ≤ Ar ≤ 149.4·108 | 0.1 ≤ Re ≤ 200,000 |
| Nguyen et al. [30] | 1997 | 4.19 | 2.49 | 1.8 ≤ Ar ≤ 353,250 | 0.1 ≤ Re ≤ 1000 |
| Brown–Lawler, their Equation (37) in [31] | 2003 | 3.57 | 2.97 | 1.8 ≤ Ar ≤ 27·105 | 0.1 ≤ Re ≤ 4000 |
| Present work, Equation (15) | 2023 | 1.22 | 1.16 | 1.8 ≤ Ar ≤ 353,250 | 0.1 ≤ Re ≤ 1000 |
| Present work, Equation (15) | 2023 | 1.17 | 1.13 | 1.8 ≤ Ar ≤ 27·105 | 0.1 ≤ Re ≤ 4000 |
| Present work, Equation (15) | 2023 | 1.44 | 1.23 | 1.8 ≤ Ar ≤ 149.4·108 | 0.1 ≤ Re ≤ 200,000 |
| Cd Value from Equation (19) | Cd Value from Standard Drag Curve (SDC) | Relative Difference (RD) (%) | Reynolds Number Re | Archimedes Number Ar |
|---|---|---|---|---|
| 242.34 | 240 | 0.98 | 0.1 | 1.8 |
| 79.01 | 80 | −1.23 | 0.3 | 5.4 |
| 36.03 | 36.5 | −1.27 | 0.7 | 13.4 |
| 26.31 | 26.5 | −0.71 | 1 | 19.9 |
| 10.52 | 10.4 | 1.17 | 3 | 70.2 |
| 5.47 | 5.4 | 1.36 | 7 | 198.5 |
| 4.22 | 4.1 | 2.93 | 10 | 307.5 |
| 2.02 | 2.0 | 1.03 | 30 | 1350 |
| 1.24 | 1.27 | −2.55 | 70 | 4667 |
| 1.03 | 1.07 | −3.68 | 100 | 8025 |
| 0.646 | 0.65 | −0.62 | 300 | 43,875 |
| 0.502 | 0.50 | 0.32 | 700 | 183,750 |
| 0.464 | 0.46 | 0.90 | 1000 | 345,000 |
| 0.406 | 0.40 | 1.44 | 3000 | 2,700,000 |
| 0.403 | 0.39 | 3.32 | 7000 | 14,332,500 |
| 0.410 | 0.41 | 0.0 | 10,000 | 3075 × 104 |
| 0.452 | 0.47 | −3.85 | 30,000 | 31,725 × 104 |
| 0.488 | 0.50 | −2.49 | 70,000 | 18,375 × 105 |
| 0.496 | 0.48 | 3.34 | 100,000 | 36 × 108 |
| 0.487 | 0.498 | −2.19 | 200,000 | 149.4 × 108 |
| Authors | Year | Formula |
|---|---|---|
| El Hasadi–Padding, their Equation (11) [4] | 2022 | , where: |
| Hongli et al.their Equation (25) in [38] | 2015 | where: and |
| Clift–Gauvin [39] | 1970 | |
| Brown–Lawler, their Equation (19) in [31] | 2003 | |
| Cheng [40] | 2009 | |
| Terfous et al. [41] | 2013 | |
| Turton–Levenspiel [42] | 1986 | |
| Haider–Levenspiel [29] | 1989 | |
| Kahn–Richardson [28] | 1987 | |
| Kaskas [43] | 1970 | |
| Ganser [44] | 1993 | |
| Brauer [45] | 1973 | |
| Barati et al., their Equation (22) in [46] | 2014 |
| Authors | Year | Mean Relative Difference (MRD) (%) | Stand. Deviat. (SD) (%) | Highest Relative Difference (HRD) (%) | Reynolds Number Re at the HRD |
|---|---|---|---|---|---|
| SDC data [3,32] | 1940 | ||||
| Present work, Equation (19) | 2023 | 1.77 | 1.17 | −3.85 | 30,000 |
| El Hasadi-Padding their Equation (11) [4] | 2022 | 2.24 | 1.99 | −7.30 | 200,000 |
| Hongli et al. their Equation (25) [38] | 2015 | 2.51 | 2.27 | −7.13 | 70,000 |
| Barati et al. their Equation (22) [46] | 2014 | 2.67 | 2.25 | −7.31 | 70,000 |
| Clift-Gauvin [39] | 1970 | 2.68 | 1.70 | 6.56 | 0.3 |
| Brown-Lawler their Equation (19) [31] | 2003 | 2.76 | 2.30 | −7.04 | 70,000 |
| Cheng [40] | 2009 | 2.98 | 2.01 | −7.13 | 70,000 |
| Terfous et al. [41] | 2013 | 3.92 | 4.93 | 20.52 | 200,000 |
| Turton-Levenspiel [42] | 1986 | 3.93 | 1.97 | 7.84 | 0.3 |
| Haider-Levenspiel [29] | 1989 | 4.06 | 2.17 | 8.30 | 0.3 |
| Kahn-Richardson [28] | 1987 | 4.88 | 4.97 | −17.39 | 70,000 |
| Kaskas [43] | 1970 | 9.70 | 6.43 | 20.26 | 3000 |
| Ganser [44] | 1993 | 10.22 | 8.35 | −24.79 | 100 |
| Brauer [45] | 1973 | 12.63 | 14.66 | 41.53 | 3000 |
| Authors | Year | Mean Relative Difference (MRD) (%) | Stand. Deviat. (SD) (%) | Highest Relative Difference (HRD) (%) | Reynolds Number Re at the HRD |
|---|---|---|---|---|---|
| SDC data [3,46] | 1940 | ||||
| Present work, Equation (20) | 2023 | 2.20 | 1.53 | −6.36 | 30,000 |
| Barati et al., their Equation (22) [46] | 2014 | 2.12 | 2.22 | −7.31 | 70,000 |
| El Hasadi–Padding, their Equation (11) [4] | 2022 | 2.34 | 1.77 | −7.30 | 200,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friso, D. Mathematical Modeling of Particle Terminal Velocity for Improved Design of Clarifiers, Thickeners and Flotation Devices for Wastewater Treatment. Clean Technol. 2023, 5, 921-933. https://doi.org/10.3390/cleantechnol5030046
Friso D. Mathematical Modeling of Particle Terminal Velocity for Improved Design of Clarifiers, Thickeners and Flotation Devices for Wastewater Treatment. Clean Technologies. 2023; 5(3):921-933. https://doi.org/10.3390/cleantechnol5030046
Chicago/Turabian StyleFriso, Dario. 2023. "Mathematical Modeling of Particle Terminal Velocity for Improved Design of Clarifiers, Thickeners and Flotation Devices for Wastewater Treatment" Clean Technologies 5, no. 3: 921-933. https://doi.org/10.3390/cleantechnol5030046
APA StyleFriso, D. (2023). Mathematical Modeling of Particle Terminal Velocity for Improved Design of Clarifiers, Thickeners and Flotation Devices for Wastewater Treatment. Clean Technologies, 5(3), 921-933. https://doi.org/10.3390/cleantechnol5030046






