Abstract
Installation of new wind farms in areas such as the north coast of the Yucatan peninsula is of vital importance to face the local energy demand. For the proper functioning of these facilities it is important to perform wind data analysis, the data having been collected by anemometers, and to consider the particular characteristics of the studied area. However, despite the great development of anemometers, forecasting methods are necessary for the optimal harvesting of wind energy. For this reason, this study focuses on developing an enhanced wind forecasting method that can be applied to wind data from the north coast of the Yucatan peninsula (in general, any type of data). Thus, strategies can be established to generate a greater amount of energy from the wind farms, which supports the local economy of this area. Four variants have been developed based on the traditional double and single exponential methods. Furthermore, these methods were compared to the experimental data to obtain the optimal forecasting method for the Yucatan area. The forecasting method with the highest performance has obtained an average relative error of 7.9510% and an average mean error of 0.3860 m/s.
1. Introduction
With the increase of Renewable Energy Sources (RES) the demand for oil and gas has been decreasing. Moreover, 238 GW of installed wind and solar power capacity has been added during 2021, thus demonstrating the ability of RES to overcome the world’s energy crisis [1,2]. Likewise, RES provided approximately 29% of the world’s electricity generation [3].
Wind energy is among the main RES. This energy source already provides a significant portion of the electrical energy consumption in several countries of the European Union. In Latin America and the Caribbean, 4.7 GW were added for a regional total of 33.9 GW. In Mexico, during 2020, only 0.6 GW were added to its installed capacity. Therefore, Mexico, which was considered one of the top 10 installers in Latin America, disappeared from the list [3]. However, many regions in Mexico such as Baja California, Veracruz, Oaxaca, and Yucatan have wind power capacity potential [4]. Particularly, the Yucatan Peninsula has a technical capacity and annual generation potential of 6125 MW and 14,802 GWh, respectively [5]. With three wind farms in operation, the state of Yucatan has an installed capacity of 244.7 MW [6,7,8].
With the installation of wind farms being more frequent in these types of regions (i.e., flat areas and at sea level), a proper evaluation of the wind resource for each determined site is essential for the successful development of the power grid, since the turbine production depends mainly on wind speed. It is possible to calculate energy production by having the turbine power curve and the resource assessment. To carry out this evaluation, the main anemometric variables to be measured are wind speed, wind direction, temperature, and atmospheric pressure (the first two parameters are key values since, as the wind is an airflow, not all the wind is used to generate) [9]. However, recording wind speed data using different devices as anemometers can present errors due to different wind conditions, which represents a problem in obtaining the best performance from a power grid [10]. This affects the electricity service and the economy of the people who live in areas such as Yucatan, especially people with low income. To solve this problem, many researchers have developed different mathematical models depending on the lapse of time to be able to anticipate wind conditions. Prediction models, depending on the period, can be classified into very short term (a few seconds to 30 min), short term (30 min to 6 h), medium-term (6 h to 24 h), long term (24 h to 72 h), and very long term (>72 h) [11,12,13,14,15,16].
Another classification is made according to methodology. In this way, the models can be deterministic (or physical), statistical, and hybrid. Physical methods use previous wind power data and Numerical Weather Prediction (NWP) data. These models require a more detailed physical description of the site including roughness, obstacles, temperature, pressure, etc., which makes them computationally complex. This approach requires considerable resources, both computationally and economically since, although the data required are common to all wind forecast models, they will vary with the location of the wind farm and it will be necessary to obtain them for each location. Physical approaches are satisfactory for short-term and long-term forecasting [16,17,18]. Statistical methods are based on historical data series to make a forecast for the next few hours. These models present good results for short periods. Its main disadvantage is that, as the time in the forecast increases, the prediction error also increases. Specifically, these methods can be divided into traditional models, time series based, and Artificial Neural Networks (ANN). The most frequently used statistical models include autoregressive model, moving average, autoregressive moving average (ARMA), autoregressive integrated moving average (ARIMA), exponential smoothing, Markov chain, Generalized Autoregressive Conditional Heteroskedasticity (GARCH), among others [19,20,21,22]. Hybrid or mixed methods are due to the combination of different approaches (physical and statistical) and different time windows. The main objective of this method is to benefit from each method and improve the accuracy of the forecasts. Although it is not always achieved, it has been proved that there are lower risks in most situations. Among these methods are ANN-ARIMA, wavelet-ANN, wavelet-ARIMA, Kalman filter-ANN (KF + ANN), Wavelet-Support vector machine optimized by genetic algorithm (WT-SVM-GA), Isolation Forest (IF)-deep learning-ANN, CEE-CC-FS, among others [20,21,22,23,24,25].
In particular, the exponential smoothing method has great variability, adaptation, and a large number of applications. This method is characterized by giving weight to the error caused by the forecast and the experimental data and using the previous forecasts to generate the following predictions. Therefore, the latest observations significantly influence the current forecast, as is the case with short-term measurements of wind speed. However, according to works reported in the literature, the use of the exponential smoothing method in the prediction of wind speed is scarce [19]. In [19], the authors have analyzed the wind speed data collected in Chetumal, Quintana Roo by using a statistical analysis of the time series and the Single Exponential Smoothing (SES) method. Finally, in the work [19], the SES method has been compared with the artificial neural network method to prove that the SES method is very useful for wind speed forecasting (in particular for Chetumal, Quintana Roo). In [26], the authors have developed a combined forecasting system and validated it by comparing it with wind speed data sets from three different wind farms in Penglai, China. Furthermore, in the work [26], the performance of the model has been proved by contrasting it with an extension of the exponential smoothing method and two machine learning models. In the paper [27], two-hybrid forecasting systems based on the structural characteristics of wind speed have been proposed to capture the linear and nonlinear factors hidden in wind speed data. This is because the authors have used a decomposition algorithm to eliminate noise from raw data and reconstruct more reliable wind speed time data. So, a linear model based on the exponential smoothing method or autoregressive moving average model captures the linear patterns hidden and a nonlinear model based on the backpropagation neural network extracts the nonlinear patterns hidden in the data.
Although the use of the exponential smoothing method for the development of new forecasting methods for wind speed is scarce, different forecasting methods have been developed based on other traditional methods. In [10], the authors have evaluated the effects of a set of various moving average filter durations and turbulence intensities on the recorded maximum gust wind speed to present a function dependent on the average duration and turbulence intensity. In [28], a new forecasting method is proposed by the combination of the local convolutional neural network. The authors have transformed the non-convex problems into convex problems to obtain the globally optimal solutions for the convex problems by using heuristic optimization algorithms. Therefore, a more stable model can be constructed to deal with various wind speed data sets. In the work [29], the authors have developed a forecasting method to assess and predict wind speed by integrating Sentinel satellite imagery analysis. This process has been carried out by using multi-sensor satellites and machine learning methods. Furthermore, the developed method has been applied to assess wind energy potential around the Favignana island in Sicily, Italy. In [30], the authors have improved the accuracy of forecasting the short-term wind speed by developing a hybrid wind speed forecasting model based on four modules: crow search algorithm, wavelet transform, feature selection based on entropy and mutual information, and deep learning time series prediction based on long short term memory neural networks. Moreover, the proposed method developed in this work was applied to wind data from Galicia, Spain, and Iran. In [31], a combined prediction system has been proposed to develop a new forecasting method based on optimal sub-model selection, point prediction based on a modified multi-objective optimization algorithm, interval forecasting based on distribution fitting, and forecasting system evaluation.
From the current state of the art, this work focuses on developing four variants of the exponential smoothing forecasting method to optimize the forecast of wind speed. Thus, it is possible to propose strategies to improve the energy harvested from wind farms (in this case, for Yucatan peninsula wind farms) avoiding the main grid as much as possible. This would support the local economy and improve energy services. Furthermore, these methods can be applied to any kind of data.
This paper is divided into six sections. After the introduction, in Section 2 the characteristics of the experiment are described (i.e., experimental test set-up and characteristics of the area where the data were collected). In Section 3, a brief description of the SES method and the Double Exponential Smoothing (DES) method is provided. Later in Section 4, the optimization of the SES and DES methods is developed and explained. Subsequently, results and discussion of these forecasting methods developed are presented in Section 5. Finally, the conclusion of this work is given in Section 6.
2. Measurements Site and Characteristics
Data collection was carried out on the north coast of the state of Yucatan, Mexico. The surface of the territory is mainly flat and its elevation is 2 m above mean sea level. The climate of the site is warm semi-dry with rains in summer. Its average temperature is 26 °C with prevailing winds from the south-east [32].
The geographical characteristics of the measurement site are presented in Table 1 and its location in Figure 1.

Table 1.
Geographical characteristics of the measurement station.

Figure 1.
Location of the north coast of the Yucatan peninsula.
An ultrasonic wind sensor (Gill windsonic anemometer) was used to measure the speed and direction of the wind, placed at 40 m in a mobile phone tower; see Figure 2. This sensor records the horizontal components of the wind vector to generate the scalar values of wind speed and wind direction. The technical parameters of the ultrasonic sensor used are presented in Table 2 [33].

Figure 2.
Telecommunication tower with ultrasonic wind sensor.

Table 2.
Main technical characteristics of the measurement sensor.
The monitoring frequency for both variables was 1 Hz and the average data of every 10 min was stored in a data logger. The measurements were carried out during a year from January to December of 2011, Figure 3.
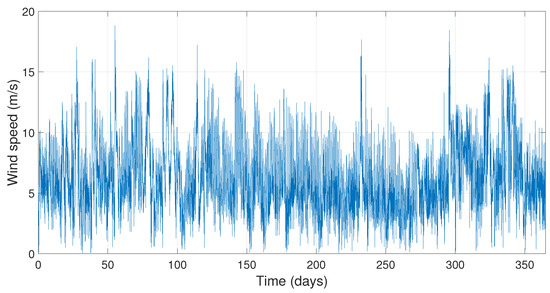
Figure 3.
Wind speed data behavior over a year.
The descriptive statistics for the site are presented in Table 3.

Table 3.
Descriptive statistics of the site.
The frequency distribution of the wind speed series and their probability distributions (Weibull and Normal) are shown in Figure 4.
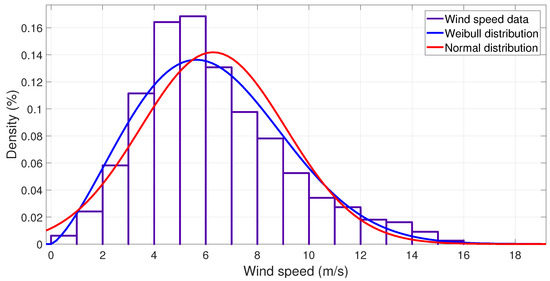
Figure 4.
Probability distributions for wind speed data.
The shape () and scale parameters () of the Weibull distribution () for the wind speed (v) are calculated as in [34].
where is the Gamma function.
3. Forecasting Methods for the Wind Speed
One way to analyze the wind speed data is by forecasting methods, since this type of data is essentially a complex process to be analytically modeled [35]. Moreover, as has been proved, some forecasting methods for the wind speed depend not only on the experimental data values, but can also be a function of the residuals of past forecasts, which corresponds to small periods [13,36]. Therefore, due to the behavior of the experimental data, the analysis has been carried out using these methods.
3.1. Moving Average
There are many wind speed forecasting methods. One of the most common is the moving average method, which is a time series constructed by taking averages of several sequential values of another time series [37]. In this study, the data analysis began with the average method, since the time series have demonstrated accuracy in wind speed forecasting [14]. Moreover, in the application of the wind speed, the moving average method is used to extract the wind power fluctuations [11].
To start the analysis of the experimental data, the moving average methods to forecast were as follows:
- (1)
- The Two-Period Simple Moving Average (2-SMA):
- (2)
- The Three-Period Simple Moving Average (3-SMA):
- (3)
- The Two-Period Double Moving Average (2-DMA):
- (4)
- The Three-Period Double Moving Average (3-DMA):
For all cases, and are the experimental data and the predictive value corresponding at time t, respectively.
3.2. Exponential Smoothing
Exponential smoothing is one of the classical methods used for forecasting. This method has been used in diverse fields of research [38,39]. In addition to forecasting, this method allows smoothing the analyzed function. Therefore, the data can be presented in a more convenient form and the random errors can be removed [19].
An efficient implementation of the method together with the descriptive and the inferential statistic is allowed due to its robustness [19]. This method is based on the intuitive application of movable averages, in where the tool to smooth the function is the combination of the error of the last observations and one or some constants [40]. In this work, the SES and DES methods are described.
The SES method used in this study is based on the methodology described in [19], which is presented as:
where is a constant taking values within the interval [0, 1] [19]. However, as will be shown later in Section 5, the optimal was greater than 1 for some cases.
For the DES method, the equations presented in [40] are used:
where and are constants. Like , the values of and must be between 0 and 1 [40]. However, as is presented in Section 5, the optimal was greater than 1 and the optimal was lower than 1 for some cases.
4. Proposed Optimization of SES and DES Methods for Wind Speed Data
The non-linear least squares function (Equation (10)) has been implemented to optimally calculate the parameters , , and for each day of the year according to the experimental data obtained, as an optimization for the SES and DES methods. The minimum daily error of the SES and DES methods was calculated by adjusting the parameters , , and . With these parameters, it is possible to develop variants of the traditional SES and DES methods as described in this section.
where n is the number of data, p is the set of parameters of the equations (i.e., for (8) and for (9)).
With optimal parameters, two variants from the SES method and two variants from the DES method have been proposed. The first variant for the SES method is given by:
where
where is the optimal parameter of the day k and N is the number of days of the month (i.e., N is equal to 28, 30, or 31 depending on the month). has been calculated by using the command lsqcurvefit in the software MATLAB. As can be seen, this variant consists in obtaining the average of the optimal s corresponding to a month. Then this average is implemented in the classical SES method.
The second variant for the SES method is given by:
In this variant, the classical SES method has been adapted by iterations of the optimal value of , in other words, it is the optimal parameter of the previous day k, the optimum value has been used for the first day of each month ().
Similarly, the variants of the DES method are similar to the variants of the SES method. The first variant of the DES method is given by:
where and are similarly as
where and are the optimal parameter of the day k and they have been calculated by using the command lsqcurvefit in Matlab.
Finally, the second variant of the DES method is given by:
As for Equation (13), the optimum values and have been used for the first day of each month ().
5. Results and Discussion
To apply the methods developed in Section 4, the optimal constants , , and for each day have been calculated using MATLAB. Figure 5 and Figure 6 illustrate the optimal behavior from the months January–June.
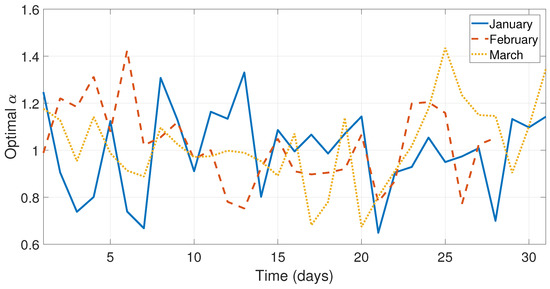
Figure 5.
Optimal values of for the days from the months January, February, and March.
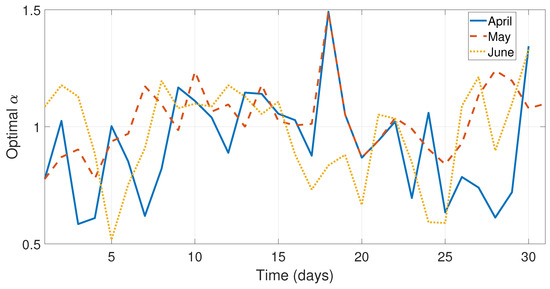
Figure 6.
Optimal values of for the days from the months April, May, and June.
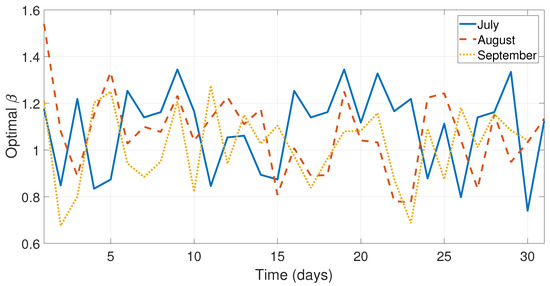
Figure 7.
Optimal values of for the days from the months July, August, and September.
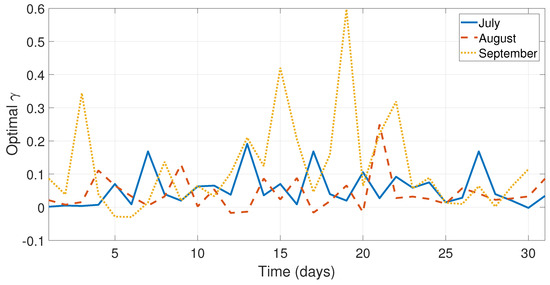
Figure 8.
Optimal values of for the days from the months July, August, and September.
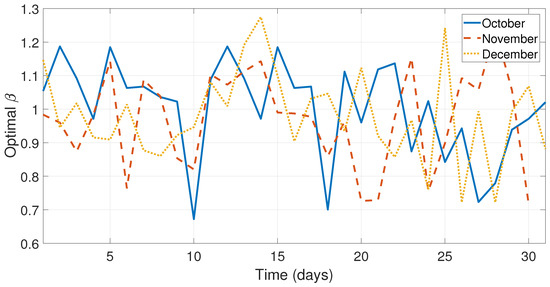
Figure 9.
Optimal values of for the days from the months October, November, and December.
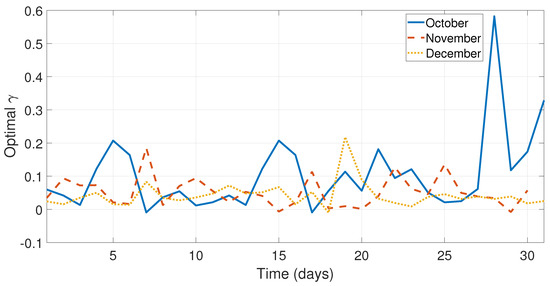
Figure 10.
Optimal values of for the days from the months October, November, and December.
As can be seen in Figure 5, Figure 6 and Figure 7 and Figure 9, the values of the optimal constants and in some cases are greater than 1, which contrasts the theory of the classical SES and DES methods, since the values and are assumed to be between 0 and 1 [19,40]. Similarly, the value of the optimal constant in some cases is lower than 1, when it is speculated that the value oscillates between 0 and 1 according to the classic DES method [40], see Figure 8 and Figure 10.
With the values of the optimal constants , , and , the values of , , and have been calculated for each month of the year, as presented in Table 4.

Table 4.
Value of , , and for each month of the year.
Once the values of constants , , and have been obtained, the methods developed in Section 4 are applied.
5.1. Simulation
To evaluate and compare forecasting methods, the relative error , the mean error , the mean squared error , the root mean square error , and the coefficient of determination have been calculated as follows:
where is the mean of the month
As mentioned in Section 3, the first forecasting methods for wind speed were based on the moving average method. Moreover, the recursive function was analyzed. This is due to the similarity with the proposed method. Table 5 reports the relative errors of the methods 2-SMA, 3-SMA, 2-DMA, 3-DMA, and the recursive function .

Table 5.
Relative error of each month for the moving average methods and the recursive function.
As presented in Table 5, the recursive function reports the best performance between these five methods. However, the methods developed in Section 4 are implemented to reduce the relative and mean errors obtained by the recursive function.
With the values obtained for , , , , , and in the previous subsection, the methods developed in Section 4 have been applied. After that, the forecasts with these methods have been analyzed and compared to the experimental data using different error flags. A summary of the results obtained from this analysis is presented in Table 6, Table 7, Table 8, Table 9 and Table 10.

Table 6.
Relative error of each month for the methods developed.

Table 7.
Mean error of each month for the methods developed.

Table 8.
Mean squared error of each month for the methods developed.

Table 9.
Root mean square error of each month for the methods developed.

Table 10.
Coefficient of determination of each month for the methods developed.
As can be seen in Table 6, the ranges of the relative error were: 5.8199% to 10.4158% for SES method with ; 6.0283% to 11.1853% for DES method with and ; 5.8835% to 10.5249% for SES method with ; and 7.3060% to 18.6109% for DES method with and . Furthermore, the average relative errors were 7.9510%, 8.4128%, 8.0213%, and 10.0586% for SES with , DES with and , SES with , and DES with and , respectively.
In the analysis of the relative error , the method with the best performance for each month was the SES method with except for February and June where the SES method with obtained the smallest error, see Table 4. However, the SES method with generally performed the best as its average relative error was the lowest.
As presented in Table 7, the ranges of the mean error were: 0.3524 m/s to 0.4241 m/s for SES method with ; 0.3620 m/s to 0.4506 m/s for DES method with and ; 0.3564 m/s to 0.4249 m/s for SES method with ; and 0.4079 m/s to 1.0123 m/s for DES method with and . Moreover, the average mean errors were 0.3860 m/s, 0.4074 m/s, 0.3905 m/s, and 0.5062 m/s for SES with , DES with and , SES with , and DES with and , respectively.
In the analysis of mean error , the method with the best performance for each month was the SES method with , see Table 6. Therefore, based on the mean error analysis, the SES method with has the best performance.
In Table 8 and Table 9, the mean squared errors and the root mean squared errors are reported. The ranges of the mean squared error were: 0.2485 to 0.5009 for SES method with ; 0.2805 to 0.5511 for DES method with and ; 0.2558 to 0.5046 for SES method with ; and 0.3455 to 11.2723 for DES method with and . Furthermore, the average mean squared errors were 0.3615, 0.4046, 0.3681, and 1.4478 for SES with , DES with and , SES with , and DES with and , respectively. The ranges of the root mean squared error were: 0.4985 m/s to 0.7077 m/s for SES method with ; 0.5296 m/s to 0.7423 m/s for DES method with and ; 0.5058 m/s to 0.7423 m/s for SES method with ; and 0.5878 m/s to 3.3574 m/s for DES method with and . Moreover, the average root mean squared error were 0.5974 m/s, 0.6319 m/s, 0.6029 m/s, and 0.9555 m/s for SES with , DES with and , SES with , and DES with and , respectively.
Based on the analysis of mean squared error and the root mean squared error, the method with the best performance was the SES method with .
Table 10 reports the coefficients of determination. These values had the following ranges: 0.9132 to 0.9755 for SES method with ; 0.9081 to 0.9727 for DES method with and ; 0.9117 to 9748 for SES method with ; and 0.4691 to 0.9621 for DES method with and . The average coefficients of determination were 0.9459, 0.9426, 0.9447, and 0.8882 for SES with , DES with and , SES with , and DES with and , respectively. In this case, the SES method with has reported better performance.
Once the analysis had been carried out, the simulations were carried out to be able to observe the behavior of the forecasting methods developed in this work. The simulations compared the SES with , DES with and , SES with , DES with and , and 2-SMA methods, which have shown the lowest relative and mean errors. In Figure 11 and Figure 12 the behavior of the data taken on the first day of January and the simulations of the forecasting methods proposed in this work can be appreciated. In Figure 13 and Figure 14, the errors between experimental data and the forecast for the first day of May have been illustrated, which is the month with the lowest relative errors (see Table 6). The last four simulations illustrate the behavior and comparison of the forecasts with the highest relative and mean error, see Table 6 and Table 7. In Figure 15 and Figure 16, the behaviors of the data taken and the forecasts corresponding to the first day August have been shown, in this month the SES with , DES with and , and 2-SMA methods incurred their largest relative error. Finally, Figure 17 and Figure 18 illustrate the behavior of the error of the comparison between experimental data and the forecasts for the first day of September, where the SES method with and DES method with and obtained their largest relative error.
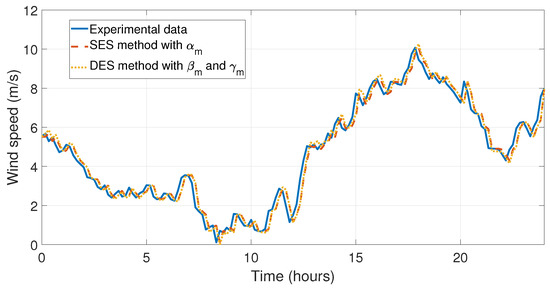
Figure 11.
Simulation and comparison of the SES method with and DES method with and with the experimental data for the first day of January.
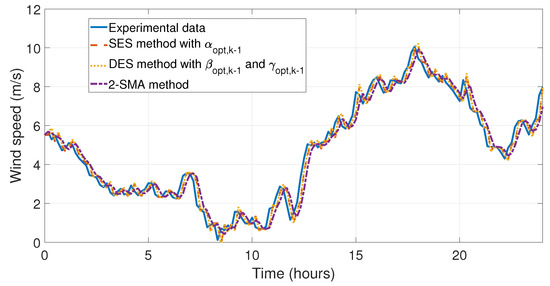
Figure 12.
Simulation and comparison of the SES method with , DES method with and , and 2-SMA method with the experimental data for the first day of January.
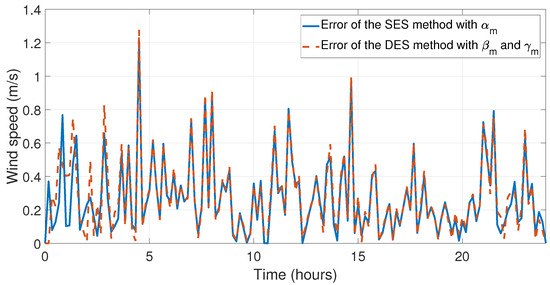
Figure 13.
Error when comparing the experimental data with the simulation data of the SES method with and DES method with and for the first day of May (month with the lowest relative errors).
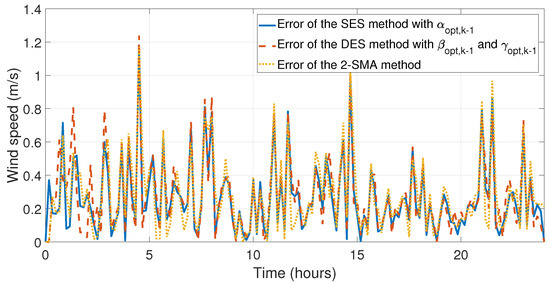
Figure 14.
Error when comparing the experimental data with the simulation data of the SES method with , DES method with and , and 2-SMA method for the first day of May (month with the lowest relative errors).
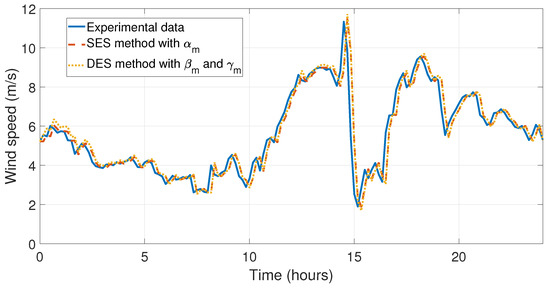
Figure 15.
Simulation and comparison of the SES method with and DES method with and with the experimental data for the first day of August.
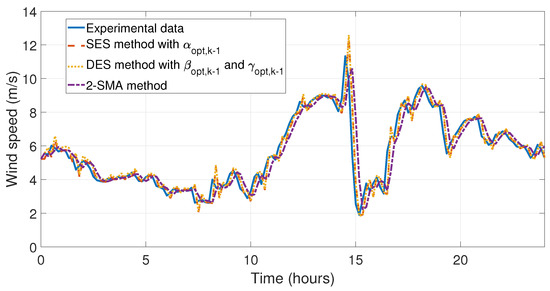
Figure 16.
Simulation and comparison of the SES method with , DES method with and , and 2-SMA method with the experimental data for the first day of August (these methods obtained their largest relative error in this month).
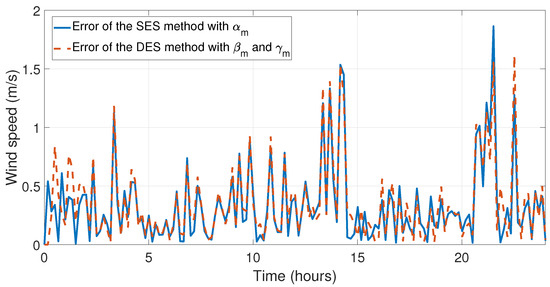
Figure 17.
Error when comparing the experimental data with the simulation data of the SES method with and DES method with and for the first day of September (these methods obtained their largest relative error in this month).
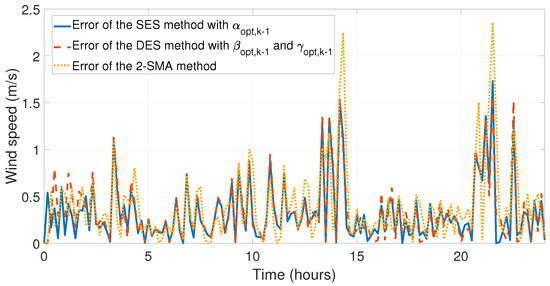
Figure 18.
Error when comparing the experimental data with the simulation data of the SES method with , DES method with and , and 2-SMA method for the first day of September.
5.2. Discussion
With the methods developed in this work, it is possible to obtain up to an average relative error %, an average mean error m/s, an average mean squared error , an average root mean square error m/s, and an average coefficient of determination , which indicate a high degree of accuracy of the proposed methods (i.e., due to the amount of experimental data used in this work, 52,560 wind speed data). Moreover, based on the analysis carried out, the SES method with has reported the best performance by having the lowest errors. Therefore, the developed method in this work is effective in forecasting wind speed data. However, the estimation of the model is not optimal, and errors between the experimental data and the model can be observed. Furthermore, the obtained errors are particularly noticeable in some months, which are complex to forecast according to the weather conditions. Thus, taking into account the weather conditions, it is possible to increase the reliability of this forecasting method.
6. Conclusions
In this study, four methods have been developed based on the classic SES and DES methods to forecast the wind speed in the north coast of the Yucatan peninsula. Statistical tests have demonstrated the effectiveness of these methods. Thus, strategies to optimize the energy harvests from wind farms in this region can be established. However, the variability of the weather affects the performance of the proposed methods. To solve this, it is necessary to collect more data from the studied area to find patterns for improving forecasting methods. It is also worth mentioning that forecasting methods developed in this work can be applied not only for wind speed data but for different kinds of data.
Author Contributions
Conceptualization, C.P.-A., Á.H.-G. and V.R.; methodology, C.P.-A. and V.R.; software, Á.H.-G.; validation, C.P.-A. and Á.H.-G.; formal analysis, Á.H.-G.; investigation, C.P.-A. and V.R.; resources, D.G.; data curation, C.P.-A.; writing—original draft preparation, Á.H.-G.; writing—review and editing, C.P.-A., Á.H.-G., V.R. and D.G.; visualization, C.P.-A. and V.R.; supervision, V.R.; project administration, Á.H.-G.; funding acquisition, D.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
This work has been supported by Consejo Nacional de Ciencia y Tecnología (CONACYT) Mexico.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RES | Renewable Energy Sources |
| NWP | Numerical Weather Prediction |
| ANN | Artificial Neural Networks |
| AMA | Autoregressive Moving Average |
| ARIMA | Autoregressive Integrated Moving Average |
| GARCH | Generalized Autoregressive Conditional Heteroskedasticity |
| KF+ANN | Kalman filter-ANN |
| WT-SVM-GA | Wavelet-Support vector machine optimized by genetic algorithm |
| IF | Isolation Forest |
| SES | Single Exponential Smoothing |
| DES | Double Exponential Smoothing |
| 2-SMA | Two-Period Simple Moving Average |
| 3-SMA | Three-Period Simple Moving Average |
| 2-DMA | Two-Period Double Moving Average |
| 3-DMA | Three-Period Double Moving Average |
References
- Looney, B.; Dale, S. Statistical Review of World Energy 2021. 2021. Available online: www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/statistical-review/bp-stats-review-2021-full-report.pdf (accessed on 15 July 2021).
- GWEC. Global Wind Report 2021. 2021. Available online: https://gwec.net/global-wind-report-2021/ (accessed on 15 July 2021).
- REN21 Renewables Now. Renewables 2021 Global Status Report. 2021. Available online: https://www.ren21.net/wp-content/uploads/2019/05/GSR2021_Full_Report.pdf (accessed on 15 July 2021).
- SENER. Inventario Nacional de Energías Limpias, Estadísticas. 2018. Available online: https://dgel.energia.gob.mx/inel/index.html (accessed on 15 July 2021).
- Brancho, R.; Flores-Espino, F.; Morgenstein, J.; Aznar, A.; Castillo, R.; Settle, E. The Yucatan Peninsula Energy Assessment: Pathways for a Clean and Sustainable Power System, 1st ed.; National Renewable Energy Laboratory: Golden, CO, USA, 2021. Available online: https://www.nrel.gov/docs/fy21osti/79680.pdf (accessed on 15 July 2021).
- de México, H. Mauricio vila Dosal Inaugura Parque Eólico “Dzilam de Bravo” en Yucatán, Tech. Rep., El Heraldo de México. 2019. Available online: https://heraldodemexico.com.mx/nacional/2019/5/4/mauricio-vila-dosal-inaugura-parque-eolico-dzilam-de-bravo-en-yucatan-91367.html (accessed on 15 July 2021).
- de México, H. Inauguran Parque Eólico en Tizimín, Yucatán y Anuncian Construcción de Otro. el Heraldo de México, Tech. Rep., El Heraldo de México. 2020. Available online: https://heraldodemexico.com.mx/nacional/2020/12/14/inauguran-parque-eolico-en-tizimin-yucatan-anuncian-construccion-de-otro-235574.html (accessed on 15 July 2021).
- Yucatán, N. Inauguran el Parque Eólico “Progreso”; Generará Energía Para 215 mil Viviendas, Tech. Rep., Novedades Yucatán. 2020. Available online: https://sipse.com/novedades-yucatan/inauguracion-parque-eolico-progreso-inversion-yucatan-energia-renovables-374631.html (accessed on 15 July 2021).
- I. 61400-12-1:2017; Wind Energy Generation Systems—Power Performance Measurements of Electricity Producing Wind Turbines. Tech. Rep.; International Standard, S&P Global Inc.: New York City, NY, USA, 2017. Available online: https://webstore.iec.ch/publication/26603 (accessed on 15 July 2021).
- Safaei Pirooz, A.A.; Flay, R.G.; Minola, L.; Azorin-Molina, C.; Chen, D. Effects of sensor response and moving average filter duration on maximum wind gust measurements. J. Wind. Eng. Ind. Aerodyn. 2020, 206, 104354. [Google Scholar] [CrossRef]
- Xin, P.; Liu, Y.; Yang, N.; Song, X.; Huang, Y. Probability distribution of wind power volatility based on the moving average method and improved nonparametric kernel density estimation. Glob. Energy Interconnect. 2020, 3, 247–258. [Google Scholar] [CrossRef]
- Miller, C.; Holmes, J.; Henderson, D.; Ginger, J.; Morrison, M. The response of the dines anemometer to gusts and comparisons with cup anemometers. J. Atmos. Ocean. Technol. 2013, 30, 1320–1336. [Google Scholar] [CrossRef]
- Erdem, E.; Shi, J. Arma based approaches for forecasting the tuple of wind speed and direction. Appl. Energy 2011, 88, 1405–1414. [Google Scholar] [CrossRef]
- Tascikaraoglu, A.; Uzunoglu, M. A review of combined approaches for prediction of short-term wind speed and power. Renew. Sustain. Energy Rev. 2014, 34, 243–254. [Google Scholar] [CrossRef]
- Wang, X.; Guo, P.; Huang, X. A review of wind power forecasting models. Energy Procedia 2011, 12, 770–778. [Google Scholar] [CrossRef]
- Hanifi, S.; Liu, X.; Lin, Z.; Lotfian, S. A critical review of wind power forecasting methods—past, present and future. Energies 2020, 13, 3764. [Google Scholar] [CrossRef]
- Nazir, M.S.; Alturise, F.; Alshmrany, S.; Nazir, H.M.J.; Bilal, M.; Abdalla, A.N.; Sanjeevikumar, P.; Ali, Z.M. Wind generation forecasting methods and proliferation of artificial neural network: A review of five years research trend. Sustainability 2020, 12, 3778. [Google Scholar] [CrossRef]
- Saroha, S.; Aggarwal, S.K.; Rana, P. Wind power forecasting. In Forecasting in Mathematics; Jaoude, A.A., Ed.; IntechOpen: Rijeka, Croatia, 2021; Chapter 4; pp. 1–15. [Google Scholar] [CrossRef]
- Cadenas, E.; Jaramillo, O.; Rivera, W. Analysis and forecasting of wind velocity in chetumal, quintana roo, using the single exponential smoothing method. Renew. Energy 2010, 35, 925–930. [Google Scholar] [CrossRef]
- Barbosa de Alencar, D.; De Mattos Affonso, C.; Limão de Oliveira, R.C.; Moya Rodríguez, J.L.; Leite, J.C.; Reston Filho, J.C. Different models for forecasting wind power generation: Case study. Energies 2017, 10, 1976. [Google Scholar] [CrossRef]
- Jiang, P.; Wang, B.; Li, H.; Lu, H. Modeling for chaotic time series based on linear and nonlinear framework: Application to wind speed forecasting. Energy 2019, 173, 468–482. [Google Scholar] [CrossRef]
- Yousuf, M.U.; Al-Bahadly, I.; Avci, E. Wind speed prediction for small sample dataset using hybrid first-order accumulated generating operation-based double exponential smoothing model. Energy Sci. Eng. 2022, 10, 726–739. [Google Scholar] [CrossRef]
- Chen, Q.; Folly, K.A. Short-term wind power forecasting using mixed input feature-based cascade-connected artificial neural networks. Front. Energy Res. 2021, 9, 634639. [Google Scholar] [CrossRef]
- Santhosh, M.; Venkaiah, C.; Vinod Kumar, D.M. Current advances and approaches in wind speed and wind power forecasting for improved renewable energy integration: A review. Eng. Rep. 2020, 2, e12178. [Google Scholar] [CrossRef]
- Tipi, N. Supply Chain Analytics and Modelling: Quantitative Tools and Applications, Kogan Page. 2021. Available online: https://books.google.com.mx/books?id=VVAlEAAAQBAJ (accessed on 23 August 2021).
- Wang, J.; Li, Q.; Zeng, B. Multi-layer cooperative combined forecasting system for short-term wind speed forecasting. Sustain. Energy Technol. Assess. 2021, 43, 100946. [Google Scholar] [CrossRef]
- Huang, X.; Wang, J.; Huang, B. Two novel hybrid linear and nonlinear models for wind speed forecasting. Energy Convers. Manag. 2021, 238, 114162. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, J.; Xiao, L.; Fu, T. Short-term wind speed time series forecasting based on a hybrid method with multiple objective optimization for non-convex target. Energy 2021, 215, 119180. [Google Scholar] [CrossRef]
- Nezhad, M.M.; Heydari, A.; Pirshayan, E.; Groppi, D.; Garcia, D.A. A novel forecasting model for wind speed assessment using sentinel family satellites images and machine learning method. Renew. Energy 2021, 179, 2198–2211. [Google Scholar] [CrossRef]
- Memarzadeh, G.; Keynia, F. A new short-term wind speed forecasting method based on fine-tuned lstm neural network and optimal input sets. Energy Convers. Manag. 2020, 213, 112824. [Google Scholar] [CrossRef]
- Jiang, P.; Liu, Z.; Niu, X.; Zhang, L. A combined forecasting system based on statistical method, artificial neural networks, and deep learning methods for short-term wind speed forecasting. Energy 2021, 217, 119361. [Google Scholar] [CrossRef]
- INAFED. Enciclopedia de los Municipios y Delegaciones de Mexico. Dzilam de Bravo. 2021. Available online: https://www.inafed.gob.mx/work/enciclopedia/EMM31yucatan/municipios/31028a.html (accessed on 15 July 2021).
- Gill Instruments Limited. Wind Sonic. Wind Speed & Direction Sensor. 2019. Available online: https://pdf.directindustry.com/pdf/gill-instruments/windsonic-wind-speed-direction-sensor/57743-69689-_2.html (accessed on 15 July 2021).
- Pramod, J. Wind Energy Engineering, 1st ed.; McGraw Hill: New York, NY, USA, 2010. [Google Scholar]
- Huang, Z.; Chalabi, Z. Use of time-series analysis to model and forecast wind speed. J. Wind. Eng. Ind. Aerodyn. 1995, 56, 311–322. [Google Scholar] [CrossRef]
- Torres, J.; García, A.; De Blas, M.; De Francisco, A. Forecast of hourly average wind speed with arma models in navarre (spain). Sol. Energy 2005, 79, 65–77. [Google Scholar] [CrossRef]
- Seong, B. Smoothing and forecasting mixed-frequency time series with vector exponential smoothing models. Econ. Model. 2020, 91, 463–468. [Google Scholar] [CrossRef]
- Nafil, A.; Bouzi, M.; Anoune, K.; Ettalabi, N. Comparative study of forecasting methods for energy demand in morocco. Energy Rep. 2020, 6, 523–536. [Google Scholar] [CrossRef]
- Jung, J.; Tam, K.-S. A frequency domain approach to characterize and analyze wind speed patterns. Appl. Energy 2013, 103, 435–443. [Google Scholar] [CrossRef]
- Gardner, E.S. Exponential smoothing: The state of the art—Part II. Int. J. Forecast. 2006, 22, 637–666. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).