Analyzing the Applicability of Random Forest-Based Models for the Forecast of Run-of-River Hydropower Generation
Abstract
:1. Introduction
- time series of climate data (precipitation and temperature),
- time series of the hydropower production at level of a country, and
- hydropower yearly installed capacity.
2. Materials
2.1. Climate Input Data
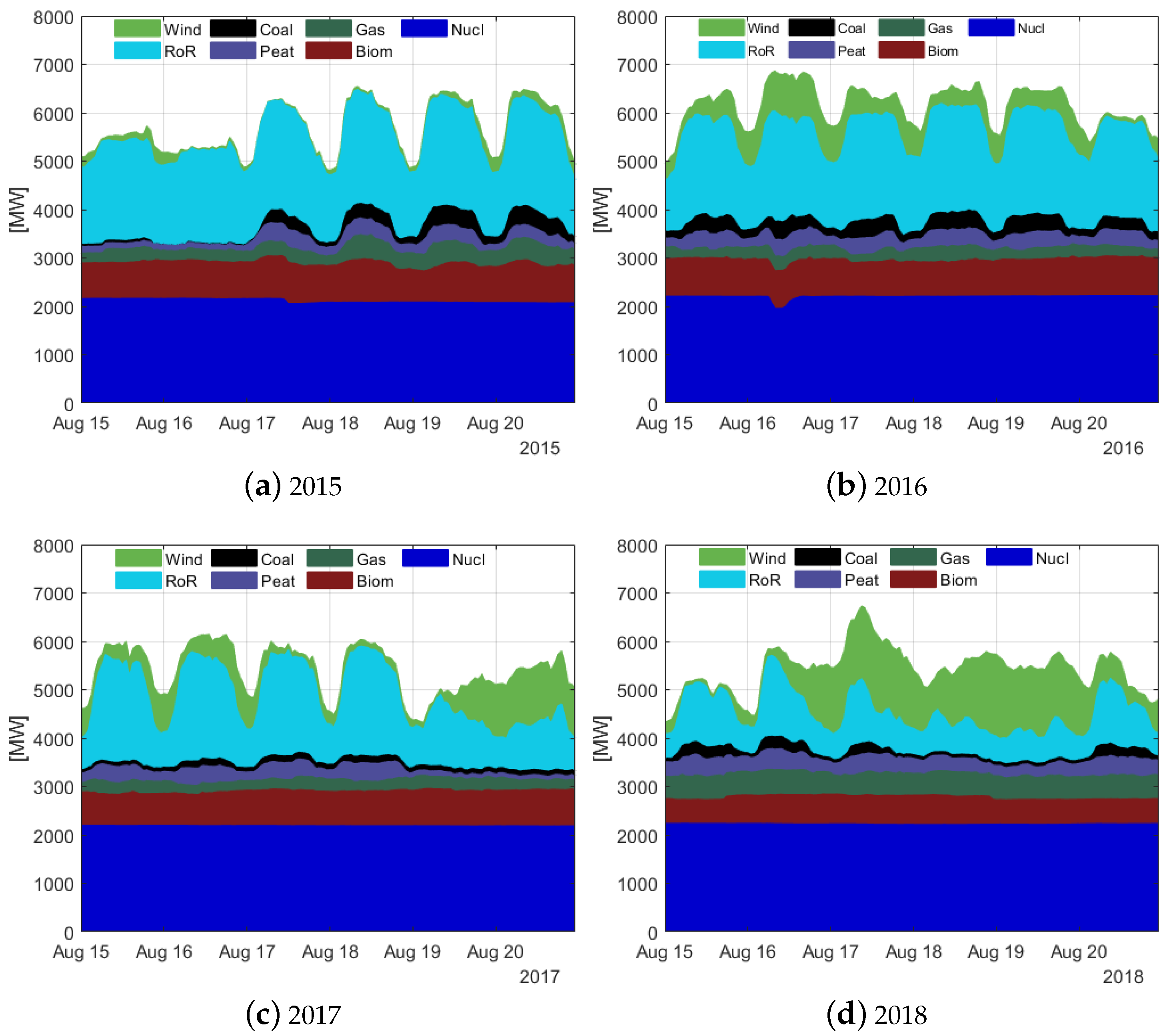
2.2. Hydropower Production and Installed Capacity Data
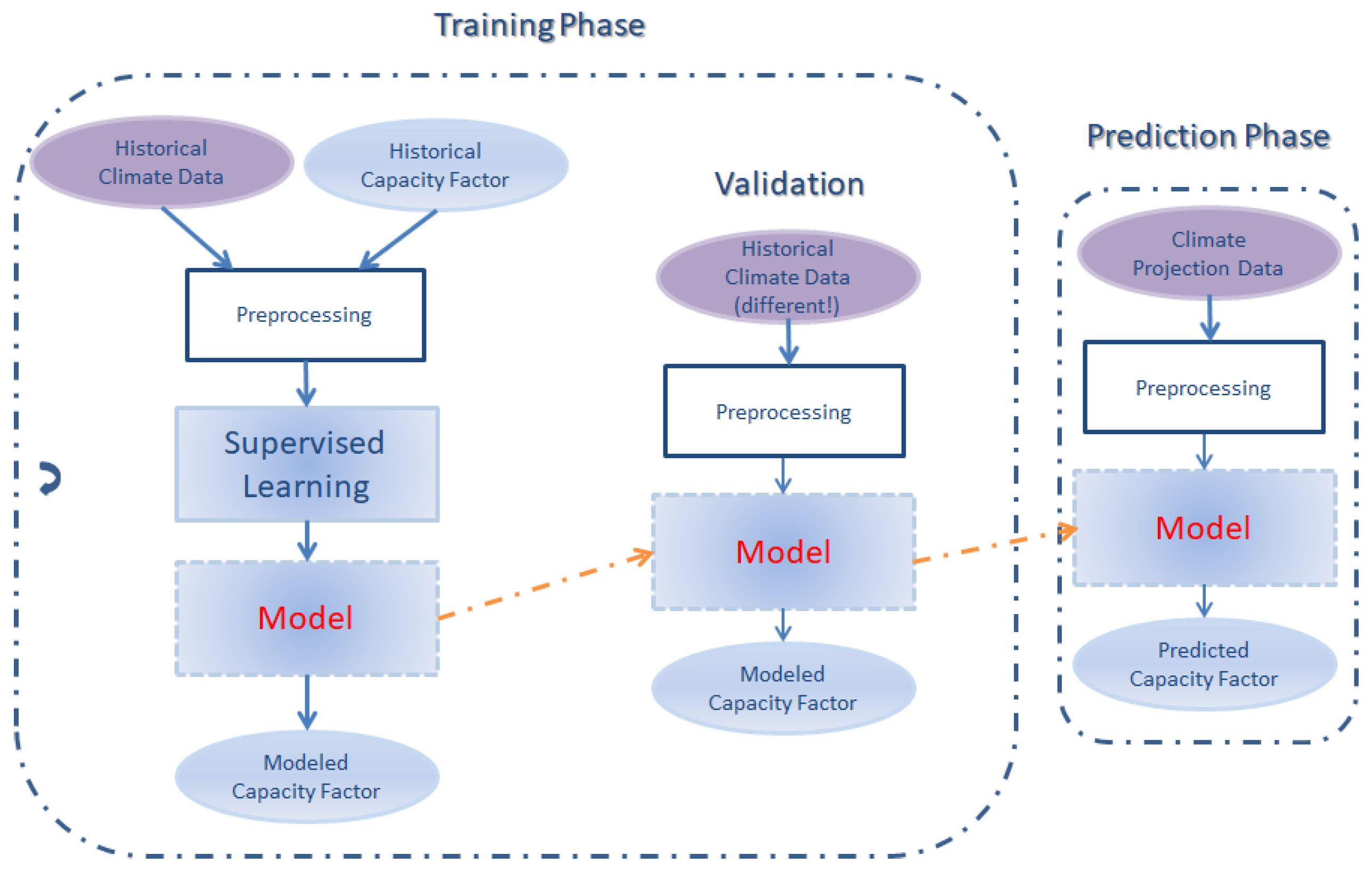
3. Methodology
3.1. Machine Learning
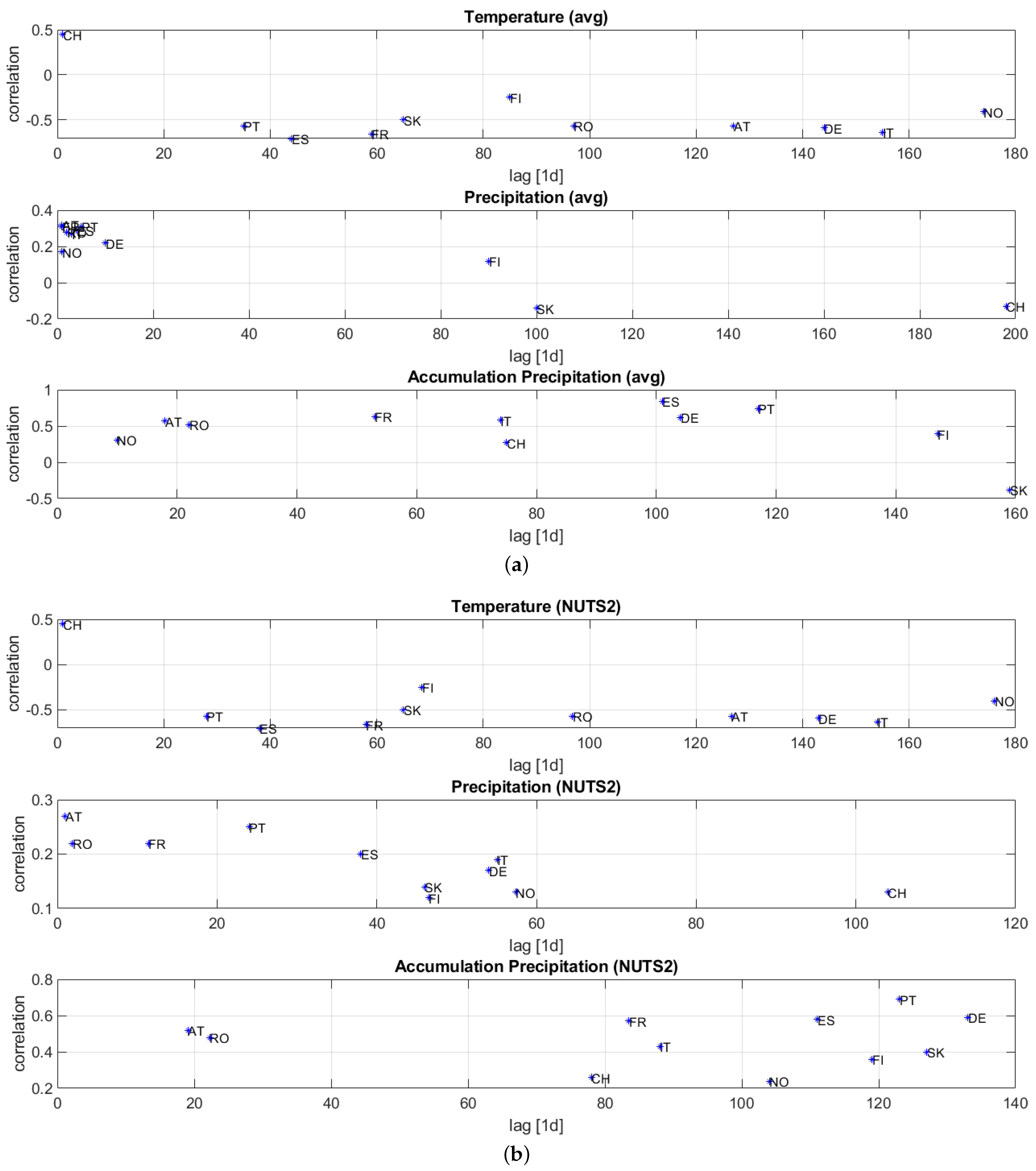
3.2. Choice of the Predictors
- air temperature, i.e., the time series ;
- precipitation, i.e., the time series ; and
- capacity factor of hydropower generation, i.e., the time series .
- the air temperature at the preceding -th day with respect to , where is computed by considering the lag that maximizes the sample Pearson correlation [22] between the time series of the hydropower generation y and of the air temperature , say ;
- the precipitation at the preceding -th day with respect to , where is computed similarly to by considering ; and
- the sum of precipitation in the last days with respect to , with defined as explained above.
3.3. Model Validation
- Correlation coefficient (R)where is the covariance, and and are the standard deviation of and , respectively. It is a measure of the strength and direction of the linear relationship between the observed and the modeled variables.
- Normalized Mean Absolute Error ()Note that the normalized version of MAE is preferred in this case as the actual CF may include also zero or close to zero values, then the classical mean absolute percentage error would lead to large error values.
- Normalized Root Mean Square Error ()where .
4. Results
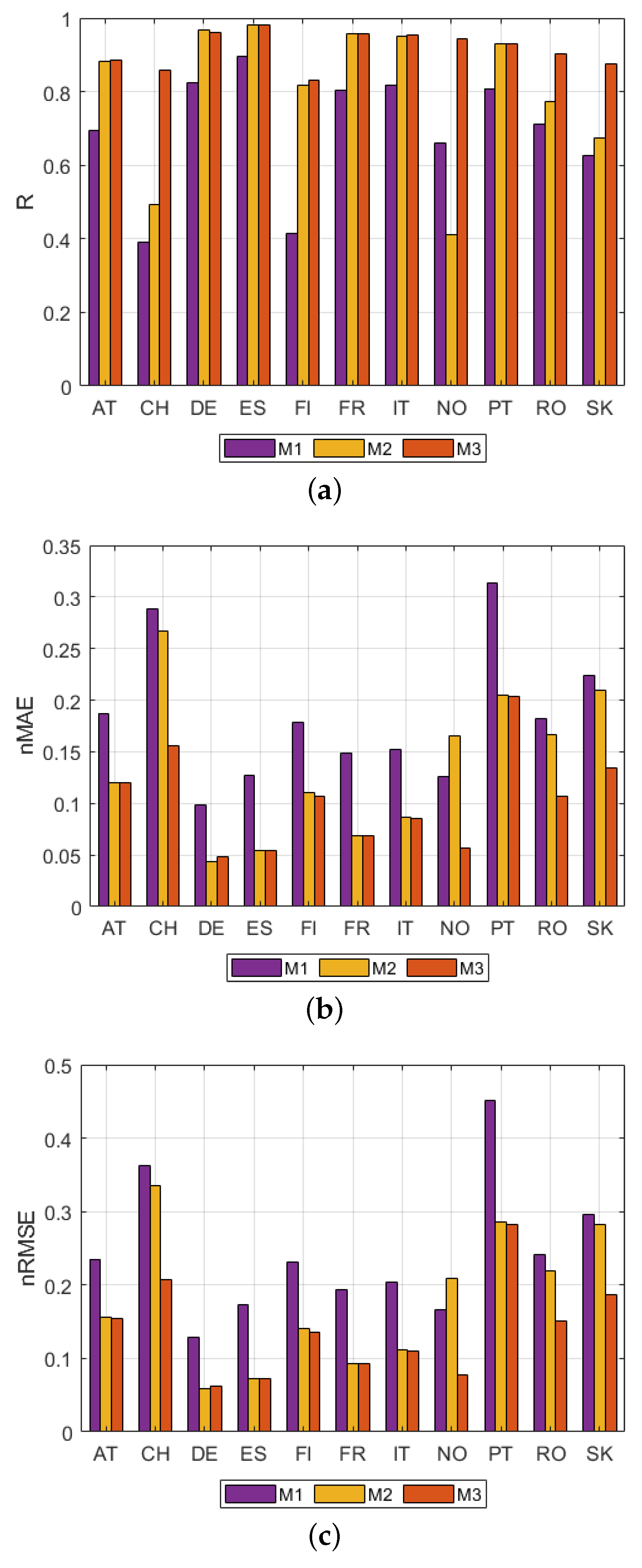
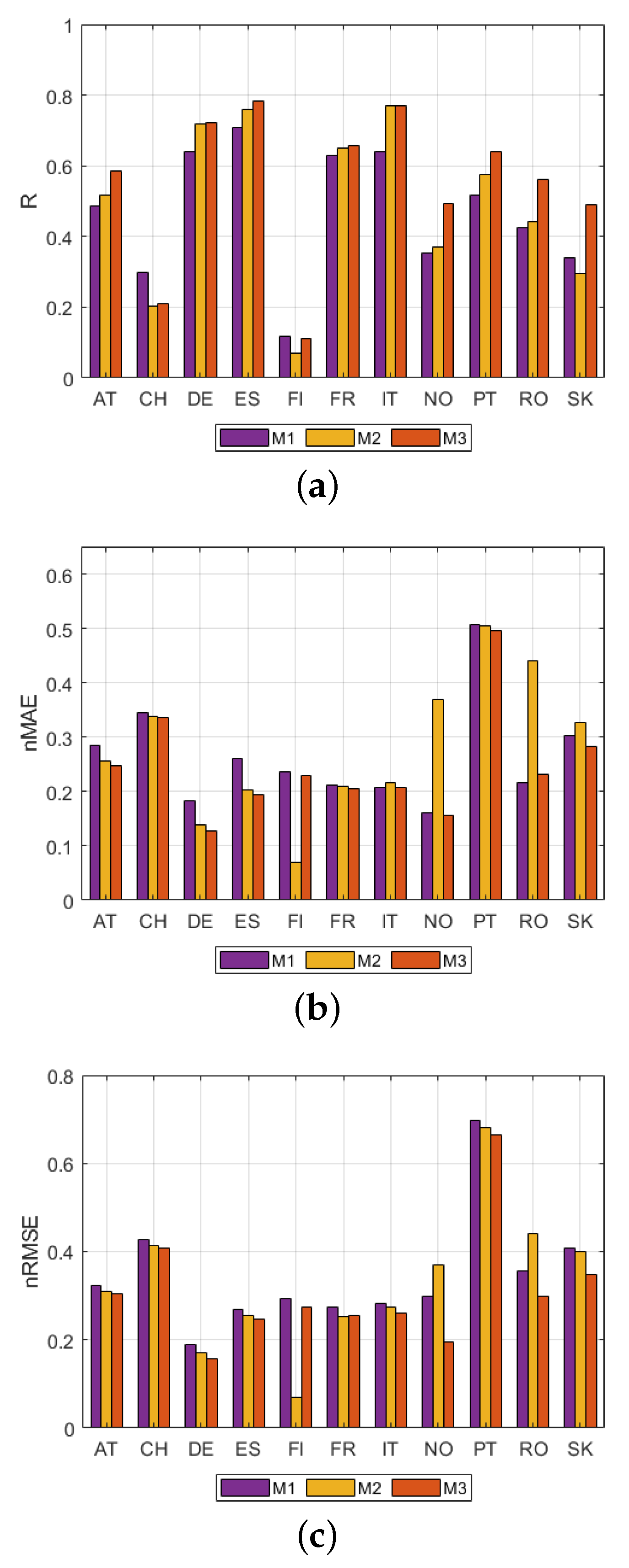
4.1. Model Selection
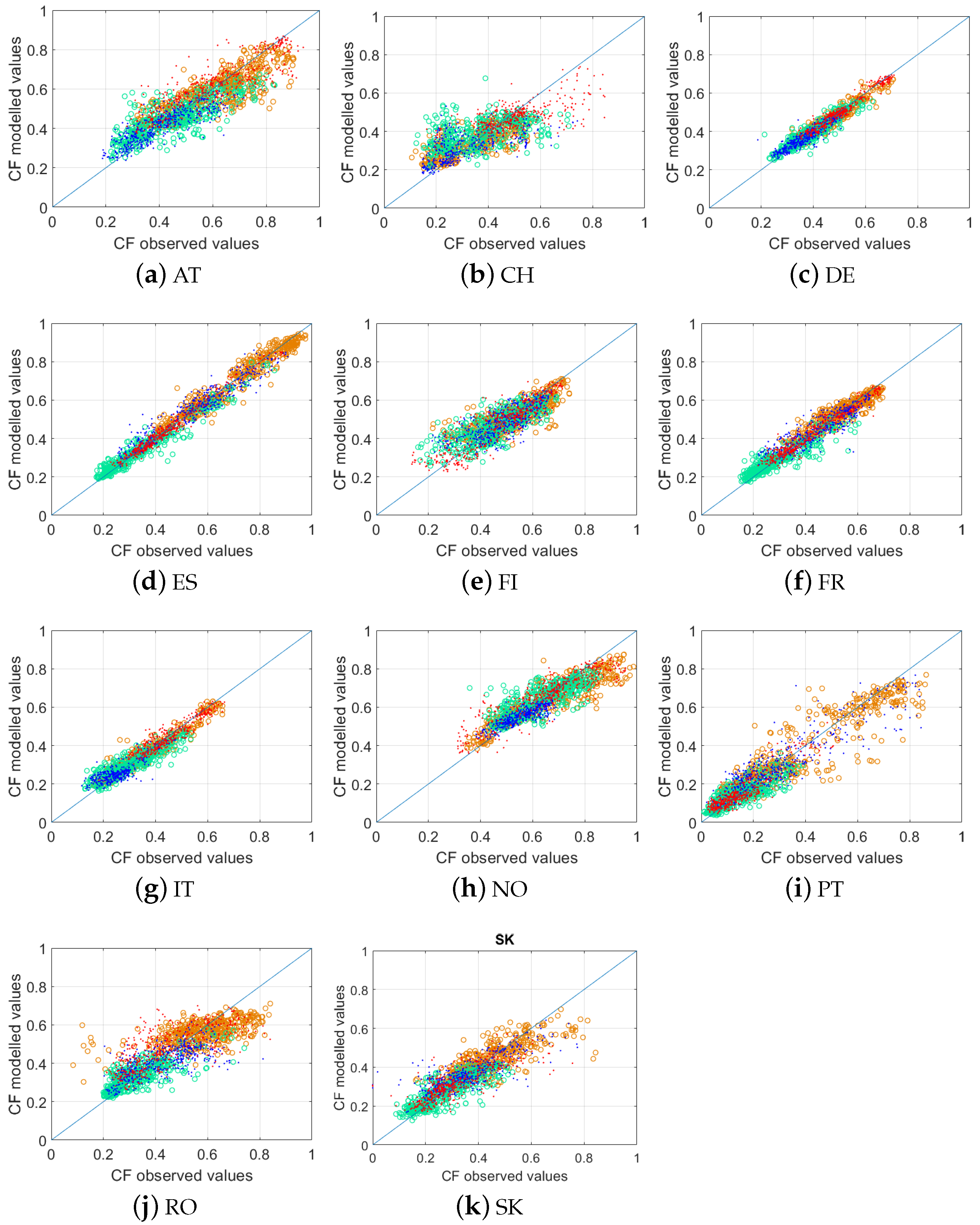
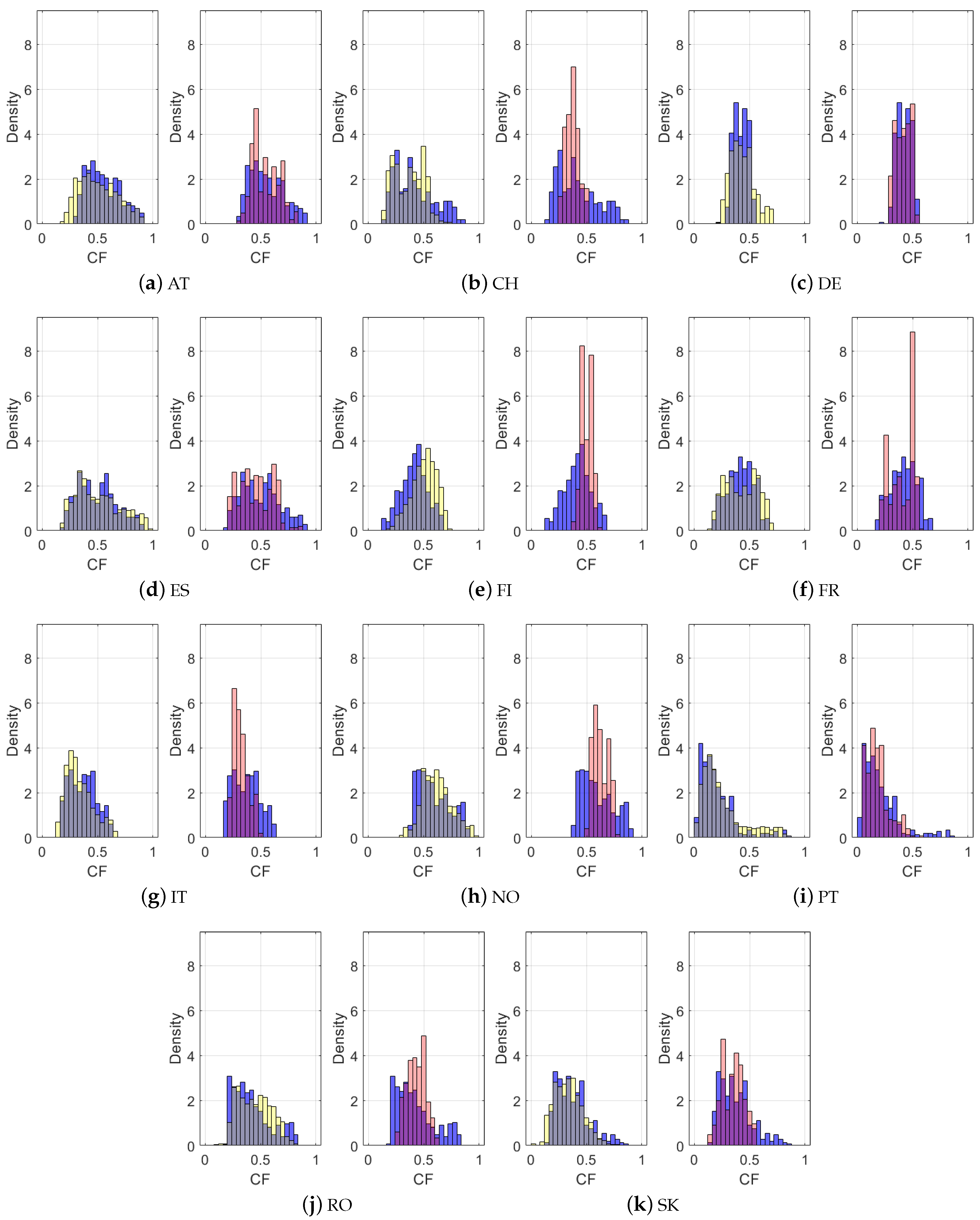
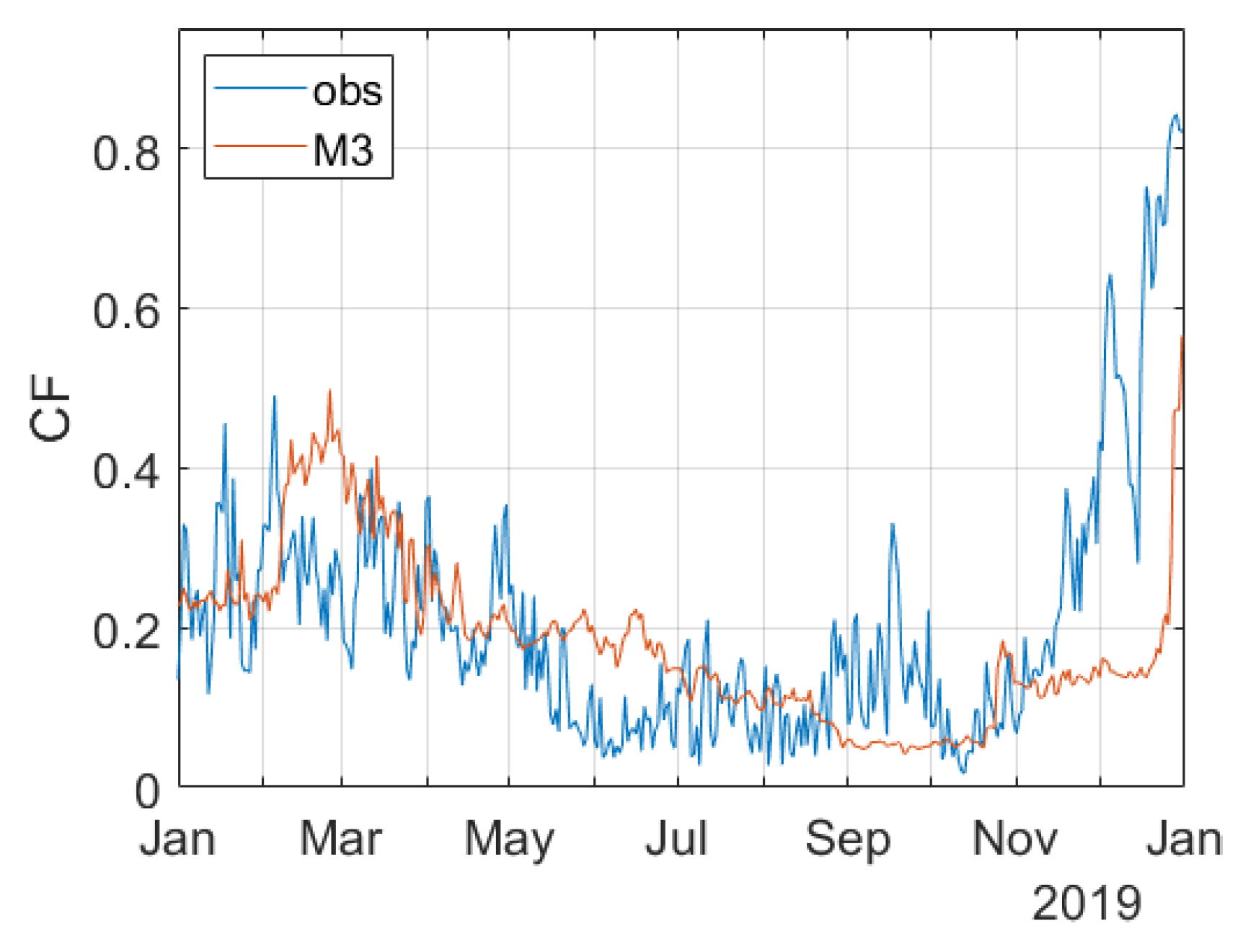
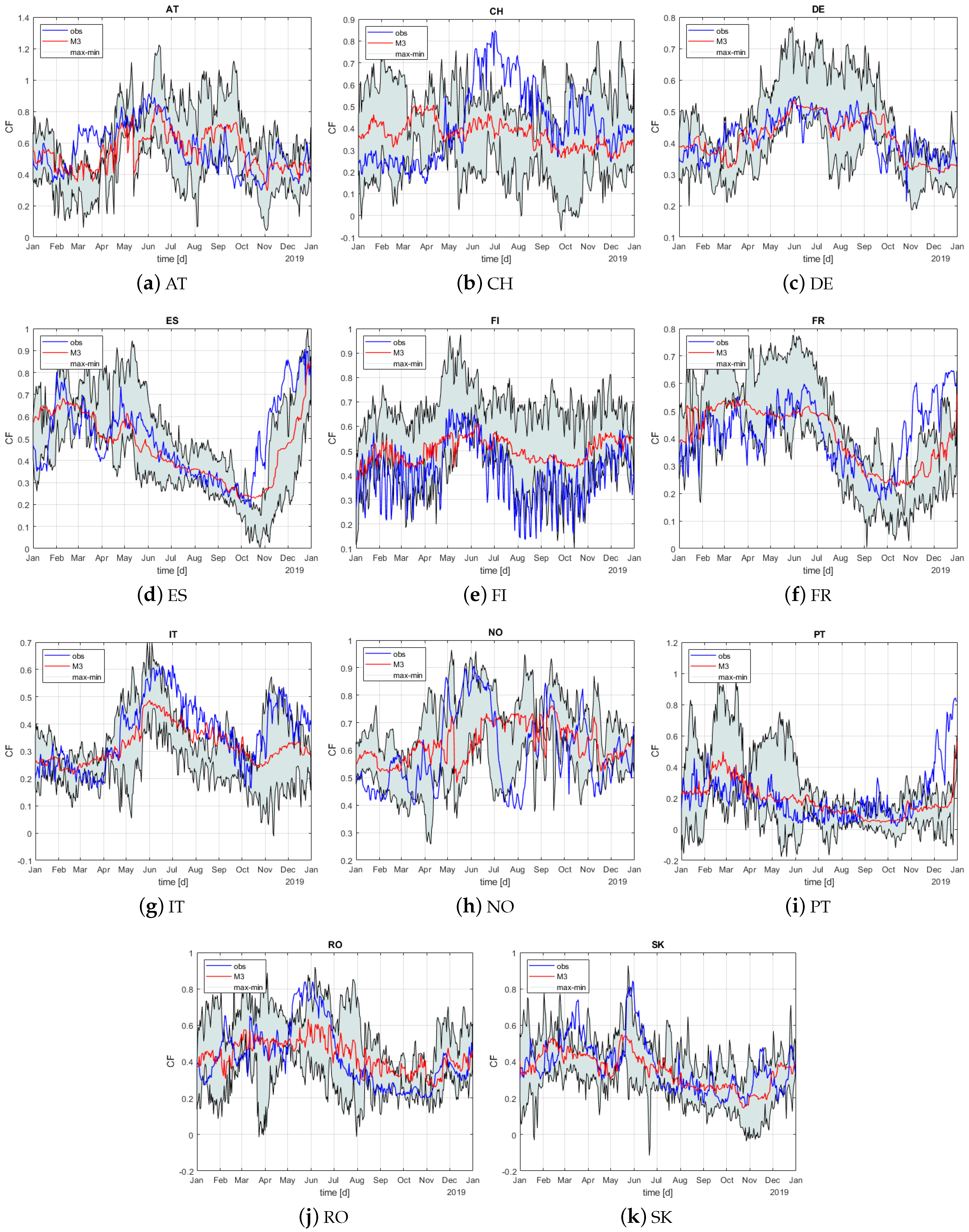
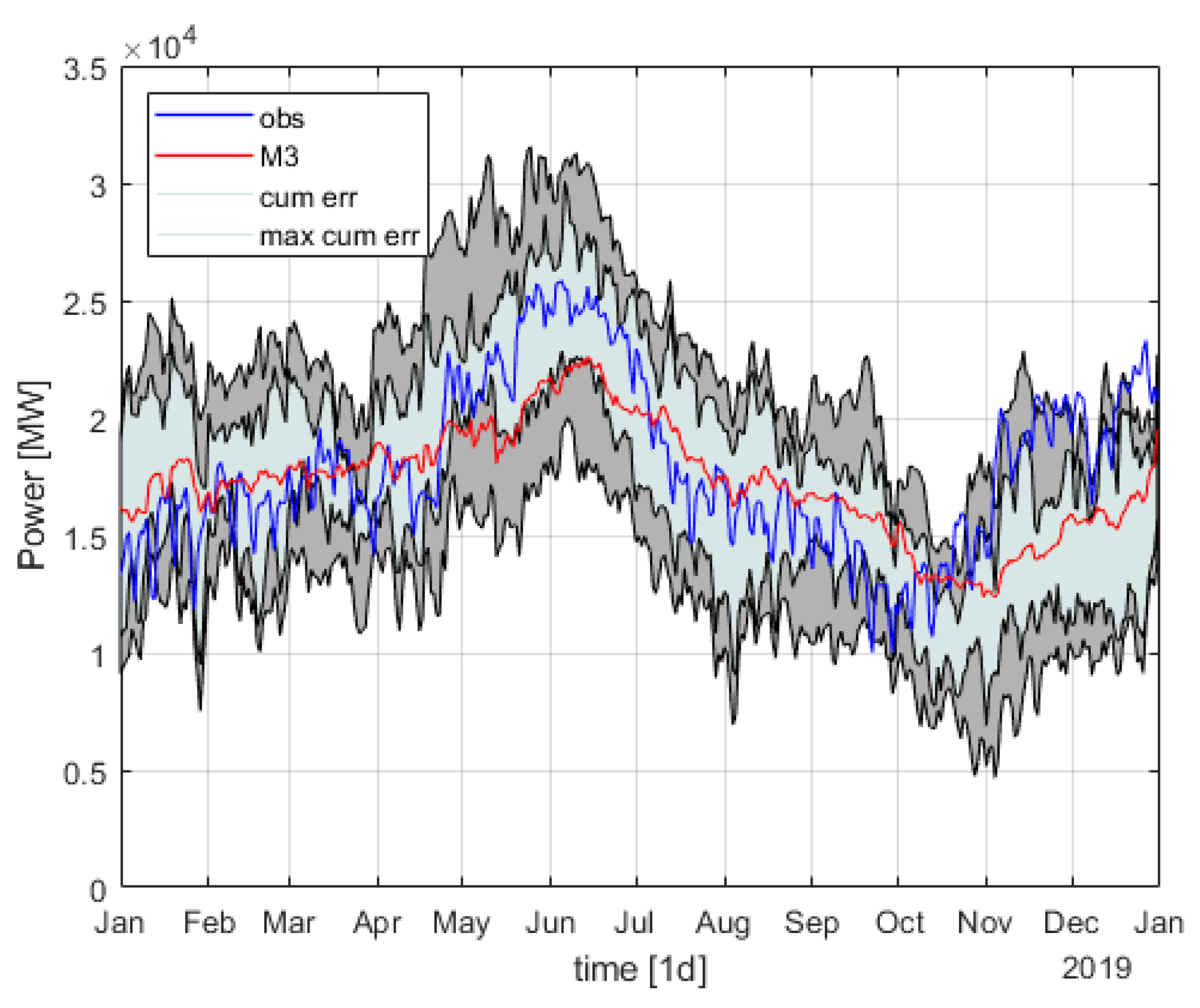
4.2. Accuracy of Prediction
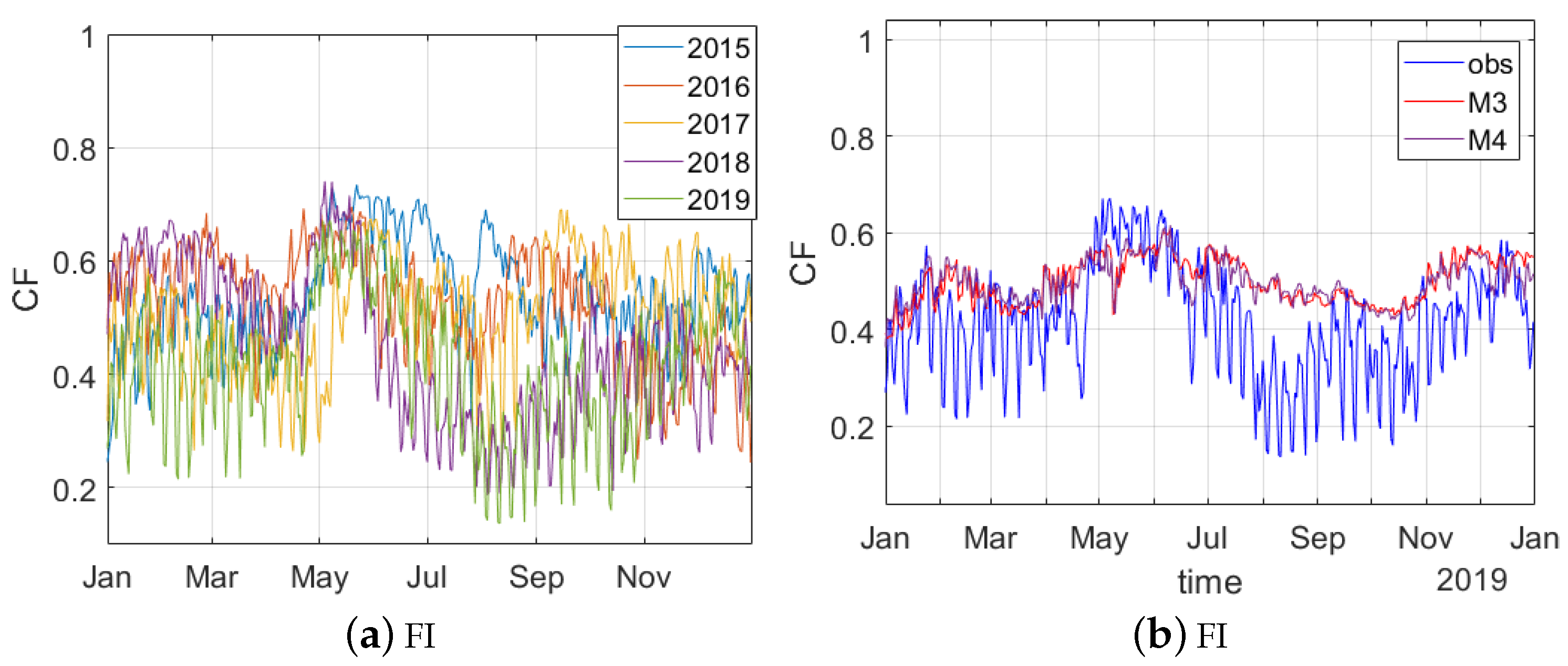
4.2.1. Modeling Challenge: Representativeness of the Training Set
4.2.2. Modeling Challenge: Insights on Country Specific Issues
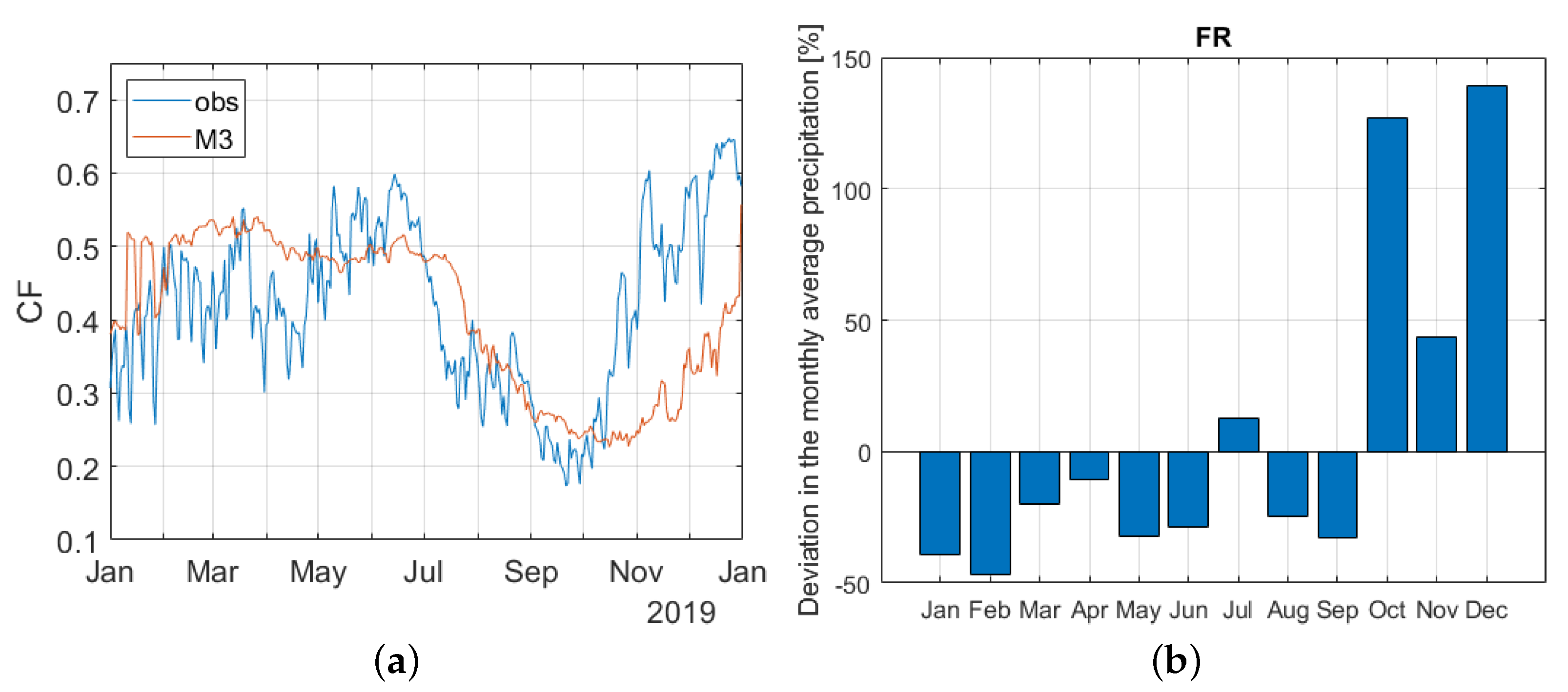
4.2.3. Relevance for Operational Use
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| RF | Random Forest |
| RoR | Run-of-River |
| Res | Reservoir |
| CF | Capacity Factor |
Appendix A
Appendix A.1. Optimal Lags in Model Training
| NUTS2 Features | Avg Features | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Country | AT | TP | Acc TP | AT | TP | Acc TP | ||||||
| Min | Avg | Max | Min | Avg | Max | Min | Avg | Max | ||||
| AT | 126 | 126.66 | 128 | 1 | 1 | 1 | 18 | 19.11 | 23 | 127 | 1 | 18 |
| CH | 1 | 1 | 1 | 67 | 104.71 | 198 | 71 | 78 | 89 | 1 | 198 | 75 |
| DE | 143 | 143.63 | 144 | 1 | 54.78 | 156 | 40 | 133.15 | 200 | 144 | 10 | 104 |
| ES | 9 | 38 | 46 | 2 | 38.94 | 102 | 23 | 111.35 | 200 | 44 | 4 | 101 |
| FI | 52 | 68.50 | 85 | 1 | 46.50 | 91 | 36 | 119.25 | 147 | 85 | 90 | 147 |
| FR | 44 | 58.59 | 79 | 1 | 11.40 | 103 | 20 | 83.59 | 154 | 59 | 1 | 53 |
| IT | 140 | 154.76 | 161 | 1 | 55.14 | 198 | 23 | 87.90 | 200 | 155 | 3 | 74 |
| NO | 174 | 176.71 | 184 | 1 | 57.42 | 198 | 5 | 104 | 200 | 174 | 1 | 10 |
| PT | 18 | 28.80 | 35 | 4 | 24.40 | 103 | 113 | 123.60 | 131 | 35 | 5 | 117 |
| RO | 96 | 96.87 | 97 | 1 | 1.87 | 2 | 17 | 22.25 | 32 | 97 | 2 | 22 |
| SK | 65 | 65 | 65 | 1 | 46 | 63 | 19 | 127.75 | 176 | 65 | 100 | 159 |
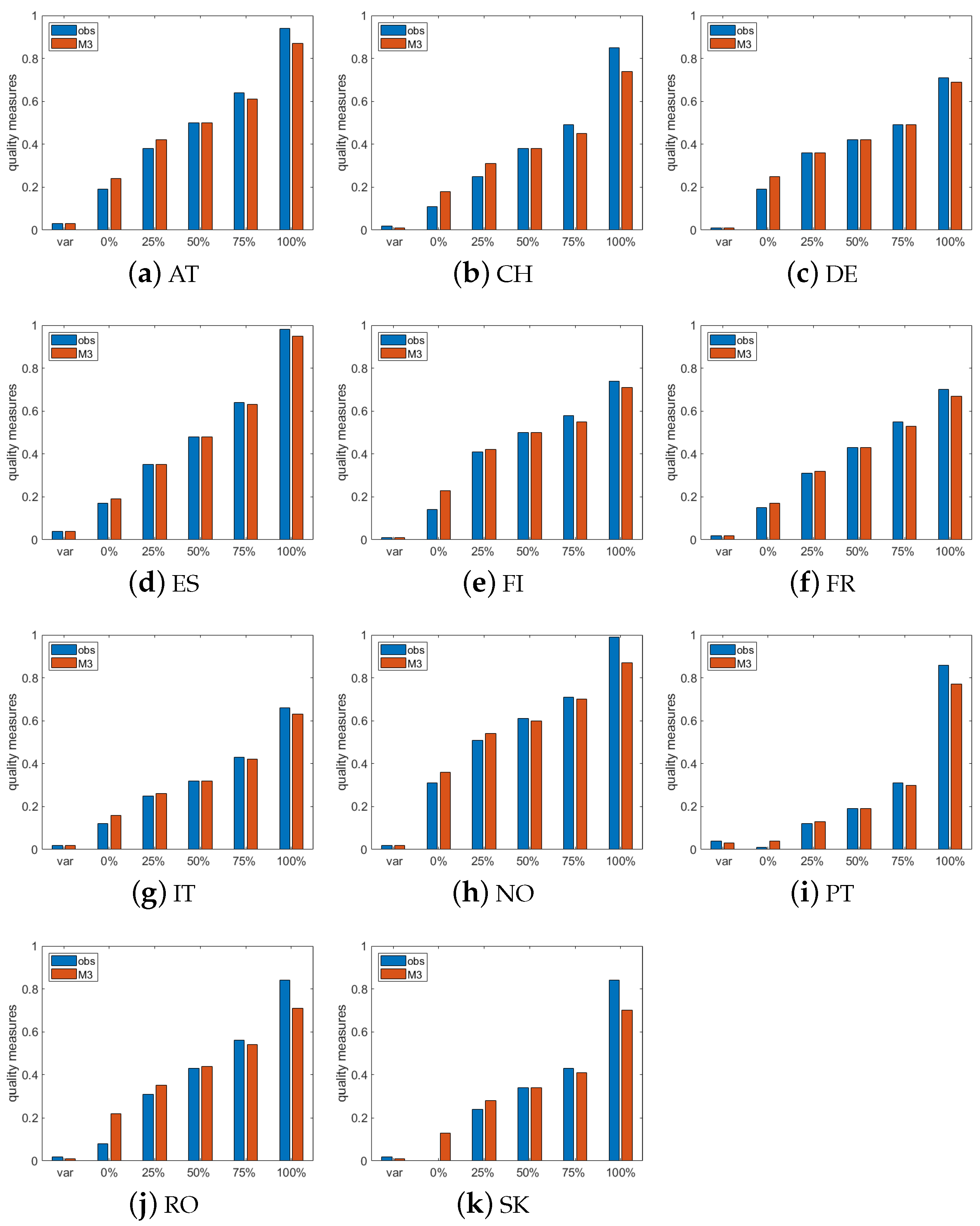
Appendix A.2. Time Series Quality Measures
| Observations | M3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Var | 0% | 25% | 50% | 75% | 100% | Var | 0% | 25% | 50% | 75% | 100% | |
| AT | 0.03 | 0.19 | 0.38 | 0.50 | 0.64 | 0.94 | 0.03 | 0.24 | 0.42 | 0.50 | 0.61 | 0.87 |
| CH | 0.02 | 0.11 | 0.25 | 0.38 | 0.49 | 0.85 | 0.01 | 0.18 | 0.31 | 0.38 | 0.45 | 0.74 |
| DE | 0.01 | 0.19 | 0.36 | 0.42 | 0.49 | 0.71 | 0.01 | 0.25 | 0.36 | 0.42 | 0.49 | 0.69 |
| ES | 0.04 | 0.17 | 0.35 | 0.48 | 0.64 | 0.98 | 0.04 | 0.19 | 0.35 | 0.48 | 0.63 | 0.95 |
| FI | 0.01 | 0.14 | 0.41 | 0.50 | 0.58 | 0.74 | 0.01 | 0.23 | 0.42 | 0.50 | 0.55 | 0.71 |
| FR | 0.02 | 0.15 | 0.31 | 0.43 | 0.55 | 0.70 | 0.02 | 0.17 | 0.32 | 0.43 | 0.53 | 0.67 |
| IT | 0.02 | 0.12 | 0.25 | 0.32 | 0.43 | 0.66 | 0.02 | 0.16 | 0.26 | 0.32 | 0.42 | 0.63 |
| NO | 0.02 | 0.31 | 0.51 | 0.61 | 0.71 | 0.99 | 0.02 | 0.36 | 0.54 | 0.60 | 0.70 | 0.87 |
| PT | 0.04 | 0.01 | 0.12 | 0.19 | 0.31 | 0.86 | 0.03 | 0.04 | 0.13 | 0.19 | 0.30 | 0.77 |
| RO | 0.02 | 0.08 | 0.31 | 0.43 | 0.56 | 0.84 | 0.01 | 0.22 | 0.35 | 0.44 | 0.54 | 0.71 |
| SK | 0.02 | 0.00 | 0.24 | 0.34 | 0.43 | 0.84 | 0.01 | 0.13 | 0.28 | 0.34 | 0.41 | 0.70 |
References
- IRENA. Smart Grids and Renewables: A Guide for Effective Deployment; Technical Report; IRENA: Abu Dhabi, United Arab Emirates, 2013. [Google Scholar]
- International Hydropower Association. Hydropower Status Report: Sector Trends and Insights. Available online: www.hydropower.org/status2019 (accessed on 1 January 2020).
- Stoll, B.; Andrade, J.; Cohen, S.; Brinkman, G.; Brancucci Martinez-Anido, C. Hydropower Modeling Challenges; Technical Report WFGX. 1040; National Renewable Energy Laboratory: Golden, CO, USA, 2017.
- Hamududu, B.; Killingtveit, A. Assessing climate change impacts on global hydropower. Energies 2012, 5, 305–322. [Google Scholar] [CrossRef] [Green Version]
- Jakeman, A.J.; Hornberger, G.M. How much complexity is warranted in a rainfall-runoff model? Water Resour. Res. 1993, 29, 2637–2649. [Google Scholar] [CrossRef]
- Bergstra, J.S.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. Adv. Neural Inf. Process. Syst. 2011, 9, 2546–2554. [Google Scholar]
- Bellin, A.; Majone, B.; Cainelli, O.; Alberici, D.; Villa, F. A continuous coupled hydrological and water resources management model. Environ. Model. Softw. 2016, 75, 176–192. [Google Scholar] [CrossRef]
- Treiber, N.A.; Heinermann, J.; Kramer, O. Computational Sustainability, Studies in Computational Intelligence; Section: Wind Power Prediction with Machine Learning; Springer International Publishing: Cham, Switzerland, 2016; Volume 645. [Google Scholar]
- Baumgartner, J.; Gruber, K.; Simoes, S.G.; Saint-Drenan, Y.M.; Schmidt, J. Less Information, Similar Performance: Comparing Machine Learning-Based Time Series of Wind Power Generation to Renewables.ninja. Energies 2020, 13, 2277. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Drobinski, P. Wind and solar renewable energy potential resources estimation. Encycl. Life Support Syst. (EOLSS) 2012, 8, 1–12. [Google Scholar]
- Ho, L.T.T.; Dubus, L.; De Felice, M.; Troccoli, A. Reconstruction of Multidecadal Country-Aggregated Hydro Power Generation in Europe Based on a Random Forest Model. Energies 2020, 13, 1786. [Google Scholar] [CrossRef] [Green Version]
- German Meteorological Service (DWD—Deutscher Wetterdienst). Available online: https://www.dwd.de/EN/Home/home_node.html (accessed on 1 December 2021).
- Fröhlich, K.; Dobrynin, M.; Isensee, K.; Gessner, C.; Paxian, A.; Pohlmann, H.; Haak, H.; Brune, S.; Früh, B.; Baehr, J. The German Climate Forecast System: GCFS. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002101. [Google Scholar] [CrossRef]
- European Commission; Statistical Office of the European Union. Statistical Regions in the European Union and Partner Countries: NUTS and Statistical Regions 2021: 2020 Edition; Publications Office of the EU: Luxembourg, 2020.
- European Network of Transmission System Operator for Electricity. Available online: https://www.entsoe.eu/ (accessed on 1 December 2021).
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar]
- Sessa, V.; Assoumou, E.; Bossy, M.; Carvalho, S.; Simoes, S.G. Machine Learning for Assessing Variability of the Long-Term Projections of the Hydropower Generation on a European Scale; Technical Report, 2020; Available online: https://hal-mines-paristech.archives-ouvertes.fr/hal-02507400 (accessed on 1 December 2021).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- MATLAB and Deep Learning Toolbox. Available online: https://fr.mathworks.com/products/deep-learning.html (accessed on 1 December 2021).
- Pearson, K. Notes on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1895, 58, 240–242. [Google Scholar]
- De Felice, M.; Dubus, L.; Suckling, E.; Troccoli, A. The impact of the North Atlantic Oscillation on European hydropower generation. arXiv 2018. [Google Scholar] [CrossRef] [Green Version]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Janitza, S.; Hornung, R. On the overestimation of random forest’s out-of-bag error. PLoS ONE 2018, 13, e0201904. [Google Scholar] [CrossRef] [PubMed]
- Ashraf, F.B.; Haghighi, A.T.; Riml, J.; Alfredsen, K.; Koskela, J.J.; Kløve, B.; Marttila, H. Changes in short term river flow regulation and hydropeaking in Nordic rivers. Sci. Rep. 2018, 8, 17232. [Google Scholar] [CrossRef] [PubMed]

| Country | Total Installed Capacitity (RoR + Res) [MW] | Total Generated [TWh] |
|---|---|---|
| Norway (NO) | 29,334 (1149 + 28,185) | 141.69 |
| Spain (ES) | 20,294 (1155 + 19,139) | 33.34 |
| France (FR) | 16,947 (9759 + 7188) | 64.84 |
| Italy (IT) | 14,900 (10,441 + 4459) | 47.62 |
| Austria (AT) | 8160 (5724 + 2436) | 42.52 |
| Switzerland (CH) | 6194 (606 + 5588) | 40.62 |
| Romania (RO) | 6134 (2746 + 3388) | 15.53 |
| Germany (DE) | 5117 (3819 + 1298) | 24.75 |
| Portugal (PT) | 4372 (2857 + 1515) | 13.96 |
| Finland (FI) | 3153 (3153 + -) | 15.56 |
| Greece (GE) | 2702 (299 + 2403) | 3.43 |
| Serbia (RS) | 2477 (2005 + 472) | 9.66 |
| Bulgaria (BG) | 2347 (537 + 1810) | 3.37 |
| Croatia (HR) | 1865 (1444 + 334) | 3.40 |
| Slovakia (SK) | 1626 (1208 + 418) | 4.67 |
| Predictors | M1 (avg) | M2 (NUTS2) | M3 (avg + NUTS2) |
|---|---|---|---|
| Temperature | |||
| sync | ✓ | ✓ | ✓ |
| lagged (opt) | ✓ | ✓ | ✓ |
| Precipitation | |||
| sync | ✓ | ✓ | ✓ |
| lagged (opt) | ✓ | ✓ | ✓ |
| accum (opt) | ✓ | ✓ | ✓ |
| 2015 | 2016 | 2017 | 2018 | 2019 |
|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sessa, V.; Assoumou, E.; Bossy, M.; Simões, S.G. Analyzing the Applicability of Random Forest-Based Models for the Forecast of Run-of-River Hydropower Generation. Clean Technol. 2021, 3, 858-880. https://doi.org/10.3390/cleantechnol3040050
Sessa V, Assoumou E, Bossy M, Simões SG. Analyzing the Applicability of Random Forest-Based Models for the Forecast of Run-of-River Hydropower Generation. Clean Technologies. 2021; 3(4):858-880. https://doi.org/10.3390/cleantechnol3040050
Chicago/Turabian StyleSessa, Valentina, Edi Assoumou, Mireille Bossy, and Sofia G. Simões. 2021. "Analyzing the Applicability of Random Forest-Based Models for the Forecast of Run-of-River Hydropower Generation" Clean Technologies 3, no. 4: 858-880. https://doi.org/10.3390/cleantechnol3040050
APA StyleSessa, V., Assoumou, E., Bossy, M., & Simões, S. G. (2021). Analyzing the Applicability of Random Forest-Based Models for the Forecast of Run-of-River Hydropower Generation. Clean Technologies, 3(4), 858-880. https://doi.org/10.3390/cleantechnol3040050






