Estimating Smart Wi-Fi Thermostat-Enabled Thermal Comfort Control Savings for Any Residence
Abstract
:1. Introduction
2. Background
3. Case Study
4. Methodology
4.1. Model Improvements Considering Solar Heating Inputs
4.1.1. Data Collection and Preprocessing
4.1.1.1. Data Employed
4.1.1.2. Data Preprocessing
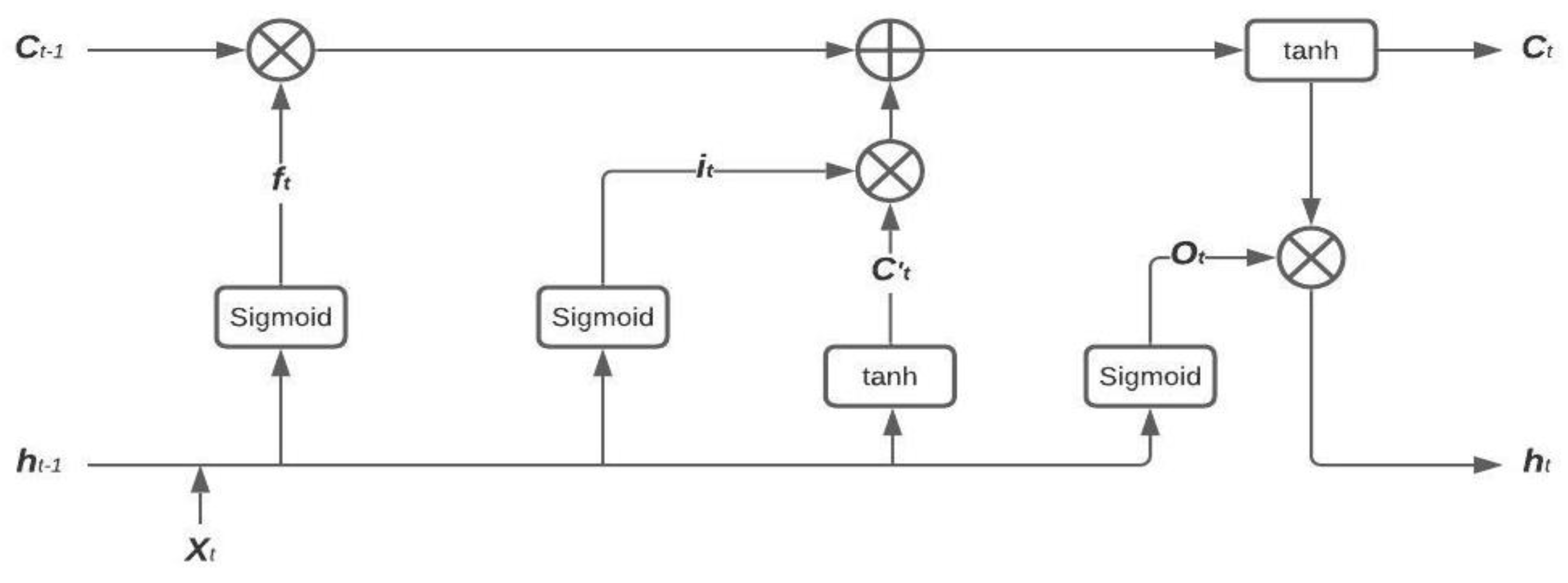
4.1.2. Model Development and Improvement
4.2. Estimating Changes in Cooling Required When Solar Heating Is Included
4.3. Estimating Impact of Solar Heat Gain on PMV Control
4.3.1. PMV Model
4.3.2. MRT Estimation
4.3.3. Summary of PMV Calculations
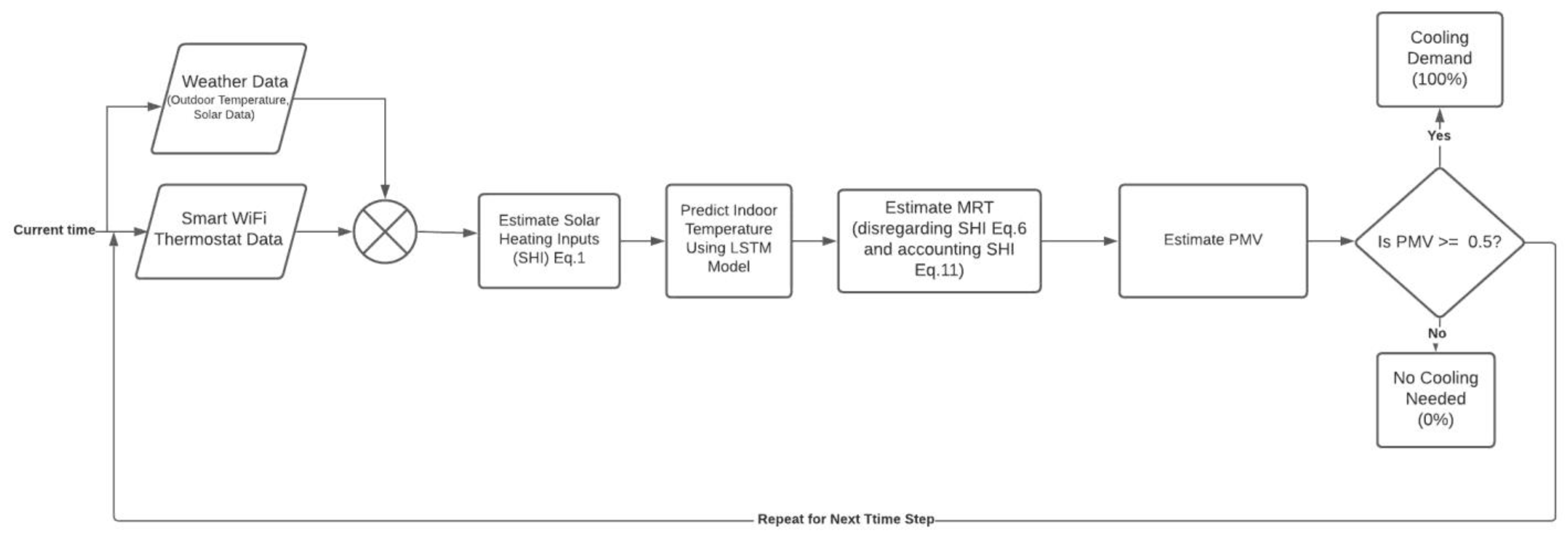
4.3.4. Thermal Comfort Control Logic
4.4. Evaluating Savings from PMV Control with Solar Contributions Accounted For
5. Results
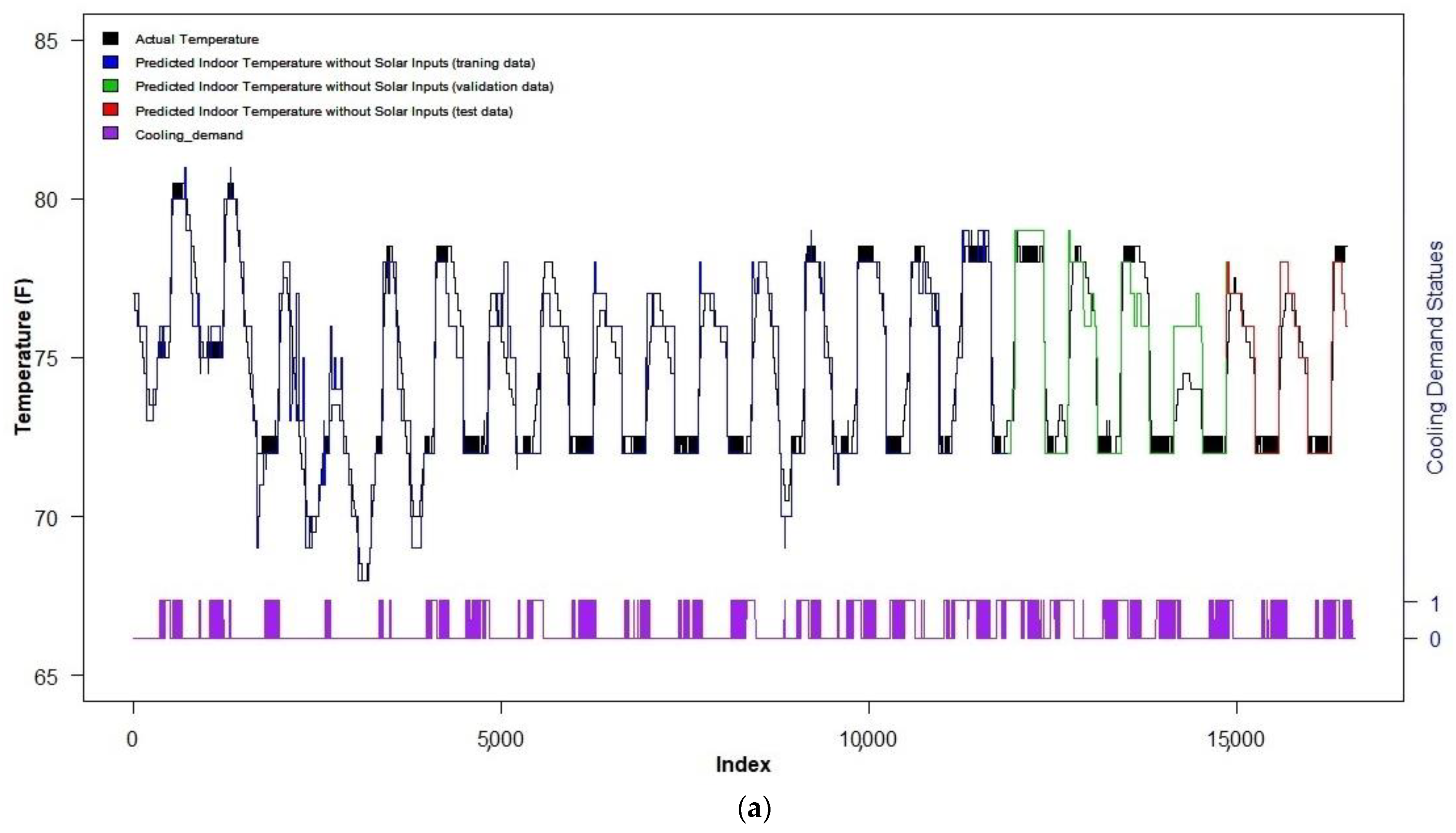
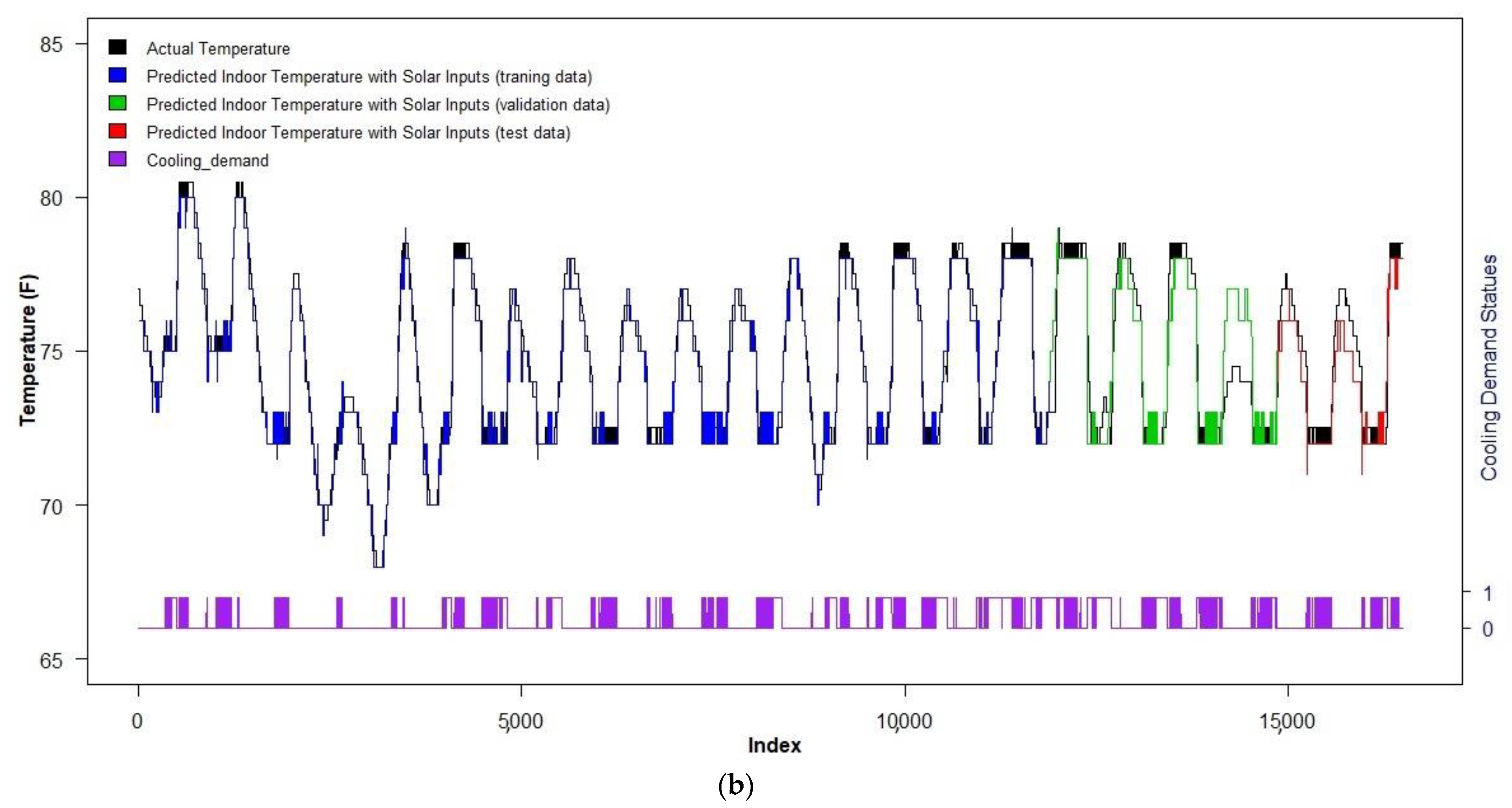
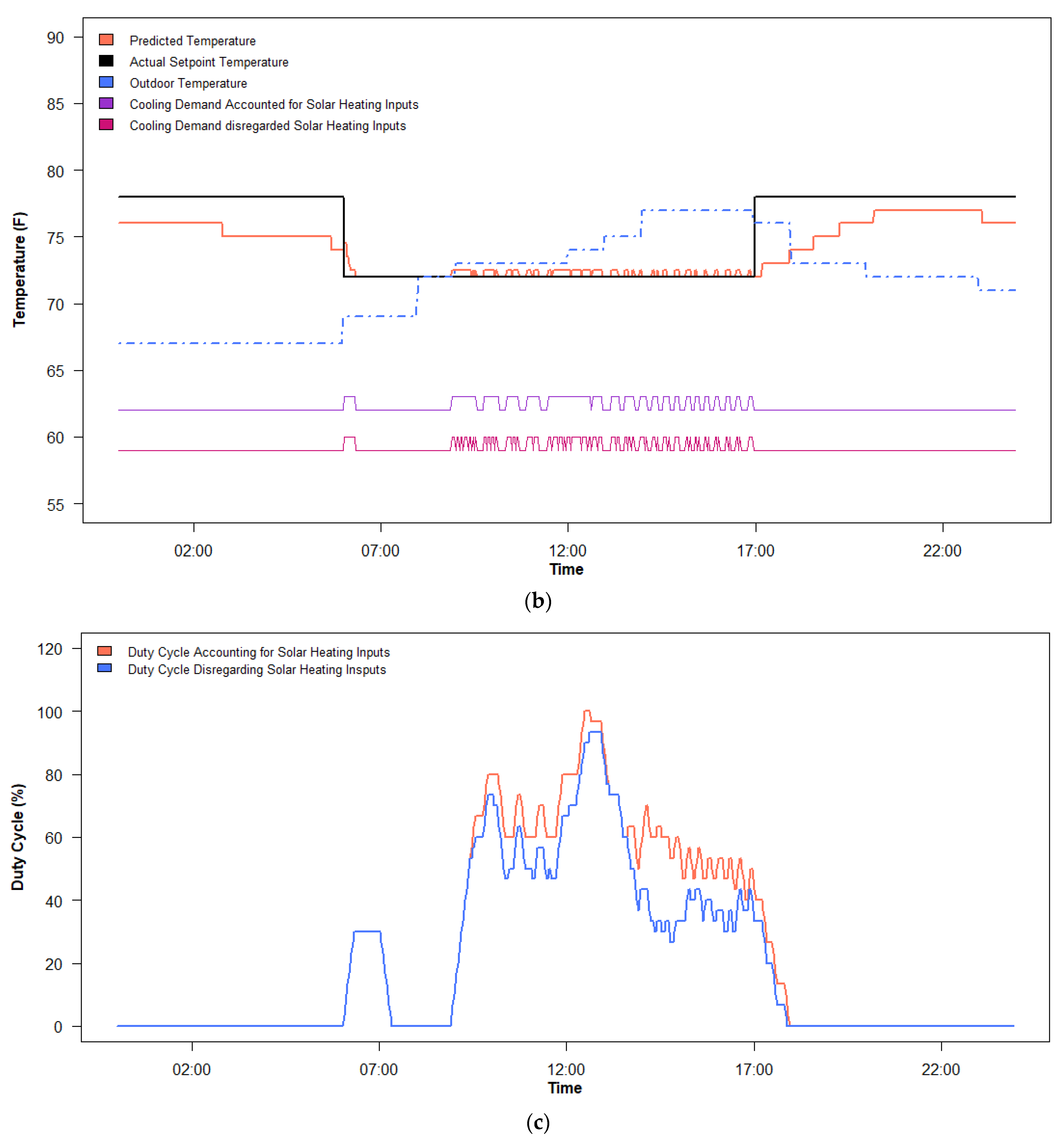
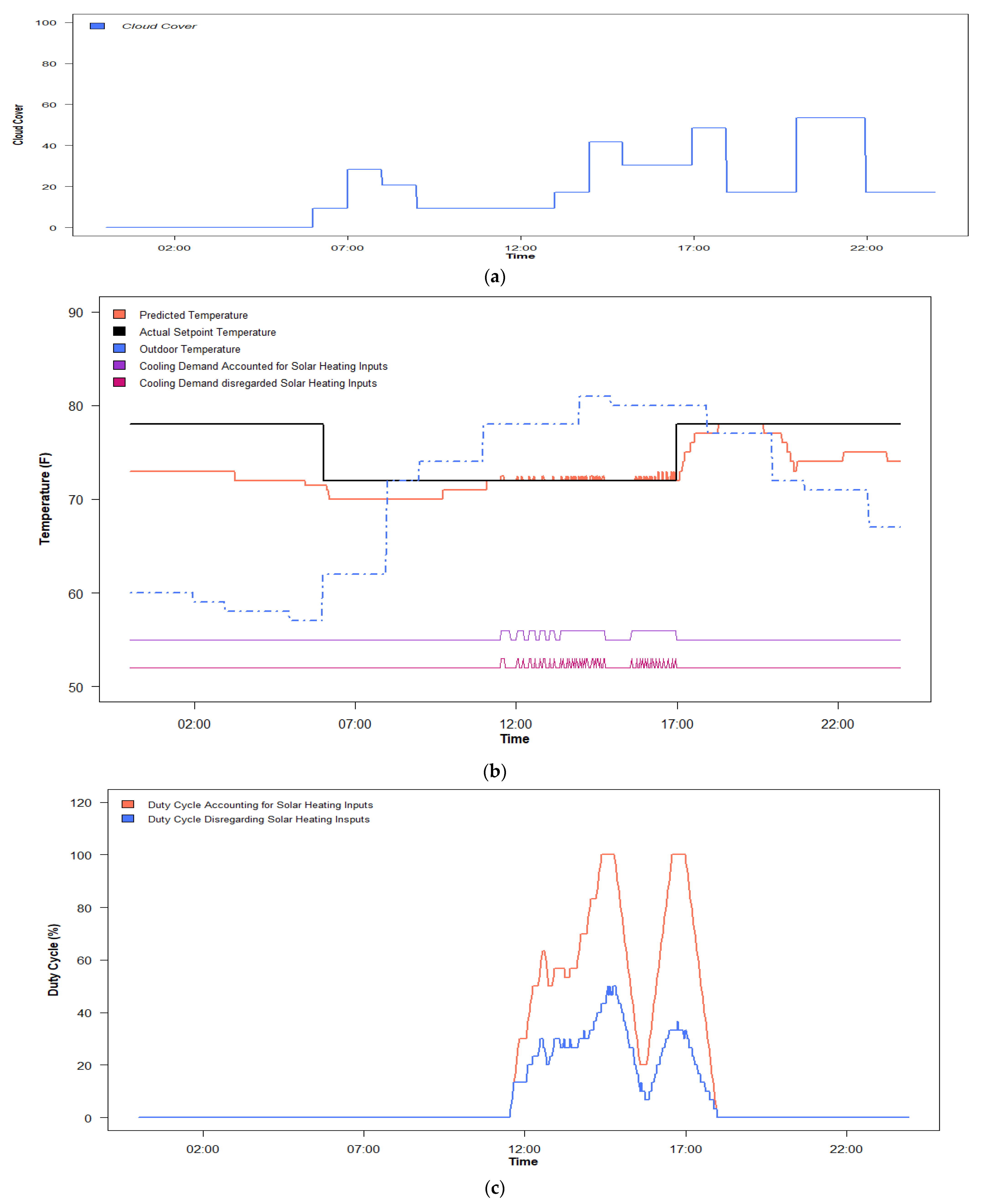
5.1. Cooling Reduction from Thermal Comfort Control versus Traditional Temperature Control with and without Consideration of Solar Heat Gain
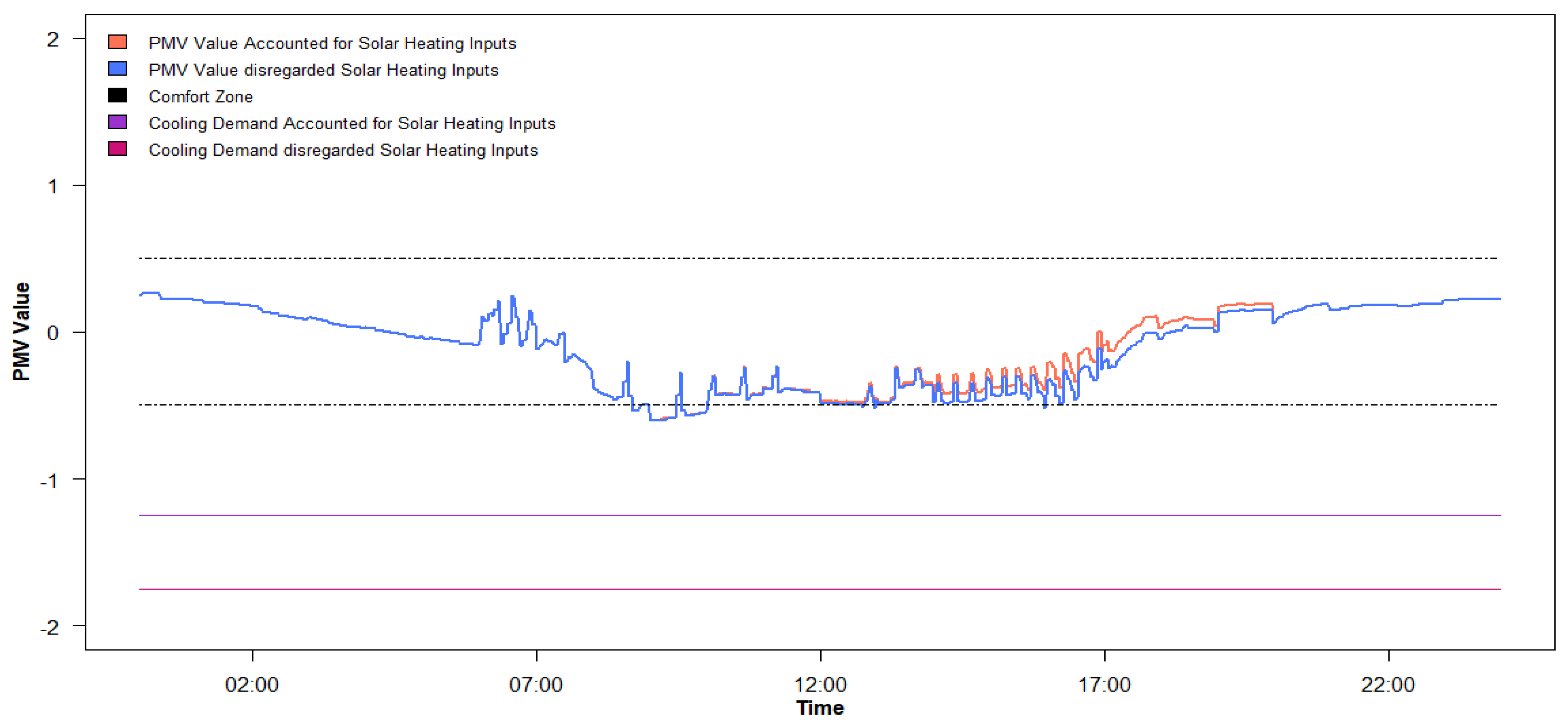
5.2. Impact of Solar Heat Gain on PMV Value
5.3. Savings from PMV Control with Solar Heat Gain Contributions Accounted For
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature List
| Symbol | Description | Unit | Symbol | Description | Unit |
| PMV | Predicted mean vote | - | Radiant heat transfer | W/m2 | |
| MRT | Mean radiant temperature | K | Solar incidence angle per building’s surface | degree | |
| Building floor area | m2 | Beam solar irradiance per building’s surface | W/m2 | ||
| Building wall area | m2 | Diffuse solar irradiance per building’s surface | W/m2 | ||
| Single window area | m2 | Ground-reflected solar irradiance per building’s surface | W/m2 | ||
| Wall thermal resistance | m2 K/W | Total solar irradiance per building’s surface | W/m2 | ||
| Window thermal resistance | m2 K/W | Transmitted solar radiation through windows | W/m2 | ||
| Attic thermal resistance | m2 K/W | Solar heat gain coefficient | - | ||
| Conductive thermal resistance through envelope | m2 K/W | Solar-air temperature | °C | ||
| Overall thermal resistance on interior surface | m2 K/W | Indoor room temperature | °C | ||
| Overall thermal resistance on exterior surface | m2 K/W | Outdoor temperature | °C | ||
| Absorptance of surface for solar radiation | - | Cooling setpoint temperature | °C | ||
| Hemispherical emittance of surface | - | Interior surface temperature of envelope | °C | ||
| Difference between long wave radiation incident on surface from sky and surroundings and radiation emitted by black body at outdoor air temperature | W/ m2 | RH | Indoor relative humidity | % | |
| Coefficient of heat transfer for long wave radiation and convection outer surface | W/m2 °C | Radiation heat transfer coefficient | W/m2 °C |
References
- Masson-Delmotte, V.; Zhai, P.; Pörtner, H.-O.; Roberts, D.; Skea, J.; Shukla, P.R.; Pirani, A.; Moufouma-Okia, W.; Péan, C.; Pidcock, R. (Eds.) IPCC, 2018: Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; in press; IPCC: Geneva, Switzerland, 2018. [Google Scholar]
- Stanford University Energy and Climate Plan. Available online: https://sustainable.stanford.edu/sites/default/files/E%26C%20Plan%202016.6.7.pdf (accessed on 26 June 2021).
- Hand, M.M.; Baldwin, S.; DeMeo, E.; Reilly, J.M.; Mai, T.; Arent, D.; Porro, G.; Meshek, M.; Sandor, D. (Eds.) Renewable Electricity Futures Study (Entire Report) National Renewable Energy Laboratory. Renewable Electricity Futures Study; NREL/TP-6A20-52409; National Renewable Energy Laboratory: Golden, CO, USA, 2012. Available online: http://www.nrel.gov/analysis/re_futures/ (accessed on 13 April 2021).
- Puget Sound Energy: Major HVAC Controls Upgrade Rebates. PSE. Available online: https://www.pse.com/en/business-incentives/commercial-hvac-upgrade-incentives/major-hvac-controls-upgrade-rebates (accessed on 13 April 2021).
- Masoso, O.; Grobler, L.J. The dark side of occupants’ behaviour on building energy use. Energy Build. 2010, 42, 173–177. [Google Scholar] [CrossRef]
- Vakiloroaya, V.; Samali, B.; Fakhar, A.; Pishghadam, K. A review of different strategies for HVAC energy saving. Energy Convers. Manag. 2014, 77, 738–754. [Google Scholar] [CrossRef]
- Ghahramani, A.; Dutta, K.; Yang, Z.; Ozcelik, G.; Becerik-Gerber, B. Quantifying the influence of temperature setpoints, building and system features on energy consumption. In Proceedings of the Winter Simulation Conference (WSC); Huntington Beach, CA, USA, 6–9 December 2015, IEEE: Piscataway, NJ, USA, 2015; pp. 1000–1011. [Google Scholar]
- Ghahramani, A.; Dutta, K.B. Becerik-gerber, energy trade off analysis of optimized daily temperature setpoints. J. Build. Eng. 2018, 19, 584–591. [Google Scholar] [CrossRef]
- Kaam, S.; Raftery, P.; Cheng, H.; Paliaga, G. Time-averaged ventilation for optimized control of variable-air-volume systems. Energy Build. 2017, 139, 465–475. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Yan, H.; Lok, C. Thermal comfort and building energy consumption implications—A review. Appl. Energy 2014, 115, 164–173. [Google Scholar] [CrossRef]
- Park, J.; Kim, T.; Lee, C. Development of Thermal Comfort-Based Controller and Potential Reduction of the Cooling Energy Consumption of a Residential Building in Kuwait. Energies 2019, 12, 3348. [Google Scholar] [CrossRef] [Green Version]
- Lou, R.; Hallinan, K.; Huang, K.; Reissman, T. Smart Wifi Thermostat-Enabled Thermal Comfort Control in Residences. Sustainability 2020, 12, 1919. [Google Scholar] [CrossRef] [Green Version]
- Fanger, P.O. Thermal Comfort: Analysis and Applications in Environmental Engineering; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Khovalyg, D.; Kazanci, O.; Gundlach, I.; Bahnfleth, W.; Toftum, J.; Olesen, B.W. Impact of Indoor Environmental Quality Standards on the Simulated Energy Use of Classrooms. In Proceedings of the Windsor Conference 2020, Windsor, UK, 16–19 April 2020. [Google Scholar]
- Azuatalam, D.; Lee, W.; de Nijs, F.; Liebman, A. Reinforcement Learning for Whole-building HVAC Control and Demand Response. Energy AI 2020, 2, 100020. [Google Scholar] [CrossRef]
- Li, Y.; de la Ree, J.; Gong, Y. The Smart Thermostat of HVAC Systems Based on PMV-PPD Model for Energy Efficiency and Demand Response. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Deng, Z.; Chen, Q. Artificial neural network models using thermal sensations and occupants’ behavior for predicting thermal comfort. Energy Build. 2018, 174, 587–602. [Google Scholar] [CrossRef]
- Chemingui, Y.; Gastli, A.; Ellabban, O. Reinforcement Learning-Based School Energy Management System. Energies 2020, 13, 6354. [Google Scholar] [CrossRef]
- Hong, S.; Lee, J.; Moon, J.; Lee, K. Thermal Comfort, Energy and Cost Impacts of PMV Control Considering Individual Metabolic Rate Variations in Residential Building. Energies 2018, 11, 1767. [Google Scholar] [CrossRef] [Green Version]
- Smart Thermostat Market. Market Research Firm. Available online: https://www.marketsandmarkets.com/Market-Reports/smart-thermostat-market-266618794.html (accessed on 15 April 2021).
- Alanezi, A.M.; Hallinan, K.; Huang, K. Automated Residential Energy Audits Using a Smart WiFi Thermostat-Enabled Data Mining Approach. Energies 2021, 14, 2500. [Google Scholar] [CrossRef]
- Altarhuni, B.; Naji, A.; Brodrick, P.; Hallinan, K.; Brecha, R.J.; Yao, Z. Large scale residential energy efficiency prioritization enabled by machine learning. Energy Efficiency 2019, 12, 2055–2078. [Google Scholar] [CrossRef]
- Responsible Party DOC/NOAA/NESDIS/NCEI. National Centers for Environmental Information, NESDIS, NOAA, U.S. Department of Commerce (Point of Contact). NOAA’s Climate Divisional Database (nCLIMDIV). NOAA’s Climate Divisional Database (nCLIMDIV)—CKAN. Available online: https://catalog.data.gov/dataset/noaas-climate-divisional-database-nclimdiv (accessed on 10 January 2021).
- NASA. Prediction of Worldwide Energy Resources (Power). (2020, November 12). Available online: https://catalog.data.gov/dataset/prediction-of-worldwide-energy-resources-power (accessed on 24 March 2021).
- Duffie, J. Solar Engineering of Thermal Processes; John Wiley: Hoboken, NJ, USA, 2020. [Google Scholar]
- Xu, P.; Han, S.; Huang, H.; Qin, H. Redundant features removal for unsupervised spectral feature selection algorithms: An empirical study based on nonparametric sparse feature graph. Int. J. Data Sci. Anal. 2018, 8, 77–93. [Google Scholar] [CrossRef]
- Huang, K.; Hallinan, K.; Lou, R.; Alanezi, A.M.; Alshatshati, S. Sun, Q. Self-Learning Algorithm to Predict Indoor Temperature and Cooling Demand from Smart WiFi Thermostat in a Residential Building. Sustainability 2020, 12, 3685. [Google Scholar]
- Sepp, H.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- AHSRAE. ASHRAE Handbook—Fundamentals; ASHRAE, Inc.: Atlanta, GA, USA, 2005. [Google Scholar]
- Arens, E.; Hoyt, T.; Zhou, X.; Huang, L.; Zhang, H.; Schiavon, S. Modeling the comfort effects of short-wave solar radiation indoors. Build. Environ. 2015, 88, 3–9. [Google Scholar] [CrossRef] [Green Version]
- d’Ambrosio Alfano, F.R.; Olesen, B.W.; Palella, B.I.; Pepe, D.; Riccio, G. Fifty Years of PMV Model: Reliability, Implementation and Design of Software for Its Calculation. Atmosphere 2020, 11, 49. [Google Scholar] [CrossRef] [Green Version]



| Ref. | Building Type | Technologies/Sensors Employed | Model/Algorithm Applied | Control Strategy Implemented | Savings Estimation |
|---|---|---|---|---|---|
| [15] | Commercial Building | Simulation Software | Deep Reinforcement Learning (DRL) | Reinforcement Learning Agent | Up to 50% |
| [11] | Residential Building | Temperature, Relative Humidity, and Occupancy Sensors | No Simulation | Thermal Comfort-Based Controller | Up to 39.5% |
| [16] | Residential Building | Thermostat Data Occupant Surveys of Comfort | Second-Order Equivalent Thermal Parameter (ETP) | PMV-PPD-Based Smart Thermostats Control | Up to 11.5% |
| [17] | Commercial Building | Thermostat Building Automation System | Artificial Neural Network (ANN) | No Control. Merely Assessed Thermal Comfort | Not Mentioned |
| [18] | Commercial Building | Simulation Software | Deep Reinforcement Learning (DRL) | Deep Reinforcement Learning Agent | Up to 21% |
| [19] | Residential Building | Simulation Software | No Details | PMV and Metabolic Rate-Based Controller | Up to 28.8% |
| House Characteristics | House #1 | House #2 | House #3 | House #4 | House #5 |
|---|---|---|---|---|---|
| Afloor (m2) | 54 | 84 | 54 | 59 | 45 |
| Awall (m2) | 159 | 187 | 156 | 152 | 149 |
| Awindow (m2) | 2–3 | 2–3 | 2–3 | 2–3 | 2–3 |
| Rwall (m2 °K/W) | 0.88 | 0.7 | 0.7 | 2.5 | 0.88 |
| Rwindow (m2 °K/W) | 0.35 | 0.35 | 0.35 | 0.35 | 0.35 |
| RAttic (m2 °K/W) | 3.87 | 2.15 | 1.1 | 6.69 | 3.17 |
| Shaded Faces | North/West | North/East/West | North/West | North/East/West | North/West |
| Compressor Cooling Size (kW) | 10.5 | 8.8 | 10.5 | 10.5 | 12.25 |
| Date | Time | Solar Altitude Angle (Degree) | Solar Incidence Angle (South) (Degree) | Cloud Cover (%) | Beam Solar Radiation (South) (W/m2) | Diffuse Solar Radiation (South) (W/m2) | Ground Reflective (South) (W/m2) | Total Solar Radiation Received by South Side (W/m2) |
|---|---|---|---|---|---|---|---|---|
| 07/06/2018 | 09:02 | 41.139 | 86.837 | 24 | 38 | 97 | 10 | 109 |
| … | … | … | … | … | … | … | … | … |
| 14/06/2018 | 14:28 | 70.252 | 74.385 | 41.7 | 229 | 135 | 46 | 243 |
| … | … | … | … | … | … | … | … | … |
| 23/06/2018 | 16:14 | 42.096 | 87.691 | 91.7 | 16 | 96 | 6 | 103 |
| Date | Time | Outdoor Temperature (F) | Indoor Temperature (F) | Cooling Setpoint Temperature (F) | Cooling Demand Status (0/1) | Cloud Cover (%) | Solar Altitude Angle (degree) | Southern Beam Solar Radiation (W/m2) | Western Beam Solar Radiation (W/m2) |
|---|---|---|---|---|---|---|---|---|---|
| 02/6/2018 | 0:00:00 | 69 | 77 | 80 | 0 | 53.5 | −27.549 | 0 | 0 |
| … | |||||||||
| 12/6/2018 | 10:16:00 | 76 | 72.5 | 72 | 1 | 96.2 | 55.93 | 57 | 0 |
| … | |||||||||
| 24/6/2018 | 16:06:00 | 83 | 72 | 72 | 0 | 35.2 | −27.714 | 137 | 448 |
| Model | Lookback Steps | Hidden Layers (Units) | Batch Size | MAE | R2 | MAPE (%) | RMSE | ||
|---|---|---|---|---|---|---|---|---|---|
| LSTM w/o Solar Inputs | 30 | 40 | 25 | 15 | 128 | 0.66296 | 0.847 | 0.866 | 1.003 |
| LSTM w/Solar Inputs | 30 | 40 | 25 | 15 | 128 | 0.406 | 0.912 | 0.537 | 0.627 |
| House #1 | House #2 | House #3 | House #4 | House #5 | |
|---|---|---|---|---|---|
| Insulation Level | Medium | Low | Low | High | Medium |
| Savings from Thermal Comfort Control w/ and w/out Solar Heat Gain Consideration | 40%/53% | 47%/56% | 46%/60% | 33%/43% | 40%/52% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhamayani, A.D.; Sun, Q.; Hallinan, K.P. Estimating Smart Wi-Fi Thermostat-Enabled Thermal Comfort Control Savings for Any Residence. Clean Technol. 2021, 3, 743-760. https://doi.org/10.3390/cleantechnol3040044
Alhamayani AD, Sun Q, Hallinan KP. Estimating Smart Wi-Fi Thermostat-Enabled Thermal Comfort Control Savings for Any Residence. Clean Technologies. 2021; 3(4):743-760. https://doi.org/10.3390/cleantechnol3040044
Chicago/Turabian StyleAlhamayani, Abdulelah D., Qiancheng Sun, and Kevin P. Hallinan. 2021. "Estimating Smart Wi-Fi Thermostat-Enabled Thermal Comfort Control Savings for Any Residence" Clean Technologies 3, no. 4: 743-760. https://doi.org/10.3390/cleantechnol3040044
APA StyleAlhamayani, A. D., Sun, Q., & Hallinan, K. P. (2021). Estimating Smart Wi-Fi Thermostat-Enabled Thermal Comfort Control Savings for Any Residence. Clean Technologies, 3(4), 743-760. https://doi.org/10.3390/cleantechnol3040044






