Optimization of a Hybrid Solar PV and Gas Turbine Generator System Using the Loss of Load Probability Index
Abstract
1. Introduction
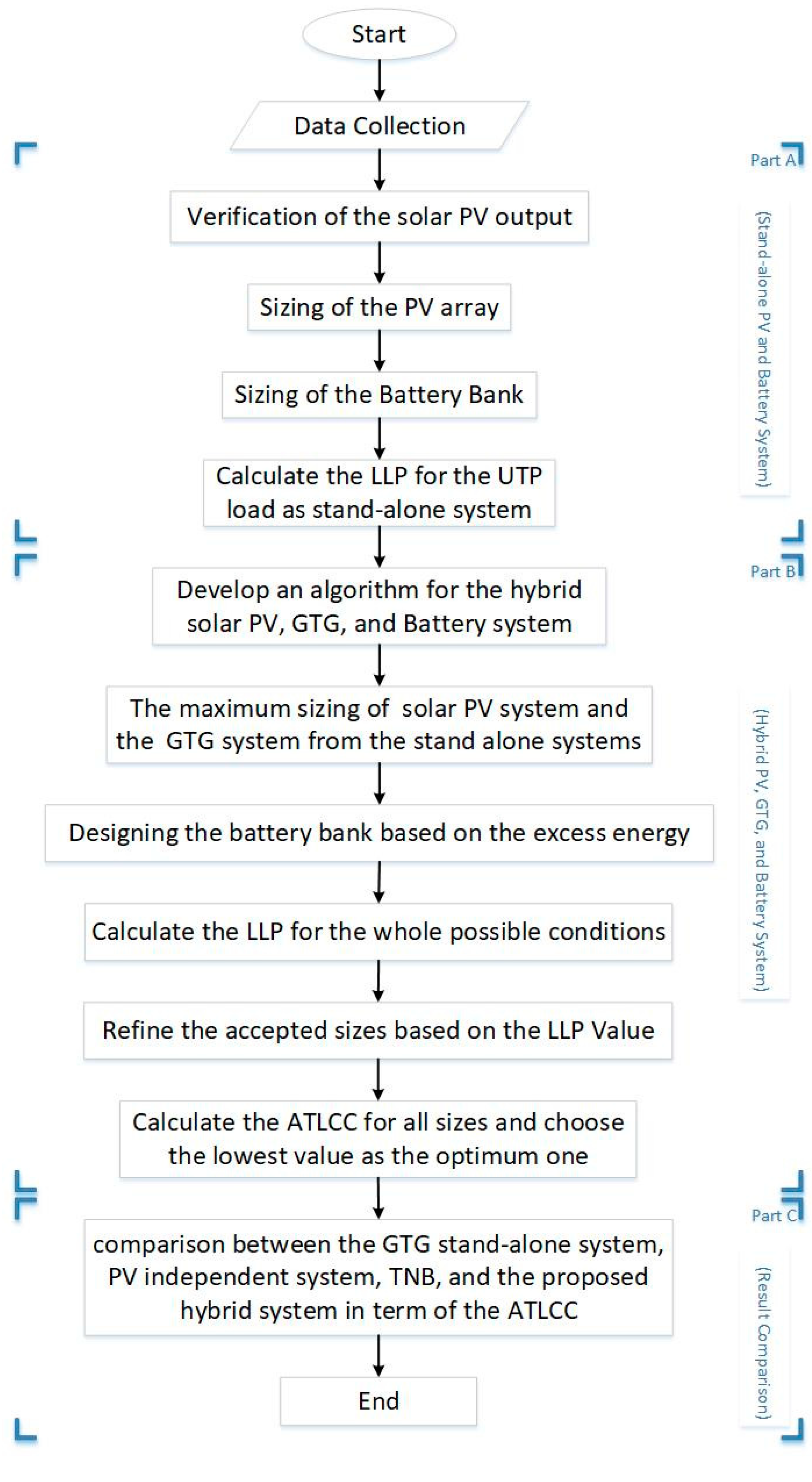
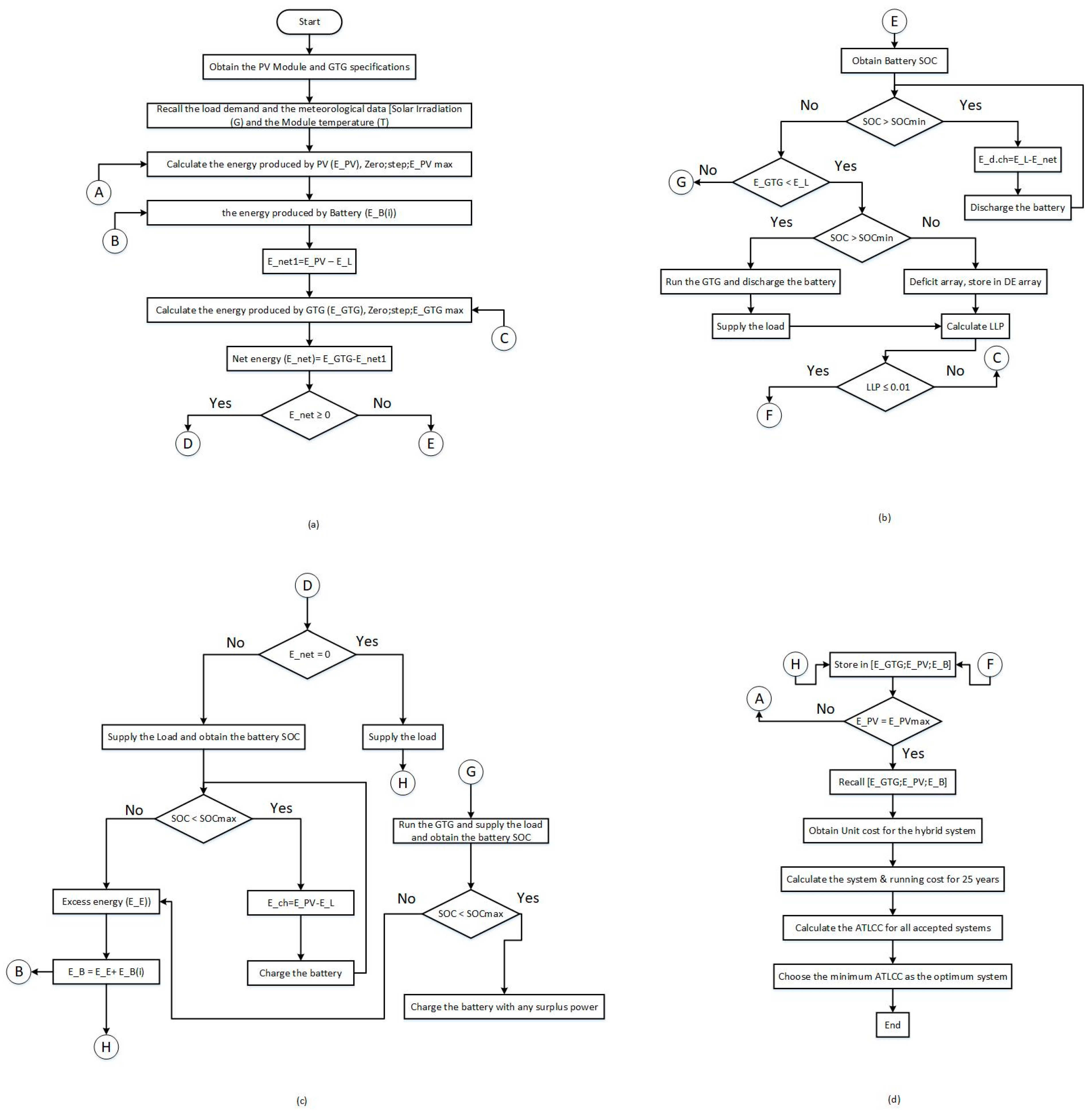
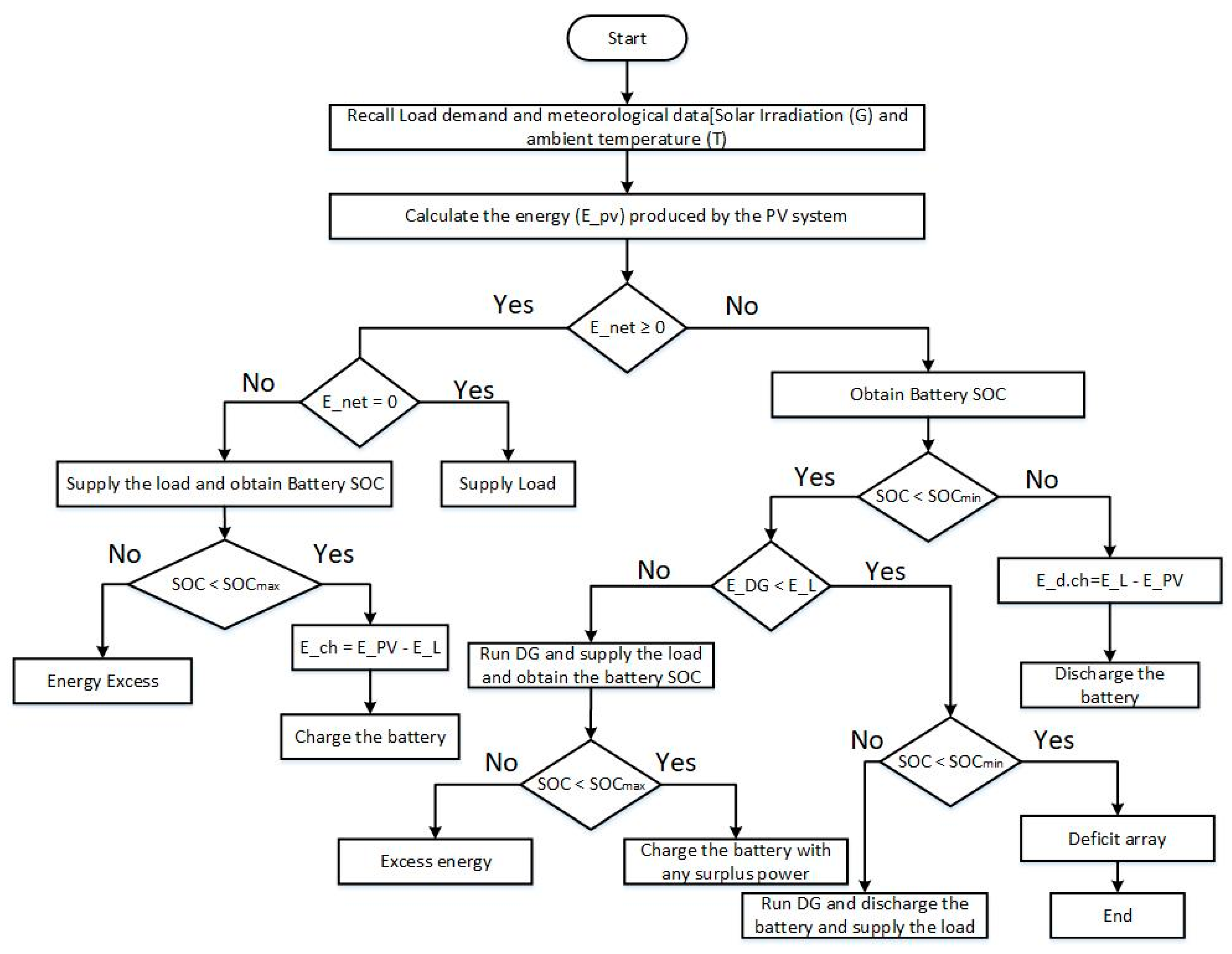
2. Proposed Optimization Methodology
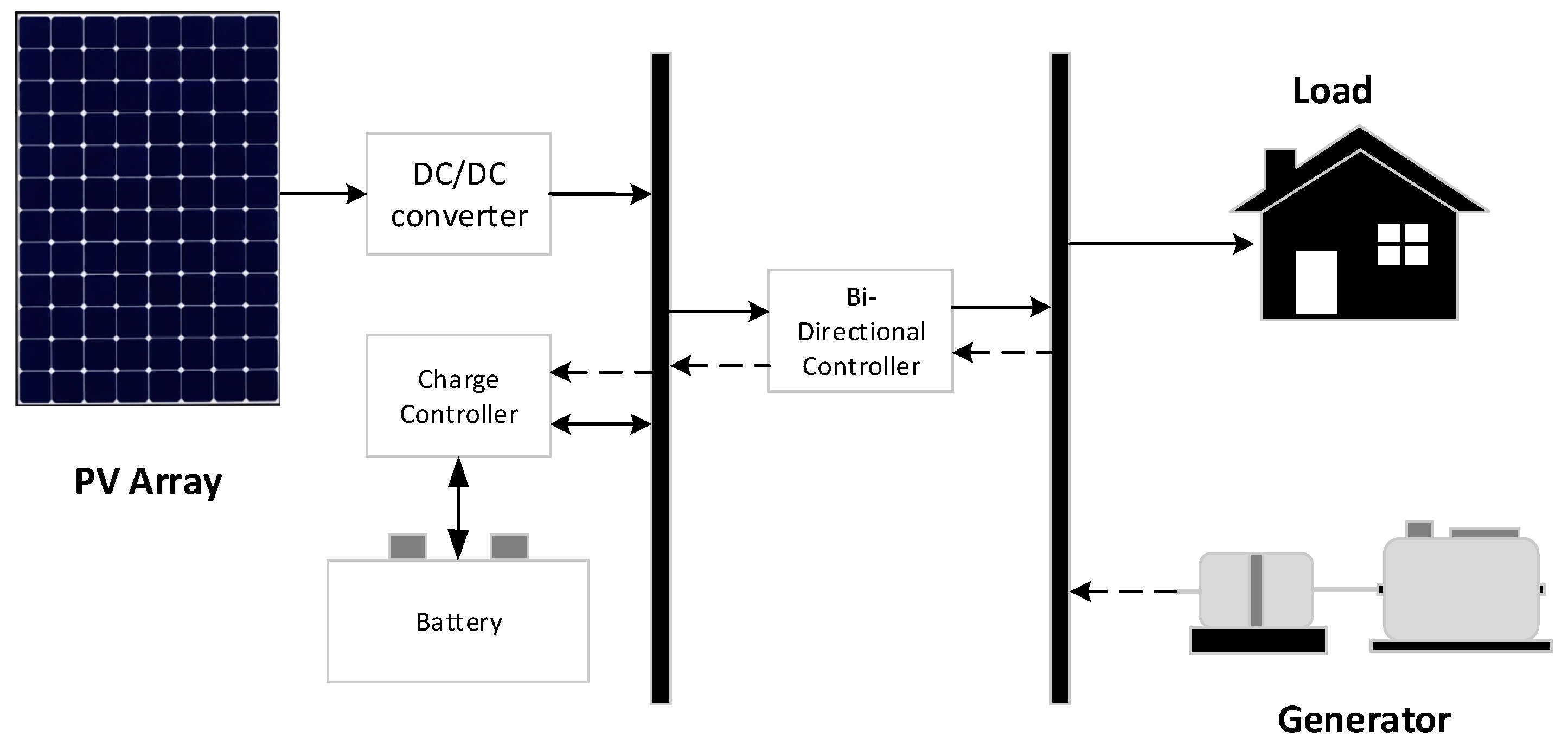
Modelling of the System
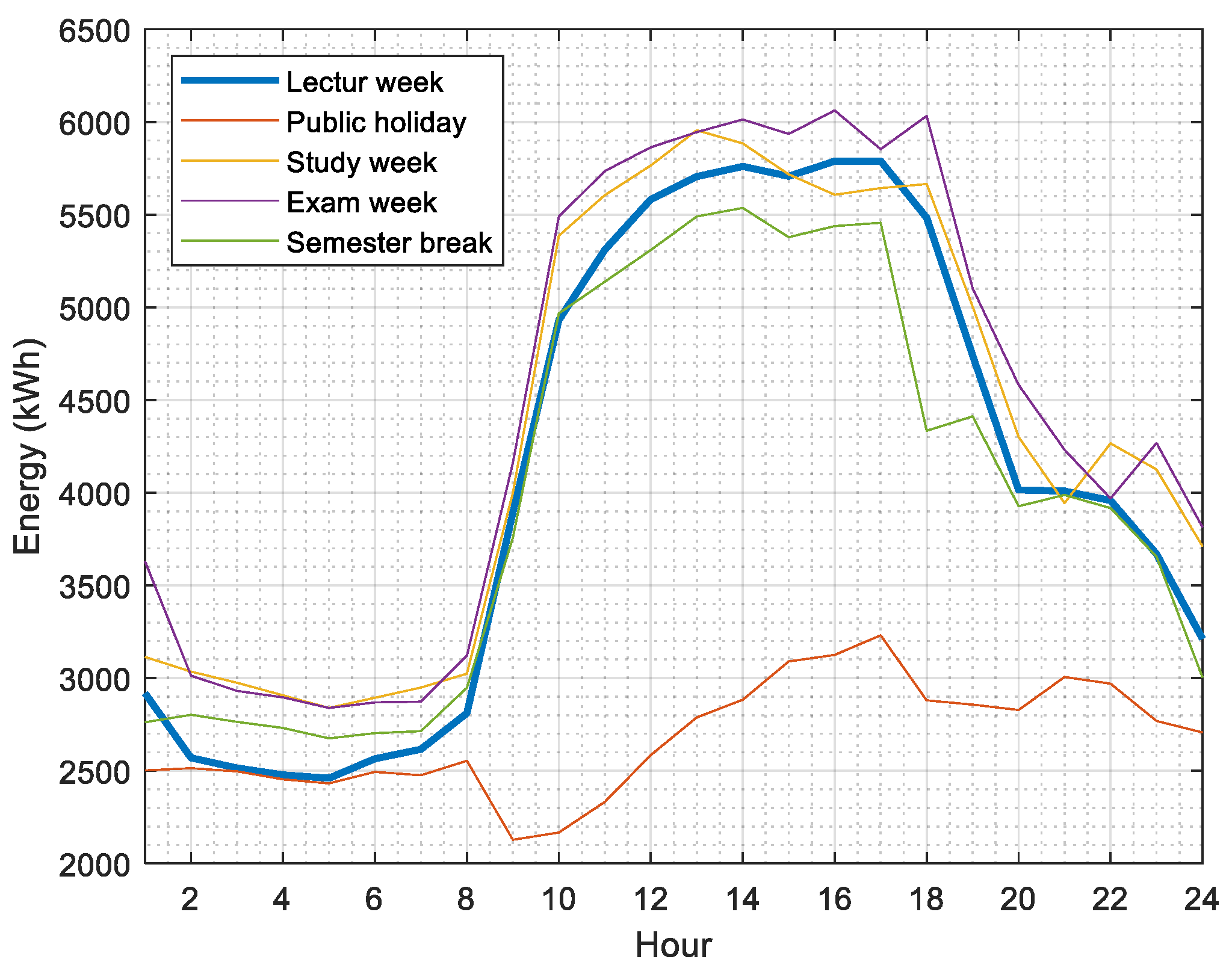
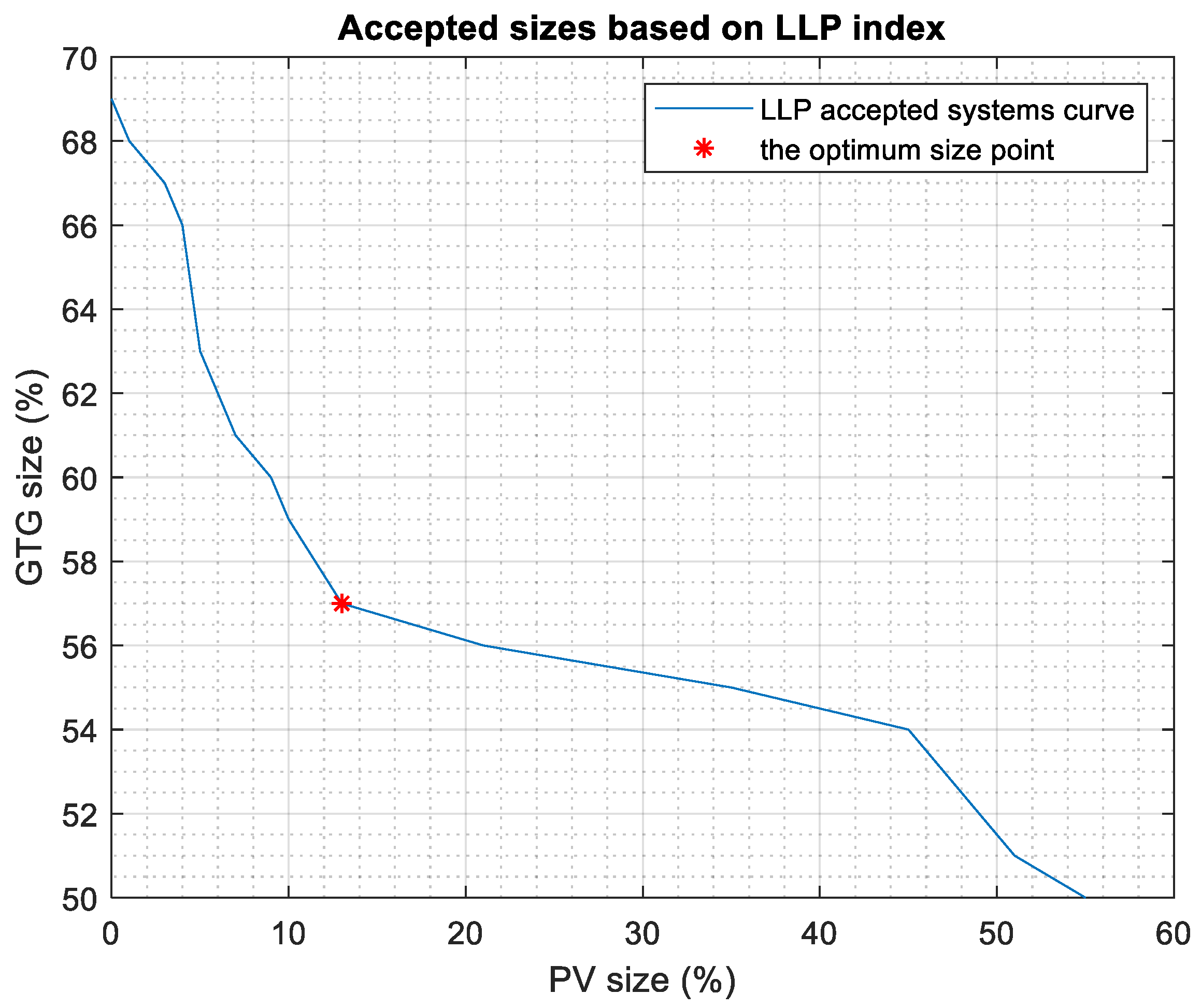
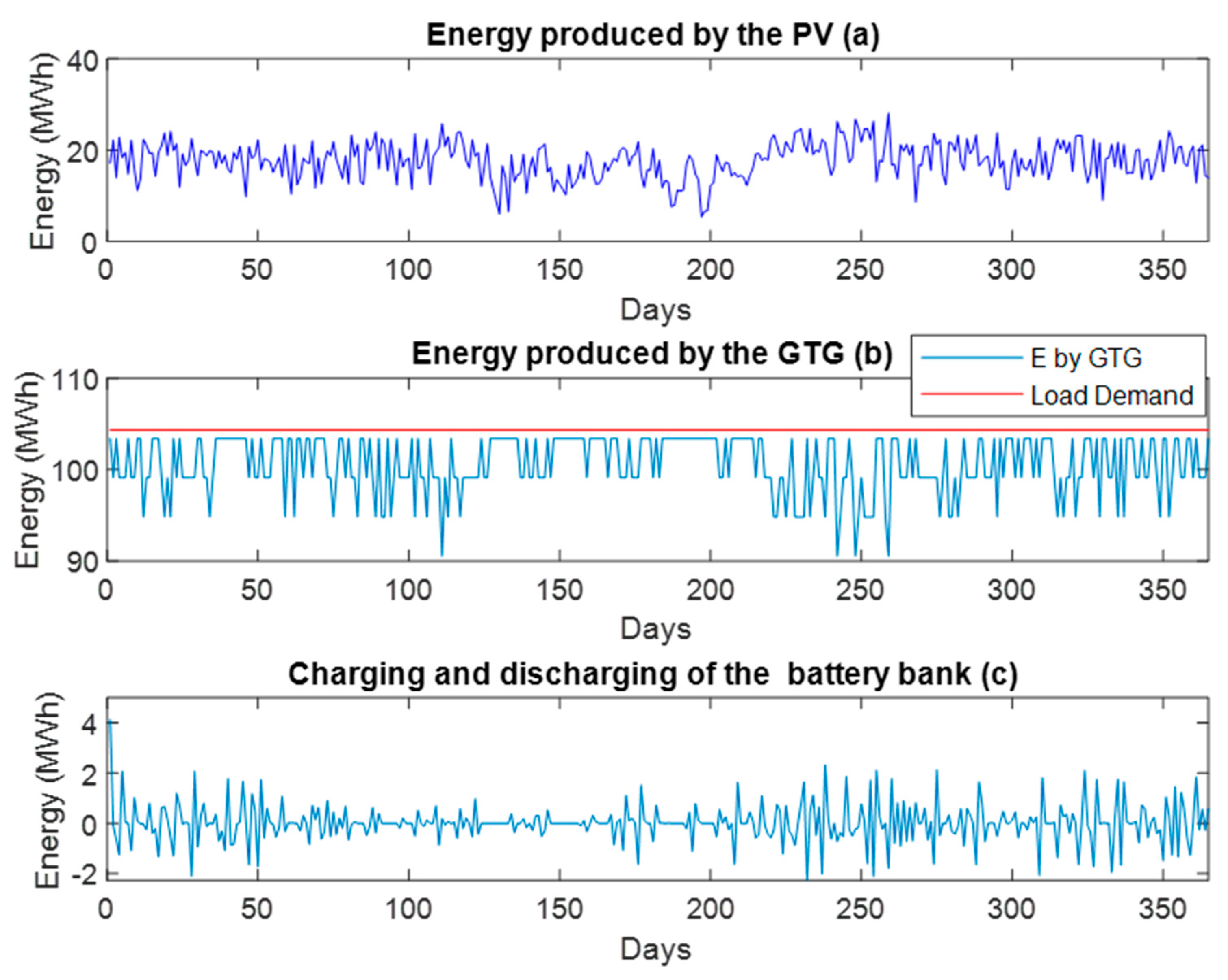
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bhattacharya, M.; Paramati, S.R.; Ozturk, I.; Bhattacharya, S. The effect of renewable energy consumption on economic growth: Evidence from top 38 countries. Applied Energy 2016, 162, 733–744. [Google Scholar] [CrossRef]
- Mamaghani, A.H.; Escandon, S.A.A.; Najafi, B.; Shirazi, A.; Rinaldi, F. Techno-economic feasibility of photovoltaic, wind, diesel and hybrid electrification systems for off-grid rural electrification in Colombia. Renew. Energy 2016, 97, 293–305. [Google Scholar] [CrossRef]
- Saboori, H.; Hemmati, R.; Jirdehi, M.A. Reliability improvement in radial electrical distribution network by optimal planning of energy storage systems. Energy 2015, 93, 2299–2312. [Google Scholar] [CrossRef]
- Pavković, D.; Hoić, M.; Deur, J.; Petrić, J. Energy storage systems sizing study for a high-altitude wind energy application. Energy 2014, 76, 91–103. [Google Scholar] [CrossRef]
- Cucchiella, F.; D’Adamo, I.; Gastaldi, M.; Stornelli, V. Solar Photovoltaic Panels Combined with Energy Storage in a Residential Building: An Economic Analysis. Sustainability 2018, 10, 3117. [Google Scholar] [CrossRef]
- Mohd Shatar, N.; Abdul Rahman, M.A.; Muhtazaruddin, M.N.; Shaikh Salim, S.A.Z.; Singh, B.; Muhammad-Sukki, F.; Bani, N.A.; Mohd Saudi, A.S.; Ardila-Rey, J.A. Performance Evaluation of Unconcentrated Photovoltaic-Thermoelectric Generator Hybrid System under Tropical Climate. Sustainability 2019, 11, 6192. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Sopian, K. Optimization of a PV/wind micro-grid for rural housing electrification using a hybrid iterative/genetic algorithm: Case study of Kuala Terengganu, Malaysia. Energy Build. 2012, 47, 321–331. [Google Scholar] [CrossRef]
- Chen, P.-J.; Wang, F.-C. Design optimization for the hybrid power system of a green building. Int. J. Hydrogen Energy 2018, 43, 2381–2393. [Google Scholar] [CrossRef]
- Sadeghi, S.; Ameri, M. Comparison the combination of different power generators with photovoltaic panels and batteries. In Computer Applications for Security, Control and System Engineering; Springer: Berlin/Heidelberg, Germany, 2012; pp. 376–387. [Google Scholar]
- Basrawi, F.; Yamada, T.; Obara, S.Y. Economic and environmental based operation strategies of a hybrid photovoltaic–microgas turbine trigeneration system. Appl. Energy 2014, 121, 174–183. [Google Scholar] [CrossRef]
- Comodi, G.; Renzi, M.; Cioccolanti, L.; Caresana, F.; Pelagalli, L. Hybrid system with micro gas turbine and PV (photovoltaic) plant: Guidelines for sizing and management strategies. Energy 2015, 89, 226–235. [Google Scholar] [CrossRef]
- Jaber, J.; Odeh, S.; Probert, S. Integrated PV and gas-turbine system for satisfying peak-demands. Appl. Energy 2003, 76, 305–319. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S. Review of recent trends in optimization techniques for solar photovoltaic–wind based hybrid energy systems. Renew. Sustain. Energy Rev. 2015, 50, 755–769. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Sopian, K. A review of photovoltaic systems size optimization techniques. Renew. Sustain. Energy Reviews 2013, 22, 454–465. [Google Scholar] [CrossRef]
- Shen, W. Optimally sizing of solar array and battery in a standalone photovoltaic system in Malaysia. Renewable energy 2009, 34, 348–352. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, S.; Liu, D.; Li, R.; Chu, Y. Operation optimization strategy for wind-concentrated solar power hybrid power generation system. Energy Convers. Manag. 2018, 160, 243–250. [Google Scholar] [CrossRef]
- Bataineh, K.; Dalalah, D. Optimal configuration for design of stand-alone PV system. Smart Grid Renew. Energy 2012, 3, 139–147. [Google Scholar] [CrossRef]
- Kouro, S.; Leon, J.I.; Vinnikov, D.; Franquelo, L.G. Grid-connected photovoltaic systems: An overview of recent research and emerging PV converter technology. IEEE Ind. Electron. Mag. 2015, 9, 47–61. [Google Scholar] [CrossRef]
- Vivas, F.; De las Heras, A.; Segura, F.; Andújar, J. A review of energy management strategies for renewable hybrid energy systems with hydrogen backup. Renew. Sustain. Energy Rev. 2018, 82, 126–155. [Google Scholar] [CrossRef]
- Ogunjuyigbe, A.; Ayodele, T.; Akinola, O. Optimal allocation and sizing of PV/Wind/Split-diesel/Battery hybrid energy system for minimizing life cycle cost, carbon emission and dump energy of remote residential building. Appl. Energy 2016, 171, 153–171. [Google Scholar] [CrossRef]
- Kaabeche, A.; Ibtiouen, R. Techno-economic optimization of hybrid photovoltaic/wind/diesel/battery generation in a stand-alone power system. Solar Energy 2014, 103, 171–182. [Google Scholar] [CrossRef]
- Belaid, S.; Mellit, A. Prediction of daily and mean monthly global solar radiation using support vector machine in an arid climate. Energy Convers. Manag. 2016, 118, 105–118. [Google Scholar] [CrossRef]
- Ameen, A.M.; Pasupuleti, J.; Khatib, T. Simplified performance models of photovoltaic/diesel generator/battery system considering typical control strategies. Energy Convers. Manag. 2015, 99, 313–325. [Google Scholar] [CrossRef]


| Yearly (USD) | Proposed System | GTG System | TNB System |
|---|---|---|---|
| Tariff | 0.046681 | 0.07530421 | 0.05952902 |
| Savings | 2,171,345.0175 | 0 | 1,167,514.0812 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atef, M.; Khatib, T.; Abdullah, M.F.; Romlie, M.F. Optimization of a Hybrid Solar PV and Gas Turbine Generator System Using the Loss of Load Probability Index. Clean Technol. 2020, 2, 240-251. https://doi.org/10.3390/cleantechnol2030016
Atef M, Khatib T, Abdullah MF, Romlie MF. Optimization of a Hybrid Solar PV and Gas Turbine Generator System Using the Loss of Load Probability Index. Clean Technologies. 2020; 2(3):240-251. https://doi.org/10.3390/cleantechnol2030016
Chicago/Turabian StyleAtef, Mohamed, Tamer Khatib, Muhammad Faris Abdullah, and Mohd Fakhizan Romlie. 2020. "Optimization of a Hybrid Solar PV and Gas Turbine Generator System Using the Loss of Load Probability Index" Clean Technologies 2, no. 3: 240-251. https://doi.org/10.3390/cleantechnol2030016
APA StyleAtef, M., Khatib, T., Abdullah, M. F., & Romlie, M. F. (2020). Optimization of a Hybrid Solar PV and Gas Turbine Generator System Using the Loss of Load Probability Index. Clean Technologies, 2(3), 240-251. https://doi.org/10.3390/cleantechnol2030016






