Simulated Biogeochemical Effects of Seawater Restoration on Diked Salt Marshes, Cape Cod National Seashore, Massachusetts, U.S.
Abstract
1. Introduction
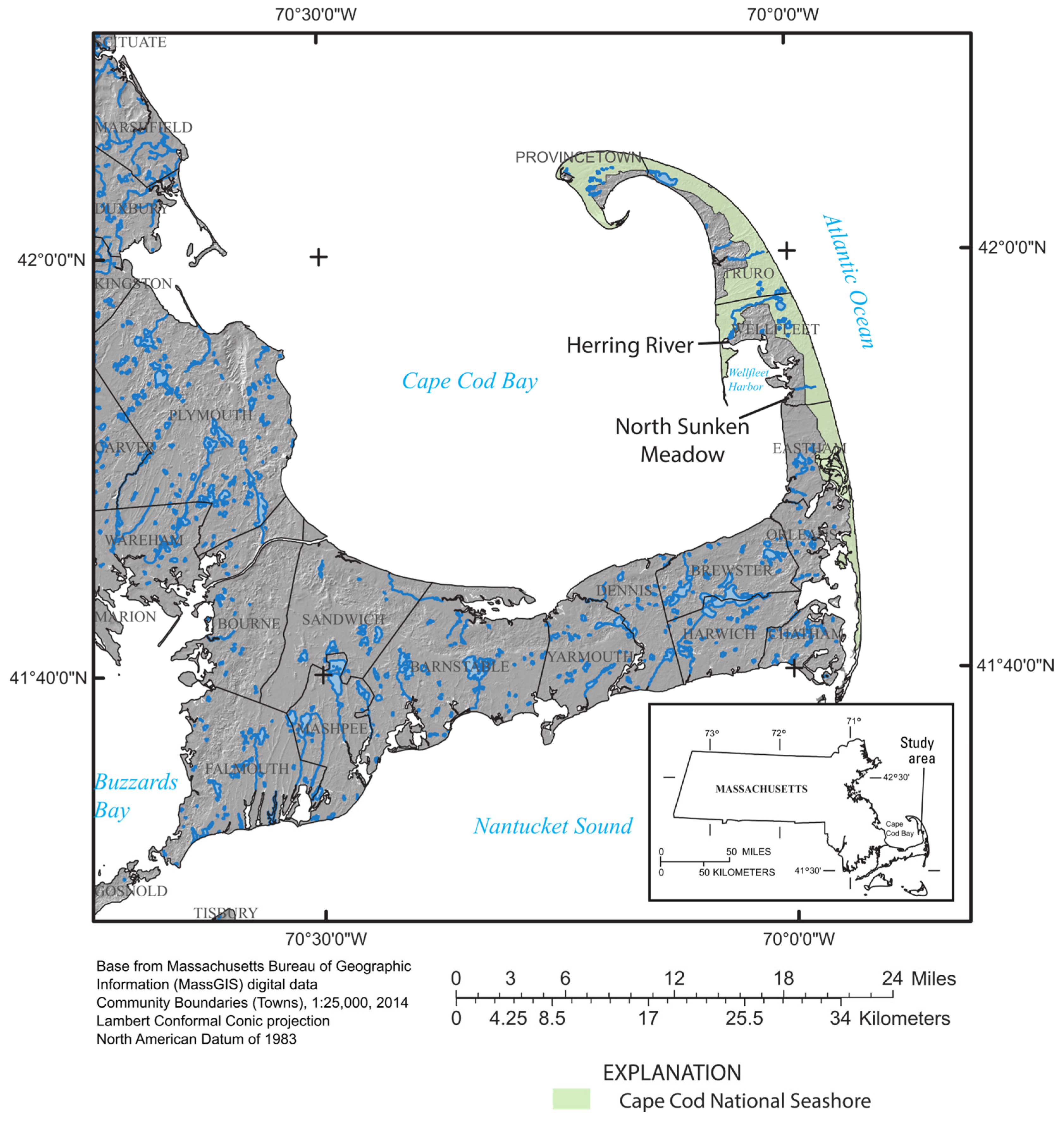
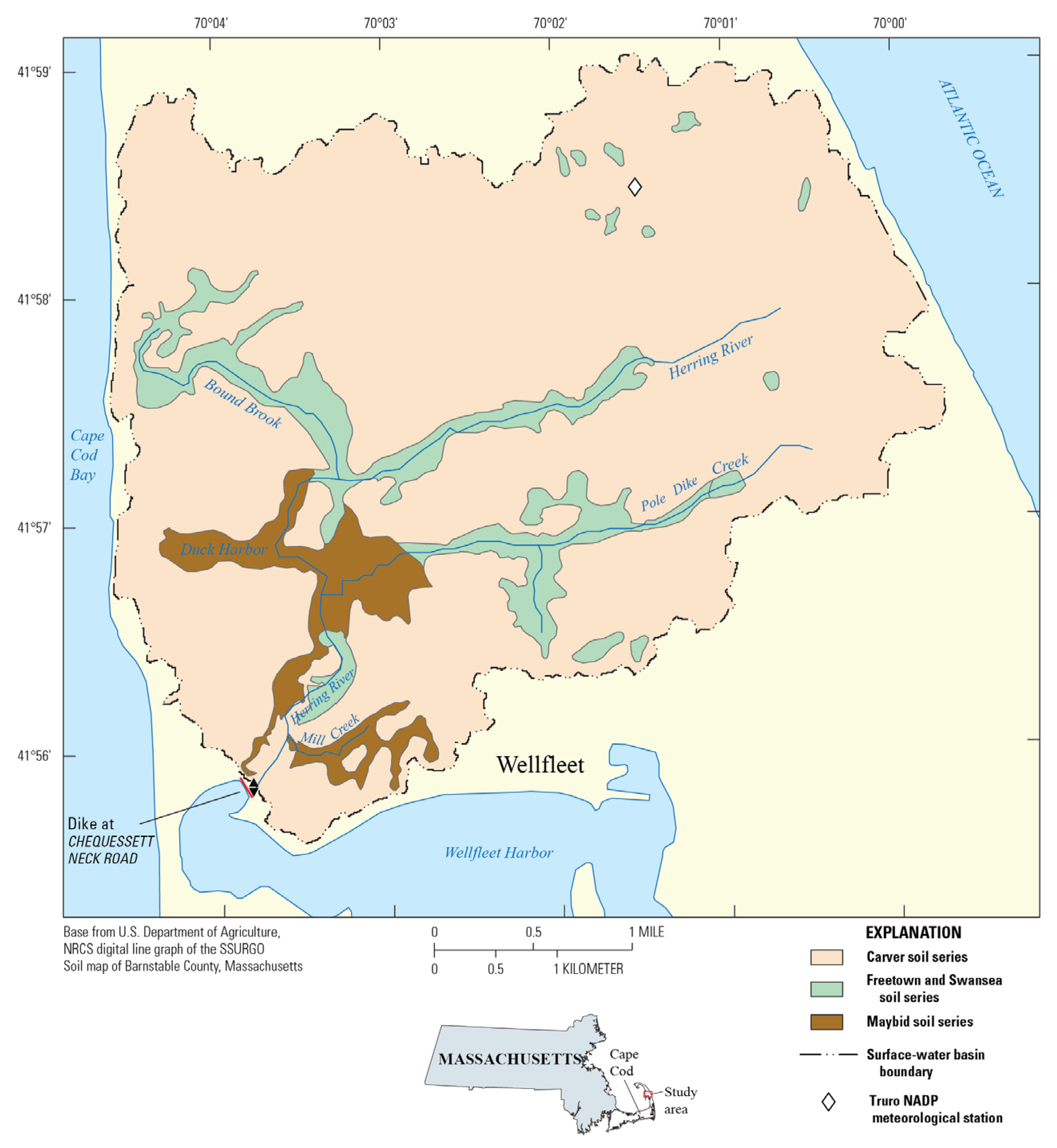
2. Methods
| Simulation | Microcosm Flow, Saltwater (Solution 0) | Porosity (%) | Number of Pore Volumes | Number of Shifts | Time per Shift (Seconds) | Velocity a (Meters/Second) | |
|---|---|---|---|---|---|---|---|
| Volume (Liters) | Time Period | DF/DD | |||||
| Microcosm column experiment models [4] | 10 | 12 h | 90/55 | 1.38/2.29 | 62/103 | 687/419 | 1.4 × 10−5/2.4 × 10−5 |
| 3 | 3 mos | 90/55 | 0.42/0.69 | 18.9/30.9 | 412,031/251,793 | 2.4 × 10−8/3.97 × 10−8 | |
| 1.5 | 10 mos | 90/55 | 0.21/0.34 | 9.44/15.4 | 2,746,872/1,678,618 | 3.7 × 10−9/5.96 × 10−9 | |
| 3.5 | 7 mos | 90/55 | 0.49/0.80 | 22/36 | 824,062/503,585 | 1.2 × 10−8/1.99 × 10−8 | |
| Basecase models | 72.9 | 12 yrs | 90/55 | 10.2/16.7 | 458/750 | 828,818/506,573 | 1.2 × 10−8/1.97 × 10−8 |
| 605 | 100 yrs | 90/55 | 9.9 × 104/1.6 × 105 | 3808/ 6230 | 828,718/ 506,543 | 1.2 × 10−8/1.97 × 10−8 | |
2.1. Study Area and Marsh Restoration Biogeochemistry
2.2. Microcosm Geochemical Models and Calibration
2.2.1. Model Assumptions and Set Up
| Reaction Number | Reaction | Reaction Type | Equation | Rates (1/s): Determined by Calibration for DF Sediments | Rates (1/s): Determined by Calibration for DD Sediments |
|---|---|---|---|---|---|
| 1 | Oxidation of SOM by reduction of Fe(III) [ammonium jarosite is source of the Fe(III) used in the model] | Redox, kinetically controlled | DOM a + 4x Fe3+4xOH− → xCO2(g) + 4x Fe2+ + 3/xH2O + y NH3 + z H3PO4 | Rate = 3.5 × 10−9 | Rate = 7 × 10−9 |
| 2 | Oxidation of SOM by reduction of SO42− | Redox, kinetically controlled | DOM a + (x/2)SO42− + (y-2z)CO2 + (y-2z)H2O → (x/2)H2S + (x+y−2z)HCO3− + yNH4+ + zHPO42− | IF(tot(“Fe(+3)”) ≤ 2 × 10−6, THEN rate = 2.5 × 10−10 | IF(tot(“Fe(+3)”) ≤ 2 × 10−6, THEN rate = 1.76 × 10−9 |
| 3 | Oxidation of SOM by methanogenesis | Redox, kinetically controlled | DOM a + (y−2z)H2O → x/2CH4 + (x−2y+4z/2)CO2 + (y−2z)HCO3− + yNH4+ + zHPO42− | IF (tot(“Fe(+3)”) ≤ 2 × 10−6, AND (tot(“SO42−)”) ≤ 2 × 10−6, THEN rate = 3 × 10−11 | IF (tot(“Fe(+3)”) ≤ 2 × 10−6, AND (tot(“SO42−)”) ≤ 2 × 10−6, THEN rate = 1.76 × 10−10 |
| 4 | FeS precipitation | Equilibrium | FeS = Fe+2 + S−2 | NA | NA |
| 5 | Al(OH)3 (amorphous) precipitation and dissolution | Equilibrium | Al(OH)3 + 3H+ = Al+3 + 3 H2O | NA | NA |
| Constituent or Property | DF Solution 1–45 | DD Solution 1–45 | Seawater Composition, Solution 0 |
|---|---|---|---|
| Temperature °C | 25 | 25 | 25 |
| pH | 6.7 | 4 | 8.5 a |
| pe | -- | -- | 8.45 |
| Na | 0.026 a | 0.026 a | 468 c |
| Ca | 0.004 a | 0.004 a | 10.2 c |
| Mg | 0.0015 a | 0.0015 a | 53.2 c |
| K | 0.001 a | -- | 10.2 c |
| Cl | 0.040 | 0.715 a | 545 c |
| S(6), sulfate | -- | -- | 28.2 c |
| Alkalinity as HCO3- | 4 a | 0.1 a | 2.3 c |
| N(-3), ammonium | 0.001 | 0.075 a | - |
| S2− | 0.1 a | 0 a | -- |
| P | 0.001 b | 0.002 a | -- |
| Fe(II) | 0.0001 a | 0.1 a | -- |
| Fe(III) | 0.0001 a | 0.001 | -- |
| Si | -- | -- | 0.07 c |
| O(0), diss. oxygen | 0.01 | 0.01 | 0.75 |
| Al | 0.01 a | 0.3 a | -- |
| Parameter | DF Biogeochemistry | DD Biogeochemistry |
|---|---|---|
| Exchange concentrations (mol/L) | 0.50 | 0.85 |
| Surfaces sites (mol/L) | 0.027 | 0.2 |
| Equilibrium phases—ammonium jarosite concentration (mol/L) | 0.0001 throughout (0.005 in basecase) | Varies with profile [5] |
| Rate of reaction | DF rates (Table 2) | DD rates (Table 2) |
| Solutions | DF freshwater; artificial seawater (Table 3) | DD freshwater; artificial seawater (Table 3) |
2.2.2. Sedimentary Organic Matter (SOM) Degradation Rates
2.2.3. Solution Chemistry, Ion Exchange, and Surface Complexation (Sorption)
2.3. Basecase Geochemical Models
3. Results and Discussion
3.1. Geochemical Modeling of Microcosm Experiments
3.1.1. Biogeochemical Model of Diked, Flooded (DF) Sediments
3.1.2. Biogeochemical Model of Diked, Drained (DD) Sediments
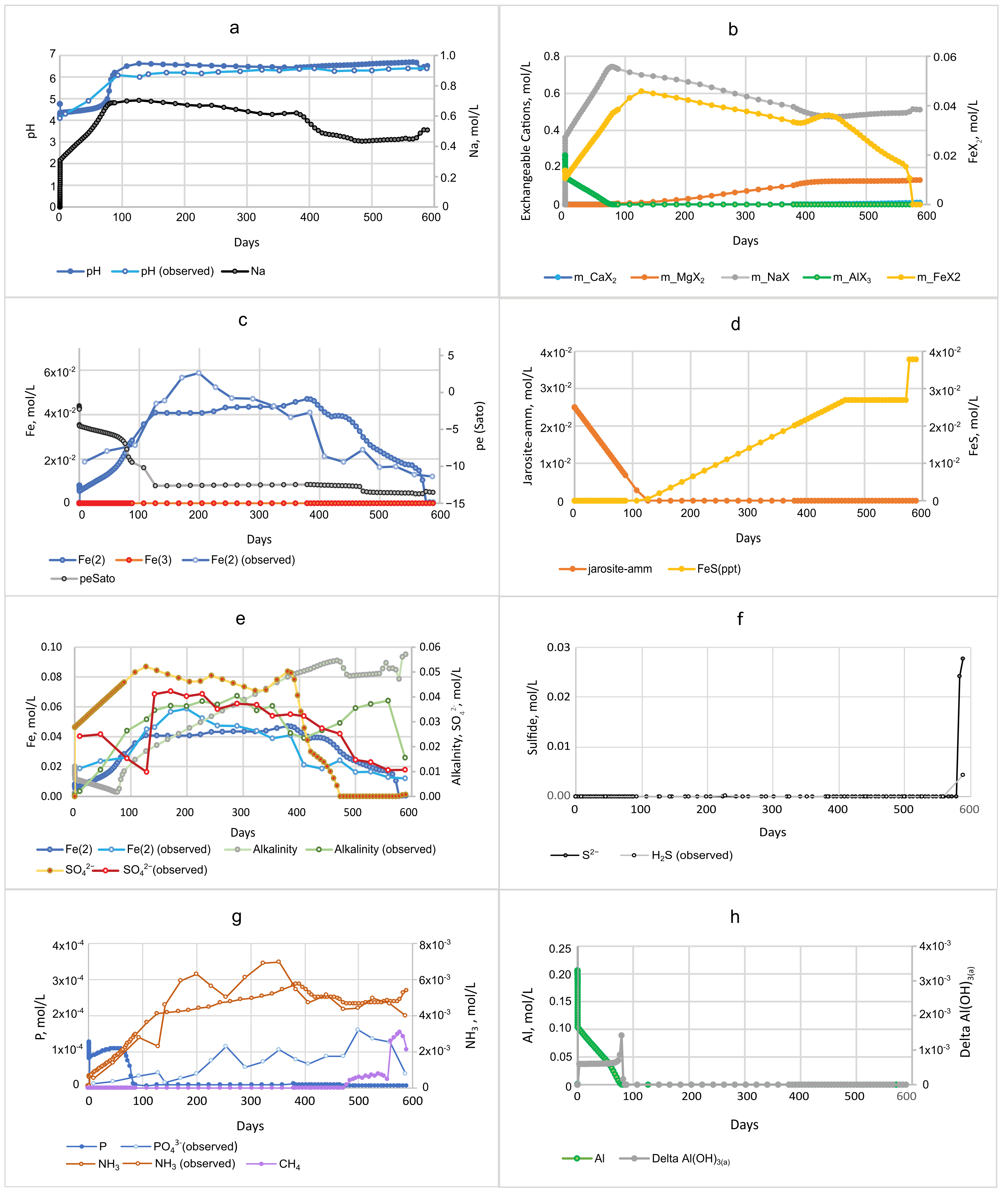
3.1.3. Comparison of DF and DD Models
3.2. Basecase Simulations of Seawater Flooding in Diked Marsh Sediments
3.3. Biogeochemical Implications of Seawater Restoration
4. Summary and Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Previous Marsh Sediment Microcosm Experiments
References
- Soukup, M.A.; Portnoy, J.W. Impacts from mosquito control-induced sulphur mobilization in a Cape Cod estuary. Environ. Conserv. 1986, 13, 47–50. [Google Scholar] [CrossRef]
- Dent, D.L.; Pons, L.J. A world perspective on acid sulphate soils. Geoderma 1995, 67, 263–276. [Google Scholar] [CrossRef]
- Portnoy, J. Summer oxygen depletion in a diked New England estuary. Estuaries 1991, 14, 122–129. [Google Scholar] [CrossRef]
- Portnoy, J.W.; Giblin, A.E. Biogeochemical effects of seawater restoration to diked salt marshes. Ecol. Appl. 1997, 7, 1054–1063. [Google Scholar] [CrossRef]
- Portnoy, J.W.; Giblin, A.E. Effects of historic tidal restrictions on salt marsh sediment chemistry. Biogeochemistry 1997, 36, 275–303. [Google Scholar] [CrossRef]
- Anisfeld, S.C. Biogeochemical Responses to Tidal Restoration. In Tidal Marsh Restoration: A Synthesis of Science and Management; Roman, C.T., Burdick, D.M., Eds.; Island Press/Center for Resource Economics: Washington, DC, USA, 2012; pp. 39–58. ISBN 978-1-61091-229-7. [Google Scholar] [CrossRef]
- Adams, J.B.; Niekerk, L.V. Ten principles to determine environmental flow requirements for temporarily closed estuaries. Water 2020, 12, 1944. [Google Scholar] [CrossRef]
- Gedan, K.B.; Silliman, B.R.; Bertness, M.D. Centuries of Human-Driven Change in Salt Marsh Ecosystems. Annu. Rev. Mar. Sci. 2009, 1, 117–141. [Google Scholar] [CrossRef]
- Bromberg, K.D.; Bertness, M.D. Reconstructing New England salt marsh losses using historical maps. Estuaries 2005, 28, 823–832. [Google Scholar] [CrossRef]
- Niering, W.A.; Bowers, R.M. Our disappearing tidal marshes. In Connecticut Coastal Marshes: A Vanishing Resource; The Connecticut Aboretum Bulletin No. 12; Connecticut College: New London, CT, USA, 1966; p. 36. Available online: https://digitalcommons.conncoll.edu/arbbulletins/12/ (accessed on 1 August 2024).
- Holmquist, J.R.; Eagle, M.; Molinari, R.L.; Nick, S.K.; Stachowicz, L.C.; Kroeger, K.D. Mapping methane reduction potential of tidal wetland restoration in the United States. Commun. Earth Environ. 2023, 4, 353. [Google Scholar] [CrossRef]
- Kroeger, K.D.; Crooks, S.; Moseman-Valtierra, S.; Tang, J. Restoring tides to reduce methane emissions in impounded wetlands: A new and potent Blue Carbon climate change intervention. Sci. Rep. 2017, 7, 11914. [Google Scholar] [CrossRef] [PubMed]
- Crooks, S.; Sutton-Grier, A.E.; Troxler, T.G.; Herold, N.; Bernal, B.; Schile-Beers, L.; Wirth, T. Coastal wetland management as a contribution to the US National Greenhouse Gas Inventory. Nat. Clim. Change 2018, 8, 1109–1112. [Google Scholar] [CrossRef] [PubMed]
- Sanders-DeMott, R.; Eagle, M.J.; Kroeger, K.D.; Wang, F.; Brooks, T.W.; O’Keefe Suttles, J.A.; Nick, S.K.; Mann, A.G.; Tang, J. Impoundment increases methane emissions in Phragmites-invaded coastal wetlands. Glob. Change Biol. 2022, 28, 4539–4557. [Google Scholar] [CrossRef]
- Cape Cod National Seashore. East Harbor Tidal Restoration Project. National Park Service. 2022. Available online: http://www.nps.gov/caco/naturescience/east-harbor-tidal-restoration-project-page.htm (accessed on 1 August 2024).
- Burton, E.D.; Bush, R.T.; Johnston, S.G.; Sullivan, L.A.; Keene, A.F. Sulfur biogeochemical cycling and novel Fe-S mineralization pathways in a tidally re-flooded wetland. Geochim. Cosmochim. Acta 2011, 75, 3434–3451. [Google Scholar] [CrossRef]
- Lucas, L.V.; Brown, C.J.; Robertson, D.M.; Baker, N.T.; Johnson, Z.C.; Green, C.T.; Cho, S.J.; Erickson, M.L.; Gellis, A.C.; Jasmann, J.R.; et al. Gaps in Water-Quality Modeling of Hydrologic Systems, Intended outlet. Water 2025, 17, 98. [Google Scholar] [CrossRef]
- DeLaune, R.; Patrick Jr, W.; Van Breemen, N. Processes governing marsh formation in a rapidly subsiding coastal environment. Catena 1990, 17, 277–288. [Google Scholar] [CrossRef]
- Nyman, J.A.; Carloss, M.; DeLaune, R.; Patrick, W., Jr. Erosion rather than plant dieback as the mechanism of marsh loss in an estuarine marsh. Earth Surf. Process. Landf. 1994, 19, 69–84. [Google Scholar] [CrossRef]
- Thom, R.M. Accretion rates of low intertidal salt marshes in the Pacific Northwest. Wetlands 1992, 12, 147–156. [Google Scholar] [CrossRef]
- Capone, D.G.; Kiene, R.P. Comparison of microbial dynamics in marine and freshwater sediments: Contrasts in anaerobic carbon catabolism 1. Limnol. Oceanogr. 1988, 33, 725–749. [Google Scholar] [CrossRef]
- Wong, V.N.L.; Johnston, S.G.; Burton, E.D.; Bush, R.T.; Sullivan, L.A.; Slavich, P.G. Seawater causes rapid trace metal mobilisation in coastal lowland acid sulfate soils: Implications of sea level rise for water quality. Geoderma 2010, 160, 252–263. Available online: https://www.sciencedirect.com/science/article/pii/S0016706110003034 (accessed on 1 August 2024). [CrossRef]
- Yvanes-Giuliani, Y.A.M.; Waite, T.D.; Collins, R.N. Exchangeable and secondary mineral reactive pools of aluminium in coastal lowland acid sulfate soils. Sci. Total Environ. 2014, 485–486, 232–240. [Google Scholar] [CrossRef]
- Appelo, C.A.J.; Postma, D. Geochemistry, Groundwater, and Pollution, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2005; 649p. [Google Scholar]
- Davis, J.A.; Kent, D.B. Chapt. 5. Mineral-Water Interface Geochemistry. In Reviews in Mineralogy, Volume 23: Mineral-Water Interface Geochemistry; Hochella, M.F., Jr., White, A.F., Eds.; Mineralogical Society of America: Washington, DC, USA, 1990; pp. 177–260. Available online: http://www.minsocam.org/MSA/RIM/Rim23.html (accessed on 1 August 2024).
- Kent, D.B.; Wilkie, J.A.; Davis, J.A. Modeling the movement of a pH perturbation and its impact on adsorbed zinc and phosphate in a wastewater-contaminated aquifer. Water Resour. Res. 2007, 43, 4841. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Stollenwerk, K.G.; Colman, J.A. Reactive-transport simulation of phosphorus in the sewage plume at the Massachusetts Military Reservation, Cape Cod, Massachusetts. In Water-Resources Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2003. [Google Scholar] [CrossRef]
- Dzombak, D.A.; Morel, F.M. Surface Complexation Modeling: Hydrous Ferric Oxide; Wiley-Interscience: New York, NY, USA, 1990; ISBN 0471637319. [Google Scholar]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3: A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations; U.S. Geological Survey Techniques and Methods 6-A43: Reston, VA, USA, 2013; p. 519. [CrossRef]
- Hare, J.A.; Borggaard, D.L.; Alexander, M.A.; Bailey, M.M.; Bowden, A.A.; Damon-Randall, K.; Didden, J.T.; Hasselman, D.J.; Kerns, T.; McCrary, R.; et al. A review of river herring science in support of species conservation and ecosystem restoration. Mar. Coast. Fish. 2021, 13, 627–664. [Google Scholar] [CrossRef]
- Portnoy, J.; Phipps, C.; Samora, B. Mitigating the effects of oxygen depletion on Cape Cod NS anadromous fish. Park Sci. 1987, 8, 12–13. [Google Scholar]
- MassDCR. Wellfleet Harbor Resource Summary, Area of Critical Environmental Concern (ACEC); Massachusetts Department of Conservation & Recreation: Boston, MA, USA, 2003; 4p. Available online: https://www.mass.gov/doc/wellfleet-harbor-resource-summary (accessed on 1 August 2024).
- Brown, C.J. Data and Model Archive for Simulations of Seawater Restoration on Diked Salt Marshes; U.S. Geological Survey Data Release: Reston, VA, USA, 2024. [CrossRef]
- Mullaney, J.R.; Barclay, J.R.; Laabs, K.L.; Lavallee, K.D. Hydrogeology and interactions of groundwater and surface water near Mill Creek and the Herring River, Wellfleet, Massachusetts, 2017–2018. Sci. Investig. Rep. 2020, 60, 5145. [Google Scholar] [CrossRef]
- NRCS Soil Survey Staff. Official Soil Series Descriptions; Natural Resources Conservation Service, United States Department of Agriculture: Washington, DC, USA, 2024. Available online: https://www.nrcs.usda.gov/resources/data-and-reports/official-soil-series-descriptions-osd (accessed on 11 August 2024).
- Huntington, T.G.; Spaetzel, A.B.; Colman, J.A.; Kroeger, K.D.; Bradley, R.T. Assessment of water quality and discharge in the Herring River, Wellfleet, Massachusetts, November 2015 to September 2017. Sci. Investig. Rep. 2021, 59, 5120. [Google Scholar] [CrossRef]
- Friends of the Herring River. Transitioning Flow to the Chequessett Neck Road Bridge. Project Updates. 2025. Available online: https://herringriver.org/news/restoration-updates/ (accessed on 12 May 2025).
- Hansel, C.M.; Lentini, C.J.; Tang, Y.; Johnston, D.T.; Wankel, S.D.; Jardine, P.M. Dominance of sulfur-fueled iron oxide reduction in low-sulfate freshwater sediments. ISME J. 2015, 9, 2400–2412. [Google Scholar] [CrossRef] [PubMed]
- Berner, R.A. Early Diagenesis: A Theoretical Approach; Princeton University Press: Princeton, NJ, USA, 1980; ISBN 069108260X. [Google Scholar]
- Capooci, M.; Seyfferth, A.L.; Tobias, C.; Wozniak, A.S.; Hedgpeth, A.; Bowen, M.; Biddle, J.F.; McFarlane, K.J.; Vargas, R. High methane concentrations in tidal salt marsh soils: Where does the methane go? Glob. Change Biol. 2024, 30, e17050. [Google Scholar] [CrossRef]
- Rickard, D. The composition of mackinawite. Am. Mineral. 2024, 109, 401–407. [Google Scholar] [CrossRef]
- Rickard, D. Chapter 5—Metastable Sedimentary Iron Sulfides. In Developments in Sedimentology; Rickard, D., Ed.; Elsevier: Amsterdam, The Netherlands, 2012; Volume 65, pp. 195–231. ISBN 0070-4571. [Google Scholar] [CrossRef]
- Lan, Y.; Butler, E.C. Monitoring the transformation of mackinawite to greigite and pyrite on polymer supports. Appl. Geochem. 2014, 50, 1–6. [Google Scholar] [CrossRef]
- Fanning, D.S.; Rabenhorst, M.C.; Fitzpatrick, R.W. Historical developments in the understanding of acid sulfate soils. Geoderma 2017, 308, 191–206. [Google Scholar] [CrossRef]
- Singer, P.C.; Stumm, W. Acidic mine drainage: The rate-determining step. Science 1970, 167, 1121–1123. [Google Scholar] [CrossRef]
- Moses, C.O.; Nordstrom, D.K.; Herman, J.S.; Mills, A.L. Aqueous pyrite oxidation by dissolved oxygen and by ferric iron. Geochim. et Cosmochim. Acta 1987, 51, 1561–1571. [Google Scholar] [CrossRef]
- Brown, A.D.; Jurinak, J.J. Mechanism of Pyrite Oxidation in Aqueous Mixtures. J. Environ. Qual. 1989, 18, 545–550. [Google Scholar] [CrossRef]
- Luther, G.W.; Kostka, J.E.; Church, T.M.; Sulzberger, B.; Stumm, W. Seasonal iron cycling in the salt-marsh sedimentary environment: The importance of ligand complexes with Fe(II) and Fe(III) in the dissolution of Fe(III) minerals and pyrite, respectively. Mar. Chem. 1992, 40, 81–103. [Google Scholar] [CrossRef]
- Daoud, J.; Karamanev, D. Formation of jarosite during Fe2+ oxidation by Acidithiobacillus ferrooxidans. Miner. Eng. 2006, 19, 960–967. [Google Scholar] [CrossRef]
- Nordstrom, D.K.; Blowes, D.W.; Ptacek, C.J. Hydrogeochemistry and microbiology of mine drainage: An update. Appl. Geochem. 2015, 57, 3–16. [Google Scholar] [CrossRef]
- Appelo, C.A.J. Cation and proton exchange, pH variations, and carbonate reactions in a freshening aquifer. Water Resour. Res. 1994, 30, 2793–2805. [Google Scholar] [CrossRef]
- Brown, C.J.; Misut, P.E. Aquifer geochemistry at potential aquifer storage and recovery sites in coastal plain aquifers in the New York city area, USA. Appl. Geochem. 2010, 25, 1431–1452. [Google Scholar] [CrossRef]
- Lombard, M.A.; Lombard, P.J.; Brown, C.J.; Degnan, J.R. A multi-model approach toward understanding iron fouling at rock-fill drainage sites along roadways in New Hampshire, USA. SN Appl. Sci. 2020, 2, 1073. [Google Scholar] [CrossRef]
- USEPA. Aquatic Life Criteria and Methods for Toxics; U.S. Environmental Protection Agency: Washington, DC, USA, 2023. Available online: https://www.epa.gov/wqc/aquatic-life-criteria-and-methods-toxics (accessed on 15 March 2025).
- USEPA. Ambient Water Quality Criteria for Ammonia (Saltwater); U.S. Federal Register: Washington, DC, USA, 1989. Available online: https://www.epa.gov/sites/default/files/2019-02/documents/ambient-wqc-ammonia-saltwater-1989.pdf (accessed on 1 August 2024).
- Ceazan, M.L.; Thurman, E.M.; Smith, R.S.U. Retardation of ammonium and potassium transport through a contaminated sand and gravel aquifer: The Role of cation exchange. Environ. Sci. Technol. 1989, 23, 1402–1408. [Google Scholar] [CrossRef]
- Baker, J.P.; Schofield, C.L. Aluminum toxicity to fish in acidic waters. Water Air Soil Pollut. 1982, 18, 289–309. [Google Scholar] [CrossRef]
- Khalidy, R.; Santos, R.M. Assessment of geochemical modeling applications and research hot spots—A year in review. Environ. Geochem. Health 2021, 43, 3351–3374. [Google Scholar] [CrossRef]
- Brown, C.J.; Lucas, L.V.; Robertson, D.M.; Baker, N.T.; Johnson, Z.C.; Green, C.T.; Cho, S.J.; Erickson, M.L.; Gellis, A.C.; Jasmann, J.R.; et al. Model and Data Resources Supporting Water-Quality Modeling of Hydrologic Systems; U.S. Geological Survey Data Release 2025; USGS: Reston, VA, USA, 2025. [CrossRef]
- Van Cappellen, P.; Gaillard, J.-F. Biogeochemical dynamics in aquatic sediments. Rev. Mineral. 1996, 34, 335–376. [Google Scholar] [CrossRef]
- Nordstrom, D.; Plummer, L.; Wigley, T.; Wolery, T.; Ball, J.; Jenne, E.; Bassett, R.; Crerar, D.; Florence, T.; Fritz, B. A comparison of computerized chemical models for equilibrium calculations in aqueous systems. In Chemical Modeling in Aqueous Systems—Speciation, Sorption, Solubility, and Kinetics; Jenne, E., Ed.; Series 93; American Chemical Society: Washington, DC, USA, 1979; pp. 857–892. ISBN 0841204799. [Google Scholar] [CrossRef]
- Dent, D. Acid Sulphate Soils: A Baseline for Research and Development; Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1986; 250p, ISBN 9070260980. [Google Scholar]
- Redfield, A.C. On the proportions of organic derivations in sea water and their relation to the composition of plankton. In James Johnstone Memorial Volume; University Press of Liverpool: Liverpool, UK, 1934; pp. 177–192. [Google Scholar]
- Van Cappellen, P.; Wang, Y. STEADYSED1, A Steady-State Reaction-Transport Model for C, N, S, O, Fe and Mn in Surface Sediments-Version 1.0 User’s Manual; School of Earth and Atmospheric Science: Atlanta, GA, USA; Georgia Institute of Technology: Atlanta, GA, USA, 1995. [Google Scholar] [CrossRef]
- Wan, D.; Yu, P.; Kong, L.; Zhang, J.; Chen, Y.; Zhao, D.; Liu, J. Effects of inland salt marsh wetland degradation on plant community characteristics and soil properties. Ecol. Indic. 2024, 159, 111582. [Google Scholar] [CrossRef]
- Valiela, I.; Costa, J.E. Eutrophication of Buttermilk Bay, a Cape Cod coastal embayment: Concentrations of nutrients and watershed nutrient budgets. Environ. Manag. 1988, 12, 539–553. [Google Scholar] [CrossRef]
- Harvey, J.W.; Chambers, R.M.; Hoelscher, J.R. Preferential flow and segregation of porewater solutes in wetland sediment. Estuaries 1995, 18, 568–578. [Google Scholar] [CrossRef]
- Howarth, R.; Chan, F.; Conley, D.J.; Garnier, J.; Doney, S.C.; Marino, R.; Billen, G. Coupled biogeochemical cycles: Eutrophication and hypoxia in temperate estuaries and coastal marine ecosystems. Front. Ecol. Environ. 2011, 9, 18–26. [Google Scholar] [CrossRef]
- Sato, M. Oxidation of sulfide ore bodies; 1, Geochemical environments in terms of Eh and pH. Econ. Geol. 1960, 55, 928–961. [Google Scholar] [CrossRef]
- Krairapanond, A.; Jugsujinda, A.; Patrick, W.H. Phosphorus sorption characteristics in acid sulfate soils of Thailand: Effect of uncontrolled and controlled soil redox potential (Eh) and pH. Plant Soil 1993, 157, 227–237. [Google Scholar] [CrossRef]
- Blanc, P.; Lassin, A.; Piantone, P.; Azaroual, M.; Jacquemet, N.; Fabbri, A.; Gaucher, E.C. Thermoddem: A geochemical database focused on low temperature water/rock interactions and waste materials. Appl. Geochem. 2012, 27, 2107–2116. [Google Scholar] [CrossRef]
- Arndt, S.; Jørgensen, B.B.; LaRowe, D.E.; Middelburg, J.J.; Pancost, R.D.; Regnier, P. Quantifying the degradation of organic matter in marine sediments: A review and synthesis. Earth-Sci. Rev. 2013, 123, 53–86. [Google Scholar] [CrossRef]
- Sterling, S.M.; MacLeod, S.; Rotteveel, L.; Hart, K.; Clair, T.A.; Halfyard, E.A.; O’Brien, N.L. Ionic aluminium concentrations exceed thresholds for aquatic health in Nova Scotian rivers, even during conditions of high dissolved organic carbon and low flow. Hydrol. Earth Syst. Sci. 2020, 24, 4763–4775. [Google Scholar] [CrossRef]
- USEPA. Quality Criteria for Water; U.S. Environmental Protection Agency: Washington, DC, USA, 1986. Available online: https://www.epa.gov/sites/default/files/2018-10/documents/quality-criteria-water-1986.pdf (accessed on 1 August 2024).
- Cadmus, P.; Brinkman, S.; May, M. Chronic Toxicity of Ferric Iron for North American Aquatic Organisms: Derivation of a Chronic Water Quality Criterion Using Single Species and Mesocosm Data. Arch. Environ. Contam. Toxicol. 2018, 74, 605–615. [Google Scholar] [CrossRef]
- Romano, N.; Kumar, V.; Sinha, A.K. Implications of excessive water iron to fishhealth and some mitigation strategies. Glob. Seaf. Alliance. 2021. Available online: https://www.globalseafood.org/advocate/implications-of-excessive-water-iron-to-fish-health-and-some-mitigation-strategies/ (accessed on 1 August 2024).
- USEPA. Nutrient and Sediment Estimation Tools for Watershed Protection. 2018. Available online: https://www.epa.gov/sites/default/files/2018-08/documents/loadreductionmodels2018.pdf (accessed on 1 August 2024).
- USEPA. Final Aquatic Life Ambient Water Quality Criteria For Ammonia-Freshwater 2013; Environmental Protection Agency: Washington, DC, USA, 2013. Available online: https://www.federalregister.gov/documents/2013/08/22/2013-20307/final-aquatic-life-ambient-water-quality-criteria-for-ammonia-freshwater-2013 (accessed on 1 August 2024).
- DeForest, D.K.; Brix, K.V.; Tear, L.M.; Adams, W.J. Multiple linear regression models for predicting chronic aluminum toxicity to freshwater aquatic organisms and developing water quality guidelines. Environ. Toxicol. Chem. 2018, 37, 80–90. [Google Scholar] [CrossRef]
- Gensemer, R.W.; Playle, R.C. The bioavailability and toxicity of aluminum in aquatic environments. Crit. Rev. Environ. Sci. Technol. 1999, 29, 315–450. [Google Scholar] [CrossRef]
- Besser, J.; Cleveland, D.; Ivey, C.; Blake, L. Toxicity of Aluminum to Ceriodaphnia dubia in Low-Hardness Waters as Affected by Natural Dissolved Organic Matter. Environ. Toxicol. Chem. 2019, 38, 2121–2127. [Google Scholar] [CrossRef]
- Lind, C.J.; Hem, J.D. Effects of organic solutes on chemical reactions of aluminum. Water Supply Pap. 1975, 1827, 83. [Google Scholar] [CrossRef]
- Lydersen, E. The solubility and hydrolysis of aqueous aluminium hydroxides in dilute fresh waters at different temperatures. Hydrol. Res. 1990, 21, 195–204. [Google Scholar] [CrossRef]
- Schofield, C.L.; Trojnar, J.R. Aluminum toxicity to brook trout (Salvelinus fontinalis) in acidified waters. In Polluted Rain. Environmental Science Research; Toribara, T.Y., Miller, M.W., Morrow, P.E., Eds.; Springer: Boston, MA, USA, 1980; pp. 341–366. ISBN 1461330629. [Google Scholar] [CrossRef]
- USEPA. Final Aquatic Life Ambient Water Quality Criteria for Aluminum; U.S. Environmental Protection Agency: Washington, DC, USA, 2018; p. 161. Available online: https://www.epa.gov/wqc/aquatic-life-criteria-and-methods-toxics (accessed on 1 August 2024).
- Driscoll, C.T.; Schecher, W.D. The chemistry of aluminum in the environment. Environ. Geochem. Health 1990, 12, 28–49. [Google Scholar] [CrossRef] [PubMed]
- Rozsa, R. An Overview of Wetland Restoration Projects in Connecticut; University of Connecticut: Storrs, CT, USA, 1988; pp. 1–11. [Google Scholar]
- Burdick, D.M.; Dionne, M.; Boumans, R.M.; Short, F.T. Ecological responses to tidal restorations of two northern New England salt marshes. Wetl. Ecol. Manag. 1996, 4, 129–144. [Google Scholar] [CrossRef]
- Mendelssohn, I.A.; McKee, K.L. Spartina Alterniflora Die-Back in Louisiana: Time-Course Investigation of Soil Waterlogging Effects. J. Ecol. 1988, 76, 509–521. [Google Scholar] [CrossRef]
- Luo, M.; Huang, J.-F.; Zhu, W.-F.; Tong, C. Impacts of increasing salinity and inundation on rates and pathways of organic carbon mineralization in tidal wetlands: A review. Hydrobiologia 2019, 827, 31–49. [Google Scholar] [CrossRef]
- Golding, L.A.; Angel, B.M.; Batley, G.E.; Apte, S.C.; Krassoi, R.; Doyle, C.J. Derivation of a water quality guideline for aluminium in marine waters. Environ. Toxicol. Chem. 2014, 34, 141–151. [Google Scholar] [CrossRef]
- Eftekhari, N.; Kargar, M.; Zamin, F.; Rastakhiz, N.; Manafi, Z. A Review on Various Aspects of Jarosite and Its Utilization Potentials. Ann. De Chim.Sci. Des Matériaux 2020, 44, 43–52. [Google Scholar] [CrossRef]
- Charlton, S.R.; Parkhurst, D.L. Modules based on the geochemical model PHREEQC for use in scripting and programming languages. Comput. Geosci. 2011, 37, 1653–1663. [Google Scholar] [CrossRef]
- McCleskey, R.B.; Cravotta III, C.A.; Miller, M.P.; Tillman, F.; Stackelberg, P.; Knierim, K.J.; Wise, D.R. Salinity and total dissolved solids measurements for natural waters: An overview and a new salinity method based on specific conductance and water type. Appl. Geochem. 2023, 154, 105684. [Google Scholar] [CrossRef]
- Laudelout, H.; Van Bladel, R.; Bolt, G.H.; Page, A.L. Thermodynamics of heterovalent cation exchange reactions in a montmorillonite clay. Trans. Faraday Soc. 1968, 64, 1477–1488. [Google Scholar] [CrossRef]
- Dutrizac, J. Factors affecting alkali jarosite precipitation. Metal. Trans. B 1983, 14, 531–539. [Google Scholar] [CrossRef]
- Neubauer, S.C.; Givler, K.; Valentine, S.; Megonigal, J.P. Seasonal patterns and plant-mediated controls of subsurface wetland biogeochemistry. Ecology 2005, 86, 3334–3344. [Google Scholar] [CrossRef]
- Portnoy, J.W. Effects of Diking, Drainage and Seawater Restoration on Biogeochemical Cycling in New England Salt Marshes; Boston University: Boston, MA, USA, 1996. [Google Scholar]
- NADP. National Atmospheric Deposition Program Annual Precipitation Data. 2021. Available online: https://nadp.slh.wisc.edu/wp-content/uploads/2022/11/2021as.pdf (accessed on 15 October 2024).

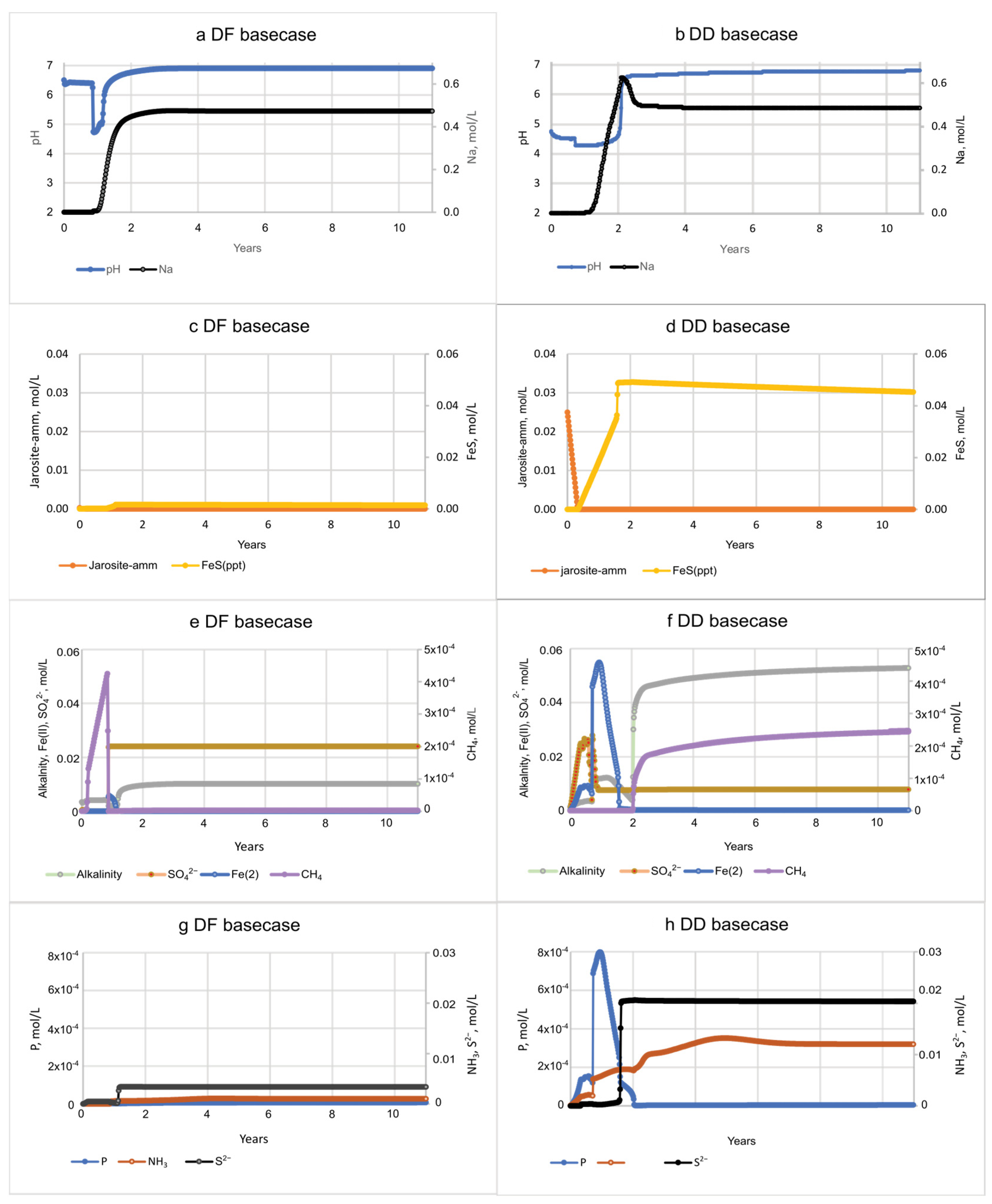

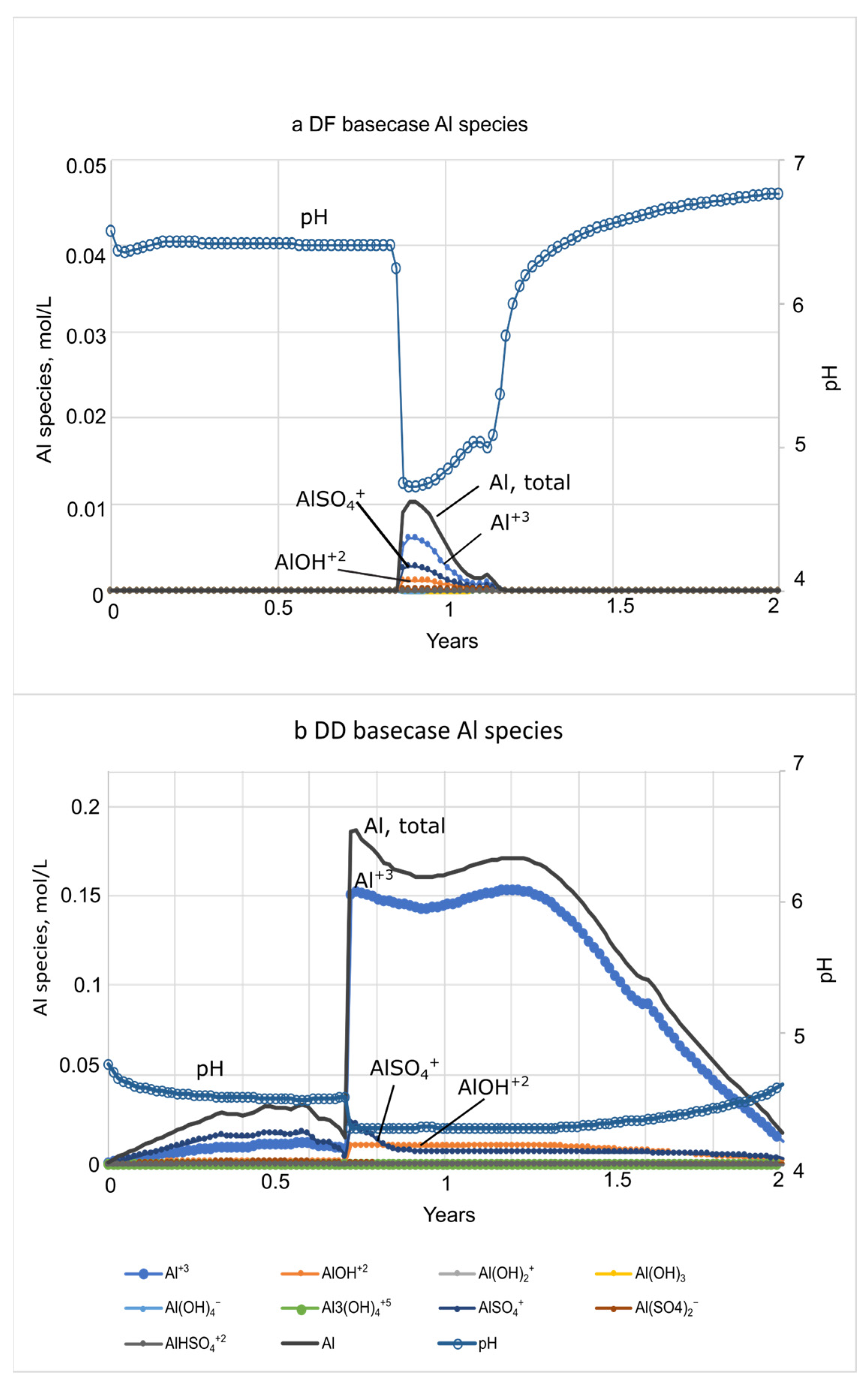

| Diked, Flooded (DF) | Diked, Drained (DD) |
|---|---|
| Conditions before tidal restoration | |
| • Freshwater-submerged marsh sediments, methanogenic | • Subaerially exposed marsh sediments, oxic at surface and reducing with depth |
| • Sedimentary organic matter (SOM) buildup (absence of inorganic sediments from flood tides, and slow, methanogenic decomposition); low NH4+ | • SOM oxidation and subsidence; high N, P, Fe, H2S or S2−; high sorbed Fe(II) |
| • Mackinawite/pyrite present • Low amount of Fe(III) minerals and dissolved Fe(II) (Fe < 5 µg/g) | • FeS and FeS2 oxidation and release of H+ (pH < 4), Fe(II), SO42− to create acid SO42− soils • High amounts of Fe(III) minerals (0.2–0.7 mg/g Fe) and dissolved Fe(II), most is sorbed |
| Simulated tidal restoration conditions | |
| • Oxidation of SOM coupled to the reduction of O2, Fe(III), SO42−, following re-entry of seawater into seasonally flooded and drained marshes. | |
| • Salination increases SO42− levels, promotes SO42−-reducing conditions (oxic at the sediment surface), and subsequent desorption of acidity (H+), S2−, Fe, Al, and nutrients. | |
| • NH4+ and P released due to accelerated organic decomposition (and some NH4+ by desorption) | |
| • SO42− reduction; S−2 gradually increases to 6.1 mmol/L; Fe sulfide formation | • Fe sulfide oxidation; acidity mobilized; S−2 increase to 28 mmol/L by 578 days, coincident with Fe(II) depletion |
| • Dissolved Fe peaks at 0.24 mmol/L at 15 days, then decreases as jarosite-amm is depleted | • Dissolved Fe peaks at 46 mmol/L at 385 days (desorption and reductive dissolution of jarosite) then depleted by 583 days from Fe sulfide formation |
| • CH4 concentrations are very low | • CH4 concentrations are generally low but increase at end of simulation to peak at 2.8 mmol/L at 578 days |
| • Al peak of 15 mmol/L at 8–12 h | • Al peak of 206 mmol/L at 8–12 h |
| • Low P gradual increase to 3.3 µmol/L by 580 days | • High P peak early to 119 µmol/L, gradual decline to 3.5 µmol/L by 589 days |
| • NH4+, gradual increase to 0.52 mmol/L | • NH4+, steady increase to 5.7 mmol/L |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brown, C.J. Simulated Biogeochemical Effects of Seawater Restoration on Diked Salt Marshes, Cape Cod National Seashore, Massachusetts, U.S. Soil Syst. 2025, 9, 89. https://doi.org/10.3390/soilsystems9030089
Brown CJ. Simulated Biogeochemical Effects of Seawater Restoration on Diked Salt Marshes, Cape Cod National Seashore, Massachusetts, U.S. Soil Systems. 2025; 9(3):89. https://doi.org/10.3390/soilsystems9030089
Chicago/Turabian StyleBrown, Craig J. 2025. "Simulated Biogeochemical Effects of Seawater Restoration on Diked Salt Marshes, Cape Cod National Seashore, Massachusetts, U.S." Soil Systems 9, no. 3: 89. https://doi.org/10.3390/soilsystems9030089
APA StyleBrown, C. J. (2025). Simulated Biogeochemical Effects of Seawater Restoration on Diked Salt Marshes, Cape Cod National Seashore, Massachusetts, U.S. Soil Systems, 9(3), 89. https://doi.org/10.3390/soilsystems9030089





