Abstract
Phosphate sorption data are often analyzed by least-squares fitting to the two- or three-parameter Freundlich model. The standard methods are flawed by (1) treating the measured pseudo-equilibrium concentration C as the independent (hence error-free) variable and (2) neglecting the weighting that should accommodate the varying precision of the data. Here, we address both of these shortfalls and use a global fit model to achieve optimal precision in fitting data for five acidic Australian soil types. Each individual dataset consists of measured C values for up to nine phosphate spiking levels C0. For each soil type, there are three–five such datasets from varying levels of phosphate fertilizer pre-exposure (Pf) two years earlier. These datasets are fitted simultaneously by expressing the Freundlich capacity factor a and exponent b as theoretically predicted functions of the assay amounts of Fe, Al, and P measured for each Pf. The analysis allows for uncertainty in both C and C0, with inverse-variance weighting from variance functions estimated by residuals analysis. The estimated presorbed P amounts Q depend linearly on Pf, with positive intercepts at Pf = 0, indicating residual phosphate in the soils prior to the laboratory phosphate treatments. The key takeaway points are as follows: (1) global analysis yields optimal estimates and improved precision for the fit parameters; (2) allowing for uncertainty in C is essential when the data include C values near 0; (3) varying data precision requires weighting to yield optimal parameter estimates and reliable uncertainties.
1. Introduction
Phosphate soil sorption data are typically fitted to simple isotherms for the purpose of compactly summarizing the experimental results and extrapolating beyond the range of the measurements [1,2,3,4,5,6,7,8]. The Langmuir, Tempkin, and Freundlich models have been used commonly, with recent work showing a preference for the last of these, which was clearly superior in one statistical comparison [9]. The work in [9] allowed for an aspect of such analysis that has usually been neglected—the weighting of the data, as called for by their varying precision, or heteroscedasticity [5]. It also dealt with a second problem in most treatments of sorption data—that the variable commonly taken as independent and thus assumed to be error-free is the measured pseudo-equilibrium concentration C of phosphate. The analysis was enabled by parallel experiments from four laboratories in the work of Nair et al. [4], which permitted estimation of the variance function (VF) for C, needed for inverse-variance weighting.
In the present work, we use the Freundlich model to analyze sorption data for five acidic Australian soils at from three to five different prior amendments with phosphate fertilizer and typically nine C0 values in each set of measurements. We use nonlinear least squares (LS) to fit all the data for each soil collectively in what we think is the first such global analysis, with the Freundlich coefficients represented as functions of the oxalate assays of Fe, Al, and P in the same soil samples. We also allow for uncertainty in both C and C0, acknowledging that the latter, though nominally a precisely prepared concentration, may effectively capture some of the experimental variability (from, e.g., the preparation and handling of the different soil samples). This is in fact consistent with the usual treatment of such data, where the sorbed amount X is taken as the dependent variable (see below). Lacking replicate measurements, we estimate the VFs for C and C0 from the statistics of their residuals. This is accomplished through comparison with Monte Carlo (MC) simulations to match the statistics of the experimental data analyzed the same way. We believe that this procedure, too, is a first use of such methods on multiple uncertain variables.
The heart of this work is the simultaneous LS fitting of up to five datasets having 45 data points, in place of five separate fits of nine points each, to obtain optimal estimates of the fit parameters and their uncertainties. Since this type of fitting may be unfamiliar to readers, we describe below a simpler example of two datasets fitted to two straight lines having a common slope. We also briefly compare three algorithmic methods for handling LS problems with uncertainty in both variables, showing that all three can be expected to give reliable results.
2. Theory and Computations
Background. In sorption studies, the Freundlich model is expressed as
with X being the sorbed amount, related to the initial and pseudo-equilibrium concentrations by
where R is the ratio of solution volume to soil mass and a and b are the Freundlich parameters. With solution concentrations in mg/L and X in mg/kg, R has units L/kg; in our experiments, the soil samples were 5.00 g and the solution volumes 50.0 mL, giving R = 10 L/kg.
X = a Cb,
X = R (C0 − C),
If the total sorbed phosphate includes a presorbed quantity Q, X in Equation (1) is replaced by X + Q. Equivalently, Equation (1) can be rewritten as
where Q can be treated as a third adjustable parameter in the nonlinear least-squares (NLS) fit or held constant at its measured value if this is considered reliable.
X = a Cb − Q,
As was noted, the usual procedure of fitting X with Equations (1) and (3) is flawed by treating C as error-free. This problem can be handled several ways. First, one can combine Equations (2) and (3) to obtain
This gives C0 explicitly as a function of C, making it directly suitable for analysis, considering C error-free and C0 as the dependent variable. Indeed, with these assumptions, analyses with Equations (3) and (4) produce identical results. For the Freundlich isotherm there is no closed-form functional relation, C = f(C0), for analysis with C as the dependent variable and C0 as the independent one. (This can be done through numerical algorithms; see below). The work in [9] accomplished the same goal by using the effective-variance (EV) method [10] to translate uncertainty in C into an effective uncertainty in C0. In this approach, Equation (4) remains the fit relation, and C is still treated as error-free in the fitting.
C0 = C + (a Cb − Q)/R.
In the present work, we use the “total variance” (TV) method, which allows for uncertainty in C0, C, or both. In this method, algorithms for which have been available since at least 1972 [11,12], the minimization target for a function of x and y, both uncertain, is
Here, the weights are wxi = α/σxi2 and wyi = α/σyi2, and the δs are the residuals (adjusted–observed) in x and y, with α a single proportionality constant. The TV results have the satisfying property of being independent of the way the fit relation is expressed [13,14]. The algorithms typically require that the model be expressed in the form f(x,y) = 0, for which purpose it is useful to rewrite Equation (4) in an implicit form, like
STV = ∑ wxiδxi2 + wyiδyi2.
f(C,C0) = 0 = R(C0 − C) − a Cb + Q.
Through the weights wxi and wyi, proper implementation of the TV method requires information about the variances σi2 in x and y at the ith point. In the present work, we do not have replicate measurements from which to estimate these. Yet, it would be inappropriate to simply ignore heteroscedasticity, since previous work has shown that the data variance can span several orders of magnitude [9]. Accordingly, we have used the statistics of the fit residuals for this purpose, in an iterative procedure that is described below.
In the context of this effort to correctly weight the data, it may be reassuring to note that incorrect weighting rarely results in drastically bad parameter estimates. Rather, the primary effects are increased dispersion of the parameter estimates and importantly, incorrect estimation of their uncertainties (which can be either optimistic or pessimistic). The increased parameter dispersion can sometimes give estimates that are outside of the confidence limits of properly weighted estimates.
Global Fit Model. The word “global” in this context can be taken to mean “all-encompassing”, and it refers to all datasets that contribute to the determination of one or more of the adjustable fit parameters. Since global LS fitting may not be familiar to some readers, we first describe a simpler example that may help clarify how it works. Suppose there are two datasets expected to follow a linear model, y = c + dx, and the slopes d are theoretically expected to be the same. One approach to this problem would be to fit the two datasets, then average the two d values and refit both datasets with d now fixed at its average, to obtain the two intercepts, c1 and c2. In the global alternative, both datasets are fitted together to give the three parameters, c1, c2, and d. The parameter estimates from the two approaches will likely be identical or nearly so, but the parameter standard errors (SE) will not: the global model will yield reliable SEs from the covariance matrix, while the two-step procedure will do so only if interparameter correlation is properly taken into account. While simple LS programs may not accommodate global models, programs that permit user-defined fit models (including, e.g., Excel) can easily handle such problems.
In the present sorption global fit model, we simultaneously fit the three–five datasets recorded for a given soil type after differing fertilizer pre-exposures Pf two years earlier. These datasets are connected through theory-based definitions of their a and b parameters [1,7,15],
and
where Feox, Alox, and Pox are from the oxalate assays (mmol/kg) for each Pf, and A and B are offsets used to center the values of the linear term argument and the [H+] term in Equation (7a). In this way, we reduce the number of a and b fit parameters from 6–10 to at most 5 that follow predicted behaviors. In cases where a parameter is found to be statistically insignificant (|parameter| < parameter standard error) [16], it is set to zero and the fit is repeated.
a = a0+ a1(Feox + Alox − A) + a2 10(B–pH),
b = b0 − b1 Pox/(Feox + Alox),
Initially, individual Q parameters were included for each sample. Thus, for example, for five samples of a given soil type (five Pf treatments), the number of adjustable parameters was reduced from fifteen (5 × 3) in the individual fits to five Q values plus at most the five parameters in Equation (7) in the global analysis. For all five soil types, the dependence of Q on Pf appeared to be linear, so the several Q parameters were further reduced to two by incorporating them in the global model using
Q = q0 + q1 Pf.
Data Variance Functions from Residuals Analysis. The data variances are needed for the computation of the σxi2 and σyi2 values that occur in the weights in Equation (5). In the usual situation of a single uncertain variable, estimation of data variance functions (VF) from residuals is straightforward [17]. After “studentization” (see below), each squared residual is an estimate of the data variance. If heteroscedasticity is indicated, a VF is fitted to these, and the data are then refitted using this VF to obtain new residuals. After several cycles, this procedure usually converges on a final VF and a corresponding set of parameters and their standard errors (SEs).
With multiple uncertain variables, there are problems with this approach. For example, although STV in Equation (5) closely follows the χ2 distribution [13], the x- and y-components of the sum do not. Further, we know of no easy way to set the relative contributions of these components to the sum. For example, on re-examining the results from the Monte Carlo (MC) simulations in ref [13] for the York model [18], we found that the x- and y-components comprised 27% and 73% of the total, respectively. This breakdown did depend on the slope but not the intercept, with, for example, the y contribution dropping to 63% when the slope was changed from −0.48 to ±1.0.
To deal with this situation, we have devised a trial-and-error procedure that uses MC simulations to match observed residuals with predictions for synthetic data analyzed the same way. This procedure is described in detail in the online Supplementary Materials (SI). It includes studentization of the residuals to convert them to estimates of the variance. (This is needed because observed residuals have variance that undershoots the data variance at each point [17]).
Some simple VFs for heteroscedasticity in, for example, C, are [19]
and
In ref. [9] two three-parameter VFs gave comparable performance, one with a linear term added to Equation (9a), the other with the power two in the second term of (9a) made variable (becoming 1.6). The addition of a linear term to (9a) is consistent with expectations for spectrophotometric measurements [20]. Here, we have needed VFs with a faster rise in σ in the mid-range of C, like replacing C in Equation (9b) with C1/2.
σC2 = c2 + (dC)2,
σC2 = (c + dC)2.
In displaying the dispersion information for the experimental data, we show the standard deviation (SD) for C0 from the statistics for all residuals sharing a common C0, and similarly for C (where residuals for differing C are grouped by their proximity for the statistical averaging). This means typically 10–20 residuals for each displayed value, for which the relative SD (RSD) is (2(n − 1))−1/2, where n is the number of averaged residuals. The displayed error bars are based on these values.
Computational Methods. The global fitting, MC simulations, and residuals analysis were conducted with in-house FORTRAN codes run in Microsoft FORTRAN. For single uncertain variables, similar codes are given in refs. [16,21]. The codes for the TV method are as described in refs. [11,13,22,23]. We also used the KaleidaGraph (KG) program for simple linear and nonlinear models, both unweighted and weighted. The KG nonlinear fitting routine does not appear capable of implementing the TV method; however, it and similar analysis packages can handle multiple uncertain variables with the effective variance (EV) methods.
In the EV method used in [9] with Equation (6) as the fit model, the effective variance is
The weights are then taken as wi = σeff,i−2 and must be adjusted iteratively to obtain convergence, usually in ~10 cycles. A variation of this method gives near-TV results for nonlinear models and identical results for straight-line models. This EV2 method [13,14] is also easy to implement in KG and Excel [24]. Again, using Equation (6) as the fit model, the minimization target is the sum over all points of f(C,C0)i2/σeff,i2. The dependence of the weights on the parameters [through (∂f/∂C)] is thus automatically a part of the iterative parameter adjustment process in the EV2 method.
Our reported parameter SEs are the square roots of the diagonal elements of the covariance matrix. There are two choices here [19]: (1) If the data variances are thought to be known absolutely, the factor α after Equation (5) is taken as 1.0 to give Vprior. (2) Alternatively, the factor α = STV/ν is incorporated to give Vpost, where ν is the number of statistical degrees of freedom, equal to the number of fitted points n minus the number of adjustable parameters p. Given the approximate nature of our estimation of the data VFs, we report post-SEs.
3. Experiments and Data
The experimental details are given elsewhere [25] and discussed briefly in the Supplementary Materials (SI). The five soils are acidic pasture soils from the higher rainfall coastal zone of Eastern Australia: Camden (KA), Flaxley (FL), Glenmore (MO), Moss Vale (MA), and Richmond (D). A table summarizing their key properties is included in the Supplementary Materials (SI), where all the data are also presented.
4. Results and Discussion
Preliminary Least-Squares Analysis. Figure 1 illustrates results from sorption experiments on MO soil having two different fertilizer pre-exposures, Pf. The need for Q in the fit model of Equation (3) is clear from the fit results with and without this term. As has been noted, analysis of these data using Equations (3) and (4) usually treats C as error-free and C0 as uncertain and gives identical results for the parameters and their SEs (see Supplementary Materials (SI) for an example). On the other hand, analysis using Equations (4) and (6) with C0 error-free and C with constant uncertainty gives consistently larger and more uncertain estimates of Q, as is shown for the KA soils in Figure 2.
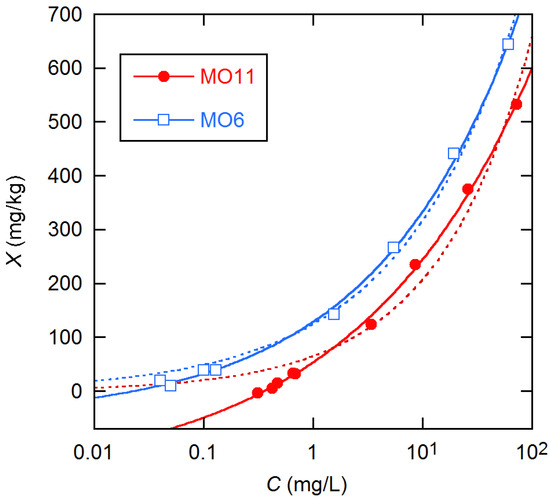
Figure 1.
Sorbed P vs. pseudo-equilibrium P solution concentration for two MO soils having fertilizer amendments of 71 mg/kg (MO6) and 602 mg/kg (MO11). The curves are LS fit results to the model of Equation (3) with (solid) and without (dashed) Q. Omission of the Q term gives increases in the sums of squared residuals in these unweighted fits by factors of 5 (MO6) and 20. The estimated Q values are 52 (14) and 168 (30) mg/kg for MO6 and MO11, respectively. (Figures in parentheses are estimated SEs in terms of final digits, e.g., 168 ± 30). Note the logarithmic scale for C.
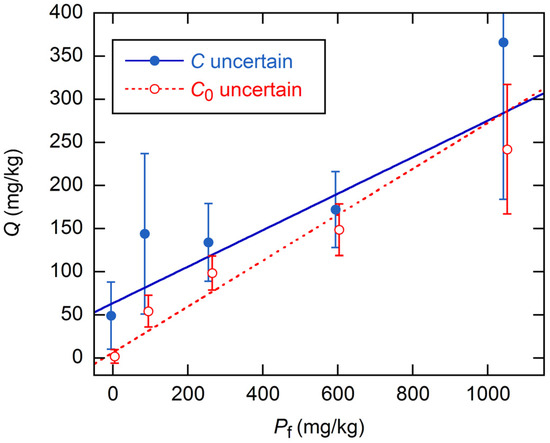
Figure 2.
Sorption Q estimates for KA soils from analyses of individual Pf datasets, using Equation (6) and assuming uncertain C and uncertain C0, with the other variable treated as error-free. The illustrated lines are results of weighted fits giving intercepts 63 (33) and 8 (7), and slopes 0.21 (9) and 0.27 (4), for C and C0 uncertain, respectively. Displayed error bars are 1 SE. Points have been displaced on the Pf axis for clarity of display.
Figure 3 shows the Qs obtained for the KA soils with the global model, for the assumptions of constant error in C0 alone and in C alone. For comparison, we include results obtained by inverse-variance weighting with the final data VFs (discussed below). For all three error models, the linearity of Q from the global fits is improved over that from individual fits, as was shown for the KA soils in Figure 2. Further, all slopes are smaller by a factor of ~2, and all intercepts are statistically significant.
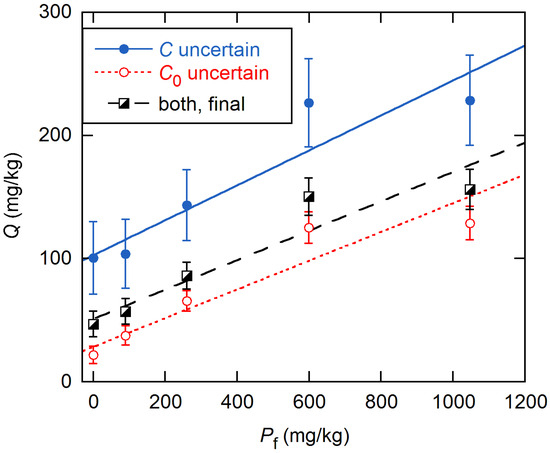
Figure 3.
Sorption Q estimates for KA soils from global analysis using Equation (6), for three different assumptions about the data error. In the first two, the other variable was taken to be error-free; in the third, both were weighted using the final data VFs (see below). The illustrated lines are results of weighted fits giving, in legend order, intercepts 103 (19), 28 (5), and 51 (7); and slopes 0.14 (4), 0.12 (1), and 0.12 (2).
To show the sensitivity of results to the choice of fitting method, we compare in Table 1 results obtained for one soil sample analyzed with the three different NLS methods described above. The EV2 results are closer to TV than are the EV results, but in no case are the differences large compared with the parameter SEs. This general agreement is maintained with heteroscedastic variables, and the differences become even less significant when the uncertainties in estimating the data VFs are acknowledged. Thus, users can expect satisfactory results from all three methods.

Table 1.
Comparison of results obtained for the MO5 soil analyzed with three NLS methods, for constant uncertainty in C, C0, and both.
Data Variance Function Estimation. Initially, the data for each soil type and fertilizer Pf were fitted to the three-parameter model of Equation (6) assuming constant uncertainty for C0 and zero for C, and the reverse. The residuals from all data for a given soil type were then examined for systematic effects. Three of the soil types gave no clear such effects, but two did, as shown in Figure 4, before and after removal of the largest outlier values at C0 = 63.5 mg/L. For the FL soils, the systematic effects are negligible in frame D, but they persist for the KA soils in frame C. The behavior for FL is consistent with an erroneously prepared solution, but that for KA could as well indicate limitations in the Freundlich model for this soil. In this regard, removal of the highest concentration data (C0 = 125.6 mg/L) improved the fit S values as much as did removal of those at C0 = 63.5 mg/L. As is discussed below, these two choices give significantly different Q estimates for the KA soils. The residuals patterns for C-uncertain resembled those for C0 but with reversed signs (from Equation (6)) and ~30% smaller magnitude.
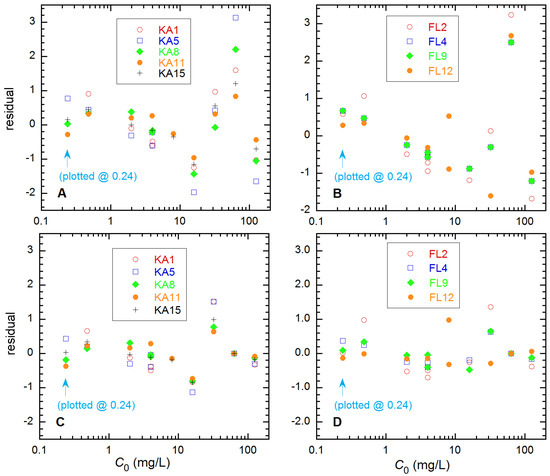
Figure 4.
Least-squares fit residuals from C0-uncertain analyses of the KA (left) and FL (right) soils, displayed vs. C0. From Equation (6), the residuals are 10 times the C0 disparities. Results at top (A,B) are from fitting all data, at bottom (C,D) after removal of the values at C0 = 63.5 (shown with a value of 0.0). (The left-most points in each frame are for C0 = 0 but have been displaced for the log display).
Figure 5 shows the residual SDs for analysis with the global model, treating in turn C and C0 as having constant uncertainty. (The MA soil data were much noisier, with several outliers, so they were omitted from these computations). If either of these simple error models were correct, the residual variances would be approximately constant for one of these. Both displays show a rise with increasing C and C0, indicating heteroscedasticity, error contributions from both variables, or both effects. By comparing these results with results from MC simulations for various assumptions about the data errors, we can hope to discern the actual situation.
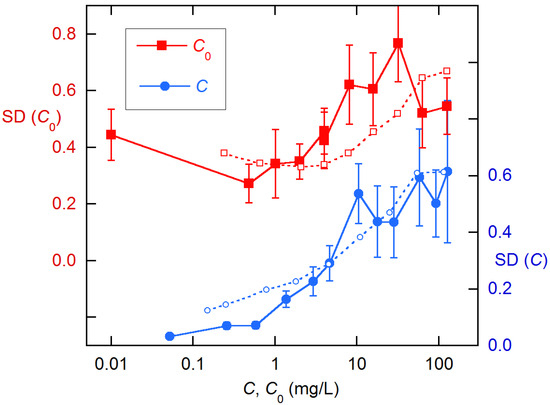
Figure 5.
Standard deviations from studentized residuals obtained fitting data for all soils except MA to the global model, assuming, in turn, constant uncertainty for C and C0 and no error for the other variable. For C0 (SD scale left), the lowest abscissa values were 0.0 but were increased to 0.01 for this logarithmic display. For C, the abscissa is the mean of close-lying values; for C0, it is the employed concentration. Dashed lines and open points are results for final estimated VFs (see below and Supplementary Materials (SI)).
The MC procedures used to obtain the final estimated VFs shown in Figure 5 are discussed in the Supplementary Materials (SI). The results are
The agreement in Figure 5 is less than stellar, but it should suffice to yield high-quality results, considering that even the most extreme assumptions about the data error do not drastically alter the Qs, for example, as illustrated above in Figure 3.
σC = 0.05 + 0.02 C1/2,
σC0 = 0.2 + 0.05 C01/2.
Weighted Global Analysis. In Figure 6, we compare results for the a and b parameters from standard (unweighted fits of individual datasets using Equation (3)) and global fits (with weighting based on the SD expressions in Equation (11)) of the MO soil data. Because of the pH dependence, the global a values from Equation (7a) do not fall on a straight line, while the global b values are linear in the abscissa by definition. Most of the values for the two methods disagree by more than their combined SEs, which can be taken as a measure of inconsistency.
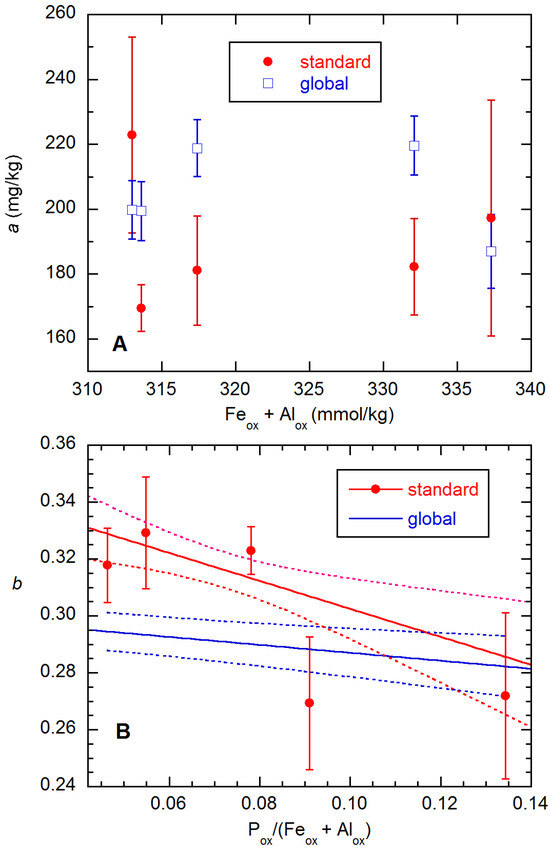
Figure 6.
Results for Freundlich a (frame A) and b (B) from standard and global analyses of the MO data (5 Pf values). All error bars are 1 σ. In (B), the dotted lines represent the 1-σ error bands on the weighted linear fit of the displayed standard points and on the linear fitted function in the global model.
Figure 7 shows the Qs obtained analyzing all data with the weighted global model. The dependence on Pf is linear in all cases, and all intercepts are statistically significant. The slopes for the last four soils range from 0.072 to 0.119, while that for MA is three times larger.
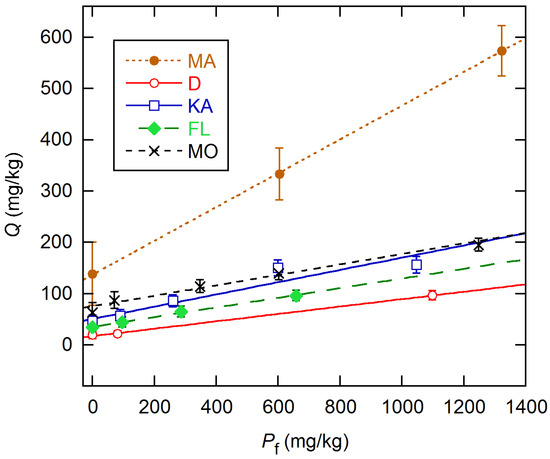
Figure 7.
Sorption Q estimates as a function of phosphate fertilizer amendment for five soils, from global TV analyses using Equations (6) and (7), with inverse-variance weighting using the SD expressions of Equation (11). Displayed error bars are 1 SE. Lines are from weighted LS fits.
When the global model was changed to incorporate the linear dependence of Q on Pf through Equation (8), results for four of the soils remained close to those obtained with individual Q values, as shown in Figure 7. However, for the KA soil type, the apparently modest deviations in Figure 3 and Figure 7 are much more significant than they appear, because the Q values are highly correlated through their common assessment in the global model. Accordingly, the reduced χ2 (RCS = STV/ν) rose by a factor of 6 to 10.6. The KA results given in Table 2 were obtained by deleting the data for the fifth concentration. Results for other data selections are discussed in the Supplementary Materials (SI). As can be seen from Table 2, the pH parameter a2 was statistically significant for only the MO and FL soils. The other parameters were significant except for one case for a1 (MA). The RCS values vary somewhat more than the expected ~1.0(3) for equivalent data for all soils, but they are not drastically in conflict with this, which was an assumption in the estimation of the VFs.

Table 2.
Results from global analyses of sorption data for five soil types.
The much stronger dependence of Q on Pf for the MA soils prompted us to examine the MA fits more closely. We found that the results for both global models were unduly sensitive to the deletion of high-C0 points for the MA1 samples (Pf = 0). These results are discussed in more detail in the Supplementary Materials (SI), and we include the results obtained deleting all MA1 data in a footnote in Table 2.
Similarly, the great sensitivity of the KA results to the choice of included data means that those results must be considered more uncertain than is indicated by the KA parameter SEs in Table 2. This behavior heightens concern that the Freundlich model may not be suitable for the KA soils. The problem is discussed in more detail in the Supplementary Materials (SI), which also includes all the data, tabulated results for the individual-Q global model, and results from several alternative global fits of the KA data. All these results assume error-free oxalate assays and pHs, when in fact these are all measured quantities subject to uncertainty. Allowing for their uncertainty is not simple, as single measurements of each of these apply to all the data for a given Pf. Spot checks of ±4% changes in Pox and (Feox + Alox) in selected datasets gave smaller % changes in q0 and q1, so such effects are likely much smaller than the SEs reported in Table 2.
5. Conclusions
Although we have found possible use of global fitting methods in analysis of the time dependence of sorption (methods not described) [26,27], we believe the present work is the first such analysis of the dependence on fertilizer treatment. In this, we have also addressed common shortfalls—the tacit treatment of the measured C values as error-free and the failure to weight the data in accord with their often strong heteroscedasticity. We have allowed for uncertainty in both C and C0, the latter considered as a stand-in for experimental procedures other than direct measurement, like the preparation of soil/solution mixtures. To estimate the variances in C and C0, we have used residuals analysis incorporating a novel Monte Carlo trial-and-error procedure.
It is worth emphasizing that the most important result of the VF estimation efforts was the need to include some uncertainty in C. This need can be understood from the observation that most of the sorption experiments included some experiments where, within uncertainty, the measured C was 0.00 (see Supplementary Materials (SI)) [28,29]. To avoid computational problems, such values were typically set to a very small value, like C = 0.0001 mg/L, which is reasonable, since simplest residuals analysis indicated σC ~ 0.1 mg/L. (Note that σC is numerically ~500 times the absorbance uncertainty, from the conversion of the spectrophotometric absorbance to C). Taking typical a and b values of 100 mg/kg and 0.3, respectively, the values of aCb range from 50 down to 6 mg/kg as C drops from 0.1 to 0.0001 mg/L. The differences in these values hugely exceed any reasonable uncertainty for X and C0—roughly 0.3 mg/L for the latter from simplest residuals analysis. Allowing for even a small uncertainty in C completely neutralizes such problems. Anyone analyzing sorption data without allowing for uncertainty in C, as is customary in the use of Equation (3) as the fit model, should take care to ensure that these low-C problems do not affect the analysis.
The practical motivation for phosphate sorption studies of the type treated here is optimizing the balance between the needs for plant nutrition and the environment. The global analysis of data from multiple fertilizer pretreatments provides greatly improved estimates of the parameters in the Freundlich model, of which Q, the pre-existing P, is mainly of interest in this regard. The linear increase in Q with Pf implies that the increase is attributable to the fertilizer, hence represents bioavailable P. However, since Q is just a parameter in an empirical model, we cannot be sure that it is quantitatively reliable. Further, the finite Q0 values for Pf = 0 represent P of unknown origin. These are among several questions about precisely what is measured in P sorption studies and various assays, answers to which are needed for a complete and reliable assessment of the crops-vs.-environment phosphate balance [25].
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/soilsystems9010022/s1: Table S1: Initial soil characteristics; Figure S1: Standard deviations from studentized residuals obtained from MC simulations; Table S2: Sorption data; Table S3: Results from individual-Q global analyses of sorption data for five soils; Table S4. Results from four linear-Q global analyses of sorption data for KA soil type; Figure S2: Effect of deletion of Pf = 0 data for the MA soil type; Figure S3: Weighted fits of KA data to 3-parameter Freundlich model, as X vs. C (left, Equation (3) in text) and C0 vs. C (Equation (4)).
Author Contributions
Conceptualization, J.T., P.H., and P.J.M.; methodology, J.T., P.H., and P.J.M.; software, J.T.; formal analysis, J.T. and P.J.M.; resources, P.J.M.; data, P.H. and P.J.M.; writing—original draft, J.T.; writing—review and edition, J.T., P.H., and P.J.M.; project administration, P.J.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work received no specific financial support.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All analyzed data are presented in the Supplementary Materials (SI).
Acknowledgments
We thank Damian Collins for his critical reading and helpful comments on this manuscript.
Conflicts of Interest
The authors declare no competing financial interests or personal relationships that might have influenced the work reported in this paper.
References
- Fitter, A.H.; Sutton, C.D. Use of Freundlich isotherm for soil phosphate sorption data. J. Soil Sci. 1975, 26, 241–246. [Google Scholar] [CrossRef]
- Barrow, N.J. The description of phosphate adsorption curves. J. Soil Sci. 1978, 29, 447–462. [Google Scholar] [CrossRef]
- Mead, J.A. A comparison of the Langmuir, Freundlich and Temkin equations to describe phosphate adsorption properties of soils. Aust. J. Soil Res. 1981, 19, 332–342. [Google Scholar] [CrossRef]
- Nair, P.S.; Logan, T.J.; Sharpley, A.N.; Sommers, L.E.; Tabatabai, M.A.; Yuan, T.L. Interlaboratory comparison of a standardized phosphorus adsorption procedure. J. Environ. Qual. 1984, 13, 591–595. [Google Scholar] [CrossRef]
- Kinniburgh, D.G. General purpose adsorption isotherms. Environ. Sci. Technol. 1986, 20, 895–904. [Google Scholar] [CrossRef]
- Tolner, L.; Fuleky, G. Determination of the originally adsorbed soil-phosphorus by modified Freundlich isotherm. Commun. Soil Sci. Plant Anal. 1995, 26, 1213–1231. [Google Scholar] [CrossRef]
- Barrow, N.J. Towards a single-point method for measuring phosphate sorption by soils. Aust. J. Soil Res. 2000, 38, 1099–1113. [Google Scholar] [CrossRef]
- Barrow, N.J. The description of sorption curves. Eur. J. Soil Sci. 2008, 59, 900–910. [Google Scholar] [CrossRef]
- Tellinghuisen, J.; Bolster, C.H. Least-Squares Analysis of Phosphorus Soil Sorption Data with Weighting from Variance Function Estimation: A Statistical Case for the Freundlich Isotherm. Environ. Sci. Technol. 2010, 44, 5029–5034. [Google Scholar] [CrossRef]
- Clutton-Brock, M. Likelihood distributions for estimating functions when both variables are subject to error. Technometrics 1967, 9, 261–269. [Google Scholar] [CrossRef]
- Powell, D.R.; Macdonald, J.R. A rapidly convergent iterative method for the solution of the generalized nonlinear least squares problem. Computer J. 1972, 15, 148–155. [Google Scholar] [CrossRef]
- Britt, H.I.; Luecke, R.H. The estimation of parameters in nonlinear, implicit models. Technometrics 1973, 15, 233–247. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Least-squares analysis of data with uncertainty in x and y: A Monte Carlo methods comparison. Chemom. Intell. Lab. Syst. 2010, 103, 160–169. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Least Squares Methods for Treating Problems with Uncertainty in x and y. Anal. Chem. 2020, 92, 10863–10871. [Google Scholar] [CrossRef] [PubMed]
- Sposito, G. Derivation of the Freundlich equation for ion exchange reactions. Soil Sci. Soc. Am. J. 1980, 44, 652–654. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes; Cambridge Univ. Press: Cambridge, UK, 1986. [Google Scholar]
- Tellinghuisen, J. Variance function estimation by replicate analysis and generalized least squares: A Monte Carlo comparison. Chemom. Intell. Lab. Syst. 2009, 99, 138–149. [Google Scholar] [CrossRef]
- York, D. Least-squares fitting of a straight line. Can. J. Phys. 1966, 44, 1079–1086. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Calibration: Detection, Quantification, and Confidence Limits Are (Almost) Exact When the Data Variance Function Is Known. Anal. Chem. 2019, 91, 8715–8722. [Google Scholar] [CrossRef]
- Ingle, J.D., Jr.; Crouch, S.R. Evaluation of precision of quantitative molecular absorption spectrometric measurements. Anal. Chem. 1972, 44, 1375–1386. [Google Scholar] [CrossRef]
- Bevington, P.R. Data Reduction and Error Analysis for the Physical Science; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Lybanon, M. A better least-squares method when both variables have uncertainties. Am. J. Phys. 1984, 52, 22–26. [Google Scholar] [CrossRef]
- Boggs, P.T.; Donaldson, J.R.; Byrd, R.H.; Schnabel, R.B. ALGORITHM 676 ODRPACK: Software for Weighted Orthogonal Distance Regression. ACM Trans. Math. Softw. 1989, 15, 348–364. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Least-squares analysis of data with uncertainty in y and x: Algorithms in Excel and KaleidaGraph. J. Chem. Educ. 2018, 95, 970–977. [Google Scholar] [CrossRef]
- Milham, P.J.; Carlson-Perret, N.; Morrison, R.J.; Harvey, D.; Andersson, K.O.; Burkitt, L.L.; Collins, D.; Haigh, A.M.; Hannah, M.C.; Tellinghuisen, J.; et al. Estimating Existing Sorbed Soil Phosphate from its Effect on Subsequent Sorption: 1 Relations of Freundlich Parameters and Soil Properties 2023. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4461675 (accessed on 18 February 2025).
- Tan, B.; Barrow, N.J.; Longguo, L.; Zhou, P.; Zhuang, W. Phosphorus Sorption by Purple Soils in Relation to Their Properties: Investigation, Characterization, and Explanation. Sustainability 2023, 15, 14609. [Google Scholar] [CrossRef]
- Barrow, N.J. Equations to describe the amount and rate of sorption. Eur. J. Soil Sci. 2023, 74, e13355. [Google Scholar] [CrossRef]
- Dougherty, W.J.; Mason, S.D.; Burkitt, L.L.; Milham, P.J. Relationship between phosphorus concentration in surface runoff and a novel soil phosphorus test procedure (DGT) under simulated rainfall. Soil Res. 2011, 49, 523–528. [Google Scholar] [CrossRef]
- Murphy, J.; Riley, J.P. A modified single solution method for the determination of phosphate in natural waters. Anal. Chim. Acta 1962, 27, 31–36. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).