Determining Drought and Salinity Stress Response Function for Garlic

Abstract

Garlic (Allium sativum L.) is an important crop cultivated in arid and semi-arid climates. To quantify the tolerance of garlic to drought and salinity stresses in terms of parameter values of the stress response function, we conducted pot experiments in a greenhouse for two years. Nine 1/5000a Wagner pots were used for three treatments, namely drought-treated, salinity-treated, and control pots, for estimating the relative transpiration. Daily transpiration rates were observed by weighing pots, and the soil surface of each pot was covered. The soil water contents were measured hourly using two soil moisture probes for drought-treated pots, and two salinity probes for both soil water content and bulk electrical conductivity were monitored for salinity-treated pots. When the ratio of actual to potential transpiration fell below 50%, the root length distributions were obtained by dismantling the pots. The parameter values for both drought-stress and salinity-stress functions were estimated using inverse-analysis and bulk-analysis methods. The parameter values of drought-stress and salinity-stress functions obtained by the simpler and cheaper bulk method gave similar results to the inverse method when the root length distributions were relatively uniform.

1. Introduction

In arid and semi-arid climates, drought and salinity stresses limit root water uptake, resulting in poor crop production. Wang et al. [1] documented that drought stress causes severe crop production losses of more than 50% worldwide, whereas Singh [2] mentioned that more than one billion hectares of arable land has been affected by salinity and might be continuous to expand worldwide. Irrigation with saline water results in salt accumulation in the plant root zone which may have a detrimental effect on plant growth and crop establishment [3], and this depends on the ability of each crop to tolerate the salinity level. A plant might end its life cycle in early growth stages due to the hypertonic and hyperosmotic stresses [4]. On the other hand, severe drought stress can significantly affect the plant metabolism [5] and reduce root length density [6]. Quantifying the plant response to such severe conditions may help for better crop and irrigation management, as well as salinity control.

To quantify the response of a crop to salinity and water stress, a macroscopic root water uptake model which uses the reduction function was developed [7]. It has been employed to manage irrigation and salt/sodic reclamation strategies in saline agriculture [8] and for evaluating the plant root water uptake under various water deficits [9]. The reduction function is a central component of the root water uptake model, which is used in the sink term in the Richards [10] equation commonly used in the numerical simulations of water flow, solute movement, and root water uptake, such as HYDRUS [11], SWAP [12], or WASH_2D [13], all of which have been used for irrigation management scenarios. Therefore, determining the parameter values in the stress response function can be useful to avoid significant yield losses owing to both drought stress and salinity stresses while saving irrigation water. The parameter values of drought $(h_{50}$, $p)$, and salinity $(h_{050}$, $p$) stress response function (SRF) are plant-specific and thus must be determined for each crop.

Garlic (Allium sativum L.) is one of the major crops and consumed in many dishes (3.5 kg/head/year) and used even for medical care worldwide. It is expected to be produced in severe water scarcity and more saline conditions, and some researchers have evaluated its tolerance to drought and salinity in terms of plants’ agronomic aspects.

Zhou et al. [14] reported that drought stress affected the garlic growth component, whereas Francois [15] reported its tolerance in salinity. In a study, Francois found that garlic is tolerant at a threshold value of 3.9 dSm⁻¹, but bulb yield decreased to 50% at a threshold value of 7.4 dSm⁻¹ of saturated extract [15] and at a threshold value of 8 dSm⁻¹ of saline irrigation water applied [16]. High saline irrigation conditions might cause severe abiotic stress on garlic, and such conditions cause chlorophyll degradation and decrease carotenoid content [17]. However, none of those previous studies evaluated its tolerance to drought and salinity stresses in terms of parameter values of SRF, using a numerical simulation model of water flow in soils and root water uptake, although accuracy in prediction of water flow and root water uptake is critical for a proper evaluation of the response of rain and irrigation on crop yield. Again, optimizing parameter values of Feddes reduction function is very complex, and few have been made to attempts to inversely determine the parameters values of SRF of root water uptake. Yanagawa and Fujimaki [18] presented a method to inversely determine parameter values of drought $(h_{50}$, $p)$ and salinity $(h_{050}$, $p$) stresses for soybean and canola using plural soil moisture probes for each pot. Those methods, however, require soil moisture probes and dataloggers that make it a bit costly to be implemented by the researchers in developing countries. Moreover, it requires laborious accurate calibration of the probes for each soil, under climatic condition [9]; restricted measurement volumes in pots; and the use of parameter estimator software for the reduction function of root water uptake (PERF) [19].

The objective of this study was to firstly determine the parameter values of drought $(h_{50}$, $p)$ and salinity $(h_{050}$, $p$) stresses of garlic using the inverse method (Yanagawa and Fujimaki [18]).

Recently, Ebrahimian et al. [20] presented a simpler method to determine the drought stress response function (DSRF) and salinity stress response function (SSRF) for sesame and reported that a close value was obtained compared to the inverse method. This method was only tested for one crop and one season. Therefore, more experiments should be carried out to validate its effectiveness.

The method [20] may help irrigation scientists and breeders to easily determine such parameter values. The reliability of the simpler method may depend on plant and other experimental conditions. Therefore, the second objective of this study was to evaluate the accuracy of a simplified bulk method to determine both parameter values of drought $(h_{50}$, $p)$ and salinity $(h_{050}$, $p$) stresses by comparing them with the results of the inverse method using garlic crop for the two consecutive seasons.

2. Materials and Methods

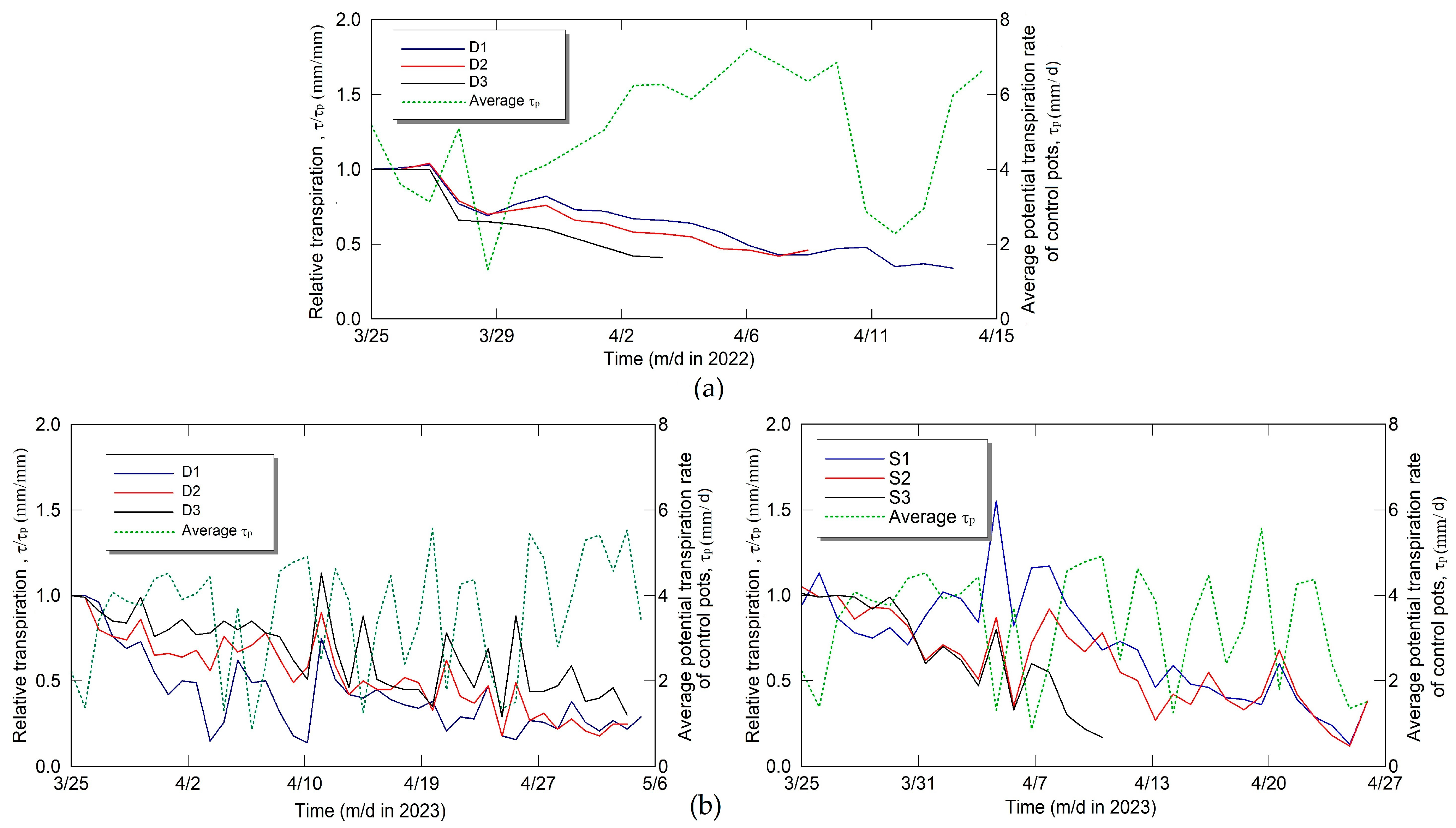
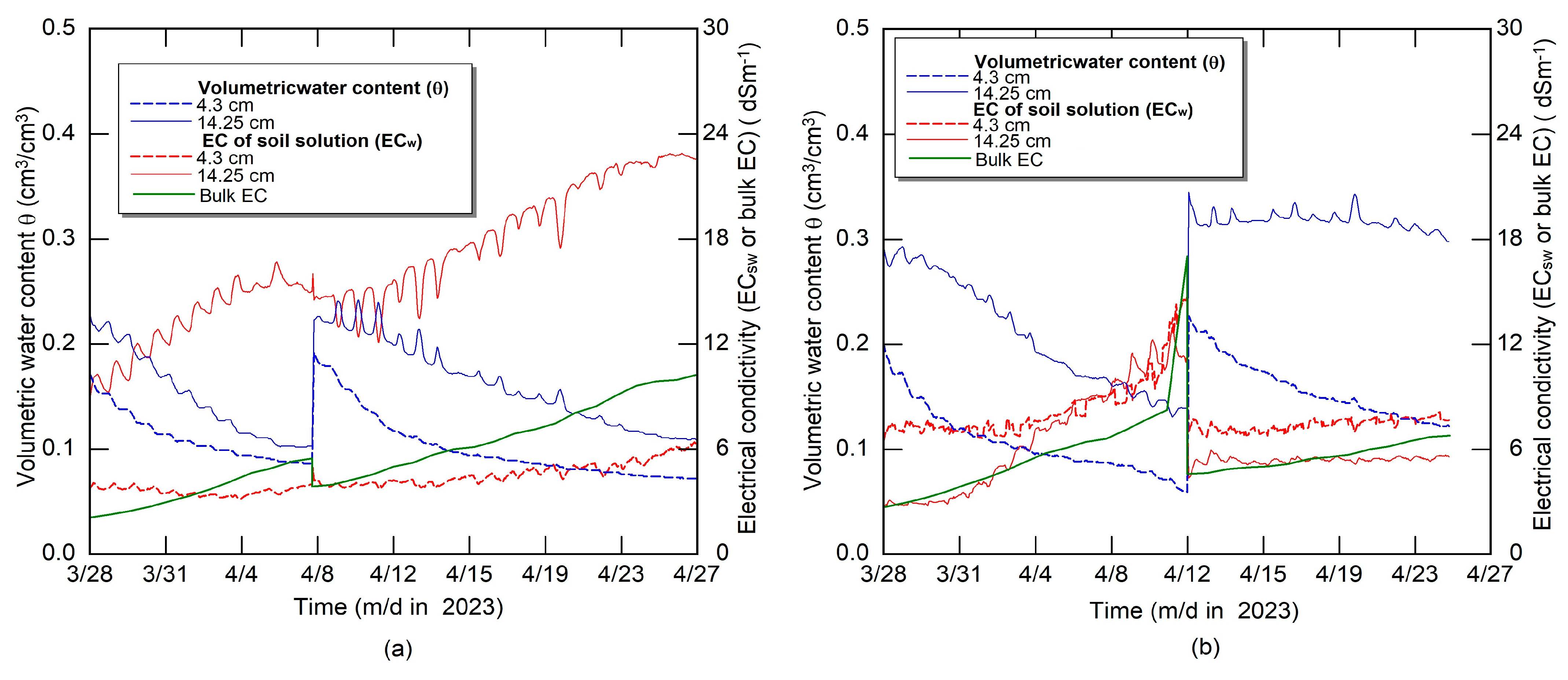
2.1. Description of Pot Experiments

We carried out two pot experiments in a greenhouse at the Arid Land Research Center, Tottori University, for two consecutive seasons in 2022 and 2023. In each experiment year, we set up nine 1/5000a Wagner pots (height, upper diameter, and lower diameter: 20 cm, 15.90, and 14.95, respectively) for three treatments with three replicates pots: drought-treated pots (D1, D2, and D3), salinity-treated-pots (S1, S2, and S3), and control pots (C1, C2, and C3) for estimating daily relative transpiration ($\mathsf{\tau }/\mathsf{\tau }\mathrm{p}$) (the ratio of actual transpiration to potential transpiration) during the stress period.

Tottori sand was packed in control and salinity-treated pots, whereas Kanto loam was used for the drought-treated pots due to its higher water holding capacity compared with the sandy soil. In other words, drought undergoes too fast in coarse soil (e.g., sandy soil) compared to finer soils (e.g., Kanto loam soil). In addition, in coarse soil, small errors in soil moisture measurement may lead to large errors in estimating suction. For salinity stress, we can use sandy soil, because during the salinity stress period, we keep soil moisture high and sandy soil allows us rapid replacement of soil solution, i.e., imposition of salinity stress. The two soils properties are shown in

Table 1. Parameter values of van Genuchten equation [21] (Equation (8)) for the two soils.

Soil	θsat	θr	αv	n
	cm3 cm−3	cm3 cm−3	cm−1
Tottori sand	0.42	0.03	0.018	4.0
Kanto loam	0.64	0	0.0025	1.26

.

In 2022, the garlic (Allium sativum L.) cloves were sown on 14 October, and the experiment ended on 18 April. In 2023, the cloves were sown on 4 November, and the experiment ended on 6 May. One seed-clove of garlic was sown in each pot, and each plant received 3 g of N-P-K fertilizer of 8-8-8 in solid form at 14 and 21 days after sowing and grown until middle age to impose drought and salinity stresses.

Drought-treated pots were saturated by applying tap water until leaching occurred from the drainage orifice at the bottom of each replicated pot. The drought stress was imposed by suspending irrigation water at all drought-treated pots until the termination of the experiment when the relative transpiration was steadily less than 0.4.

Before the imposition of salinity stress, salinity-treated pots were sufficiently irrigated with tap water to firstly estimate the parameter values due to drought stress in sandy soil, and when the relative transpiration reached 0.5, we applied NaCl solution to impose salinity stress on the plant, and the experiment was terminated when the relative transpiration reached 0.5. The amounts of saline irrigation water were determined for each pot by refilling the loss from transpiration to the previous irrigation. We repeated this scenario twice to impose salinity stress on salinity-treated pots. We terminated the experiment when the relative transpiration of the plant was steadily less than 0.4.

During the imposition of drought and salinity stresses, evaporation from soil was not allowed by covering the soil surface for each pot with styrene foam or aluminum paper. The average volumetric water content of control pots was maintained around 0.2, larger than field capacity by adding tap water consumed since the previous irrigation every morning.

In the first year, 2022, drought-treated pots were exposed to drought stress from 27 March to 16 April, while in the second year, 2023, they were exposed from 25 March to 5 May. Plants in salinity-treated pots received saline water two times of 2000 ppm of NaCl solution from 12 March to 12 April, in 2022, whereas the plants received in 2023 two times of 3000 ppm of NaCl solution from 25 March to 6 May.

Two soil moisture sensors were installed horizontally at a depth of 4.5 and 13.5 cm into each drought-treated pot to monitor daily soil moisture. In 2022, 10HS (METER Inc., Pullman, Washington, WA, USA) sensors were used, while TEROS 10 sensors were used in 2023, and the measured data in drought-treated pots were recorded using data loggers ZL6 (METER Inc., Pullman, Washington, WA, USA). We also installed two soil moisture and salinity sensors horizontally at depths of 4.3 and 14.3 cm into each salinity-treated pot to monitor soil moisture, bulk electrical conductivity, and soil temperature. TEROS 12 (METER, Inc., Pullman, WA, USA) sensors were installed in all salinity-treated pots in 2022 and used for pot S2 in 2023, while 5TE (Decagon Devices, Inc. Pullman, WA, USA) sensors were installed in only two pots, S1 and S3, in 2023. In both years, soil moisture, bulk electrical conductivity, and soil temperature were recorded using data loggers Em50 (Decagon Devices, Inc., Pullman, WA, USA) and ZL6 (METER, Inc., Pullman WA, USA).

The weight of each pot was measured every morning at 9:30, using an electronic balance.

To correct for individual differences in growth mainly owing to micrometeorological difference and genetic difference, we multiplied a correction factor to the mean value of transpiration rate of the control pot to estimate the potential transpiration rate of each pot.

2.2. Plant Root Water Uptake

2.2.1. Theorical Expression

In the macroscopic root water uptake model, the rate of root water uptake is calculated as follows [22]:

$$S=\mathsf{\alpha }{T}_{rp}\mathsf{\beta }$$

(1)

where $S$ is root water uptake rate (h⁻¹); $T_{rp}$ is the potential transpiration rate (cm h⁻¹); β is the normalized root density or root activity (cm⁻¹); and $\mathsf{\alpha }$ is a reduction coefficient, which is calculated as a function of matric and osmotic potentials:

$$\mathsf{\alpha }=\frac{1}{1+{\left(\frac{h}{h_{50}}+\frac{h_0}{h_{050}}\right)}^p}$$

(2)

where $h$ and $h_0$ are the matric and osmotic heads, respectively; $h_{50}$ and $h_{050}$ are the matric and osmotic potentials when the water uptake is 50% of its potential rate; and $p$ is an empirical parameter. Equation (2) is the SRF.

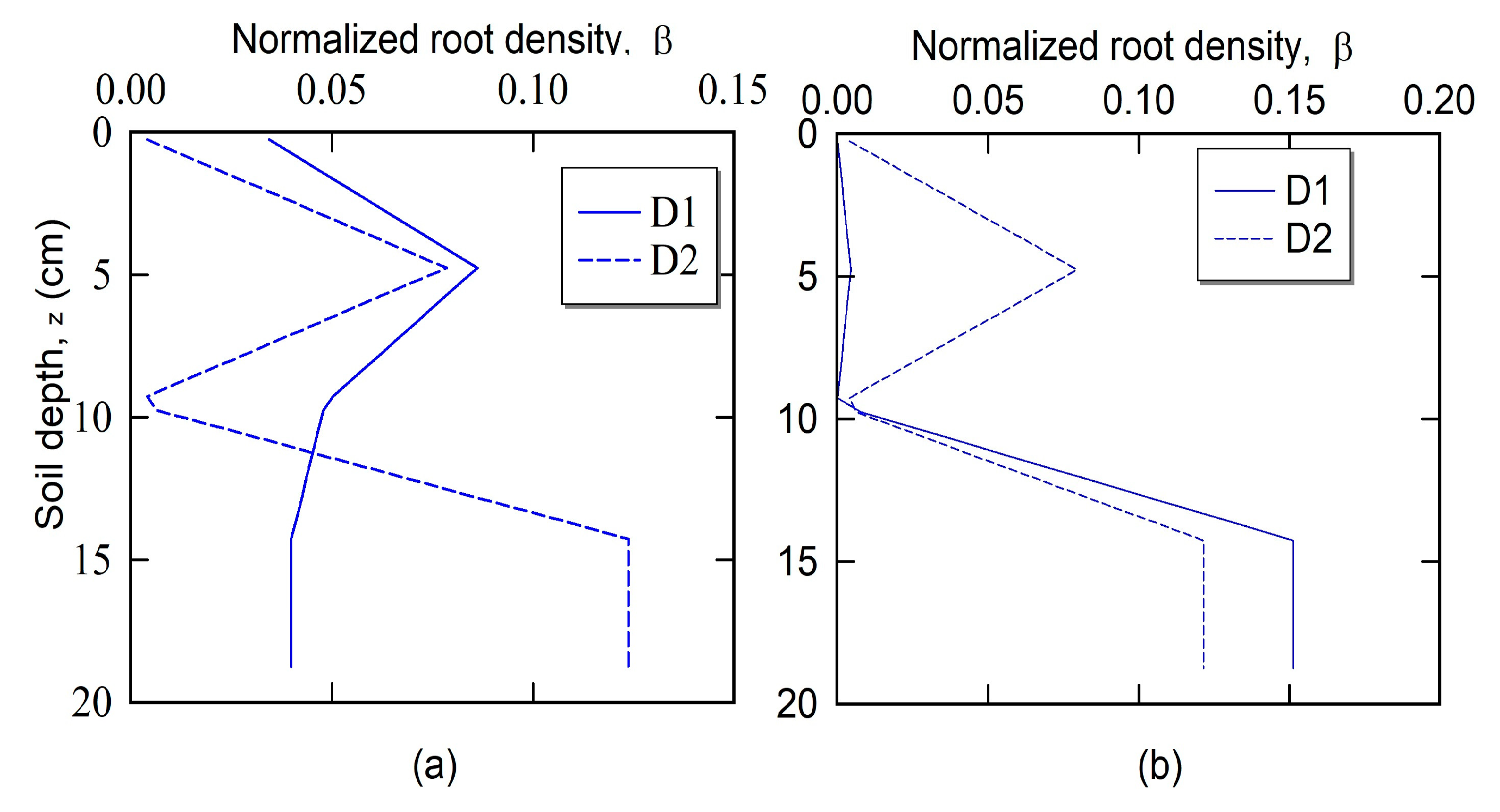
2.2.2. Survey for Root Length Distribution

During both years, we quantified the root length distribution at the end of the experiment to determine β used in the inverse analysis of the SRF. We proceeded as follows: we took the entire soil from each treated pot from the four layers, namely 0–4.5, 4.5–9.5, 9.5–14.5, and 14.5 cm to the bottom. We then we rinsed and wet-sieved using a steel mesh and then washed and air-dried in a mesh screen. The air-dried root was scanned on a flatbed screen at 300 dpi. The total length of the root obtained in an image was obtained using the Newman method [23].

2.3. Bulk Method

The bulk method was based on mass balance calculation using the daily weight of pots and applied salt [20]. The intermediate daily average water contents $\left({\overline{\theta }}_i\right)$ of the morning and next morning for drought-treated pots were used to calculate the representative matric potential of the day using the soil water retention curve (Equation (8)) to estimate the parameter values, $h_{50}$ and $p$, of drought stress by fitting the curve using Equation (2). ${\overline{\theta }}_i$ can be estimated as follows:

$${\overline{\theta }}_i=\frac{W_i-W_f}{V_t}+{\overline{\theta }}_f$$

(3)

where $W_i$ is the pot weight on day i (g), $W_f$ is the pot weight on the final day of the experiment (g), $V_t$ is the total soil volume (cm³), and ${\overline{\theta }}_f$ is average soil water content at the end of experiment (cm³ cm⁻³).

The average salt concentration $\left({\overline{C}}_i\right)$ on the morning of day i in the salinity-treated pot is calculated by the intermediate daily average salt mass content before $\left(C_{bi}\right)$ and the intermediate salt mass content after $\left(C_{ai}\right)$ saline water applied the morning.

$${\overline{C}}_i=\frac{C_{bi}+C_{ai+1}}{2}$$

(4)

The ${\overline{C}}_i$ was used to calculate the representative osmotic potential of the day using Equation (9) [19], and then the parameter value $h_{050}$ and the $p$ of the salinity stress were obtained via a fitting curve, using Equation (2).$C_{ai}$ and $C_{bi}$ were calculated as follows:

$$C_{bi}=\frac{M_{bi}}{{\overline{\theta }}_{bi}{V_t\rho }_w} \mathrm{and} C_{ai}=\frac{M_{ai}}{{{{\overline{\theta }}_{ai}V}_t\rho }_w}$$

(5)

$$M_{ai}=M_{bi}+\frac{W_{ai}-W_{bi}}{{\rho }_w}{C}_w$$

(6)

$${\overline{\theta }}_{bi}=\frac{W_{bi}-W_f}{V_t}+{\overline{\theta }}_f \mathrm{a}\mathrm{n}\mathrm{d} {\overline{\theta }}_{ai}=\frac{W_{ai}-W_f}{V_t}+{\overline{\theta }}_f$$

(7)

where ${\overline{\theta }}_{bi}$ and ${\overline{\theta }}_{ai}$ are the soil water contents before and after irrigation (cm³ cm⁻³), and $W_{bi}$ and $W_{ai}$ are the pot weights, respectively, before and after irrigation (g); $M_{bi}$ and $M_{ai}$ are mass of salts (g) in the soil at the morning of i-th before and after irrigation, respectively; $\rho w$ is the density of water (g cm⁻³); ${\overline{C}}_i$ is the soil salt concentration at the morning of i-th day (g cm⁻³); and $C_w$ (g cm⁻³) is the salt concentration of the irrigation water.

In drought-treated samples, the matric head, h(cm), was obtained using the van Genuchten Equation (8):

$$h=\frac{1}{{\alpha }_v}{\left[{\left(\frac{\theta -{\theta }_r}{{\theta }_s-{\theta }_r}\right)}^{1-n}-1\right]}^{\frac{1}{n}}$$

(8)

where $\theta$ is the soil water content (cm³ cm⁻³), $\theta$_s is the saturated soil water content (cm³ cm⁻³), $\theta$_r is the residual soil water content (cm³ cm⁻³), α_v is the inverse of the air-entry value (cm⁻¹), and n is the pore-size distribution index (dimensionless).

In salinity-treated pots, the osmotic potential, $h_0$ (cm), of soil water content can be calculated using Equation (9) [19]:

$$h_0=2\omega \nu C\chi \mathrm{RT}$$

(9)

where $\omega$ is a unit-conversion factor (10.2 cm kg J⁻¹); $\nu$ is the number of ions per molecule; $C$ is the salt concentration (mol kg⁻¹); χ is the osmotic coefficient, which is assumed to be unity; R is the universal gas constant (8.31 J mol⁻¹ K⁻¹); and T is the temperature in Kelvin.

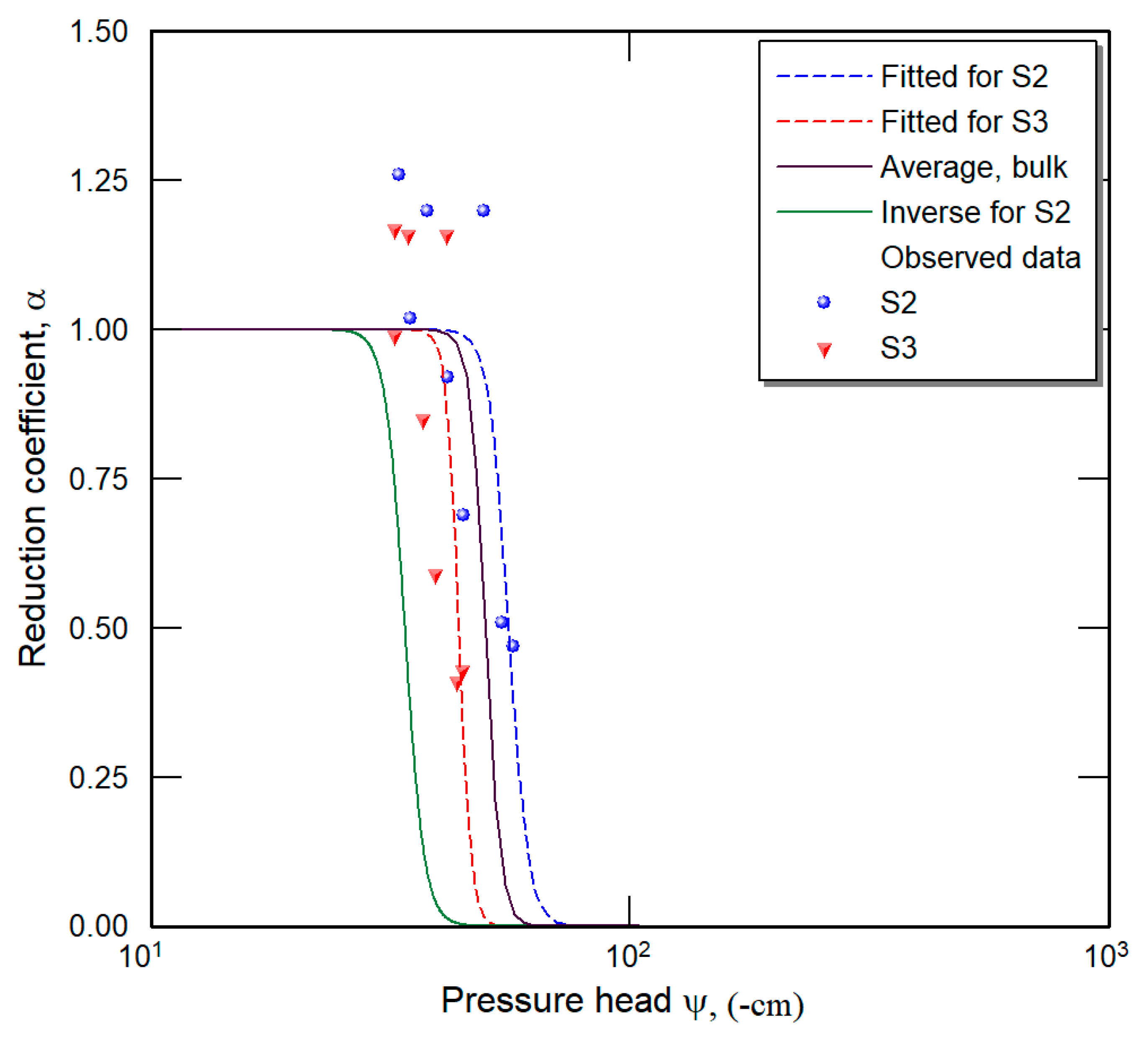
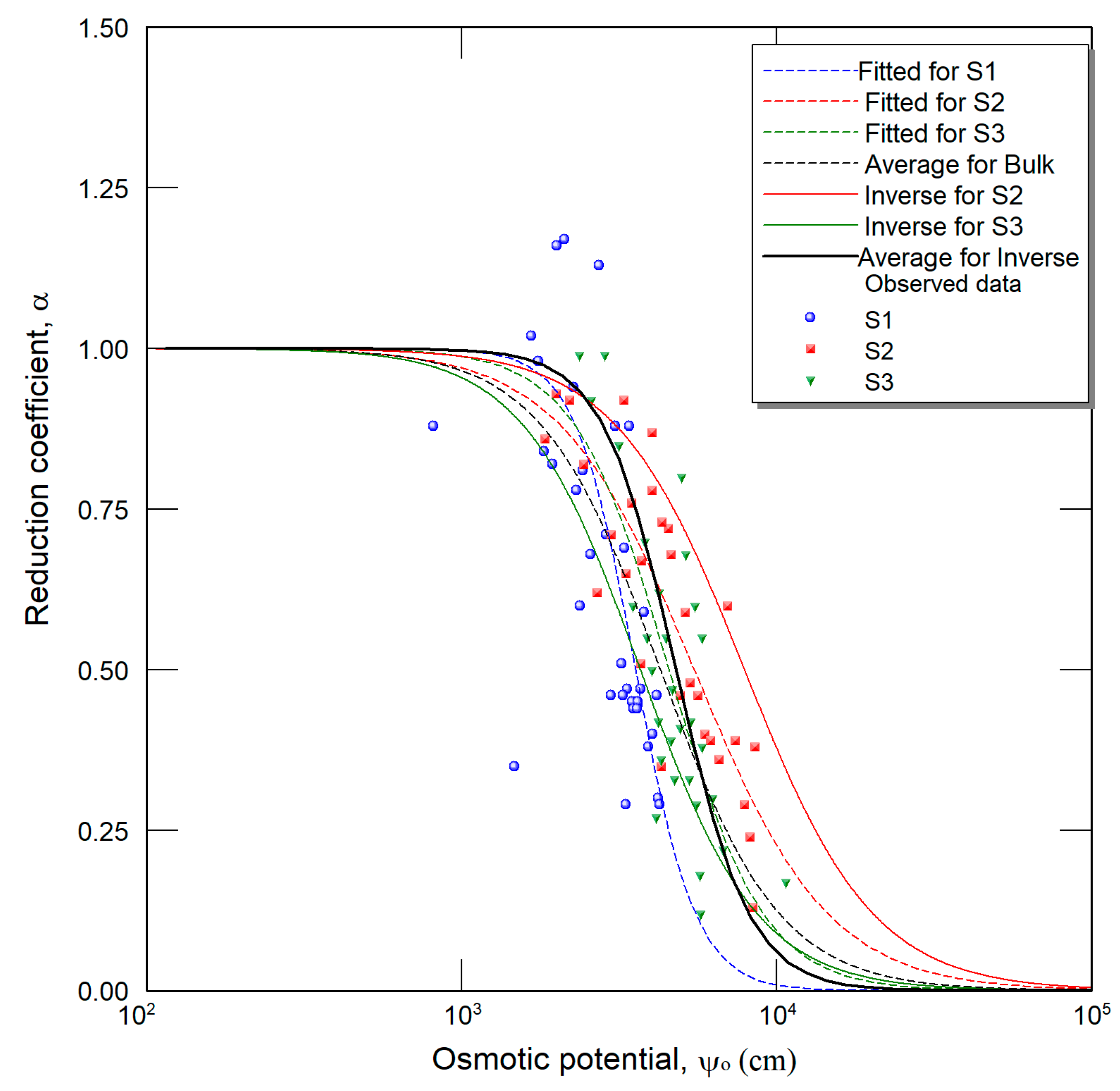
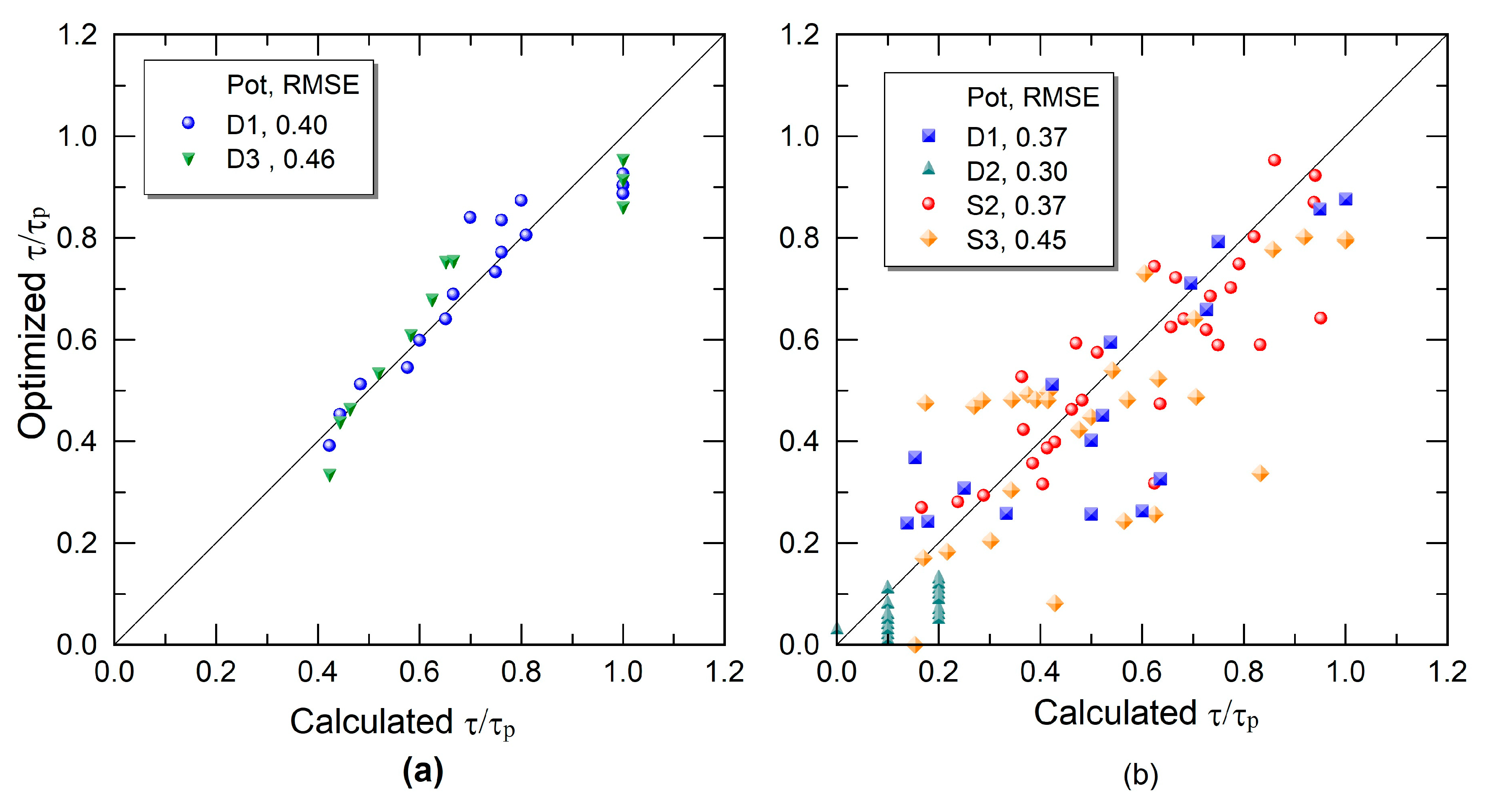
2.4. Inverse Method

We employed the method presented by Yanagawa and Fujimaki [18] for both drought and salinity stresses’ data analysis. In this method, the accurate calibration of sensors is critical [18]. We calibrated the sensors using final θ and salt concentration distribution and ${\overline{\theta }}_i$ and ${\overline{C}}_i$.

The obtained θ for drought-treated pots and both the measured θ and electrical conductivity of the soil solution of salinity-treated pots were used for inverse analysis to obtain the parameter values, $(h_{50}$, $p)$ and $(h_{050}$, $p$), using a reduction function of root water uptake (perf) [19], which is freely accessible on the website of Arid Land Research Center, Tottori University (https://www.alrc.tottori-u.ac.jp/fujimaki/download/perf/, accessed on 15 June 2022).

The calculated transpiration rate, $T_{cal}$, was estimated while assuming that the pattern of transpiration is the same as that of the short wave radiation, R_a (W m⁻²) [18].

$$T_{rp}={\tau }_p\frac{R_a}{{\int }_{0:00}^{24:00}{R}_{a}dt}$$

(10)

where τ_p is the potential daily transpiration rate (cm). The daily transpiration value was calculated by integration of hourly calculated transpiration rate, ${\tau }_{cal}$ (cm s⁻¹).

$${\tau }_{cal}(\overrightarrow{B)}={\int }_{0:00}^{24:00}{T}_{cal}(\overrightarrow{B)}dt$$

(11)

where $(\overrightarrow{B)}$ is the vector of the optimized parameter. We used the root mean square error between the actual and calculated daily transpiration, $\tau$ and ${\tau }_{cal}$, as the objective function that was to be minimized. T_cal is the simulated transpiration rate, which is the integration of the root water uptake, S, across the root zone (cm h⁻¹).

The root mean square error value was used as an objective function to minimize the difference between actual and calculated daily transpiration [18].

$$RMSE(\overrightarrow{B)}={\left\{\frac{1}{N}\sum _{\tau =1}^N{\left[{\tau }_{cal}(\overrightarrow{B)}-\tau \right]}^2\right\}}^{0.5}$$

(12)

3. Results and Discussion

The time evolution of the relative transpiration rate, τ/τ_p, since suspending water supplied to drought-treated pots and starting the application of saline water to salinity-treated pots is shown in Figure 1. Having the τ/τ_p significantly below 1.0 indicates the imposition of drought stress (Figure 1a,b, left). The experiment in 2022 was terminated on 12 April, 17 April, and 7 April for D1, D2, and D3, respectively (Figure 1a); meanwhile, in 2023, it was terminated on 12 April for both D1 and D2, and on 5 May for D3 (Figure 1b-left). For the salinity-treated pots, the experiment in 2023 was terminated on 06 May for S1, and on 27 April for both S2 and S3 (Figure 1b-right), when the τ/τ_p values were less than 0.4 in both of the two years.

In response to the depletion of salt build-up, the τ/τ_p gradually decreased after saline water applied (Figure 1b, right), except for observed plant recovery on the next day after saline water was firstly applied.

Large fluctuations in 2023 may have been mainly caused by that of potential transpiration, as shown by the right axes. The τ/τ_p tends to be large when τ_p is small, owing to the smaller microscopic gradient of matric or osmotic potential near each root. In other words, the stress response function may also depend on the potential transpiration rate. However, the development of alternative equations is beyond the scope of this study (Figure 1b, left).

The variation in the period of drought-treated pots and salinity-treated pots across each year experiment is due to the different transpiration demands of each experiment for the same calendar days between the two years. Higher transpiration demands in 2022 could shorten the duration under the stress, where the actual plant transpiration instantly decreased compared with 2023, as show in Figure 1a.

The dynamic changes in average θ in drought-treated pots using bulk analysis and the observed one using probes during the experiment run in 2022 and 2023 are shown in Figure 2a,b, respectively. Regarding the output of the sensor, the difference in water content between the two depths (4.5 and 13.5 cm) was minor compared to the drastic change from field capacity to wilting point. Unfortunately, the data were erroneous for pot D2 in 2022 and for pot D3 in 2023.

The changes in the θ and EC of soil solution (EC_sw) are shown in Figure 3 for salinity-treated pots in 2023. Plants in S2 and S3 were under drought stress (before 25 March) just before the application of NaCl solution both first (25 March) and second (8 April) for S2 to near field capacity, and the θ decreased, while the EC_sw increased (Figure 3a). The EC_sw temporary decreased just after irrigation, particularly in S3 (Figure 3b).

Figure 4 shows the normalized root length density of drought-treated pots. In the first year of the experiment, 2022, pot D1 had the largest density at the top layer, around 5 cm in depth, while pot D2 had the largest density near the bottom (Figure 4a). The same trend was observed in pot D2 and pot D1 in 2023 (Figure 4b). In both of the two years, a large density was observed in all drought-treated pots near the bottom, except for pot D1 (Figure 4a), possibly owing to the limited soil depth. Under severe drought stress, garlic may respond by extending its root length to the deeper layers in order to explore available water. Mahajan [4] mentioned that, under severe drought condition, root activity tends to develop into deeper layers because plants tend to reduce photosynthesis by reducing leaf area index and to invest more in root development to adapt to the drought-environment condition [24].

The profiles of normalized root length density of salinity-treated pots are shown in Figure 5. There were almost no roots in the surface layer. Since the period of salinity stress was short compared with the entire growing season, salinity stress may have not largely impacted the distribution of root. The difference in soil texture may have caused difference in root distribution. Garlic may tend to extend its roots to a deeper layer, and sand may have been easier to extend than Kanto loam.

The fitted and inversely determined drought stress response functions are shown in Figure 6, and the results of $h_{50} \mathrm{and} p_{50}$ are listed in

Table 2. The estimated parameter values of stress response function for drought stress in 2022 and 2023. STD refers to the standard deviation.

Method	Replicate	2022		2023
		h50 (-cm)		p50
	D1	5592	1.25	5884	1.73
Bulk	D2	7312	1.8	1974	1.34
	D3	4839	0.92	2812	1.43
	Mean ± STD	5914 ± 1035	1.32 ± 0.36	3557 ± 1681	1.50 ± 0.17
	D1	4589	1.43	6623	1.49
Inverse	D2	-	-	1180	0.81
	D3	4738	1.48	-	-
	Mean ± STD	4664 ± 75	1.46 ± 0.03	3902 ± 2722	1.15 ± 0.34

. The fitted curves (bulk) in Figure 6a for the three pots gave an average h₅₀ of −5914 cm, with a standard deviation of 1035 cm, while the inverse analysis gave an average of −4664 cm, slightly higher than that using the bulk method. This might be due to the large differences in the root length density of the pots, as shown in Figure 4a. In contrast, both average parameter values, h₅₀, of −3902 cm determined with the inverse method and that −3557 cm using the bulk method (Figure 6b) were fairly close, possibly because the root length distributions were fairly uniform (Figure 4b). Overall, in each experiment, the average parameter values of bulk and inverse methods were close, indicating that the bulk method might be fairly acceptable for researchers to simply determine the DSRF of local varieties at a low cost. Compared with the published h₅₀ using the inverse method, the value for garlic is lower (i.e., more tolerant) than it is for canola (−1019 cm) [18], sesame (−1642 cm) [20], and alfalfa (−1800 cm) [25].

We also determined the DSRF for Tottori sand (Figure 7) using data for salinity-treated pots just before starting salinity stress, and the average h₅₀ was—50 cm by bulk method and—34 cm using the inverse method (

Table 3. The estimated parameter values of stress response function for drought and salinity stresses using Tottori sand in 2023. STD refers to the standard deviation.

Method	Replicate	h50 (-cm)	p50	h050 (-cm)	p050
	S1	-	-	3516	2.42
Bulk	S2	56	21.32	5509	2.08
	S3	44	33.67	4589	2.99
	Mean ± STD	50 ± 6	27.5 ± 6.18	4538 ± 814	2.5 ± 0.37
	S1	-	-	-	-
Inverse	S2	34	21.3	7621	5.82
	S3	-	-	2020	1.68
	Mean ± STD	-	-	4821 ± 2801	3.8 ± 2.07

), which is marvelously higher (a smaller absolute value) than those obtained for Kanto loam soil. Unfortunately, the sensor output of S3 before 27 March was poor, and we could not inversely analyze it. This dependence of parameter value on soil type, mainly caused by a sharp drop in water diffusivity below the field capacity for sand, may be a drawback of the macroscopic root water uptake model and suggests the necessity of determining DSRF for sand, in addition to a finer soil, if the crop is grown in sandy soils.

The resulting SSRFs are plotted in Figure 8 and the results of $h_{050} \mathrm{and} p_{050}$ are listed in Table 3. The fitted curves for the three pots analyzed by the bulk method gave an average h₀₅₀ of −4538 cm, with a standard deviation of −814 cm. The inverse analysis gave an average of −4821, fairly close to the average obtained using the bulk method in spite of the non-uniform root and salinity distribution. Unfortunately, we failed to record the data of S1 before imposing salinity stress (25 March). The results of the salinity stress response function in 2022 are not presented here owing the fact that salinity stress could not be imposed by maturity owing to the low salinity of applied saline water (2 g/L). Note that, in 2022, the salinity-treated pots were terminated on 15 April for S1, 07 April for S2, and 14 April for S3. Compared with the published h₀₅₀ using the inverse method, the value for garlic is lower (i.e., more tolerant) than soybean (−3221 cm) [19] and canola (−4396 cm) [18] and higher than sesame (−5659 cm) [20].

Measured and optimized relative daily transpiration τ/τ_p using parameter values obtained by the inverse method are plotted in Figure 9a,b for 2022 and 2023, respectively. The optimized τ/τ_p agreed well with the measured values. A few large discrepancies in Figure 10 occurred mainly on cloudy days. This implies that SRF may also somewhat depend on the potential transpiration rate. Except for those days, the agreement between optimization and calculated over the two-years indicates the reliability of the proposed methods presented by Yanagawa and Fujimaki [18] for determining parameter values of the SRF for crops.

4. Conclusions

We determined the parameter values of the drought and salinity stress response function for garlic under two different soil textures. The average value of (h₅₀, p) determined with the inverse method was (−4288 cm, 1.30), while (h₀₅₀, p) was (−4821 cm, 3.75); meanwhile, the bulk method gave (h₅₀, p) of (−4736 cm, 1.40) and (h₀₅₀, p) of (−4538 cm, 2.50). The simpler and cheaper bulk method used gave fairly close results to the inverse method.

Those parameters values could be used as trigger values of sensor-based automated irrigation system and to optimize irrigation depth for garlic under severe drought and salinity conditions while preventing salt accumulation in the root zone.

To meet the increasing food demand in developing countries facing expanding drought and saline conditions, where numerous irrigation agriculture infrastructure projects are underway and irrigation lands are being expanded, irrigation operators or agricultural decision-supporting companies are encouraged to optimize irrigation depth using a simulation model with parameter values specifically determined for local crops, thus avoiding irrigation-induced salinity hazard. If soil moisture/salinity sensors are not available, or if researchers are not familiar with sensor calibration, the bulk method may be employed. An alternative stress response function incorporating the effect of the potential transpiration rate may enhance the accuracy in predicting transpiration.