Assessing Soil Prediction Distributions for Forest Management Using Digital Soil Mapping

Abstract

Texture, soil organic matter (SOM), and soil depth (SoD) are crucial properties in forest management because they can supply spatial information on forest site productivity and guide fertilizer applications. However, soil properties possess an inherent uncertainty that must be mapped to enhance decision making in management applications. Most digital soil mapping predictions primarily concentrate on the mean of the distribution, often neglecting the estimation of local uncertainty in soil properties. Additionally, there is a noticeable scarcity of practical soil examples to demonstrate the prediction uncertainty for the benefit of forest managers. In this study, following a digital soil mapping (DSM) approach, a Quantile Regression Forest (QRF) model was developed to generate high-resolution maps and their uncertainty regarding the texture, SoD, and SOM, which were expressed as standard deviation (Sd) values. The results showed that the SOM (R² = 0.61, RMSE = 2.03% and with an average Sd = 50%), SoD (R² = 0.74 and RMSE = 19.4 cm), clay (R² = 0.63, RMSE = 10.5% and average Sd = 29%), silt (R² = 0.59, RMSE = 6.26% and average Sd = 33%), and sand content (R² = 0.55, RMSE = 9.49% and average Sd = 35%) were accurately estimated for forest plantations in central south Chile. A practical demonstration of precision fertilizer application, utilizing the predictive distribution of SOM, effectively showcased how uncertainty in soil attributes can be leveraged to benefit forest managers. This approach holds potential for optimizing resource allocation and maximizing economic benefits.

1. Introduction

Environmental characteristics and soil site conditions have a significant impact on forest growth and stand development [1], and as a result, understanding them is critical for forecasting planting limits on specific forest species and their productivity [2]. Soils, in particular, play an important role in regulating, supporting, and provisioning ecosystem services, and data on soil properties represent critical information for forest planning and management schemes [3]. Key soil properties such as the texture and organic matter content are essential to estimate site productivity, which is defined as a quantitative estimate of a site’s potential to produce a volume of trees in a given time [4].

Soil texture has shown to be strongly related to the movement, retention, capacity, and availability of nutrients and water content, as well as the ease with which plant roots may penetrate the ground and absorb water [5]. Previous research on forest growth has observed that soil texture is one of the most important properties for evaluating soil compaction recovery to guide future planting procedures [6]. For example, Ref. [7] found a strong correlation (R² = 0.84) between the soil texture content and soil density. Soil organic matter (SOM) is an important chemical property for evaluating forest site fertility because it has a large influence on the soil cation exchange capacity [8], which is a vital factor for nutrient supply to plants [9]. Previous research found that increasing the SOM by 1% raised the site index (the height of dominant trees per stand in a target year) by approximately 20% in Pinus banksiana plantations and by 7% in Picea glauca plantations [10]. Additionally, soil depth (SoD), described as the depth of the soil profile from the top surface to the bedrock or root barriers [11], is also correlated to nutrient capacity and the plant’s available water content, and it controls biological activity [12]. This soil property has been linked to site index prediction in Pinus plantations [13] as well as overall productivity in forest plantations [14]. Changes in the SoD have also been linked to variations in the basal area within hardwood plantations. Specifically, the loss of soil thickness due to erosion is projected to decrease the basal area from an initial estimate of 18 to 26 m²/ha to a range of 8 to 21 m²/ha in future generations of forest plantations [15].

Understanding the interplay between physical and chemical soil properties that contribute to forest biomass production and carbon storage is vital, particularly in managed forest plantations where the goal is to maximize productivity over short rotation cycles. Enhancing the spatial characterization of soil properties not only facilitates an increased understanding of site productivity [4] but also optimizes fertilizer applications. Forests planted on sites with high nutrient contents tend to be less responsive to fertilizer applications, potentially eliminating the need for such interventions [16]. Ref. [17], for instance, observed a 400% increase in volume in Pinus ponderosa plantations due to fertilizer applications at sites with low concentrations of organic matter and nitrogen content. Consequently, identifying site fertility is critical for reducing fertilization management costs without significantly compromising potential growth. Furthermore, soil property data helps in optimizing heavy machinery allocation during timber harvesting and site preparation in plantations to minimize soil compaction.

Conventionally, the representation of soil properties and their relationships with environmental characteristics are traditionally obtained through field surveys, soil pit samples, and laboratory analyses [18]. Several approaches for interpolating the spatial information of soil properties, commonly employing geostatistical models, have emerged in recent decades based on field and laboratory measurements and spatially explicit environmental data [19]. The introduction of the SCORPAN theoretical model has proven to provide the best approximation for the development of digital soil mapping (DSM), improving the spatial representation of numerous soil properties. This theoretical model posits that soil properties are the result of the interactions between seven factors or variables that describe soil formation: S (previously measured soil information), C (climate), O (land cover), R (topography), P (parent material), A (soil age), and N (spatial position) [18]. This approach has been frequently used to predict and map soil properties such as depth gradients of soil organic carbon [9] and soil texture [20]. These soil maps are designed to provide decision-makers with accurate and precise information, which is necessary in forest plantation management to improve and enable site-specific management operations [21], mainly in relation to precise fertilization treatments based on granular assessments of soil nutrient deficiencies [22]. Nonetheless, it is also well recognized that the maps produced using DSM techniques are not error-free [23].

Uncertainty in digital soil mapping can originate from modeling errors and measurement inaccuracies associated with the input data [23]. Quantifying uncertainty is a crucial step because it assesses the reliability of the prediction data, typically expressed within a range of confidence intervals [24]. In the context of precision silviculture, possessing a comprehensive understanding of the confidence intervals for predicted variables, such as soil fertility, holds significant importance when making site-specific fertilization management decisions [25]. This knowledge provides valuable advantages by allowing resources to be directed towards areas based on the inherent variability in soil properties. However, the majority of digital soil mapping predictions tend to focus solely on the mean of the prediction distribution and often avoid estimating local uncertainty in soil predictions. This is due to inherent challenges, particularly with machine learning models, which are the preferred and most common approach for DSM [26]. For instance, the Random Forest (RF) method has gained widespread use in digital soil mapping, attributable to its ensemble of regression trees that yield more robust estimations with less biased internal error estimates [27]. Nevertheless, this approach only retains the mean of the prediction observations while disregarding other valuable information [28]. Other statistical models, such as the Bayesian Maximum Entropy (BME) model for spatial prediction, address the integration of data with uncertainty into the modeling process, aiming to enhance their predictive capabilities compared with traditional estimation methods [29]. However, this is normally challenged by computational complexity, sample size limitations [30], uncertainty in interpretability, and the complexity of parameter estimation [31].

The Quantile Regression Forest (QRF) [32] approach is a tree-based ensemble method which has the advantage of allowing the measurement of prediction uncertainties for each soil property as well as the depiction of probability distributions of dependent environmental variables [28]. A QRF, akin to an RF, offers valuable information regarding both the median and the distribution of the target variable. The principal difference lies in the treatment of observations within each node and tree: while an RF retains only the mean of the observations, thereby discarding additional data, a QRF preserves the values of all observations [32]. In recent years, QRFs have been gaining popularity in soil investigations, providing accurate estimates of the SOM [23,33,34], clay content, and other soil parameters [28,35], including in-depth 3D representations of the SOM, pH, and clay content, among others [36]. While most studies have centered on comparing the QRF method with other machine learning algorithms concerning their predictive prowess—for example, for soil organic carbon [37] and soil organic matter [28,34]—with favorable results, there remains a gap in terms of its use for management decisions in the soil domain. The application of uncertainty for management is undoubtedly beneficial for decision making. Still, recent research lacks practical examples on harnessing this uncertainty for the benefit of forest managers.

Recognizing the significant gap in current research, this study introduces an innovative approach to soil science by developing probabilistic maps to aid forest management decisions. The ability to visualize a range of possible soil conditions across a given area presents a substantial advancement over conventional methods, which typically rely on less descriptive, average-based data. This probabilistic approach becomes essential for making informed, data-driven decisions crucial for sustainable forest management. By focusing on these maps, this study aims to enhance operational strategies and decision-making processes in forestry. The purpose of this study therefore is to evaluate the spatial uncertainty distribution for soil depth, texture, and organic matter, with the intention of applying these findings to forest management operations at a 10 m spatial resolution. For this, we utilized the Quantile Regression Forest (QRF) model approach. To do so, we investigated (1) the uncertainty of soil property mapping products, (2) elaborating a 3D map for the texture and SOM based on the SoD, and (3) practical management application examples that leverage fine resolution and its associated prediction distribution.

2. Study Area

The study area was located at a specific site in central south Chile, in the Región del Maule (35°14′ S, 73°20′ W). The diverse terrain of this region comprises the coastal Andes ranges, the central valley, and the Andes foothills. Alfisol soils, found along the coast, are described as highly fertile with high concentrations of aluminum (Al) and iron (Fe), and rich in clay content [38]. Ultisols are present on the Andes’ coastal range and inceptisols occur in the valley [39] (Figure 1). Ultisols have a kandic or argillic horizon and few basic cations that have formed under forest vegetation in humid climates [40]. Inceptisols are soils with minimal horizon development, with some evidence of clay minerals, metal oxides, or humus accumulating in layers, but not enough to classify the soil into an order defined by characteristic surfaces [41]. The parent material in the study area varies from marine sediments at the coast, to metamorphic and granitic sediments in the valley. The climate is rainy and temperate, with the annual precipitation varying widely from 1219 mm along the coast to 2835 mm along the Andes coastal range, showing dry periods in the summer and wetter periods in the rest of the year. The elevation on the study area ranges from sea level (~1 m) to 1280 m.a.s.l. A land-use map for the area is illustrated in the Appendix A section (Figure A1).

3. Materials

3.1. LiDAR

Airborne LiDAR technology, also known as airborne laser scanning (ALS), was used to collect data over 160,000 ha (Figure 1), spanning over a continuous region of forest plantations. Data acquisition took place between February and October of 2020–2021 following the specifications shown in

Table 1. Airborne laser scanning (ALS) data acquisition parameters.

Acquisition Parameter	Value
Sensor	Optech Galaxy Prime (Teledyne Optech, Vaughan, Ontario, Canada).
Utilized plane	Tecnam P2006
Flying height	3000 m AGL
Average flying speed (knots)	115
Pulse repetition frequency (kHz)	700
Scan angle	26 deg
Returns recorded	Up to 5
Overlap	60%
Average overall point density	29.2 points/m2
Average pulse density	20.8 pulses/m2

.

3.2. Soil Pit and Auger Data

Within the ALS survey area, a soil profile legacy database collected by Forestal Arauco was used in this study, comprising 654 soil pits and 1442 soil depth samples obtained utilizing an auger in bore holes up to 4.1 m deep (auger length), with their spatial location recorded using a Garmin Handheld GPSMAP 64 2.6″ GPS (Garmin Ltd., Olathe, Kansas, USA). Data for all soil profiles were collected just after harvesting between 1994 and 2018 and were distributed across Pinus radiata plantations.

Soil pits were 150 cm deep × 150 cm wide and their profile properties were evaluated using the recommendations provided in [17]: (i) horizon nomenclature, including master horizons and other modifiers, as well as horizon thickness (in cm); (ii) soil matrix color in the moist state using the Munsell notation; (iii) texture class determined using the field hand test; (iv) carbonates determined using the effervescence field test; and (v) stoniness in vol. %.

Soil pit samples were analyzed in the laboratory to obtain sand, clay, and silt content measurements, as well as SOM, determined using wet oxidation throughout the entire soil pit profile and horizon thickness (cm). Soil depth information was based on 2096 observations, which included both soil pits and auger samples.

Table 2. Soil information. Values shown represent the number of observations (N) and the mean, standard deviation, and minimum and maximum values.

Soil Property	N	Mean	Standard Deviation	Min	Max
SoD (cm)	2096	158.7	65.6	30	420
Silt%	654	26.1	9.25	6	71
Clay%	654	41.8	17.3	11	87
Sand%	654	32.1	12.9	1	64
SOM%	654	6.7	3.2	0.3	18.2

contains a summary of all of the information for SoD, texture, and SOM.

3.3. Climate

Long-term monthly temperature (maximum and minimum) and rainfall data from 1990 to 2020 were obtained at 500 m resolution from CR2 (Center for Climate and Resilience Research) [42], available online. This dataset encompasses the continental region of Chile on a consistent 0.05-degree latitude–longitude grid. It was developed using statistical models that calibrate various climatic variables against rigorously controlled observational data, including atmospheric variables from weather stations, topographical details, and land surface temperature data derived from the MODIS satellite sensor.

3.4. Existing Soil Information

The Chilean Natural Resources Information Center (CIREN) provided us with vector information on the soil morphological properties and parent material, available online [39], including soil class data following the USDA Soil Classification System at order, suborder, great-group, subgroup, family, and series levels.

3.5. Forest Cover

Landsat 8 OLI remote sensing imagery that covered the study area was acquired for the period from 2013 to 2022, ensuring a maximum cloud cover of no more than 20%. These images provided observations at 16-day intervals with a moderate spatial resolution of 30 m. They served as proxies for land-cover representation, and further details are discussed in Section 4.

4. Methodology

4.1. Digital Elevation Model

The raw ALS data were processed using conventional routines to build a digital elevation model (DEM), which included tiling, filtering, and ground classification at a 10 m spatial resolution. For processing, the LAStools software package (version 211206) was employed [43]. The lasground algorithm was used to classify the ground data (with default parameters), and then blast2dem was used to create the DEM.

4.2. Modeling Soil Properties

The SCORPAN approach was used to model the SoD, SOM, and soil texture. The input variables for the SCORPAN model encompassed all of the aforementioned soil properties. For our research, we chose to produce a 10 m spatial resolution map for DSM. This decision was primarily driven by the increasing demand for site-specific precision in silviculture management and precision fertilization treatments within forest stands based on a granular assessment of the soil nutrient deficiencies. According to [44], fast-growing trees in plantation environments have a root lateral extension of 1.5 to 2.5 times the tree height, ranging from 10 m and up, depending on their age, for which a 10 m resolution map could account for individual tree interactions with chemical and physical soil properties affecting growth. An overview of the approach is showed in Figure 2.

First, a set of input variables (environmental covariates) related to soil-forming factors were produced using the SCORPAN approach. Second, a variable selection method, specifically Recursive Feature Elimination, was used to determine the best variables for each soil attribute. Third, Quantile Regression Forest (QRF) [32] models were employed for digital soil mapping. Data were split into training (80%) and testing (20%) datasets, and their spatial distribution is illustrated in Figure 1. Models were assessed using coefficient of determination (R²), root mean square error (RMSE), and mean absolute percent error (MAPE) values. In the fourth step, we derived a percentile distribution, focusing on the median—which offers more reliable predictions than the mean for soil attributes with outliers or skewed distributions—and assessed the uncertainty of each predicted soil attribute. In addition, by utilizing the entire range of the distribution of SOM, we informed the creation of a probabilistic map tailored for precision management applications. Further details are provided in Section 4.5.

For the soil depth data, an extra step was required due to the unbalanced distribution of the data (60% of observations were above 180 cm). First, to prevent the regression model from forecasting values predominantly over the class with the most data, the soil depth information was pre-classified using an RF classification model into either ‘above 180 cm’ or ‘below 180 cm’. The model was then validated with a confusion matrix using the testing dataset (above 180 cm only). The value of 180 was assigned for the SoD in pixels so that the model could predict the class ‘above 180 cm’. Second, a QRF model was developed for the subset of the data corresponding to soil depths below 180 cm. The final soil depth prediction was an ensemble of both classification and regression models, with the regression output being applied to areas classified as less than 180 cm deep.

4.3. Input Environmental Covariates for DSM

4.3.1. Topographic Variables

Topographic attributes are important variables for soil formation [18] as they determine the pathways of surface water movement across a watershed and therefore affect watershed hydrologic responses to rainfall, as well as soil properties such as the organic matter decomposition rate and soil texture [45,46]. Primary topographic variables can be computed directly from the DEM [47]. We applied the Automated Geoscientific Analysis (SAGA) [48] approach to obtain nineteen primary topographic variables affecting soil formation properties (

Table 3. List of topographic input variables.

Code	Description
DEM	Digital elevation model
Aspect	Aspect degree (%)
CNBL	Channel network base level (m.a.s.l)
CND	Channel network distance
CI	Convergence index
DiffI	Diffuse insolation
DirI	Direct insolation
LS_factor	Slope length and steepness factor
MRRTF	Multiresolution Index of Ridge-Top Flatness
MRBVF	Multiresolution Index of Valley-Bottom Flatness
PC	Plan curvature
ProfC	Profile curvature
Slope	Slope degree
TanC	Tangential curvature
TSC	Terrain surface convexity
TWI	Topographic wetness index
TC	Total catchment area
TIns	Total insolation
ValDepth	Valley depth

). All of these variables were derived directly from the DEM at a 10 m resolution.

4.3.2. Forest Cover

Previous studies have successfully utilized satellite information and satellite indices as proxies to represent the land cover. Examples include the use of GlobeLand30 data, acquired from Landsat TM and ETM+ sensors [33], and NDVI data from Landsat 8 [49] to predict soil organic carbon. According to [50], maximum-value vegetation indices can capture the dynamics of green vegetation while reducing typical issues such as cloud contamination, surface directional reflectance, atmospheric attenuation, and view and lighting geometry. To reflect historical forest cover for the SCORPAN vegetation variables, two vegetation indices—the Enhanced Vegetation Index (EVI) and the Normalized Difference Vegetation index (NDVI)—were computed using Landsat 8 OLI at a 30 m resolution using Google Earth Engine. For this study, the EVI and NDVI were calculated from 2013 to 2022; to minimize the effect of clouds or the influence of atmospheric constituents on these vegetation indices, the maximum value per year was chosen to reflect the yearly NDVI and EVI. The final NDVI and EVI values were calculated as the 10-year average maximum values and then resampled to 10 m using the bilinear interpolation method.

4.3.3. Climate Variables

Climate variables are useful in forecasting soil properties and have been applied to digital soil mapping [51]. Previous studies have used kriging with external drift (KED) in order to interpolate and downscale temperature data using elevation as an external drift, improving the final forecast over kriging based solely on spatial information [52,53]. KED is a type of interpolation technique that combines spatial information from the data as related to an external drift defined by an auxiliary variable [54]. To verify that the climatic variables were integrated with the other SCORPAN variables (topography, parental material, and satellite vegetation indices), they were resampled to 10 m. For this, we applied the KED approach using the association between each monthly climatic variable (rainfall, minimum temperature, and maximum temperature described in the data) and the DEM as the external drift. This process was implemented using 10-fold cross-validation with the covariance function automatically chosen. The covariance function was selected automatically from either a Spherical, Exponential, Gaussian, or Matérn function via minimizing the prediction RMSE and coefficient of correlation.

These variables were then used to create 19 bioclimatic variables, calculated as a function of the monthly minimum and maximum temperatures and precipitation (mm) and elaborated with the KED approach (variables listed in

Table A1. List of environmental input raster variables.

Code	Category	Description
biovar.1	Climate	bio1 = Mean annual temperature (°C)
biovar.2	Climate	bio2 = Mean diurnal range (mean of max temp - min temp) (°C)
biovar.3	Climate	bio3 = Isothermality (bio2/bio7) (× 100) (%)
biovar.4	Climate	bio4 = Temperature seasonality (standard deviation × 100) (%)
biovar.5	Climate	bio5 = Max temperature of warmest month (°C)
biovar.6	Climate	bio6 = Min temperature of coldest month (°C)
biovar.7	Climate	bio7 = Temperature annual range (bio5-bio6) (°C)
biovar.8	Climate	bio8 = Mean temperature of the wettest quarter (°C)
biovar.9	Climate	bio9 = Mean temperature of driest quarter (°C)
biovar.10	Climate	bio10 = Mean temperature of warmest quarter (°C)
biovar.11	Climate	bio11 = Mean temperature of coldest quarter (°C)
biovar.12	Climate	bio12 = Total (annual) precipitation (mm)
biovar.13	Climate	bio13 = Precipitation of wettest month (mm)
biovar.14	Climate	bio14 = Precipitation of driest month (mm)
biovar.15	Climate	bio15 = Precipitation seasonality (coefficient of variation) (%)
biovar.16	Climate	bio16 = Precipitation of wettest quarter (mm)
biovar.17	Climate	bio17 = Precipitation of driest quarter (mm)
biovar.18	Climate	bio18 = Precipitation of warmest quarter (mm)
biovar.19	Climate	bio19= Precipitation of coldest quarter (mm)
DEM	Topography	Digital elevation model
Aspect	Topography	Aspect Degree (%)
CNBL	Topography	Channel Network Base Level (m.a.s.l)
CND	Topography	Channel Network Distance
CI	Topography	Convergence Index
DiffI	Topography	Diffuse Insolation
DirI	Topography	Direct Insolation
LS_factor	Topography	Slope Length and Steepness Factor
MRRTF	Topography	Multiresolution Ridge Top Flatness
MRBVF	Topography	Multiresolution Index of Valley Bottom Flatness
PC	Topography	Plan curvature
ProfC	Topography	Profile curvature
Slope	Topography	Slope Degree (%)
TanC	Topography	Tangential curvature
TSC	Topography	Terrain Surface Convexity
TWI	Topography	Topographic Wetness Index
TC	Topography	Total catchment area
TIns	Topography	Total Insolation
ValDepth	Topography	Valley Depth
NDVI	Vegetation	Normalized Difference Vegetation index
EVI	Vegetation	Enhanced Vegetation Index
PRM	Soil Morphology	Parent rock material
SC	Soil Morphology	Soil Class

), using the climate-based models provided by the United States Geological Survey (USGS).

4.3.4. Parent Material and Other Soil Information

Parent material and lithology information are considered to be fundamental variables for digital soil mapping [18]. Parent material has been shown to have a considerable influence on soil properties such as texture, color, pH, and mineral composition [55]. The soil class information and parent material, available in vector format, were rasterized to a 10 m resolution.

4.4. Variable Selection

According to [56], a large number of independent variables in machine learning models can lead to poor prediction performance and overfitting. Recursive Feature Elimination (RFE) is a feature selection method that tries to find the best feature subset based on the learned model and classification accuracy by removing features that have the least effect on training errors [57]. RFE is essentially a backward predictor selection method that selects features by recursively considering smaller and smaller subsets of features, then builds a model with the remaining attributes and calculates the model’s accuracy using internal cross-validation [58]. This step is critical for avoiding overfitting issues caused by a high-dimensional dataset with an excessive number of features [59]. The RFE pre-processing method was used to extract a subset of relevant variables from the 44 covariates available. The top variables were selected based on a measure of the percent increase in mean squared error. This score indicates how much each predictor variable contributes to the accuracy of the model. We used 5 folds and 5 repeats while running the RFE.

4.5. Quantile Regression Forest

As previously mentioned, a QRF not only estimates the conditional mean but also retains information on other quantiles of the response variable, which can be used to generate the prediction distribution. The QRF framework employs the power of Random Forests by building multiple decision trees, which then aggregate the predicted quantiles from each tree, offering a comprehensive distributional forecast rather than a single point estimate [28]. This method proves especially valuable when the interest lies in understanding the relationship between a set of predictor variables and specific percentiles of the response variable [32]. Hereafter, these will be referred to as percentiles for clarity. For instance, a prediction at the 50th percentile corresponds to the median of the dependent variable. Similarly, predictions at the 25th and 75th percentiles provide estimates of the lower and upper quartiles, respectively, thus providing a more detailed perspective on the range of potential outcomes. In the context of soil analysis, this allows us to observe the variability in predictions of soil properties, thereby aiding in more targeted soil management strategies.

The QRF technique was used to develop a regression model for predicting the soil texture, SOM, and SoD under 180 cm.

4.5.1. Uncertainty, Soil Property Predictions, and Forest Management Practical Example

For each soil property, the median (50th percentile) and standard deviation (SD) (representing uncertainty) were determined. Sd is determined based on the entire prediction distribution per pixel. Additionally, for the four selected sites across the study area (see Figure 1), various percentiles were calculated to understand the conditional distribution and variability in the response outcome. The percentiles selected for this purpose were the 10th, 25th, 50th, 75th, and 90th percentiles. These sites were selected for their variability in terms of DEM at the study site, located at 227, 8, 942, and 817 m above sea level for sites 1, 2, 3, and 4, respectively, and covered different types of soil orders.

Subsequently, R² and RMSE values were calculated using the testing dataset, based on the median.

To incorporate predictive uncertainty and the entire distribution of soil properties for forest management applications, we constructed a practical example. In this example, we used predictions of SOM to identify sites with varying fertility levels. We established a threshold of 5% SOM, directing the allocation of fertilizers to sites where fertility levels were at or below this threshold. This 5% SOM threshold was selected arbitrarily to suit the needs of our example; however, this value can be adjusted based on fertility research that examines the relationship between SOM and forest yield, thereby establishing a more appropriate threshold for fertilizer application. Using the QRF, we modeled the SOM content across a range of quantiles, from the 1st to the 99th percentile (0.01 to 0.99). This method allowed us to estimate the conditional distribution of SOM content given the selected environmental variables (RFE). Predictions were generated for each pixel in the raster dataset, with the model outputting the predicted SOM content at specified quantiles. We specifically targeted the percentile that most closely approached the 5% SOM threshold. The results were stored spatially, enabling us to visualize and assess areas likely to meet or exceed this SOM content threshold. To represent the probability of having values equal to or above the target threshold, we used the following equation:

$$P=1-argpmin\mid Qp\left(Y\mid X\right)-yt\mid$$

(1)

where Y denotes the SOM content, X represents the set of the selected variables (post RFE for SOM), Qp(Y∣X) is the pth percentile of the conditional distribution of Y given X, yt is the target SOM content (5%), and P is the probability of having pixel values above or equal to the established SOM threshold.

We then set an 80% probability threshold to guide fertilizer application decisions. This level offers a pragmatic balance between certainty and practicality in decision making. Setting the threshold at 80% establishes a high level of confidence that the soil genuinely meets the required SOM content before applying fertilizers. Additionally, an 80% threshold minimizes the risk of under-fertilizing, which can occur if the threshold is set too high (e.g., 95%), potentially leading to suboptimal forest yields and economic losses.

4.5.2. Three-Dimensional Soil Property Predictions

To obtain the prediction values at different depths (3D representation) for the SOM, clay, silt, and sand content, we used depth information from soil pit chemical analyses at different horizon thicknesses (in cm) as the dependent variables in the QRF model, and the depth along with the value of the selected environmental covariates as independent variables, as used in [36]. For this case, the average depth value assigned at the center of the observed depth interval per soil-pit thickness was used. This model can be generalized as follows:

Sa_(x,y) = f(depth_(x,y), topography_(x,y), forest land cover_(x,y), climate_(x,y), parent material_(x,y), soil_(x,y))

(2)

where Sa is the soil property of interest, depth is the depth at which this property was measured, and topography, forest land cover, climate, parent material, and soil are the selected environmental variables (code available on [60]).

These models were then used to predict the soil property over the spatial distribution of the environmental variables and values of depth between 0 and 180, every 10 cm. The prediction maps for the clay, silt, and sand content were used to classify soil texture according to the USDA textural soil classification [61]. Here, the soil texture class is derived based on the different proportions of sand, silt, and clay. For instance, an equal proportion of sand, silt, and clay results in a loam soil class, while a higher proportion of clay (30–45%) compared to sand (20–45%) and silt (20–45%) will result in a clay loam classification.

4.6. Software Implementation

R (version 4.3.3) was used for all simulations and validations for producing climatic variables, regression models, and classification models. The 10-fold cross-validation for downscaling the temperature (max and min) and precipitation data using KED was performed using autoKrige.cv (Version: 1.1-9) [62] from the ‘automap’ package (Version 1.1-9) [63]. The biovars function in the ‘dismo’ (Version 1.3-14) [64] package was used to obtain 19 bioclimatic variables based on the monthly minimum and maximum temperature and precipitation (mm). The QRF was implemented via the quantregForest R-package [65]. The RF classification model was implemented using the caret package (Version 6.0-94) [66], as well as tuning the hyperparameters, including the number of randomly selected predictors, the minimum node size, and the splitting rule. Soil texture classification was implemented using the soiltexture package (Version: 1.5.3) and the USDA.TT classification [67].

5. Results

5.1. Climate Variables

The cross-validation results demonstrated that KED downscaling provided accurate estimates of the climatic variables. For all months, the RMSE difference between the original and downscaled resolution was low, ranging from 0.04 to 0.62 mm for precipitation, from 0.04 to 0.09 °C for the minimum temperature, and from 0.08 to 0.12 °C for the maximum temperature. Due to an increase in rainfall throughout the winter (May to August), there was a slight increase in error for precipitation during this time period, coming to an average of 0.44 mm. For all months and variables, an r value of 0.99 resulted in the cross-validation process.

5.2. Variable Selection

The RFE reduced the 44 available input variables to the 10 most important for every soil property. Predominantly, these variables were generally of a topographic nature (60%), followed by climatic variables (37%), and forest land-cover variables (3%). For the prediction of all properties (SoD, SOM%, clay%, silt%, sand%), the DEM and total annual precipitation (bioclimatic variable) were selected as the top variables. The channel network base level (CNBL) was the second most important topographic variable, influencing every soil property. Furthermore, the mean annual temperature was one of the top ten input variables for the SoD and SOM, while temperature seasonality affected the SOM, clay, silt, and sand content.

Table 4. Selected input variables for the SoD, SOM, clay content, silt content, and sand content predictions. The first section of this table contains climatic variables, followed by topographic variables, and, finally, remote sensing proxies of the forest and land cover. A more detailed description of each variable is given in Table A1.

Input Variable	SoD	SOM%	Clay%	Silt%	Sand%
Total precipitation (mm)	✓	✓	✓	✓	✓
Precipitation seasonality (%)	✓
Mean temperature (°C)	✓	✓
Mean diurnal range (°C)		✓
Temperature seasonality (%)		✓	✓	✓	✓
Precipitation of the wettest month (mm)			✓	✓	✓
Temperature annual range (°C)			✓	✓	✓
Channel network distance	✓		✓	✓
DEM	✓	✓	✓	✓	✓
Channel network base level (m.a.s.l)	✓	✓	✓		✓
Valley depth	✓		✓	✓	✓
Aspect	✓
Slope length and steepness factor	✓			✓
Terrain surface convexity	✓
Diffuse insolation		✓	✓
Slope		✓
Multiresolution Index of Valley-Bottom Flatness		✓		✓	✓
Multiresolution Index of Ridge-Top Flatness				✓
Total insolation			✓
EVI					✓
NDVI					✓

summarizes the 10 input variables selected for each soil property prediction.

5.3. Validation

5.3.1. Soil Depth Classification

The SoD classification model achieved an overall accuracy of 0.84, as evaluated using a confusion matrix, with a 95% confidence interval ranging from 78.99% to 87.46%. The matrix revealed 164 true positive cases of soil depths correctly predicted to be greater than 180 cm, and 100 true negative cases where soil depths were accurately identified as less than or equal to 180 cm. There were 36 commission errors and 16 omission errors, indicating instances of overestimation and underestimation, respectively (

Table 5. Confusion matrix for SoD classification.

Reference Prediction	Depths over 180 cm	Depths under 180 cm
Depth over 180 cm	164	36
Depth under 180 cm	16	100

). Additionally, the Kappa statistic, which measures the agreement between predictions and references corrected for chance agreement, was 0.66.

5.3.2. Soil Attributes

The results of the soil attribute modeling using the QRF are presented in

Table 6. Accuracy of the modeled soil properties.

Variable	R2	RMSE	MAPE
Using the testing dataset:
SoD	0.74	19.4	10.53
SOM%	0.61	2.03	41.18
Clay%	0.63	10.5	20.91
Silt%	0.59	6.26	20.73
Sand%	0.55	9.49	42
Using the training dataset:
SoD	0.86	10.4	7.6
SOM%	0.84	1.29	21.8
Clay%	0.78	8.75	16.9
Silt%	0.68	6.08	18.4
Sand%	0.73	8.21	40

, which includes both the training and testing sets for validating the accuracy of the predictions. The most accurate predictions using the testing dataset were for SoD (below 180 cm), with an R² of 0.74 and an RMSE of 19.4. In contrast, the sand predictions were the least accurate, exhibiting the lowest R² at 0.55 and a MAPE of 42. Other variables such as SOM, clay, and silt were modeled with R² values ranging from 0.59 to 0.61. However, the MAPE for SOM was 41.18, while for clay and silt, it fluctuated between 20.73 and 20.91. Predicted versus observed plots for SOM, clay, sand, silt, and SoD (below 180 cm) are illustrated in Appendix A.

The spatial representation of the SoD data is illustrated in Figure 3. This map combines the regression output applied to areas classified as less than 180 cm deep in the classification prediction map. Deep soils are located on the foothills of the Andes coastal range, whereas shallow soils (less than 180 cm deep) are found in areas with a slope steepness greater than 35° and channel network areas.

5.4. Mapping the Uncertainty and Soil Property Predictions

Figure 4 depicts the spatial representations of the SOM, clay, silt, and sand predictions. In the upper soil layer, there is a noticeably high content of SOM across the study area, with values peaking at 18.1%. Some pockets of land in the coastal range exhibit increased uncertainty (Figure 4B). A significant portion of the study area has a high clay content, reaching up to 79%, especially near the Andes foothills (in areas with ultisols) and within some parts of the valley (alfisols). However, there is a higher uncertainty associated with this soil property in the coast and along channel network pathways (Figure 4D). Silt is primarily concentrated in the northern region of the Andes foothills, while sand is more prevalent at higher altitudes. Across all soil properties, with the exception of silt, there is greater uncertainty along the channel network located within the valley.

Figure 1 displays four sites selected based on their variability within the study area. The distribution of these four sites is detailed in Figure 5, presenting the 10th, 25th, 50th, 75th, and 90th percentiles. From this, we can observe the variability in soil properties. Generally, sites 2 and 3 exhibit lower SOM levels compared to other areas. Meanwhile, sites 3 and 4 demonstrate more balanced concentrations of sand, silt, and clay.

Figure 5. Percentile distribution of SOM, clay, silt, and sand contents for the four sites depicted in Figure 1.

Figure 5. Percentile distribution of SOM, clay, silt, and sand contents for the four sites depicted in Figure 1.

In our practical example, we created a probabilistic map indicating areas with 5% SOM content, as illustrated in Figure 6A. This analysis facilitated the development of a probabilistic map based on the entire range of distribution for the SOM, which was used to identify areas of high or low fertility for targeted fertilizer application. Figure 6B highlights the designated zones for fertilization: regions with at least an 80% probability of surpassing 5% SOM content are colored green, while those with a 5% or lower probability are colored purple and marked for fertilizer application.

5.5. Three-Dimensional Soil Map

The QRF provided a 3D representation of the SOM and texture class (as a combination of clay, silt, and sand) predictions across different soil depth layers. Figure 7 displays this 3D visualization of the soil properties at a sample site selected for its topographic relief variations. Figure 8 illustrates the entire depth variation of the SOM, clay, silt, and sand contents in the study area by soil order, which aids in better illustrating depth changes. In Figure 7, the predicted SoD is used as a base layer to represent the soil thickness. The spatial information for the SOM demonstrates that as depth increases, the amount of organic content decreases, with the highest concentrations occurring only in the first 40 cm of soil depth. Figure 7B shows the soil texture classification based on different proportions of clay, silt, and sand. Within the study area, the soil texture class is predominantly clay (61.4%) and clay loam (28%). The observed soil classifications show only small variations at different depths. In Figure 8, the median values of clay, silt, and sand show minimal variation, consistent with the observations for the soil texture classes. Most notably, there is an increase in sand content beyond 70 cm in the inceptisol layer.

6. Discussion

This study presents a method for obtaining spatial predictions and their associated uncertainties for digital soil mapping. Additionally, it demonstrates how to integrate the distributions of these predictions of soil properties into forest management operations.

Our results show that the soil properties were well represented spatially when using the QRF. The chosen 10 m spatial resolution, selected to observe soil property changes within the forest stand, provided accurate results when compared to other studies on SoD prediction using a regression model (R² = 0.74, MAPE = 10.53%, and RMSE = 19.4 cm). Although SoD is a difficult soil property to predict, we obtained a significant improvement by considering all of the SCORPAN input variables when compared to other studies using only topographic variables [68], indicating an overall good performance in line with the results presented in [69].

In the validation analysis, the SOM map showed reliable results, with R² = 0.61, MAPE = 41.18%, and RMSE = 2.03%. When compared to previous studies, we can observe that the general level of validation accuracy for SOM predictions ranges between R² = 0.45 at 10 m using topographic attributes only [70], R² = 0.51 at 30 m [71], and R² = 0.53 using a QRF at 30 m resolution [34]. In our study, the observed standard deviation of the prediction distribution ranged from 1.7% to 7.7%. In most of the valley and the Andes foothills, the variability hovered at around 17% of the mean. However, in the Andes, it rose to approximately 50%. This trend can potentially be attributed to the fact that as topographic heterogeneity increases, soil properties vary significantly [72].

Soil texture also showed accurate results given the successful validation of the clay, silt, and sand contents. Clay had the higher accuracy, followed by silt and lastly by sand (Table 5), with mean standard deviations of 29%, 33%, and 35%, respectively. Similar results were reported by other studies [20,73,74], which account for their good prediction accuracy based on the strength of the used input variables of the SCORPAN approach, emphasizing the importance of integrating key soil formation variables for reliable predictions of soil texture.

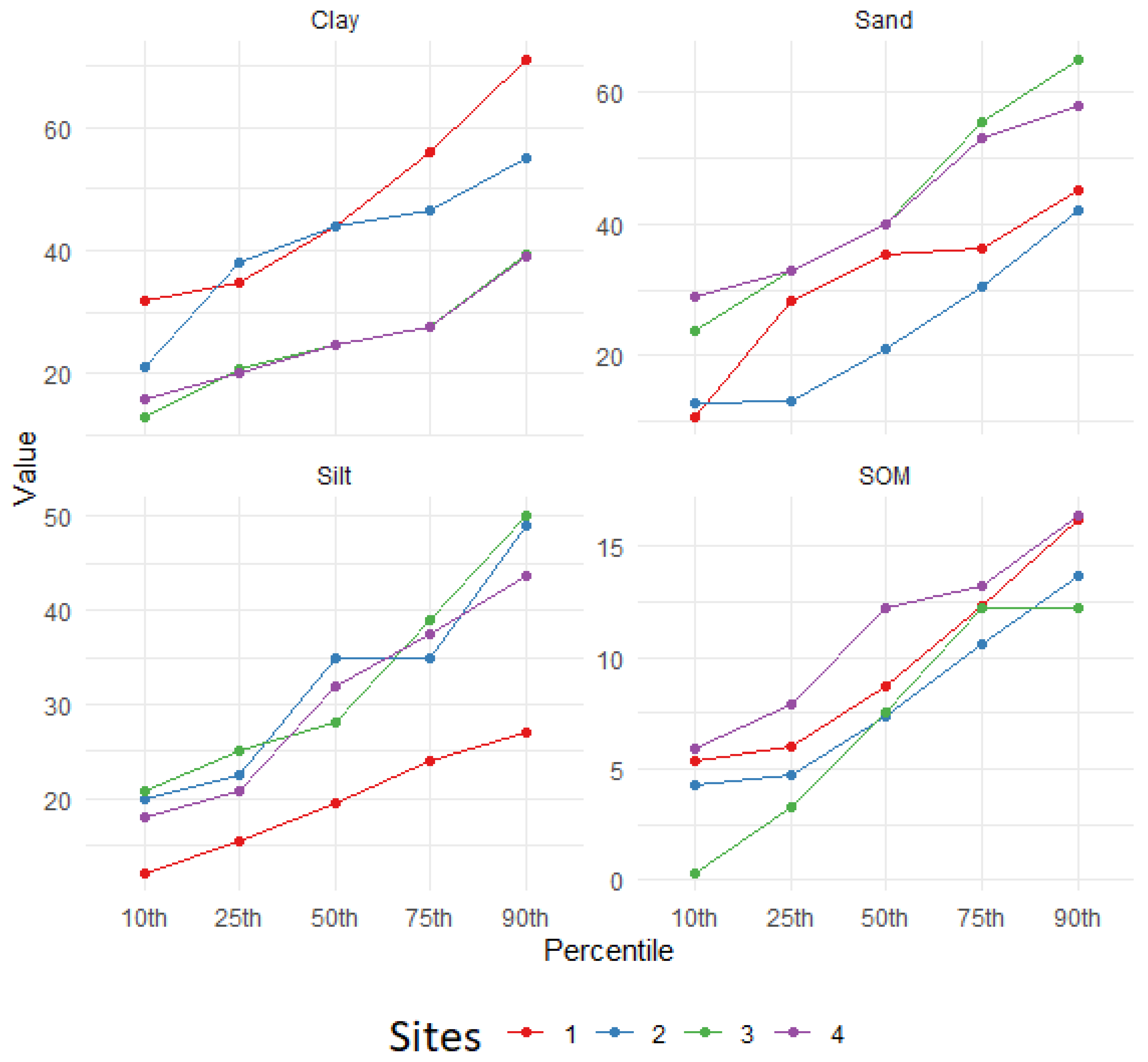
Observing the spatial distribution of standard deviation values and the spread of prediction distributions for the four selected sites depicted in Figure 1 and explained in Figure 5, it becomes apparent that there is significant variability in the prediction distributions across all predicted soil properties. This variability is particularly pronounced, as anticipated, on the foothills of the Andes coastal range, where the topography is highly heterogeneous and maximum variation occurs [75]. For example, the SOM ranges from 3.2% (25th percentile) to 12.2% (75th percentile). Surprisingly, even in the valley, where the topographic relief is relatively consistent, a notably variable prediction distribution of soil properties persists. Following the SOM example, it varies from 7.9% to 13.2% in the 25th and 75th percentiles, respectively. Capturing the spatial predictive distribution of soil properties is crucial to reducing uncertainty and enhancing the quality of digital soil mapping (DSM) products. As Ref. [25] noted, one direct application of soil prediction uncertainty is in optimizing soil sampling designs, with a focus on areas of high uncertainty. Furthermore, the use of prediction variability and the entire distribution of soil properties is also beneficial to managers in reducing uncertainty in forest growth responses to fertilizer application, as illustrated in the practical management application example. This phenomenon, where responses to fertilizer application are heightened in areas of low soil fertility, has been substantiated by previous research [16,17]. Relying solely on the mean for decision-supporting purposes, as exemplified in Figure 6, and using the same 5% SOM as a threshold to identify areas for fertilization, would imply that in 50% of cases, values will exceed the decided threshold. This translates to 50% of areas exhibiting a low response or no response to fertilizer application. As demonstrated in the example, utilizing the entire distribution range can ensure positive responses of forest growth to management applications, depending on the level of probability chosen for decisions (80% in our example), thereby minimizing resource allocation and maximizing the economic benefits.

As discussed in previous research [12], detecting the presence of shallow soils is crucial for soil protection management in forested areas. It is vital to understand the forest roots’ capacity to reach available nutrients and to enhance our knowledge of the plants’ available water content and the variation in nutrient availability at different soil depths for tree root uptake. As shown in Figure 7, the 3D map demonstrates a significant variation in SOM content at different depths. The decrease in SOM with increasing soil depths has been mentioned several times in the literature [76,77]. This occurs because SOM is produced near the surface due to superficial leaf decomposition in forested areas and fine-root decomposition in grasslands. This shift in distribution is also linked to varying microbial community structures at different soil depths, which influence the rate of organic matter decomposition [78]—a reduction rate that can be visualized with the methodology presented in this study. Although there is some variation in soil texture at different depths, it is not significant. Similar results found in [79] were explained by the soil’s age since most of the horizons were still forming, as may be the case in our study area. Furthermore, particularly around the coast, the soil is classified as clay through several depth levels, likely because they are on alfisols—classified by the USDA soil taxonomy as clay-enriched with a relatively high natural fertility [61].

Regarding the SCORPAN variables selected for this research, DEM has emerged as one of the top variables related to soil texture and depth. This correlation can primarily be attributed to its association with soil erosion and redistribution, as well as its impact on the SOM accumulation cycle [75]. Previous research has found that elevation, the topographic wetness index (TWI), plan curvature, the total catchment area, and the channel network base level are the key topography characteristics most closely connected to soil organic carbon concentration in flat-slope locations [80]. Furthermore, for hydrologic and geomorphic purposes, the Multiresolution Index of Ridge-Top Flatness (MRRTF), Multiresolution Index of Valley-Bottom Flatness (MRVBF), slope, and valley depth have shown strong links with sediment deposits and influence deposit depth [81]. As observed in [82], the distance to water channels provides essential information on sediment accumulation, altering the SOM content, SoD, and soil texture, which are also reflected in this study. Besides elevation, this variable has also been recognized as one of the most critical topographic parameters for the digital soil mapping of SOM [80]. According to the literature, one of the most important environmental variables influencing the rate of weathering and organic decomposition, which cause new layers of soil to accumulate at depth, is the mean annual temperature [83,84]. Furthermore, precipitation notably impacts hydrological processes such as surface runoff and groundwater flow, which are vital for organic matter decomposition rates and infiltration from the litter layer to mineral soil, as extensively reported [45,46]. This notion is corroborated in this study, wherein these two climatic variables are selected as some of the most significant predictors of among all of the predicted soil properties.

The most significant advantage of the proposed methodology is that it enables the prediction of accurate high-spatial-resolution maps of soil properties and their predictive distributions, based on soil formation factors (SCORPAN). The application of QRFs in DSM, as used in this study, demonstrates the utility of this methodology for the spatial interpolation of key soil properties and its uncertainty within the forest stand, which has been previously applied in SoilGrids250m [23]. As mentioned in previous research [28,35], the QRF model is a promising alternative for observing the probabilistic distribution of soil predictions, especially for precision silviculture tasks. Nonetheless, the primary advantage of using a QRF for high-resolution soil properties lies in its ability to capture variable distributions. This aspect is frequently overlooked in conventional soil prediction models and management applications.

Similar to previous soil property mapping efforts [85,86], spatial soil information has proven to be a valuable tool for enhancing our understanding of site productivity variations within forested areas, especially when utilizing the spatial resolution chosen for this study (10 m). This approach to digital soil property analysis, along with its associated uncertainties, enhances fertilizer prescription capabilities by identifying areas with fertility issues, thereby facilitating precision in fertilizer application during forest operations, as demonstrated in the example provided. Moreover, granulometric information at a fine spatial resolution using the QRF method, alongside SoD data, can be employed to improve assessments of water-holding capacity and soil fertility ratings. These enhancements are crucial for process-based models used in predicting forest growth, as well as for precision planning in timber harvesting and site preparation to mitigate soil compaction risks. Integrating predictive soil property distribution into decision management strategies can further contribute to reductions in fertilization costs and increases in productivity. This methodology holds promise for transferability, as it is applicable to various soil properties, soil-related management practices, and diverse locations or countries. Future research should use high-resolution soil property information and its predictive distribution combined with ALS individual tree metrics to develop tree growth models in order to better understand the effects of site productivity on growth.

7. Conclusions

Quantile Regression Forests have proven to be both accurate and reliable in predicting soil properties and their distribution, especially in digital soil mapping applications. The methodology showcases spatial precision, making it invaluable for site-specific precision in silviculture management and precision fertilization treatments within forest stands. Incorporating prediction distribution is vital, as it plays a crucial role in minimizing uncertainty in decision-supporting applications within forest management. This is particularly true for operations such as fertilizer application, road construction planning, and forest growth modeling, especially in the context of site-specific management.