High Average Current Electron Beam Generation Using RF Gated Thermionic Electron Gun
Abstract
1. Introduction
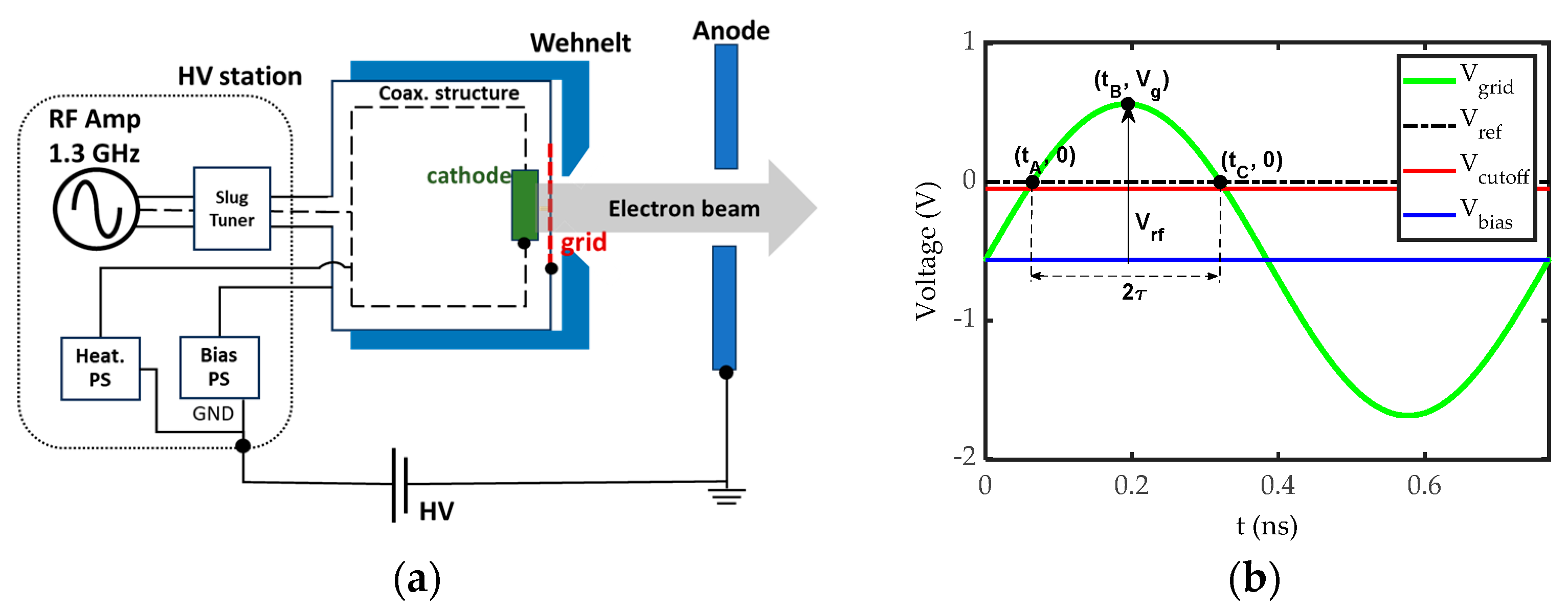
2. Thermionic Gridded Electron Gun
3. Theoretical Model and Simulation Setup for RF Gating
3.1. RF Gating Mechanism
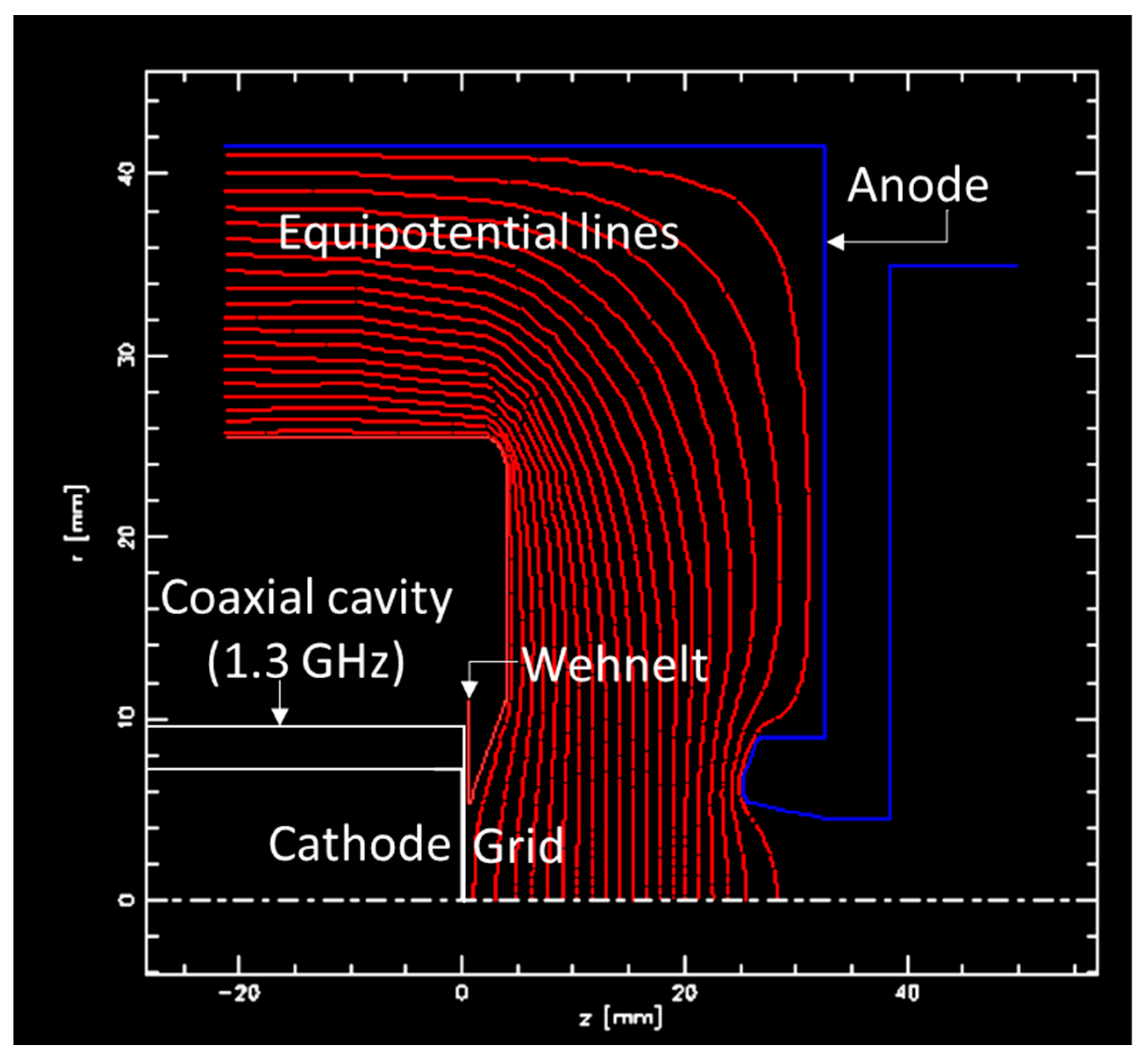
3.2. Simulation Setup for RF Gating in KUCODE
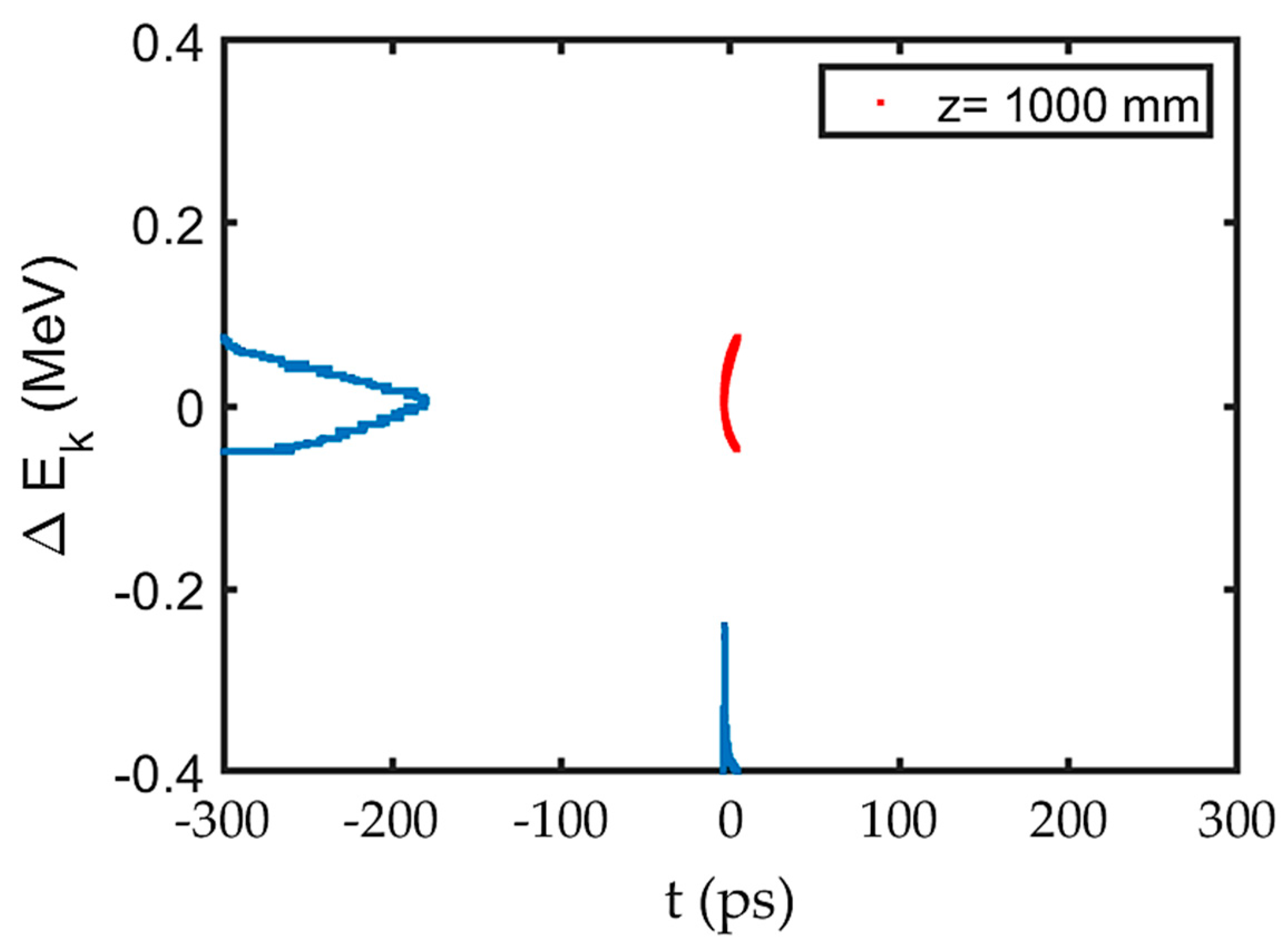
4. Results and Discussion
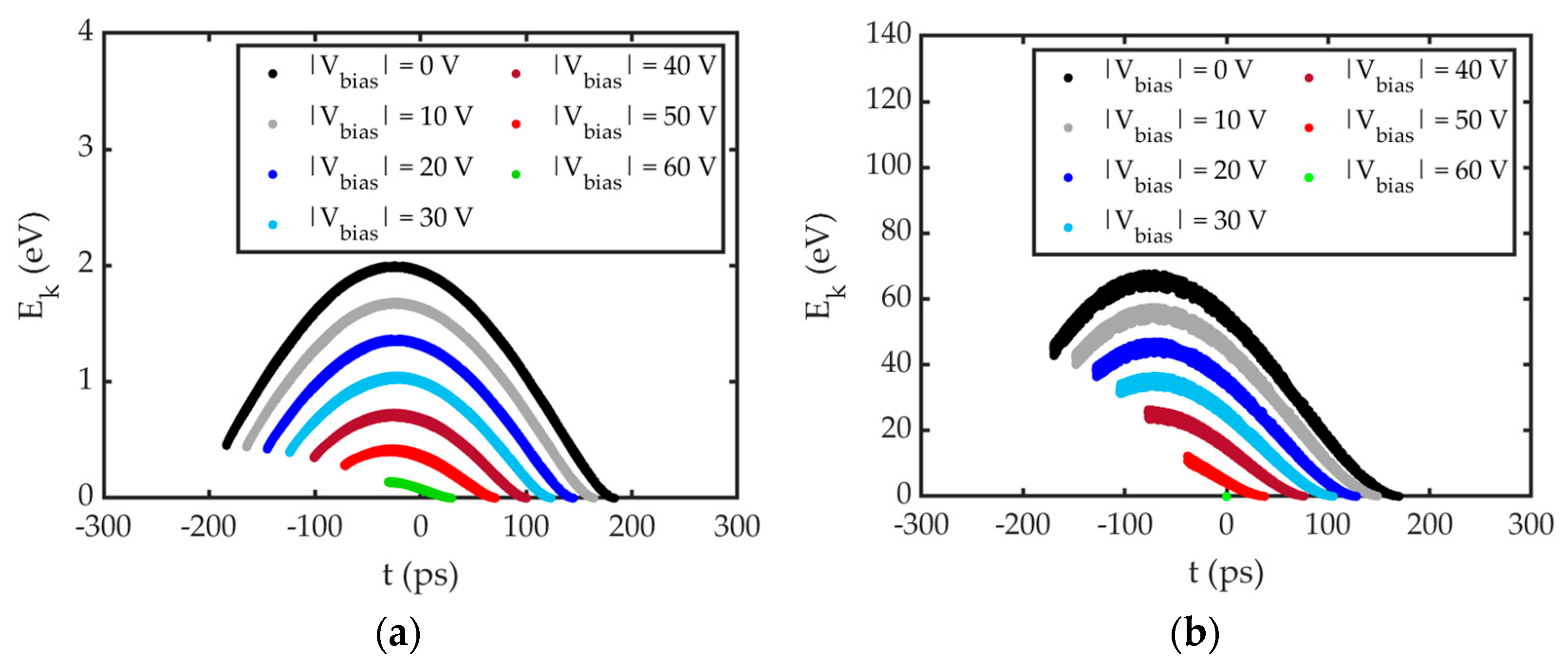
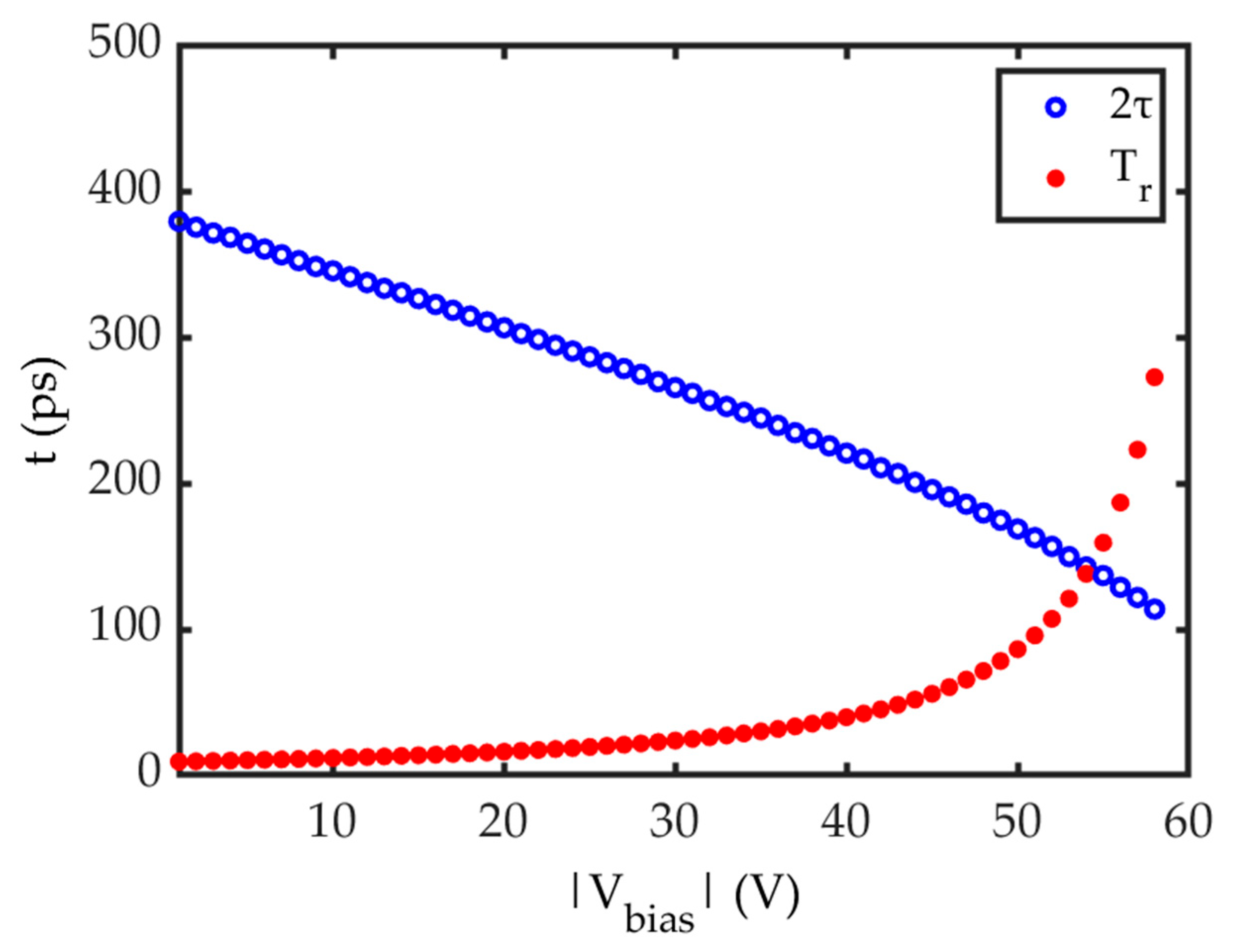
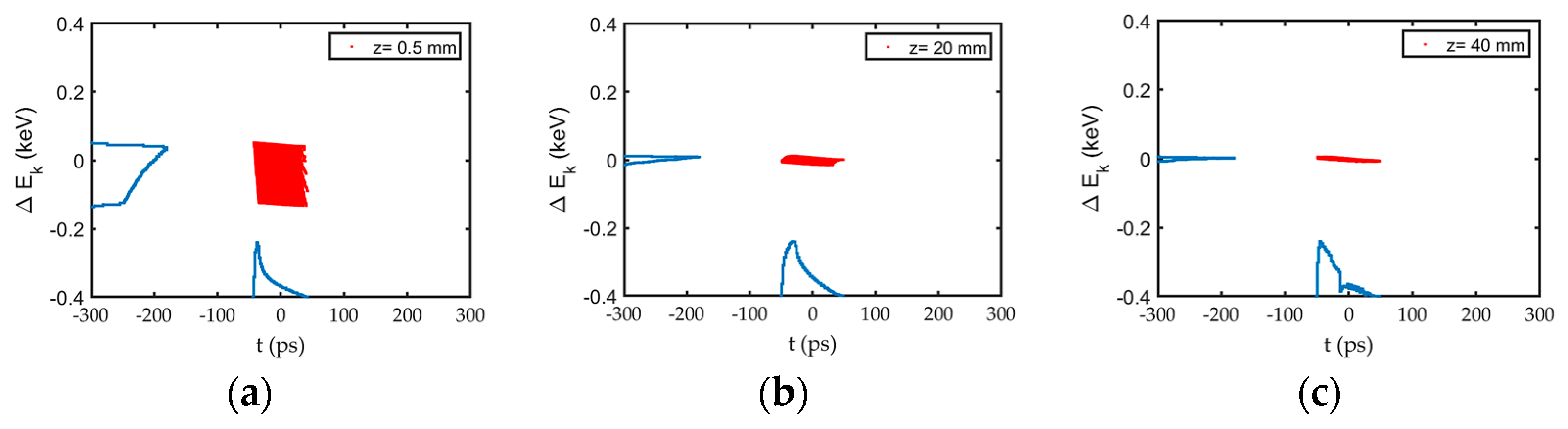
4.1. Performance of the RF Gated Gun (Cathode—Grid Space)
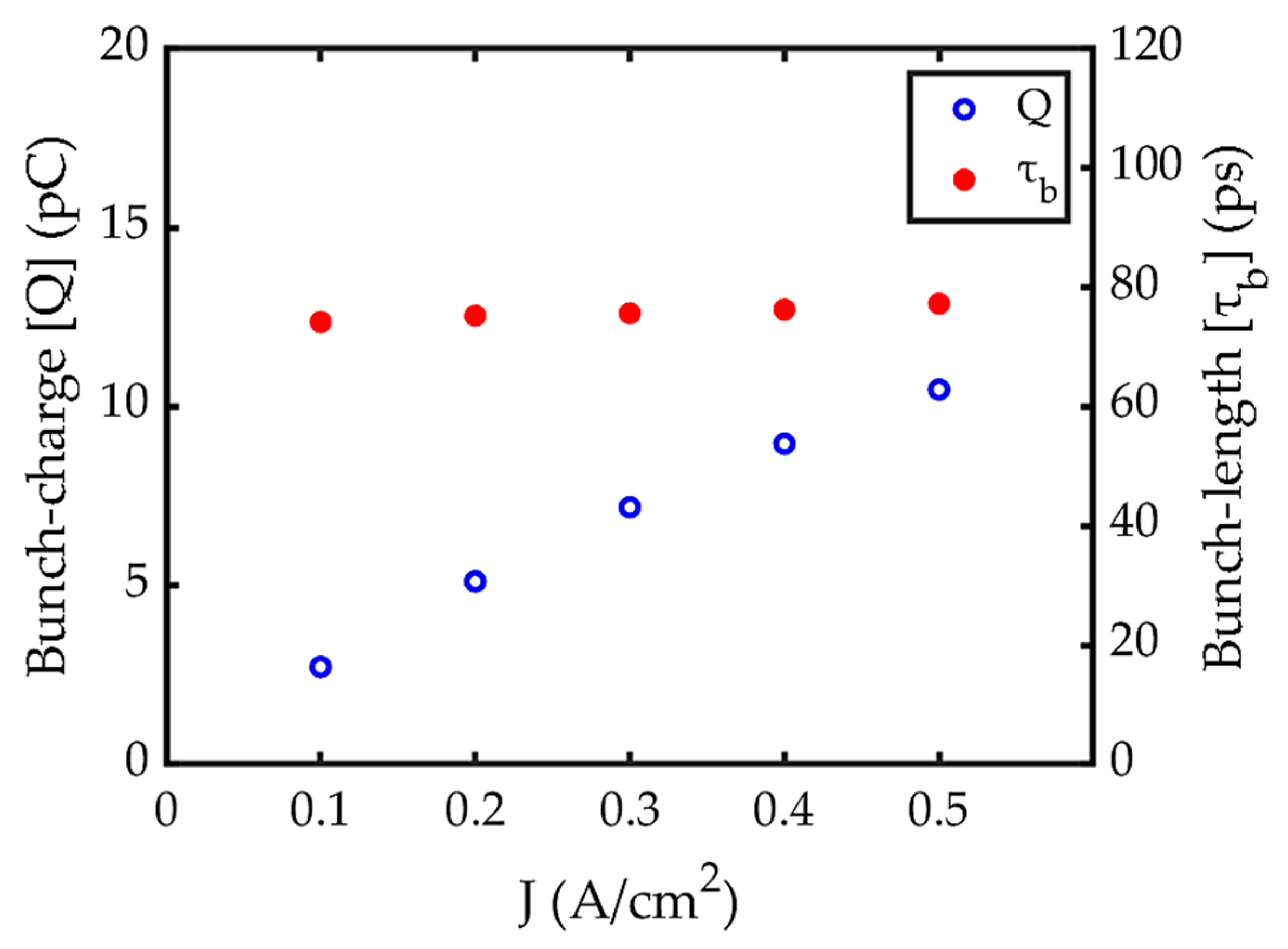
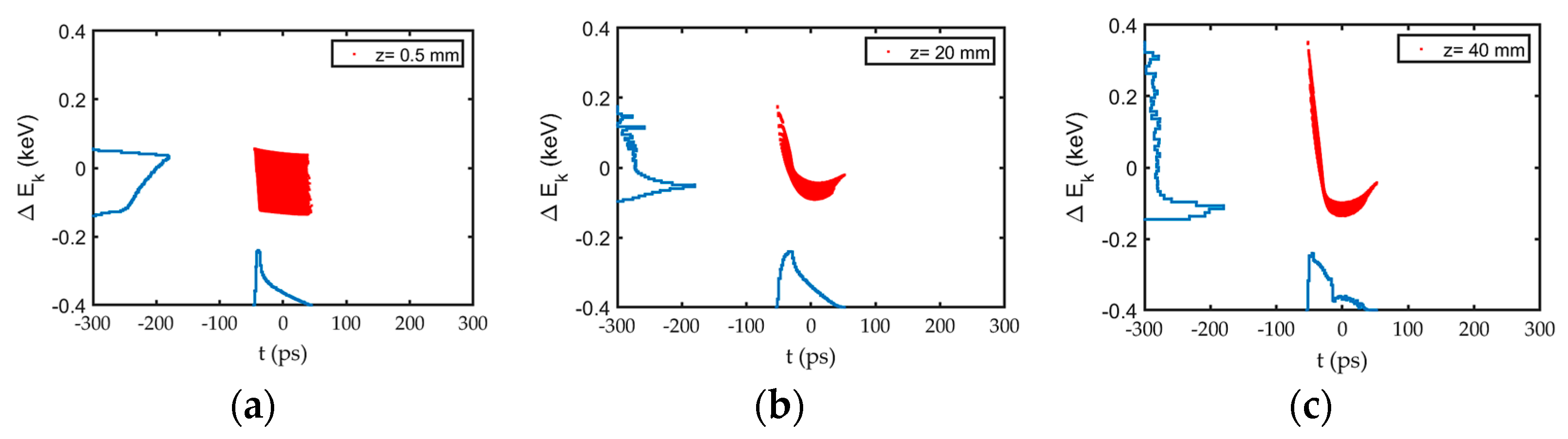
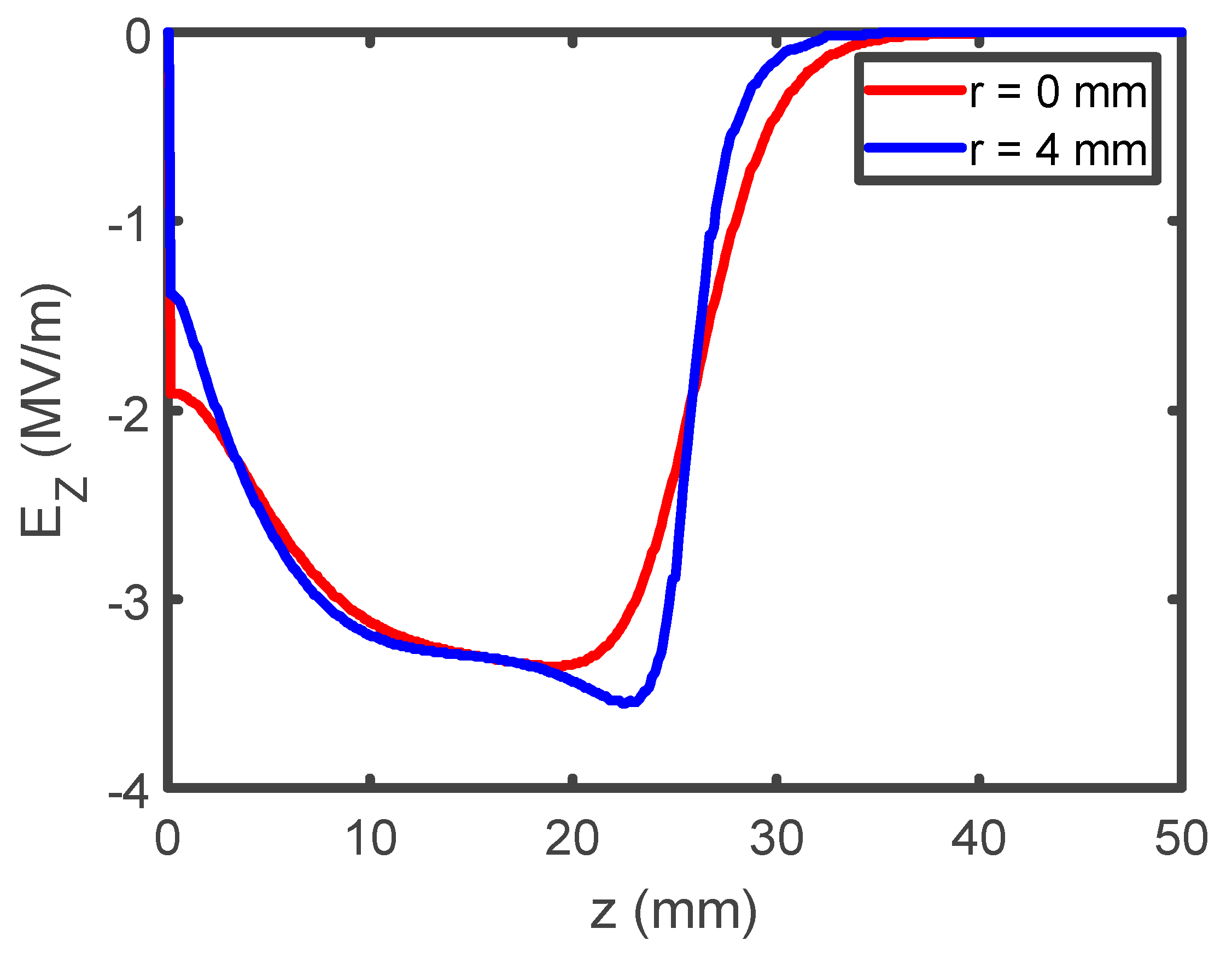
4.2. Performance of the RF Gated Gun (Grid—Anode Space)
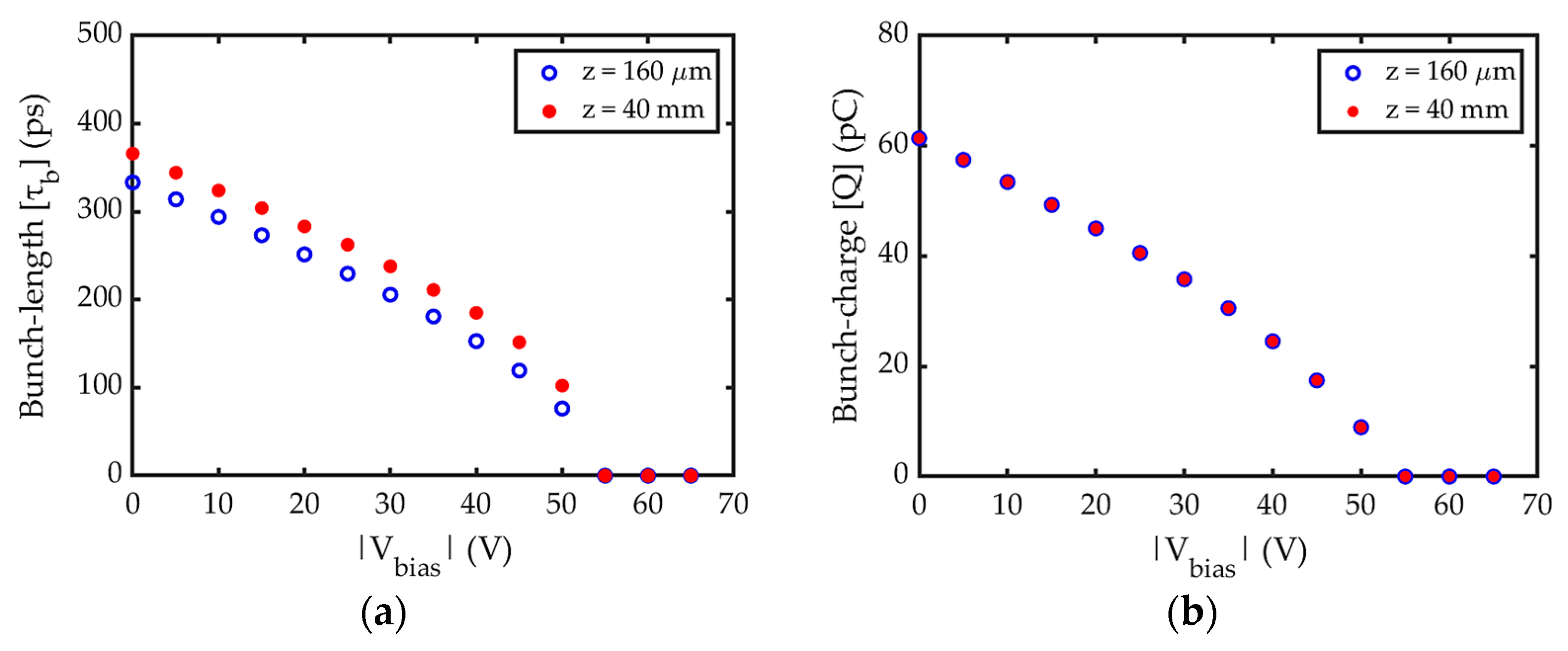
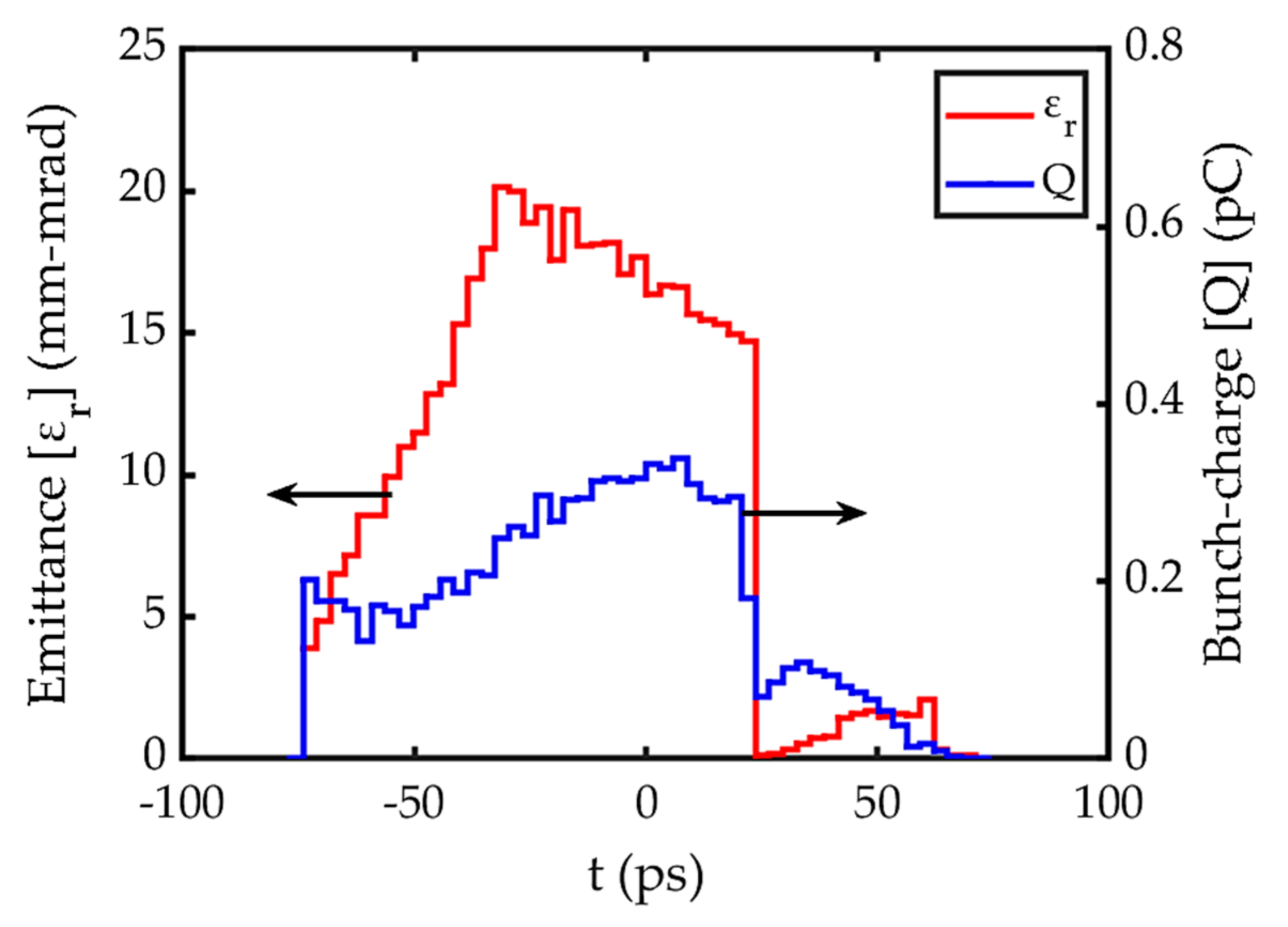
4.3. Performance of the RF Gated Gun (Anode—Buncher Space)
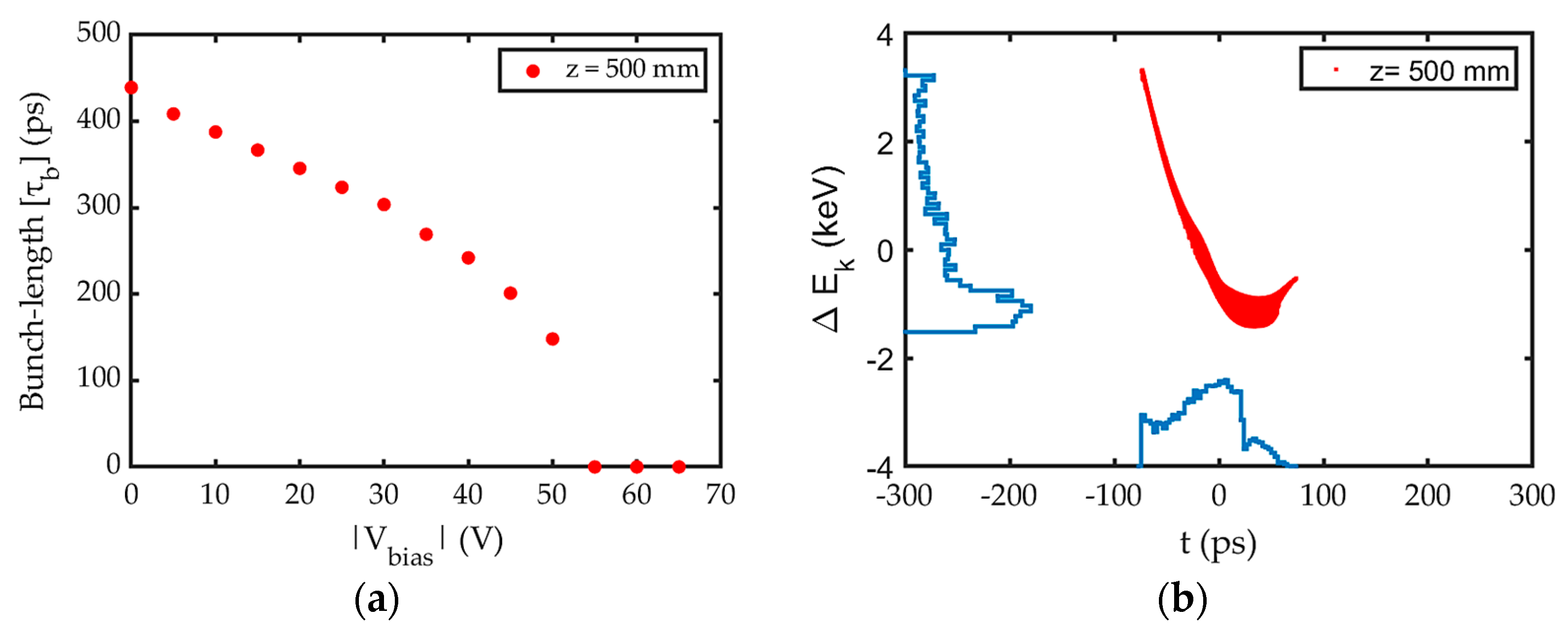
4.4. Other Ways to Reduce the Bunch-Length Further
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Diamond, W.T.; Ross, C.K. Actinium-225 production with an electron accelerator. J. Appl. Phys. 2021, 129, 10. [Google Scholar] [CrossRef]
- Starovoitova, V.N.; Tchelidze, L.; Wells, D.P. Production of medical radioisotopes with linear accelerators. Appl. Radiat. Isot. 2014, 85, 39–44. [Google Scholar] [CrossRef] [PubMed]
- Chmielewski, A.G.; Han, B. Electron beam technology for environmental pollution control. Appl. Radiat. Chem. Fields Ind. Biotechnol. Environ. 2016, 374, 37–66. [Google Scholar] [CrossRef] [PubMed]
- Borrely, S.I.; Cruz, A.C.; Del Mastro, N.L.; Sampa, M.H.O.; Somessari, E.S. Radiation processing of sewage and sludge. A review. Prog. Nucl. Energy 1998, 33, 3–21. [Google Scholar] [CrossRef]
- Londhe, K.; Lee, C.S.; Zhang, Y.; Grdanovska, S.; Kroc, T.; Cooper, C.A.; Venkatesan, A.K. Energy evaluation of electron beam treatment of perfluoroalkyl substances in water: A critical review. ACS EST Eng. 2021, 1, 827–841. [Google Scholar] [CrossRef]
- Trojanowicz, M.; Bobrowski, K.; Szreder, T.; Bojanowska-Czajka, A. Gamma-ray, X-ray and electron beam based processes. In Advanced Oxidation Processes for Waste Water Treatment; Academic Press: London, UK, 2018; pp. 257–331. [Google Scholar] [CrossRef]
- Hama, H.; Miura, S. Toward superconducting electron accelerators for various applications. Phys. Status Solidi (A) 2021, 218, 2000294. [Google Scholar] [CrossRef]
- Pavlov, Y.S.; Petrenko, V.V.; Alekseev, P.A.; Bystrov, P.A.; Souvorova, O.V. Trends and opportunities for the development of electron-beam energy-intensive technologies. Radiat. Phys. Chem. 2022, 198, 110199. [Google Scholar] [CrossRef]
- Ciovati, G.; Anderson, J.; Coriton, B.; Guo, J.; Hannon, F.; Holland, L.; LeSher, M.; Marhauser, F.; Rathke, J.; Rimmer, R.; et al. Design of a cw, low-energy, high-power superconducting linac for environmental applications. Phys. Rev. Accel. Beams 2018, 21, 091601. [Google Scholar] [CrossRef]
- Hara, T.; Aoki, T.; Dewa, H.; Fujita, T.; Fukami, K.; Fukui, T.; Hiraiwa, T.; Hosoda, N.; Inagaki, T.; Itoga, T.; et al. Low-emittance beam injection for a synchrotron radiation source using an X-ray free-electron laser linear accelerator. Phys. Rev. Accel. Beams 2021, 24, 110702. [Google Scholar] [CrossRef]
- Asaka, T.; Ego, H.; Hanaki, H.; Hara, T.; Hasegawa, T.; Hasegawa, T.; Inagaki, T.; Kobayashi, T.; Kondo, C.; Maesaka, H.; et al. Low-emittance thermionic-gun-based injector for a compact free-electron laser. Phys. Rev. Accel. Beams 2017, 20, 080702. [Google Scholar] [CrossRef]
- Sprangle, P.; Penano, J.; Hafizi, B.; Gordon, D.; Gold, S.; Ting, A.; Mitchell, C. High average current electron guns for high-power free electron lasers. Phys. Rev. Spec. Top.—Accel. Beams 2011, 14, 020702. [Google Scholar] [CrossRef]
- Arnold, A.; Teichert, J. Overview on superconducting photoinjectors. Phys. Rev. Spec. Top.—Accel. Beams 2011, 14, 024801. [Google Scholar] [CrossRef]
- Gonin, I.; Kazakov, S.; Kephart, R.; Khabiboulline, T.; Nicol, T.; Solyak, N.; Thangaraj, J.; Yakovlev, V. Built-in thermionic electron source for an SRF linacs. In Proceedings of the IPAC2021 (Brazil, 2021) THPAB156, Campinas, Brazil, 24–28 May 2021. [Google Scholar] [CrossRef]
- Ha, G.; Kim, K.J.; Power, J.G.; Sun, Y.; Piot, P. Bunch shaping in electron linear accelerators. Rev. Mod. Phys. 2022, 94, 025006. [Google Scholar] [CrossRef]
- Jenkins, R.O. A review of thermionic cathodes. Vacuum 1969, 19, 353–359. [Google Scholar] [CrossRef]
- Masuda, K. Development of Numerical Simulation Codes and Application to Klystron Efficiency Enhancement. Ph.D. Thesis, Department of Engineering, Kyoto University, Kyoto, Japan, 1998. [Google Scholar]
- Kavar, A.B.; Kashiwagi, S.; Muto, T.; Abiko, H.; Hinode, F.; Nagasawa, I.; Nanbu, K.; Shibata, K.; Takahashi, K.; Kudo, K.; et al. Numerical Study of 5 MeV Srf Electron Linac For Wastewater Purification. In Proceedings of the 32nd Linear Accelerator Conference, LINAC 2024, Chicago, IL, USA, 25–30 August 2024; JACoW Publishing: Geneva, Switzerland, 2024. [Google Scholar]
- Nishimori, N.; Nagai, R.; Hajima, R.; Shizuma, T.; Minehara, E.J. A thermionic electron gun system for the JAERI superconducting FEL. In Proceedings of the EPAC2000, Vienna, Austria, 26–30 June 2000. MOP5A06. [Google Scholar]
- Sheng, S.G.; Lin, G.Q.; Gu, Q.; Li, D.M. Electron Gun for SSRF. In Proceedings of the Second Asian Particle Accelerator Conference (APAC’01), Beijing, China, 17–21 September 2001. TUBU04. [Google Scholar]
- Bakker, R.J.; van der Geer, C.A.J.; van der Meer, A.F.G.; van Amersfoort, P.W.; Gillespie, W.A.; Saxon, G. 1 GHz modulation of a high-current electron gun. Nucl. Instrum. Methods Phys. Res. Sect. A 1991, 307. [Google Scholar] [CrossRef]
- Gold, S.H.; Ting, A.; Jabotinski, V.; Zhou, B.; Sprangle, P. Development of a high average current rf linac thermionic injector. Phys. Rev. Spec. Top.—Accel. Beams 2013, 16, 083401. [Google Scholar] [CrossRef]
- Zhang, L.; Adam, G.; Militsyn, B.; He, W.; Cross, A.W. Electron injector based on thermionic RF-modulated electron Gun for particle accelerator applications. IEEE Trans. Electron Devices 2019, 67, 347–353. [Google Scholar] [CrossRef]
- Kavar, A.B.; Kashiwagi, S.; Masuda, K.; Muto, T.; Hinode, F.; Nagasawa, I.; Nanbu, K.; Kanomata, K.; Shibata, K.; Takahashi, K.; et al. Numerical Study of a High Current Thermionic Electron Gun for a Superconducting Radio Frequency Linac. e-J. Surf. Sci. Nanotechnol. 2024, 22, 212–219. [Google Scholar] [CrossRef]
- Available online: https://www.mppinc.com/product/power-grid-devices-eimac-22/electron-sources-131 (accessed on 17 June 2025).

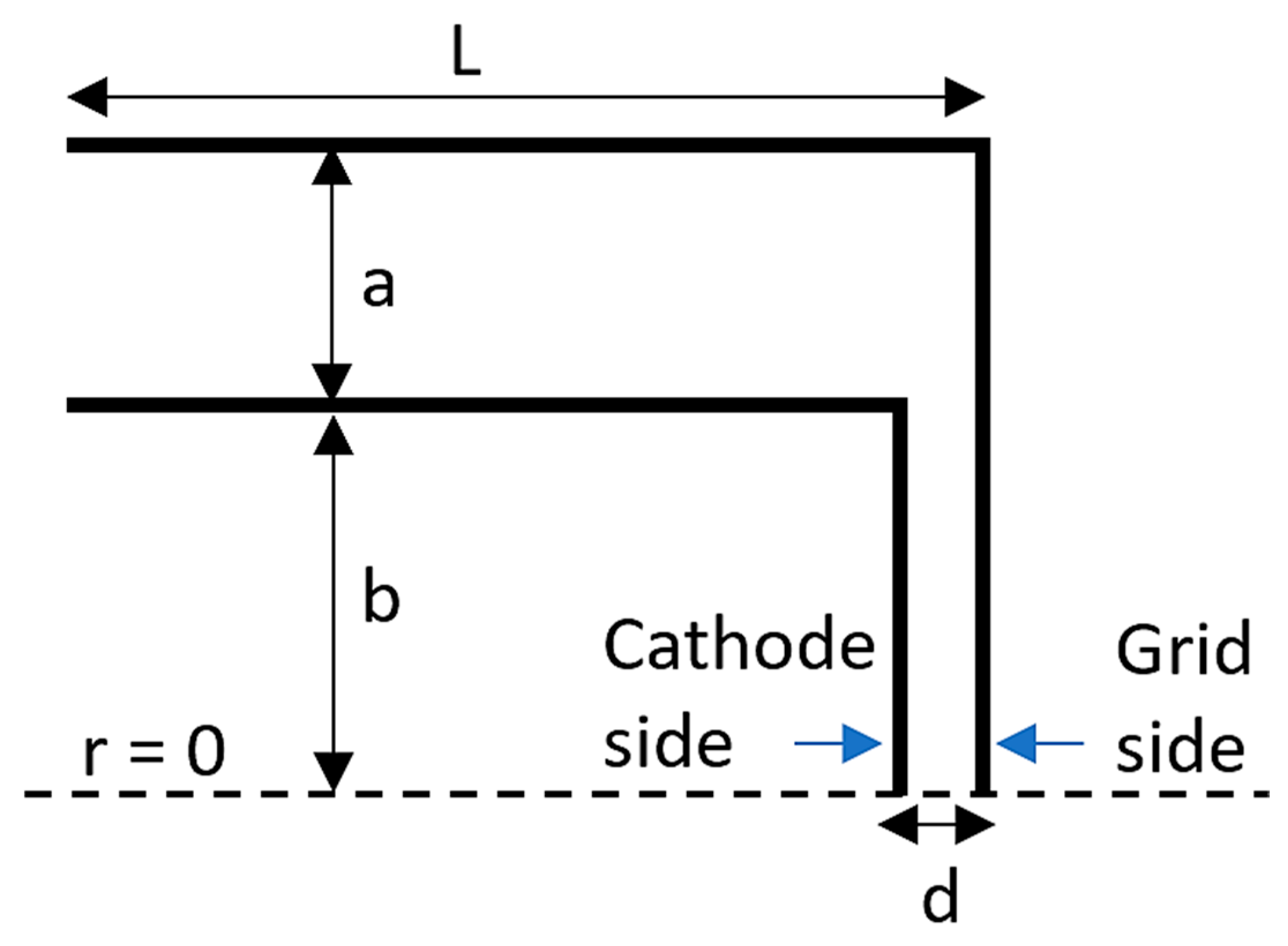




| L | 72.54355 mm |
| a | 4.455 mm |
| b | 7.175 mm |
| d | 160 µm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kavar, A.B.; Kashiwagi, S.; Masuda, K.; Muto, T.; Hinode, F.; Nanbu, K.; Nagasawa, I.; Shibata, K.; Takahashi, K.; Yamada, H.; et al. High Average Current Electron Beam Generation Using RF Gated Thermionic Electron Gun. Particles 2025, 8, 68. https://doi.org/10.3390/particles8030068
Kavar AB, Kashiwagi S, Masuda K, Muto T, Hinode F, Nanbu K, Nagasawa I, Shibata K, Takahashi K, Yamada H, et al. High Average Current Electron Beam Generation Using RF Gated Thermionic Electron Gun. Particles. 2025; 8(3):68. https://doi.org/10.3390/particles8030068
Chicago/Turabian StyleKavar, Anjali Bhagwan, Shigeru Kashiwagi, Kai Masuda, Toshiya Muto, Fujio Hinode, Kenichi Nanbu, Ikuro Nagasawa, Kotaro Shibata, Ken Takahashi, Hiroki Yamada, and et al. 2025. "High Average Current Electron Beam Generation Using RF Gated Thermionic Electron Gun" Particles 8, no. 3: 68. https://doi.org/10.3390/particles8030068
APA StyleKavar, A. B., Kashiwagi, S., Masuda, K., Muto, T., Hinode, F., Nanbu, K., Nagasawa, I., Shibata, K., Takahashi, K., Yamada, H., Kudo, K., Abiko, H., Kitisri, P., & Hama, H. (2025). High Average Current Electron Beam Generation Using RF Gated Thermionic Electron Gun. Particles, 8(3), 68. https://doi.org/10.3390/particles8030068






