Calculation of α Decay Half-Lives for Tl, Bi, and At Isotopes

Abstract

We investigated the reaction Q-value ($Q_{\alpha }$) for the $\alpha$ decay of Tl, Bi, and At isotopes using the deformed relativistic Hartree–Bogoliubov theory in continuum (DRHBc) with the covariant density functional PC-PK1. The $\alpha$ decay half-lives of Tl, Bi, and At isotopes are evaluated using various empirical formulas, based on both experimental $Q_{\alpha }$ and those obtained from DRHBc calculations. The calculated $Q_{\alpha }$ and $\alpha$ decay half-lives are compared with experimental data. On the basis of these results, we also predicted the $\alpha$ decay half-lives of isotopes for which experimental data are unavailable.

1. Introduction

Various nuclear decay modes have been experimentally observed, including $\alpha$ decay, $\beta$ decay, proton decay, neutron decay, spontaneous fission, and electron capture [1]. Among these, $\alpha$ decay is one of the most crucial decay modes, widely recognized as a key tool for investigating unstable and neutron-deficient isotopes, as well as superheavy elements. Since its discovery by Becquerel in 1896, $\alpha$ decay has become a major research topic in nuclear physics. This decay mode also provides essential insights into the structure and stability of atomic nuclei, as well as the mechanisms behind decay. Additionally, $\alpha$ decay plays a crucial role in the synthesis of superheavy elements, providing valuable insights for predicting and understanding the existence of specific elements. For example, it enables the prediction of the half-lives of superheavy elements and the discovery of new decay pathways. As such, $\alpha$ decay remains a central focus of various nuclear physics research.

Owing to the significant advancements in experimental technology, substantial progress has been made in both the experimental [2,3] and theoretical [4,5] aspects of $\alpha$ decay. Experimentally, various heavy nuclei have been successfully discovered through the analysis of alpha decay chains in recent years. For example, ²¹⁴U, a new $\alpha$-emitting nucleus, has been successfully produced through the ¹⁸²W(³⁶Ar, 4n)²¹⁴U reaction [2]. Theoretically, several empirical formulas have been developed to study $\alpha$ decay half-lives, including the Royer formula [6], AKRA [7], Viola–Seaborg–Sobiczewski (VSS) formula [8,9], Sobiczewski–Parkhomenko (SP) formula [10], Universal Decay Law (UDL) [11,12], and others.

$Q_{\alpha }$ is one of the significant characteristic quantities of an alpha-emitting nucleus. It is given as follows:

$$Q_{\alpha }=E_b(Z-2,N-2)-E_b(Z,N)+E_b(2,2),$$

(1)

where $E_b$ is the binding energy of the nucleus, and the binding energy of ⁴He ($E_b$(2,2)) is 28.30 MeV.

The nuclear masses of over 2000 nuclei have been experimentally measured. However, $\alpha$ decay is still anticipated to occur in the vast, unexplored regions of the nuclear chart, which remain beyond the reach of experimental techniques in the near future. Therefore, a detailed analysis of $Q_{\alpha }$ must depend on reliable theoretical nuclear mass models.

For addressing the mentioned issue, a well-refined and state-of-the-art relativistic nuclear model is essential. This model should simultaneously account for the deformation, pairing correlations, and continuum effects within a microscopic framework capable of covering the entire nuclear mass range. In this context, the deformed relativistic Hartree–Bogoliubov theory in continuum (DRHBc), based on point-coupling density functionals, has been developed [13,14]. The DRHBc theory has been shown to provide a robust description of nuclear masses with high predictive power [15,16], and it has also been applied to study the nuclear structure of various isotopes [17,18,19,20,21,22,23,24,25].

Generally, even–even nuclei are more suitable for $\alpha$ decay studies due to their abundant experimental data, well-defined decay paths, and theoretical simplicity. In Ref. [26], the $\alpha$ decay of even–even actinides and super-heavy nuclei with $Z\ge 90$ was carefully analyzed. Additionally, in our previous study [27], we investigated the $\alpha$-decay half-lives of even–even nuclei in the range from W to U using DRHBc theory and the semiclassical WKB approximation. In this article, we investigate the $\alpha$ decay half-lives of Tl, Bi, and At isotopes using empirical formulas and the DRHBc theory with the PC-PK1 density functional [28]. The article is organized as follows. Section 2 introduces a brief overview of the DRHBc theory and the empirical formulas used in this study, along with the numerical details for DRHBc calculations. The results and discussions for Tl, Bi, and At isotopes are presented in Section 3. Finally, the summary and conclusions are provided in Section 4.

2. Theoretical Framework

2.1. Deformed Relativistic Hartree–Bogoliubov Theory in Continuum

The detailed formalism of the DRHBc theory can be found in Refs. [29,30,31]. Here, we provide only a brief overview of the formalism of the DRHBc theory. In the DRHBc theory, the relativistic Hartree–Bogoliubov (RHB) equation [32] is expressed as follows.

$$\left(\begin{array}{cc}{h}_D-\lambda & \Delta \\ -{\Delta }^{*}& -h_D^{*}+\lambda \end{array}\right)\left(\begin{array}{c}{U}_k\\ V_k\end{array}\right)=E_k\left(\begin{array}{c}{U}_k\\ V_k\end{array}\right).$$

(2)

Here, $\lambda$ is the Fermi energy, and $E_k$ and ${(U_k,V_k)}^T$ are the quasiparticle energy and quasiparticle wave function. In the coordinate space, the Dirac Hamiltonian $h_D$ can be defined as

$$h_D\left(r\right)=\alpha ·p+V\left(r\right)+\beta [M+S\left(r\right)],$$

(3)

where $\alpha$ and p are the Dirac matrices and the momentum operator, M is the nucleon mass, and $V\left(r\right)$ and $S\left(r\right)$ are the vector and scalar potentials, respectively. The paring potential $\Delta$ is expressed in terms of the pairing tensor $\kappa (r,r^{\prime })$ as follows:

$$\Delta (r,r^{\prime })=V(r,r^{\prime })\kappa (r,r^{\prime }),$$

(4)

using a density-dependent zero range force

$$\begin{array}{c}\hfill V(r,r^{\prime })={\displaystyle \frac{V_0}{2}}\left(1-P^{\mathbf{\sigma }}\right)\mathbf{\delta }(r-r^{\prime })\left(1-{\displaystyle \frac{\rho \left(r\right)}{{\rho }_{sat}}}\right).\end{array}$$

(5)

Here, $P^{\sigma }$ is the spin exchange operator, and ${\rho }_{sat}$ is the nuclear saturation density.

The total energy can be computed as

$$\begin{array}{ccc}\hfill {\mathit{E}}_{\mathrm{tot}}& =& \sum _{k>0}({\lambda }_{\tau }-E_k)v_k^2-{\displaystyle \frac{1}{2}}\int {\mathrm{d}}^{3}r\kappa \left(r\right)\Delta \left(r\right)+{\mathit{E}}_{\mathrm{c}.\mathrm{m}.}\hfill \\ & & -\int {\mathrm{d}}^{3}r\left({\displaystyle \frac{1}{2}}{\alpha }_S{\rho }_S^2+{\displaystyle \frac{1}{2}}{\alpha }_V{\rho }_V^2+{\displaystyle \frac{1}{2}}{\alpha }_{TV}{\rho }_{TV}^2+{\displaystyle \frac{2}{3}}{\beta }_S{\rho }_S^3+{\displaystyle \frac{3}{4}}{\gamma }_S{\rho }_S^4+{\displaystyle \frac{3}{4}}{\gamma }_V{\rho }_V^4\right.\hfill \\ & & \left.+{\displaystyle \frac{1}{2}}{\delta }_S{\rho }_S\Delta {\rho }_S+{\displaystyle \frac{1}{2}}{\delta }_V{\rho }_V\Delta {\rho }_V+{\displaystyle \frac{1}{2}}{\delta }_{TV}{\rho }_{TV}\Delta {\rho }_{TV}+{\displaystyle \frac{1}{2}}{\rho }_{p}e{A}^0\right),\hfill \end{array}$$

(6)

where $E_k$ is the single-particle energy, $v_k^2$ is the occupation probability, e is the unit of charge, and $A^0$ is the electromagnetic field, respectively. The coupling constant ${\alpha }_i$ for the four-fermion terms is specified by the superscripts $(i=S,V$ and $T)$, which stand for the scalar, vector, and isovector channels, respectively. ${\beta }_S$, ${\gamma }_S$, and ${\gamma }_V$ are the higher-order terms, while ${\delta }_i$ refers to the gradient terms. Finally, $E_{\mathrm{c}.\mathrm{m}.}$ denotes the center of mass correction energy.

For the numerical calculations of the Tl, Bi, and At isotopes, we employ the energy cut-off $E_{cut}^{+}=$ 300 MeV and the angular momentum cutoff $J_{max}=(23/2)\hslash$ for the Dirac Woods–Saxon basis. The pairing strength $V_0$ = −325.0 MeV fm³, a pairing window of 100 MeV, and a saturation density of ${\rho }_{sat}$ = 0.152 fm⁻³ are taken, respectively. The numerical details can be found in Refs. [13,14].

2.2. Empirical Formula for $\alpha$ Decay Half-Lives

Empirical formulas for the $\alpha$ decay half-lives typically depend on the proton number (Z), the mass number (A), and the reaction Q-value ($Q_{\alpha }$) for the $\alpha$ decay. The most crucial factor in the $\alpha$ decay process of the heavy nuclei is the accurate determination of $Q_{\alpha }$, as it reflects the structure of the heavy nuclei through the binding energy. The significance of $Q_{\alpha }$ is clearly mentioned in Refs. [8,33]. For $Q_{\alpha }$, we use both experimental data and DRHBc mass table data, particularly when experimental $Q_{\alpha }$ are unavailable.

2.2.1. Royer Formula

The Royer formula [6] is given by

$${log}_{10}{T}_{1/2}=a+b{A}^{1/6}\sqrt{Z}+{\displaystyle \frac{cZ}{\sqrt{Q_{\alpha }}}},$$

(7)

where A, Z, and $Q_{\alpha }$ are the mass number, proton number, and the reaction Q-value for the $\alpha$ decay, respectively. Additionally, the parameters a, b, and c are $a=$ −25.68, $b=$ −1.1423, and $c=$ 1.592 for odd Z–even N nuclei, and $a=$ −29.48, $b=$ −1.113, and $c=$ 1.6971 for odd Z–odd N nuclei, respectively [34].

2.2.2. AKRA Formula

Akrawy and Poenaru presented [7] a new expression for calculating the $\alpha$ decay half-life by incorporating nuclear isospin asymmetry $I=(N-Z)/A$.

$${log}_{10}{T}_{1/2}=a+b{A}^{1/6}\sqrt{Z}+{\displaystyle \frac{cZ}{\sqrt{Q_{\alpha }}}}+dI+e{I}^2.$$

(8)

For the odd Z–even N nuclei case (odd Z–odd N nuclei case), the parameters a, b, c, d, and e are as follows: $a=$ −31.79248 (−26.27896), $b=$ −1.07636 (−1.20130), $c=$ 1.75354 (1.65906), $d=$ −2.22627 (−0.08411), and $e=$ 0.39378 (67.59728) [35].

2.2.3. Viola–Seaborg–Sobiczewski (VSS) Formula

The VSS [8,9] formula proposed by Sobiczewski extended the original Viola–Seaborg formula to better account for heavy and superheavy nuclei are widely used to calculate and predict the $\alpha$ decay half-lives.

$${log}_{10}{T}_{1/2}={\displaystyle \frac{aZ+b}{\sqrt{Q_{\alpha }}}}+cZ+d+h_{log},$$

(9)

where $a=$ 1.66175, $b=$ −8.5166, $c=$ −0.20228, and $d=$ −33.9069, respectively. The term $h_{log}$ describes the hindrance effects related to odd-Z and/or odd-N. Its value is 0.772 for odd-Z even-N nuclei and 1.114 for odd-Z odd-N nuclei [36].

2.2.4. Parkhomenko–Sobiczewski (SP) Formula

The Parkhomenko–Sobiczewski (SP) formula, which is a phenomenological expression used to explain the $\alpha$ decay half-lives of nuclei heavier than ²⁰⁸Pb, was introduced by Parkhomenko and Sobiczewski [10]. The (SP) formula is given by

$${log}_{10}{T}_{1/2}={\displaystyle \frac{aZ}{\sqrt{Q_{\alpha }-E_i}}}+bZ+c,$$

(10)

where the values of the coefficients [36] are $a=$ 1.5372, $b=$ −0.1607, and $c=$ −36.573. The $E_i$ represents the average excitation energy, with values of 0.113 and 0.284 for odd–even and odd–odd nuclei, respectively.

2.2.5. Universal Decay Law (UDL) Formula

Qi et al. [11,12] derived a linear universal decay law (UDL) based on an R-matrix theory that describes the microscopic mechanism of $\alpha$ emission and is applicable to $\alpha$ decay. The UDL formula is expressed as follows:

$${log}_{10}{T}_{1/2}=a{Z}_p{Z}_d\sqrt{{\displaystyle \frac{\mu }{Q_{\alpha }}}}+b\sqrt{\mu Z_p{Z}_d(A_p^{1/3}+A_d^{1/3})}+c.$$

(11)

Here, $\mu =A_a{A}_d/(A_a+A_d)$, where $A_a$ denotes the mass number of the emitted alpha particle and $A_d$ represents the mass number of the daughter nucleus. In Equation (11), the coefficients for the UDL formula, as provided in Ref. [35], are as follows: $a=$ 0.4314, $b=$ −0.4087, and $c=$ −25.7725.

3. Results

It is well-known that the $\alpha$ decay half-lives are highly sensitive to $Q_{\alpha }$. Therefore, selecting an accurate $Q_{\alpha }$ is crucial for making reliable predictions. First, we examined the $Q_{\alpha }$ of the Tl, Bi, and At by the DRHBc theory. In Figure 1, the $Q_{\alpha }$ for Tl, Bi, and At obtained from the DRHBc calculations are plotted against the neutron number, along with the available experimental data [37]. Additionally, for a quantitative comparison, we present the differences between the calculated results and the experimental data, with uncertainties represented by standard deviation of less than 1.14, 1.03, and 0.95 MeV for Tl, Bi, and At, respectively, as shown in Figure 1.

The $\alpha$ decay half-lives calculated using five empirical formulas (AKRA, Royer, SP, UDL, and VSS) are presented in Figure 2. The results were obtained using the experimental $Q_{\alpha }^{EXP}$ values and the $Q_{\alpha }^{DRHBc}$ values derived from DRHBc calculations, as shown in panels (a) and (b) of Figure 2, respectively. For comparison with the experiment, we use the experimental $\alpha$ decay half-lives from NNDC [38]. Since multiple decay modes can exist for each nucleus, we consider only 17 experimental data points where the branching ratio of $\alpha$ decay is close to 100%. The logarithmic differences between the experimental half-lives and the calculated values are shown in Figure 2c,d. Additionally, the calculated $\alpha$ decay half-lives are listed in

Table 1. The calculated half-life of $\alpha$ decay using selected empirical formulas. The experimental data for $Q_{\alpha }^{EXP}$ and half-lives are taken from AME2020 [37] and NNDC [38], respectively. The units of $Q_{\alpha }^{EXP}$ and ${log}_{10}{T}_{1/2}$ are MeV and seconds (s), respectively.

		${log}_{10}{\mathit{T}}_{1/2}$
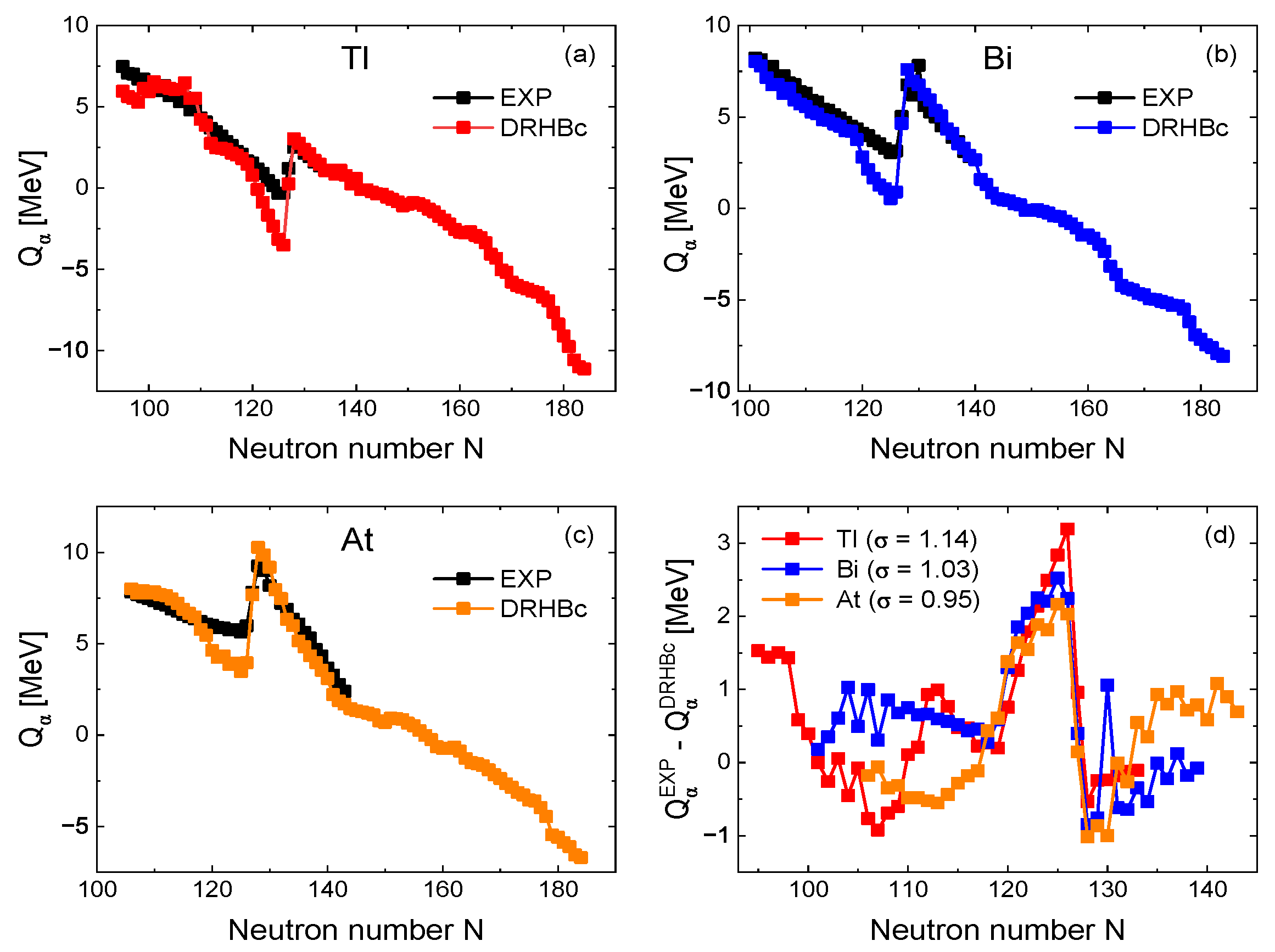
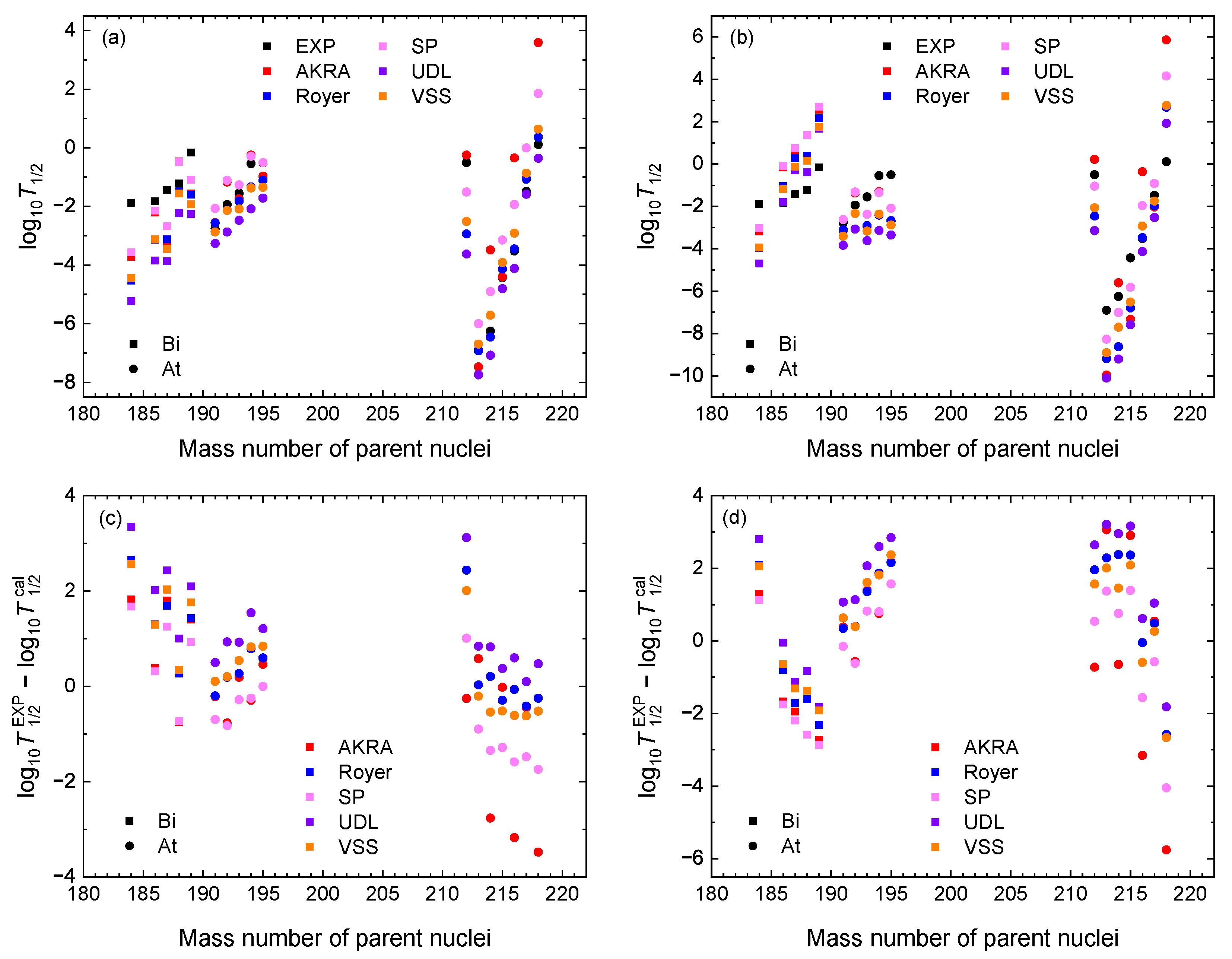
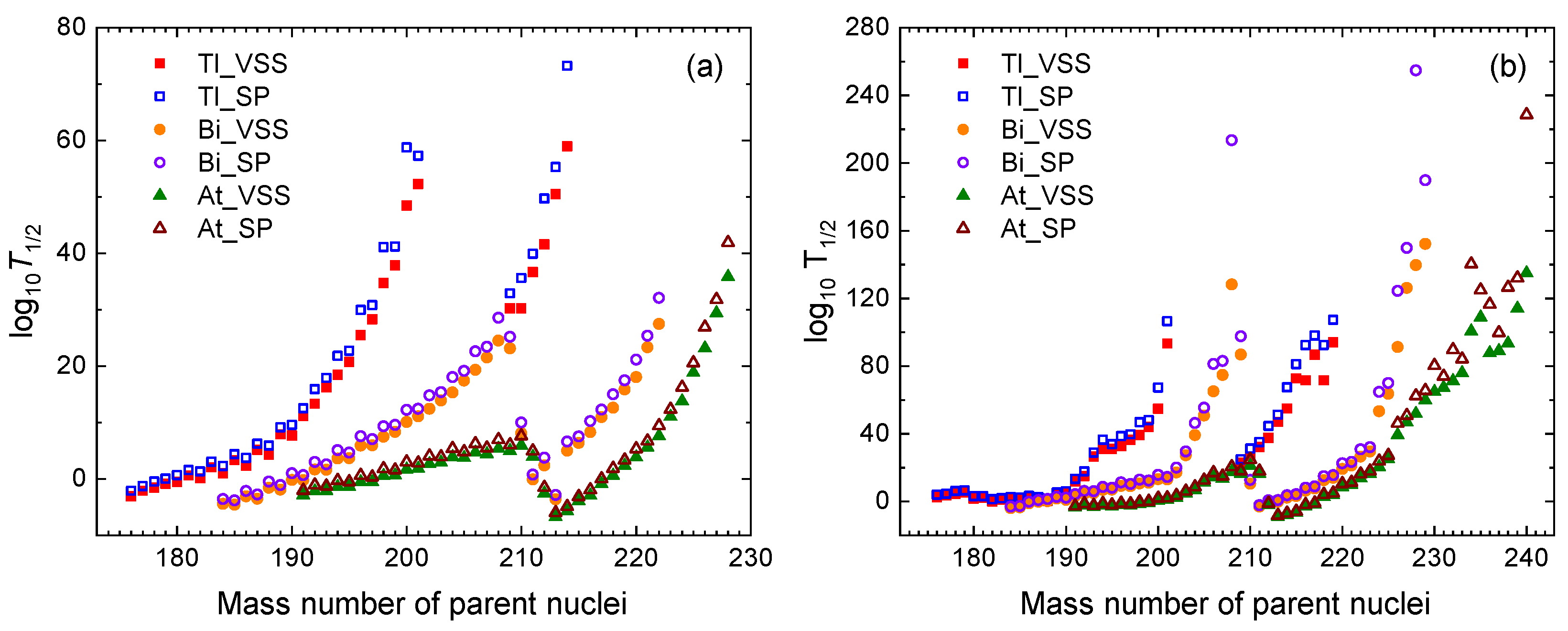
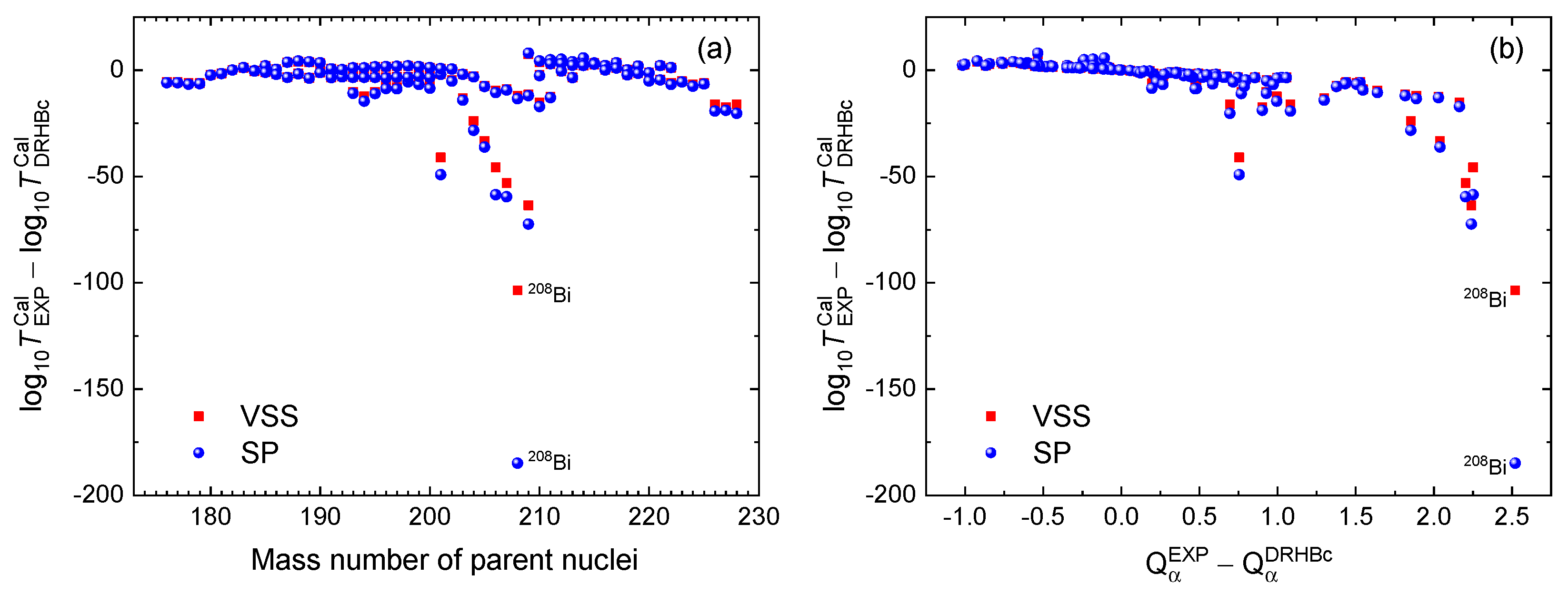
$\mathit{\alpha }$ Transition	${\mathit{Q}}_{\mathit{\alpha }}^{\mathit{EXP}}$	EXP	AKRA	Royer	SP	UDL	VSS
184Bi →180Tl	8.22	−1.89	−3.71	−4.53	−3.56	−5.23	−4.45
186Bi →182Tl	7.76	−1.83	−2.21	−3.13	−2.15	−3.85	−3.12
187Bi →183Tl	7.76	−1.43	−3.23	−3.12	−2.68	−3.87	−3.46
188Bi →184Tl	7.26	−1.22	−0.47	−1.49	−0.49	−2.23	−1.57
189Bi →185Tl	7.27	−0.16	−1.56	−1.60	−1.10	−2.26	−1.92
191At →187Bi	7.82	−2.77	−2.55	−2.57	−2.07	−3.27	−2.87
192At →188Bi	7.70	−1.94	−1.17	−2.13	−1.12	−2.87	−2.14
193At →189Bi	7.57	−1.55	−1.74	−1.82	−1.27	−2.47	−2.09
194At →190Bi	7.45	−0.54	−0.25	−1.33	−0.29	−2.09	−1.37
195At →191Bi	7.34	−0.51	−0.97	−1.11	−0.50	−1.72	−1.35
212At →208Bi	7.82	−0.50	−0.25	−2.94	−1.51	−3.62	−2.51
213At →209Bi	9.25	−6.90	−7.48	−6.93	−6.00	−7.75	−6.70
214At →210Bi	8.99	−6.25	−3.49	−6.46	−4.91	−7.08	−5.71
215At →211Bi	8.18	−4.43	−4.41	−4.14	−3.15	−4.81	−3.91
216At →212Bi	7.95	−3.52	−0.35	−3.45	−1.94	−4.12	−2.91
217At →213Bi	7.20	−1.49	−1.04	−1.07	−0.01	−1.58	−0.87
218At →214Bi	6.88	0.11	3.59	0.36	1.85	−0.36	0.63
standard deviation			1.55	1.11	1.09	1.61	1.16

and

Table 2. The same as Table 1, but with results obtained using $Q_{\alpha }^{DRHBc}$ from the DRHBc calculations. The standard deviation ($\pm \sigma$) are the results obtained using $Q_{\alpha }^{DRHBc}$ ($\pm \sigma$) $(\sigma =2.2)$, respectively.

		${log}_{10}{\mathit{T}}_{1/2}$
$\mathit{\alpha }$ Transition	${\mathit{Q}}_{\mathit{\alpha }}^{\mathit{DRHBc}}$	EXP	AKRA	Royer	SP	UDL	VSS
184Bi →180Tl	8.04	−1.89	−3.18	−3.98	−3.02	−4.69	−3.94
186Bi →182Tl	7.15	−1.83	−0.16	−1.03	−0.08	−1.79	−1.19
187Bi →183Tl	6.75	−1.43	0.52	0.28	0.76	−0.31	−0.13
188Bi →184Tl	6.77	−1.22	1.36	0.38	1.36	−0.39	0.15
189Bi →185Tl	6.27	−0.16	2.57	2.15	2.70	1.66	1.75
191At →187Bi	8.00	−2.77	−3.15	−3.11	−2.62	−3.84	−3.40
192At →188Bi	7.76	−1.94	−1.37	−2.33	−1.32	−3.08	−2.33
193At →189Bi	7.92	−1.55	−2.94	−2.91	−2.37	−3.62	−3.16
194At →190Bi	7.77	−0.54	−1.30	−2.41	−1.35	−3.14	−2.36
195At →191Bi	7.83	−0.51	−2.69	−2.67	−2.08	−3.35	−2.88
212At →208Bi	7.67	−0.50	0.22	−2.46	−1.04	−3.15	−2.07
213At →209Bi	10.27	−6.90	−9.97	−9.19	−8.27	−10.11	−8.91
214At →210Bi	9.86	−6.25	−5.61	−8.63	−7.01	−9.21	−7.71
215At →211Bi	9.18	−4.43	−7.34	−6.79	−5.82	−7.59	−6.52
216At →212Bi	7.96	−3.52	−0.37	−3.48	−1.96	−4.14	−2.93
217At →213Bi	7.46	−1.49	−2.03	−1.97	−0.91	−2.52	−1.75
218At →214Bi	6.33	0.11	5.86	2.68	4.15	1.93	2.77
standard deviation			2.33	1.77	1.75	2.11	1.62
standard deviation (+$\sigma$)			6.07	6.62	5.59	7.38	6.24
standard deviation (−$\sigma$)			11.12	9.81	10.98	9.29	9.26

. Table 1 shows the results derived using experimental $Q_{\alpha }^{EXP}$ values, while Table 2 displays the results obtained using $Q_{\alpha }^{DRHBc}$ values from DRHBc calculations. The standard deviations $\sigma$ between the experimental data and the calculated results, as defined by

$$\sigma =\sqrt{{\displaystyle \frac{1}{N}}\Sigma {(lo{g}_{10}{T}_{1/2}^{EXP}-lo{g}_{10}{T}_{1/2}^{cal})}^2},$$

(12)

are provided in the last row of Table 1 and Table 2. The $Q_{\alpha }$ calculated based on the DRHBc masses has uncertainty due to the deviation from experimental values ($\sigma$ = 2.2 MeV). This uncertainty can also affect the accuracy of the $\alpha$ decay half-life calculated using $Q_{\alpha }^{DRHBc}$. The results are summarized in Table 2.

The predicted $\alpha$ decay half-lives of Tl (Z = 81), Bi (Z = 83), and At (Z = 85) isotopes, calculated using the VSS and SP formulas—two models with the smallest standard deviations among the five models, as shown in Table 2—are shown in Figure 3a,b, with $Q_{\alpha }$ values taken from AME2020 [37] and the DRHBc mass table. We also compared the results obtained using $Q_{\alpha }$ values derived from AME2020 and the DRHBc mass table. For a given isotope chain, the calculated half-lives generally increase as the neutron number increases. This trend decreases near the N = 126 shell closure and then increases again.

In Figure 4a, the logarithmic differences of $\alpha$ decay half-lives for Tl (Z = 81), Bi (Z = 83), and At (Z = 85) isotopes between the results obtained using $Q_{\alpha }$ values derived from AME2020 and those derived from the DRHBc mass table versus the mass number of the parent nucleus are presented. The results of the two formulas, VSS and SP, are nearly identical, except for ²⁰⁸Bi. Additionally, the differences with respect to ($Q_{\alpha }^{EXP}-Q_{\alpha }^{DRHBc}$) are presented in Figure 4b. We can observe that, as the value of ($Q_{\alpha }^{EXP}-Q_{\alpha }^{DRHBc}$) increases, the logarithmic differences between the results predicted using $Q_{\alpha }$ values from AME2020 and those from the DRHBc mass table also increase, particularly when it exceeds 2.0. Finally, we can see that the difference between the results of VSS and SP formulas increases. We will calculate and predict the $\alpha$ decay half-lives using the predicted densities in the DRHBc theory within the WKB approximation framework [39,40] in the following study.

4. Summary

In this work, we evaluated the reaction Q-value ($Q_{\alpha }$) for the $\alpha$ decay of Tl, Bi, and At isotopes using the DRHBc theory and compared the results with experimental data from AME2020. Since multiple decay modes exist for each nucleus, we considered only 17 experimental data points where the branching ratios for $\alpha$ decay modes are almost 100%. The $\alpha$ decay half-lives of these isotopes were calculated using five different empirical formulas, based on both experimental $Q_{\alpha }$ values and those obtained from the DRHBc calculations. The calculated $\alpha$ decay half-lives were also compared with experimental data from NNDC. The VSS and SP formulas have the smallest standard deviations ($\sigma$) between the calculated results and the experimental data among the five models. Based on these results, we calculated and predicted the $\alpha$ decay half-lives of Tl, Bi, and At isotopes using VSS and SP formulas. In the future study, we will calculate and predict the $\alpha$ decay half-lives using the densities obtained from the DRHBc theory within the WKB approximation framework.