Abstract
Bubble nuclei, characterized by a depletion in nucleon density at the nuclear center, are investigated within the atomic number range using the Deformed Relativistic Hartree–Bogoliubov theory in continuum. This study extends previous investigations, which were limited to even–even isotopes, by incorporating even–odd, odd–even, and odd–odd nuclei within this range. The extension is achieved by introducing the blocking effect into the point-coupling approach to ensure self-consistency. Following previous studies, we define a nucleus as a bubble candidate if the bubble parameter exceeds , and identify five bubble nuclei in both even-Z and odd-Z nuclei groups, based on the highest values. The formation of bubble structures is confirmed through an analysis of proton single-particle energy levels of the most centrally depleted nuclei across four categories: even–odd, even–even, odd–even, and odd–odd.
1. Introduction
The exploration of atomic nuclei, particularly those near the neutron drip line, has progressed significantly in recent years, driven by advancements in experimental facilities worldwide [1,2]. The discovery of over 3000 isotopes has broadened our understanding of the nuclear landscape, revealing previously uncharted regions of a nuclear structure. These findings play a crucial role in deepening our knowledge of the nuclear structure and the evolution of heavy nuclei. However, despite these advancements, the evolution of nuclear density distributions remains incompletely understood, particularly regarding the shape decoupling effect, which leads to distinct deformations between the core and the halo, and the existence of bound nuclei beyond the neutron drip line.
A key issue in nuclear structure research is understanding exotic nuclei, which exhibit unique phenomena such as bubble structures and shape coexistence in their ground states [3]. Bubble nuclei, in particular, arise when the central region of the nucleus exhibits a substantial depletion in nucleon density. These nuclei, characterized by reduced proton and neutron densities, have been extensively studied theoretically. It has been suggested that bubble formation originates from the reduced occupation of s states near the Fermi surface, which suppresses the central density [3,4,5,6,7,8,9,10,11,12]. Additionally, pairing correlations and nuclear deformation are known to further weaken the bubble structure [3,6,13,14,15,16,17].
In this study, we employ the deformed relativistic Hartree–Bogoliubov theory in continuum (DRHBc) to investigate the nuclear density distributions and internal structure. This framework is well suited for studying exotic nuclear phenomena, such as neutron-rich nuclei and bubble structures, as it incorporates deformation and treats self-consistently continuum effects and pairing [18,19,20].
This paper is organized as follows. In Section 2, we introduce the DRHBc framework and discuss its application to bubble structures. Section 3 presents our results on bubble nuclei with atomic numbers ranging , identifying those with the most significant central density depletion and analyzing their structural properties. Finally, a conclusion of our findings is provided in Section 4.
2. Theoretical Framework
2.1. DRHBc
In this study, we employ the relativistic mean-field (RMF) framework to investigate nuclear structure and density distributions while incorporating pairing correlations. The blocking effect is included to account for the presence of unpaired nucleons in odd-mass and odd–odd nuclei. This modifies the pairing potential and alters single-particle occupation probabilities, which in turn affect central density depletion in bubble structures. The Lagrangian density used in our calculations is given by [21]
where m is the nucleon mass, and , , and are the coupling constants for four-fermion contact interactions. The terms with , , and account for density-dependent effects, while those with , , and describe the finite-range effects. and represent the four-vector potential and the field strength tensor of the electromagnetic field, respectively. The subscripts S, V, and denote scalar, vector, and isovector components. Further details on the DRHBc theory can be found in Refs. [19,20], and numerical implementations are described in Ref. [21].
Both automatic and orbital-fixed blocking methods are employed in the DRHBc framework. The automatic method iteratively excludes the lowest-energy quasiparticle state, ensuring self-consistency during convergence. The orbital-fixed method, on the other hand, enforces the occupation of a specific single-particle state. These approaches enable reliable calculations for odd-mass and odd–odd nuclei. Applying the mean-field approximation to the Lagrangian density and performing a Legendre transformation, we derive the mean-field Hamiltonian density. By employing the variational method and the Bogoliubov transformation, we obtain the relativistic Hartree–Bogoliubov (RHB) equation [22], given by
where is the Dirac Hamiltonian, is the chemical potential, represents the pairing potential, and are the quasiparticle wavefunctions.
To account for nuclear deformation, the DRHBc framework expands the density distribution in terms of Legendre polynomials as
where are the expansion coefficients, and are the Legendre polynomials.
In odd-mass and odd–odd nuclei, the blocking effect changes the pairing field by excluding specific quasiparticle states. This leads to modifications in single-particle occupation probabilities and the energy spectrum. The automatic blocking method is particularly effective in cases where a well-defined lowest quasiparticle state exists, facilitating rapid convergence. However, when several low-energy quasiparticle states are closely spaced, the orbital-fixed blocking method is used to investigate the impact of blocking different states on nuclear properties. This ensures a robust and reliable description of pairing suppression and structural evolution in exotic nuclei [20].
2.2. Bubble Parameter
Proton bubble nuclei are identified by a significant reduction in central proton density relative to the maximum proton density within the nucleus. The central density depletion is quantified using the proton depletion fraction, which serves as a key parameter for characterizing bubble structures. In previous studies [6,8,9,14], the bubble parameter was defined as the ratio of the maximum proton density, which is uniquely defined and does not depend on the direction. However, for deformed nuclei described within the DRHBc framework, the proton density distribution varies with the polar angle , leading to anisotropic density profiles. Consequently, the maximum proton density also depends on , making the original definition unsuitable for deformed nuclei.
To address this issue, a modified bubble parameter was introduced in the previous study [3]. This incorporates an angle-averaged maximum proton density, providing a more consistent measure of central density depletion in deformed nuclei:
where the angle averaged maximum proton density is defined as
Here, denotes the radial coordinate where the proton density reaches its local maximum for a given . This formulation ensures that represents an effective maximum density, accounting for directional variations in deformed nuclei. For spherical nuclei, where the proton density distribution is isotropic, the bubble parameter naturally reduces to its conventional definition, i.e., , ensuring consistency with the previous studies.
3. Results
Using Equation (4), we systematically calculate the bubble parameter for nuclei with described in DRHBc and analyze the result. Table 1 represents the list of nuclei, which show the highest 5 bubble parameter for even-Z and odd-Z nuclei, respectively. We adopt the point coupling density functional (PC-PK1) [23] to extend and compare the previous study. The neutron numbers of the nuclei in Table 1 are close to the neutron magic number 184, with the bubble parameter exceeding 28%. Compared to previous study [3], which identified Hf as the most depleted nucleus, these results reveal that the presence of unpaired nucleons, particularly in odd-Z or odd-N nuclei, significantly contributes to the bubble parameter. In other words, this finding aligns with earlier studies, which indicates that paired nucleons tend to limit the bubble structure. For even-Z nuclei, the nucleus with the most central depletion is Hg, while for odd-Z nuclei, Lu exhibits the most central depletion.

Table 1.
List of the nuclei which show the highest 5 bubble parameters for even-Z and odd-Z nuclei, respectively.
Additionally, we observe the effect of quadrupole deformation () on the bubble parameter. For even-Z nuclei, a comparison between 258W and 253W indicates that 253W exhibits a smaller bubble parameter. Note that 258W has a magic neutron number, but 253W has a non-magic neutron number. Similarly, for odd-Z nuclei, a comparison between 257Ta and 256Ta shows that 256Ta, with an odd neutron number, has a lower value. These effects can be attributed to the quadrupole deformation (), which reduces the bubble parameter. Additionally, the presence of an unpaired nucleon can alter pairing correlations and subsequently influence the bubble parameter, consistent with previous studies [3,6,13,14,15,16,17].
The density distributions of 263Hg, 256Hf, 255Lu, and 254Re are presented in Figure 1, representing even–odd, even–even, odd–even, and odd–odd nuclei, respectively. The scaled density distributions of protons and neutrons are provided to facilitate comparison with the total baryon density. Since nuclear interactions depend on the nucleon composition, direct comparisons between different nuclides are challenging due to variations in the mass numbers, which correspond to different nuclear systems. Nevertheless, a qualitative analysis provides useful insights. First, both 255Lu and 256Hf have a neutron magic number of 184. Compared to the other two nuclides, their neutron density distributions appear relatively smooth. This suggests that deviation from a neutron magic number significantly affects the overall nuclear density distribution. Furthermore, an analysis of proton density distributions indicates that both odd and even proton numbers consistently result in lower central densities. However, inherent differences between these nuclear systems make direct quantitative comparisons challenging.
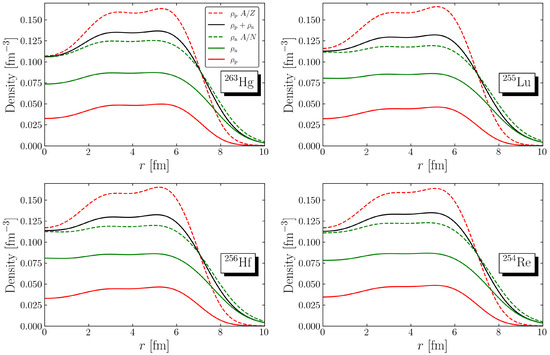
Figure 1.
Density profiles for 263Hg, 255Lu, 256Hf, 254Re. For comparison with the total baryon density, the scaled proton density and neutron density are also displayed.
Figure 2 presents the proton single-particle levels for the ground states of 263Hg, 256Hf, 255Lu, and 254Re. The states above the Fermi surface appear due to the inclusion of the pairing potential in the DRHBc framework. For the spherical nuclei 263Hg, 256Hf, and 255Lu, only the orbital contributes to the central density because angular momentum l is a conserved quantum number. In contrast, 254Re exhibits slight quadrupole deformation (), leading to the splitting of single-particle states. Despite this deformation, a low occupation probability of orbital is observed in all nuclei, resulting in a depleted central proton density. For even-Z nuclei, the and states are fully occupied because their energy levels lie far below the Fermi surface, consistent with previous findings [3]. In odd-Z nuclei, however, one proton occupies either the or state near the Fermi surface with an occupation probability of 0.5, rather than the state. These high-angular-momentum states () contribute minimally to the central density due to their spatial distribution, effectively acting as blocked protons. This suggests that a lower central density reduces destabilizing interactions between the surface and center, leading to a more stable nuclear structure. In other words, structures with lower central proton densities tend to be more stable than those with denser centers.
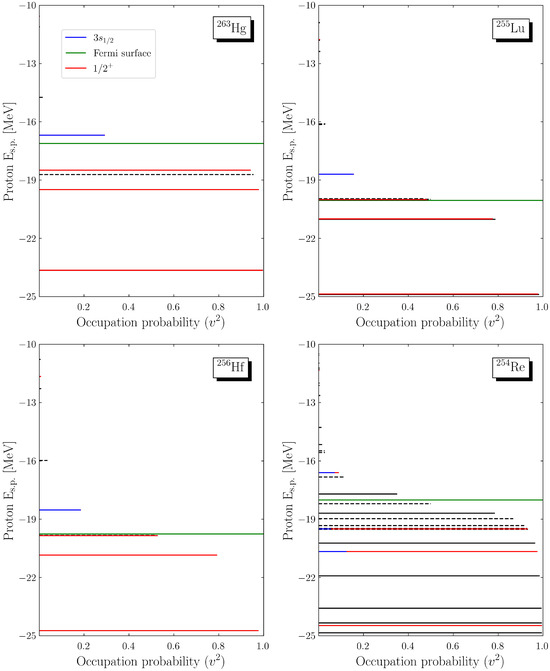
Figure 2.
Proton single-particle levels near the Fermi surface for 263Hg, 255Lu, 256Hf, and 254Re. The solid line means the positive-parity state and dashed line means the negative parity. Only states contribute to the s states. Note that the occupation probability of the state of the near Fermi surface is low.
In the case of the deformed nucleus 254Re, the angular momentum l is not a good quantum number, but its projection onto the symmetry axis remains well defined. Consequently, the states in deformed nuclei can still contribute to the central density. The occupancy of the s state in deformed nuclei is estimated using the formalism from [24]:
where m stands for the total angular momentum projection on the symmetry axis. For 254Re, as shown in Figure 2, the occupation of states remains low, leading to a depleted central region. Both 255Lu, and 254Re are odd-Z nuclides, exhibiting the odd-proton blocking effect. As previously mentioned, 254Re features more single-particle levels in its ground state than 263Hg, 256Hf, and 255Lu. This is attributed to quadrupole deformation, which alters the nuclear structure and enables the inclusion of the state. These results suggest that in odd-Z nuclides, nuclear deformation influences the bubble structure but does not necessarily suppress it, instead modifying the spatial distribution of nucleons within the nucleus.
4. Conclusions
In this study, we systematically calculated the bubble parameter for nuclei with , extending the scope of the previous research [3]. We first identified the five nuclei with the highest bubble parameter in both even-Z and odd-Z nuclei groups. These ten nuclei were found to be either spherical or only slightly deformed, consistent with previous findings that nuclear deformation weakens the bubble structure. Next, we selected 263Hg, 256Hf, 255Lu, and 254Re as representative examples of even–odd, even–even, odd–even, and odd–odd bubble nuclei. These nuclei were analyzed in detail through their density distributions and proton single-particle levels. As anticipated from previous studies, the depletion in central density is primarily driven by lower occupations of s states near the Fermi surface. Furthermore, our results emphasized that that quadrupole deformation () plays a critical role in moderating the bubble structure, with more deformed nuclei exhibiting weaker central density depletion. Additionally, for odd-Z nuclei such as 255Lu and 254Re, the proton blocking effect was observed, influencing the distribution of single-particle levels and contributing to the distinct characteristics of central density depletion in these nuclei. These findings provide further insight into the interplay between deformation, single-particle structure, and central density depletion, advancing our understanding of bubble structures in exotic nuclei.
Author Contributions
Conceptualization, Y.K.; methodology, Y.C.; formal analysis, C.S. and Y.C.; investigation, C.S. and Y.C.; writing—original draft preparation, C.S. and Y.C.; writing—review and editing, All authors; visualization, C.S. and Y.C.; supervision, C.-H.L.; project administration, C.-H.L.; funding acquisition, C.-H.L. All authors have read and agreed to the published version of the manuscript.
Funding
C.S. and C.-H.L. were supported by National Research Foundation of Korea (NRF) grants funded by the Korean government (Ministry of Science and ICT) (No. RS-2023-NR076639, and No. 2018R1D1A1B07048599). C.S. also was supported in part by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (Grant Nos. RS-2024-00460031). Y.C. was supported in part by the National Key R&D Program of China (2022YFA1602401) and the National Natural Science Foundation of China (No. 12335009 & 12435010). This work was supported partly by the Rare Isotope Science Project of Institute for Basic Science funded by Ministry of Science, ICT, and Future Planning and NRF (No. 2013M7A1A1075764). A portion of the computational resources were provided by the National Supercomputing Center including technical support (No. KSC-2020-CRE-0329 and No. KSC-2021-CRE-0126).
Data Availability Statement
The data supporting the reported results can be found in the publicly available dataset at the following website: https://drhbctable.jcnp.org/, accessed on 20 March 2025.
Acknowledgments
C.S. and C.-H.L. were supported by National Research Foundation of Korea (NRF) grants funded by the Korean government (Ministry of Science and ICT) (No. RS-2023-NR076639, and No. 2018R1D1A1B07048599). C.S. also was supported in part by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (Grant Nos. RS-2024-00460031). Y.C. was supported in part by the National Key R&D Program of China (2022YFA1602401) and the National Natural Science Foundation of China (No. 12335009 & 12435010). This work was in part supported by the Institute for Basic Science, Korea (Grant No. IBS-R031-D1).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tarasov, O.B.; Gade, A.; Fukushima, K.; Hausmann, M.; Kwan, E.; Portillo, M.; Smith, M.; Ahn, D.S.; Bazin, D.; Chyzh, R.; et al. Observation of New Isotopes in the Fragmentation of Pt198 at FRIB. Phys. Rev. Lett. 2024, 132, 072501. [Google Scholar] [CrossRef] [PubMed]
- Dronchi, N.; Charity, R.J.; Sobotka, L.G.; Brown, B.A.; Weisshaar, D.; Gade, A.; Brown, K.W.; Reviol, W.; Bazin, D.; Farris, P.J.; et al. Evolution of shell gaps in the neutron-poor calcium region from invariant-mass spectroscopy of Sc37,38, Ca35, and K34. Phys. Rev. C 2024, 110, L031302. [Google Scholar] [CrossRef]
- Choi, Y.B.; Lee, C.H.; Mun, M.H.; Kim, Y. Bubble nuclei with shape coexistence in even-even isotopes of Hf to Hg. Phys. Rev. C 2022, 105, 024306. [Google Scholar] [CrossRef]
- Wong, C. Bubble nuclei. Phys. Lett. B 1972, 41, 451–454. [Google Scholar] [CrossRef]
- Todd-Rutel, B.G.; Piekarewicz, J.; Cottle, P.D. Spin orbit splitting in low j neutron orbits and proton densities in the nuclear interior. Phys. Rev. C 2004, 69, 021301. [Google Scholar] [CrossRef]
- Yao, J.M.; Baroni, S.; Bender, M.; Heenen, P.H. Beyond-mean-field study of the possible ‘bubble’ structure of 34Si. Phys. Rev. C 2012, 86, 014310. [Google Scholar] [CrossRef]
- Wang, Y.; Hou, Z.; Zhang, Q.; Tian, R.; Gu, J. Effect of a tensor force on the proton bubble structure of Hg206. Phys. Rev. C 2015, 91, 017302. [Google Scholar] [CrossRef]
- Duguet, T.; Somà, V.; Lecluse, S.; Barbieri, C.; Navrátil, P. Ab initio calculation of the potential bubble nucleus 34Si. Phys. Rev. C 2017, 95, 034319. [Google Scholar] [CrossRef]
- Saxena, G.; Kumawat, M.; Kaushik, M.; Jain, S.; Aggarwal, M. Bubble Structure in Magic Nuclei. Phys. Lett. B 2019, 788, 1–6. [Google Scholar] [CrossRef]
- Li, J.J.; Long, W.H.; Margueron, J.; Van Giai, N. 48Si: An atypical nucleus? Phys. Lett. B 2019, 788, 192–197. [Google Scholar] [CrossRef]
- Arthuis, P.; Barbieri, C.; Vorabbi, M.; Finelli, P. AbInitio Computation of Charge Densities for Sn and Xe Isotopes. Phys. Rev. Lett. 2020, 125, 182501. [Google Scholar] [CrossRef] [PubMed]
- Kumawat, M.; Saxena, G.; Kaushik, M.; Jain, S.; Deegwal, J.; Aggarwal, M. Novel feature of doubly bubble nuclei in 50 ≤ Z(N) ≤ 82 region along with magicity and weakly bound structure. Int. J. Mod. Phys. E 2020, 29, 2050068. [Google Scholar] [CrossRef]
- Khan, E.; Grasso, M.; Margueron, J.; Van Giai, N. Detecting bubbles in exotic nuclei. Nucl. Phys. A 2008, 800, 37–46. [Google Scholar] [CrossRef]
- Grasso, M.; Gaudefroy, L.; Khan, E.; Niksic, T.; Piekarewicz, J.; Sorlin, O.; Giai, N.; Vretenar, D. Nuclear ‘bubble’ structure in Si-34. Phys. Rev. C 2009, 79, 034318. [Google Scholar] [CrossRef]
- Shukla, A.; Åberg, S. Deformed bubble nuclei in the light-mass region. Phys. Rev. C 2014, 89, 014329. [Google Scholar] [CrossRef]
- Luo, Z.J.; Yu, K.; Zhou, X.R.; Cui, J.W.; Sagawa, H. Effects of deformation, pairing and tensor correlation on the evolution of bubble structure within the Skyrme-Hartree-Fock method. Eur. Phys. J. A 2018, 54, 193. [Google Scholar] [CrossRef]
- Saxena, G.; Kumawat, M.; Agrawal, B.; Aggarwal, M. A systematic study of the factors affecting central depletion in nuclei. J. Phys. G 2019, 46, 065105. [Google Scholar] [CrossRef]
- Meng, J.; Toki, H.; Zhou, S.G.; Zhang, S.Q.; Long, W.H.; Geng, L.S. Relativistic Continuum Hartree Bogoliubov theory for ground state properties of exotic nuclei. Prog. Part. Nucl. Phys. 2006, 57, 470–563. [Google Scholar] [CrossRef]
- Zhang, K.; Cheoun, M.-K.; Choi, Y.-B.; Chong, P.S.; Dong, J.; Geng, L.; Ha, E.; He, X.; Heo, C.; Ho, M.C.; et al. Deformed relativistic Hartree-Bogoliubov theory in continuum with point coupling functional: Examples of even-even Nd isotopes. Phys. Rev. C 2020, 102, 024314. [Google Scholar] [CrossRef]
- Pan, C.; Cheoun, M.-K.; Choi, Y.-B.; Dong, J.; Du, X.; Fan, X.H.; Gao, W.; Geng, L.; Ha, E.; He, X.-T.; et al. Deformed relativistic Hartree-Bogoliubov theory in continuum with a point-coupling functional. II. Examples of odd Nd isotopes. Phys. Rev. C 2022, 106, 014316. [Google Scholar] [CrossRef]
- Guo, P.; Cao, X.; Chen, K.; Chen, Z.; Cheoun, M.-K.; Choi, Y.-B.; Lam, P.C.; Deng, W.; Dong, J.; Du, P.; et al. Nuclear mass table in deformed relativistic Hartree–Bogoliubov theory in continuum, II: Even-Z nuclei. Atom. Data Nucl. Data Tabl. 2024, 158, 101661. [Google Scholar] [CrossRef]
- Kucharek, H.; Ring, P. Relativistic field theory of superfluidity in nuclei. Hadron. Nucl. 1991, 339, 23–35. [Google Scholar] [CrossRef]
- Zhao, P.; Li, Z.; Yao, J.; Meng, J. New parametrization for the nuclear covariant energy density functional with point-coupling interaction. Phys. Rev. C 2010, 82, 054319. [Google Scholar] [CrossRef]
- Sun, X.X.; Zhou, S.G. Rotating deformed halo nuclei and shape decoupling effects. Sci. Bull. 2021, 66, 2072–2078. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).