Abstract
This study investigates the masses and quadrupole deformations of even-Z nuclei within the range using the triaxial relativistic Hartree–Bogoliubov model (TRHB) with the PC-PK1 density functional. For odd-mass nuclei, the global minima were determined using the automatic blocking method and their dynamical correlation energies (DCEs) were approximated using the average values of neighboring even–even nuclei calculated from a microscopic, five-dimensional, collective Hamiltonian (5DCH). The mean-field results underestimate the binding energies of most open-shell nuclei, with an initial root–mean–square (rms) deviation of 2.56 MeV for 1223 even-Z nuclei. Incorporating DCEs significantly reduces this deviation to 1.36 MeV. Additionally, the descriptions of two-neutron and one-neutron separation energies are improved, with rms deviations decreasing to 0.75 MeV and 0.65 MeV, respectively. Further refinement through accounting for odd–even differences in DCEs reduces the rms deviations for binding energies and one-neutron separation energies to 1.30 MeV and 0.63 MeV, respectively. Regarding the quadrupole deformations, TRHB calculations reveal spherical shapes near shell and subshell closures, well-deformed shapes at the mid-shell, and rapid shape transitions in medium- and heavy-mass regions. Oblate shapes dominate in regions , and , and the neutron-deficient Pb region, with notable odd–even shape staggering attributed to the blocking effect of the odd nucleon. Triaxial shapes are favored in the mass regions and .
1. Introduction
Nuclear mass (or binding energy) is a fundamental property of atomic nuclei. To date, more than 3300 nuclides have been identified or synthesized in laboratories [1], with approximately 300 occurring naturally. Using advanced experimental techniques such as time-of-flight measurements, storage ring mass spectrometry, and ion trap methods [2,3], researchers have accurately determined the masses of more than 2500 nuclides [4].
Theoretical models predict that there are approximately 7000 to 12,000 bound nuclei [5,6], with the location of the neutron drip line for remaining highly uncertain. The search for the limits of nuclear binding is deeply intertwined with the need to understand the origin of elements [7]. In particular, the astrophysical rapid neutron-capture process, which is responsible for the formation of many heavy elements, critically depends on the properties of nuclei near the neutron drip line. These properties, however, will remain experimentally inaccessible in the foreseeable future, making theoretical predictions across the nuclear landscape indispensable. Over the past few decades, significant progress has been made using macroscopic–microscopic models [8,9,10,11], achieving remarkable accuracy with root–mean–square deviations of approximately 300 keV [12].
Nuclear density functional theory (DFT), based on effective nucleon–nucleon interactions, is a highly promising microscopic approach in the field of nuclear physics. It is built upon a universal energy density functional and, with just a limited number of parameters, it is able to describe not only the nuclear binding energies but also other crucial quantities relevant to simulating the nucleosynthesis process, such as -decay rates and fission rates, in a unified and comprehensive manner [13].
A number of Hartree–Fock–Bogoliubov (HFB) mass-table-type calculations have been performed based on the non-relativistic Skyrme [5,14,15,16,17,18] and Gogny [19,20,21] density functionals. The Skyrme mass model HFB-27* [18] determines its 24 parameters in functionals and corrections by fitting 2353 nuclear masses, achieving an accuracy of 0.512 MeV. The Gogny mass model D1M [20] incorporates the beyond-mean-field dynamical correlation energies (DCEs) and fits its 14 parameters to 2149 measured masses, resulting in a final rms deviation of 0.798 MeV.
The relativistic DFT was proven to be a powerful theory in nuclear physics and has been successfully employed to describe a variety of nuclear phenomena [22,23,24,25,26,27,28,29,30]. Significant progress in mass description has also been achieved based on relativistic DFT. In 2015, we performed a systematic calculation for 575 even–even nuclei using the relativistic mean-field plus Bardeen–Cooper–Schrieffer (RMF+BCS) framework with the PC-PK1 functional [31], and the beyond-mean-field DCEs were taken into account using a microscopically mapped, five-dimensional, collective Hamiltonian (5DCH) without additional free parameters. The root–mean–square (rms) deviation of nuclear masses was significantly reduced to 1.14 MeV [32]. In 2021, we extended our previous work to the nuclear landscape of even–even nuclei using an advanced triaxial relativistic Hartree–Bogoliubov (TRHB) framework [33]. It was emphasized that the nuclear landscape is considerably extended using the PC-PK1 functional compared to previous results obtained with the relativistic density functionals DD-PC1 [34] and TMA [35]. Moreover, the calculations reproduced the measured mass regions for the shape and the coexistence of multiple shapes and predict new regions [36].
Our final goal is to establish a global calculation for the nuclear ground state and low-lying excitation properties across the entire nuclear landscape using the TRHB with the PC-PK1 functional. As mentioned above, for the first step, we fulfilled this aim for even–even nuclei [33,36]. Here, we will conduct a study of the properties of odd-mass nuclei, focusing on the masses and quadrupole deformations of the even-Z odd-N nuclei whose masses have been measured. The key aspect is the appropriate handling of the blocking of odd nucleon and the beyond-mean-field DCEs. The blocking of odd nucleon was introduced in the TRHB model and successfully applied to numerous studies, such as the Yrast band of 109Ag [37], magnetic rotations in 198Pb and 199Pb [38], chirality in 106Ag [39], and nuclear decay [40]. As the variation in DCEs is gentle [33,41], in this work, we will approximately calculate the DCEs of odd-mass nuclei through the interpolation of those of neighboring even–even nuclei, and further phenomenologically take into account the odd–even differences in DCEs.
In Section 2, we introduce the Relativistic Hartree–Bogoliubov (RHB) theory and the blocking effect for odd-mass nuclei. Section 3 presents a systematic analysis of the binding energies, quadrupole deformations, and dynamical correlation energies (DCEs) of 1223 even-Z nuclei. Finally, the conclusions and future perspectives are summarized.
2. Theoretical Framework and Numerical Details
The RHB theory provides a unified and self-consistent treatment of mean fields and pairing correlations [42,43,44,45]. The RHB equation is as follows:
where is the Dirac Hamiltonian, is the pairing field, is the Fermi energy for neutron or proton (), is the quasiparticle energy, and and are the quasiparticle wave functions.
The Dirac Hamiltonian in the coordinate space is
with the scalar and vector potentials
constructed using the following densities:
According to the no-sea approximation, the summations in the above equations were performed over the quasiparticle states with positive energies in the Fermi sea. In Equations (3), we use PC-PK1 parametrization [31] for the parameters .
The pairing potential is as follows:
where, for simplicity, the spin and isospin degrees of freedom are not shown, and is the pairing tensor [46]. In principle, the same relativistic interaction used in Equations (2) and (3) can be applied to the pairing channel. In 1991, Kucharek and Ring [43] derived the Dirac–Hartree–Fock–Bogoliubov equations using a unified relativistic interaction within a quantum field theory framework. However, their analysis of pairing correlations in symmetric nuclear matter yielded excessively large pairing gaps due to the strongly repulsive nature of the relativistic nuclear interaction. Subsequent studies demonstrated that adopting the finite-range Gogny interaction or a separable pairing force [47] for the pairing channel produces more realistic pairing gaps. Therefore, in this work, we adopted the latter approach, employing the separable pairing force for :
The selected pairing interaction fails to maintain covariance. However, since a fully covariant treatment of paring dynamics in RMF theory is still an open question, we followed the widely practiced approach and used Equation (6) in the nuclear rest frame. Here, and denote the center of mass and the relative coordinates, respectively, and has a Gaussian expression
The projector allows only the states with a total spin . The two parameters G and a were determined in Ref. [47] through fitting to the density dependence of pairing gaps at the Fermi surface for nuclear matter obtained with the Gogny forces.
For an odd-mass nucleus, the blocking effect of the unpaired nucleon needs to be considered [46]. The ground state of a system with an unpaired particle can be described using a one-quasiparticle state:
where corresponds to the quasiparticle state that is properly blocked. In other words, the one-quasiparticle state is the vacuum with respect to the set of quasiparticle operators . That is, the blocking effect can be realized through the exchange of . According to Equation (1), this exchange corresponds to the exchange of the columns and that of the energy . In principle, the blocked orbital breaks the time reversal symmetry and the currents appear. However, in general, the contribution of the currents is very weak for the bulk properties of odd-mass nuclei [48], and thus the currents were neglected in the present calculation. To determine the ground state of an odd-mass nucleus, one needs to find the correct deformation minimum with the correct blocking orbital. Here, we blocked the lowest quasiparticle orbital in each iteration of TRHB equation, which is referred to as “automatic blocking”. Moreover, for the shape-coexisting nuclei or soft nuclei, one has to perform automatic blocking calculations staring from various initial states with different deformations.
The TRHB equation is solved through expanding the quasiparticle wavefunctions in terms of a three-dimensional harmonic oscillator basis in Cartesian coordinates [49]. For nuclei with Z < 20, , and , the harmonic oscillator basis contains 12, 14, and 16 major shells, respectively, and these were examined to determine their ability to provide converged results.
3. Results and Discussion
Figure 1 illustrates the differences between the experimental binding energies [4] and the theoretical ones calculated by the TRHB using the PC-PK1 functional for 1223 even-Z nuclei. The mean-field results for the nuclei around the neutron shell closure () and proton shell closure () agree well with the data. However, the binding energies were underestimated for most open-shell nuclei, and large discrepancies (>3 MeV) were found in the transitional regions (c.f. Figure 2). The root–mean–square (rms) deviation from the experimental nuclear binding energies is 2.56 MeV.
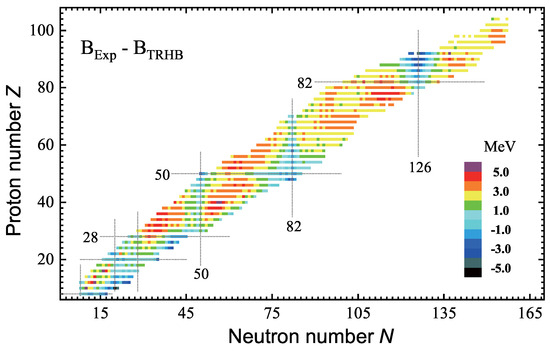
Figure 1.
Differences between the experimental binding energies [4] and the theoretical ones calculated by the TRHB with the PC-PK1 functional for 1223 even-Z nuclei. Considering the non-convergency of PC-PK1 for 14O, 23−26Mg, 26,27Si, 33,34S, and 34Ar, the PCF-PK1 functional [50] was adopted for these nuclei.
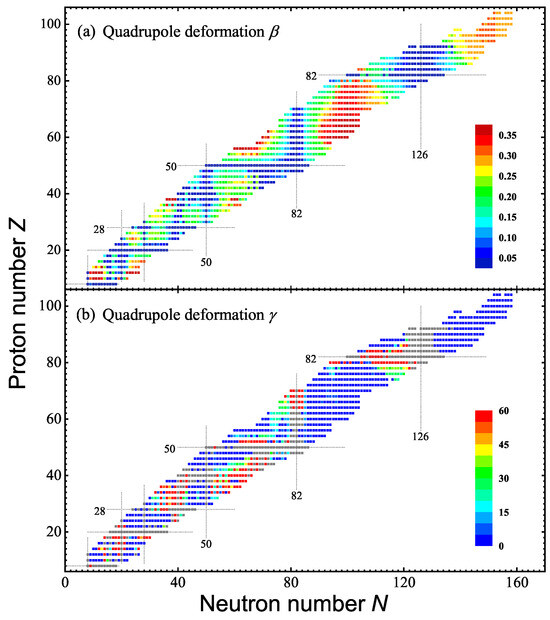
Figure 2.
Quadrupole deformations (panel (a)) and (panel (b)) of the mean-field ground state, calculated using TRHB with the PC-PK1 functional, are shown for 1223 even-Z nuclei. The gray color in panel (b) denotes the spherical nuclei, where is meaningless.
Figure 2 displays the quadrupole deformations and of the mean-field ground state, calculated using TRHB with PC-PK1 functional. Here, represents the quadrupole deformation, which is distinct from the 4 × 4 Dirac matrix in Equation (2). In general, the nuclei close to the shells and subshell () are spherical, while the mid-shell nuclei are well-deformed. Between these areas, rapid shape transitions or even shape phase transitions can be observed in the medium- and heavy-mass regions. Shape phase transitions are characterized by abrupt changes in the ground-state nuclear shape. In panel (b), most of the deformed nuclei are prolate and oblate shapes are favored in the regions , and , as well as in neutron-deficient Pb region, which are well-known to contain coexisting shapes [51,52]. Moreover, in these regions, the quadrupole deformations in the odd nuclei are quite different from those of the neighboring even nuclei, presenting with an odd–even staggered shape. This is due the subtle balance between the coexisting shapes with different blocking configurations occupied by the odd nucleon [53]. These results are consistent with those of DRHBc mass table [41] and HFB calculations using Gogny D1S [21]. In panel (b), it is also interesting to observe that triaxial shapes are favored in the mass regions and .
The TRHB results were obtained based on the static mean-field approximation, which is characterized through the breaking of symmetries in the underlying Hamiltonian, including translational, rotational, and particle number symmetries. This leads to the inclusion of static correlations such as deformations and pairing. However, to incorporate the dynamical correlations, one has to move beyond the mean-field approximation by restoring the broken symmetries and mixing the configurations of symmetry-breaking product states. For even–even nuclei, we utilized a TRHB-based, five-dimensional collective Hamiltonian (5DCH) to take into account the quadrupole dynamical correlations. The resulting ground-state energy of the state (laboratory frame) is derived without phenomenological adjustments, providing a direct comparison with the experimental data [33,36]. The dynamical correlation energy (DCE) can be defined as the energy difference between the mean-field global minimum in the intrinsic frame and the ground state with good angular momentum in the laboratory frame, representing the energy correction from the dynamical collective correlations. This aligns with the standard many-body techniques for symmetry restoration.
In Figure 3a, we take even–even Th isotopes as examples to illustrate the DCEs calculated from 5DCH based on TRHB with a PC-PK1 functional. These vary in a relatively mild manner with the neutron number, except for the nuclei close to the neutron shells. For the odd-mass nuclei, recently, rotational DCEs were extracted using the state-of-the-art angular momentum projection method, and it was found that they change smoothly from a light- to a heavy-mass region [54]. They also proved the validity of the cranking approximation for the odd-mass nuclei, which is used to construct a DRHBc mass table for the even-Z nuclei. Figure 3b displays the odd–even differences for the rotational DCEs, which were taken from the DRHBc mass table [41]. These are basically oscillated around 0.2 MeV. For nuclei in the gaps in Figure 3b, the DCE was set to zero, and the corresponding odd–even differences were consequently assigned a value of zero.
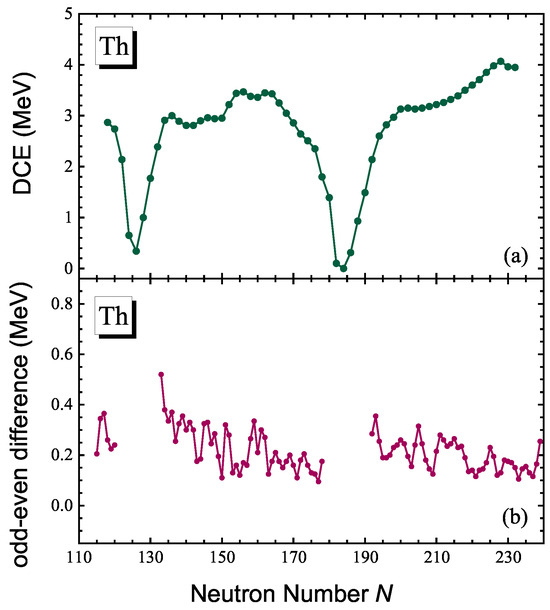
Figure 3.
(a) DCEs of the even–even Th isotopic chain calculated using 5DCH based on TRHB as a function of neutron number N. (b) Odd–even difference for the rotational DCEs of Th isotopes. The rotational DCEs are taken from the DRHBc mass table [41].
The above findings enable us to approximate the DCEs of odd-mass nuclei by averaging those of their neighboring even–even nuclei. In Figure 4 and Table 1, we present the differences between the experimental binding energies [4] and the theoretical values incorporating DCEs. Notably, the theoretical results exhibit excellent agreement with the experimental data, with the energy deviations for most nuclei falling within MeV. Larger deviations (>3 MeV) were primarily observed in light nuclei and the mass region. For the 1223 even-Z nuclei, the rms deviation from the experimental binding energies was significantly reduced to 1.36 MeV. Furthermore, in Figure 5 and Table 1, the description for both the two-neutron and one-neutron separation energies was optimized by considering the DCEs, and their rms deviations were reduced from 0.98 and 0.75 MeV to 0.75 and 0.65 MeV, respectively. Notably, this accurate description of nuclear binding energies was achieved using a global density functional, without introducing any additional phenomenological parameters.

Figure 4.
Differences between the experimental binding energies [4] and the theoretical ones calculated using the TRHB with DCEs for 1223 even-Z nuclei.

Table 1.
The rms deviations for the binding energies, two-neutron separation energies , and one-neutron separation energies in the TRHB calculations without (first row) and with (second row) DCEs, in comparison with the AME2020 data [4]. The dataset comprises 1223 nuclei from AME2020 data [4], including 606 even-Z odd-N nuclei and 617 neighboring even–even nuclei. The DCE* in the last row means that all the DCEs of 617 odd-mass nuclei were subtracted with a constant 0.20 MeV. All the values in the table are in the unit of MeV.
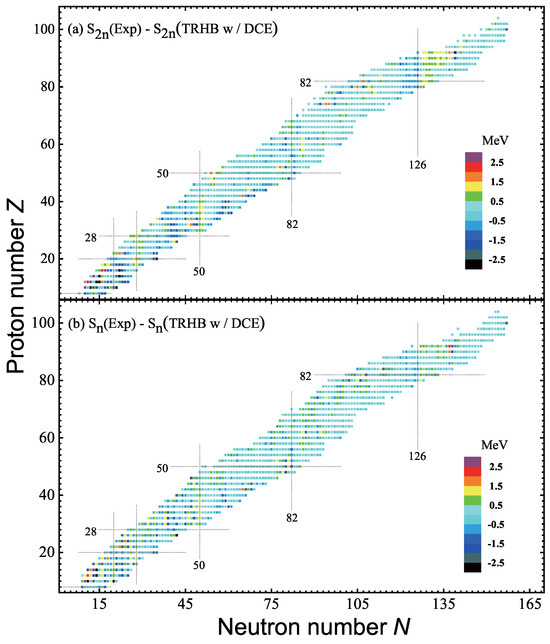
Figure 5.
Differences between the experimental separation energies [4] and the theoretical ones calculated using the TRHB with DCEs for 1223 even-Z nuclei. The two-neutron separation energies are shown in panel (a), while the one-neutron separation energies are shown in panel (b).
Finally, we considered the odd–even differences for DCEs through phenomenologically subtracting a constant from those of odd-mass nuclei. For odd-mass nuclei with an initial DCE = 0 or those whose DCEs would become negative after subtraction (i.e., DCE < 0), the DCEs were clamped at zero to ensure physical consistency. When the constant was chosen as 0.20 MeV, we obtained the best description for the binding energies and , whose rms deviations were further reduced to 1.30 and 0.63 MeV, respectively (see the last row of Table 1). This serveed as a valuable reference for future refinements of odd-A nuclei.
4. Summary and Outlook
In summary, the masses and quadrupole deformations of even-Z nuclei within the range were calculated using the triaxial relativistic Hartree–Bogoliubov model with the PC-PK1 density functional. For odd-mass nuclei, the global minima were determined via the automatic blocking method, while their dynamical correlation energies (DCEs) were approximated using the average values of adjacent even–even nuclei, derived from a microscopic five-dimensional collective Hamiltonian (5DCH) [33].
The mean-field results underestimate the nuclear binding energies for most open-shell nuclei, and the root–mean–square (rms) deviation is 2.56 MeV for the total 1223 even-Z nuclei. After incorporating dynamical correlation energies (DCEs), the rms deviation is significantly reduced to 1.36 MeV. Additionally, the description of two-neutron and one-neutron separation energies improves, with rms deviations decreasing from 0.98 MeV and 0.75 MeV to 0.75 MeV and 0.65 MeV, respectively. Further refinement is achieved by accounting for odd–even differences in DCEs through a phenomenological adjustment, where a constant 0.20 MeV is subtracted from the DCEs of odd-mass nuclei. This reduces the rms deviations for binding energies and one-neutron separation energies to 1.30 MeV and 0.63 MeV, respectively.
Regarding quadrupole deformations, nuclei near-shell and subshell closures have spherical shapes, while those at the mid-shell are very deformed. In the medium- and heavy-mass regions, rapid shape transitions—or even shape-phase transitions—are observed. Triaxial shapes are predicted in the mass regions and . Oblate shapes are favored in the regions , and , as well as in the neutron-deficient Pb region, where we also can also observe that the quadrupole deformations of odd nuclei differ significantly from those of the neighboring even nuclei, manifesting as an odd–even shape staggering. This phenomenon arises due to the delicate balance between coexisting shapes, influenced by the blocking configurations of the odd nucleon [53].
In the future, we will continue to investigate the covariance issues in the pairing interaction. The microscopic 5DCH framework can be extended to explicitly account for the contributions of odd nucleons. This would enable precise calculations of dynamical correlation energies (DCEs) for odd-mass and odd–odd nuclei, as well as the construction of a comprehensive nuclear landscape based on the PC-PK1 density functional or its advanced counterpart, PCF-PK1 [50].
Author Contributions
Writing—original draft preparation, Q.Z.; writing—review and editing, Z.L.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was partly supported by the National Natural Science Foundation of China (Grant No. 12375126) and the Fundamental Research Funds for the Central Universities.
Data Availability Statement
The dataset can be accessed upon request to the corresponding author.
Acknowledgments
Q. Zhou gratefully acknowledges the fruitful discussions and valuable assistance from P. W. Zhao, Y. K. Wang, Y. L. Yang, and T. Qu at Peking University, as well as M. H. Zhou at Southwest University. The helpful discussions with members of the DRHBc Mass Table Collaboration are highly appreciated.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Thoennessen, M. The Discovery of Isotopes; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Wang, M. Nuclear Mass Measurement and Evaluation. Nucl. Phys. Rev. 2017, 34, 380–386. [Google Scholar]
- Wang, M.; Zhang, Y.H.; Zhou, X.H. Nuclear mass measurements. Sci. Sin. Phys. Mech. Astron. 2020, 50, 052006. [Google Scholar]
- Wang, M.; Huang, W.J.; Kondev, F.G.; Audi, G.; Naimi, S. The AME 2020 atomic mass evaluation (II). Tables, graphs and references. Chin. Phys. C 2021, 45, 030003. [Google Scholar] [CrossRef]
- Erler, J.; Birge, N.; Kortelainen, M.; Nazarewicz, W.; Olsen, E.; Perhac, A.M.; Stoitsov, M. The limits of the nuclear landscape. Nature 2012, 486, 509–512. [Google Scholar] [CrossRef]
- Xia, X.W.; Lim, Y.; Zhao, P.W.; Liang, H.Z.; Qu, X.Y.; Chen, Y.; Liu, H.; Zhang, L.F.; Zhang, S.Q.; Kim, Y.; et al. The limits of the nuclear landscape explored by the relativistic continuum Hartree—Bogoliubov theory. At. Data Nucl. Data Tables 2018, 121–122, 1–215. [Google Scholar] [CrossRef]
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the elements in stars. Rev. Mod. Phys. 1957, 29, 547. [Google Scholar] [CrossRef]
- Möller, P.; Myers, W.; Swiatecki, W.; Treiner, J. Nuclear mass formula with a finite-range droplet model and a folded-Yukawa single-particle potential. At. Data Nucl. Data Tables 1988, 39, 225–233. [Google Scholar] [CrossRef]
- Moller, P.; Nix, J.; Myers, W.; Swiatecki, W. Nuclear Ground-State Masses and Deformations. At. Data Nucl. Data Tables 1995, 59, 185–381. [Google Scholar] [CrossRef]
- Möller, P.; Sierk, A.; Ichikawa, T.; Sagawa, H. Nuclear ground-state masses and deformations: FRDM(2012). At. Data Nucl. Data Tables 2016, 109–110, 1–204. [Google Scholar] [CrossRef]
- Haustein, P.E. An overview of the 1986–1987 atomic mass predictions. At. Data Nucl. Data Tables 1988, 39, 185–200. [Google Scholar] [CrossRef]
- Wang, N.; Liu, M.; Wu, X.Z.; Meng, J. Surface diffuseness correction in global mass formula. Phys. Lett. B 2014, 734, 215–219. [Google Scholar] [CrossRef]
- Bender, M.; Heenen, P.H.; Reinhard, P.G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 2003, 75, 121. [Google Scholar] [CrossRef]
- Samyn, M.; Goriely, S.; Heenen, P.H.; Pearson, J.; Tondeur, F. A hartree–fock–bogoliubov mass formula. Nucl. Phys. A 2002, 700, 142–156. [Google Scholar] [CrossRef]
- Stoitsov, M.; Dobaczewski, J.; Nazarewicz, W.; Pittel, S.; Dean, D. Systematic study of deformed nuclei at the drip lines and beyond. Phys. Rev. C—Nucl. Phys. 2003, 68, 054312. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J. Skyrme-Hartree-Fock-Bogoliubov Nuclear Mass Formulas: Crossing the 0.6 MeV Accuracy Threshold with Microscopically Deduced Pairing. Phys. Rev. Lett. 2009, 102, 152503. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J. Further explorations of Skyrme-Hartree-Fock-Bogoliubov mass formulas. XIII. The 2012 atomic mass evaluation and the symmetry coefficient. Phys. Rev. C—Nucl. Phys. 2013, 88, 024308. [Google Scholar] [CrossRef]
- Goriely, S.; Chamel, N.; Pearson, J. Hartree-Fock-Bogoliubov nuclear mass model with 0.50 MeV accuracy based on standard forms of Skyrme and pairing functionals. Phys. Rev. C—Nucl. Phys. 2013, 88, 061302. [Google Scholar] [CrossRef]
- Hilaire, S.; Girod, M. Large-scale mean-field calculations from proton to neutron drip lines using the D1S Gogny force. Eur. Phys. J. A 2007, 33, 237–241. [Google Scholar] [CrossRef]
- Goriely, S.; Hilaire, S.; Girod, M.; Peru, S. The Gogny-Hartree-Fock-Bogoliubov nuclear-mass model. Phys. Rev. Lett. 2009, 102, 242501. [Google Scholar] [CrossRef]
- Delaroche, J.P.; Girod, M.; Libert, J.; Goutte, H.; Hilaire, S.; Péru, S.; Pillet, N.; Bertsch, G. Structure of even-even nuclei using a mapped collective Hamiltonian and the D1S Gogny interaction. Phys. Rev. C—Nucl. Phys. 2010, 81, 014303. [Google Scholar] [CrossRef]
- Ring, P. Relativistic mean field theory in finite nuclei. Prog. Part. Nucl. Phys. 1996, 37, 193–263. [Google Scholar] [CrossRef]
- Vretenar, D.; Afanasjev, A.; Lalazissis, G.; Ring, P. Relativistic Hartree–Bogoliubov theory: Static and dynamic aspects of exotic nuclear structure. Phys. Rep. 2005, 409, 101–259. [Google Scholar] [CrossRef]
- Meng, J.; Toki, H.; Zhou, S.G.; Zhang, S.Q.; Long, W.H.; Geng, L.S. Relativistic continuum Hartree Bogoliubov theory for ground-state properties of exotic nuclei. Prog. Part. Nucl. Phys. 2006, 57, 470–563. [Google Scholar] [CrossRef]
- Nikšić, T.; Vretenar, D.; Ring, P. Relativistic nuclear energy density functionals: Mean-field and beyond. Prog. Part. Nucl. Phys. 2011, 66, 519–548. [Google Scholar] [CrossRef]
- Meng, J.; Peng, J.; Zhang, S.Q.; Zhao, P.W. Progress on tilted axis cranking covariant density functional theory for nuclear magnetic and antimagnetic rotation. Front. Phys. 2013, 8, 55–79. [Google Scholar] [CrossRef]
- Meng, J.; Zhou, S.G. Halos in medium-heavy and heavy nuclei with covariant density functional theory in continuum. J. Phys. G Nucl. Part. Phys. 2015, 42, 093101. [Google Scholar] [CrossRef]
- Zhou, S.G. Multidimensionally constrained covariant density functional theories—nuclear shapes and potential energy surfaces. Phys. Scr. 2016, 91, 063008. [Google Scholar] [CrossRef]
- Meng, J. Relativistic Density Functional for Nuclear Structure; World Scientific: Singapore, 2016; Volume 10. [Google Scholar]
- Shen, S.H.; Liang, H.Z.; Long, W.H.; Meng, J.; Ring, P. Towards an ab initio covariant density functional theory for nuclear structure. Prog. Part. Nucl. Phys. 2019, 109, 103713. [Google Scholar] [CrossRef]
- Zhao, P.W.; Li, Z.P.; Yao, J.M.; Meng, J. New parametrization for the nuclear covariant energy density functional with a point-coupling interaction. Phys. Rev. C 2010, 82, 054319. [Google Scholar] [CrossRef]
- Lu, K.Q.; Li, Z.X.; Li, Z.P.; Yao, J.M.; Meng, J. Global study of beyond-mean-field correlation energies in covariant energy density functional theory using a collective Hamiltonian method. Phys. Rev. C 2015, 91, 027304. [Google Scholar] [CrossRef]
- Yang, Y.L.; Wang, Y.K.; Zhao, P.W.; Li, Z.P. Nuclear landscape in a mapped collective Hamiltonian from covariant density functional theory. Phys. Rev. C 2021, 104, 054312. [Google Scholar] [CrossRef]
- Agbemava, S.; Afanasjev, A.; Ray, D.; Ring, P. Global performance of covariant energy density functionals: Ground state observables of even-even nuclei and the estimate of theoretical uncertainties. Phys. Rev. C 2014, 89, 054320. [Google Scholar] [CrossRef]
- Geng, L.S.; Toki, H.; Meng, J. Masses, Deformations and Charge Radii—Nuclear Ground-State Properties in the Relativistic Mean Field Model. Prog. Theor. Phys. 2005, 113, 785–800. [Google Scholar] [CrossRef]
- Yang, Y.L.; Zhao, P.W.; Li, Z.P. Shape and multiple shape coexistence of nuclei within covariant density functional theory. Phys. Rev. C 2023, 107, 024308. [Google Scholar] [CrossRef]
- Wang, Y.K. Yrast band of 109Ag described by tilted axis cranking covariant density functional theory with a separable pairing force. Phys. Rev. C 2017, 96, 054324. [Google Scholar] [CrossRef]
- Wang, Y.K. Magnetic rotations in 198Pb and 199Pb within covariant density functional theory with pairing correlations. Phy. Rev. C 2018, 97, 064321. [Google Scholar] [CrossRef]
- Zhao, P.W.; Wang, Y.K.; Chen, Q.B. Microscopic resolution of the nuclear chiral conundrum with crossing twin bands in 106Ag. Phys. Rev. C 2019, 99, 054319. [Google Scholar] [CrossRef]
- Wang, Y.K.; Zhao, P.W.; Meng, J. Relativistic configuration-interaction density functional theory: Nonaxial effects on nuclear ββ decay. Sci. Bull. 2024, 69, 2017–2020. [Google Scholar] [CrossRef] [PubMed]
- Guo, P.; Cao, X.J.; Chen, K.M.; Chen, Z.H.; Cheoun, M.K.; Choi, Y.B.; Lam, P.C.; Deng, W.M.; Dong, J.M.; Du, P.X.; et al. Nuclear mass table in deformed relativistic Hartree–Bogoliubov theory in continuum, II: Even-Z nuclei. At. Data Nucl. Data Tables 2024, 158, 101661. [Google Scholar] [CrossRef]
- Meng, J. Relativistic continuum Hartree-Bogoliubov theory with both zero range and finite range Gogny force and their application. Nucl. Phys. A 1998, 635, 3–42. [Google Scholar] [CrossRef]
- Kucharek, H.; Ring, P. Relativistic field theory of superfluidity in nuclei. Z. Für Phys. A Hadron. Nucl. 1991, 339, 23–35. [Google Scholar] [CrossRef]
- Gonzalez-Llarena, T.; Egido, J.; Lalazissis, G.; Ring, P. Relativistic Hartree-Bogoliubov calculations with finite range pairing forces. Phys. Lett. B 1996, 379, 13–19. [Google Scholar] [CrossRef]
- Serra, M.; Ring, P. Relativistic Hartree-Bogoliubov theory for finite nuclei. Phys. Rev. C 2002, 65, 064324. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Many Body Nuclear Problem; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Tian, Y.; Ma, Z.Y.; Ring, P. A finite range pairing force for density functional theory in superfluid nuclei. Phys. Lett. B 2009, 676, 44–50. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, K.Y.; Zhang, S.Q. Nuclear magnetism in the deformed halo nucleus 31Ne. Phys. Lett. B 2024, 855, 138792. [Google Scholar] [CrossRef]
- Nikšić, T.; Paar, N.; Vretenar, D.; Ring, P. DIRHB—A relativistic self-consistent mean-field framework for atomic nuclei. Comput. Phys. Commun. 2014, 185, 1808–1821. [Google Scholar] [CrossRef]
- Zhao, Q.; Ren, Z.X.; Zhao, P.W.; Meng, J. Covariant density functional theory with localized exchange terms. Phys. Rev. C 2022, 106, 034315. [Google Scholar] [CrossRef]
- Heyde, K.; Wood, J.L. Shape coexistence in atomic nuclei. Rev. Mod. Phys. 2011, 83, 1467–1521. [Google Scholar] [CrossRef]
- Quan, S.; Liu, W.P.; Li, Z.P.; Smith, M.S. Microscopic core-quasiparticle coupling model for spectroscopy of odd-mass nuclei. Phys. Rev. C 2017, 96, 054309. [Google Scholar] [CrossRef]
- Pan, C.; Cheoun, M.K.; Choi, Y.B.; Dong, J.M.; Du, X.K.; Fan, X.H.; Gao, W.; Geng, L.S.; Ha, E.; He, X.T.; et al. Deformed relativistic Hartree-Bogoliubov theory in continuum with a point-coupling functional. II. Examples of odd Nd isotopes. Phys. Rev. C 2022, 106, 014316. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, E.F.; Yao, J.M. Benchmarking rotational correction energies in odd-mass nuclei. arXiv 2024, arXiv:2409.12402. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).