The Impact of Asymmetric Dark Matter on the Thermal Evolution of Nucleonic and Hyperonic Compact Stars
Abstract
1. Introduction
2. Baryonic and Dark Matter EoSs
2.1. Baryonic Matter
2.2. Dark Matter
3. Two-Fluid Formalism
4. NS Thermal Evolution
5. Results
5.1. Hyperonic and Nucleonic DU Onsets
5.2. Mapping the Nucleonic and Hyperonic DU Regions Inside the Star
5.3. Cooling Curves
5.4. Thermal Evolution of Cassiopeia A as a DM-Admixed NS
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EoS | equation of state |
| NS | neutron star |
| BM | baryonic matter |
| DM | dark matter |
| DU | direct Urca |
| MU | modified Urca |
| GW | gravitational wave |
| PBF | pair breaking and formation |
| IST | Induced Surface Tension |
| TOV | Tolmann–Oppenheimer–Volkoff |
| JWST | James Webb Space Telescope |
Appendix A. Observational Data
References
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rep. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Wex, N.; Deller, A.T.; Coles, W.A.; Ali, M.; Burgay, M.; Camilo, F.; Cognard, I.; et al. Strong-Field Gravity Tests with the Double Pulsar. Phys. Rev. X 2021, 11, 041050. [Google Scholar] [CrossRef]
- Goldman, I.; Mohapatra, R.N.; Nussinov, S.; Rosenbaum, D.; Teplitz, V. Possible Implications of Asymmetric Fermionic Dark Matter for Neutron Stars. Phys. Lett. B 2013, 725, 200–207. [Google Scholar] [CrossRef]
- Ivanytskyi, O.; Sagun, V.; Lopes, I. Neutron stars: New constraints on asymmetric dark matter. Phys. Rev. D 2020, 102, 063028. [Google Scholar] [CrossRef]
- Karkevandi, D.R.; Shakeri, S.; Sagun, V.; Ivanytskyi, O. Bosonic dark matter in neutron stars and its effect on gravitational wave signal. Phys. Rev. D 2022, 105, 023001. [Google Scholar] [CrossRef]
- Giangrandi, E.; Sagun, V.; Ivanytskyi, O.; Providência, C.; Dietrich, T. The Effects of Self-interacting Bosonic Dark Matter on Neutron Star Properties. Astrophys. J. 2023, 953, 115. [Google Scholar] [CrossRef]
- Das, A.; Malik, T.; Nayak, A.C. Dark matter admixed neutron star properties in light of gravitational wave observations: A two fluid approach. Phys. Rev. D 2022, 105, 123034. [Google Scholar] [CrossRef]
- Dutra, M.; Lenzi, C.H.; Lourenço, O. Dark particle mass effects on neutron star properties from a short-range correlated hadronic model. Mon. Not. R. Astron. Soc. 2022, 517, 4265–4274. [Google Scholar] [CrossRef]
- Diedrichs, R.F.; Becker, N.; Jockel, C.; Christian, J.E.; Sagunski, L.; Schaffner-Bielich, J. Tidal deformability of fermion-boson stars: Neutron stars admixed with ultralight dark matter. Phys. Rev. D 2023, 108, 064009. [Google Scholar] [CrossRef]
- Lenzi, C.H.; Dutra, M.; Lourenço, O.; Lopes, L.L.; Menezes, D.P. Dark matter effects on hybrid star properties. Eur. Phys. J. C 2023, 83, 266. [Google Scholar] [CrossRef]
- Heger, A.; Fryer, C.L.; Woosley, S.E.; Langer, N.; Hartmann, D.H. How Massive Single Stars End Their Life. Astrophys. J. 2003, 591, 288–300. [Google Scholar] [CrossRef]
- Yang, W.; Chen, H.; Liu, S. The effect of dark matter on the Jeans instability with the q-nonextensive velocity distribution. AIP Adv. 2020, 10, 075003. [Google Scholar] [CrossRef]
- Meyer, M.; Petrushevska, T. Search for Axionlike-Particle-Induced Prompt γ-ray Emission from Extragalactic Core-Collapse Supernovae with the Fermi Large Area Telescope. Phys. Rev. Lett. 2020, 124, 231101, Erratum in Phys. Rev. Lett. 2020, 125, 119901. [Google Scholar] [CrossRef]
- Brito, R.; Cardoso, V.; Okawa, H. Accretion of Dark Matter by Stars. Phys. Rev. Lett. 2015, 115, 111301. [Google Scholar] [CrossRef]
- Kouvaris, C.; Tinyakov, P. Constraining Asymmetric Dark Matter through observations of compact stars. Phys. Rev. D 2011, 83, 083512. [Google Scholar] [CrossRef]
- Bramante, J.; Kavanagh, B.J.; Raj, N. Scattering Searches for Dark Matter in Subhalos: Neutron Stars, Cosmic Rays, and Old Rocks. Phys. Rev. Lett. 2022, 128, 231801. [Google Scholar] [CrossRef]
- Erickcek, A.L.; Sigurdson, K. Reheating Effects in the Matter Power Spectrum and Implications for Substructure. Phys. Rev. D 2011, 84, 083503. [Google Scholar] [CrossRef]
- Buckley, M.R.; DiFranzo, A. Collapsed Dark Matter Structures. Phys. Rev. Lett. 2018, 120, 051102. [Google Scholar] [CrossRef]
- Dengler, Y.; Schaffner-Bielich, J.; Tolos, L. Second Love number of dark compact planets and neutron stars with dark matter. Phys. Rev. D 2022, 105, 043013. [Google Scholar] [CrossRef]
- Maselli, A.; Pnigouras, P.; Nielsen, N.G.; Kouvaris, C.; Kokkotas, K.D. Dark stars: Gravitational and electromagnetic observables. Phys. Rev. D 2017, 96, 023005. [Google Scholar] [CrossRef]
- Kouvaris, C.; Nielsen, N.G. Asymmetric dark matter stars. Phys. Rev. D 2015, 92, 063526. [Google Scholar] [CrossRef]
- Ellis, J.; Hektor, A.; Hütsi, G.; Kannike, K.; Marzola, L.; Raidal, M.; Vaskonen, V. Search for Dark Matter Effects on Gravitational Signals from Neutron Star Mergers. Phys. Lett. B 2018, 781, 607–610. [Google Scholar] [CrossRef]
- Giudice, G.F.; McCullough, M.; Urbano, A. Hunting for Dark Particles with Gravitational Waves. J. Cosmol. Astropart. Phys. 2016, 10, 001. [Google Scholar] [CrossRef]
- Emma, M.; Schianchi, F.; Pannarale, F.; Sagun, V.; Dietrich, T. Numerical Simulations of Dark Matter Admixed Neutron Star Binaries. Particles 2022, 5, 24. [Google Scholar] [CrossRef]
- Bezares, M.; Viganò, D.; Palenzuela, C. Gravitational wave signatures of dark matter cores in binary neutron star mergers by using numerical simulations. Phys. Rev. D 2019, 100, 044049. [Google Scholar] [CrossRef]
- Hippert, M.; Dillingham, E.; Tan, H.; Curtin, D.; Noronha-Hostler, J.; Yunes, N. Dark matter or regular matter in neutron stars? How to tell the difference from the coalescence of compact objects. Phys. Rev. D 2023, 107, 115028. [Google Scholar] [CrossRef]
- Rüter, H.R.; Sagun, V.; Tichy, W.; Dietrich, T. Quasiequilibrium configurations of binary systems of dark matter admixed neutron stars. Phys. Rev. D 2023, 108, 124080. [Google Scholar] [CrossRef]
- Bauswein, A.; Guo, G.; Lien, J.H.; Lin, Y.H.; Wu, M.R. Compact dark objects in neutron star mergers. Phys. Rev. D 2023, 107, 083002. [Google Scholar] [CrossRef]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quant. Grav. 2010, 27, 194002. [Google Scholar] [CrossRef]
- Mills, C.; Tiwari, V.; Fairhurst, S. Localization of binary neutron star mergers with second and third generation gravitational-wave detectors. Phys. Rev. D 2018, 97, 104064. [Google Scholar] [CrossRef]
- Ackley, K.; Adya, V.B.; Agrawal, P.; Altin, P.; Ashton, G.; Bailes, M.; Baltinas, E.; Barbuio, A.; Beniwal, D.; Blair, C.; et al. Neutron Star Extreme Matter Observatory: A kilohertz-band gravitational-wave detector in the global network. Publ. Astron. Soc. Austral. 2020, 37, e047. [Google Scholar] [CrossRef]
- Shakeri, S.; Karkevandi, D.R. Bosonic Dark Matter in Light of the NICER Precise Mass-Radius Measurements. arXiv 2022, arXiv:2210.17308. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Elshamouty, K.G.; Heinke, C.O.; Potekhin, A.Y. Tests of the nuclear equation of state and superfluid and superconducting gaps using the Cassiopeia A neutron star. Phys. Rev. C 2015, 91, 015806. [Google Scholar] [CrossRef]
- Sagun, V.; Giangrandi, E.; Dietrich, T.; Ivanytskyi, O.; Negreiros, R.; Providência, C. What Is the Nature of the HESS J1731-347 Compact Object? Astrophys. J. 2023, 958, 49. [Google Scholar] [CrossRef]
- Sales, T.; Lourenço, O.; Dutra, M.; Negreiros, R. Revisiting the thermal relaxation of neutron stars. Astron. Astrophys. 2020, 642, A42. [Google Scholar] [CrossRef]
- Page, D.; Lattimer, J.M.; Prakash, M.; Steiner, A.W. Minimal cooling of neutron stars: A New paradigm. Astrophys. J. Suppl. 2004, 155, 623–650. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Pethick, C.J. Neutron star cooling. Ann. Rev. Astron. Astrophys. 2004, 42, 169–210. [Google Scholar] [CrossRef]
- Maxwell, O.V. Neutrino Emission Processes in Hyperon Populated Neutron Stars. Astrophys. J. 1987, 316, 691–707. [Google Scholar] [CrossRef][Green Version]
- Prakash, M.; Prakash, M.; Lattimer, J.M.; Pethick, C.J. Rapid cooling of neutron stars by hyperons and Delta isobars. Astrophys. J. Lett. 1992, 390, L77. [Google Scholar] [CrossRef]
- Kaminker, A.D.; Yakovlev, D.G.; Haensel, P. Theory of neutrino emission from nucleon–hyperon matter in neutron stars: Angular integrals. Astrophys. Space Sci. 2016, 361, 267. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M.; Pethick, C.J.; Haensel, P. Direct URCA process in neutron stars. Phys. Rev. Lett. 1991, 66, 2701–2704. [Google Scholar] [CrossRef]
- Page, D.; Geppert, U.; Weber, F. The Cooling of compact stars. Nucl. Phys. A 2006, 777, 497–530. [Google Scholar] [CrossRef]
- Potekhin, A.Y.; Pons, J.A.; Page, D. Neutron stars—Cooling and transport. Space Sci. Rev. 2015, 191, 239–291. [Google Scholar] [CrossRef]
- Tolos, L.; Centelles, M.; Ramos, A. The Equation of State for the Nucleonic and Hyperonic Core of Neutron Stars. Publ. Astron. Soc. Austral. 2017, 34, e065. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Weber, F. Competition between delta isobars and hyperons and properties of compact stars. Phys. Lett. B 2018, 783, 234–240. [Google Scholar] [CrossRef]
- Sedrakian, A.; Harutyunyan, A. Delta-resonances and hyperons in proto-neutron stars and merger remnants. Eur. Phys. J. A 2022, 58, 137. [Google Scholar] [CrossRef]
- Fortin, M.; Providencia, C.; Raduta, A.R.; Gulminelli, F.; Zdunik, J.L.; Haensel, P.; Bejger, M. Neutron star radii and crusts: Uncertainties and unified equations of state. Phys. Rev. C 2016, 94, 035804. [Google Scholar] [CrossRef]
- Raduta, A.R.; Sedrakian, A.; Weber, F. Cooling of hypernuclear compact stars. Mon. Not. R. Astron. Soc. 2018, 475, 4347–4356. [Google Scholar] [CrossRef]
- Demorest, P.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. Shapiro Delay Measurement of A Two Solar Mass Neutron Star. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Togashi, H.; Tamagawa, T.; Furumoto, T.; Yasutake, N.; Rijken, T.A. Neutron-star radii based on realistic nuclear interactions. Phys. Rev. C 2017, 96, 065804. [Google Scholar] [CrossRef]
- Shahrbaf, M.; Blaschke, D.; Typel, S.; Farrar, G.R.; Alvarez-Castillo, D.E. Sexaquark dilemma in neutron stars and its solution by quark deconfinement. Phys. Rev. D 2022, 105, 103005. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef]
- Ivanytskyi, O.; Blaschke, D. Density functional approach to quark matter with confinement and color superconductivity. Phys. Rev. D 2022, 105, 114042. [Google Scholar] [CrossRef]
- Ivanytskyi, O.; Blaschke, D.B. Recovering the Conformal Limit of Color Superconducting Quark Matter within a Confining Density Functional Approach. Particles 2022, 5, 38. [Google Scholar] [CrossRef]
- Gärtlein, C.; Ivanytskyi, O.; Sagun, V.; Blaschke, D. Hybrid star phenomenology from the properties of the special point. Phys. Rev. D 2023, 108, 114028. [Google Scholar] [CrossRef]
- Fortin, M.; Raduta, A.R.; Avancini, S.; Providência, C. Relativistic hypernuclear compact stars with calibrated equations of state. Phys. Rev. D 2020, 101, 034017. [Google Scholar] [CrossRef]
- Fortin, M.; Raduta, A.R.; Avancini, S.; Providência, C. Thermal evolution of relativistic hyperonic compact stars with calibrated equations of state. Phys. Rev. D 2021, 103, 083004. [Google Scholar] [CrossRef]
- Baryakhtar, M.; Bramante, J.; Li, S.W.; Linden, T.; Raj, N. Dark Kinetic Heating of Neutron Stars and An Infrared Window On WIMPs, SIMPs, and Pure Higgsinos. Phys. Rev. Lett. 2017, 119, 131801. [Google Scholar] [CrossRef]
- Raj, N.; Tanedo, P.; Yu, H.B. Neutron stars at the dark matter direct detection frontier. Phys. Rev. D 2018, 97, 043006. [Google Scholar] [CrossRef]
- Chatterjee, S.; Garani, R.; Jain, R.K.; Kanodia, B.; Kumar, M.S.N.; Vempati, S.K. Faint light of old neutron stars and detectability at the James Webb Space Telescope. Phys. Rev. D 2023, 108, L021301. [Google Scholar] [CrossRef]
- Wijnands, R.; Degenaar, N.; Page, D. Cooling of Accretion-Heated Neutron Stars. J. Astrophys. Astron. 2017, 38, 49. [Google Scholar] [CrossRef]
- Aguilera, D.N.; Pons, J.A.; Miralles, J.A. The impact of magnetic field on the thermal evolution of neutron stars. Astrophys. J. Lett. 2008, 673, L167–L170. [Google Scholar] [CrossRef]
- Hamaguchi, K.; Nagata, N.; Yanagi, K. Dark Matter Heating vs. Rotochemical Heating in Old Neutron Stars. Phys. Lett. B 2019, 795, 484–489. [Google Scholar] [CrossRef]
- Berryman, J.M.; Gardner, S.; Zakeri, M. Neutron Stars with Baryon Number Violation, Probing Dark Sectors. Symmetry 2022, 14, 518. [Google Scholar] [CrossRef]
- Baym, G.; Beck, D.; Geltenbort, P.; Shelton, J. Testing Dark Decays of Baryons in Neutron Stars. Physical Review Letters 2018, 121, 061801. [Google Scholar] [CrossRef] [PubMed]
- Motta, T.F.; Guichon, P.A.M.; Thomas, A.W. Implications of neutron star properties for the existence of light dark matter. J. Phys. G Nucl. Part. Phys. 2018, 45, 05LT01. [Google Scholar] [CrossRef]
- Motta, T.F.; Guichon, P.A.M.; Thomas, A.W. Neutron to dark matter decay in neutron stars. Int. J. Mod. Phys. A 2018, 33, 1844020. [Google Scholar] [CrossRef]
- De Lavallaz, A.; Fairbairn, M. Neutron stars as dark matter probes. Phys. Rev. D 2010, 81, 123521. [Google Scholar] [CrossRef]
- Ángeles Pérez-García, M.; Grigorian, H.; Albertus, C.; Barba, D.; Silk, J. Cooling of Neutron Stars admixed with light dark matter: A case study. Phys. Lett. B 2022, 827, 136937. [Google Scholar] [CrossRef]
- Kouvaris, C. WIMP annihilation and cooling of neutron stars. Phys. Rev. D 2008, 77, 023006. [Google Scholar] [CrossRef]
- Bramante, J.; Raj, N. Dark matter in compact stars. Phys. Rep. 2024, 1052, 1–48. [Google Scholar] [CrossRef]
- Haberl, F. AXPs and X-ray-dim isolated neutron stars: Recent XMM-Newton and Chandra results. Adv. Space Res. 2004, 33, 638–644. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Cassano, R.; Fender, R.; Ferrari, C.; Merloni, A.; Akahori, T.; Akamatsu, H.; Ascasibar, Y.; Ballantyne, D.; Brunetti, G.; Corbelli, E.; et al. SKA-Athena Synergy White Paper. arXiv 2018, arXiv:1807.09080. [Google Scholar]
- In’t Zand, J.J.M.; Bozzo, E.; Qu, J.; Li, X.D.; Amati, L.; Chen, Y.; Donnarumma, I.; Doroshenko, V.; Drake, S.A.; Hernanz, M.; et al. Observatory science with eXTP. Sci. China Phys. Mech. Astron. 2019, 62, 029506. [Google Scholar] [CrossRef]
- Ray, P.S.; STROBE-X Steering Committee & Working Group. STROBE-X: X-ray Timing and Spectroscopy on Dynamical Timescales from Microseconds to Years. arXiv 2019, arXiv:1903.03035. [Google Scholar]
- Kumar, A.; Das, H.C.; Patra, S.K. Thermal relaxation of dark matter admixed neutron star. Mon. Not. R. Astron. Soc. 2022, 513, 1820–1833. [Google Scholar] [CrossRef]
- Garani, R.; Palomares-Ruiz, S. Evaporation of dark matter from celestial bodies. J. Cosmol. Astropart. Phys. 2022, 5, 042. [Google Scholar] [CrossRef]
- Dietrich, T.; Clough, K. Cooling binary neutron star remnants via nucleon-nucleon-axion bremsstrahlung. Phys. Rev. D 2019, 100, 083005. [Google Scholar] [CrossRef]
- Sedrakian, A. Axion cooling of neutron stars. Phys. Rev. D 2016, 93, 065044. [Google Scholar] [CrossRef]
- Buschmann, M.; Co, R.T.; Dessert, C.; Safdi, B.R. Axion Emission Can Explain a New Hard X-ray Excess from Nearby Isolated Neutron Stars. Phys. Rev. Lett. 2021, 126, 021102. [Google Scholar] [CrossRef] [PubMed]
- Buschmann, M.; Dessert, C.; Foster, J.W.; Long, A.J.; Safdi, B.R. Upper Limit on the QCD Axion Mass from Isolated Neutron Star Cooling. Phys. Rev. Lett. 2022, 128, 091102. [Google Scholar] [CrossRef] [PubMed]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Ávila, A.; Giangrandi, E.; Sagun, V.; Ivanytskyi, O.; Providência, C. Rapid neutron star cooling triggered by dark matter. arXiv 2024, arXiv:2309.03894. [Google Scholar] [CrossRef]
- Sagun, V.V.; Ivanytskyi, A.I.; Bugaev, K.A.; Mishustin, I.N. The statistical multifragmentation model for liquid-gas phase transition with a compressible nuclear liquid. Nucl. Phys. A 2014, 924, 24–46. [Google Scholar] [CrossRef]
- Bugaev, K.A.; Vitiuk, O.V.; Grinyuk, B.E.; Panasiuk, P.P.; Yakovenko, N.S.; Zherebtsova, E.S.; Sagun, V.V.; Ivanytskyi, O.I.; Bravina, L.V.; Blaschke, D.B.; et al. Induced surface and curvature tension equation of state for hadron resonance gas in finite volumes and its relation to morphological thermodynamics. Int. J. Mod. Phys. A 2021, 36, 2141009. [Google Scholar] [CrossRef]
- Sagun, V.V.; Bugaev, K.A.; Ivanytskyi, A.I.; Yakimenko, I.P.; Nikonov, E.G.; Taranenko, A.V.; Greiner, C.; Blaschke, D.B.; Zinovjev, G.M. Hadron Resonance Gas Model with Induced Surface Tension. Eur. Phys. J. A 2018, 54, 100. [Google Scholar] [CrossRef]
- Sagun, V.V.; Bugaiev, K.A.; Ivanytskyi, A.I.; Oliinychenko, D.R.; Mishustin, I.N. Effects of Induced Surface Tension in Nuclear and Hadron Matter. EPJ Web Conf. 2017, 137, 09007. [Google Scholar] [CrossRef]
- Sagun, V.V.; Lopes, I.; Ivanytskyi, A.I. The induced surface tension contribution for the equation of state of neutron stars. Astrophys. J. 2019, 871, 157. [Google Scholar] [CrossRef]
- Sagun, V.; Panotopoulos, G.; Lopes, I. Asteroseismology: Radial oscillations of neutron stars with realistic equation of state. Phys. Rev. D 2020, 101, 063025. [Google Scholar] [CrossRef]
- Chen, W.C.; Piekarewicz, J. Building relativistic mean field models for finite nuclei and neutron stars. Phys. Rev. C 2014, 90, 044305. [Google Scholar] [CrossRef]
- Gal, A.; Hungerford, E.V.; Millener, D.J. Strangeness in nuclear physics. Rev. Mod. Phys. 2016, 88, 035004. [Google Scholar] [CrossRef]
- Li, J.J.; Long, W.H.; Sedrakian, A. Hypernuclear stars from relativistic Hartree-Fock density functional theory. Eur. Phys. J. A 2018, 54, 133. [Google Scholar] [CrossRef]
- Haensel, P.; Zdunik, J.L. Non-equilibrium processes in the crust of an accreting neutron star. Astron. Astrophys. 1990, 227, 431–436. [Google Scholar]
- Negele, J.W.; Vautherin, D. Neutron star matter at subnuclear densities. Nucl. Phys. A 1973, 207, 298–320. [Google Scholar] [CrossRef]
- Nelson, A.; Reddy, S.; Zhou, D. Dark halos around neutron stars and gravitational waves. J. Cosmol. Astropart. Phys. 2019, 7, 012. [Google Scholar] [CrossRef]
- Bell, N.F.; Melatos, A.; Petraki, K. Realistic neutron star constraints on bosonic asymmetric dark matter. Phys. Rev. D 2013, 87, 123507. [Google Scholar] [CrossRef]
- Eckert, D.; Ettori, S.; Robertson, A.; Massey, R.; Pointecouteau, E.; Harvey, D.; McCarthy, I.G. Constraints on dark matter self-interaction from the internal density profiles of X-COP galaxy clusters. Astron. Astrophys. 2022, 666, A41. [Google Scholar] [CrossRef]
- Clowe, D.; Bradač, M.; Gonzalez, A.H.; Markevitch, M.; Randall, S.W.; Jones, C.; Zaritsky, D. A Direct Empirical Proof of the Existence of Dark Matter. Astrophys. J. 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Randall, S.W.; Markevitch, M.; Clowe, D.; Gonzalez, A.H.; Bradac, M. Constraints on the Self-Interaction Cross-Section of Dark Matter from Numerical Simulations of the Merging Galaxy Cluster 1E 0657-56. Astrophys. J. 2008, 679, 1173–1180. [Google Scholar] [CrossRef]
- Goodman, J.; Ibe, M.; Rajaraman, A.; Shepherd, W.; Tait, T.M.P.; Yu, H.B. Constraints on Dark Matter from Colliders. Phys. Rev. D 2010, 82, 116010. [Google Scholar] [CrossRef]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J1810+1744: Companion Darkening and a Precise High Neutron Star Mass. Astrophys. J. Lett. 2021, 908, L46. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Greif, S.K.; Hebeler, K.; Hinderer, T.; Nissanke, S.; Schwenk, A.; Riley, T.E.; Watts, A.L.; Lattimer, J.M.; Ho, W.C.G. Constraints on the Dense Matter Equation of State and Neutron Star Properties from NICER’s Mass–Radius Estimate of PSR J0740+6620 and Multimessenger Observations. Astrophys. J. Lett. 2021, 918, L29. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼3.4M⊙. Astrophys. J. Lett. 2020, 892, L3. [Google Scholar] [CrossRef]
- Doroshenko, V.; Suleimanov, V.; Pühlhofer, G.; Santangelo, A. A strangely light neutron star within a supernova remnant. Nat. Astron. 2022, 6, 1444–1451. [Google Scholar] [CrossRef]
- Hessels, J.W.T.; Ransom, S.M.; Stairs, I.H.; Freire, P.C.C.; Kaspi, V.M.; Camilo, F. A radio pulsar spinning at 716-Hz. Science 2006, 311, 1901–1904. [Google Scholar] [CrossRef]
- Yakovlev, D.G.; Kaminker, A.D.; Gnedin, O.Y.; Haensel, P. Neutrino emission from neutron stars. Phys. Rep. 2001, 354, 1. [Google Scholar] [CrossRef]
- Schaab, C.; Balberg, S.; Schaffner-Bielich, J. Implications of hyperon pairing for cooling of neutron stars. Astrophys. J. Lett. 1998, 504, L99. [Google Scholar] [CrossRef][Green Version]
- Providência, C.; Fortin, M.; Pais, H.; Rabhi, A. Hyperonic stars and the symmetry energy. Front. Astron. Space Sci. 2019, 6, 13. [Google Scholar] [CrossRef]
- Iwamoto, N. Quark beta decay and the cooling of neutron stars. Phys. Rev. Lett. 1980, 44, 1637–1640. [Google Scholar] [CrossRef]
- Iwamoto, N. Neutrino emissivities and mean free paths of degenerate quark matter. Annals Phys. 1982, 141, 1–49. [Google Scholar] [CrossRef]
- Page, D. NSCool: Neutron Star Cooling Code. Astrophysics Source Code Library, Record ascl:1609.009. 2016. Available online: http://xxx.lanl.gov/abs/1609.009 (accessed on 1 March 2023).
- Yakovlev, D.G.; Levenfish, K.P.; Shibanov, Y.A. Cooling neutron stars and superfluidity in their interiors. Phys. Usp. 1999, 42, 737–778. [Google Scholar] [CrossRef]
- Baiko, D.A.; Haensel, P.; Yakovlev, D.G. Thermal conductivity of neutrons in neutron star cores. Astron. Astrophys. 2001, 374, 151. [Google Scholar] [CrossRef]
- Schwenk, A.; Friman, B.; Brown, G.E. Renormalization group approach to neutron matter: Quasiparticle interactions, superfluid gaps and the equation of state. Nucl. Phys. A 2003, 713, 191–216. [Google Scholar] [CrossRef]
- Chen, J.M.C.; Clark, J.W.; Davé, R.D.; Khodel, V.V. Pairing gaps in nucleonic superfluids. Nucl. Phys. A 1993, 555, 59–89. [Google Scholar] [CrossRef]
- Negreiros, R.; Tolos, L.; Centelles, M.; Ramos, A.; Dexheimer, V. Cooling of Small and Massive Hyperonic Stars. Astrophys. J. 2018, 863, 104. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Heinke, C.O. A Neutron Star with a Carbon Atmosphere in the Cassiopeia A Supernova Remnant. Nature 2009, 462, 71–73. [Google Scholar] [CrossRef] [PubMed]
- Heinke, C.O.; Ho, W.C.G. Direct Observation of the Cooling of the Cassiopeia A Neutron Star. Astrophys. J. Lett. 2010, 719, L167–L171. [Google Scholar] [CrossRef]
- Shternin, P.S.; Yakovlev, D.G.; Heinke, C.O.; Ho, W.C.G.; Patnaude, D.J. Cooling neutron star in the Cassiopeia~A supernova remnant: Evidence for superfluidity in the core. Mon. Not. R. Astron. Soc. Lett. 2011, 412, L108–L112. [Google Scholar] [CrossRef]
- Elshamouty, K.G.; Heinke, C.O.; Sivakoff, G.R.; Ho, W.C.G.; Shternin, P.S.; Yakovlev, D.G.; Patnaude, D.J.; David, L. Measuring the Cooling of the Neutron Star in Cassiopeia A with all Chandra X-ray Observatory Detectors. Astrophys. J. 2013, 777, 22. [Google Scholar] [CrossRef]
- Wijngaarden, M.J.P.; Ho, W.C.G.; Chang, P.; Heinke, C.O.; Page, D.; Beznogov, M.; Patnaude, D.J. Diffusive nuclear burning in cooling simulations and application to new temperature data of the Cassiopeia A neutron star. Mon. Not. R. Astron. Soc. Lett. 2019, 484, 974–988. [Google Scholar] [CrossRef]
- Shternin, P.S.; Ofengeim, D.D.; Heinke, C.O.; Ho, W.C.G. Constraints on neutron star superfluidity from the cooling neutron star in Cassiopeia A using all Chandra ACIS-S observations. Mon. Not. R. Astron. Soc. Lett. 2022, 518, 2775–2793. [Google Scholar] [CrossRef]
- Page, D.; Prakash, M.; Lattimer, J.M.; Steiner, A.W. Rapid Cooling of the Neutron Star in Cassiopeia A Triggered by Neutron Superfluidity in Dense Matter. Phys. Rev. Lett. 2011, 106, 081101. [Google Scholar] [CrossRef]
- Taranto, G.; Burgio, G.F.; Schulze, H.J. Cassiopeia A and direct URCA cooling. Mon. Not. R. Astron. Soc. Lett. 2016, 456, 1451–1458. [Google Scholar] [CrossRef]
- Blaschke, D.; Grigorian, H.; Voskresensky, D.N.; Weber, F. On the Cooling of the Neutron Star in Cassiopeia A. Phys. Rev. C 2012, 85, 022802. [Google Scholar] [CrossRef]
- Hamaguchi, K.; Nagata, N.; Yanagi, K.; Zheng, J. Limit on the Axion Decay Constant from the Cooling Neutron Star in Cassiopeia A. Phys. Rev. D 2018, 98, 103015. [Google Scholar] [CrossRef]
- Tsiopelas, S.; Sagun, V. Neutron star cooling within the equation of state with induced surface tension. Particles 2020, 3, 45. [Google Scholar] [CrossRef]
- Tsiopelas, S.; Sagun, V. Thermal evolution of neutron stars described within the equation of state with induced surface tension. Astron. Nachr. 2021, 342, 332–336. [Google Scholar] [CrossRef]
- Takatsuka, T. Energy Gap in Neutron-Star Matter. Prog. Theor. Phys. 1972, 48, 1517–1533. [Google Scholar] [CrossRef]
- Nan, R.; Li, D.; Jin, C.; Wang, Q.; Zhu, L.; Zhu, W.; Zhang, H.; Yue, Y.; Qian, L. The Five-Hundred-Meter Aperture Spherical Radio Telescope (FAST) Project. Int. J. Mod. Phys. D 2011, 20, 989–1024. [Google Scholar] [CrossRef]
- Carilli, C.L.; Rawlings, S. Science with the Square Kilometer Array: Motivation, key science projects, standards and assumptions. New Astron. Rev. 2004, 48, 979. [Google Scholar] [CrossRef]
- Amiri, M.; Bandura, K.M.; Boyle, P.J.; Brar, C.; Cliche, J.F.; Crowter, K.; Cubranic, D.; Demorest, P.B.; Denman, N.T.; Dobbs, M.; et al. The CHIME Pulsar Project: System Overview. Astrophys. J. Supp. 2021, 255, 5. [Google Scholar] [CrossRef]
- Skidmore, W. TMT International Science Development Teams & TMT Science Advisory Committee Thirty Meter Telescope Detailed Science Case: 2015. Res. Astron. Astrophys. 2015, 15, 1945–2140. [Google Scholar] [CrossRef]
- Beznogov, M.V.; Yakovlev, D.G. Statistical theory of thermal evolution of neutron stars. Mon. Not. R. Astron. Soc. 2015, 447, 1598–1609. [Google Scholar] [CrossRef]
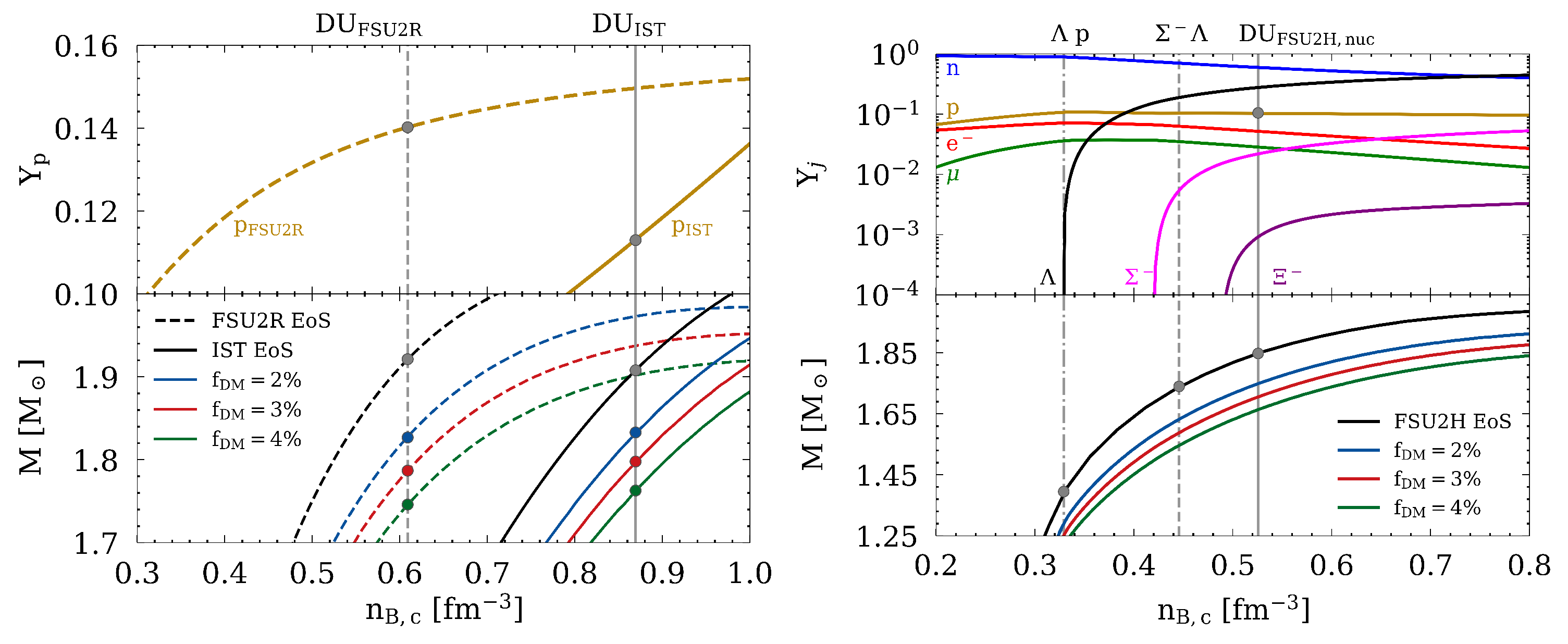

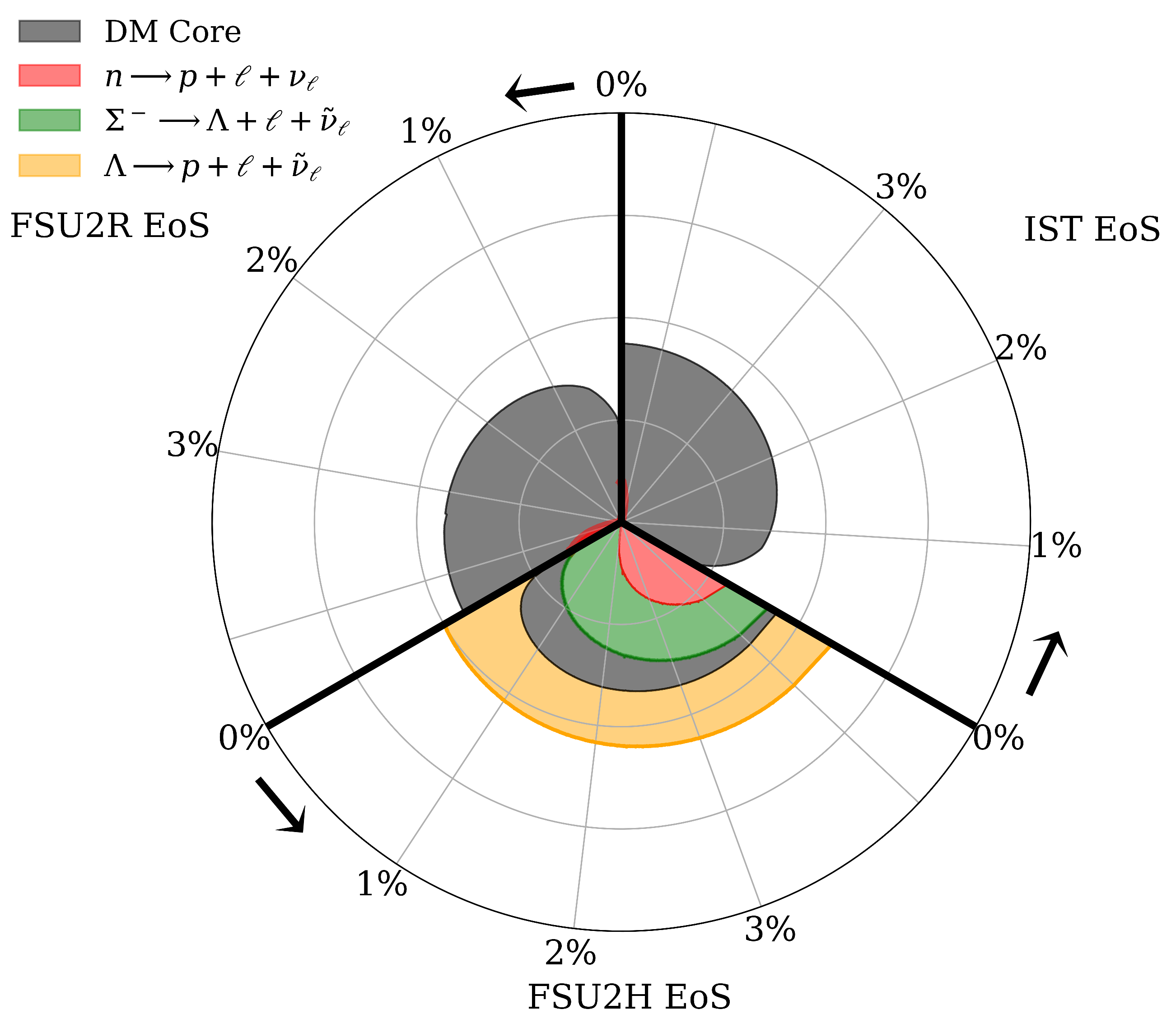




[fm−3] | [MeV] | [MeV] | [MeV] | L [MeV] | [MeV] | [MeV] | |
|---|---|---|---|---|---|---|---|
| IST EoS | 0.16 | −16.00 | 201.0 | 30.0 | 93.19 | 2.084 | 11.4 |
| FSU2R EoS | 0.1505 | −16.28 | 238.0 | 30.7 | 46.90 | 2.048 | 12.8 |
| FSU2H EoS | 0.1505 | −16.28 | 238.0 | 30.5 | 44.50 | 1.992 | 12.7 |
| IST EoS | nDU [] | MDU [] | FSU2R EoS | nDU [] | MDU [] | ||
|---|---|---|---|---|---|---|---|
| 0% | 0.869 | 1.908 | 0% | 0.608 | 1.921 | ||
| 2% | 1.83 | 2% | 1.83 | ||||
| 3% | 1.80 | 3% | 1.79 | ||||
| 4% | 1.76 | 4% | 1.75 | ||||
| FSU2H EoS | |||||||
|---|---|---|---|---|---|---|---|
| nDU [] | MDU [] | nDU [] | MDU [] | nDU [] | MDU [] | ||
| 0% | 0.332 | 1.40 | 0.446 | 1.74 | 0.534 | 1.85 | |
| 2% | 1.32 | 1.63 | 1.75 | ||||
| 3% | 1.28 | 1.59 | 1.71 | ||||
| 4% | 1.24 | 1.54 | 1.66 | ||||
| IST EoS | ||||
|---|---|---|---|---|
| [] | [km] | |||
| 1.20 | 11.29 | 11.11 | 11.03 | 10.94 |
| 1.60 | 11.10 | 10.91 | 10.81 | 10.70 |
| 1.90 | 10.58 | 10.35 | 10.20 | 10.05 |
| FSU2R EoS | ||||
| [] | [km] | |||
| 1.20 | 12.18 | 12.09 | 12.01 | 11.93 |
| 1.60 | 12.39 | 12.25 | 12.15 | 12.05 |
| 1.90 | 12.16 | 11.93 | 11.73 | 11.47 |
| FSU2H EoS | ||||
| [] | [km] | |||
| 1.20 | 12.43 | 12.30 | 12.24 | 12.16 |
| 1.50 | 12.77 | 12.62 | 12.53 | 12.44 |
| 1.70 | 12.86 | 12.63 | 12.50 | 12.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giangrandi, E.; Ávila, A.; Sagun, V.; Ivanytskyi, O.; Providência, C. The Impact of Asymmetric Dark Matter on the Thermal Evolution of Nucleonic and Hyperonic Compact Stars. Particles 2024, 7, 179-200. https://doi.org/10.3390/particles7010010
Giangrandi E, Ávila A, Sagun V, Ivanytskyi O, Providência C. The Impact of Asymmetric Dark Matter on the Thermal Evolution of Nucleonic and Hyperonic Compact Stars. Particles. 2024; 7(1):179-200. https://doi.org/10.3390/particles7010010
Chicago/Turabian StyleGiangrandi, Edoardo, Afonso Ávila, Violetta Sagun, Oleksii Ivanytskyi, and Constança Providência. 2024. "The Impact of Asymmetric Dark Matter on the Thermal Evolution of Nucleonic and Hyperonic Compact Stars" Particles 7, no. 1: 179-200. https://doi.org/10.3390/particles7010010
APA StyleGiangrandi, E., Ávila, A., Sagun, V., Ivanytskyi, O., & Providência, C. (2024). The Impact of Asymmetric Dark Matter on the Thermal Evolution of Nucleonic and Hyperonic Compact Stars. Particles, 7(1), 179-200. https://doi.org/10.3390/particles7010010







