Abstract
Electric Dipole Moments (EDM) of particles (leptons, nucleons, and light nuclei) are currently deemed one of the best indicators for new physics, i.e., phenomena which lie outside the Standard Model (SM) of elementary particle physics—so-called physics “Beyond-the-Standard-Model” (BSM). Since EDMs of the SM are vanishingly small, a finite permanent EDM would indicate charge-parity (CP) symmetry violation in addition to the well-known sources of the SM, and could explain the baryon asymmetry of the Universe, while an oscillating EDM would hint at a possible Dark Matter (DM) field comprising axions or axion-like particles (ALPs). A new approach exploiting polarized charged particles (proton, deuteron, 3He) in precision storage rings offers the prospect to push current experimental EDM upper limits significantly further, including the possibility of an EDM discovery. In this paper, we describe the scientific background and the steps towards the realization of a precision storage ring, which will make such measurements possible.
1. Introduction
1.1. Scientific Background
During the past century mankind has made mind-blowing progress in the understanding of nature, which continues to this day and age with spectacular new discoveries, such as the observation of the Higgs-boson or the detection of gravitational waves. Nevertheless, there is a plethora of fundamental questions which wait to be answered [1]. As will be illustrated below, some of them relate the largest scales (i.e., cosmology) to the smallest ones (elementary particle physics), and answers to them will point towards physics not contained in the celebrated respective Standard Model.
Electric Dipole Moments (EDM) of elementary particles—the permanent separation of positive and negative electric charge centroids—have a very strong science case [2] as they aim to solve two of the most pressing problems in contemporary cosmology and particle physics:
- Reason for the Baryon-asymmetric Universe (BAU) (Why is there matter and no antimatter?) [3]
- Composition of Dark Matter (DM) in the Universe (What is Dark Matter made of?) [4,5].
EDMs do not conserve discrete symmetries [6]; they violate time-reversal invariance (T), parity (P), and—if the combined charge-parity-time reversal (CPT) symmetry holds—in addition, charge-parity (CP) is “broken”. These symmetries and conservation laws play a very important role in modern physics; via Noether´s theorem [7], the invariance of a system subject to a continuous symmetry transformation (e.g., a time-translation, a spacial translation or a rotation) leads to a conservation law (energy, momentum and, angular momentum, respectively). In addition to continuous symmetries, there are discrete symmetries—parity (P) (reflection of space coordinates at the origin: (x, y, z) → (−x, −y, −z)), charge conjugation (C) (replacing a particle by its antiparticle, thus changing the sign of the electric charge: (+) → (−)), and time reversal (T) (change of the direction of the time coordinate: (t) → (−t))—as well as combinations thereof: charge-parity (CP) and charge-parity-time (CPT). Until around the middle of the 20th century, it was taken for granted that all discrete symmetry transformations are good ones—that is these operations do not make a difference in the experimental outcome—but then parity-violation and later CP-violation were discovered experimentally, implying that nature does distinguish between left and right, and between matter and antimatter. Today, only the combined CPT-symmetry is assumed to be exact (the so-called CPT theorem [8]). As a consequence, this means that CP-violation implicates T-reversal violation and vice versa to preserve CPT. CP-violation is one prerequisite to explain the observed matter–antimatter asymmetry in the Universe. The size of CP-violation, which has been found up to now and is implemented in the Standard Model (SM) of particle physics, falls short of explaining this asymmetry by many orders of magnitude.
No particle EDM has been found so far—only impressive experimental upper limits exist, e.g., for the electron [9] (indirectly deduced in atomic measurements) and for the neutron [10]. It turns out that the well-established CP-violation of the Standard Model of particle physics leads only to very tiny EDMs, below the sensitivity of current experiments. The discovery of a finite EDM value would signal the presence of additional CP-violation, which is required for an understanding of the apparent matter–antimatter asymmetry of our Universe. Observation of a finite EDM could thus solve this puzzle.
A new symmetry (called “Peccei–Quinn”(PQ) after its inventors) has originally been suggested to account for the smallness of CP-violation in the strong interaction (dubbed the “strong CP-problem”) [11]. One consequence of PQ symmetry breaking is the existence of a new spin-0 (“scalar”) particle called an “axion”. These particles (or its generalization, axion-like particles (ALP)) [12] are considered promising candidates for Dark Matter (DM), which represents a large fraction (about 25%) of the energy content of the Universe, but its nature is still unknown. No experimental indications for axions/ALPs have been found yet. Axions/ALPs will couple to gluons (the exchange particles that bind quarks inside hadrons) and induce oscillating EDMs, e.g., of nucleons (protons and neutrons) [13]. Observation of such an oscillating EDM could thus clarify the nature of DM.
A discovery of static (not changing with time) EDMs and/or time-dependent (oscillating) EDMs (oEDM) would provide a breakthrough in the quest to understand the set-up and evolution of the Universe on a deeper, more fundamental level. The current model of elementary particle physics—the Standard Model (SM), which is spectacularly successful in many other areas of fundamental particle physics—is not able to explain both the Baryon-asymmetric Universe (BAU) and Dark Matter. Finding an EDM experimentally will therefore inevitably also imply an extension to physics beyond the SM (BSM).
Recently, it has been realized that charged particles, in particular the proton and the deuteron can be used to search for EDMs with unprecedented sensitivity, improving current limits by orders of magnitude [14]. For these experiments, a dedicated—not yet existing—new type of precision storage ring is required, which will allow the measurement of the corresponding observable, the time-development of the polarization in a stored polarized particle beam under investigation.
In the following two chapters the science case is outlined in more detail.
1.1.1. The Ambition to Solve the Matter–Antimatter Asymmetry
We live in a Universe that apparently contains an overwhelming amount of matter compared to antimatter.
Our Universe was created 13.8 billion years ago in a singular event known as the Big Bang. According to our current understanding, it created matter and antimatter in equal amounts. However, in the Universe we live in and investigate today, we only find matter (except for tiny amounts created in violent particle interactions), from our immediate neighbourhood to the largest distances. During the past decades, cosmology, assisted by nuclear and particle physics, advanced our understanding of the evolution of the Universe tremendously. The fate of the antimatter in this evolution is one of the biggest remaining mysteries. During the early evolution of the Universe, antimatter particles annihilated with corresponding matter particles into photons, leaving behind only a tiny fraction of matter—for reasons yet unknown. This tiny fraction constitutes the material foundation of today’s Universe and of our very existence. Diverse research is ongoing in the quest to understand the formation of a matter-dominated Universe.
In the 1960s, the work of Andrei Sakharov [15] provided the following conditions for matter to escape the annihilation:
- Baryon number violation—a change in the difference between the number of baryons and antibaryons at the particle level,
- Charge conjugation (C) and charge-parity (CP) violation—a different behaviour of matter and antimatter—and
- Thermal non-equilibrium (i.e., effective during a phase transition of the Universe)—to prevent a subsequent compensation of the asymmetry between matter and antimatter.
The Standard Models of cosmology and particle physics meet these conditions qualitatively, but fail by 8 to 9 orders of magnitude at a quantitative description (see below). The models predict an insufficient amount of matter that survived the annihilation phase in the early Universe. It is frequently believed that the failure may arise from the second condition, i.e., from yet undiscovered violations of fundamental symmetries between matter and antimatter (particles and antiparticles), in particular additional CP-violation not yet found.
Here, EDMs enter the stage. Subatomic particles with nonzero spin (regardless of either elementary or composite nature) can only support a nonzero permanent EDM if both time-reversal (T) and parity (P) symmetries are violated explicitly, while the charge symmetry (C) can be maintained. Assuming the conservation of the combined CPT symmetry, T-violation also implies CP-violation. The CP-violation generated by the Kobayashi–Maskawa mechanism of weak interactions contributes a very small EDM that is several orders of magnitude below current experimental limits [16]. However, many models for physics beyond the Standard Model (BSM) predict EDM values near the current experimental limits (see, e.g., [17]).
Finding a non-zero EDM value of any subatomic particle would be a signal that there exists a new source of CP-violation, either induced by the strong CP-violation via the so-called “θQCD angle” or by a genuine BSM effect. In fact, the best upper limit on θQCD follows from the experimental bound on the EDM of the neutron. As indicated above, CP-violation beyond the SM is also essential for explaining the mystery of the observed baryon-antibaryon asymmetry of our Universe (BAU). A measurement of a single EDM will not be sufficient to establish the sources of any new CP-violation. Complementary observations of EDMs in multiple systems will thus prove essential.
Up to now, measurements have focused on neutral systems (neutron, atoms, molecules); Figure 1 gives a summary of the EDM upper limits (for a recent summary, see [18]). Note that the limit for the proton has been deduced from a 199Hg measurement and no limit for the deuteron exists.
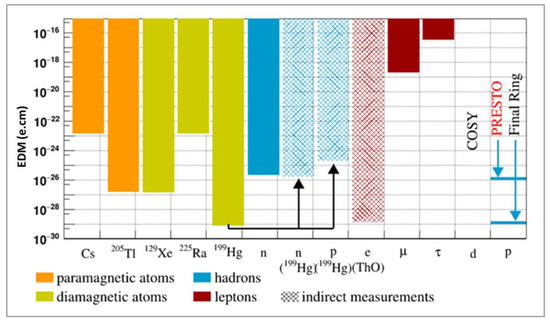
Figure 1.
Current status of EDM searches (95% upper limits) of molecules, atoms, and particles: the full-colour bars represent direct measurements, while the shaded bars are deduced results for these systems. In particular, the proton result has been obtained indirectly from the experimental EDM limit for 199Hg; this is indicated by the black arrows. Impressive EDM limits for the electron come from Thorium-oxide (ThO) and HfF+ measurements [9]—still many orders of magnitude larger than the SM-prediction. It generally holds that the contribution from the SM is negligible at the sensitivity level accessible with current experimental techniques. For the deuteron (d), for which neither a direct nor an indirect limit is known, an EDM limit from the measurement at the Cooler Synchrotron (COSY) of Forschungszentrum Jülich (Germany) will soon be available (see below). The expected sensitivity is comparable to the muon (µ) [19] and tau (τ) limits [20]. The goal of the proton EDM (p) of the final ring is to reach a sensitivity of 10−29 e·cm, and the goal for the intermediate step—a prototype storage ring (called PRESTO in the figure)—is to reach 10−26 e·cm.
In order to directly measure the EDM of charged particles, the design of a dedicated precision storage ring needs to be developed [21]. The goal is to provide optimal experimental conditions to investigate the time evolution of the polarization of stored polarized beams of protons and/or deuterons.
The advantages of the storage ring method are:
- Direct observation of the EDM effect of the system (proton, deuteron, and possibly other light ions such as 3He) under investigation, i.e., no need to extract particle EDM from measurement in a complex system;
- Virtually no limit to the number of particles used in the investigation, i.e., no limitation in the achievable statistical accuracy;
- There are theoretical relations between EDMs for protons and deuterons (see, e.g., [21]), which will serve as consistency checks for theory.
On a more general level, there will be different systematic errors and fake effects compared to neutral systems, and in the end—once EDMs for all of them have been obtained—they must all be internally consistent within the theoretical interpretation.
Due to the smallness of the effect, the measurements will need an excessive sensitivity, and this poses technological and metrological challenges, which will be discussed below in the section “methodology”.
1.1.2. The Intent to Understand the Nature of Dark Matter
Since the earliest times of mankind, people have looked at the night sky with awe, wondering what these tiny luminous objects in heaven might be. Today, though few of us have had a chance to see even our own galaxy (Milky Way) in full glory, it is known to most people that we are only able to see a small fraction of the Milky Way and an even tinier part of the vast visible Universe—as, e.g., observed through electromagnetic radiation, ranging from radio waves to visible light and beyond. It may come as no surprise that astronomical observations over the past almost 100 years have accumulated more and more evidence that this luminous part (stars, galaxies, and clusters) only constitutes a portion of the mass in our Universe. In fact only about one fifth of the matter is made of fundamental particles that we know and understand; the majority of the matter is not visible and thus dubbed “Dark Matter” (DM) [22].
DM has been postulated by the need for much more mass than actually seen in rotating galaxies in order to bind them by the gravitational force, compensating the centrifugal force. This is shown schematically in Figure 2.
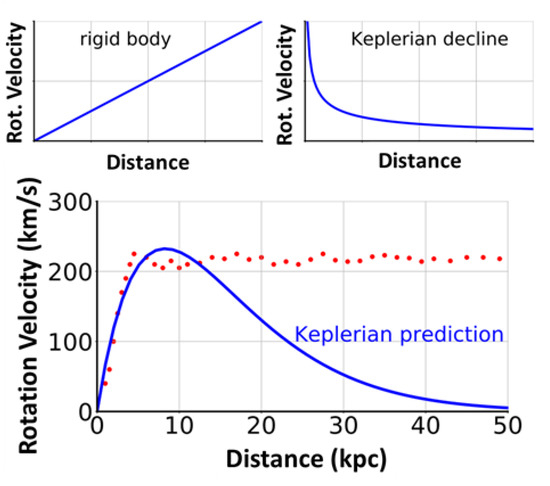
Figure 2.
Rotational speed for a rigid body (top left) and for Keplerian motion, e.g., our solar system, with most of the mass centred at zero (top right). Below, the result (red dots) for a typical spiral galaxy is shown. The disagreement of the rotational speed of galaxies from the Keplerian prediction for R > 10 kpc (i.e., the constant speed) was first observed by F. Zwicky [23,24] in the 1930s in the Coma Cluster, and indicates that more mass than visible must be present.
There are further compelling observations indicating the existence of DM [25], e.g., via gravitational lensing and its role in the evolution of structure in the Universe. However, what DM actually is remains a mystery. It is important to note that none of the known building blocks of the (otherwise remarkably successful) Standard Model (SM) of elementary particle physics can serve as DM. This implies that the SM is incomplete and that a discovery of DM particles would be conclusive evidence for physics beyond the SM (BSM). There is mounting evidence for the need of DM, and the search is ongoing by a suite of dedicated experiments, but no DM particle(s) has(have) been observed to date, although there have been claims. The allowed DM-parameters of mass and coupling to SM particles spans a huge range, which requires very different techniques for discovery (see, e.g., [26]).
The following principal search strategies for Dark Matter are currently exploited:
- Direct production of DM particles at accelerators;
- Detection of galactic DM particles through interactions with SM matter; and
- Detection of DM as coherently oscillating waves.
EDMs will exploit the third option, assuming a high occupation number per unit volume, i.e., a field rather than individual particles. The effect of DM on the spin motion of an ensemble of particles (a beam) in a storage ring would then be observed as oscillating Electric Dipole Moments (oEDM) in nucleons and nuclei [13].
To conclude a discussion of motivations, the science case is summarized in Figure 3.
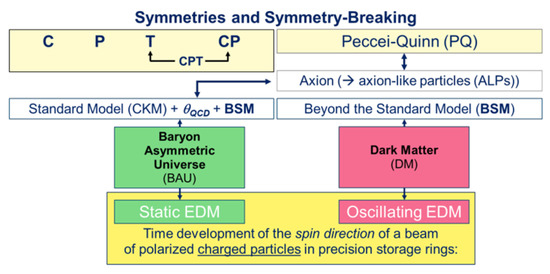
Figure 3.
Summary of the scientific background: discrete symmetries (C, P, T, and combinations thereof) and the presumed Peccei–Quinn symmetry (PQ) together with their breaking (CP and PQ symmetry violation) can be related to static and oscillating EDMs. Static EDMs may be responsible for the Baryon-asymmetric Universe (BAU), while oscillating EDMs could be due to the axion and/or axion-like particles (ALP) as Dark Matter candidates. Experimentally, both can be investigated by a measurement of the time development of the spins of a beam of charged particles circulating in a storage ring.
1.2. State-of-the-Art Knowledge
EDMs can be searched for in elementary particles such as leptons (electrons, muons, taus), composite particles (e.g., neutrons and protons), and—indirectly—in complex systems, for example atoms and molecules.
At first, two important remarks seem to be indicated:
- The connection between any finite experimental EDM result and its sources is less complex for simpler systems—this is schematically shown in Figure 4. A more detailed picture of such connections is given, e.g., in [27].
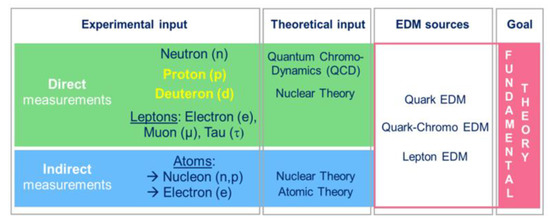 Figure 4. Schematic connection between experiment and a fundamental theory as the ultimate goal of EDM investigations. There are two major paths to experimentally search for EDMs: direct measurements, which study a sole particle species, and indirect measurements, which use atoms or molecules (or even bulk matter). Although indirect experiments have resulted in impressive upper limits, direct investigations are clearly preferable, since they will be much easier to interpret.
Figure 4. Schematic connection between experiment and a fundamental theory as the ultimate goal of EDM investigations. There are two major paths to experimentally search for EDMs: direct measurements, which study a sole particle species, and indirect measurements, which use atoms or molecules (or even bulk matter). Although indirect experiments have resulted in impressive upper limits, direct investigations are clearly preferable, since they will be much easier to interpret.
While results from indirect searches—i.e., experiments with systems which contain the respective particle—are available for the electron and the proton (see Figure 1), in the end, one has to strive for the observation of the pure (naked) object under investigation. For charged particles, this will imply the use of stored beams to extend the observation times to such a level that the miniscule expected effects of an EDM can be observed with available experimental techniques.
- 2.
- EDM results from different systems will be needed to pin down the (set of) EDM sources.
Experimental results—EDM upper limits of the order of 10−26 e·cm—are available for the free neutron [10] (see Figure 1), and it can be expected that they will be further improved by ongoing and upcoming new experiments, although the limitations for the provision of ultracold neutrons (and the finite neutron lifetime) will finally limit the achievable sensitivity. In order to complement these results, experimental EDM searches for free protons must be conducted, and this is now in reach with a new class of measurements of the spin motion of polarized protons, which are circulating in a precision trap called a storage ring. In such experiments, the number of stored protons is hardly limited, which implies that the statistical uncertainty (relating to the achievable sensitivity) can be higher than for the neutron. The challenge will be, as outlined below, to reduce the systematic uncertainties to a comparable level.
2. Methodology of Charged-Particle EDM Searches
The basis for observing an EDM is its interaction with an external electric field. The possible observables are given by the fact that the EDM vector (which can be thought of as connecting the negative and the positive electric charge that forms the EDM) and the intrinsic angular momentum (“spin”) vector are parallel to each other. Thus, one way to detect an EDM is to observe the impact it has on the spin of a particle (in practice: an ensemble of particles with spins oriented in a preferred direction, a polarized beam). In the following, we focus on charged particles (proton, deuteron), which need to be confined in a trap—in this case a storage ring—since otherwise they would be accelerated out-of-sight by the electric field. While a full description of the spin-motion of particles in the electric and magnetic fields of the ring requires the use of the Thomas–BMT equation [28,29], the following discussion focuses on a generic description of the method.
In order to introduce the basic principle of an EDM measurement of polarized charged particles in a storage ring, it is reasonable to start by describing what is happening to them as they go around the ring, when no EDM of the particles would exist. To simplify the situation further, it is assumed that at the beginning the spins are pointing in the direction of motion (i.e., parallel to the particle´s momentum vector):
- Since the spin s of a particle is linked to a magnetic moment µ = (G + 1) (q/m) s, where G is the magnetic anomaly, q the charge, and m the mass, the particles will precess in the electric and/or magnetic field of the storage ring, which are necessary to keep them on a closed orbit. The total angular precession frequency of the spin is given by ds/dt = Ωs × s, where Ωs has components due to the magnetic and electric dipole moments of the particle.
- For any particle and energy, the electric and magnetic fields bending the beam can be chosen such that the angular rotation of the spin vector s from turn to turn vanishes, the spin is then said to “be frozen”, and, e.g., an initial longitudinal polarization of the particle beam is maintained.
- For particles with G > 0, such as protons, the above frozen-spin condition can be fulfilled with electric fields only by operating the ring at a specific energy, the so-called “magic” energy.
Now consider that the particles possess also an EDM d = ds (parallel to the spin s) and are exposed to a radial electric field E:
- The interaction between electric field and EDM will produce a torque d × E that rotates the spin out of the ring plane, as schematically shown in Figure 5.
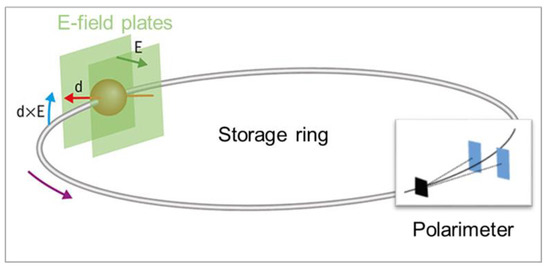 Figure 5. Basic principle of an EDM measurement. For clarity, only a single particle is shown and the magnetic moment precession is neglected. The particle is kept on its orbit by the transverse electric field E, generated by the electrostatic deflector plates that are depicted in green. Initially, all particle spins s in the beam point along the direction of motion. An electric dipole moment d= ds tilts the spin s out of the horizontal plane due to the torque d × E. This effect is experimentally observable, because the vertical polarization component of the beam can be detected in the polarimeter.
Figure 5. Basic principle of an EDM measurement. For clarity, only a single particle is shown and the magnetic moment precession is neglected. The particle is kept on its orbit by the transverse electric field E, generated by the electrostatic deflector plates that are depicted in green. Initially, all particle spins s in the beam point along the direction of motion. An electric dipole moment d= ds tilts the spin s out of the horizontal plane due to the torque d × E. This effect is experimentally observable, because the vertical polarization component of the beam can be detected in the polarimeter.
As a result, the principle for searching/observing EDMs of charged particles is as follows:
- Inject a polarized charged particle beam with its spin vectors pointing in the direction of the momentum vector into a storage ring fulfilling the “frozen spin” condition. Thus, when the particles possess only a magnetic dipole moment (MDM), the beam will remain polarized in longitudinal direction.
- Let the particles interact with an electric field that couples to the possible EDM.
- Observe the rotation of the beam polarization out of the storage ring plane due to a non-zero EDM as a function of time. This can be observed with a dedicated detector system inside the ring, called a polarimeter.
At this point, it is important to note that the MDM of the particle completely dominates the spin motion if no special provisions are taken. In order to maximise the sensitivity to EDM, the MDM contributions must vanish.
This can be achieved by the following measures:
- Switch off the external magnetic field: B = 0 (i.e., use an all-electric storage ring and shield all external magnetic fields);
- Arrange that bunches are polarized in the longitudinal direction during the duration of the measurement by choosing a “magic momentum”; this is possible for particles with a positive magnetic anomaly (G > 0), e.g., for the proton for a momentum of p = 700.7 MeV/c (corresponding to a kinetic energy of 232.8 MeV).
For particles with G < 0 (such as the deuteron), an all-electric solution is not possible and one needs to use a combination of radial electric and vertical magnetic fields to make the spin “frozen” along the particle momentum. Though this measurement procedure sounds straightforward and simple, a closer look indicates substantial intricacy. As mentioned earlier, this can be investigated using the Thomas–BMT equation, which describes the temporal behaviour of the spin of a particle with a magnetic dipole moment (MDM) and an electric dipole moment (EDM) in the presence of electric (E) and magnetic (B) fields.
In the remainder of this chapter, challenges will be discussed which come along with the vastly different magnitude of response of a particle’s spin to electric (via an EDM) and magnetic (via its MDM) fields. In order to set a benchmark, it may suffice to mention that the minuscule (radial) magnetic field of ≈10−17 T (10 aT (atto-Tesla)) mimics the effect of an EDM of 10−29 e·cm—the sensitivity goal for the final EDM ring. It has been shown [21] that with reasonable assumptions for beam intensity, beam polarization, measurement time, applied electric field, and polarimetry, a statistical accuracy of d = 10−29 e·cm can be achieved in one year of measurement time; the task, therefore. is to conceive and realise a research infrastructure which allows to bring the systematic uncertainty to a similar level. This implies to identify all sources of false effects to be able to remove all of them or to mitigate their effects to the highest possible level.
The research infrastructure—an all-electric precision storage ring for polarized proton beams of 232.8 MeV—is in many fundamental aspects a blank area; many questions will have to be answered and technological solutions will need to be scrutinised before one can start to realise the facility.
This comprises the following list of items:
- Beam characteristics: storage time of the intensive beams, spin coherence time of the beam polarization and beam emittance; need of phase space cooling;
- Hardware: electric bends, storage ring vacuum; need of cryogenics, instrumentation for beam and spin manipulation, monitoring and control, polarimetry/polarimeter, injection scheme into the storage ring, and stability of power supplies;
- Other: alignment and metrology of ring elements, systematics investigations, and beam and spin tracking simulations.
3. Strategy towards Realization
Research and development towards a precision storage ring has been vigorously advanced at the storage ring COSY, which currently is the only facility worldwide where corresponding tests and measurements can be conducted. A schematic layout of the COSY facility is given in Figure 6.
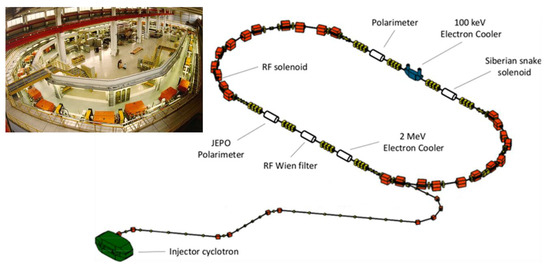
Figure 6.
Layout of the Cooler Synchrotron (COSY) storage ring at Forschungszentrum Jülich (Germany) together with an early photograph: the ring has a circumference of 184 m and can accelerate and store unpolarized and polarized beams of protons and deuterons from the injector cyclotron with momenta up to 3.7 GeV/c. The equipment comprises electron and stochastic cooling apparatuses, as well as spin manipulation and detection devices. The unique capabilities of COSY have been used by the JEDI collaboration to investigate manipulations of polarized particle beams and its response to external electric and magnetic fields as preparation for EDM measurements—both at COSY and future dedicated storage rings.
COSY [30] was conceived and built in the late 1980s, and originally used for hadron physics experiments with both unpolarized and polarized proton and deuteron beams at different internal and external target stations until about 2015. Starting from 2010, the JEDI collaboration used COSY beams for the development of hardware (e.g., a new beam polarimeter, beam-position monitors, and a radio-frequency Wien-filter), measurement techniques (e.g., optimization of the so-called “spin-coherence time”, the “pilot-bunch method”, and feedback loops) and—last, but not the least—first experiments with polarized deuteron beams.
3.1. Stage 1: R&D and Measurements at COSY as “Proof-of-Capability”
Over the years, the following achievements have been accomplished at COSY [31,32,33,34]:
- Development and implementation of techniques to preserve, manipulate, and observe the polarization of polarized beam bunches in a storage ring (optimization of the spin coherence time, use of a radio-frequency Wien filter, including the pilot-bunch method, design and set-up of an in-beam polarimeter), since they are essential prerequisites for a successful measurement of electric dipole moments of charged particles.
- A Rogowski beam-position monitor has been developed, optimized, installed into COSY, and used in the deuteron EDM (dEDM) measurements.
- A new polarimeter to determine the polarization direction of a circulating polarized beam, based on LYSO scintillators with a silicon photosensor readout, has been developed, optimized, installed into COSY, and used in the dEDM measurements [35].
- A radio-frequency Wien filter has been designed, built, and installed in COSY [36]. In a magnetic (B-field) storage ring such as COSY, the effect of a possible EDM on the particle spin (i.e., on the polarization of an ensemble of polarized particles) will exactly cancel, since the torque due to EDM changes sign—this is why the final EDM storage ring will be an all-electric ring with E-fields only. However, with the concept of such a Wien filter, it is possible in principle to observe the EDM effect (at reduced sensitivity). This device has been exploited for the so-called “precursor experiments” [37] with a polarized deuteron beam.
- In order to study the influence of the RF WF on the polarization (and possibly the orbit), two beam-bunches were injected into the COSY ring, and the RF WF was upgraded such that it could be switched on/off when one of the two bunches passes through the device. After successful tests, this so-called “pilot bunch” method was exploited in the second dEDM precursor experiment.
Scientific Results
- A successful measurement of an oscillating electric dipole moment (limit) for a polarized deuteron beam has been performed in COSY—this was not anticipated originally, but it demonstrates that small changes of the beam polarization can be observed reliably [38]. A preliminary exclusion plot for the size of the oscillating EDM is given in Figure 7.
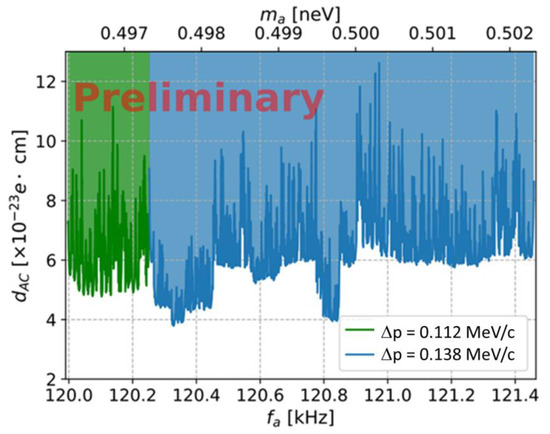 Figure 7. Preliminary result for the 90% confidence level sensitivity for excluding an ALP’s induced oscillating EDM (oEDM) in the frequency range 120.0–121.4 kHz (corresponding to a mass range ma = 0.496–0.502 neV/c2). A dedicated paper has been submitted [38].
Figure 7. Preliminary result for the 90% confidence level sensitivity for excluding an ALP’s induced oscillating EDM (oEDM) in the frequency range 120.0–121.4 kHz (corresponding to a mass range ma = 0.496–0.502 neV/c2). A dedicated paper has been submitted [38]. - A proof-of-capability of measuring a limit for a deuteron electric dipole moment in a magnetic storage ring (COSY) has also been achieved; the EDM result has not been finalized up to now due to very complex investigations required to quantify the systematic uncertainty.
COSY has been an indispensable development tool and test device for the storage ring EDM venture. The efforts have been supported by a grant of the European Research Council (ERC AdG srEDM with Principal Investigator H.S., with additional beneficiaries from RWTH Aachen University (Germany), J.P., and the University of Ferrara (Italy), P.L.) from 2016 to 2022. Unfortunately, the operation of COSY will be terminated by the end of 2024 within the context of the transfer of the Institute for Nuclear Physics (IKP) of Forschungszentrum Jülich to the GSI Helmholtz Center Darmstadt, which forfeits the community its current centre-of-gravity.
3.2. Stage 2: A Prototype Storage Ring (PSR) for EDM Searches
COSY is a magnetic storage ring, thus many issues listed above cannot be investigated there. Before starting the construction of the final ring, which is supposed to be one with a circumference of the order of 500 m for a purely electric ring [14], or even larger for a hybrid machine [39,40], and thus constitutes a major investment, members of the JEDI and the CPEDM (Charged Particle EDM) collaboration have concluded that the next step must be the design and construction of a prototype storage ring (PSR) [21]. Because COSY will no longer be available, the PSR cannot rely on the facility, e.g., as a tool for beam preparation and injector.
The PSR should operate at a beam kinetic energy between 30 and 45 MeV in two modes:
- as an all-electric ring for CW/CCW operation, but not at the magic momentum; and
- in the “frozen spin” mode after complementing the ring with B-fields; this will allow to perform a first competitive proton (pEDM) experiment with a sensitivity similar to the neutron EDM, i.e., about 10−26 e·cm.
Activities have started for a design study of the PSR, including discussions of the host institution as well as its financing and timeline.
3.3. Stage 3: Design and Implementation of the Final Precision Storage Ring
There are suggestions to build a precision storage ring to search for charged-particle EDMs with a sensitivity of the order of 10−29 e·cm with the knowledge acquired by now—mainly based on paper work [39,40]. If there is a lesson that we have learned over the past 10 years or so in our experimental investigations of production, preservation, manipulation and detection of polarized beams in a storage ring, it is that one is always facing unexpected challenges. Thus, a final ring which should yield an unprecedented sensitivity must be very carefully approached—also having in mind that the construction cost is significant. The JEDI/CPEDM collaborations are convinced that starting to construct this ring now is premature, and consequently are suggesting to design and build a PSR first. Only after the experience gained in operating the PSR, including a first competitive EDM measurement, the holy grail EDM ring should be approached.
4. Summary and Outlook
According to our present understanding, the early Universe contained the same amount of matter and antimatter and, if the Universe had behaved symmetrically as it developed, every particle would have been annihilated by one of its antiparticles. One of the great mysteries is therefore why matter dominates over antimatter in the visible Universe. Furthermore, among the deepest mysteries in natural sciences stands the question of what the Universe is made of. Visible matter, comprising Standard Model particles, accounts only for a small fraction. As inferred from cosmological observations, about 5 times more matter is invisible and is called Dark Matter (DM).
Electric Dipole Moments of particles offer the possibility of providing answers to both enigmas: static EDMs would imply new sources of CP-violation, required for the baryon asymmetry, and oscillating EDMs could be due to axions/ALPs, a prime candidate for DM.
EDM searches with charged particles in storage rings are a new approach, which may be a game-changer due to its projected sensitivity of 10−29 e·cm. However, technological and metrological challenges abound and require a staged approach, i.e., a PSR as next step before embarking on the final ring—as outlined in Figure 8.
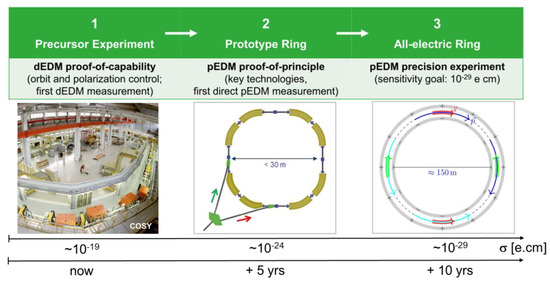
Figure 8.
Stages of the strategy for charged particle EDM searches as outlined by the CPEDM collaboration. The EDM sensitivity goals are given for each step. Stage 1 is currently ongoing, while the timeline for stages 2 and 3 is of the order of 5 and 10 years, respectively.
The storage ring EDM enterprise is a long-term project. For further information, we refer the reader to a “CERN Yellow Report” [21], in which the current status of the accumulated knowledge for searches of charge-particle EDMs in storage rings has been summarized. An additional source of detailed information is the web-site given in Supplementary Materials below.
Supplementary Materials
Additional information can be downloaded at: http://collaborations.fz-juelich.de/ikp/jedi/.
Author Contributions
Conceptualization, H.S., S.M.S., P.L. and J.P.; methodology, H.S., P.L. and J.P.; writing—original draft preparation, H.S.; writing—review and editing, S.M.S., P.L. and J.P. All authors have read and agreed to the published version of the manuscript.
Funding
H.S., P.L. and J.P. acknowledge the support of the European Commission via the European Research Council (ERC) by the Advanced Grant “Search for electric dipole moments using storage rings” (ERC-2015-AdG, Grant Agreement number 694340).
Data Availability Statement
The study does not report any finalized data yet.
Acknowledgments
The authors want to acknowledge the long-term cooperation within the JEDI and the CPEDM collaborations, as well as the outstanding support of the scientists and technicians operating the COSY facility.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, R.E.; Lidström, S. Life, the Universe, and everything—42 fundamental questions. Phys. Scr. 2017, 92, 12501. [Google Scholar] [CrossRef]
- Alarcon, R.; Alexander, J.; Anastassopoulos, V.; Aoki, T.; Baartman, R.; Baeßler, S.; Bartoszek, L.; Beck, D.H.; Bedeschi, F.; Berger, R.; et al. Electric dipole moments and the search for new physics. arXiv 2022, arXiv:2203.08103. [Google Scholar] [CrossRef]
- Canetti, L.; Drewes, M.; Shaposhnikov, M. Matter and Antimatter in the Universe. New J. Phys. 2012, 14, 95012. [Google Scholar] [CrossRef]
- Chadha-Day, F.; Ellis, J.; Marsh, D.J. Axion dark matter: What is it and why now? arXiv 2021, arXiv:2105.01406v2. [Google Scholar] [CrossRef] [PubMed]
- Boveia, A.; Berkat, M.; Chen, T.Y.; Desai, A.; Doglioni, C.; Drlica-Wagner, A.; Gardner, S.; Gori, S.; Greaves, J.; Harding, P.; et al. Snowmass 2021 Dark Matter Complementarity Report. arXiv 2022, arXiv:2211.07027v2. 17. [Google Scholar] [CrossRef]
- Ramsey, N.F. Electric-dipole moments of elementary particles. Rep. Prog. Phys. 1982, 45, 95. [Google Scholar] [CrossRef]
- Leach, P.; Paliathanasis, A. (Eds.) Noether’s Theorem and Symmetry; MDPI: Basel, Switzerland, 2020; ISBN 978-3-03928-234-0/978-3-03928-235-7. [Google Scholar] [CrossRef]
- Blum, A.S.; de Velasco, A. The genesis of the CPT theorem. Eur. Phys. J. H 2022, 47, 5. [Google Scholar] [CrossRef]
- Roussy, T.S.; Caldwell, L.; Wright, T.; Cairncross, W.B.; Shagam, Y.; Ng, K.B.; Schlossberger, N.; Park, S.Y.; Wang, A.; Ye, J.; et al. A new bound on the electron’s electric dipole moment. arXiv 2022, arXiv:2212.11841v3. [Google Scholar] [CrossRef]
- Abel, C.; Afach, S.; Ayres, N.J.; Baker, C.A.; Ban, G.; Bison, G.; Bodek, K.; Bondar, V.; Burghoff, M.; Chanel, E.; et al. Measurement of the Permanent Electric Dipole Moment of the Neutron. Phys. Rev. Lett. 2020, 124, 81803. [Google Scholar] [CrossRef]
- Peccei, R.D. The Strong CP Problem and Axions; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 741, pp. 3–17. [Google Scholar] [CrossRef]
- Ringwald, A. Axions and Axion-Like Particles. arXiv 2014, arXiv:1407.0546v1. [Google Scholar] [CrossRef]
- Kim, O.; Semertzidis, Y.K. New method of probing an oscillating EDM induced by axionlike dark matter using an RF Wien Filter in storage rings. Phys. Rev. D 2021, 104, 96006. [Google Scholar] [CrossRef]
- Anastassopoulos, V.; Andrianov, S.; Baartman, R.; Baessler, S.; Bai, M.; Benante, J.; Berz, M.; Blaskiewicz, M.; Bowcock, T.; Brown, K.; et al. A storage ring experiment to detect a proton electric dipole moment. Rev. Sci. Instr. 2016, 87, 115116. [Google Scholar] [CrossRef] [PubMed]
- Sakharov, A.D. Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe. Sov. Phys. Usp. 1991, 34, 392. [Google Scholar] [CrossRef]
- Mohanmurthy, P.; Winger, J.A. Estimation of CP violating EDMs from known mechanisms in the SM. arXiv 2020, arXiv:2009.00852v3. 66. [Google Scholar] [CrossRef]
- Fukuyama, T. Searching for New Physics beyond the Standard Model in Electric Dipole Moment. Int. J. Mod. Phys. A 2012, 27, 1230015. [Google Scholar] [CrossRef]
- Kirch, K.; Schmidt-Wellenburg, P. Search for electric dipole moments. EPJ Web Conf. 2020, 234, 1007. [Google Scholar] [CrossRef]
- Ema, Y.; Gao, T.; Pospelov, M. Improved indirect limits on muon EDM. arXiv 2021, arXiv:2108.05398. [Google Scholar]
- Bernreuther, W.; Chen, L.; Nachtmann, O. Electric dipole moment of the tau lepton revisited. Phys. Rev. D 2021, 103, 96011. [Google Scholar] [CrossRef]
- Abusaif, F.; Aggarwal, A.; Aksentev, A.; Alberdi-Esuain, B.; Andres, A.; Atanasov, A.; Barion, L.; Basile, S.; Berz, C.; Böhme, C.; et al. Storage Ring to Search for Electric Dipole Moments of Charged Particles: Feasibility Study; CERN Yellow Reports: Monographs; CERN: Meyrin, Switzerland, 2021; Volume 3. [Google Scholar] [CrossRef]
- Trimble, V. Existence and Nature of Dark Matter in the Universe. Ann. Rev. Astron. Astrophys. 1987, 25, 425–472. [Google Scholar] [CrossRef]
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helv. Phys. Acta 1933, 6, 110–127. [Google Scholar]
- Johnson, J., Jr. Zwicky: The Outcast Genius Who Unmasked the Universe; Harvard University Press: Cambridge, MA, USA, 2019; ISBN 9780674979673. [Google Scholar]
- Bahcall, N.A. Dark matter universe. Proc. Natl. Acad. Sci. USA 2015, 112, 12243–12245. [Google Scholar] [CrossRef] [PubMed]
- Rajendran, S. New Directions in the Search for Dark Matter. arXiv 2022, arXiv:2204.03085v1.84. [Google Scholar] [CrossRef]
- Chupp, T.E.; Fierlinger, P.; Ramsey-Musolf, M.J.; Singh, J.T. Electric dipole moments of atoms, molecules, nuclei, and particles. Rev. Mod. Phys. 2019, 91, 15001. [Google Scholar] [CrossRef]
- Lee, S.Y. The Thomas–BMT equation. In Spin Dynamics and Snakes in Synchrotrons; World Scientific: Singapore, 1997; pp. 9–24. [Google Scholar]
- Fukuyama, T.; Silenko, A.J. Derivation of Generalized Thomas-Bargmann-Michel-Telegdi Equation for a Particle with Electric Dipole Moment. Int. J. Mod. Phys. A 2013, 28, 1350147. [Google Scholar] [CrossRef]
- Wilkin, C. The legacy of the experimental hadron physics programme at COSY. Eur. Phys. J. A 2017, 53, 114. [Google Scholar] [CrossRef]
- Annual Report 2018, Institut für Kernphysik COSY, Jül-4418, ISSN 0944-2952 (Forschungszentrum Jülich). pp. 15–21. Available online: https://www.fz-juelich.de/de/ikp/service/downloads (accessed on 25 February 2023).
- Annual Report 2019, Institut für Kernphysik COSY, Jül-4423, ISSN 0944-2952 (Forschungszentrum Jülich). pp. 8–13. Available online: https://www.fz-juelich.de/de/ikp/service/downloads (accessed on 25 February 2023).
- Annual Report 2020, Institut für Kernphysik COSY, Jül-4427, ISSN 0944-2952 (Forschungszentrum Jülich). pp. 7–13. Available online: https://www.fz-juelich.de/de/ikp/service/downloads (accessed on 25 February 2023).
- Annual Report 2021, Institut für Kernphysik COSY, Jül-4429, ISSN 0944-2952 (Forschungszentrum Jülich). pp. 6–11. Available online: https://www.fz-juelich.de/de/ikp/service/downloads (accessed on 25 February 2023).
- Müller, F.; Javakhishvili, O.; Shergelashvili, D.; Keshelashvili, I.; Mchedlishvili, D.; Abusaif, F.; Aggarwal, A.; Barion, L.; Basile, S.; Böker, J.; et al. A new beam polarimeter at COSY to search for electric dipole moments of charged particles. J. Instrum. 2020, 15, P12005. [Google Scholar] [CrossRef]
- Slim, J.; Nikolaev, N.N.; Rathmann, F.; Wirzba, A.; Nass, A.; Hejny, V.; Pretz, J.; Soltner, H.; Abusaif, F.; Aggarwal, A.; et al. (JEDI Collaboration), First detection of collective oscillations of a stored deuteron beam with an amplitude close to the quantum limit. Phys. Rev. Accel. Beams 2021, 24, 124601. [Google Scholar] [CrossRef]
- Lehrach, A.; Lorentz, B.; Morse, W.; Nikolaev, N.; Rathmann, F. Precursor Experiments to Search for Permanent Electric Dipole Moments (EDMs) of Protons and Deuterons at COSY. arXiv 2012, arXiv:1201.5773. [Google Scholar]
- Karanth, S.; Stephenson, E.J.; Chang, S.P.; Hejny, V.; Park, S.; Pretz, J.; Semertzidis, Y.; Wrońska, A.; Abusaif, F.; Aksentev, A.; et al. First Search for Axion-Like Particles in a Storage Ring Using a Polarized Deuteron Beam. arXiv 2022, arXiv:2208.07293v2. [Google Scholar] [CrossRef]
- Hacıömeroğlu, S.; Semertzidis, Y.K. Hybrid ring design in the storage-ring proton electric dipole moment experiment. Phys. Rev. Accel. Beams 2019, 22, 34001. [Google Scholar] [CrossRef]
- Omarov, Z.; Davoudiasl, H.; Hacıömeroğlu, S.; Lebedev, V.; Morse, W.M.; Semertzidis, Y.K.; Silenko, A.J.; Stephenson, E.J.; Suleiman, R. Comprehensive symmetric-hybrid ring design for a proton EDM experiment at below 10−29 e⋅cm. Phys. Rev. D 2022, 105, 32001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).