Abstract
Over the past several years, there has been enormous interest in massive neutron stars and white dwarfs due to either their direct or indirect evidence. The recent detection of gravitational wave event GW190814 has confirmed the existence of compact stars with masses as high as ∼2.5–2.67 within the so-called mass gap, indicating the existence of highly massive neutron stars. One of the primary goals to invoke massive compact objects was to explain the recent detections of over a dozen Type Ia supernovae, whose peculiarity lies with their unusual light curve, in particular the high luminosity and low ejecta velocity. In a series of recent papers, our group has proposed that highly magnetised white dwarfs with super-Chandrasekhar masses can be promising candidates for the progenitors of these peculiar supernovae. The mass-radius relations of these magnetised stars are significantly different from those of their non-magnetised counterparts, which leads to a revised super-Chandrasekhar mass-limit. These compact stars have wider ranging implications, including those for soft gamma-ray repeaters, anomalous X-ray pulsars, white dwarf pulsars and gravitational radiation. Here we review the development of the subject over the last decade or so, describing the overall state of the art of the subject as it stands now. We mainly touch upon the possible formation channels of these intriguing stars as well as the effectiveness of direct detection methods. These magnetised stars can have many interesting consequences, including reconsideration of them as possible standard candles.
1. Introduction
In the last several years, there has been much interest in massive compact objects. Sometimes the evidence is direct; however, it is indirect on some other occasions. For instance, the detection of gravitational wave (GW) event GW190814 [1] directly confirms the existence of a compact star with a mass of 2.5–2.67. Thus far, the minimum mass of an astrophysical black hole is understood to be around [2,3] (also see [4]) while the maximum mass of a neutron star (NS) is argued to be about [5], leading to a so-called mass gap. Therefore, the above observation fills in the gap, arguing the compact object to be a massive NS. Note, however, that some researchers also claim against this mass gap. There indeed can be a depression in mass distribution. Nevertheless, there is other evidence for massive NSs (although not as massive as that inferred from GW190814) based on pulsar observations [6] with mass . Indeed, the statistics based on observation showed that while the averaged mass of NSs is about , the accreted millisecond pulsars have masses, on average, of [7,8]. Hence, there is no surprise with the discovery of more than two solar mass pulsars.
On the other hand, for more than 15 years, at least a dozen objects have been detected as peculiar over-luminous Type Ia Supernovae (SNeIa), whose unusually high luminosity, along with their violation of Khokhlov’s limit [9], argue for progenitor masses that are as high as [10,11]. This is evidence for a significant violation of the Chandrasekhar mass-limit of ∼1.4 of white dwarfs (WDs) and a super-Chandrasekhar mass-limit.
An important question to ask is: how do we argue for the existence of such unconventional and massive compact objects? Numerous investigations have been carried out by our group aimed at uncovering this mystery over the last one decade. We have shown that strong magnetic field: its strength and anisotropic effect [12,13,14,15,16,17,18,19,20,21,22], modified Einstein’s gravity [23,24], and matter encountering noncommutative physics at high density in the core of compact stars [25,26] can each independently lead to highly massive WDs and NSs. After our initiation, several other groups independently started looking at this issue based on other ideas, e.g., the ungravity effect [27], WDs having net electric charge [28,29], lepton number violation [30] and anisotropic pressure [31]. Additionally, there appears to be a relation between equation of state (EoS) and compact mass [32].
Magnetic fields in WDs and NSs, in general, degenerate stars, have been explored for a long time (see the review [33] from three decades ago). In general, it is not difficult to understand the surface field of WDs and NSs to be ∼ and G, respectively [33,34], based on their different origins, e.g., fossil effect, dynamo, binary evolution etc. [35,36]. Spectropolarimetric observations suggest that the magnetic flux of majority magnetic WDs is similar to that of main-sequence Ap-Bp stars [34]. This argues for an evolutionary link of magnetism between the main sequence stars and WDs. A similar argument can be made for isolated NSs if the underlying O-type progenitors have effective dipolar fields ∼ G [34]. It has been statistically found that magnetic WDs are, in general, massive, and their number with fields at high as ∼ G could even be of the total population [35]. However, magnetic field evolutions for isolated and accreting WDs are different. This is no surprise because in the outer layers of WDs, the field structure is expected to be modified due to accretion, particularly above a critical accretion rate . This results in a shorter Ohmic decay time, leading to an apparent lack of field ∼ G in observed accreting WDs [37,38].
Among other consequences of magnetized and modified gravity-induced WDs are WD pulsars. These stars can also behave as soft gamma-ray repeaters (SGRs) and anomalous X-ray pulsars (AXPs) [39,40,41], generating significant gravitational radiation that can be detected by space-based detectors [42,43,44]. Many of these transients can eventually turn out to be WDs with super-Chandrasekhar masses. Observational data from the Sloan Digital Sky Survey (SDSS) suggest that magnetic WDs can have larger masses compared to their non-magnetic counterparts, although they span the same temperature range [45,46]. Regardless of the rotation rate, strong magnetic fields have been shown to modify the EoS of electron degenerate matter and yield super-Chandrasekhar WDs with masses up to ∼ [12,13,14,17].
The effect of strong magnetic fields on the mass-radius relation has been explored previously by our group for both Newtonian [12] and general relativistic [15,16,17,21] formalisms. These studies were performed for various different field configurations and were in good agreement with the results from independent studies [29,47,48]. All the above ventures, including the underlying observations, by the aforementioned groups have brought super-Chandrasekhar WDs into the limelight in recent times. Magnetized WDs (B-WDs) have many important implications other than their apparent link to peculiar SNeIa, and, therefore, their other properties should also be explored [39,40]. Strong magnetic fields can influence the thermal properties of WDs, namely their luminosity, temperature gradient and cooling rate [18,20,21,22]. Moreover, the magnetic field of WD has a crucial role in their binary evolution as progenitors of SNeIa or accretion-induced collapse [49,50,51]. Additionally, a possible merger through binary evolution leading to a peculiar SNeIa could be an alternate explanation for super-Chandrasekhar progenitors [52].
In this review paper, we discuss the broad implications of these compact stars as well as the current status of observations. We aim at gathering all the underlying results obtained in last decade or so and try to assess the overall state of the art of the subject as it stands now, in particular regarding the effects of magnetic fields in NS and WD. This paper is organised as follows. In Section 2, we discuss the origin and evolution of strong magnetic fields inside WD stars. In Section 3, we simulate the rotating and magnetized B-WDs based on their structural stability for toroidal and poloidal magnetic field geometries. In Section 4, we compute the mass-radius relation for non-rotating B-WDs, assuming a spherical geometry and radially varying field strength. In Section 5, we explore the effect of cooling as well as magnetic field dissipation on the modified mass limit and the suppressed luminosities of B-WDs. In Section 6, we briefly describe the quantisation of energy states of matter in B-WDs and derive their modified mass limit, assuming both constant and varying magnetic fields. In Section 7, we investigate the GW emission originating from WDs with misaligned rotation and magnetic axes, along with their detection prospects. Finally, we discuss the effect of anisotropy of dense matter in the presence of strong magnetic fields on the properties of B-WDs in Section 8 and conclude in Section 9.
2. Origin and Evolution of Magnetic Fields inside White Dwarfs
Here, we discuss the origin of strong fields inside magnetised WDs and their evolution at the end of the main sequence during the asymptotic giant phase. We present both numerical results from the Cambridge stellar evolution code STARS and analytical estimates from virial theorem that provide a relation between various energy components of the WD.
2.1. Origin of Magnetic Field
Magnetic fields in stars exhibit complex behaviour with structure on both small and large scales. The origin of large-scale fields is debated. They can be fossil fields (e.g., [14,34]) that can be dated back to the formation of the star or fields generated by a dynamic effect. Additionally, the field can be generated due to WD mergers (e.g., [34]). As large-scale magnetic fields in stars can be unstable, dynamo effects are interesting because they can regenerate these fields. It is well known that purely poloidal or toroidal fields in stars are both structurally unstable [53,54]. However, magnetized stars and B-WDs with a toroidally dominated mixed field configuration, along with a small poloidal component, are among the most plausible cases [55] and also have an approximately spherical shape [17]. Unlike the surface magnetic field, which can be observationally inferred, fields in the interior of the WD cannot be directly constrained. However, there is a sufficient evidence that stars exhibit dipolar fields in their outer regions and are expected to have stronger toroidally dominated fields in their interior. Numerical simulations have already shown that the central fields of B-WDs can be several orders of magnitude higher than those at the surface [17,56,57].
2.1.1. Dynamo-Model Based STARS Simulations
The evolution of magnetic field components along with the angular momentum during stellar evolution has been modelled recently with the Cambridge stellar evolution code STARS [56] using advection-diffusion equations coupled to the structural and compositional equations. It has been shown that the magnetic field is likely to be dipolar in nature, decaying as an inverse square law for most of the star. The simulation results also suggest that, at the end of main sequence, stars have toroidally dominated magnetic fields. The authors reported [56] the evolution of toroidal field in the interior of the WD as a function of mass coordinate at various times in the end of main sequence after the exhaustion of helium nuclei in the core, i.e., during the asymptotic giant phase, as displayed in Figure 1 for completeness.
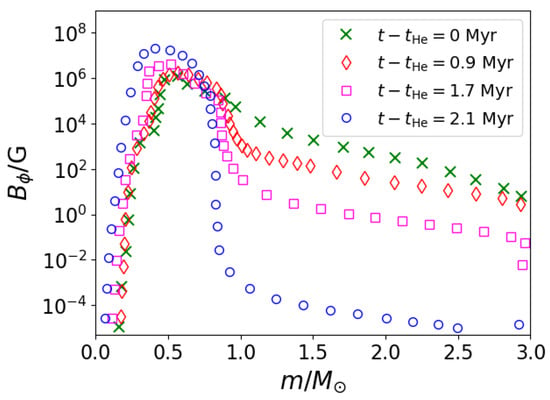
Figure 1.
Toroidal field inside the star is shown as a function of the mass coordinate at various times after the helium exhaustion in the core, during the asymptotic giant phase. See [56] for details.
Large-scale magnetic fields can be present in the degenerate core of magnetised WDs or B-WDs; even during the late stages of stellar evolution [56] very high fields can develop based on the conservation of magnetic flux, as well as from the dynamo mechanism. Therefore, strong fields inside magnetized WDs can also be of fossil origin. While the mass of the WD increases due to accretion, the magnetic field is advected into its interior. Consequently, the gravitational power dominates over the degeneracy pressure, which leads to the contraction of the star. Hence, the initial seed magnetic field is amplified as the total magnetic flux remains conserved.
For magnetic field within a star of size , the resultant flux will be ∼. From flux freezing, for a 1000 km size B-WD, the magnetic field can then grow up to ∼. Once the field increases, the total outward force further builds up to balance the inward gravitational force, and the whole cycle is repeated multiple times. Therefore, the magnetic fields of B-WDs are likely to be fossil remnants from their main-sequence progenitor stars.
2.1.2. Modified Virial Theorem
Virial theorem relates the integrated gravitational potential, thermal, kinetic and magnetic energies of a physical system to provide insight into its equilibrium configuration. By invoking magnetic flux conservation and based on the variation of the internal magnetic field with the matter density as a power law, the modified virial theorem can be derived using the equation of magnetostatic equilibrium [58]. The well-known form of the virial theorem is
where T, W, and are the kinetic, gravitational, thermal and magnetic energies, respectively. For the case of a static non-rotating WD, we have . Assuming that a polytropic EoS is satisfied through the entire star such that , where K and are polytropic constants, and with is the mean density, the scalar virial theorem reduces to
After rearranging the terms, we obtain
for any . For , appropriate for extremely relativistic non-magnetic degenerate electrons, we obtain a mass which is independent of radius for a fixed magnetic flux, as expected from Chandrasekhar’s theory. We evaluate the coefficients , and to establish the modified virial theorem for a high magnetic field.
In the presence of a strong magnetic field, the contribution of the magnetic pressure to the magnetostatic balance cannot be neglected. The new momentum balance condition, neglecting the effect of magnetic tension, is then given by
at an arbitrary radius r with mass enclosed at that radius , where includes the contribution from magnetic field and is the pressure due to the magnetic field of the star. We consider two different approaches to compute the modified virial theorem (see [58]): (i) invoke flux conservation (freezing), which is quite common in stars when conductivity is high, and (ii) assume the magnetic field varies as a power law with respect to density, just as the EoS of thermal pressure, throughout.
For the case (i), the coefficients of the modified virial theorem are obtained as
When for , the situation simplifies to that of a non-magnetized or weakly magnetized WD or a B-WD with constant magnetic field and hence constant throughout. For power-law fields of case (ii), corresponding coefficients are
where is the constant from the relation . It is important to note that is related to the scaling of B with . Therefore, the presence of magnetic pressure allows either a more massive or smaller star. For , the result reduces to that of the non-magnetic case with a redefined K. Figure 2 shows the variation of radius with indices n and for the conserved flux and power-law field models, respectively, with various and total masses.
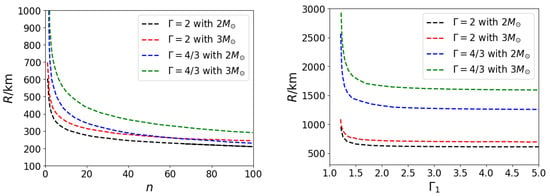
Figure 2.
Left panel: Variation of radius with n for the conserved flux model with various and total masses. Right panel: Variation of radius with for the power-law field model with various and total masses. In each case, corresponds to , and corresponds to , with being the average magnetic field. Parameter sets from top to bottom mentioned in the figures correspond to the lines sequentially from bottom to top in the low n and regimes. See [58].
2.2. Evolution of Magnetic Field
Highly magnetised WDs can possibly result from repeated episodes of accretion and spin-down [57]. The entire evolution of the B-WD can be classified in two phases: accretion-powered and rotation-powered. The accretion-powered phase is governed by three conservation laws: linear and angular momenta conservation and conservation of magnetic flux around the stellar surface, given as
where accounts for the dominance of gravitational force over the centrifugal force, I is the stellar moment of inertia and is the angular velocity of the star that also includes the contribution acquired due to accretion. Here, we neglect any possible field decay and assume a specific field geometry. Solving the above equations simultaneously gives the time evolutions of the radius, magnetic field and angular velocity during the accretion phase. Accretion discontinues when
where is the density of the inner disk edge.
If the magnetic field is dipolar, for a fixed magnetic field. Generalizing it to with constant k giving for the spin-powered phase, we obtain
Here, is the initial angular velocity for the spin-powered phase (once accretion stops) at time , and is the angle between the rotation and magnetic axes. The value of k is fixed such that can be constrained at , which is known from the field evolution in the preceding accretion-powered phase. Here, corresponds to the dipole field configuration; therefore m represents the deviation from the dipolar field, especially for . Figure 3 shows the sample evolutions of angular velocity and magnetic field as functions of stellar mass. The initial angular velocity and particularly the magnetic field are chosen in such a way that they do not affect the stellar structure with respect to when they are zero. In both cases, initially larger with accretion drops significantly during the spin-powered phase, followed by a phase of its increasing trend. At the end of the evolution, the star can be left either as a super-Chandrasekhar WD and/or an SGR/AXP candidate with a higher spin frequency. Other initial conditions do not produce qualitatively different results.
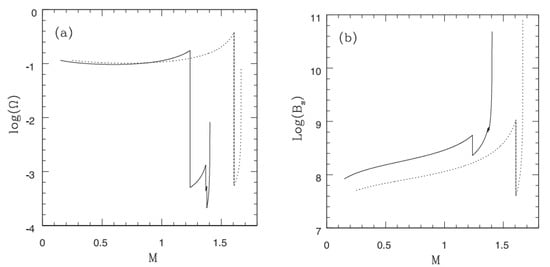
Figure 3.
Time evolution of angular velocity ((a) panel) and magnetic field ((b) panel) as functions of mass. The solid curves correspond to the case with , , , and dotted curves correspond to the case with , , , and . The other parameters are fixed with , , and at . See [57].
3. Simulating Magnetized and Rotating White Dwarfs and Their Stability
In nature, WDs are expected to consist of mixed field geometry, including both toroidal and poloidal magnetic field components. However, here we consider toroidally dominated magnetic fields as they ensure the stability of these stars. Note, in fact, that the core of WDs may contain a stronger toroidal field, which contributes to the stellar structure, mostly including mass, with a weaker surface poloidal field. We simulate WDs and B-WDs based on the Einstein equation solver, XNS code [59]. It has been shown that toroidally dominated and purely toroidal fields not only make the star slightly prolate but also increases its equatorial radius [17,60,61]. It is seen that the deformation at the core is more prominent than the outer region. Nevertheless, the rotation of a star makes it oblate, and hence, there is always a competition between these two opposing effects to decide whether the star will be an overall oblate or prolate.
The combined effect of toroidal field and rotation (uniform and differential) was already explored in detail earlier [42]. It was shown that as the angular frequency is small, it does not affect the star considerably and results in a marginally prolate star due to magnetic effects. However, for high angular velocity, the low density region is affected more due to rotation than the high density central region, resulting in an oblate shaped star. For both the explorations, the magnetic to gravitational energies ratio (ME/GE) as well as kinetic to gravitational energies ratio (KE/GE) are chosen to be to maintain stable equilibrium [62,63,64]. The authors found that for the central density , the magnetic field at the interior (close to the center) of the WD is . Several WDs are observed with the surface magnetic field [45,65,66]; hence, the central field might be much larger than . In fact, it has already been argued in the literature that the central field could be as large as [48,67].
For differentially rotating B-WDs [17], the angular velocity profile is specified as [68,69]
which is implemented in the XNS code used to simulate them, where A is a constant that indicates the extent of differential rotation, , , is the angular velocity at the center and is the angular velocity at radius r. Previous works (e.g., [16,17,42]) reported in detail the density isocontours of differentially rotating B-WDs for toroidal and poloidal fields. It was shown that ‘polar hollow’ structure can form with differential rotation regardless of the specific geometry of the magnetic field.
4. Mass-Limit and Luminosity Suppression in Non-Rotating White Dwarfs
Apart from increasing the limiting mass of WDs, strong magnetic fields can also influence the thermal properties of the star, such as its luminosity, temperature gradient and cooling rate [18,19,20,21,22]. To model such a WD, the total pressure inside the star is modelled by including the contributions from the degenerate electron gas, ideal gas and magnetic pressures. The interface is at the radius where the contributions from electron degenerate core and outer ideal gas pressures are the same. The presence of strong fields gives rise to additional pressure and density inside the magnetized WDs [70] when c is the speed of light.
For an approximately spherical B-WD, the model equations for magnetostatic equilibrium, photon diffusion and mass conservation can be written within a Newtonian framework as
where we have ignored the magnetic tension term for radially varying magnetic field strength. In these equations, and are the electron degeneracy pressure and the ideal gas pressure, is the matter density, T is the temperature, is the mass enclosed within radius r, is the radiative opacity, is the luminosity at radius r, and is the adiabatic index of the gas.
The opacity in the surface layers of non-magnetised WD is approximated with Kramers’ formula, , where , and X and Z are the mass fractions of hydrogen and heavy elements (other than hydrogen and helium) in the stellar interior, respectively. Assuming helium WDs for our study here, we set the helium mass fraction to and . The radiative opacity in the surface layers is mainly due to the bound-free and free-free transitions of electrons [71]. For the radial variation of the field magnitude within the B-WD, we adopt a profile used extensively to model magnetized NSs and B-WDs [15,72], given by
where is the surface magnetic field, is a fiducial magnetic field, and and are dimensionless parameters along with , which determine how the magnetic field decays from the degenerate core to the surface. We set , and for all calculations, unless stated otherwise.
Radial luminosity is assumed to be constant, , as there is no hydrogen burning or other nuclear fusion reactions that take place within the WD core. The differential equations are solved by providing the matter density at the surface, total WD mass and surface temperature as the boundary conditions. For strong magnetic fields, the variation of radiative opacity with B can be modelled as [73,74]. The field-dependent Potekhin’s opacity is used instead of Kramers’ opacity if , which is relevant for the strong fields that we consider.
The left panel of Figure 4 shows the effect of luminosity on the mass-radius relation for non-magnetized WDs compared to Chandrasekhar’s results [75]. Although the increase in L leads to progressively higher masses for larger WDs, Chandrasekhar mass limit is retained irrespective of the luminosity. The right panel of Figure 4 shows the effect of magnetic field on the mass-radius relation for B-WDs with and compares them with the non-magnetic Chandrasekhar results. It can be seen that the magnetic field affects the mass-radius relation in a manner analogous to increasing L by shifting the curve towards higher masses for these WDs having larger radii. The mass-radius curves for practically overlap with each other in the smaller radius regime and retain the Chandrasekhar mass limit. However, for strong central fields with , super-Chandrasekhar WDs are obtained, with masses as high as ∼.
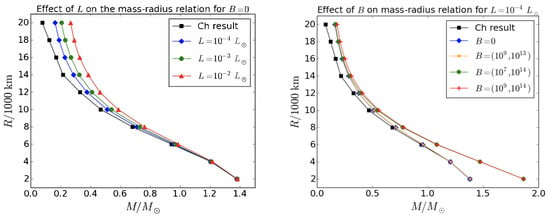
Figure 4.
Left panel: The effect of L on the mass–radius relation of non-magnetised WDs is shown for (blue diamonds), (green circles) and (red triangles), along with the Chandrasekhar result (black squares). Right panel: The effect of field strength on the mass–radius relation of B-WDs is shown for (blue diamonds), (orange crosses), (green circles) and (red pluses), along with the Chandrasekhar result (black squares) for . See [22].
To ensure structural stability of B-WD, an increase in magnetic energy density has to be compensated by a corresponding decrease in the thermal energy and hence the luminosity. This effect is especially prominent for B-WDs with larger radii where the magnetic, thermal and gravitational energies are comparable with each other. We find that in the presence of stronger field, a slight decrease in the luminosity for 12,000 km WDs leads to masses that are similar to their non-magnetic counterparts. However, the smaller radius B-WDs require a substantial drop in their luminosity (well outside the observable range) and still do not really achieve masses that are similar to the non-magnetized WDs. As a result, for stars with 10,000, even if the luminosity decreases substantially with , the resulting mass of the B-WD remains larger than its non-magnetic counterpart. This leads to an extended branch in the mass-radius relation.
5. Effect of Magnetic Field Dissipation and Cooling Evolution
Magnetic fields inside WD undergo decay by Ohmic dissipation and Hall drift processes with timescales given by [37,76], respectively,
where , , , and is the characteristic length scale of the flux loops through the outer core of WD. Ohmic decay is the dominant field dissipation process for , while for , the decay occurs via Hall drift, and for , the principal decay mechanism is likely to be ambipolar diffusion [76].
The field decay can be solved using
where denotes the ambipolar diffusion time scale. We consider two separate cases: (a) when only Ohmic dissipation occurs for both the surface and central magnetic fields, and (b) while continues to evolve over , Hall drift determines the evolution until the central field drops to about , below which Ohmic dissipation sets in.
The thermal energy is radiated away gradually over time in the observed luminosity from the surface layers as the star evolves. Because most of the electrons occupy the lowest energy states in a degenerate gas, the thermal energy of ions is the only significant energy source that can be radiated. The rate at which thermal energy of ions is transported to surface and radiated depends on the specific heat, given by
where is the specific heat at constant volume. Given an initial L and temperature at time , final temperature after cooling is given by , where is the WD age. It is important to note that for simplicity in calculations, we have assumed self-similarity of the cooling process over the entire evolution.
Table 1 lists the luminosities and masses for WDs with radii 20,000 and initial at time and . The fraction of time when the Hall drift dominates, i.e., , falls significantly with increasing stellar radius. Therefore, the magnetic field decays considerably more because the faster Ohmic dissipation process turns out to be critical for much of the cooling evolution. The mass-radius relations merge for WDs. The inferred luminosities are also much less suppressed for the intermediate radius WDs with 12,000. However, for low radius B-WDs, field decay affects mass and luminosity significantly. As it is the high magnetic pressure which helps to hold more mass, the field decay significantly sheds off mass in its new equilibrium if the radius is fixed. The limiting mass for small radius B-WDs with a fixed drops to about due to field decay compared to without field evolution. The majority of these small radius B-WDs still remain practically hidden throughout their cooling evolution because of their strong fields and correspondingly low luminosity.

Table 1.
The effect of magnetic field on luminosity when the initial field is fixed at for all the radii. The topmost entry for each radius is the initial time, whereas the bottom two entries list corresponding parameters for . We evaluate fields assuming Ohmic dissipation is the dominant process for the top entries of , and for the bottom entries, we assume Hall drift is the primary process until the field parameter decays to ∼, below which Ohmic dissipation dominates.
The left panel of Figure 5 shows the effect of B-WD evolution on their mass-radius relations, including both magnetic field decay and thermal cooling effects but neglecting neutrino cooling. The luminosities are varied with field strength such that the B-WD masses can match those obtained for the non-magnetized WDs. For , the mass-radius relation is shifted more towards the Chandrasekhar result as a result of cooling, and the mass limit remains unaltered. However, for , although the maximum mass ∼ at a small radius turns out to be much larger than the Chandrasekhar limit, we find that it is lowered considerably to ∼ primarily as a result of magnetic field decay and also thermal cooling over . The right panel of Figure 5 shows the radial variation of matter density for the same cases. Matter density at the core is slightly suppressed in the presence of strong field and also as a result of the evolution. As the total stellar energy is conserved, an increase in the magnetic energy has to be compensated by a similar decrease in gravitational energy, and, hence, the central density. Once the field decays and luminosity drops due to cooling, the central density adjusts itself to be slightly lower to balance the loss of magnetic and thermal energies with time.
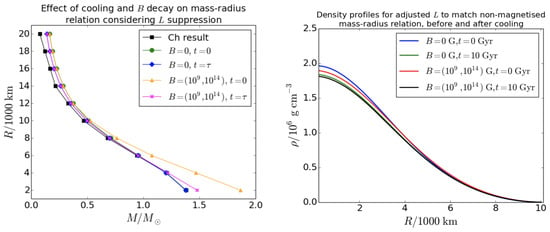
Figure 5.
Left panel: Effect of magnetic field on L set to match the non-magnetised mass-radius relation. Results are shown for at (green circles), at (blue diamonds), at (orange triangles) and at (magenta crosses). Right panel: The matter density profiles for the same cases are shown for R = 10,000 km. See [22].
We also use the STARS stellar evolution code to qualitatively investigate the B-WD mass-radius relationship at different field strengths, with the objective of numerically validating our semi-analytical models. We find that the numerical results are in good agreement with our analytical formalism, and the magnitude of dictates the shape of the mass-radius curve. In validation of our analytical approach, we have found that the limiting mass ∼ obtained with the STARS numerical models is in very good agreement with , which is inferred from the semi-analytical calculations for B-WDs with strong fields [22] for a given magnetic field profile.
We argue that the young super-Chandrasekhar B-WDs only sustain their large masses up to ∼ since their formation, and this essentially explains their apparent scarcity even without the difficulty of detection owing to their suppressed luminosities. We plan to explore this issue in detail in the future, particularly the timescale of their formation considering simultaneously the growth (e.g., by accretion [57]) and decay of fields. It is important to note that if matter accretes at a higher rate such that the total mass accreted exceeds ∼0.1–0.2 before the field diffuses, the field may be restructured [38], leading to a reduced polar field independent of the initial field. We also plan to rigorously explore the fate of B-WDs once the fields decay, if they actually collapse, in place of keeping the radius fixed.
6. Mass Limit Estimate including Quantum Effects
Several magnetized WDs have been discovered with surface fields as high as ∼. It is likely that stronger fields (∼) exist at their interiors. Energy states of a free electron in a uniform strong magnetic field are quantized into Landau orbitals, which defines the motion of the electron in a plane perpendicular to the field. The maximum number of Landau levels occupied by cold electrons in a magnetic field is given by , where is the rest mass of the electron, is the maximum Fermi energy of the system and , where , is the critical field strength. High magnetic field strength therefore modifies the equation of state (EoS) of degenerate matter by causing Landau quantization of electrons [77]. The larger the magnetic field, the smaller is the number of Landau levels occupied [13]. This results in a significant modification of the mass-radius relation of the underlying WD, particularly for .
To obtain the revised mass-radius relation for a strongly magnetized WD, the modified EoS has to be combined with the condition of magnetostatic equilibrium. If the B-WD is approximated to be spherical, then its mass is obtained from
If the field is uniform or highly fluctuating, the magnetic terms can be neglected in the above equations, and following Lane–Emden formalism [78], the scalings of mass and radius with central density are obtained as
Here, (), which is the case for a high as shown in Figure 6, corresponds to central density independent mass, unlike Chandrasekhar’s case when is independent of the field strength, and limiting mass corresponds to .
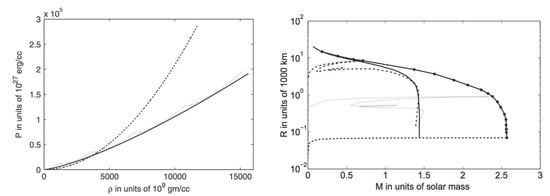
Figure 6.
Left panel: EoS for different cases: solid line represents Chandrasekhar’s EoS, and the dotted and dashed lines represent the 5-level (corresponding to very strong B) and 1-level (corresponding to ultimate EoS for extreme B) systems of Landau quantization, respectively. Right panel: Mass-radius relations: pure solid line represents Chandrasekhar’s result, and the one marked with filled circles represents the evolutionary track of WD with an increase in B. The dot-dashed, dotted and dashed lines represent WDs with 50124-level, 200-level and 1-level systems of Landau quantization, respectively (corresponding to increasing B). We set for both panels. See [13,14].
Substituting the proportionality constants appropriately, the limiting mass is obtained as
when the limiting radius . For , which is the case for a carbon-oxygen WD, we obtain . For a finite but high-density and magnetic field, e.g., and when , and . It should be noted that these and B are similar or below their respective upper limits set by the instabilities of pycnonuclear fusion, inverse- decay and general relativistic effects [15]. Note, however, that pycnonuclear reaction rates are quite uncertain and not well constrained. Moreover, slightly lower and B still would lead to B-WD mass well above the Chandrasekhar mass-limit.
The left panel of Figure 6 shows how the EoS of electron degenerate matter is modified as a result of magnetic field. With increasing field, the inward gravitational force is balanced by the outward force due to modified matter pressure, and a quasi-equilibrium state is attained. Consequently, with decreasing stellar radius due to a higher gravitational field, a very high magnetic field is generated, which prevents the WD from collapsing, thus making its equilibrium configuration more massive. Subsequently, with the continuation of accretion the WD approaches the new mass limit . This new limiting mass WD plausibly sparks off a violent thermonuclear reaction with further accretion, as is the case with the idea of the limit of nonmagnetic WDs, thus exploding it and giving rise to an over-luminous type Ia supernova.
The evolution of the mass-radius relationship with the evolution of magnetic field for a super-Chandrasekhar WD of maximum possible mass is shown in the right panel of Figure 6, along with a few typical mass-radius relations for different fixed magnetic field strengths describing possible stars in intermediate equilibrium states. The ultimate WD, corresponding to the maximum mass , lies on the mass-radius relation for a one-Landau-level system, but the intermediate WDs having weaker magnetic fields correspond to multilevel systems. The said one-Landau-level system corresponds to the hypothetical high central magnetic field . This is in the spirit of a Chandrasekhar mass-limit for a non-magnetic WD, which also corresponds to the hypothetical high (even infinity) central density. However, the mass for still appears to be significantly super-Chandrasekhar. The intermediate systems of 200-level and 50124-level systems correspond to central magnetic fields of and , respectively.
7. Detectability of Gravitational Waves from Magnetised White Dwarfs
One question that remains to be answered is how can B-WDs be detected directly. Continuous gravitational waves can be among the alternate ways to detect super-Chandrasekhar WD candidates. If B-WDs are rotating with certain angular frequency, then they can efficiently emit gravitational radiation, provided that their magnetic field and rotation axes are not aligned [79], and these gravitational waves can be detected by upcoming instruments. The dimensionless amplitudes of the two polarizations of a gravitational wave (GW) at a time t are given by [79,80]
with , where is the quadrupole moment of the distorted star, is the angle between the rotation axis and the body’s third principal axis z, and i is the angle between the rotation axis of the object and our line of sight. The left panel of Figure 7 shows a schematic diagram of a pulsar with being the rotational axis and z the magnetic field axis, where the angle between these two axes is . The GW amplitude is
where is the ellipticity of the body, and , , are the principal moments of inertia. We have used XNS code [59] to simulate the underlying axisymmetric equilibrium configuration of B-WDs in general relativity. Moreover, we assume the distance between the WD and the detector to be 100 pc.
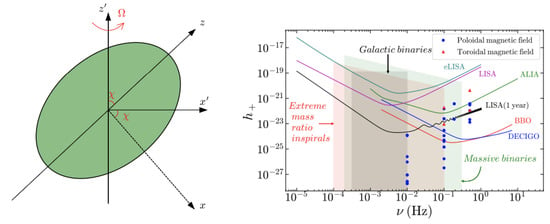
Figure 7.
Left panel: Schematic diagram of a B-WD with being the rotational axis and z as the magnetic axis. Right panel: The dimensionless GW amplitudes for WDs are shown as functions of frequency, along with the sensitivity curves of various detectors. Optimum i is chosen for at . See [43].
Since a pulsating WD can emit both dipole and GW radiations simultaneously, it is associated with both dipole and quadrupolar luminosities. Dipole luminosity for an axisymmetric WD is [81]
where , is the magnetic field strength at the pole, is the radius of the pole and is the average WD radius. The function is defined as
Similarly, the quadrupolar GW luminosity is given by [80]
It should be noted that this formula is valid if is very small. The total luminosity is due to both dipole and gravitational radiations. Therefore, and decay with time due to both and , given by [81]
where is the moment of inertia about the -axis. Equations (26) and (27) need to be solved simultaneously to obtain the timescale over which a WD can radiate.
The right panel of Figure 7 shows the dimensionless GW amplitudes for WDs as functions of their frequencies, along with the sensitivity curves of various detectors. We find that the isolated WDs may not be detected directly by LISA but can be detected after integrating the signal-to-noise ratio (SNR) for 1 year. As WDs are larger in size compared to NS, they cannot rotate as fast as NS and hence ground-based GW detectors such as LIGO, Virgo and KAGRA are not expected to detect the isolated WDs. These isolated WDs are also free from the noise due to the galactic binaries as well as from the extreme mass ratio inspirals (EMRIs).
A pulsar-like object radiates GWs at two frequencies. When we observe such a GW signal whose strength remains unchanged during the observation time T, the corresponding detector’s cumulative SNR is given by [82,83]
where
where is the angle between the interferometer arms and is the detector’s power spectral density (PSD) at the frequency f with . As we mostly deal with space-based interferometers such as LISA, we assume . The average is over all possible angles, including i, which determine the object’s orientation with respect to the celestial sphere reference frame.
Figure 8 shows the SNR as a function of time for toroidal field-dominated WDs with different field strengths. We assume that these toroidal-dominated WDs have a poloidal surface field which is nearly four orders of magnitude smaller than the maximum toroidal field inside the WD. Of course, such a poloidal field cannot change the shape and size of the WD, as does the toroidal field. The surface field strength is relatively very small (as is the dipole luminosity), and so it hardly changes and within a 1 yr period. The left panel of Figure 8 shows the SNR for a B-WD with with mass . All the GW detectors except LISA can easily detect such a WD almost immediately, and LISA can detect it in 5 months of integration. In contrast, when the field strength decreases () the SNR decreases, and LISA and TianQin can no longer detect them, as shown in the right panel. However, they can still be detected by ALIA, BBO and DECIGO within 1 yr of integration time.
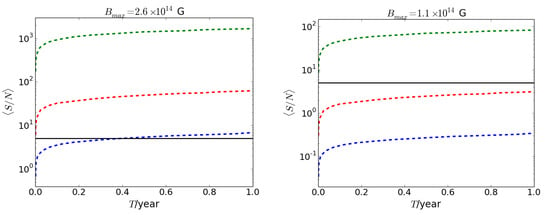
Figure 8.
SNR as a function of integration time for a toroidal field-dominated WD with central density , spin period , and . The green (top) line represents ALIA, the red (middle) line represents TianQin and blue (bottom) line represents LISA. The solid black line corresponds to . See [44].
Figure 9 shows the SNR as a function of integration time for XTE J1810-197, assuming . We choose the maximum radius of this source to be 3000 km instead of 4000 km if it is a WD because its spin is fast and the XNS code does not run for 4000 km with such high rotation frequency. The left panel of Figure 9 shows that BBO and DECIGO would be able to detect it within 20 d and 100 d, respectively, if it is a 3000 km poloidal field-dominated WD. If it is a toroidally dominated WD, BBO and DECIGO could immediately detect it, and ALIA would be able to detect it within 5 months only if it is a 3000 km toroidally dominated WD (see right panel).
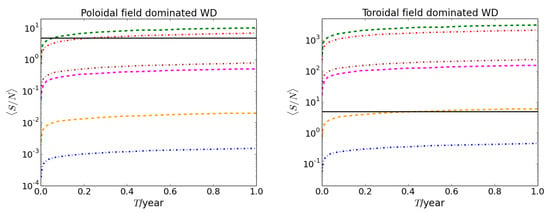
Figure 9.
SNR as a function of integration time for XTE J1810-197 assuming . The first, second and fifth lines from top correspond to a WD with radius 3000 km for BBO, DECIGO and ALIA respectively, while third, fourth and sixth lines from top represent a WD with radius 1000 km for BBO, DECIGO and ALIA respectively. The solid black line corresponds to . See [44].
There are many other plausible detectabilities, e.g., via their activity in binary systems, which will be explored in the future.
8. Matter Anisotropy Effects in Highly Magnetised White Dwarfs
It has been shown that the presence of a strong magnetic field, the anisotropy of dense matter, and the orientation of a magnetic field can significantly influence the properties of neutron and quark stars [84]. The stability of them and B-WDs is not achieved unless one considers the anisotropy of the system arising from the combined effects of [84,85]: (i) anisotropy due to strong magnetic fields and (ii) anisotropy of the system fluid.
The effective contributions from the matter and magnetic field lead to the system density given by
The system pressure along the direction of magnetic field is represented as parallel pressure and takes the form based on magnetic field orientations as
Similarly, the system pressure that aligns perpendicular to the magnetic fields is defined as transverse pressure and is based on the magnetic field orientations
The essential magnetostatic stellar equations which describe static, spherically symmetric B-WDs are
and for radial orientation (RO)
whereas for transverse orientation (TO)
We describe the effective anisotropy of the stars with , which depends on the magnetic field orientations given by in case of RO and for TO. We have for RO
and for TO
where is a dimensionless constant that describes the strength of anisotropy within the stellar structure. Note that implies the anisotropy effects that arise due to matter properties and magnetic field both vanish. However, the case of but implies that only the anisotropy due to magnetic field vanishes. We have shown that highly magnetized WD models, which do not account for the combined anisotropic effects of the fluid and field, are eliminated, as they suffer from an instability at the stellar center.
To solve the magneto-hydrostatic stellar structure equations from the stellar center to surface, it is needed to supply an EoS along with a functional form of . Here, we consider the EoS proposed by Chandrasekhar to describe degenrate electrons of WDs as
where is the mass of an electron, is the mass of a hydrogen atom, h is Planck’s constant, is the mean molecular weight per electron, and with is the Fermi momentum. For the carbon-oxygen WDs, .
We show the mass-radius relations of B-WDs for different , and in Figure 10. For TO fields with , a maximum mass B-WD of is obtained, whose radius is 1457.67 km. For an RO field with , the maximum mass drops to , and the radius of the B-WD is 454.67 km. For , the maximum mass and the corresponding radius of B-WDs increase by and , respectively, compared to the non-magnetized but anisotropic case. For , the maximum mass and the corresponding radius decrease by ∼2% and ∼52%, respectively, compared to the values of non-magnetized but anisotropic WDs. Even without considering the magnetic field and incorporating the effects of local anisotropy due to the fluid, it is possible to push the maximum mass of WDs beyond the Chandrasekhar mass limit. For example, by considering , we obtain a maximum mass for a non-magnetized but anisotropic WD of . The corresponding radius is 956.08 km. These values are and , respectively, higher than the respective values of WDs at the Chandrasekhar mass limit. Moreover, with increasing and for the TO field case, the mass of anisotropic B-WDs changes significantly, as can be seen in the right panel of Figure 10. It shows that the maximum mass of a B-WD with and increases by compared to and .
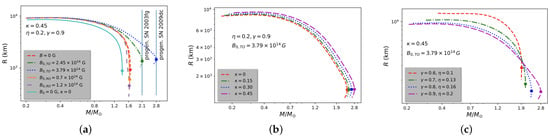
Figure 10.
Stellar radius (R) as a function of gravitational mass () for different (a) (left panel), (b) (middle panel), and (c) and (right panel). Solid circles represent the stars with the maximum-possible masses. See [85].
For RO fields, we can explain sub-, standard- and super-Chandrasekhar B-WDs by making appropriate choices of and (see Figure 11). By changing both and , as shown in the left panel of Figure 11, we successfully explain both (i) the sub- and standard-Chandrasekhar progenitor B-WDs and (ii) the standard and super-Chandrasekhar progenitor B-WDs by a single mass-radius curve for the respective cases. On the other hand, through changes of only or , sub-, standard- and super-Chandrasekhar B-WDs line up in a series of mass-radius curves; see, e.g., the middle and right panels of Figure 11. This leads to a complete explanation of under-, regular- and over-luminous SNeIa in a single theory.
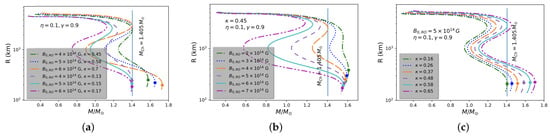
Figure 11.
Stellar radius (R) as a function of gravitational mass () for varying (a) and (left panel), (b) (middle panel), and (c) (right panel). Solid circles represent the stars with the maximum possible masses. See [85].
9. Conclusions
Reviewing the work in last decade or so, we have confirmed that, at least theoretically, massive NSs and WDs, heavier than their conventional counterparts as observed/inferred from recent data, are possibly highly magnetized, rotating stable compact stars. They have multiple implications including enigmatic peculiar over-luminous SNeIa. Numerical simulations based on Cambridge stellar evolution code STARS argue B-WDs to be toroidally (centrally) dominated with lower, maybe dipole, surface magnetic fields. The new generic mass-limit of WDs seems to be well above , around , depending on the magnetic field profile/geometry and rotational frequency.
However, these massive compact objects, particularly WDs, have hardly been observed directly due to their apparently very low luminosity. On the other hand, the presence of magnetic fields and rotation by definition brings in anisotropy in these compact objects, leading them to be triaxial when the magnetic and rotation axes are misaligned. Therefore, they are expected to emit continuous GW. Hence, B-WDs can be detected directly by the missions LISA (in one year integration time), DECIGO/BBO and the magnetised NSs can be detected by aLIGO, aVIRGO, Einstein Telescope.
Nevertheless, the magnetic fields therein start decaying beyond million years, hence these massive compact objects may not survive beyond this time. Moreover, due to their electromagnetic and gravitational radiation, the angular velocity and the misalignment angle between magnetic and rotation axes decrease, leading them to lose their pulsar nature and detection possibility. This is another reason why they are so rare and/or hard to detect unless targeted at an appropriate time. Therefore, appropriate missions in GW astronomy and otherwise, e.g., radio astronomy, should be planned to probe them.
Author Contributions
Both the authors share an equal authorship. However, various figures presented in this manuscript are based on previous works by B.M. and his collaborators. The work was conceptualized by B.M.; the methodology was initiated by B.M. and further was carried out by B.M. and M.B.; investigation was initiated by B.M. and was further taken over by M.B.; the first draft was prepared by M.B. and further was revised and edited by B.M. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
M.B. would like to acknowledge support from the Eberly Research Fellowship at the Pennsylvania State University.
Data Availability Statement
Not applicable.
Acknowledgments
B.M. thanks the organizers of “The Modern Physics of Compact Stars and Relativistic Gravity 2021” held 27–30 September 2021 in Yerevan, Armenia, for the invitation to give a talk, based on which the present paper is composed.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- MacFadyen, A.I.; Woosley, S.E. Collapsars: Gamma-Ray Bursts and Explosions in “Failed Supernovae”. Astrophys. J. 1999, 524, 262. [Google Scholar] [CrossRef]
- Pooley, D.; Kumar, P.; Wheeler, J.; Grossan, B. GW170817 Most Likely Made a Black Hole. Astrophys. J. Lett. 2018, 859, L23. [Google Scholar] [CrossRef]
- Ozel, F.; Psaltis, D.; Narayan, R.; McClintock, J.E. The Black Hole Mass Distribution in the Galaxy. Astrophys. J. 2010, 725, 1918. [Google Scholar] [CrossRef]
- Alsing, J.; O’Silva, H.; Berti, E. Evidence for a maximum mass cut-off in the neutron star mass distribution and constraints on the equation of state. Mon. Not. R. Astron. Soc. 2018, 478, 1377. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Zhang, C.M.; Wang, J.; Zhao, Y.H.; Yin, H.X.; Song, L.M.; Menezes, D.P.; Wickramasinghe, D.T.; Ferrario, L.; Chardonnet, P. Study of measured pulsar masses and their possible conclusions. Astron. Astrophys. 2011, 527, A83. [Google Scholar] [CrossRef]
- Miller, M.C. Astrophysical Constraints on Dense Matter in Neutron Stars. In Timing Neutron Stars: Pulsations, Oscillations and Explosions; Astrophysics and Space Science Library (ASSL); Springer: Berlin/Heidelberg, Germany, 2021; Volume 461. [Google Scholar] [CrossRef]
- Khokhlov, A.M. Delayed detonation model for type Ia supernovae. Astron. Astrophys. 1991, 245, 114–128. [Google Scholar]
- Scalzo, R.A.; Aldering, G.; Antilogus, P.; Aragon, C.; Bailey, S.; Baltay, C.; Bongard, S.; Buton, C.; Childress, M.; Chotard, N.; et al. Nearby Supernova Factory Observations of SN 2007if: First Total Mass Measurement of a Super-Chandrasekhar-Mass Progenitor. Astrophys. J. 2010, 713, 1073–1094. [Google Scholar] [CrossRef]
- Howell, D.A.; Sullivan, M.; Nugent, P.E.; Ellis, R.S.; Conley, A.J.; Le Borgne, D.; Carlberg, R.G.; Guy, J.; Balam, D.; Basa, S.; et al. The type Ia supernova SNLS-03D3bb from a super-Chandrasekhar-mass white dwarf star. Nature 2006, 443, 308–311. [Google Scholar] [CrossRef]
- Das, U.; Mukhopadhyay, B. Strongly magnetized cold degenerate electron gas: Mass-radius relation of the magnetized white dwarf. Phys. Rev. D 2012, 86, 042001. [Google Scholar] [CrossRef]
- Das, U.; Mukhopadhyay, B. New Mass Limit for White Dwarfs: Super-Chandrasekhar Type Ia Supernova as a New Standard Candle. Phys. Rev. Lett. 2013, 110, 071102. [Google Scholar] [CrossRef] [PubMed]
- Das, U.; Mukhopadhyay, B.; Rao, A.R. A Possible Evolutionary Scenario of Highly Magnetized Super-Chandrasekhar White Dwarfs: Progenitors of Peculiar Type Ia Supernovae. Astrophys. J. Lett. 2013, 767, L14. [Google Scholar] [CrossRef]
- Das, U.; Mukhopadhyay, B. Maximum mass of stable magnetized highly super-Chandrasekhar white dwarfs: Stable solutions with varying magnetic fields. J. Cosmol. Astropart. Phys. 2014, 2014, 050. [Google Scholar] [CrossRef]
- Das, U.; Mukhopadhyay, B. GRMHD formulation of highly super-Chandrasekhar magnetized white dwarfs: Stable configurations of non-spherical white dwarfs. J. Cosmol. Astropart. Phys. 2015, 2015, 016. [Google Scholar] [CrossRef][Green Version]
- Subramanian, S.; Mukhopadhyay, B. GRMHD formulation of highly super-Chandrasekhar rotating magnetized white dwarfs: Stable configurations of non-spherical white dwarfs. Mon. Not. R. Astron. Soc. 2015, 454, 752–765. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Mukhopadhyay, B.; Mukerjee, S. Luminosity and cooling of highly magnetized white dwarfs: Suppression of luminosity by strong magnetic fields. Mon. Not. R. Astron. Soc. 2018, 477, 2705–2715. [Google Scholar] [CrossRef]
- Bhattacharya, M.; Mukhopadhyay, B.; Mukerjee, S. Luminosity and cooling suppression in magnetized white dwarfs. arXiv 2018, arXiv:1810.07836. [Google Scholar]
- Gupta, A.; Mukhopadhyay, B.; Tout, C.A. Suppression of luminosity and mass-radius relation of highly magnetized white dwarfs. Mon. Not. R. Astron. Soc. 2020, 496, 894–902. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Bhattacharya, M.; Hackett, A.J.; Kalita, S.; Karinkuzhi, D.; Tout, C.A. Highly magnetized white dwarfs: Implications and current status. arXiv 2021, arXiv:2110.15374. [Google Scholar]
- Bhattacharya, M.; Hackett, A.J.; Gupta, A.; Tout, C.A.; Mukhopadhyay, B. Evolution of Highly Magnetic White Dwarfs by Field Decay and Cooling: Theory and Simulations. Astrophys. J. 2022, 925, 133. [Google Scholar] [CrossRef]
- Banerjee, S.; Shankar, S.; Singh, T.P. Constraints on modified gravity models from white dwarfs. J. Cosmol. Astropart. Phys. 2017, 2017, 004. [Google Scholar] [CrossRef]
- Eslam Panah, B.E.; Liu, H. White dwarfs in de Rham-Gabadadze-Tolley like massive gravity. Phys. Rev. D 2019, 99, 104074. [Google Scholar] [CrossRef]
- Kalita, S.; Mukhopadhyay, B.; Govindarajan, T.R. Significantly super-Chandrasekhar mass-limit of white dwarfs in noncommutative geometry. Int. J. Mod. Phys. D 2021, 30, 2150034. [Google Scholar] [CrossRef]
- Kalita, S.; Mukhopadhyay, B.; Govindarajan, T.R. Super-Chandrasekhar limiting mass white dwarfs as emergent phenomena of noncommutative squashed fuzzy spheres. Int. J. Mod. Phys. D 2021, 30, 2150101. [Google Scholar] [CrossRef]
- Bertolami, O.; Mariji, H. White dwarfs in an ungravity-inspired model. Phys. Rev. D 2016, 93, 104046. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, X.; Wen, D. One possible solution of peculiar type Ia supernovae explosions caused by a charged white dwarf. Phys. Rev. D 2014, 89, 104043. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Arbanil, J.D.V.; Marinho, R.M.; Malheiro, M. White dwarfs with a surface electrical charge distribution: Equilibrium and stability. Eur. Phys. J. C 2018, 78, 411. [Google Scholar] [CrossRef]
- Belyaev, V.B.; Ricci, P.; Simkovic, F.; Adam, J.; Tater, M.; Truhlik, E. Consequence of total lepton number violation in strongly magnetized iron white dwarfs. Nucl. Phys. A 2015, 937, 17–43. [Google Scholar] [CrossRef][Green Version]
- Herrera, L.; Barreto, W. Newtonian polytropes for anisotropic matter: General framework and applications. Phys. Rev. D 2013, 87, 087303. [Google Scholar] [CrossRef]
- Glendenning, N.K. Compact Stars. Nuclear Physics, Particle Physics and General Relativity; Springe: New York, NY, USA, 1996. [Google Scholar]
- Chanmugam, G. Magnetic fields of degenerate stars. Annu. Rev. Astron. Astrophys. 1992, 30, 143–184. [Google Scholar] [CrossRef]
- Ferrario, L.; Wickramasinghe, D.T. Magnetic fields and rotation in white dwarfs and neutron stars. Mon. Not. R. Astron. Soc. 2005, 356, 615–620. [Google Scholar] [CrossRef]
- Ferrario, L.; Wickramasinghe, D.T.; Kawka, A. Magnetic fields in isolated and interacting white dwarfs. Adv. Space Res. 2020, 66, 1025–1056. [Google Scholar] [CrossRef]
- Wickramasinghe, D.T.; Ferrario, L. Magnetism in Isolated and Binary White Dwarfs. Publ. Astron. Soc. Pac. 2000, 112, 873–924. [Google Scholar] [CrossRef]
- Cumming, A. Magnetic field evolution in accreting white dwarfs. Mon. Not. R. Astron. Soc. 2002, 333, 589–602. [Google Scholar] [CrossRef]
- Zhang, C.M.; Wickramasinghe, D.T.; Ferrario, L. Is there evidence for field restructuring or decay in accreting magnetic white dwarfs? Mon. Not. R. Astron. Soc. 2009, 397, 2208–2215. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Rao, A.R. Soft gamma-ray repeaters and anomalous X-ray pulsars as highly magnetized white dwarfs. J. Cosmol. Astropart. Phys. 2016, 2016, 007. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Das, U.; Rao, A.R.; Subramanian, S.; Bhattacharya, M.; Mukerjee, S.; Bhatia, T.S.; Sutradhar, J. Significantly Super-Chandrasekhar Limiting Mass White Dwarfs and their Consequences. arXiv 2017, arXiv:1611.00133. [Google Scholar]
- Mukhopadhyay, B.; Bhattacharya, M.; Rao, A.R.; Mukerjee, S.; Das, U. Possible formation of lowly luminous highly magnetized white dwarfs by accretion leading to SGRs/AXPs. arXiv 2018, arXiv:1908.10045. [Google Scholar]
- Kalita, S.; Mukhopadhyay, B. Continuous gravitational wave from magnetized white dwarfs and neutron stars: Possible missions for LISA, DECIGO, BBO, ET detectors. Mon. Not. R. Astron. Soc. 2019, 490, 2692–2705. [Google Scholar] [CrossRef]
- Kalita, S.; Mukhopadhyay, B.; Mondal, T.; Bulik, T. Timescales for Detection of Super-Chandrasekhar White Dwarfs by Gravitational-wave Astronomy. Astrophys. J. 2020, 896, 69. [Google Scholar] [CrossRef]
- Kalita, S.; Mondal, T.; Tout, C.A.; Bulik, T.; Mukhopadhyay, B. Resolving dichotomy in compact objects through continuous gravitational waves observation. Mon. Not. R. Astron. Soc. 2021, 508, 842–851. [Google Scholar] [CrossRef]
- Vanlandingham, K.; Schmidt, G.; Eisenstein, D.; Harris, H.C.; Anderson, S.F.; Hall, P.B.; Liebert, J.; Schneider, D.P.; Silvestri, N.M.; Stinson, G.S.; et al. Magnetic White Dwarfs from the SDSS. II. The Second and Third Data Releases. Astron. J. 2005, 130, 734–741. [Google Scholar] [CrossRef]
- Ferrario, L.; de Martino, D.; Gänsicke, B.T. Magnetic White Dwarfs. Space Sci. Rev. 2015, 191, 111–169. [Google Scholar] [CrossRef]
- Boshkayev, K.; Rueda, J.; Ruffini, R.; Siutsou, I. On General Relativistic Uniformly Rotating White Dwarfs. Astrophys. J. 2013, 762, 117. [Google Scholar] [CrossRef]
- Franzon, B.; Schramm, S. Effects of strong magnetic fields and rotation on white dwarf structure. Phys. Rev. D 2015, 92, 083006. [Google Scholar] [CrossRef]
- Ablimit, I.; Maeda, K. Evolution of Magnetized White Dwarf Binaries to Type Ia Supernovae. Astrophys. J. 2019, 871, 31. [Google Scholar] [CrossRef]
- Ablimit, I.; Maeda, K. Possible Contribution of Magnetized White Dwarf Binaries to Type Ia Supernova Populations. Astrophys. J. 2019, 885, 99. [Google Scholar] [CrossRef]
- Ablimit, I. The magnetized white dwarf + helium star binary evolution with accretion-induced collapse. Mon. Not. R. Astron. Soc. 2022, 509, 6061. [Google Scholar] [CrossRef]
- Ablimit, I. The CO White Dwarf + Intermediate-mass/Massive Star Binary Evolution: Possible Merger Origins for Peculiar Type Ia and II Supernovae. Publ. Astron. Soc. Pac. 2021, 133, 074201. [Google Scholar] [CrossRef]
- Markey, P.; Tayler, R.J. The adiabatic stability of stars containing magnetic fields. II. Poloidal fields. Mon. Not. R. Astron. Soc. 1973, 163, 77–91. [Google Scholar] [CrossRef]
- Tayler, R.J. The adiabatic stability of stars containing magnetic fields. I: Toroidal fields. Mon. Not. R. Astron. Soc. 1973, 161, 365–380. [Google Scholar] [CrossRef]
- Wickramasinghe, D.T.; Tout, C.A.; Ferrario, L. The most magnetic stars. Mon. Not. R. Astron. Soc. 2014, 437, 675–681. [Google Scholar] [CrossRef]
- Quentin, L.G.; Tout, C.A. Rotation and magnetism in intermediate-mass stars. Mon. Not. R. Astron. Soc. 2018, 477, 2298–2309. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Rao, A.R.; Bhatia, T.S. AR Sco as a possible seed of highly magnetized white dwarf. Mon. Not. R. Astron. Soc. 2017, 472, 3564–3569. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Sarkar, A.; Tout, C.A. Modified virial theorem for highly magnetized white dwarfs. Mon. Not. R. Astron. Soc. 2021, 500, 763–771. [Google Scholar] [CrossRef]
- Pili, A.G.; Bucciantini, N.; Del Zanna, L. Axisymmetric equilibrium models for magnetized neutron stars in General Relativity under the Conformally Flat Condition. Mon. Not. R. Astron. Soc. 2014, 439, 3541–3563. [Google Scholar] [CrossRef]
- Ioka, K.; Sasaki, M. Relativistic Stars with Poloidal and Toroidal Magnetic Fields and Meridional Flow. Astrophys. J. 2004, 600, 296–316. [Google Scholar] [CrossRef]
- Frieben, J.; Rezzolla, L. Equilibrium models of relativistic stars with a toroidal magnetic field. Mon. Not. R. Astron. Soc. 2012, 427, 3406–3426. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Fermi, E. Problems of Gravitational Stability in the Presence of a Magnetic Field. Astrophys. J. 1953, 118, 116. [Google Scholar] [CrossRef]
- Komatsu, H.; Eriguchi, Y.; Hachisu, I. Rapidly rotating general relativistic stars. I - Numerical method and its application to uniformly rotating polytropes. Mon. Not. R. Astron. Soc. 1989, 237, 355–379. [Google Scholar] [CrossRef]
- Braithwaite, J. Axisymmetric magnetic fields in stars: Relative strengths of poloidal and toroidal components. Mon. Not. R. Astron. Soc. 2009, 397, 763–774. [Google Scholar] [CrossRef]
- Heyl, J.S. Gravitational radiation from strongly magnetized white dwarfs. Mon. Not. R. Astron. Soc. 2000, 317, 310–314. [Google Scholar] [CrossRef]
- Brinkworth, C.; Burleigh, M.; Lawrie, K.; Marsh, T.R.; Knigge, C. Measuring the Rotational Periods of Isolated Magnetic White Dwarfs. Astrophys. J. 2013, 773, 47. [Google Scholar] [CrossRef]
- Shah, H.; Sebastian, K. Central Magnetic Field of a Magnetic White Dwarf Star. Astrophys. J. 2017, 843, 131. [Google Scholar] [CrossRef]
- Stergioulas, N. Rotating Stars in Relativity. Living Rev. Relativ. 2003, 6, 3. [Google Scholar] [CrossRef]
- Bucciantini, N.; Del Zanna, L. General relativistic magnetohydrodynamics in axisymmetric dynamical spacetimes: The X-ECHO code. Astron. Astrophys. 2011, 528, A101. [Google Scholar] [CrossRef]
- Sinha, M.; Mukhopadhyay, B.; Sedrakian, A. Hypernuclear matter in strong magnetic field. Nucl. Phys. A 2013, 898, 43–58. [Google Scholar] [CrossRef]
- Shapiro, S.; Teukolsky, S. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Bandyopadhyay, D.; Chakrabarty, S.; Pal, S. Quantizing Magnetic Field and Quark-Hadron Phase Transition in a Neutron Star. Phys. Rev. Lett. 1997, 79, 2176–2179. [Google Scholar] [CrossRef]
- Potekhin, A.Y.; Yakovlev, D.G. Thermal structure and cooling of neutron stars with magnetized envelopes. Astron. Astrophys. 2001, 374, 213–226. [Google Scholar] [CrossRef][Green Version]
- Ventura, J.; Potekhin, A. Neutron Star Envelopes and Thermal Radiation from the Magnetic Surface. arXiv 2001, arXiv:astro-ph/0104003. [Google Scholar]
- Chandrasekhar, S. The highly collapsed configurations of a stellar mass. Mon. Not. R. Astron. Soc. 1935, 95, 207–225. [Google Scholar] [CrossRef]
- Heyl, J.S.; Kulkarni, S.R. How Common Are Magnetars? The Consequences of Magnetic Field Decay. Astrophys. J. 1998, 506, L61–L64. [Google Scholar] [CrossRef]
- Lai, D.; Shapiro, S.L. Cold Equation of State in a Strong Magnetic Field: Effects of Inverse beta-Decay. Astrophys. J. 1991, 383, 745. [Google Scholar] [CrossRef]
- Choudhuri, A.R. Astrophysics for Physicists; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Bonazzola, S.; Gourgoulhon, E. Gravitational waves from pulsars: Emission by the magnetic-field-induced distortion. Astron. Astrophys. 1996, 312, 675–690. [Google Scholar]
- Zimmermann, M.; Szedenits, E. Gravitational waves from rotating and precessing rigid bodies: Simple models and applications to pulsars. Phys. Rev. D 1979, 20, 351–355. [Google Scholar] [CrossRef]
- Melatos, A. Radiative precession of an isolated neutron star. Mon. Not. R. Astron. Soc. 2000, 313, 217–228. [Google Scholar] [CrossRef]
- Jaranowski, P.; Krolak, A.; Schutz, B.F. Data analysis of gravitational-wave signals from spinning neutron stars: The signal and its detection. Phys. Rev. D 1998, 58, 063001. [Google Scholar] [CrossRef]
- Bennett, M.F.; van Eysden, C.A.; Melatos, A. Continuous-wave gravitational radiation from pulsar glitch recovery. Mon. Not. R. Astron. Soc. 2010, 409, 1705–1718. [Google Scholar] [CrossRef]
- Deb, D.; Mukhopadhyay, B.; Weber, F. Effects of Anisotropy on Strongly Magnetized Neutron and Strange Quark Stars in General Relativity. Astrophys. J. 2021, 922, 149. [Google Scholar] [CrossRef]
- Deb, D.; Mukhopadhyay, B.; Weber, F. Anisotropic Magnetized White Dwarfs: Unifying Under- and Overluminous Peculiar and Standard Type Ia Supernovae. Astrophys. J. 2022, 926, 66. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).