The Number of Elementary Fermions and the Electromagnetic Coupling

Abstract

Electric charges and masses of elementary fermions of the Standard Model and fundamental physical constants (speed of light in vacuum, Planck constant, gravitational constant, vacuum permittivity, electron charge) are related through a simple equation. This new relation links 10 of the free parameters of the Standard Model—the masses of the three charged leptons and six quarks, and the electromagnetic coupling—in a compact formula, leaving strong constraints for allowing further elementary charged fermions beyond the Standard Model’s physics. The formula is not derived by theoretical calculations, but it is based on the empirically measured values of the electric charges and proper masses of the known elementary fermions.

Introduction

In physics, in the framework of the Standard Model (SM), Quantum Electro-Dynamics is among the most tested theories. Measurements of the electromagnetic fine-structure constant α have reached an accuracy of 81 part-per-trillion [1,2] (see

Table 1. Fundamental physical constants [1].

Constant	Value
c = speed of light in vacuum	2.99792458 × 108 m s−1
h = Planck constant	6.62607015 × 10−34 J Hz−1
G = gravitational constant	(6.67430 ± 0.00015) × 10−11 m3 kg−1 s−2
e = electron charge	1.602176634 × 10−19 C
${\epsilon }_0$ = vacuum permittivity	(8.8541878128 ± 0.0000000013) × 10−12 F/m
$\frac{1}{\alpha }=\frac{2{\epsilon }_{0}hc}{e^2}=$ Inverse fine-structure constant	137.035999206 ± 0.000000011
$m_P={\left(\frac{hc}{2\pi G}\right)}^{1/2}$ = Planck mass	(1.220890 ± 0.000013) × 1019 GeV

). Notwithstanding the impressive level of accuracy reached, the theoretical prediction of the anomalous magnetic electron moment g − 2 is fully in agreement with the experimental value deduced by the measure of α. For muons, instead, the situation is different: the longstanding muon g − 2 anomaly may indicate the existence of new particles that couple to muons [3], opening the possibility of new physics beyond the SM.

Under the SM, electric-charged elementary fermions gain mass from their coupling to the Higgs field, through its non-zero vacuum expectation value of 246 GeV [4]. Coupling of fundamental interactions cover many orders of magnitudes, giving rise to a hierarchy problem [5,6,7]. The hierarchy problem can be also related to the small but not zero expectation value of the Higgs field, i.e., why the Higgs boson is so much lighter than the Planck mass [6] (see Table 1). In fact, the Higgs field should be expected to be either zero or as large as the Planck energy, about 16 orders of magnitude greater than the observed value that, for this reason, should be unstable, unless there is an incredible fine-tuning cancellation between the quadratic radiative corrections and the bare mass.

To complicate the individuation of the correct theoretical solution to the hierarchy problem, there is a further limiting issue: masses of elementary particles and couplings of the fundamental interactions are free parameters of the SM. In other words, the SM does not explain or predict the pattern of fermion masses, which are observed to vary over many orders of magnitude. Additionally, electric charge quantization, which refers to the fact that the magnitudes of the proton, made by three quarks, and of the electron electric charges are the same, is not explained [8]. Table 1 [1] and

Table 2. Mass and electric charge of the elementary fermions of the SM [1,9,10].

Fermion	${\mathit{M}}_{\mathit{i}}$ = Mass (GeV) [9]	${\mathit{Q}}_{\mathit{i}}$ = Electric Charges (in Units of e)
Neutrinos	<0.00000000012 (sum of the three flavors) [10]	0
Electron	0.0005109989461 ± 0.0000000000031	1
Muon	0.1056583745 ± 0.0000000024	1
Tauon	$1.77686 \begin{array}{c}+0.00012\\ -0.00012\end{array}$	1
Up	$0.00216 \begin{array}{c}+0.00049\\ -0.00026\end{array}$	2/3
Down	$0.00467 \begin{array}{c}+0.00048\\ -0.00017\end{array}$	−1/3
Charm	$1.27 \begin{array}{c}+0.02\\ -0.02\end{array}$	2/3
Strange	$0.093\begin{array}{c}+0.011\\ -0.005\end{array}$	−1/3
Top	$172.76\begin{array}{c}+0.30\\ -0.30\end{array}$	2/3
Bottom	$4.18 \begin{array}{c}+0.03\\ -0.02\end{array}$	−1/3

[1,9,10] show the mass and electric charges of the elementary fermions and the fundamental physical constants from which the electromagnetic coupling and Planck mass depend on. Figure 1 shows these masses versus the absolute value of the electric charge Q, expressed in units of the electron charge. The three points for each electric charge value are the fermions corresponding to the three families of the SM. It can be noted that these masses for charged fermions span six orders of magnitudes, which become at least 12 orders if one also considers the neutrinos, limiting our understanding of why we have precisely these mass values and not others.

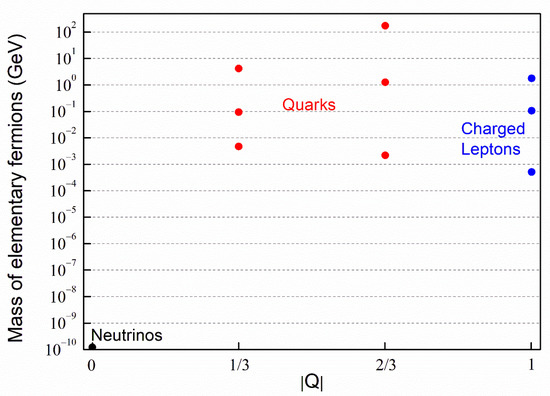
From the values reported in Table 1 and Table 2, for charged elementary fermions, it is worth noting that:

$$\frac{1}{3}{{\displaystyle \sum }}_{i=1}^{9}ln\left(\frac{m_P}{m_i}\right)=137.28 \pm 0.17,$$

(1)

very close to the inverse of the fine structure constant 1/α.

This relationship among masses of the elementary fermions and the electromagnetic coupling constant becomes more striking if we consider the following sum over all the elementary fermions of the SM:

$$R\equiv \frac{2}{\pi }\alpha {\displaystyle \sum }_{i=1}^{12}{Q}_i^{2}ln\left(\frac{m_P}{m_i}\right)$$

(2)

Indeed, inserting the masses and electric charges of the elementary fermions and the fundamental physical constants reported in Table 1 and Table 2, the following experimental value is obtained:

$$R=1.00057 \pm 0.00057.$$

(3)

Given Equation (1), Equation (2) can be readily derived by observing that the sum of the square of the four different electric charge states (0, 1, 1/3, 2/3), allowed in the SM for elementary fermions, can be approximated as follows:

$$\frac{1}{3}{\displaystyle \sum }_{i=1}^{12}{Q}_i^2=\frac{14}{9}\cong \frac{\pi }{2}.$$

(4)

Therefore, within one standard deviation, Equations (2) and (3) seems just to relate 10 free parameters of the SM: the masses of the three charged leptons, the masses of the six quarks, and the electro-magnetic coupling strength.

The probability that the above result is only the consequence of a fortuitus coincidence is very low, being involved 10 free parameters of the SM. The other possibility is that all these physical quantities are not independent and are related just through Equation (5):

$$R\equiv \frac{2}{\pi }\alpha {\displaystyle \sum }_{i=1}^{12}{Q}_i^{2}ln\left(\frac{m_P}{m_i}\right)=1.$$

(5)

Equation (5) seems to indicate that there should not be further charged elementary fermions (new families, new particles for the three families, supersymmetric fermions, etc.). The Z-pole data from CERN and SLAC, as well as the experimental evidence from the cosmological abundance of helium already implies that there are no additional fermion families beyond the three already known [8]. Moreover, also neutrinos’ masses, to avoid an indeterminate expression (division by zero), must be different from zero, as expected [10]. Supersymmetric electric-charged fermion partners of the SM particles seem to be excluded by Equation (5), since it is already satisfied by the elementary fermions of the SM (see Equation (3)). However, other fermions with masses on the TeV scale, needed to extend the theory beyond the SM [3,8,11], could satisfy an equation similar to Equation (5), with the index “i” running on more than 12 elementary fermions, but with a different multiplicative numerical constant before the sum, related to the sum of the square of the different electric charge’s states.

In any case, Equation (5) constitutes a strong constraint, satisfied by the SM 12 elementary fermions up to the fourth decimal digit (see Equation (3)). In fact, it is simple to verify that inserting quarks’ multiplicity in Equation (5), due to the three different color charges, does not allow the fulfillment of this relation up to the fourth decimal digit, even if one searches for suitable multiplicative numerical constants before the sum. The same difficulties, in satisfying Equation (5) up to the fourth decimal digit, arises if one tries to generalize the equation inserting the electro-weak bosons W and Z. These failures allow to conjecture that Equation (5) could be also considered a relation for defining the fine-structure constant, i.e., depending only on the quantized values of the electric charge of the SM elementary fermions: 0, 1, 1/3, and 2/3.

In conclusion, if Equation (5) is not a fortuitous numerical coincidence, the solutions to the hierarchy problem, for example within the theoretical framework of supersymmetric theories [8,11], or to the muon g − 2 anomaly [3], or any other theoretical extension of the SM requiring new elementary fermions, could be constrained by a relation of the type

$${\displaystyle \sum }_{i=1}^{N}C\left(Q_i^2\right)ln\left(\frac{m_P}{m_i}\right)=\frac{1}{\alpha },$$

(6)

with the multiplicative weights equal to

$$C\left(Q_i^2\right)=3Q_i^2/{\displaystyle \sum }_{j=1}^N{Q}_j^2.$$

(7)

and N the total number of elementary fermions required by the theory, by considering only the multiplicity due to the different electric charge’s states within the 3 families. The mathematical structure of Equation (6) seems to imply an entropic origin of the electro-magnetic coupling strength. Indeed, Equation (6) could be considered an extension of the Rényi entropy, which is additive ([12], p. 43): more elementary fermions, more added terms in the sum. Moreover, Compton wavelengths are proportional to the inverse of masses. In particular, the Planck length, i.e., the Compton wavelength associated to the Planck mass, is a fundamental quantity for defying area-law entropies, scaling as the size of the boundary, as shown for black holes ([12], p. 95). This finding would imply to search the explanation of the values of the elementary fermions’ masses within the geometry of the space-time at the Planck scale.