Numerical Simulations of Dark Matter Admixed Neutron Star Binaries
Abstract
:1. Introduction
2. Materials and Methods
2.1. BAM Code
2.2. Inclusion of Mirror Dark Matter
3. Single Star Simulations
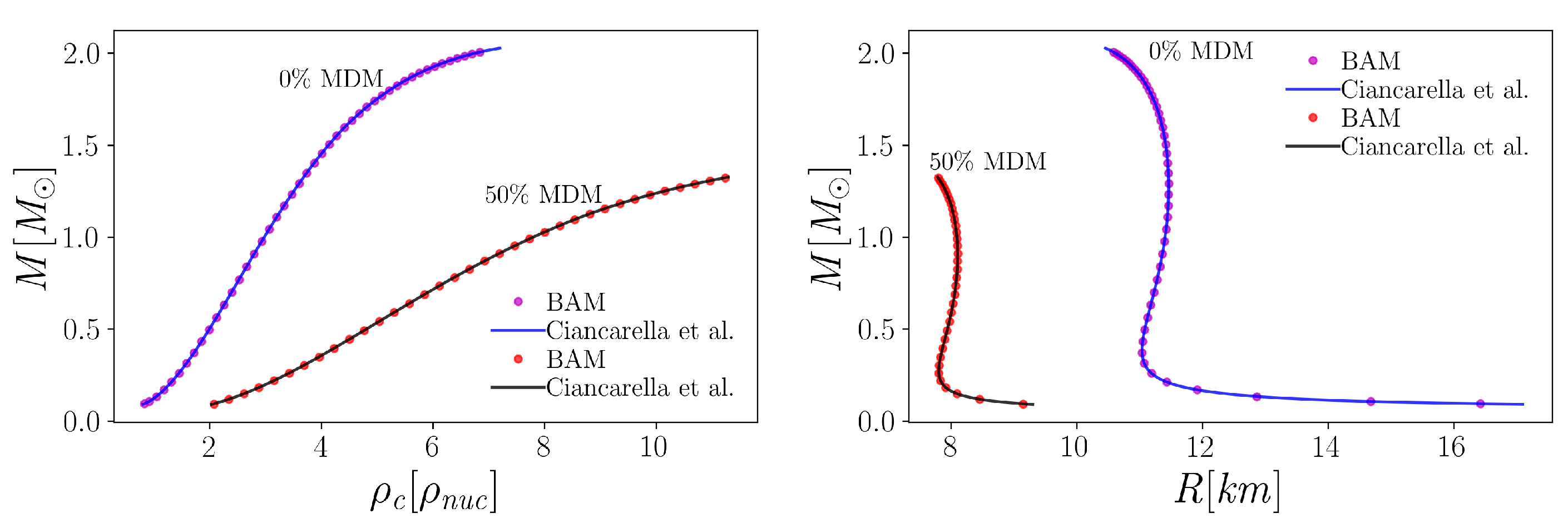
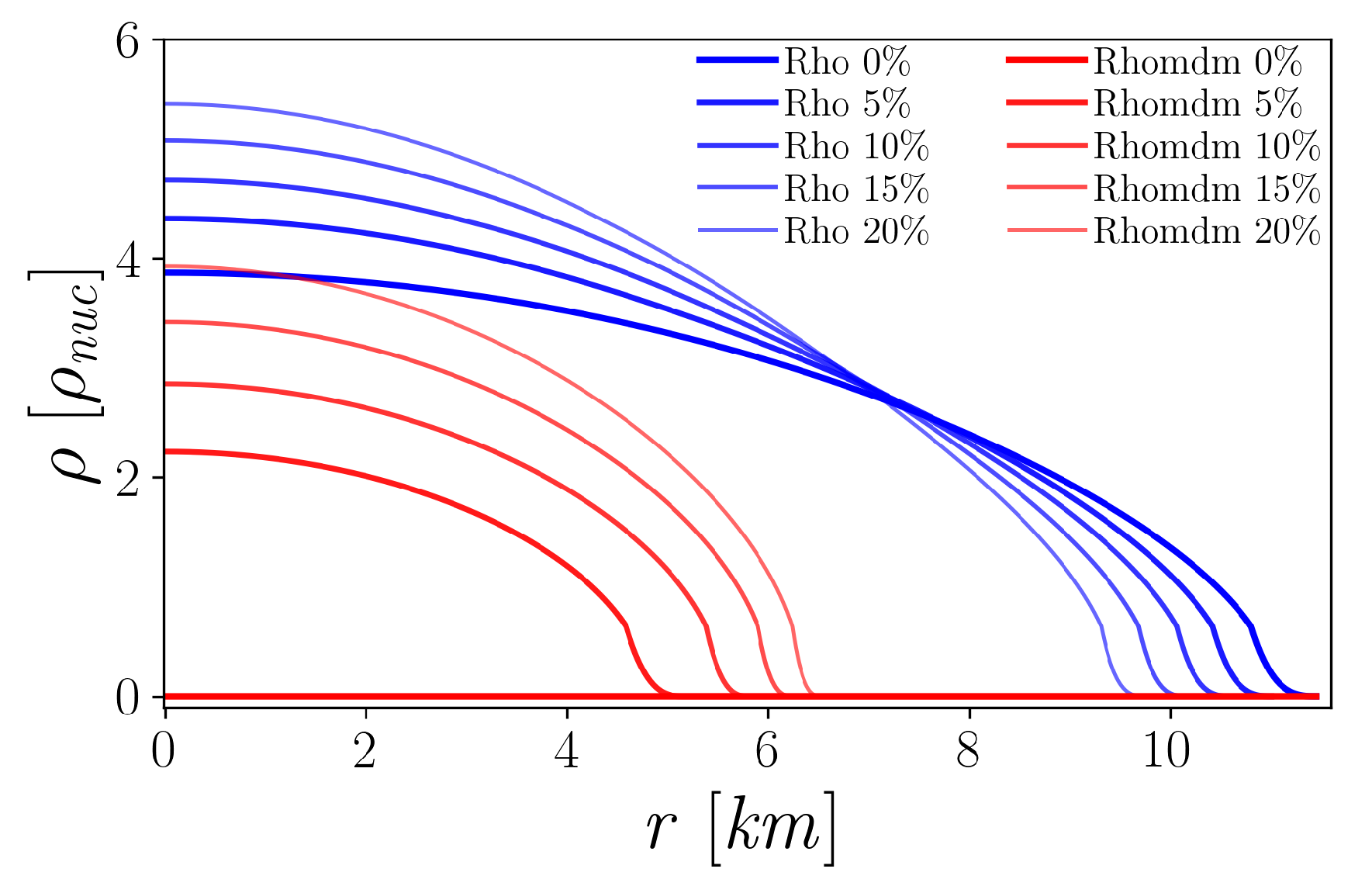
3.1. Solving the TOV Equations
3.2. Single Star Test Runs
4. Binary Neutron Star Simulations
4.1. Initial Configurations
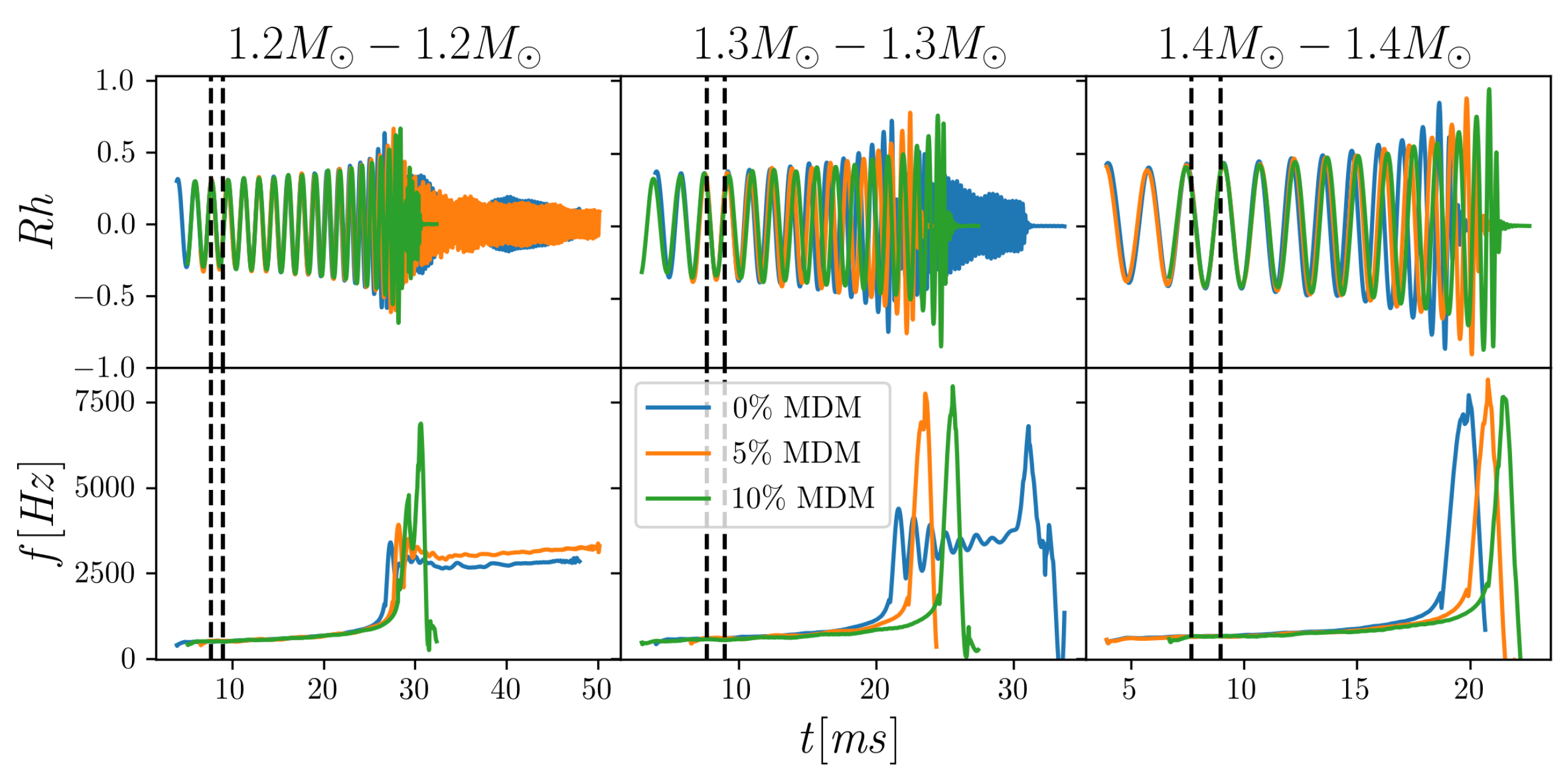
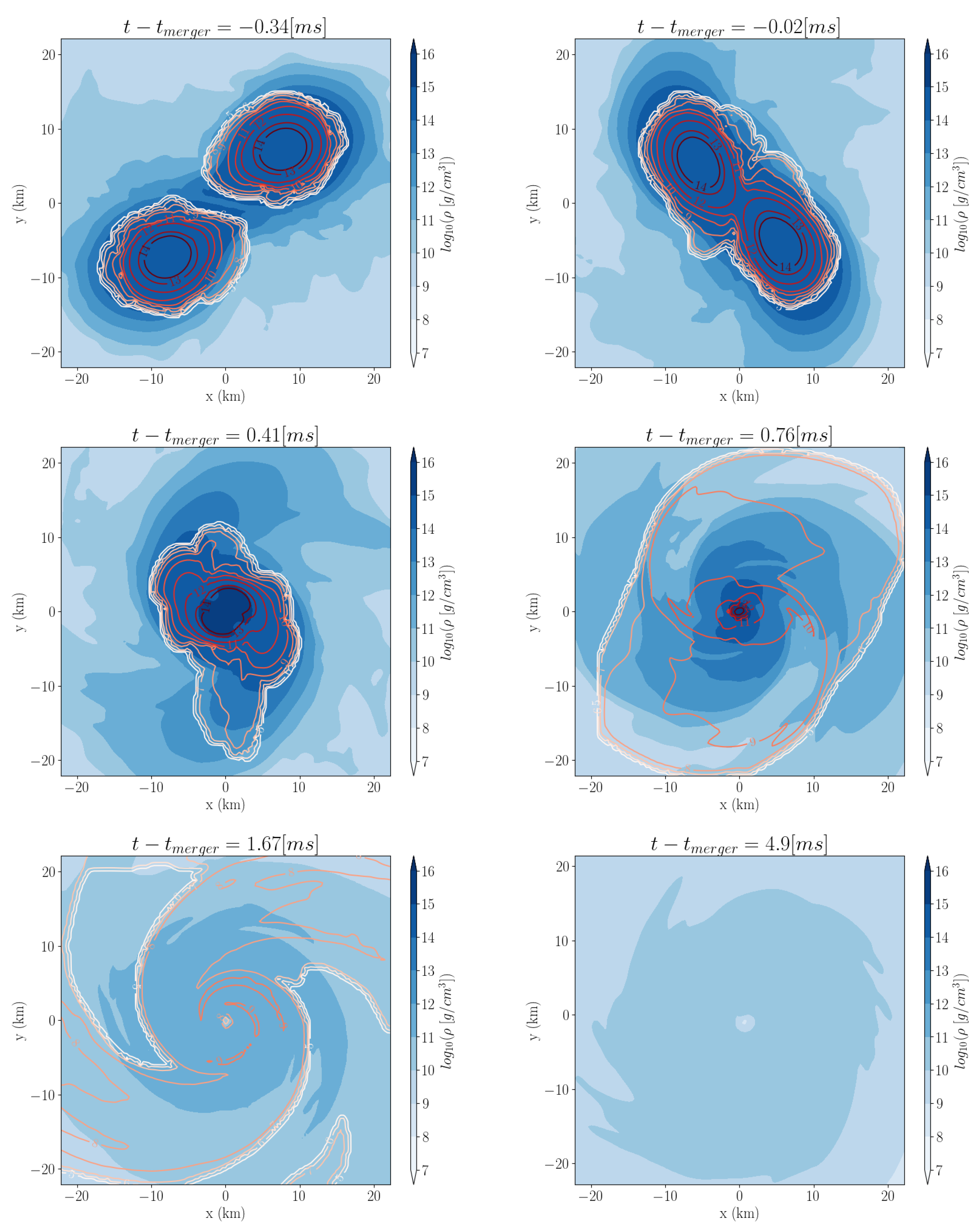
4.2. Time Evolutions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Resolution Study for the Binary Neutron Star Simulations

References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Baumgarte, T.; Shapiro, S. Numerical Relativity; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Rezzolla, L.; Zanotti, O. Relativistic Hydrodynamics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Shibata, M. Numerical Relativity; World Scientific: Singapore, 2016. [Google Scholar]
- Bauswein, A.; Guo, G.; Lien, J.H.; Lin, Y.H.; Wu, M.R. Compact Dark Objects in Neutron Star Mergers. arXiv 2020, arXiv:2012.11908. [Google Scholar]
- Miao, Z.; Zhu, Y.; Li, A.; Huang, F. Structure and pulse profiles of dark matter admixed neutron stars. arXiv 2022, arXiv:2204.05560. [Google Scholar]
- Karkevandi, D.R.; Shakeri, S.; Sagun, V.; Ivanytskyi, O. Bosonic dark matter in neutron stars and its effect on gravitational wave signal. Phys. Rev. D 2022, 105, 023001. [Google Scholar] [CrossRef]
- Narain, G.; Schaffner-Bielich, J.; Mishustin, I.N. Compact stars made of fermionic dark matter. Phys. Rev. D 2006, 74, 063003. [Google Scholar] [CrossRef]
- Bertone, G.; Fairbairn, M. Compact Stars as Dark Matter Probes. Phys. Rev. D 2008, 77, 043515. [Google Scholar] [CrossRef]
- De Lavallaz, A.; Fairbairn, M. Neutron stars as dark matter probes. Phys. Rev. D 2010, 81, 123521. [Google Scholar] [CrossRef]
- Kouvaris, C.; Tinyakov, P. Can neutron stars constrain dark matter? Phys. Rev. D 2010, 82, 063531. [Google Scholar] [CrossRef]
- Leung, S.C.; Chu, M.C.; Lin, L.M. Dark-matter admixed neutron stars. Phys. Rev. D 2011, 84, 107301. [Google Scholar] [CrossRef]
- Pérez-García, M.Á.; Silk, J. Dark matter seeding and the kinematics and rotation of neutron stars. Phys. Lett. B 2012, 711, 6–9. [Google Scholar] [CrossRef]
- Kouvaris, C. The Dark Side of Neutron Stars. arXiv 2013, arXiv:1308.3222. [Google Scholar] [CrossRef]
- Kouvaris, C.; Nielsen, N.G. Asymmetric dark matter stars. Phys. Rev. D 2015, 92, 063526. [Google Scholar] [CrossRef]
- Das, H.C.; Kumar, A.; Kumar, B.; Biswal, S.K.; Nakatsukasa, T.; Li, A.; Patra, S.K. Effects of dark matter on the nuclear and neutron star matter. Mon. Not. R. Astron. Soc. 2020, 495, 4893–4903. [Google Scholar] [CrossRef]
- Ciarcelluti, P.; Sandin, F. Have neutron stars a dark matter core? Phys. Lett. B 2011, 695, 19–21. [Google Scholar] [CrossRef]
- Sagun, V.; Giangrandi, E.; Ivanytskyi, O.; Lopes, I.; Bugaev, K. Constraints on the fermionic dark matter from observations of neutron stars. arXiv 2021. [Google Scholar] [CrossRef]
- Baryakhtar, M.; Caputo, R.; Croon, D.; Perez, K.; Berti, E.; Bramante, J.; Buschmann, M.; Brito, R.; Cole, P.S.; Coogan, A.; et al. Dark Matter In Extreme Astrophysical Environments. arXiv 2022, arXiv:2203.07984. [Google Scholar]
- Sandin, F.; Ciarcelluti, P. Effects of mirror dark matter on neutron stars. Astropart. Phys. 2009, 32, 278–284. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0927650509001406 (accessed on 21 June 2022).
- Ellis, J.; Hütsi, G.; Kannike, K.; Marzola, L.; Raidal, M.; Vaskonen, V. Dark Matter Effects On Neutron Star Properties. Phys. Rev. D 2018, 97, 123007. [Google Scholar] [CrossRef]
- Ivanytskyi, O.; Sagun, V.; Lopes, I. Neutron stars: New constraints on asymmetric dark matter. Phys. Rev. D 2020, 102, 063028. [Google Scholar] [CrossRef]
- Nelson, A.E.; Reddy, S.; Zhou, D. Dark halos around neutron stars and gravitational waves. J. Cosm. Astrop. Phys. 2019, 2019, 012. [Google Scholar] [CrossRef]
- Ciancarella, R.; Pannarale, F.; Addazi, A.; Marciano, A. Constraining mirror dark matter inside neutron stars. Phys. Dark Univ. 2021, 32, 100796. [Google Scholar] [CrossRef]
- Hotokezaka, K.; Kiuchi, K.; Kyutoku, K.; Okawa, H.; Sekiguchi, Y.i.; Shibata, M.; Taniguchi, K. Mass ejection from the merger of binary neutron stars. Phys. Rev. D 2013, 87, 024001. [Google Scholar] [CrossRef]
- Bauswein, A.; Goriely, S.; Janka, H.T. Systematics of dynamical mass ejection, nucleosynthesis, and radioactively powered electromagnetic signals from neutron-star mergers. Astrophys. J. 2013, 773, 78. [Google Scholar] [CrossRef]
- Dietrich, T.; Ujevic, M. Modeling dynamical ejecta from binary neutron star mergers and implications for electromagnetic counterparts. Class. Quant. Grav. 2017, 34, 105014. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations. Astrophys. J. Lett. 2018, 852, L29. [Google Scholar] [CrossRef]
- Fujibayashi, S.; Sekiguchi, Y.; Kiuchi, K.; Shibata, M. Properties of Neutrino-driven Ejecta from the Remnant of a Binary Neutron Star Merger: Pure Radiation Hydrodynamics Case. Astrophys. J. 2017, 846, 114. [Google Scholar] [CrossRef]
- Nedora, V.; Schianchi, F.; Bernuzzi, S.; Radice, D.; Daszuta, B.; Endrizzi, A.; Perego, A.; Prakash, A.; Zappa, F. Mapping dynamical ejecta and disk masses from numerical relativity simulations of neutron star mergers. Class. Quant. Grav. 2022, 39, 015008. [Google Scholar] [CrossRef]
- Krüger, C.J.; Foucart, F. Estimates for Disk and Ejecta Masses Produced in Compact Binary Mergers. Phys. Rev. D 2020, 101, 103002. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J.; Reed, B. GW190814: Impact of a 2.6 solar mass neutron star on the nucleonic equations of state. Phys. Rev. C 2020, 102, 065805. [Google Scholar] [CrossRef]
- Tsokaros, A.; Ruiz, M.; Shapiro, S.L. GW190814: Spin and equation of state of a neutron star companion. Astrophys. J. 2020, 905, 48. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. GW190814’s Secondary Component with Mass 2.50–2.67 M⊙ as a Superfast Pulsar. Astrophys. J. 2020, 902, 38. [Google Scholar] [CrossRef]
- Tan, H.; Noronha-Hostler, J.; Yunes, N. Neutron Star Equation of State in light of GW190814. Phys. Rev. Lett. 2020, 125, 261104. [Google Scholar] [CrossRef]
- Di Giovanni, F.; Sanchis-Gual, N.; Cerdá-Durán, P.; Font, J.A. Can fermion-boson stars reconcile multimessenger observations of compact stars? Phys. Rev. D 2022, 105, 063005. [Google Scholar] [CrossRef]
- Das, H.C.; Kumar, A.; Patra, S.K. Dark matter admixed neutron star as a possible compact component in the GW190814 merger event. Phys. Rev. D 2021, 104, 063028. [Google Scholar] [CrossRef]
- Essick, R.; Landry, P. Discriminating between Neutron Stars and Black Holes with Imperfect Knowledge of the Maximum Neutron Star Mass. Astrophys. J. 2020, 904, 80. [Google Scholar] [CrossRef]
- Tews, I.; Pang, P.T.H.; Dietrich, T.; Coughlin, M.W.; Antier, S.; Bulla, M.; Heinzel, J.; Issa, L. On the Nature of GW190814 and Its Impact on the Understanding of Supranuclear Matter. Astrophys. J. Lett. 2021, 908, L1. [Google Scholar] [CrossRef]
- Ellis, J.; Hektor, A.; Hütsi, G.; Kannike, K.; Marzola, L.; Raidal, M.; Vaskonen, V. Search for Dark Matter Effects on Gravitational Signals from Neutron Star Mergers. Phys. Lett. B 2018, 781, 607–610. [Google Scholar] [CrossRef]
- Kopp, J.; Laha, R.; Opferkuch, T.; Shepherd, W. Cuckoo’s eggs in neutron stars: Can LIGO hear chirps from the dark sector? J. High Energy Phys. 2018, 2018, 96. [Google Scholar] [CrossRef]
- Bezares, M.; Viganò, D.; Palenzuela, C. Gravitational wave signatures of dark matter cores in binary neutron star mergers by using numerical simulations. Phys. Rev. D 2019, 100, 044049. [Google Scholar] [CrossRef]
- Berezhiani, Z. Mirror World and its Cosmological Consequences. Int. J. Mod. Phys. A 2004, 19, 3775. [Google Scholar] [CrossRef]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parameterized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 2001, 380, 151. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the binary neutron star merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; Van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 6131. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef]
- Bruegmann, B.; Gonzalez, J.A.; Hannam, M.; Husa, S.; Sperhake, U.; Tichy, W. Calibration of Moving Puncture Simulations. Phys. Rev. D 2008, 77, 024027. [Google Scholar] [CrossRef]
- Thierfelder, M.; Bernuzzi, S.; Bruegmann, B. Numerical relativity simulations of binary neutron stars. Phys. Rev. D 2011, 84, 044012. [Google Scholar] [CrossRef]
- Dietrich, T.; Bernuzzi, S.; Ujevic, M.; Brügmann, B. Numerical relativity simulations of neutron star merger remnants using conservative mesh refinement. Phys. Rev. D 2015, 91, 124041. [Google Scholar] [CrossRef]
- Dietrich, T.; Ossokine, S.; Clough, K. Full 3D numerical relativity simulations of neutron star-boson star collisions with BAM. Class. Quant. Grav. 2019, 36, 025002. [Google Scholar] [CrossRef]
- Font, J.A. Numerical hydrodynamics in general relativity. Living Rev. Relativ. 2000, 3, 2. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.J.; Colella, P. Local Adaptive Mesh Refinement for Shock Hydrodynamics. J. Comp. Phys. 1989, 82, 64–84. [Google Scholar] [CrossRef]
- Berger, M.J.; Oliger, J. Adaptive Mesh Refinement for Hyperbolic Partial Differential Equations. J. Comp. Phys. 1984, 53, 484–512. [Google Scholar] [CrossRef]
- Baumgarte, T.W.; Shapiro, S.L. On the numerical integration of Einstein’s field equations. Phys. Rev. D 1998, 59, 024007. [Google Scholar] [CrossRef]
- Shibata, M.; Nakamura, T. Evolution of three-dimensional gravitational waves: Harmonic slicing case. Phys. Rev. D 1995, 52, 5428–5444. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Hilditch, D. Constraint violation in free evolution schemes: Comparing BSSNOK with a conformal decomposition of Z4. Phys. Rev. D 2010, 81, 084003. [Google Scholar] [CrossRef]
- Hilditch, D.; Bernuzzi, S.; Thierfelder, M.; Cao, Z.; Tichy, W.; Bruegmann, B. Compact binary evolutions with the Z4c formulation. Phys. Rev. D 2013, 88, 084057. [Google Scholar] [CrossRef]
- Weyhausen, A.; Bernuzzi, S.; Hilditch, D. Constraint damping for the Z4c formulation of general relativity. Phys. Rev. D 2012, 85, 024038. [Google Scholar] [CrossRef]
- Van Meter, J.R.; Baker, J.G.; Koppitz, M.; Choi, D.I. How to move a black hole without excision: Gauge conditions for the numerical evolution of a moving puncture. Phys. Rev. D 2006, 73, 124011. [Google Scholar] [CrossRef]
- Clough, K.; Dietrich, T.; Niemeyer, J.C. Axion star collisions with black holes and neutron stars in full 3D numerical relativity. Phys. Rev. D 2018, 98, 083020. [Google Scholar] [CrossRef]
- Dietrich, T.; Day, F.; Clough, K.; Coughlin, M.; Niemeyer, J. Neutron star–axion star collisions in the light of multimessenger astronomy. Mon. Not. R. Astron. Soc. 2019, 483, 908–914. [Google Scholar] [CrossRef]
- Dietrich, T.; Clough, K. Cooling binary neutron star remnants via nucleon-nucleon-axion bremsstrahlung. Phys. Rev. D 2019, 100, 083005. [Google Scholar] [CrossRef]
- Foot, R. Mirror dark matter: Cosmology, galaxy structure and direct detection. Int. J. Mod. Phys. A 2014, 29, 1430013. [Google Scholar] [CrossRef]
- Tolman, R.C. Static Solutions of Einstein’s Field Equations for Spheres of Fluid. Phys. Rev. 1939, 55, 364. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1939, 55, 374. [Google Scholar] [CrossRef]
- Gold, R.; Bernuzzi, S.; Thierfelder, M.; Brugmann, B.; Pretorius, F. Eccentric binary neutron star mergers. Phys. Rev. D 2012, 86, 121501. [Google Scholar] [CrossRef]
- Kastaun, W.; Galeazzi, F.; Alic, D.; Rezzolla, L.; Font, J.A. Black hole from merging binary neutron stars: How fast can it spin? Phys. Rev. D 2013, 88, 021501. [Google Scholar] [CrossRef]
- Palenzuela, C.; Olabarrieta, I.; Lehner, L.; Liebling, S.L. Head-on collisions of boson stars. Phys. Rev. D 2007, 75, 064005. [Google Scholar] [CrossRef]
- Bezares, M.; Bošković, M.; Liebling, S.; Palenzuela, C.; Pani, P.; Barausse, E. Gravitational waves and kicks from the merger of unequal mass, highly compact boson stars. Phys. Rev. D 2022, 105, 064067. [Google Scholar] [CrossRef]
- Baumgarte, T.W.; Shapiro, S.L. Numerical relativity and compact binaries. Phys. Rep. 2003, 376, 41–131. [Google Scholar] [CrossRef]
- Chaurasia, S.V.; Dietrich, T.; Johnson-McDaniel, N.K.; Ujevic, M.; Tichy, W.; Brügmann, B. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of large eccentricities. Phys. Rev. D 2018, 98, 104005. [Google Scholar] [CrossRef]
- Siegel, D.M.; Metzger, B.D. Three-Dimensional General-Relativistic Magnetohydrodynamic Simulations of Remnant Accretion Disks from Neutron Star Mergers: Outflows and r-Process Nucleosynthesis. Phys. Rev. Lett. 2017, 119, 231102. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, R.; Metzger, B.D. Nuclear Dominated Accretion Flows in Two Dimensions. I. Torus Evolution with Parametric Microphysics. Astrophys. J. 2013, 763, 108. [Google Scholar] [CrossRef]

| Name | Total Mass (M) | Mirror Dark Matter % | [] | [] |
|---|---|---|---|---|
| SLy_M127_0pc | 1.27 | 0% | 3.558 | 0 |
| SLy_M132_25pc | 1.32 | 25% | 5.212 | 4.045 |
| SLy_M14_50pc | 1.40 | 50% | 6.518 | 6.518 |
| SLy_M132_75pc | 1.32 | 75% | 4.045 | 5.212 |
| SLy_M127_100pc | 1.27 | 100% | 0 | 3.558 |
| M (M) | Mirror Dark Matter % | [] | [] | R [km] | |
|---|---|---|---|---|---|
| SLy_M14_0 | 1.4 | 0% | 3.866 | 0 | 11.45 |
| SLy_M14_5 | 1.4 | 5% | 4.360 | 2.234 | 11.00 |
| SLy_M14_10 | 1.4 | 10% | 4.713 | 2.854 | 10.60 |
| SLy_M13_0 | 1.3 | 0% | 3.624 | 0 | 11.46 |
| SLy_M13_5 | 1.3 | 5% | 4.058 | 2.087 | 11.04 |
| SLy_M13_10 | 1.3 | 10% | 4.366 | 2.679 | 10.63 |
| SLy_M12_0 | 1.2 | 0% | 3.398 | 0 | 11.46 |
| SLy_M12_5 | 1.2 | 5% | 3.791 | 1.960 | 11.04 |
| SLy_M12_10 | 1.2 | 10% | 4.056 | 2.499 | 10.65 |
| n | (km) | (m) | ||
|---|---|---|---|---|
| R1 | 64 | 128 | 11.81 | 369 |
| R2 | 96 | 192 | 7.88 | 246 |
| R3 | 128 | 256 | 5.91 | 185 |
| R4 | 160 | 320 | 4.73 | 148 |
| Sphere (M) | M Integral (M) | M (M) | [Hz] | |
|---|---|---|---|---|
| SLy_M14_0 | - | - | 0.001 | 1770 |
| SLy_M14_5 | - | - | 0.0008 | 2030 |
| SLy_M14_10 | - | - | 0.0014 | 2058 |
| SLy_M13_0 | 0.0168 | 4.8 × 10 | 0.062 | 1817 |
| SLy_M13_5 | 0 | 0.7 × 10 | 0.001 | 1910 |
| SLy_M13_10 | 0 | 0.8 × 10 | 0.0006 | 2221 |
| SLy_M12_0 | 0 | 0.3 × 10 | 1746 | |
| SLy_M12_5 | 0.0016 | 2.6 × 10 | 1818 | |
| SLy_M12_10 | 0.0027 | 3.3 × 10 | 0.017 | 2198 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emma, M.; Schianchi, F.; Pannarale, F.; Sagun, V.; Dietrich, T. Numerical Simulations of Dark Matter Admixed Neutron Star Binaries. Particles 2022, 5, 273-286. https://doi.org/10.3390/particles5030024
Emma M, Schianchi F, Pannarale F, Sagun V, Dietrich T. Numerical Simulations of Dark Matter Admixed Neutron Star Binaries. Particles. 2022; 5(3):273-286. https://doi.org/10.3390/particles5030024
Chicago/Turabian StyleEmma, Mattia, Federico Schianchi, Francesco Pannarale, Violetta Sagun, and Tim Dietrich. 2022. "Numerical Simulations of Dark Matter Admixed Neutron Star Binaries" Particles 5, no. 3: 273-286. https://doi.org/10.3390/particles5030024
APA StyleEmma, M., Schianchi, F., Pannarale, F., Sagun, V., & Dietrich, T. (2022). Numerical Simulations of Dark Matter Admixed Neutron Star Binaries. Particles, 5(3), 273-286. https://doi.org/10.3390/particles5030024







