Deep Learning Based Impact Parameter Determination for the CBM Experiment
Abstract
1. Introduction
2. Data Preparation
3. PointNet Models
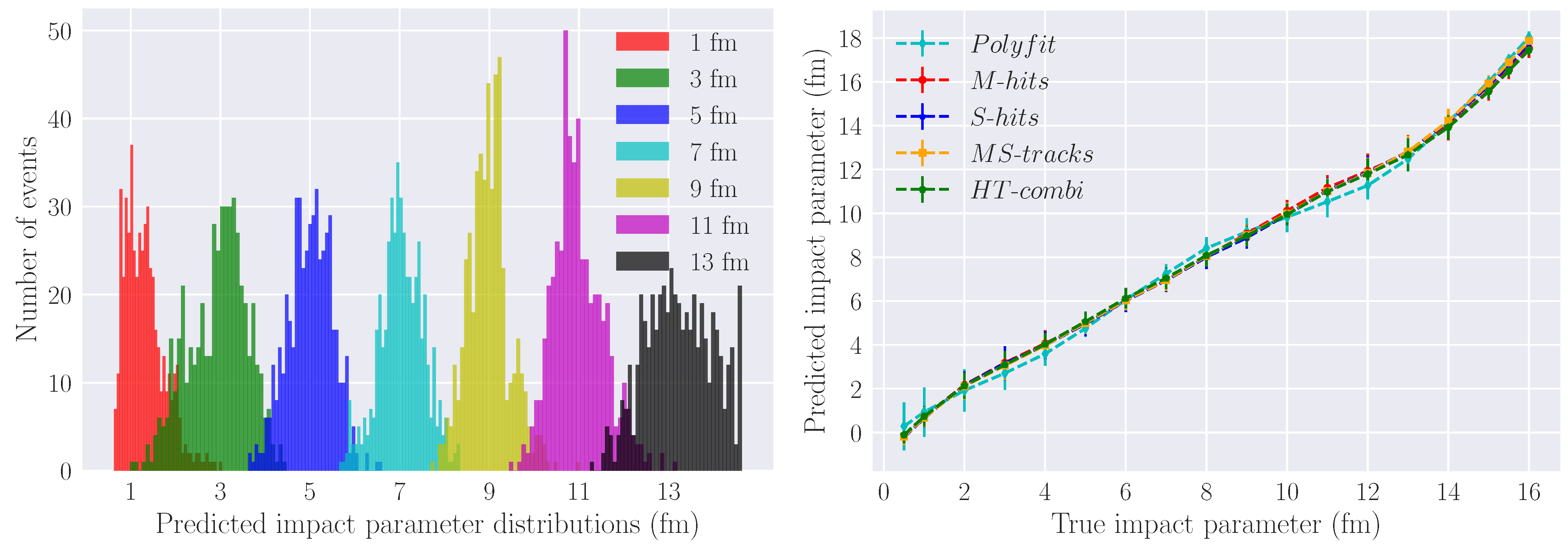
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Friese, V. The CBM experiment at GSI/FAIR. Nucl. Phys. A 2006, 774, 377–386. [Google Scholar] [CrossRef]
- Senger, P.; Cbm Collaboration. The CBM experiment at FAIR. J. Phys. Conf. Ser. 2006, 50, 357–360. [Google Scholar] [CrossRef]
- Staszel, P.; Cbm Collaboration. CBM experiment at FAIR. Acta Phys. Polon. B 2010, 41, 341–350. [Google Scholar]
- Klochkov, V.; Selyuzhenkov, I. Centrality determination in heavy-ion collisions with the CBM experiment. J. Phys. Conf. Ser. 2017, 798, 012059. [Google Scholar] [CrossRef]
- Jeon, S.; Koch, V. Event by event fluctuations. arXiv 2003, arXiv:hep-ph/0304012. [Google Scholar] [CrossRef]
- Skokov, V.; Friman, B.; Redlich, K. Volume Fluctuations and Higher Order Cumulants of the Net Baryon Number. Phys. Rev. C 2013, 88, 034911. [Google Scholar] [CrossRef]
- Chatterjee, A.; Zhang, Y.; Liu, H.; Wang, R.; He, S.; Luo, X. Effects of centrality fluctuation and deuteron formation on proton number cumulant in Au+Au collisions at = 3 GeV from JAM model. arXiv 2020, arXiv:2009.03755. [Google Scholar]
- Pang, L.G.; Zhou, K.; Su, N.; Petersen, H.; Stöcker, H.; Wang, X.N. An equation-of-state-meter of quantum chromodynamics transition from deep learning. Nat. Commun. 2018, 9, 210. [Google Scholar] [CrossRef]
- Zhou, K.; Endrődi, G.; Pang, L.G.; Stöcker, H. Regressive and generative neural networks for scalar field theory. Phys. Rev. D 2019, 100, 011501. [Google Scholar] [CrossRef]
- Steinheimer, J.; Pang, L.; Zhou, K.; Koch, V.; Randrup, J.; Stoecker, H. A machine learning study to identify spinodal clumping in high energy nuclear collisions. J. High Energy Phys. 2019, 12, 122. [Google Scholar] [CrossRef]
- Du, Y.L.; Zhou, K.; Steinheimer, J.; Pang, L.G.; Motornenko, A.; Zong, H.S.; Wang, X.N.; Stöcker, H. Identifying the nature of the QCD transition in relativistic collision of heavy nuclei with deep learning. Eur. Phys. J. C 2020, 80, 516. [Google Scholar] [CrossRef]
- Thaprasop, P.; Zhou, K.; Steinheimer, J.; Herold, C. Unsupervised Outlier Detection in Heavy-Ion Collisions. arXiv 2020, arXiv:2007.15830. [Google Scholar]
- Bourilkov, D. Machine and Deep Learning Applications in Particle Physics. Int. J. Mod. Phys. A 2020, 34, 1930019. [Google Scholar] [CrossRef]
- Radovic, A.; Williams, M.; Rousseau, D.; Kagan, M.; Bonacorsi, D.; Himmel, A.; Aurisano, A.; Terao, K.; Wongjirad, T. Machine learning at the energy and intensity frontiers of particle physics. Nature 2018, 560, 41–48. [Google Scholar] [CrossRef]
- Guest, D.; Cranmer, K.; Whiteson, D. Deep Learning and its Application to LHC Physics. Ann. Rev. Nucl. Part Sci. 2018, 68, 161–181. [Google Scholar] [CrossRef]
- Larkoski, A.J.; Moult, I.; Nachman, B. Jet Substructure at the Large Hadron Collider: A Review of Recent Advances in Theory and Machine Learning. Phys. Rep. 2020, 841, 1–63. [Google Scholar] [CrossRef]
- De Oliveira, L.; Kagan, M.; Mackey, L.; Nachman, B.; Schwartzman, A. Jet-images—Deep learning edition. J. High Energy Phys. 2016, 7, 69. [Google Scholar] [CrossRef]
- Baldi, P.; Bauer, K.; Eng, C.; Sadowski, P.; Whiteson, D. Jet Substructure Classification in High-Energy Physics with Deep Neural Networks. Phys. Rev. D 2016, 93, 094034. [Google Scholar] [CrossRef]
- Komiske, P.T.; Metodiev, E.M.; Schwartz, M.D. Deep learning in color: Towards automated quark/gluon jet discrimination. J. High Energy Phys. 2017, 1, 110. [Google Scholar]
- Almeida, L.G.; Backović, M.; Cliche, M.; Lee, S.J.; Perelstein, M. Playing Tag with ANN: Boosted Top Identification with Pattern Recognition. J. High Energy Phys. 2015, 7, 86. [Google Scholar] [CrossRef]
- Kasieczka, G.; Plehn, T.; Russell, M.; Schell, T. Deep-learning Top Taggers or The End of QCD? J. High Energy Phys. 2017, 5, 6. [Google Scholar] [CrossRef]
- Kasieczka, G.; Plehn, T.; Butter, A.; Cranmer, K.; Debnath, D.; Dillon, B.M.; Fairbairn, M.; Faroughy, D.A.; Fedorko, W.; Gay, C.; et al. The Machine Learning Landscape of Top Taggers. SciPost Phys. 2019, 7, 14. [Google Scholar]
- Qu, H.; Gouskos, L. ParticleNet: Jet Tagging via Particle Clouds. Phys. Rev. D 2020, 101, 056019. [Google Scholar] [CrossRef]
- Moreno, E.A.; Cerri, O.; Duarte, J.M.; Newman, H.B.; Nguyen, T.Q.; Periwal, A.; Pierini, M.; Serikova, A.; Spiropulu, M.; Vlimant, J.R. JEDI-net: A jet identification algorithm based on interaction networks. Eur. Phys. J. C 2020, 80, 58. [Google Scholar] [CrossRef]
- Kasieczka, G.; Marzani, S.; Soyez, G.; Stagnitto, G. Towards Machine Learning Analytics for Jet Substructure. J. High Energy Phys. 2020, 9, 195. [Google Scholar] [CrossRef]
- CMS Collaboration. Identification of heavy, energetic, hadronically decaying particles using machine-learning techniques. J. Instrum. 2020, 15, P06005. [Google Scholar] [CrossRef]
- Esmail, W.; Stockmanns, T.; Ritman, J. Machine Learning for Track Finding at PANDA. arXiv 2019, arXiv:1910.07191. [Google Scholar]
- Haake, R. Machine and deep learning techniques in heavy-ion collisions with ALICE. arXiv 2017, arXiv:1709.08497. [Google Scholar]
- Samuel, D.; Suresh, K. Artificial Neural Networks-based Track Fitting of Cosmic Muons through Stacked Resistive Plate Chambers. J. Instrum. 2018, 13, P10035. [Google Scholar] [CrossRef]
- Samuel, D.; Samalan, A.; Kuttan, M.O.; Murgod, L.P. Machine learning-based predictions of directionality and charge of cosmic muons—A simulation study using the mICAL detector. J. Instrum. 2019, 14, P11020. [Google Scholar] [CrossRef]
- Bass, S.A.; Bischoff, A.; Hartnack, C.; Maruhn, J.A.; Reinhardt, J.; Stoecker, H.; Greiner, W. Neural networks for impact parameter determination. J. Phys. G 1994, 20, L21–L26. [Google Scholar] [CrossRef]
- David, C.; Freslier, M.; Aichelin, J. Impact parameter determination for heavy-ion collisions by use of a neural network. Phys. Rev. C 1995, 51, 1453–1459. [Google Scholar] [CrossRef] [PubMed]
- Bass, S.A.; Bischoff, A.; Maruhn, J.A.; Stoecker, H.; Greiner, W. Neural networks for impact parameter determination. Phys. Rev. C 1996, 53, 2358–2363. [Google Scholar] [CrossRef] [PubMed]
- Haddad, F.; Hagel, K.; Li, J.; Mdeiwayeh, N.; Natowitz, J.B.; Wada, R.; Xiao, B.; David, C.; Freslier, M.; Aichelin, J. Impact parameter determination in experimental analysis using neural network. Phys. Rev. C 1997, 55, 1371–1375. [Google Scholar] [CrossRef]
- Sanctis, J.D.; Masotti, M.; Bruno, M.; D’Agostino, M.; Geraci, E.; Vannini, G.; Bonasera, A. Classification of the impact parameter in nucleus-nucleus collisions by a support vector machine method. J. Phys. G 2009, 36, 015101. [Google Scholar] [CrossRef]
- Li, F.; Wang, Y.; Lü, H.; Li, P.; Li, Q.; Liu, F. Application of artificial intelligence in the determination of impact parameter in heavy-ion collisions at intermediate energies. J. Phys. G 2020, 47, 115104. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Kuttan, M.O.; Steinheimer, J.; Zhou, K.; Redelbach, A.; Stoecker, H. A fast centrality-meter for heavy-ion collisions at the CBM experiment. Phys. Lett. B 2020, 811, 135872. [Google Scholar] [CrossRef]
- Heuser, J.M. The Silicon Tracking System of the CBM Experiment at FAIR. JPS Conf. Proc. 2015, 8, 022007. [Google Scholar]
- Deveaux, M.; Heuser, J.M. The Silicon Detector Systems of the Compressed Baryonic Matter Experiment; Universitätsbibliothek Johann Christian Senckenberg: Frankfurt am Main, Germany, 2013. [Google Scholar]
- Adamczewski-Musch, J.; Akishin, P.; Becker, K.H.; Belogurov, S.; Bendarouach, J.; Boldyreva, N.; Chernogorov, A.; Deveaux, C.; Dobyrn, V.; Dürr, M.; et al. The CBM RICH project. Nucl. Instrum. Meth. A 2017, 845, 434–438. [Google Scholar] [CrossRef]
- Bass, S.A.; Belkacem, M.; Bleicher, M.; Brandstetter, M.; Bravina, L.; Ernst, C.; Gerland, L.; Hofmann, M.; Hofmann, S.; Konopka, J.; et al. Microscopic models for ultrarelativistic heavy ion collisions. Prog. Part Nucl. Phys. 1998, 41, 255–369. [Google Scholar] [CrossRef]
- Bleicher, M.; Zabrodin, E.; Spieles, C.; Bass, S.A.; Ernst, C.; Soff, S.; Bravina, L.; Belkacem, M.; Weber, H.; Stoecker, H.; et al. Relativistic hadron hadron collisions in the ultrarelativistic quantum molecular dynamics model. J. Phys. G 1999, 25, 1859–1896. [Google Scholar] [CrossRef]
- Available online: https://subversion.gsi.de/cbmsoft/cbmroot/release/OCT19/ (accessed on 1 December 2019).
- Brun, R.; McPherson, A.C.; Zanarini, P.; Maire, M.; Bruyant, F. GEANT 3: User’s Guide Geant 3.10, Geant 3.11. No. CERN-DD-EE-84-01; CERN: Meyrin, Switzerland, 1987. [Google Scholar]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
| Model | Input Features | # Param. | Input Dimensions |
|---|---|---|---|
| M-hits | x, y, z of hits in all MVD planes | ||
| S-hits | x, y, z of hits in all STS planes | ||
| MS-tracks | x, y, z, dx/dz, dy/dz, q/P of tracks in first and last planes | ||
| HT-combi | combination of features of M-hits and MS-tracks | , |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuttan, M.O.; Steinheimer, J.; Zhou, K.; Redelbach, A.; Stoecker, H. Deep Learning Based Impact Parameter Determination for the CBM Experiment. Particles 2021, 4, 47-52. https://doi.org/10.3390/particles4010006
Kuttan MO, Steinheimer J, Zhou K, Redelbach A, Stoecker H. Deep Learning Based Impact Parameter Determination for the CBM Experiment. Particles. 2021; 4(1):47-52. https://doi.org/10.3390/particles4010006
Chicago/Turabian StyleKuttan, Manjunath Omana, Jan Steinheimer, Kai Zhou, Andreas Redelbach, and Horst Stoecker. 2021. "Deep Learning Based Impact Parameter Determination for the CBM Experiment" Particles 4, no. 1: 47-52. https://doi.org/10.3390/particles4010006
APA StyleKuttan, M. O., Steinheimer, J., Zhou, K., Redelbach, A., & Stoecker, H. (2021). Deep Learning Based Impact Parameter Determination for the CBM Experiment. Particles, 4(1), 47-52. https://doi.org/10.3390/particles4010006





