1. Introduction
Hadronic resonances carry a wealth of information on the reaction dynamics and hadrochemistry in heavy-ion collisions at relativistic energies. The resonance measurements at SPS, RHIC and the LHC have been used to study properties of the late hadronic phase, processes that are responsible for the enhanced production of strangeness, hadronization mechanisms and effects that shape the particle transverse momentum (
pT) spectra and the flavor-dependent parton energy loss, etc. Measurements of resonances are also foreseen in the MPD experiment at NICA [
1,
2], which is now under construction at JINR, Dubna, Russia. By design, the MPD experiment resembles the STAR and ALICE experiments at RHIC and the LHC, which have proven to be extremely effective for the reconstruction of a wide variety of resonances. Similarly to them, the MPD detector provides a high efficiency of charged particle track reconstruction in the large acceptance time-projection chamber (TPC) covering full acceptance in azimuth and |η| < 1.2 with a momentum resolution of ~1–2% and excellent particle identification capabilities based on the measurements of the particle specific energy loss in the TPC gas and time-of-flight in the TOF subsystem covering the full acceptance of the central barrel. However, an accurate estimation of the MPD potential for reconstruction of resonances requires realistic simulation of the generated signals and detector performance.
Study of the resonance properties includes measurement of their yields in a wide range of transverse momentum, reconstruction of the peak shapes to detect possible mass/width modifications, and measurement of the resonance angular distributions with respect to the event plane, other leading particles in the event or identical resonances [
3]. All these measurements are not trivial and require the development of specific analysis methods. The experimental results, which are published for the resonances, are usually obtained under several experimental and theoretical assumptions, which should be held in mind when the results are interpreted and compared to other measurements.
In this contribution, we discuss some of the most typical problems, which should be solved to measure the resonances in any modern heavy-ion experiment. The problems and the possible solutions are explained by presenting the simulation results performed for the MPD detector.
2. Reconstruction of Resonances and Experimental Challenges
In heavy-ion collisions the resonances are used as probes of the medium, study of their vacuum properties is not pursued. Therefore, the experimental study of hadronic resonances in heavy-ion collisions is usually limited to a small group of particles satisfying certain conditions. The basic properties of the resonances such as their masses, widths and decay channels should be well defined. Furthermore, the resonances should be produced at high rates in hadronic interactions at relativistic energies in order to be reconstructed. The list of resonances studied in the heavy-ion experiments is usually limited to ρ(770)0 → π+π−, K*(892)0 → π±K±, K*(892)± → π± (→ π+π−), φ(1020) → K+K−, Λ(1520) → K−p, Σ(1385)± → π±Λ (Λ → pπ−) and Ξ(1530)0 → π+Ξ− (Ξ− → π−Λ, Λ → pπ−) decays. The listed resonances have different masses, strangeness content and lifetimes, which makes them well suited for the study of different physics phenomena.
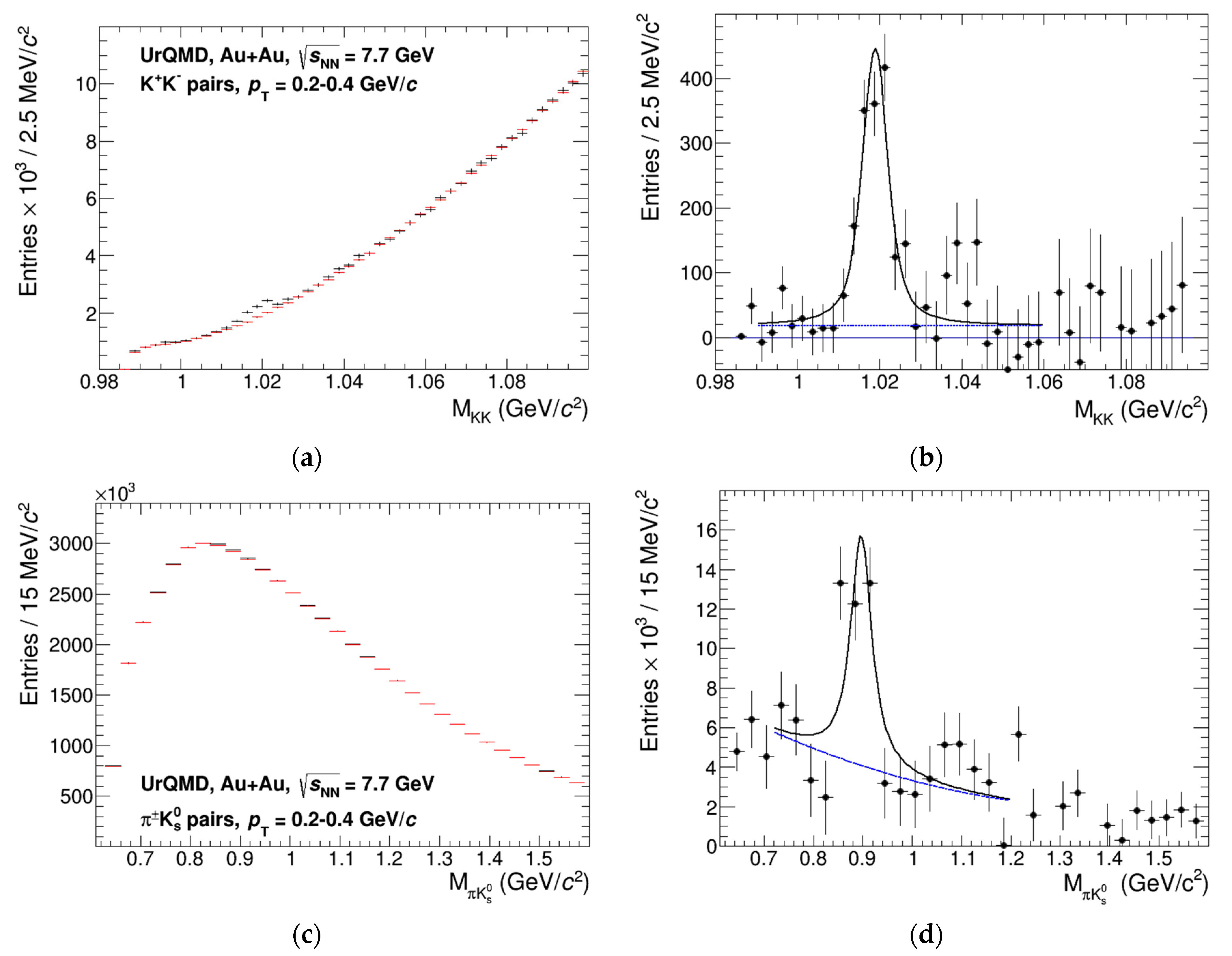
Having small lifetimes and being in many cases neutral particles, the resonances cannot be directly measured in the detector. As a result, the resonances yields are estimated by accumulating the invariant mass distributions of daughter particles according to their decay modes. Examples of the accumulated invariant mass distributions for K
+K
− and π
± pairs reconstructed in the MPD in Au + Au collisions at
= 7.7 GeV are shown in
Figure 1. Examples are shown for an interval of transverse momentum 0.2–0.4 GeV/
c in minimum bias collisions. Due to very high particle multiplicities in heavy-ion collisions, the invariant mass distributions suffer from a high level of combinatorial background (B). Very often, the background prevents observation of the resonance signals (S) in the invariant mass distributions. If in a given mass interval, the
is larger than S, then the measurement of the particle is not possible, the signal peak just cannot be distinguished from the background, or in other words, the signal is washed out by the background statistical fluctuations. Careful selection of daughter particle candidates in the event based on the particle identification signals in the TPC and TOF, matching of primary particles to the primary vertex, optimized momentum, and pair-asymmetry cuts are extremely important for minimization of the combinatorial background. For each detector and each analysis, the optimization should be run anew to provide the best significance of the measured signals. For the examples shown in
Figure 1, the S/B ratios constitute 10
−1 and 2⋅10
−2, respectively.
The situation becomes even more complicated when multi-stage decays of the resonances such as K*(892)
± → π
± (
→ π
0π
0), Σ(1385)
± → π
±Λ (Λ → pπ
−) and Ξ(1530)
0 → π
+Ξ
− (Ξ
− → π
−Λ, Λ → pπ
−) are considered. The
, Λ and Ξ
− particles cannot be directly measured and they are reconstructed by accumulating the invariant mass distributions for combinations of daughter particles as demonstrated in
Figure 2. The
, Λ and Ξ
− candidates are selected if the invariant mass of daughter particles is within 2–3 σ from the expected reconstructed mass, where σ is an expected peak width. The mass and width of the reconstructed particles are parameterized as a function of particle transverse momentum to suppress the background. The invariant mass distributions contain peaks from
, Λ or Ξ
− decays and a combinatorial background under the peaks. Part of the selected pairs is a background, which is then combined with other particles in the event to reconstruct the parent resonances. The cleaner the sample of the reconstructed
, Λ and Ξ
− signals the smaller the resulting combinatorial background that grows quadratically with the number of pairs. At the same time, the selection cuts should be loose enough to provide a reasonable reconstruction efficiency and not reject all the signal. The more stages are in the decay chain, the more challenging is the experimental analysis and the larger the number of parameters for optimization.
Most of the pairs in the combinatorial background are random pairs from uncorrelated sources. This part of the background is usually estimated with the mixed-event approach where one of the daughter particles is taken from the same event and another daughter particle is taken from another event with a similar topology (particle multiplicity, vertex coordinates, reaction plane, etc.). After proper scaling of the mixed-event invariant mass distribution, it is subtracted from the same-event distribution. The number of mixed events can be made large enough to make statistical uncertainties of the mixed-event invariant mass distribution negligible. The resulting distributions usually contain some remaining background and visible peaks from decays of the resonances as demonstrated in:
Figure 1. Another option for estimation of the background would be the accumulation of the like-sign pairs in the same event and estimation of the background as a geometrical mean,
where
N++ and
N−− are the numbers of the like-sign pairs. This method is used when a precise estimation of the background shape is critical. In this case, the like-sign invariant mass distribution accounts for a fraction of the correlated background, for example, from (mini)jets. However, this method has limited applicability because not all daughter particle combinations may have like-sign partners. Additionally, the statistical uncertainty of the estimated background is comparable to that for unlike-sign combinations, and once subtracted it increases the statistical uncertainty of the extracted signal by ~
.
The remaining background after subtraction of the mixed-event (or like-sign) background is shaped by the correlated pairs from decays of other particles and angular correlations from (mini)jets not present in the mixed events (or not fully accounted for in like-sign distributions). Extraction of the resonance peak integrals requires accurate estimation of the remaining background shape and integral. The composition of the remaining background is usually studied by running the full-event Monte Carlo simulations. In the case of the simulated data samples, the origin of each reconstructed pair of daughter particles can be tracked. The main purpose of the study is to find the optimal function to describe the background and then subtract it. For most of the cases, the remaining background is found to be a smooth function of mass in the vicinity of the peak and can be well described by a simple polynomial. Then, the invariant mass distribution is fit to a combination of a polynomial to describe the background and a peak function to describe the resonance peak, see
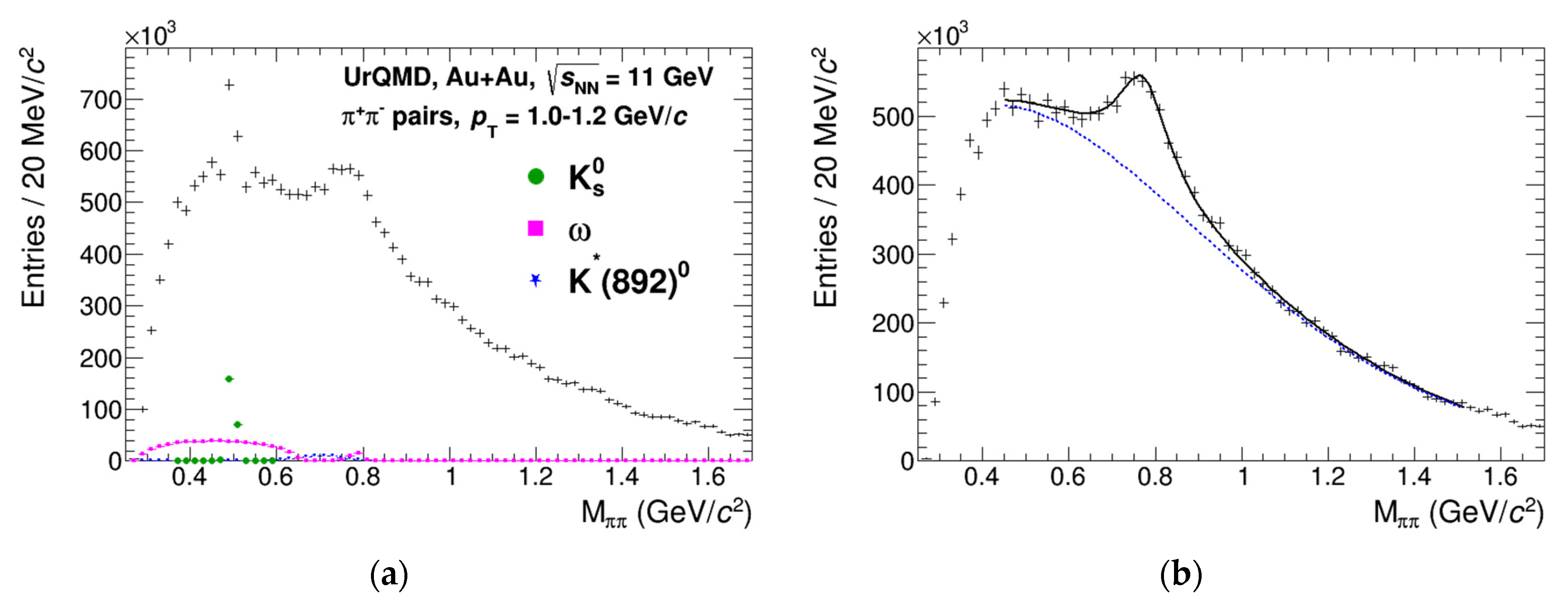
Figure 1. However, there are cases when such a simple approach does not work and the use of a smooth background function is not acceptable. An example of the decomposition of the correlated background for the case of π
+π
− invariant mass distribution is presented in the left panel of
Figure 3. The example is shown after subtraction of the mixed-event background in minimum bias Au + Au collisions at
= 11 GeV and the range of transverse momentum 1.0–1.2 GeV/
c. One can see a wide peak from the ρ(770)
0 → π
+π
− decays with a center at ~770 MeV/
c2. Additional peak-like contributions come from the
→ π
+π
−, ω → π
0π
+π
−, ω → π
+π
− decays. An additional contribution is identified to come from K*(892)
0 → π
±K
± decays, where the charged kaon is misidentified as a pion in the detector. Decays of f
0(980) and f
2(1270) mesons are not shown because they are missing in the simulation. To accurately extract the ρ(770)
0 meson yields, the peaked contributions should be estimated and subtracted or accounted for in the combined fit function as it was done in [
4]. In the particular case of ρ(770)
0 → π
+π
− analysis, the production rates of
, K*(892)
0 and ω should be measured in advance. Then, the integrals of the peaked contributions can be estimated by correcting the measured yields for the reconstruction efficiencies and the branching ratios, whereas the shapes that depend on the decay kinematics and the detector mass resolution can be borrowed from the Monte Carlo simulations as shown in
Figure 3. An example of π
+π
− invariant mass distribution after subtraction of the peaked contributions is shown in the right panel of the same figure. The background shape becomes a smooth function of mass and a simple function can be used to describe it. The estimation of the remaining background shape and integral is an important task for each resonance analysis. Depending on the detector’s capabilities to reconstruct and identify charge particles, the same analysis may require different approaches. The smooth-looking background may hide the peaked background contributions under or close to the measured resonance peaks resulting in large errors for the extracted resonance yields and line shapes.
The resonance yields that are extracted from the invariant mass distributions strongly depend on the peak shape model used in the fit function. Most often, an (r)Breit-Wigner function smeared with the estimated detector mass resolution and corrected for the mass-dependence of the reconstruction efficiency is used for the resonances. In cases when the resonance peaks are very profound and are reconstructed with large S/B ratios, the peak model can be directly verified by checking the fit quality parameters, see for example the φ(1020) → K
+K
− decay in
Figure 1. If fit converges with a reasonable probability, then the peak model is adequate for the reconstructed peak. However, in many cases due to the large combinatorial background, the resonance peaks are not very profound, the background shape is not well constrained and different peak models can result in similar fit qualities but different extracted yields and line shapes, see for example the ρ(770)
0 → π
+π
− decay in
Figure 3.
The uncertainties in the peak models can come from different sources. The peak shapes can be modified at the early stages of the interactions due to partial restoration of the chiral symmetry and high baryonic densities. The peak shape modifications can also occur at the later stages, for example in the hadronic phase. The daughter particles can rescatter with the surrounding hadrons and thus widen the reconstructed peak of the parent particle. A part of resonances can also be produced as a result of the regeneration of hadrons. Exponential
pT-shapes of the recombining hadrons favor the production of lower-mass resonances. The reconstructed peaks can also be distorted by Bose–Einstein correlations between the daughter particles and the surrounding identical hadrons. The contribution of each of these phenomena to the peak shape is not well understood and/or constrained. There is no sense to test all possible (predicted) peak models since it will result in huge uncertainties for the extracted yields. The results are reported for one of the peak models, which is expected to be the most realistic and at the same time the simplest. The peak shape and the motivations are described in the paper text, but they are not present in the measured spectra, which are usually shown or analyzed apart. When published results are interpreted or compared, one should clearly understand how it was obtained and what peak model, and what assumptions for the background distribution were used. For example, a clear demonstration of the problem is the large uncertainty reported for the ρ(770)
0 meson mass and width in the Particle Data Group [
5]. The ρ(770)
0 mesons are measured in the ρ(770)
0 → π
+π
− decay channel by different groups and experiments for many decades. Nonetheless, the reported resonance parameters significantly differ and for most of the cases, the differences come from the use of different peak models.
3. Measurement of Resonances in the MPD
The MPD detector has all important detector subsystems for the reconstruction of resonances. The yields of the resonances and background particles are estimated with the UrQMD v.3.4 [
6] event generator. Compared to other event generators such as PHSD [
7] and AMPT [
8], the UrQMD provides similar estimates for the π, K, p abundancies and somewhat lower yields for the resonances which make the obtained estimations conservatively realistic. The studies were performed in Au + Au collisions at three collision energies of
= 4, 7.7 and 11 GeV and different centrality selections, 0–20%, 20–40%, 40–60% and 60–90%. The ρ(770)
0, K*(892)
0, K*(892)
±, φ(1020), Λ(1520), Σ(1385)
± and Ξ(1530)
0 were studied in the dominant decay channels listed in the previous section. The particles were tracked through the detector materials using Geant 4 [
9]. Simulation of different detectors, reconstruction of the charged particles and pattern recognition were performed within the MpdRoot framework, which is an official software of the MPD Collaboration. In total, 10 M (5M) (5M) events of Au+Au collisions were simulated and fully reconstructed at
= 11 (7.7) (4) GeV.
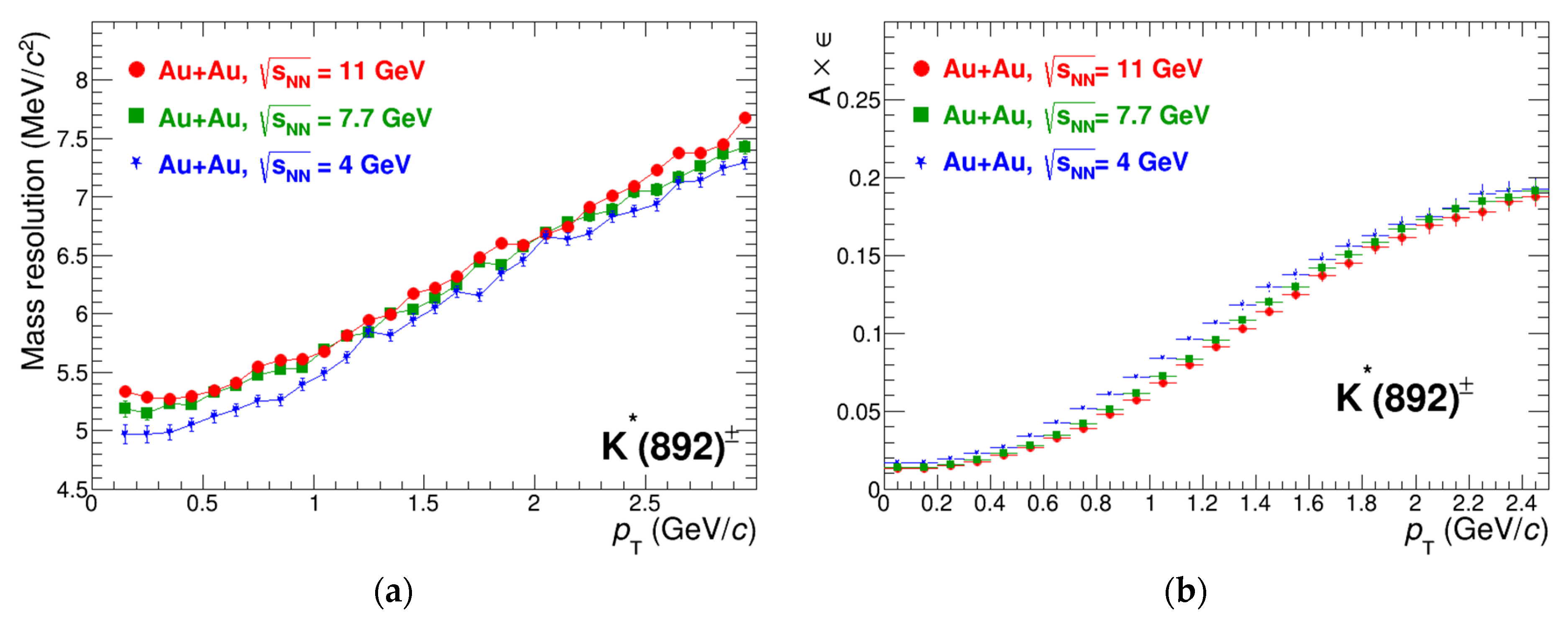
Figure 4 shows the evaluated detector mass resolution and efficiency of reconstruction for K*(892)
± → π
± decays. The mass resolution changes from 5 MeV/
c2 to 7 MeV/
c2 with the increasing transverse momentum. Such a mass resolution noticeably smears the Breit-Wigner shape of the generated peaks but preserves the possibility of the line-shape study. The reconstruction efficiency varies from ~1.5% at zero momentum to ~18% at
pT > 2.5 GeV/
c, which is comparable to that in other experiments. The mass resolution and the efficiency show a modest collision energy dependence, which is explained by the multiplicity dependence of the extracted parameters.
Examples of the invariant mass distributions reconstructed for different combinations of daughter particles are shown in
Figure 1 and
Figure 3 along with the fits, which are used to extract the particle raw yields. Additional examples can be found in [
10,
11]. The raw yields are extracted by using the known peak shape models, which are the Breit-Wigner distributions smeared with the detector mass resolution. The simulated data samples were used to estimate the S/B ratios and the signal significances in different centrality and transverse momentum intervals. The numbers were used to estimate the required data samples for a reliable measurement of resonances. Reconstruction of ρ(770)
0, K*(892)
0, K*(892)
±, φ(1020), Λ(1520) and Σ(1385)
± resonances with a significance of ~20 in each of the
pT bins with a width of 200 MeV/
c in the
pT range corresponding to ~99% of the total particle yields would require the accumulation of 10, 5, 30, 10, 15 and 25 million events in Au+Au collisions at
= 11 GeV, respectively. The numbers change to 10 (20), 5 (10), 50 (80), 10 (10), 10 (30) and 40 (70) million events in Au+Au events at
= 7.7 (4) GeV. The multiplicity dependent studies would require a factor of 10–20 higher accumulated statistics. The measurements of Ξ(1530)
0 are more challenging. With 10 M events simulated in Au+Au collisions at
= 11 GeV, only a hint of the reconstructed signal is seen at
pT > 0.4 GeV/c. Embedded simulations are needed to study the Ξ(1530)
0 production in more detail.
To obtain the fully corrected production spectra, the resonance raw yields extracted from the fits to the invariant mass distributions are corrected for the efficiencies. A comparison of the fully corrected production spectra to truly generated ones is shown in
Figure 5. In all cases, the reconstructed spectra match the generated ones within uncertainties that validate the developed reconstruction chains.
4. Conclusions
The measurement of ρ(770)0, K*(892)0, K*(892)±, φ(1020), Λ(1520), Σ(1385)± and Ξ(1530)0 resonances will be possible with the MPD detector in Au+Au collisions at NICA energies, = 4–11 GeV. The MPD will provide measurements of the resonances starting from zero transverse momentum, the high-pT reach will be limited only by the size of the available data set. The first results will become available after the accumulation of about 107 minimum bias collisions at any energy. The more differential studies as a function of centrality would need a larger data sample up to a billion events.