Direct Photons from Hot Quark Matter in Renormalized Finite-Time-Path QED
Abstract
1. Introduction
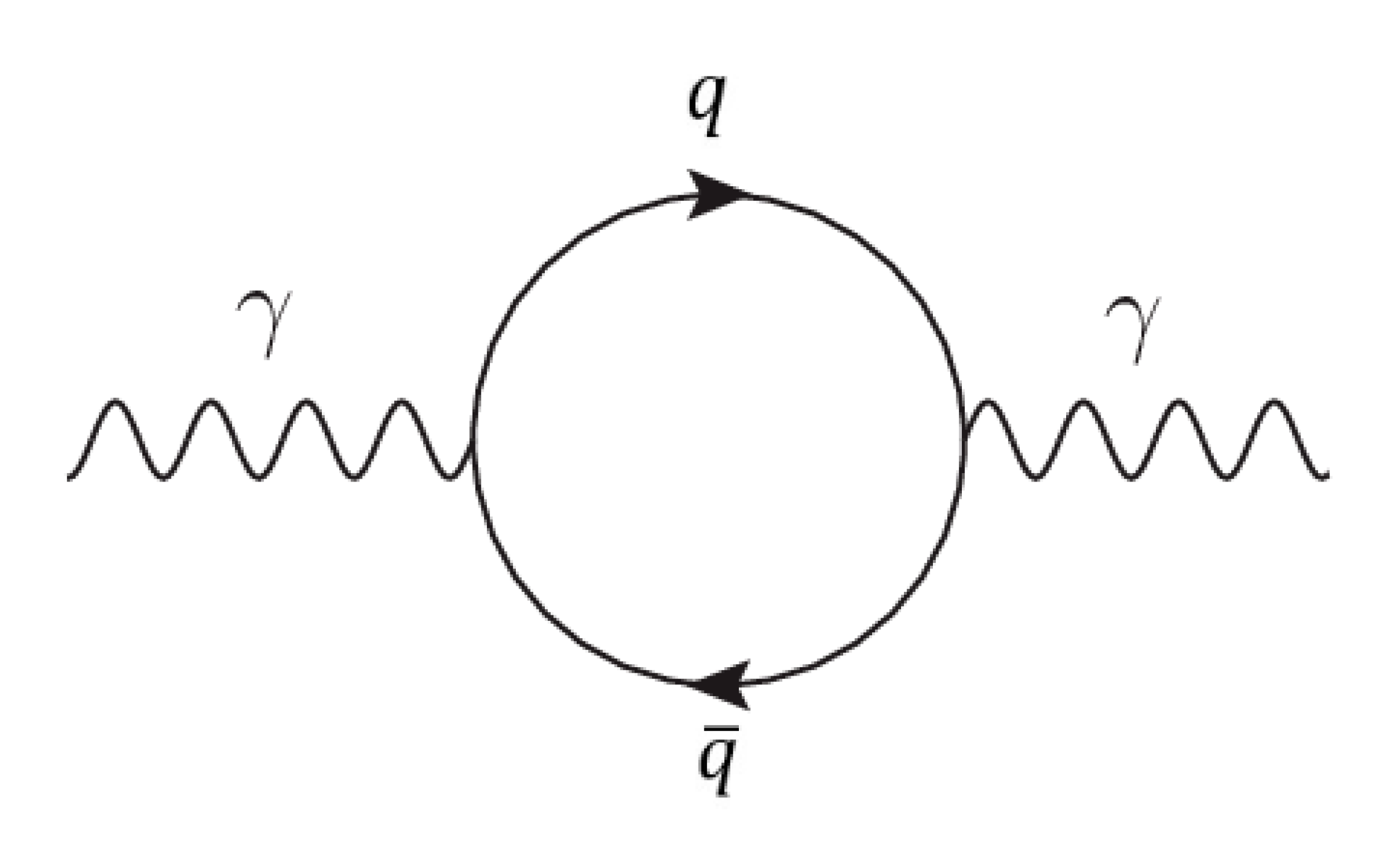
2. Direct Photon Production
- Vertices with at least one outgoing retarded propagator or incoming advanced propagator. Energy conservation is achieved by simple integration over the energy of such propagator, by closing the contour from above for the retarded and from below for the advanced propagator. This case includes the cases when there are more than one such propagators connecting the same vertex. In this case, the loop integrals should not diverge. The convolution product * containing them turns into the usual algebraic product. Examples: the vertex between the two-point functions and ; between and ; between and ; between and , as they appear in the Dyson–Schwinger equation terms .
- Vertices without any outgoing retarded propagator or incoming advanced propagator. They are lower in time than neighboring vertices. Closing the integration path always catches some singularities of the propagators. These terms will not conserve energy, but they oscillate in time, with high frequency. The examples are: the vertex between the two-point functions and ; between and ; between and ; and, between and .
- Vertices with at least one outgoing retarded propagator, or at least one incoming advanced propagator, but with two or more such propagators entering the same vertex, where the corresponding loop integral diverges. These vertices should conserve energy, but divergent integrals make them ill-defined. At , the loop integrals are regulated, and the usual closing of the integration contour leads to energy conservation. This make them group 1. vertices. Examples of such vertices are the ones between the two-point functions and , as well as and . Additionally, in the case that the mentioned vertex is connected with yet another one, where this connection satisfies the condition for the group 1 vertices, the mentioned vertex immediately belongs to the group 1.
3. Discussion of the Results
3.1. Energy Conserving Terms
- (1)
- They conserve energy.
- (2)
- They vanish for the distribution functions satisfying detailed balance principle. Indeed, the bracket from (A17) in Appendix C is the defect of detailed balance in all of the channels:In Equation (13), unpolarized photons are assumed; hence, no subscripts appear on their distribution functions .
- (3)
- They are proportional to the lowest order Collision integral. Nevertheless, their contribution vanishes, owing to the kinematical limitations. (Otherwise, these terms would correspond to the contribution from the usual S-matrix formalism.)
3.2. Term Containing
3.3. Cut Contributions
3.4. Comparison to the Wang-Boyanovsky Result
4. Conclusions
- Equation (12) contains renormalized linearly, whereas in usual S-matrix calculations it appears quadratically in higher orders of the perturbation expansion. Thus, Equation (12). at least in principle, offers a possibility, albeit challenging, to extract some information about from experiment.
- One should distinguish the direct photon stage from the later stage in which the energy uncertainties are much smaller, but higher order perturbation contributions become more important and even start to dominate (the damping phase).
- The early-time distributions of quarks () and antiquarks () are still unknown, and one should consider two very different situations: (a) the quarks are distributed isotropically and the probing functions could be taken as a thermalized Fermi–Dirac form like in Ref. [22]. Or (b) the initial distribution of quarks may reflect the early stage distribution of nucleons. Some testing of Ansätze for the distributions will be necessary before reaching the final conclusion on the importance of the presented mechanism and its result (12), but we hope this will contribute to resolving the direct photon puzzle [3].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Convolution Product
Appendix B. QED—Propagators
Appendix C. One-Loop Vacuum Polarizations
References
- Baym, G. Ultrarelativistic heavy ion collisions: The first billion seconds. Nucl. Phys. A 2016, 956, 1. [Google Scholar] [CrossRef]
- Pasechnik, R.; Šumbera, M. Phenomenological Review on Quark—Gluon Plasma: Concepts vs. Observations. Universe 2017, 3, 7. [Google Scholar] [CrossRef]
- David, G. Direct real photons in relativistic heavy ion collisions. Rept. Prog. Phys. 2020, 83, 046301. [Google Scholar] [CrossRef]
- Schwinger, J.S. Brownian motion of a quantum oscillator. J. Math. Phys. 1961, 2, 407. [Google Scholar] [CrossRef]
- Keldysh, L.V. Diagram technique for nonequilibrium processes. Sov. Phys. JETP 1965, 20, 1018–1026. [Google Scholar]
- Kadanoff, L.P.; Baym, G. Quantum Statistical Mechanics; Benjamin: New York, NY, USA, 1962. [Google Scholar]
- Danielewicz, P. Quantum Theory of Nonequilibrium Processes. 1. Ann. Phys. 1984, 152, 239. [Google Scholar] [CrossRef]
- Chou, K.C.; Su, Z.B.; Hao, B.L.; Yu, L. Equilibrium and Nonequilibrium Formalisms Made Unified. Phys. Rept. 1985, 118, 1. [Google Scholar] [CrossRef]
- Rammer, J.; Smith, H. Quantum field-theoretical methods in transport theory of metals. Rev. Mod. Phys. 1986, 58, 323. [Google Scholar] [CrossRef]
- Landsman, N.P.; van Weert, C.G. Real and Imaginary Time Field Theory at Finite Temperature and Density. Phys. Rept. 1987, 145, 141. [Google Scholar] [CrossRef]
- Calzetta, E.; Hu, B.L. Nonequilibrium Quantum Fields: Closed Time Path Effective Action, Wigner Function and Boltzmann Equation. Phys. Rev. D 1988, 37, 2878. [Google Scholar] [CrossRef]
- Niemi, A.J. Nonequilibrium Quantum Field Theories. Phys. Lett. B 1988, 203, 425–432. [Google Scholar] [CrossRef]
- Remler, E.A. Simulation of multiparticle scattering. Ann. Phys. 1990, 202, 351. [Google Scholar] [CrossRef]
- Bellac, M.L. Thermal Field Theory; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Brown, D.A.; Danielewicz, P. Partons in phase space. Phys. Rev. D 1998, 58, 094003. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Iancu, E. The Quark gluon plasma: Collective dynamics and hard thermal loops. Phys. Rept. 2002, 359, 355–528. [Google Scholar] [CrossRef]
- Boyanovsky, D.; de Vega, H.J. Anomalous kinetics of hard charged particles: Dynamical renormalization group resummation. Phys. Rev. D 1999, 59, 105019. [Google Scholar] [CrossRef]
- Boyanovsky, D.; de Vega, H.J.; Holman, R.; Simionato, M. Dynamical renormalization group resummation of finite temperature infrared divergences. Phys. Rev. D 1999, 60, 065003. [Google Scholar] [CrossRef]
- Boyanovsky, D.; de Vega, H.J.; Wang, S.Y. Dynamical renormalization group approach to quantum kinetics in scalar and gauge theories. Phys. Rev. D 2000, 61, 065006. [Google Scholar] [CrossRef]
- Boyanovsky, D.; de Vega, H.J.; Simionato, M. Nonequilibrium quantum plasmas in scalar QED: Photon production, magnetic and Debye masses and conductivity. Phys. Rev. D 2000, 61, 085007. [Google Scholar] [CrossRef]
- Wang, S.Y.; Boyanovsky, D.; de Vega, H.J.; Lee, D.S. Real time nonequilibrium dynamics in hot QED plasmas: Dynamical renormalization group approach. Phys. Rev. D 2000, 62, 105026. [Google Scholar] [CrossRef]
- Wang, S.Y.; Boyanovsky, D. Enhanced photon production from quark—gluon plasma: Finite lifetime effect. Phys. Rev. D 2001, 63, 051702. [Google Scholar] [CrossRef]
- Wang, S.Y.; Boyanovsky, D.; Ng, K.W. Direct photons: A nonequilibrium signal of the expanding quark gluon plasma at RHIC energies. Nucl. Phys. A 2002, 699, 819–846. [Google Scholar] [CrossRef]
- Boyanovsky, D.; de Vega, H.J. Are direct photons a clean signal of a thermalized quark gluon plasma? Phys. Rev. D 2003, 68, 065018. [Google Scholar] [CrossRef]
- Boyanovsky, D.; de Vega, H.J. Photon production from a thermalized quark gluon plasma: Quantum kinetics and nonperturbative aspects. Nucl. Phys. A 2005, 747, 564–608. [Google Scholar] [CrossRef]
- Arleo, F.; Aurenche, P.; Bopp, F.W.; Dadic, I.; David, G.; Delagrange, H.; d’Enterria, D.G.; Eskola, K.J. Hard probes in heavy-ion collisions at the LHC: Photon physics in heavy ion collisions at the LHC. In CERN Yellow Book CERN-2004-009-D; CERN: Geneva, Switzerland, 2004. [Google Scholar]
- Millington, P.; Pilaftsis, A. Perturbative nonequilibrium thermal field theory. Phys. Rev. D 2013, 88, 085009. [Google Scholar] [CrossRef]
- Millington, P.; Pilaftsis, A. Thermal field theory to all orders in gradient expansion. J. Phys. Conf. Ser. 2013, 447, 012071. [Google Scholar] [CrossRef]
- Dadić, I. Out-of-equilibrium thermal field theories: Finite time after switching on the interaction: Fourier transforms of the projected functions. Phys. Rev. D 2000, 63, 025011, Erratum in 2002, 66, 069903. [Google Scholar] [CrossRef]
- Dadić, I. Out-of-equilibrium TFT—energy nonconservation at vertices. Nucl. Phys. A 2002, 702, 356. [Google Scholar] [CrossRef]
- Dadić, I. Retarded propagator representation of out-of-equilibrium thermal field theories. Nucl. Phys. A 2009, 820, 267C. [Google Scholar] [CrossRef]
- Dadić, I.; Klabučar, D. Causality and Renormalization in Finite-Time-Path Out-of-Equilibrium ϕ3 QFT. Particles 2019, 2, 8. [Google Scholar] [CrossRef]
- Paquet, J.F.; Shen, C.; Denicol, G.S.; Luzum, M.; Schenke, B.; Jeon, S.; Gale, C. Production of photons in relativistic heavy-ion collisions. Phys. Rev. C 2016, 93, 044906. [Google Scholar] [CrossRef]
- Ghiglieri, J.; Kaczmarek, O.; Laine, M.; Meyer, F. Lattice constraints on the thermal photon rate. Phys. Rev. D 2016, 94, 016005. [Google Scholar] [CrossRef]
- Ding, H.T.; Karsch, F.; Mukherjee, S. Thermodynamics of strong-interaction matter from Lattice QCD. Int. J. Mod. Phys. E 2015, 24, 1530007. [Google Scholar] [CrossRef]
- Haque, N.; Bandyopadhyay, A.; Andersen, J.O.; Mustafa, M.G.; Strickland, M.; Su, N. Three-loop HTLpt thermodynamics at finite temperature and chemical potential. J. High Energy Phys. 2014, 1450, 027. [Google Scholar] [CrossRef]
- Bollini, C.G.; Giambiagi, J.J. Dimensional Renormalization: The Number of Dimensions as a Regularizing Parameter. Nuovo Cim. B 1972, 12, 20. [Google Scholar] [CrossRef]
- Hooft, G.; Veltman, M. Regularization and Renormalization of Gauge Fields. Nucl. Phys. B 1972, 44, 189–213. [Google Scholar] [CrossRef]
- Ashmore, J.F. A Method of Gauge Invariant Regularization. Lett. Nuovo Cim. 1972, 4, 289–290. [Google Scholar] [CrossRef]
- Cicuta, G.M.; Montaldi, E. Analytic renormalization via continuous space dimension. Lett. Nuovo Cim. 1972, 4, 329–332. [Google Scholar] [CrossRef]
- Wilson, K.G. Quantum field theory models in less than four-dimensions. Phys. Rev. D 1973, 7, 2911. [Google Scholar] [CrossRef]
- Kislinger, M.B.; Morley, P.D. Collective Phenomena in Gauge Theories. 2. Renormalization in Finite Temperature Field Theory. Phys. Rev. D 1976, 13, 2771. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Holstein, B.R. Renormalization and Radiative Corrections at Finite Temperature. Phys. Rev. D 1983, 28, 340, Erratum in 1984, 29, 3004. [Google Scholar] [CrossRef]
- Johansson, A.E.I.; Peressutti, G.; Skagerstam, B.S. Quantum Field Theory at Finite Temperature: Renormalization and Radiative Corrections. Nucl. Phys. B 1986, 278, 324–342. [Google Scholar] [CrossRef]
- Keil, W.; Kobes, R. Mass and Wave Function Renormalization at Finite Temperature. Phys. A 1989, 158, 47–57. [Google Scholar] [CrossRef]
- Keil, W. Radiative Corrections and Renormalization at Finite Temperature: A Real Time Approach. Phys. Rev. D 1989, 40, 1176. [Google Scholar] [CrossRef] [PubMed]
- Bellac, M.L.; Poizat, D. Renormalization of External Lines in Relativistic Field Theories at Finite Temperature. Z. Phys. C 1990, 47, 125–131. [Google Scholar] [CrossRef]
- Elmfors, P. Finite Temperature Renormalization of the (ϕ3)6- and (ϕ4)4-Models at Zero Momentum. Z. Phys. C 1992, 56, 601. [Google Scholar] [CrossRef][Green Version]
- Van Eijck, M.A.; Weert, C.G.V. Finite-temperature renormalization of the phi**4(4) model. Int. J. Mod. Phys. B 1996, 10, 1485–1497. [Google Scholar] [CrossRef]
- Chapman, I.A. Finite temperature wave function renormalization: A Comparative analysis. Phys. Rev. D 1997, 55, 6287. [Google Scholar] [CrossRef]
- Nakkagawa, H.; Yokota, H. Effective potential at finite temperature: RG improvement versus high temperature expansion. Prog. Theor. Phys. Suppl. 1997, 129, 209. [Google Scholar] [CrossRef]
- Baacke, J.; Heitmann, K.; Patzold, C. Renormalization of nonequilibrium dynamics at large N and finite temperature. Phys. Rev. D 1998, 57, 6406. [Google Scholar] [CrossRef]
- Esposito, S.; Mangano, G.; Miele, G.; Pisanti, O. Wave function renormalization at finite temperature. Phys. Rev. D 1998, 58, 105023. [Google Scholar] [CrossRef]
- Van Hees, H.; Knoll, J. Renormalization in selfconsistent approximation schemes at finite temperature. 3. Global symmetries. Phys. Rev. D 2002, 66, 025028. [Google Scholar] [CrossRef]
- Jakovac, A.; Szep, Z. Renormalization and resummation in finite temperature field theories. Phys. Rev. D 2005, 71, 105001. [Google Scholar] [CrossRef]
- Arrizabalaga, A.; Reinosa, U. Renormalized finite temperature phi**4 theory from the 2PI effective action. Nucl. Phys. A 2007, 785, 234. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Ipp, A.; Mendez-Galain, R.; Wschebor, N. Perturbation theory and non-perturbative renormalization flow in scalar field theory at finite temperature. Nucl. Phys. A 2007, 784, 376–406. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Wschebor, N. Massive renormalization scheme and perturbation theory at finite temperature. Phys. Lett. B 2015, 741, 310–315. [Google Scholar] [CrossRef]
- Ryder, L.H. Quantum Field Theory; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Garbrecht, B.; Prokopec, T.; Schmidt, M.G. Particle number in kinetic theory. Eur. Phys. J. C 2004, 38, 135–143. [Google Scholar] [CrossRef]
- Dadić, I. Two mechanisms for elimination of pinch singularities in/out of equilibrium thermal field theories. Phys. Rev. D 1999, 59, 125012. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dadić, I.; Klabučar, D.; Kuić, D. Direct Photons from Hot Quark Matter in Renormalized Finite-Time-Path QED. Particles 2020, 3, 676-692. https://doi.org/10.3390/particles3040044
Dadić I, Klabučar D, Kuić D. Direct Photons from Hot Quark Matter in Renormalized Finite-Time-Path QED. Particles. 2020; 3(4):676-692. https://doi.org/10.3390/particles3040044
Chicago/Turabian StyleDadić, Ivan, Dubravko Klabučar, and Domagoj Kuić. 2020. "Direct Photons from Hot Quark Matter in Renormalized Finite-Time-Path QED" Particles 3, no. 4: 676-692. https://doi.org/10.3390/particles3040044
APA StyleDadić, I., Klabučar, D., & Kuić, D. (2020). Direct Photons from Hot Quark Matter in Renormalized Finite-Time-Path QED. Particles, 3(4), 676-692. https://doi.org/10.3390/particles3040044




