Abstract
We construct a new equation of state for the baryonic matter under an intense magnetic field within the framework of covariant density functional theory. The composition of matter includes hyperons as well as -resonances. The extension of the nucleonic functional to the hypernuclear sector is constrained by the experimental data on and -hypernuclei. We find that the equation of state stiffens with the inclusion of the magnetic field, which increases the maximum mass of neutron star compared to the non-magnetic case. In addition, the strangeness fraction in the matter is enhanced. Several observables, like the Dirac effective mass, particle abundances, etc. show typical oscillatory behavior as a function of the magnetic field and/or density which is traced back to the occupation pattern of Landau levels.
1. Introduction
Compact stars are the end products of stellar evolution that are produced in supernova explosions. They are among the most fascinating objects in the universe that motivate theoretical studies of exotic states of matter which are difficult or impossible to produce in modern terrestrial laboratories. Among the remarkable features of compact stars are the wide range of densities covered by their interiors (from sub-saturation up to possibly 10 times the nuclear saturation density) and the huge magnetic field range to G. The compact stars are arranged in various classes according to some of their characteristic features. These include millisecond pulsars, neutron stars in X-ray binaries, radio pulsars, anomalous X-ray pulsars, soft gamma repeaters, etc. Among these, the anomalous X-ray pulsars and soft gamma repeaters are believed to be compact stars with the surface magnetic field in the range of – G [1,2] and are commonly referred as magnetars. Furthermore, there has been recently growing evidence that (at least) the repeating fast radio bursts (FRBs) are related to magnetars [3,4,5,6,7]. Since the gravitational equilibrium of compact stars admits stars with magnetic fields in the range – G, large magnetic fields beyond those currently inferred have been studied theoretically. Earlier works [8,9,10,11,12] have studied the effects of the magnetic field on the gross parameters of compact stars, such as the mass, radius, moment of inertia under intense magnetic fields. The induced deformations of the neutron stars (NSs) due to the strong magnetic fields can be important sources of gravitational waves and precession in neutron stars, see Refs. [13,14,15,16]. The structure of magnetized compact stars, in particular, their deformation, in general relativity, has been studied initially in Refs. [14,15,16] assuming various forms of the poloidal and toroidal field configurations. More recent studies [17,18,19] considered also a combination of toroidal and poloidal fields which appear to be more stable than purely poloidal or toroidal configurations. Moreover, a “universal” field profile represented by an 8th-order polynomial as a function of star’s internal radius has been proposed recently to describe the magnetic field profile inside the star [20] based on the solution of Einstein–Maxwell equations in general relativity. While large magnetic fields are required to affect the equation of state (i.e., the dependence of pressure on the energy density, hereafter abbreviated as EoS) and the structure of the star, the role of the magnetic field is still important at lower values. In particular, MeV-scale magnetic field can significantly alter the quasiparticle spectrum of baryons, leading to the suppression of the superfluidity of protons via Landau diamagnetism [21,22] and superfluidity of neutrons via Pauli paramagnetism [23], see for a review [24]. These modifications alter the neutrino emissivity of compact stars with MeV-scale magnetic fields [22] through the modifications of the neutrino production reaction rates. The anisotropy introduced by the magnetic field also affects evolutionary processes in compact stars such as their magneto-thermal evolution [25] and rotational dynamics [26,27].
Recent observations of compact stars in a wide range of electromagnetic spectra and in gravitational waves motivate detailed microscopic studies of the interior matter, in particular, its EoS and composition. A fundamental observational property of compact stars is the maximum mass, which is still a matter of debate. The mass of PSR 1913+16 (the Hulse–Taylor pulsar) M is one of the precisely determined pulsar masses [28]. The largest masses were measured for millisecond pulsars in binaries with white dwarfs, namely J1614−2230 ( M) [29], PSR J0348+0432 ( M) [30] and MSP J0740+6620 ( M with 95% credibility) [31]. The last measurement, which is based on Shapiro delay, is so far the largest measured maximum mass with relatively small error bars and, thus, sets a reliable lower bound on the maximum mass of a compact object. Another recent observation of gravitational waves by the LIGO-Virgo Collaboration (the “GW190814”event) from a binary system of a black hole and light compact object companion sets the mass of the latter at M [32], but the origin of this object (i.e., a light black hole or a heavy neutron star) is not settled. In addition, high precision mass and radius measurements for the pulsar PSR J0030+0451 are offered by the Neutron star Interior Composition ExploreR (NICER) space mission with mass–radius values M, km [33] and M, km [34].
The composition of matter at about several times the nuclear saturation density is not known. One possibility is that matter is nucleonic (with a small admixture of leptons to guarantee the charge neutrality) up to the center of a star. However, in massive compact stars, the densities can reach values exceeding the saturation density by an order of magnitude. Therefore, the appearance of new degrees of freedom is a possibility. One option is the nucleation of hyperons, which softens the EoS and results (for some models) in a maximum mass of a compact star below the value observational minimum . There are several modern covariant density functional (CDF)-based models which avoid this problem and provide sufficient repulsion to produce stars with large enough masses . A particular class of these models, which we will use in this work, is based on density functionals with density-dependent (DD) couplings [35,36,37,38,39]. The interactions in these models are mediated via the exchange of , , -mesons, and in the hypernuclear sector also via two additional (hidden strangeness) and -mesons.
An interesting possibility is an appearance of -resonances in compact stars, which has regained attention in recent years [40,41,42], after they have been neglected for a long time due to presumed high onset density of the order of 10 times the nuclear saturation density [43]. The strong interactions, in this case, are mediated by the exchange of , and -mesons only. The inclusion of -resonances in the EoS shifts the onset of hyperons to higher densities. Consequently, the high-density part of the EoS is stiffer and the maximum mass is higher when -resonances are included. They also significantly reduce the radius of the star [44,45,46] due to the softening of the EoS at intermediate densities.
In this work, we consider -resonance admixed hypernuclear matter in strong magnetic fields within the DDME2 parameterization, which has been used already for the same problem in the case of zero magnetic fields in Refs. [44,45,46,47].
2. Formalism
2.1. Model
In this work, we consider matter composed of the full baryon octet, the quartet of -resonances and leptons—electrons and muons (). The strong interaction between (non-strange) baryons is mediated by the and -mesons. In addition, the hidden-strangeness mesons (scalar) and (vector) mediate the hyperon–hyperon interactions. The total Lagrangian density of the fermionic component of matter in presence of a magnetic field is given by,
where, and are the matter and the gauge field contributions, respectively.
We take the matter part of the Lagrangian density as [42,48],
where is the covariant derivative, is the electromagnetic vector potential, is the charge of the particle (e being unit ‘+’ charge), the b-summation in the first line is over the nucleons and hyperons (spin-1/2), d-summation in the second line is over the -resonances (spin-3/2) and the l summation in the last line is over leptons. The fields , and correspond to the Dirac baryons, leptons and the Rarita–Schwinger fields for -resonances. Their masses are, respectively, , and . The third and fourth lines in Equation (2) contain the contributions from scalar meson fields and with masses and , isoscalar-vector meson fields and with masses and and, finally, the isovector-vector meson field with mass . The coupling between the mesons and baryons is described by the density-dependent couplings and , whereby stands for the iso-spin operator. Finally, the purely “gauge” mesonic contributions in Equation (2) contain the tensors
The electro-magnetic field Lagrangian density in Equation (1) has the standard form
with being the electro-magnetic field tensor. Below, we adopt the reference frame in which the four-vector potential has the form , where B is the magnitude of the magnetic field.
In the mean-field approximation, assuming that the system is infinite, the meson fields acquire the ground-state expectation values,
where the scalar and baryon (vector) number densities are defined for the baryon octet as and , respectively. For the -resonances, these are defined as and , respectively. The effective (Dirac) baryon masses in the same approximation are given by,
The scalar density, baryon number density and the kinetic energy density of the uncharged baryon (denoted by index u) at zero temperature are given by,
respectively, where, , , , are the spin, Fermi momentum, effective mass and Fermi energy of the uth-uncharged baryon.
The same quantities for a charged baryon (denoted by index c) are given by the following expressions:
- Spin-1/2 case:
- Spin-3/2 case:
where, , , are the Fermi momentum of the -Landau level, effective mass and Fermi energy of the -charged baryon. The Landau levels for spin-, baryons are denoted by , the maximum value of which is defined by,
In the case of spin- particles, the lowest Landau level has degeneracy equal unity and all other levels have degeneracy equal 2 [49]. In the case of spin- particles, the degeneracy of the lowest (first) level is 2, for the second level it is 3 and is 4 in the remaining Landau levels [50].
For the case of leptons (), the number density and contribution to the kinetic energy density is given by,
where, , , are the Fermi momentum of the -Landau level, bare mass and Fermi energy of the lepton, respectively.
In Equations (9)–(17), the Fermi momenta and are defined as,
with being the Fermi energy of the respective particle. The total energy density of the matter is thus given by,
where the sum over includes the baryon octet and the -quartet, and the l-summation is over the leptons. The matter pressure can be evaluated from the thermodynamic (Gibbs–Duhem) relation as,
where is the chemical potential of the -spin-1/2 (-spin-3/2) baryon which can be defined as,
In order to maintain thermodynamic consistency a self-energy re-arrangement term, is introduced
where is the total baryon (or vector) number density. This re-arrangement term contributes explicitly only to the matter pressure. Equations (22) and (23) provide the EoS (the relation between the pressure and energy density) of the system under consideration in a parametric form.
2.2. Meson–Baryon Coupling Parameters
In this work, we adopt the DD-ME2 parameterization proposed in Ref. [51] for nucleonic matter. The density-dependent meson–nucleon coupling constants are given by,
where , is the saturation density, N stands for a nucleon and
For the -meson, the density-dependent coupling constant is given by
The details of the procedure for fixing the values of coefficients in Equations (27) and (28) can be found in Ref. [51]. Table 1 provides the parameter values employed in this work. Note that nucleons do not couple with the and -mesons, i.e., .

Table 1.
The coupling constants for the DD-ME2 parameterization [51], at nuclear saturation density fm. For this model, the nuclear parameters are: the compression modulus MeV, the binding energy per nucleon MeV, the symmetry energy MeV, the effective nucleon Dirac mass with MeV.
For the hyperonic sector, the density-dependent vector coupling constants are determined from SU(6) symmetry [52]
For the evaluation of hyperon–-meson coupling constants, we consider the optical potentials of the and hyperons in nuclear matter to be, MeV, MeV and MeV. Due to the repulsive nature of the -potential in nuclear matter, -hyperons do not matter for the densities considered in this work. The – coupling constant is evaluated by fitting it to a potential depth MeV and further constraining the – and – couplings via the relation [53]
Table 2 provides the numerical values for the density-dependent scalar couplings. The coupling constants for the -resonances are taken as [47]

Table 2.
Scalar meson–hyperon coupling constants.
The density-dependent scalar coupling is determined by fixing the -potential to the value , where is the isoscalar nucleon potential. This implies that . Note that -resonances do not couple to and -mesons, i.e., .
2.3. Magnetic Field Profiles
To model the magnetic field profile in the neutron star interior, we adopted two types of profiles which give the dependence of the field on the position inside the star.
The exponential profile is given by [9]
where and denote the magnetic fields at surface and at center of the star, respectively. The free parameters and are commonly adjusted such as to have a fixed surface magnetic field of G for any given value of the field in the center, which is typically larger than the surface field.
The universal profile is given as [20]
where , r is the internal radius joining the center to the point of observation, is the mean radius of the star and is the value of the field at the center of the star.
3. Results
We turn now to the numerical results of our study and consider the effect of strong magnetic field on high-density stellar matter with three types of composition:
- (1)
- Nucleons (N),
- (2)
- nucleons and hyperons (NY),
- (3)
- nucleons, hyperons and -resonances (NY).
Figure 1 shows the EoS and mass–radius (hereafter M–R) relations for these three compositions of matter in the case along with some astrophysical constraints on the masses and radii of compact stars. Table 3 lists some parameters of the stars with maximum masses along the stellar sequences for the three compositions listed above.
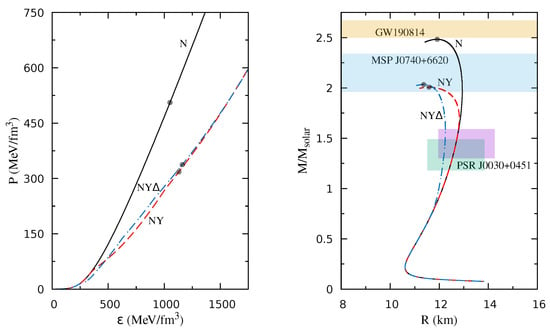
Figure 1.
Left panel: Equation of state (EoS) of matter in the absence of magnetic field for three compositions considered. Solid, dashed, dash-dotted lines correspond to the cases of nucleons only (N), nucleons and hyperons (NY), nucleons, hyperons and Delta (NY), respectively. The circles indicate the location of the maximum mass star for each composition. Right panel: the mass–radius (M–R) relations corresponding to the EoS on the left panel obtain through solutions of the TOV equations. The mass constraints from the various astrophysical observations are represented by the colored bands and correspond to the GW190814 event [32], MSP J0740+6620 [31] and the mass–radius limits inferred for PSR J0030+0451 from the Neutron star Interior Composition ExploreR (NICER) experiment [33,34].

Table 3.
Parameter values of the maximum-mass stars for non-magnetic stellar sequences derived for three different compositions. Here, , R, denote the maximum mass (in solar units), corresponding radius (in km) and central energy density (in MeV/fm), respectively.
Let us now turn to stellar configurations with magnetic field. In order to show the effect of the field in the case of the universal profile, we need a relation between the internal radius and the density, i.e., the function . This requires us to specify a stellar model. We, therefore, chose three stars from the stable region of M–R curve with parameters shown in Table 4. After fixing the value of the central field G, we are then able to use Equation (33). We note that the predicted surface magnetic field values are G.

Table 4.
The values of the energy–density, pressure and number density at the center of non-magnetized stellar models which were used to obtain the universal relation (33) as a function of density (instead of the internal radius). We also list the mass and the radius for each model.
In the case of exponential profile (32), the surface field is fixed at G and we adopt the parameter values and and for N, NY and NY matter, respectively. The resulting magnetic field profiles guarantee that the matter remains stable under the influence of strong B-field.
Figure 2 shows the variationof the magnetic field in the interior of the star as a function of internal radius and density in the cases of exponential and universal relations.
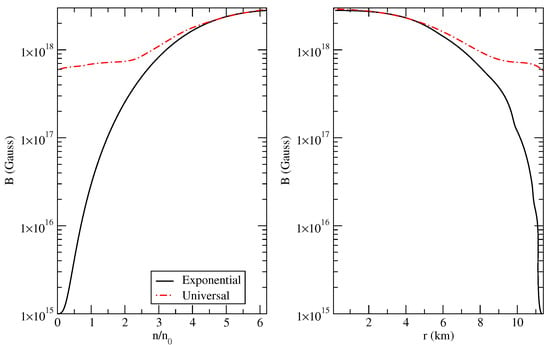
Figure 2.
Magnetic field profiles for the NY composition as a function of baryon number density, n (left panel) and internal radius r (right panel). Black solid, red dash-dotted lines denotes exponential and universal profiles, respectively.
Figure 3 and Figure 4 show the EoS in the presence of magnetic field for various compositions. In all the cases studied, it is seen that the EoSs follow the same trends with and without magnetic field. For the assumed values of the field, the changes in the EoS are marginal if viewed on the plots shown on the left panels of Figure 3 and Figure 4.
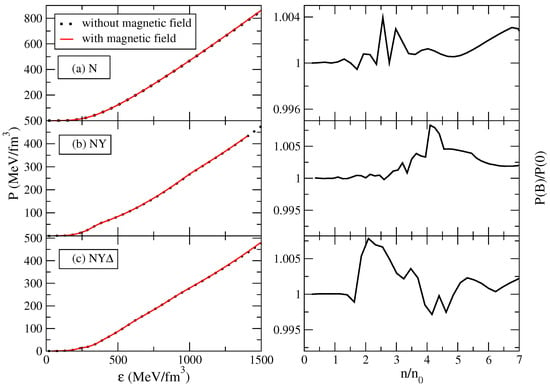
Figure 3.
A comparison of the EoS of magnetized and non-magnetized matter for three different compositions (a) nucleons only (N), (b) nucleons and hyperons (NY) and (c) nucleons, hyperons and -resonances. We assume an exponential magnetic field profile. Left panels show the dependence of pressure on energy density with (solid lines) and without (dots) magnetic field. The right panels the ratio of pressure in the presence of magnetic field to that in the absence of the field as a function of particle number density normalized to the nuclear saturation density.
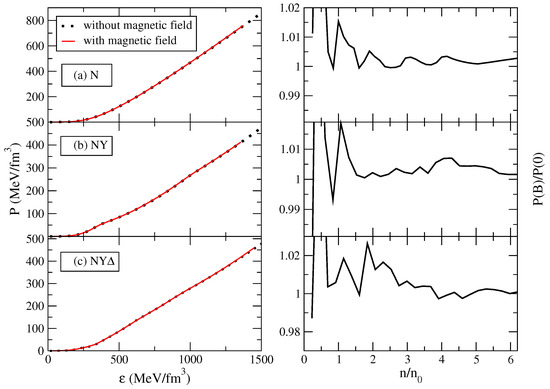
Figure 4.
Same as in Figure 3, but for the universal magnetic field profile.
The right panels of the same figures show the ratio of the pressure in presence of magnetic field to the pressure in the absence of the field. The oscillations in the pressure are associated with the occupation of the Landau levels in the strong field. It is seen that these oscillations are stronger at the surface of the star for the universal profile, because the field does not decay in this case as quickly as for the exponential profile. In the high density regime, the oscillations are comparable for both the profiles. This behavior is a consequence of the fact that close to the centre of the star, both profiles have similar values of the magnetic field (see Figure 2).
As a result of the additional pressure due to the magnetic field, the EoS is stiffened and, consequently, the maximum masses of magnetized compact stars are higher compared to their non-magnetized counterparts. This can be seen from Figure 5, where the corresponding M–R relations are displayed. More quantitatively, we find that for the N-composition the increase in maximum mass due to the effect of the magnetic field is about , in the case of NY-composition for the exponential profile and for the universal profile and, finally, for the NY-composition, about for the exponential profile and for the universal profile. We note that in the case of NY-composition the EoS is softer at high densities, than in the case of NY-composition. Therefore, the effect of the magnetic field is more sizable in the case of the softer EoS, i.e., for the NY-composition. Thus, we conclude that the changes in the maximum mass are more pronounced in the case of NY-composition and are less significant for the NY-composition.
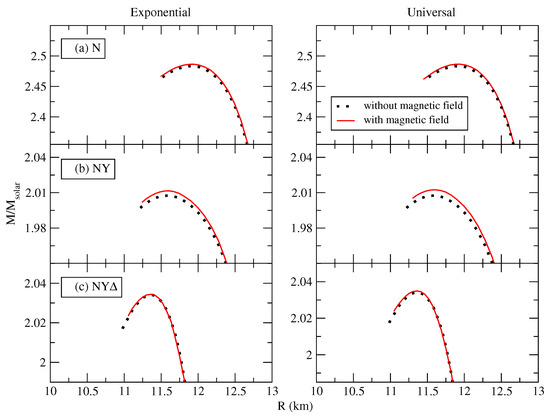
Figure 5.
The M–R relations for three compositions considered: (a) nucleons only (N), (b) nucleons and hyperons (NY) and (c) nucleons, hyperons and -resonances in the cases of with (solid lines) and without (dots) magnetic field. The left panels correspond to the exponential magnetic field profile and the right panels to universal magnetic field profile.
Figure 6 shows the ratio of fractions of different species as a function of normalized baryon number density. The oscillating nature of the fractions arises due to successive occupation of Landau levels for the charged species. The effect of the field is not substantial in the low-density regime for exponential field profile as the field strength in this case is small near the surface. In the case of the universal profile, the low-density regime shows strong fluctuations because the decay of the magnetic field with density is small and the surface magnetic field is of the order few times of G (see Figure 2). It is interesting to note that for most of the particles , but in the case of , the opposite is the case. This is a consequence of the charge neutrality. Due to the Landau quantization the fraction of electrons increases compared to non-magnetic case which causes the fraction to decrease. The pattern in Figure 6 results from the complicated interplay between the Landau quantization for charge particles entering into the two key conditions imposed—the charge neutrality and baryon number conservation, which are used in the construction of the EoS. Note also that and resonances do not appear until baryon density of for our particular choice of -potential.
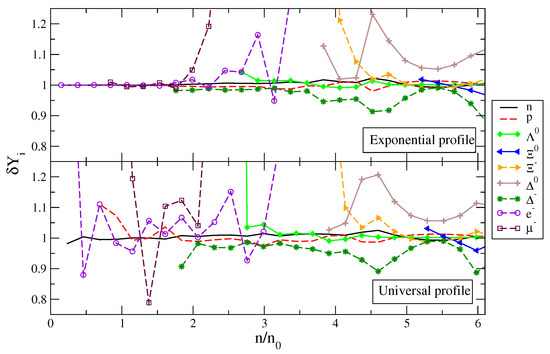
Figure 6.
Dependence of the ratio on the baryon number density normalized to the nuclear saturation density for neutrons , protons , , , , , , and . The particle markers are indicated in the panel on the right. The upper panel corresponds to the exponential field profile, the lower one to the universal field profile.
In Figure 7 we show the quantity , which is defined as the ratio of the partial fractions of strange or non-strange baryons in presence of a magnetic field to that without a magnetic field. The fraction of strange baryons is affected significantly (∼4%) by the magnetic field, whereas the fraction of the non-strange baryons is affected much less. We see that in the presence of magnetic field strange baryons appear earlier than in the non-magnetic case. This is, again, a consequence of complex interplay between the imposed charge neutrality condition and modifications of the phase-space occulation due to the Landau quantization.
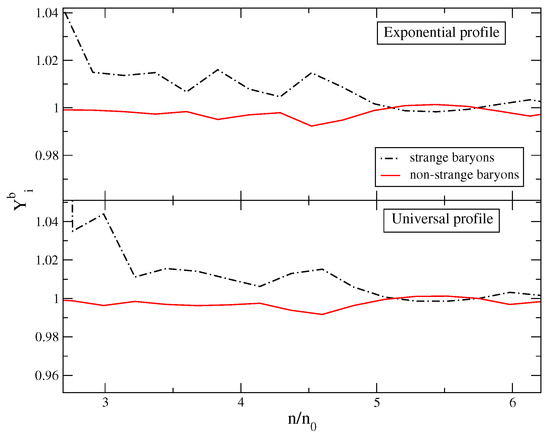
Figure 7.
The ratio of the partial fractions of strange or non-strange baryons in presence of a magnetic field to that without a magnetic field as a function of baryon number density, n in units of in the case of composition. Upper panel corresponds to the exponential field profile, the lower panel to the universal field profile.
Finally, to quantify the variations of the effective mass of a baryon in the presence of magnetic field, we show in Figure 8 the ratio of effective nucleon Dirac mass () in the magnetic field to its value in the absence of the field . It is seen that, for the exponential profile case, remains unchanged until the appearance of around times nuclear saturation density. A similar trend is observed for the universal profile case, but the amplitudes of the oscillations are larger. This is (again) due to the fact that the magnetic field value at the surface of the star is larger for this profile. With the onset of , we observe a reduction in by about in the density range ∼4–5 times saturation density for both the profiles.
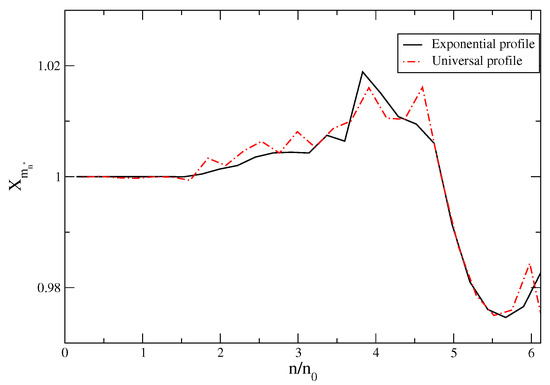
Figure 8.
Dependence of the ratio of the effective nucleon Dirac mass in the magnetic field to its value in the absence of the field on baryon number density n in units of in the case of composition. The result for the exponential field profile is shown by a solid and for universal by a dash-dotted line.
4. Conclusions and Outlook
Recent years have seen substantial progress in describing compact stars with heavy baryons (hyperons as well as -resonances) in a manner consistent with all the currently available astrophysical as well as laboratory data. Motivated by this, we have extended, for the first time, one of the standard approaches which is based on CDF theory with density-dependent couplings to the case of strongly magnetized matter. In doing so, we have taken into account fully the Landau quantization of orbits of charged particles in strong fields. We confirm previous findings that magnetic fields make EoS stiffer and lead to higher maximum masses of compact stars. To quantify these effects we employed two parameterizations of the magnetic field profiles, namely the exponential [8] and the universal [20] profiles for a fixed value of the central magnetic field G. The universal profile implies a relatively high surface magnetic field of ∼5.6 × G and flat magnetic field profile. The exponential profile, by construction, is adjusted to produce a surface magnetic field value G. In this case, the profile is steep with the magnetic field changing by orders of magnitude. Having the profiles at hand, we have explored the changes in the composition of matter and the effective mass of the nucleon. We find typical for magnetized system oscillations in these quantities which are similar to the de Haas-van Alphen oscillations of observables (e.g., the magnetic susceptibility of electronic systems) in magnetic fields. The oscillations have their origin in the occupation of the Landau levels by particles. As a result that the charged and neutral baryons are coupled by the baryon number and charge conservation, the oscillations are coupled as well and affect the fractions of neutral particles (neutrons, s and s). The oscillations of the particle fractions are substantially different for the two profiles studied if they are compared for the same value of the central magnetic field. In the case of the universal profile, these oscillations extend up to the low-density regime because the field does not change substantially. In the exponential profile case, the low-density regime has low magnetic fields, therefore the amplitudes of oscillations are low. Comparing the oscillations in the strange and non-strange sectors we observe that the hyperon fractions are more affected by the magnetic fields that the non-strange baryon fractions within the density range considered. Furthermore, the Dirac nucleon effective masses exhibit similar oscillations, which implies that a range of quantities (specific heat, baryon mean-free-path, thermal conductivity, etc.) may show oscillations as well.
Our extension of the CDF-based EoS to the non-zero magnetic field can be used to study a range of phenomena in and with magnetized compact stars in a framework that guarantees the consistency of underlying compact objects with the currently available astrophysical and experimental data.
Author Contributions
Conceptualization, M.S. and A.S.; Methodology, V.B.T.; Supervision, J.J.L. and A.S.; Writing original draft, V.B.T.; Writing review and editing, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
V.B.T. and M.S. acknowledge the funding support from Science and Engineering Research Board, Department of Science and Technology, Government of India through Project No. EMR/2016/006577 and Ministry of Education, Government of India. M.S. also thanks Alexander von Humboldt Foundation for the support of a visit to Goethe University, Frankfurt am Main. A.S. acknowledges the support through the Deutsche Forschungsgemeinschaft (Grant No. SE 1836/5-1) and European COST Actions “PHAROS” (CA16214).
Acknowledgments
V.B.T. and M.S. acknowledge the funding support from Science and Engineering Research Board, Department of Science and Technology, Government of India through Project No. EMR/2016/006577 and Ministry of Education, Government of India. M.S. also thanks Alexander von Humboldt Foundation for the support of a visit to Goethe University, Frankfurt am Main. A.S. acknowledges the support through the Deutsche Forschungsgemeinschaft (Grant No. SE 1836/5-1) and European COST Actions “PHAROS” (CA16214).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Harding, A.K.; Lai, D. Physics of strongly magnetized neutron stars. Rep. Prog. Phys. 2006, 69, 2631–2708. [Google Scholar] [CrossRef]
- Turolla, R.; Zane, S.; Watts, A.L. Magnetars: The physics behind observations. A review. Rep. Prog. Phys. 2015, 78, 116901. [Google Scholar] [CrossRef] [PubMed]
- Margalit, B.; Beniamini, P.; Sridhar, N.; Metzger, B.D. Implications of a Fast Radio Burst from a Galactic Magnetar. Astrophys. J. Lett. 2020, 899, L27. [Google Scholar] [CrossRef]
- Beniamini, P.; Wadiasingh, Z.; Metzger, B.D. Periodicity in recurrent fast radio bursts and the origin of ultralong period magnetars. Mon. Not. R. Astron. Soc. 2020, 496, 3390–3401. [Google Scholar] [CrossRef]
- Beloborodov, A.M. Blast Waves from Magnetar Flares and Fast Radio Bursts. Astrophys. J. 2020, 896, 142. [Google Scholar] [CrossRef]
- Levin, Y.; Beloborodov, A.M.; Bransgrove, A. Precessing Flaring Magnetar as a Source of Repeating FRB 180916.J0158 + 65. Astrophys. J. Lett. 2020, 895, L30. [Google Scholar] [CrossRef]
- Zanazzi, J.J.; Lai, D. Periodic Fast Radio Bursts with Neutron Star Free Precession. Astrophys. J. Lett. 2020, 892, L15. [Google Scholar] [CrossRef]
- Chakrabarty, S.; Bandyopadhyay, D.; Pal, S. Dense Nuclear Matter in a Strong Magnetic Field. Phys. Rev. Lett. 1997, 78, 2898–2901. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Chakrabarty, S.; Pal, S. Quantizing Magnetic Field and Quark-Hadron Phase Transition in a Neutron Star. Phys. Rev. Lett. 1997, 79, 2176–2179. [Google Scholar] [CrossRef]
- Broderick, A.; Prakash, M.; Lattimer, J.M. The Equation of State of Neutron Star Matter in Strong Magnetic Fields. Astrophys. J. Lett. 2000, 537, 351–367. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, P.Q.; Liu, L.G. The Influence of the Magnetic Field on the Properties of Neutron Star Matter. Mod. Phys. Lett. A 2007, 22, 623–629. [Google Scholar] [CrossRef]
- Rabhi, A.; Providência, C.; Da Providência, J. Stellar matter with a strong magnetic field within density-dependent relativistic models. J. Phys. G Nucl. Phys. 2008, 35, 125201. [Google Scholar] [CrossRef]
- Mallick, R.; Schramm, S. Deformation of a magnetized neutron star. Phys. Rev. C 2014, 89, 045805. [Google Scholar] [CrossRef]
- Bonazzola, S.; Gourgoulhon, E.; Salgado, M.; Marck, J.A. Axisymmetric rotating relativistic bodies: A new numerical approach for ‘exact’ solutions. Astron. Astrophys. 1993, 278, 421–443. [Google Scholar]
- Bocquet, M.; Bonazzola, S.; Gourgoulhon, E.; Novak, J. Rotating neutron star models with a magnetic field. Astron. Astrophys. 1995, 301, 757. [Google Scholar]
- Cardall, C.Y.; Prakash, M.; Lattimer, J.M. Effects of Strong Magnetic Fields on Neutron Star Structure. Astrophys. J. Lett. 2001, 554, 322–339. [Google Scholar] [CrossRef]
- Ciolfi, R.; Ferrari, V.; Gualtieri, L.; Pons, J.A. Relativistic models of magnetars: The twisted torus magnetic field configuration. Mon. Not. R. Astron. Soc. 2009, 397, 913–924. [Google Scholar] [CrossRef]
- Ciolfi, R.; Ferrari, V.; Gualtieri, L. Structure and deformations of strongly magnetized neutron stars with twisted-torus configurations. Mon. Not. R. Astron. Soc. 2010, 406, 2540–2548. [Google Scholar] [CrossRef]
- Ciolfi, R.; Rezzolla, L. Twisted-torus configurations with large toroidal magnetic fields in relativistic stars. Mon. Not. R. Astron. Soc. 2013, 435, L43–L47. [Google Scholar] [CrossRef]
- Chatterjee, D.; Novak, J.; Oertel, M. Magnetic field distribution in magnetars. Phys. Rev. C 2019, 99, 055811. [Google Scholar] [CrossRef]
- Sinha, M.; Sedrakian, A. Upper critical field and (non)-superconductivity of magnetars. arXiv 2014, arXiv:1403.2829. [Google Scholar] [CrossRef]
- Sinha, M.; Sedrakian, A. Magnetar superconductivity versus magnetism: Neutrino cooling processes. Phys. Rev. C 2015, 91, 035805. [Google Scholar] [CrossRef]
- Stein, M.; Sedrakian, A.; Huang, X.G.; Clark, J.W. Spin-polarized neutron matter: Critical unpairing and BCS-BEC precursor. Phys. Rev. C 2016, 93, 015802. [Google Scholar] [CrossRef]
- Sedrakian, A.; Xu-Guang, H.; Sinha, M.; Clark, J.W. From microphysics to dynamics of magnetars. J. Phys. Conf. Ser. 2017, 861, 012025. [Google Scholar] [CrossRef]
- Pons, J.A.; Miralles, J.A.; Geppert, U. Magneto-thermal evolution of neutron stars. Astron. Astrophys. 2009, 496, 207–216. [Google Scholar] [CrossRef]
- Pons, J.A.; Viganò, D. Magnetic, thermal and rotational evolution of isolated neutron stars. Living Rev. Comput. Astrophys. 2019, 5, 3. [Google Scholar] [CrossRef]
- Sedrakian, A. Rapid rotational crust-core relaxation in magnetars. Astron. Astrophys. 2016, 587, L2. [Google Scholar] [CrossRef][Green Version]
- Hulse, R.A.; Taylor, J.H. Discovery of a pulsar in a binary system. Astrophys. J. Lett. 1975, 195, L51–L53. [Google Scholar] [CrossRef]
- Özel, F.; Psaltis, D.; Ransom, S.; Demorest, P.; Alford, M. The Massive Pulsar PSR J1614-2230: Linking Quantum Chromodynamics, Gamma-ray Bursts, and Gravitational Wave Astronomy. Astrophys. J. Lett. 2010, 724, L199–L202. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 448. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Lenske, H.; Fuchs, C. Rearrangement in the density dependent relativistic field theory of nuclei. Phys. Lett. B 1995, 345, 355–360. [Google Scholar] [CrossRef]
- Fuchs, C.; Lenske, H.; Wolter, H.H. Density dependent hadron field theory. Phys. Rev. C 1995, 52, 3043–3060. [Google Scholar] [CrossRef] [PubMed]
- Typel, S.; Wolter, H.H. Relativistic mean field calculations with density-dependent meson-nucleon coupling. Nucl. Phys. A 1999, 656, 331–364. [Google Scholar] [CrossRef]
- Hofmann, F.; Keil, C.M.; Lenske, H. Application of the density dependent hadron field theory to neutron star matter. Phys. Rev. C 2001, 64, 025804. [Google Scholar] [CrossRef]
- Li, B.A.; Chen, L.W.; Ko, C.M. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys. Rep. 2008, 464, 113–281. [Google Scholar] [CrossRef]
- Drago, A.; Lavagno, A.; Pagliara, G. Can very compact and very massive neutron stars both exist? Phys. Rev. D 2014, 89, 043014. [Google Scholar] [CrossRef]
- Drago, A.; Lavagno, A.; Pagliara, G.; Pigato, D. Early appearance of Δ isobars in neutron stars. Phys. Rev. C 2014, 90, 065809. [Google Scholar] [CrossRef]
- Cai, B.J.; Fattoyev, F.J.; Li, B.A.; Newton, W.G. Critical density and impact of Δ (1232 ) resonance formation in neutron stars. Phys. Rev. C 2015, 92, 015802. [Google Scholar] [CrossRef]
- Glendenning, N.K. Neutron stars are giant hypernuclei? Astrophys. J. 1985, 293, 470–493. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Weber, F. Competition between delta isobars and hyperons and properties of compact stars. Phys. Lett. B 2018, 783, 234–240. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A. Implications from GW170817 for Δ-isobar Admixed Hypernuclear Compact Stars. Astrophys. J. Lett. 2019, 874, L22. [Google Scholar] [CrossRef]
- Sedrakian, A.; Weber, F.; Li, J.J. Confronting GW190814 with hyperonization in dense matter and hypernuclear compact stars. arXiv 2020, arXiv:2007.09683. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A. Constraining compact star properties with nuclear saturation parameters. Phys. Rev. C 2019, 100, 015809. [Google Scholar] [CrossRef]
- Tolos, L.; Centelles, M.; Ramos, A. The Equation of State for the Nucleonic and Hyperonic Core of Neutron Stars. Publ. Astron. Soc. Aust. 2017, 34, e065. [Google Scholar] [CrossRef]
- Sinha, M.; Mukhopadhyay, B.; Sedrakian, A. Hypernuclear matter in strong magnetic field. Nucl. Phys. A 2013, 898, 43–58. [Google Scholar] [CrossRef]
- De Paoli, M.G.; Castro, L.B.; Menezes, D.P.; Barros, C.C.J. Rarita-Schwinger particles under the influence of strong magnetic fields. J. Phys. G Nucl. Phys. 2013, 40, 055007. [Google Scholar] [CrossRef]
- Lalazissis, G.A.; Nikšić, T.; Vretenar, D.; Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleon couplings. Phys. Rev. C 2005, 71, 024312. [Google Scholar] [CrossRef]
- Banik, S.; Bandyopadhyay, D. Third family of superdense stars in the presence of antikaon condensates. Phys. Rev. C 2001, 64, 055805. [Google Scholar] [CrossRef]
- Li, J.J.; Long, W.H.; Sedrakian, A. Hypernuclear stars from relativistic Hartree-Fock density functional theory. Eur. Phys. J. A 2018, 54, 133. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).