Critical Behavior of (2 + 1)-Dimensional QED: 1/N Expansion
Abstract
1. Introduction
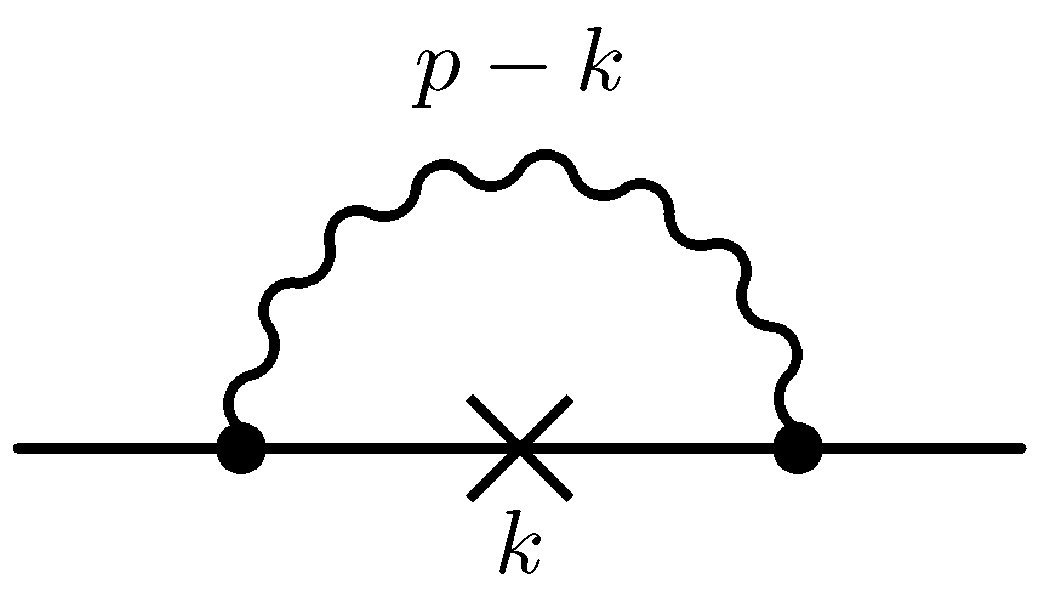
2. SD Equations
3. LO
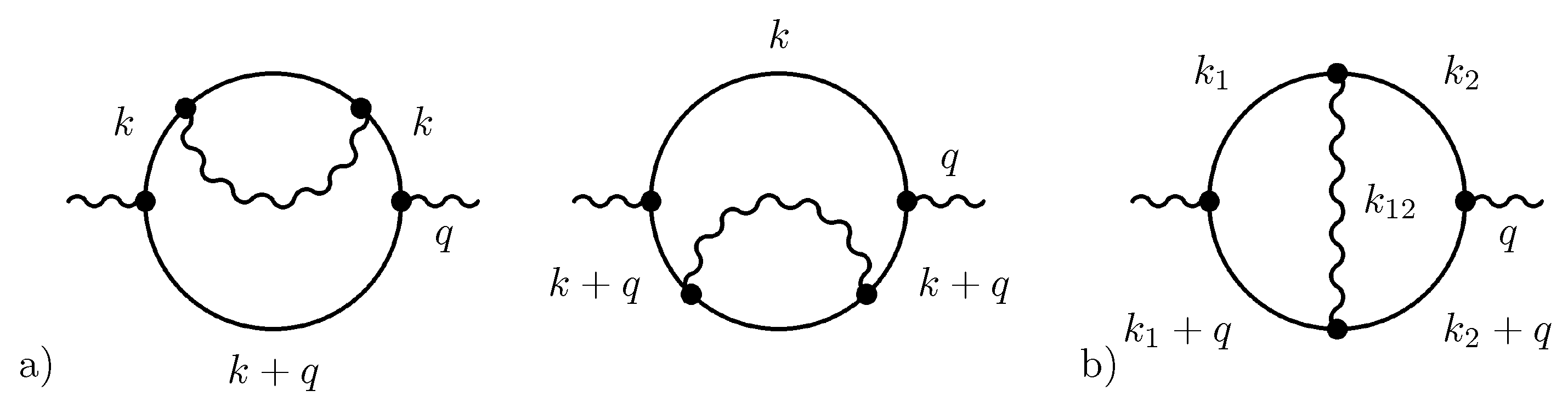
4. NLO
4.1. Extraction of the Most “Important” Terms
4.2. Gap Equation
4.3. Resummation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kotikov, A.V.; Shilin, V.I.; Teber, S. Critical behavior of (2 + 1)-dimensional QED: 1/Nf corrections in the Landau gauge. Phys. Rev. D 2016, 94, 056009. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Teber, S. Critical behavior of (2 + 1)-dimensional QED: 1/Nf corrections in an arbitrary nonlocal gauge. Phys. Rev. D 2016, 94, 114011. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Teber, S. Critical behaviour of (2 + 1)-dimensional QED: 1/N-corrections. EPJ Web Conf. 2017, 138, 06005. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Teber, S. Critical Behaviour of (2 + 1)-Dimensional QED: 1/N-Corrections; Preprint DESY-PROC-2016-04; EDP Sciences: Les Ulis, France, 2016. [Google Scholar]
- Teber, S. Field theoretic study of electron-electron interaction effects in Dirac liquids. arXiv 2018, arXiv:1810.08428. [Google Scholar]
- Appelquist, T.; Nash, D.; Wijewardhana, L.C.R. Critical Behavior in (2 + 1)-Dimensional QED. Phys. Rev. Lett. 1988, 60, 2575. [Google Scholar] [CrossRef]
- Appelquist, T.; Pisarski, R. High-Temperature Yang-Mills Theories and Three-Dimensional Quantum Chromodynamics. Phys. Rev. D 1981, 23, 2305. [Google Scholar] [CrossRef]
- Jackiw, R.; Templeton, S. How Superrenormalizable Interactions Cure their Infrared Divergences. Phys. Rev. D 1981, 23, 2291. [Google Scholar] [CrossRef]
- Appelquist, T.; Heinz, U. Three-dimensional O(n) Theories At Large Distances. Phys. Rev. D 1981, 24, 2169. [Google Scholar] [CrossRef]
- Pisarski, R. Chiral Symmetry Breaking in Three-Dimensional Electrodynamics. Phys. Rev. D 1984, 29, 2423. [Google Scholar] [CrossRef]
- Pennington, M.R.; Walsh, D. Masses from nothing: A Nonperturbative study of QED in three-dimensions. Phys. Lett. B 1991, 253, 246. [Google Scholar] [CrossRef]
- Curtis, D.C.; Pennington, M.R.; Walsh, D. Dynamical mass generation in QED in three-dimensions and the 1/N expansion. Phys. Lett. B 1992, 295, 313. [Google Scholar] [CrossRef]
- Pisarski, R. Fermion mass in three-dimensions and the renormalization group. Phys. Rev. D 1991, 44, 1866. [Google Scholar] [CrossRef]
- Azcoiti, V.; Luo, X.Q. (2 + 1)-dimensional compact QED with dynamical Fermions. Nucl. Phys. Proc. Suppl. 1993, 30, 741. [Google Scholar] [CrossRef]
- Azcoiti, V.; Laliena, V.; Luo, X.Q. Investigation of spontaneous symmetry breaking from a nonstandard approach. Nucl. Phys. Proc. Suppl. 1996, 47, 565. [Google Scholar] [CrossRef]
- Atkinson, D.; Johnson, P.W.; Maris, P. Dynamical Mass Generation in QED in Three-dimensions: Improved Vertex Function. Phys. Rev. D 1990, 42, 602. [Google Scholar] [CrossRef]
- Karthik, N.; Narayanan, R. No evidence for bilinear condensate in parity-invariant three-dimensional QED with massless fermions. Phys. Rev. D 2016, 93, 045020. [Google Scholar] [CrossRef]
- Karthik, N.; Narayanan, R. Scale-invariance of parity-invariant three-dimensional QED. Phys. Rev. D 2016, 94, 065026. [Google Scholar] [CrossRef]
- Appelquist, T.; Cohen, A.; Schmaltz, V. A New constraint on strongly coupled gauge theories. Phys. Rev. D 1999, 60, 045003. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R.; Tarnopolsky, G. Conformal QEDd, F-Theorem and the ϵ-Expansion. J. Phys. A 2016, 49, 135403. [Google Scholar] [CrossRef]
- Di Pietro, L.; Komargodski, Z.; Shamir, I.; Stamou, T. Quantum Electrodynamics in d=3 from the ϵ Expansion. Phys. Rev. Lett. 2016, 116, 131601. [Google Scholar] [CrossRef]
- Dagotto, E.; Kocic, A.; Kogut, J.B. A Computer Simulation of Chiral Symmetry Breaking in (2 + 1)-Dimensional QED with N Flavors. Phys. Rev. Lett. 1989, 62, 1083. [Google Scholar] [CrossRef]
- Dagotto, E.; Kocic, A.; Kogut, J.B. Chiral Symmetry Breaking in Three-dimensional QED With N(f) Flavors. Nucl. Phys. B 1990, 334, 279. [Google Scholar] [CrossRef]
- Hands, S.J.; Kogut, J.B.; Scorzato, L.; Strouthos, C.G. Non-compact QED(3) with N(f) = 1 and N(f)= 4. Phys. Rev. B 2004, 70, 104501. [Google Scholar] [CrossRef]
- Strouthos, C.; Kogut, J.B. The Phases of Non-Compact QED(3). arXiv 2007, arXiv:0804.0300. [Google Scholar]
- Nash, D. Higher Order Corrections in (2 + 1)-Dimensional QED. Phys. Rev. Lett. 1989, 62, 3024. [Google Scholar] [CrossRef]
- Kotikov, A.V. The Critical Behavior of (2 + 1)-Dimensional QED. JETP Lett. 1993, 58, 734. [Google Scholar] [CrossRef]
- Kotikov, A.V. On the Critical Behavior of (2 + 1)-Dimensional QED. Phys. Atom. Nucl. 2012, 75, 890. [Google Scholar] [CrossRef][Green Version]
- Gusynin, V.P.; Pyatkovskiy, P.K. Critical number of fermions in three-dimensional QED. Phys. Rev. D 2016, 94, 125009. [Google Scholar] [CrossRef]
- Herbut, I.F. Chiral symmetry breaking in three-dimensional quantum electrodynamics as fixed point annihilation. Phys. Rev. D 2016, 94, 025036. [Google Scholar] [CrossRef]
- Bashir, A.; Raya, A.; Sanchez-Madrigal, S.; Roberts, C.D. Gauge invariance of a critical number of flavours in QED3. Few Body Syst. 2009, 46, 229. [Google Scholar] [CrossRef]
- Marston, J.B.; Affleck, I. Large-n limit of the Hubbard-Heisenberg model. Phys. Rev. B 1989, 16, 11538. [Google Scholar] [CrossRef]
- Ioffe, L.B.; Larkin, A.I. Gapless fermions and gauge fields in dielectrics. Phys. Rev. B 1989, 13, 8988. [Google Scholar] [CrossRef]
- Semenoff, G.W. Condensed Matter Simulation of a Three-dimensional Anomaly. Phys. Rev. Lett. 1984, 53, 2449. [Google Scholar] [CrossRef]
- Wallace, P.R. The Band Theory of Graphite. Phys. Rev. 1947, 71, 622. [Google Scholar] [CrossRef]
- Simmons, E.H. Comment on Higher Order Corrections in (2 + 1)-dimensional QED. Phys. Rev. D 1990, 42, 2933. [Google Scholar] [CrossRef]
- Kugo, T.; Mitchard, M.G. The Chiral Ward-Takahashi identity in the ladder approximation. Phys. Lett. B 1992, 282, 162. [Google Scholar] [CrossRef]
- Ahmad, A.; Cobos-Martinez, J.J.; Concha-Sanchez, Y.; Raya, A. Landau-Khalatnikov-Fradkin transformations in Reduced Quantum Electrodynamics. Phys. Rev. D 2016, 93, 094035. [Google Scholar] [CrossRef]
- James, A.; Kotikov, A.V.; Teber, S. Landau-Khalatnikov-Fradkin transformation of the fermion propagator in massless reduced QED. Phys. Rev. D 2020, 101, 045011. [Google Scholar] [CrossRef]
- Ball, J.S.; Chiu, T.W. Analytic Properties of the Vertex Function in Gauge Theories. 1. Phys. Rev. D 1980, 22, 2542. [Google Scholar] [CrossRef]
- Kazakov, D.I. The Method Of Uniqueness, A New Powerful Technique For Multiloop Calculations. Phys. Lett. B 1983, 133, 406. [Google Scholar] [CrossRef]
- Kazakov, D.I. Analytical Methods for Multiloop Calculations: Two Lectures on the Method of Uniqueness; Preprint JINR E2-84-410; JINR Publishing Department: Dubna, Russia, 1984. [Google Scholar]
- Teber, S.; Kotikov, A.V. The method of uniqueness and the optical conductivity of graphene: New application of a powerful technique for multiloop calculations. Theor. Math. Phys. 2017, 190, 446. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Teber, S. Multi-loop techniques for massless Feynman diagram calculations. Phys. Part. Nucl. 2019, 50, 1. [Google Scholar] [CrossRef]
- Kotikov, A.V. The Gegenbauer polynomial technique: The Evaluation of a class of Feynman diagrams. Phys. Lett. B 1996, 375, 240. [Google Scholar] [CrossRef][Green Version]
- Gracey, J.A. Computation of critical exponent eta at O(1/N(f)**2) in quantum electrodynamics in arbitrary dimensions. Nucl. Phys. B 1994, 414, 614. [Google Scholar] [CrossRef]
- Fischer, C.S.; Alkofer, R.; Dahm, T.; Maris, P. Dynamical chiral symmetry breaking in unquenched QED(3). Phys. Rev. D 2004, 70, 073007. [Google Scholar] [CrossRef]
- Teber, S. Electromagnetic current correlations in reduced quantum electrodynamics. Phys. Rev. D 2012, 86, 025005. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Teber, S. Note on an application of the method of uniqueness to reduced quantum electrodynamics. Phys. Rev. D 2013, 87, 087701. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Hams, A.H.; Reenders, M. Nonperturbative infrared dynamics of three-dimensional QED with four fermion interaction. Phys. Rev. D 2001, 63, 045025. [Google Scholar] [CrossRef]
- Gracey, J.A. Electron mass anomalous dimension at O(1/(Nf(2)) in quantum electrodynamics. Phys. Lett. B 1993, 317, 415. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Teber, S. Two-loop fermion self-energy in reduced quantum electrodynamics and application to the ultrarelativistic limit of graphene. Phys. Rev. D 2014, 89, 065038. [Google Scholar] [CrossRef]
- Teber, S. Two-loop fermion self-energy and propagator in reduced QED3,2. Phys. Rev. D 2014, 89, 067702. [Google Scholar] [CrossRef]
- Teber, S.; Kotikov, A.V. Field theoretic renormalization study of reduced quantum electrodynamics and applications to the ultrarelativistic limit of Dirac liquids. Phys. Rev. D 2018, 97, 074004. [Google Scholar] [CrossRef]
- Gorbar, E.V.; Gusynin, V.P.; Miransky, V.P. Dynamical chiral symmetry breaking on a brane in reduced QED. Phys. Rev. D 2001, 64, 105028. [Google Scholar] [CrossRef]
- Marino, E.C. Quantum electrodynamics of particles on a plane and the Chern-Simons theory. Nucl. Phys. B 1993, 408, 551. [Google Scholar] [CrossRef]
- Dorey, N.; Mavromatos, N.E. QED in three-dimension and two-dimensional superconductivity without parity violation. Nucl. Phys. B 1992, 386, 614. [Google Scholar] [CrossRef]
- Kovner, A.; Rosenstein, B. Kosterlitz-Thouless mechanism of two-dimensional superconductivity. Phys. Rev. D 1990, 42, 4748. [Google Scholar] [CrossRef]
- Teber, S.; Kotikov, A.V. Review of Electron-Electron Interaction Effects in Planar Dirac Liquids. Theor. Math. Phys. 2019, 200, 1222. [Google Scholar] [CrossRef]
- Kotov, V.N.; Uchoa, B.; Pereira, V.M.; Castro Neto, A.H.; Guinea, F. Electron-Electron Interactions in Graphene: Current Status and Perspectives. Rev. Mod. Rev. 2012, 84, 1067. [Google Scholar] [CrossRef]
- Miransky, V.A.; Shovkovy, I.A. Quantum field theory in a magnetic field: From quantum chromodynamics to graphene and Dirac semimetals. Phys. Rep. 2015, 576, 1–209. [Google Scholar] [CrossRef]
- Gusynin, V.P. Graphene and quantum electrodynamics. Probl. Atomic Sci. Technol. 2013, N3, 29. [Google Scholar]
- Kotikov, A.V.; Teber, S. Critical behaviour of reduced QED4,3 and dynamical fermion gap generation in graphene. Phys. Rev. D 2016, 94, 114010. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotikov, A.V.; Teber, S. Critical Behavior of (2 + 1)-Dimensional QED: 1/N Expansion. Particles 2020, 3, 345-354. https://doi.org/10.3390/particles3020026
Kotikov AV, Teber S. Critical Behavior of (2 + 1)-Dimensional QED: 1/N Expansion. Particles. 2020; 3(2):345-354. https://doi.org/10.3390/particles3020026
Chicago/Turabian StyleKotikov, Anatoly V., and Sofian Teber. 2020. "Critical Behavior of (2 + 1)-Dimensional QED: 1/N Expansion" Particles 3, no. 2: 345-354. https://doi.org/10.3390/particles3020026
APA StyleKotikov, A. V., & Teber, S. (2020). Critical Behavior of (2 + 1)-Dimensional QED: 1/N Expansion. Particles, 3(2), 345-354. https://doi.org/10.3390/particles3020026





