Gluon Propagators in QC2D at High Baryon Density
Abstract
1. Introduction
2. Lattice Setup
3. Gluon Propagators and Screening Masses
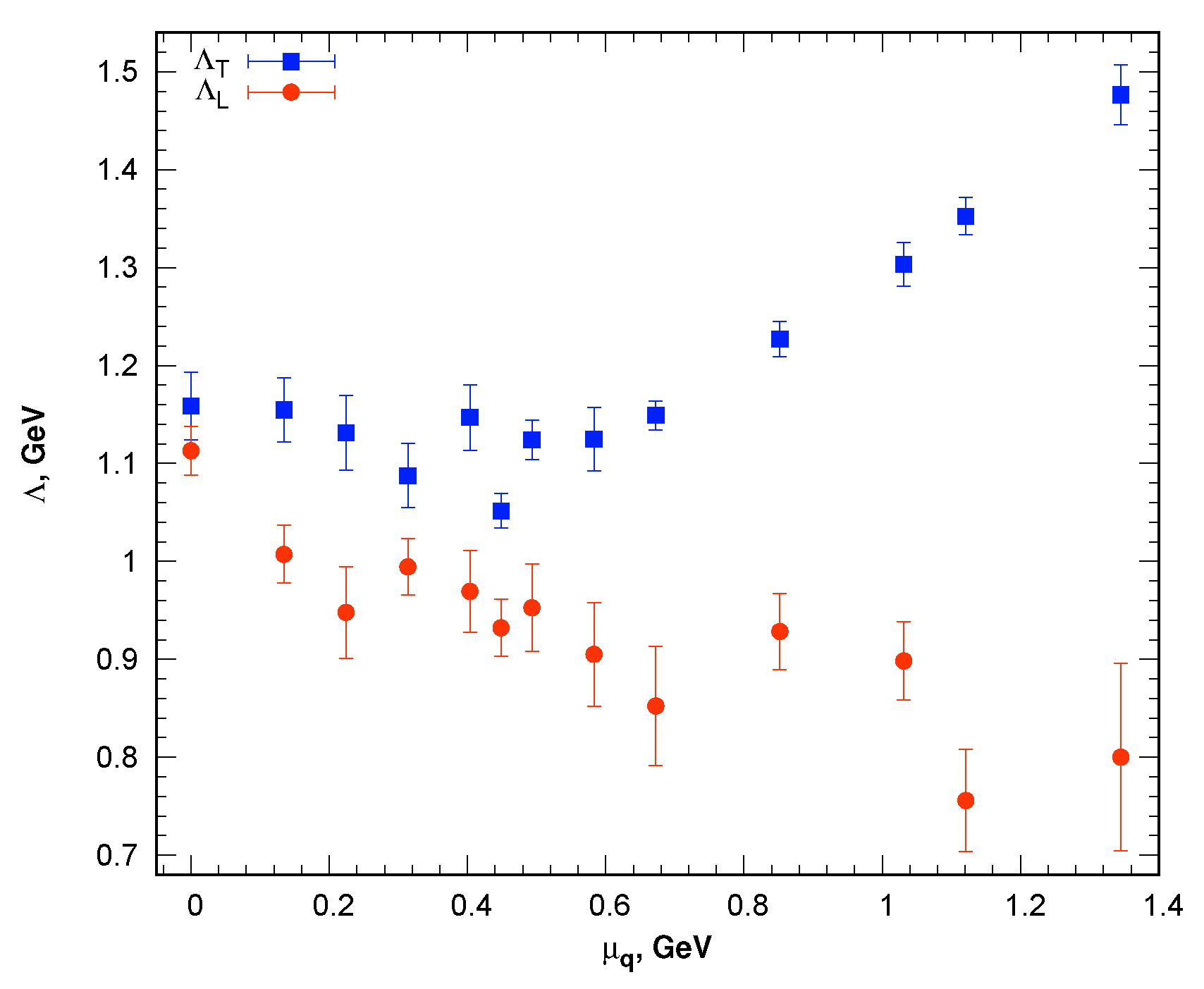
3.1. Definition of the Screening Mass
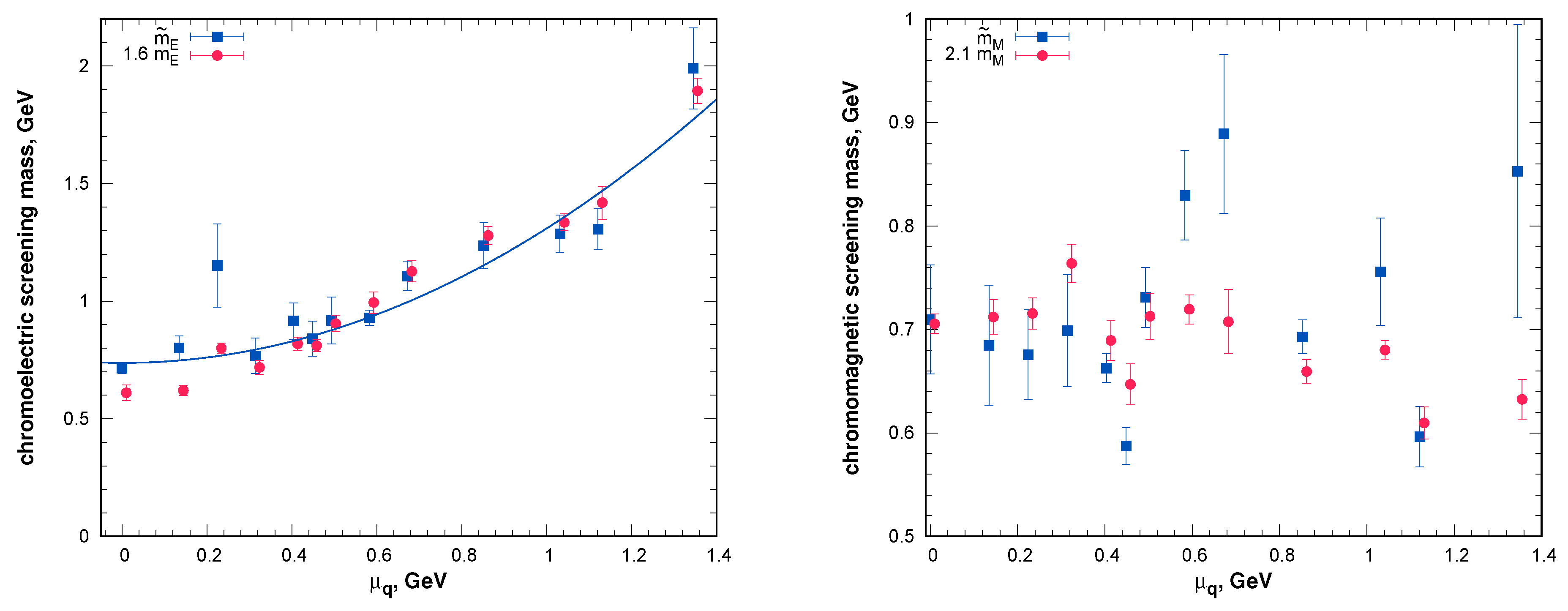
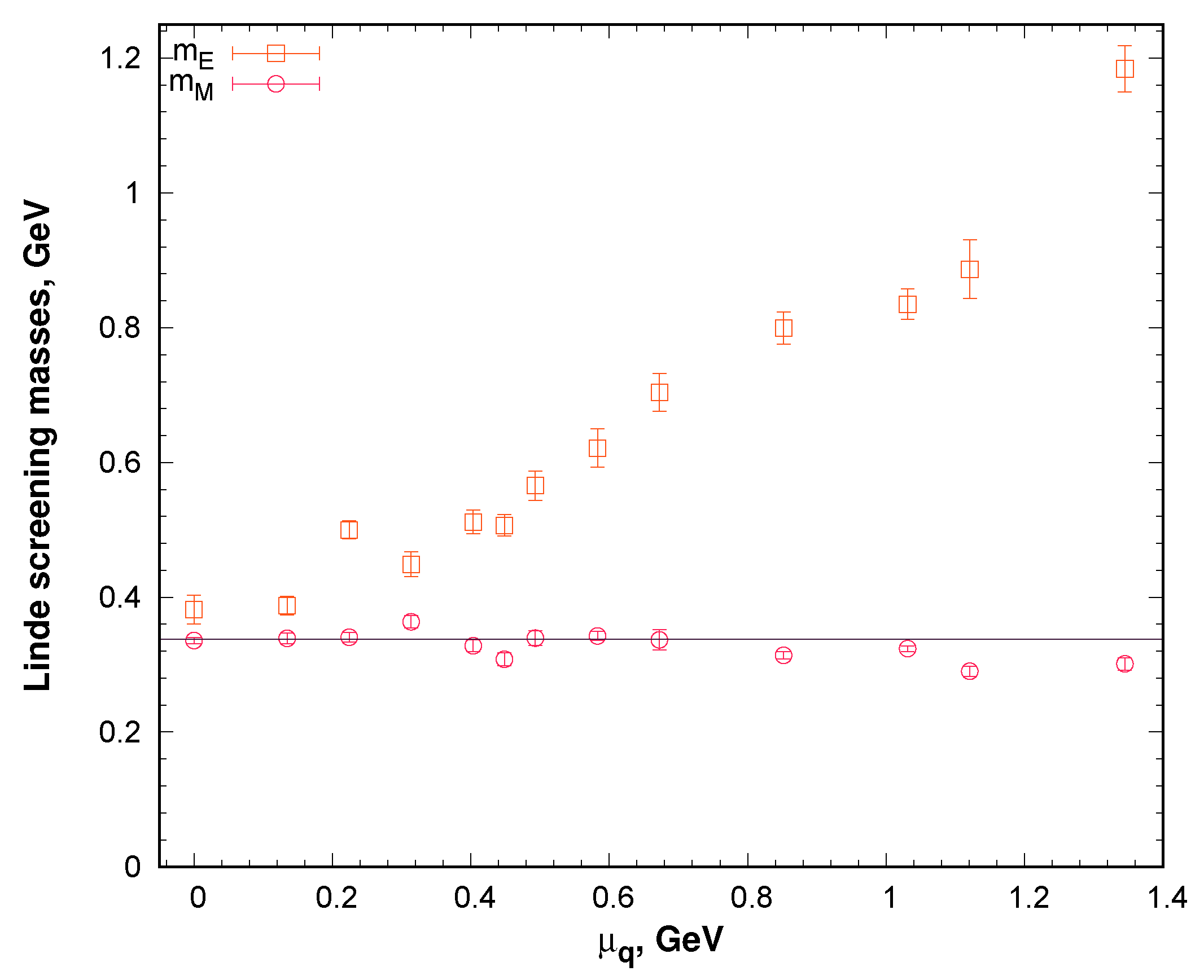
3.2. Screening Masses in QCD
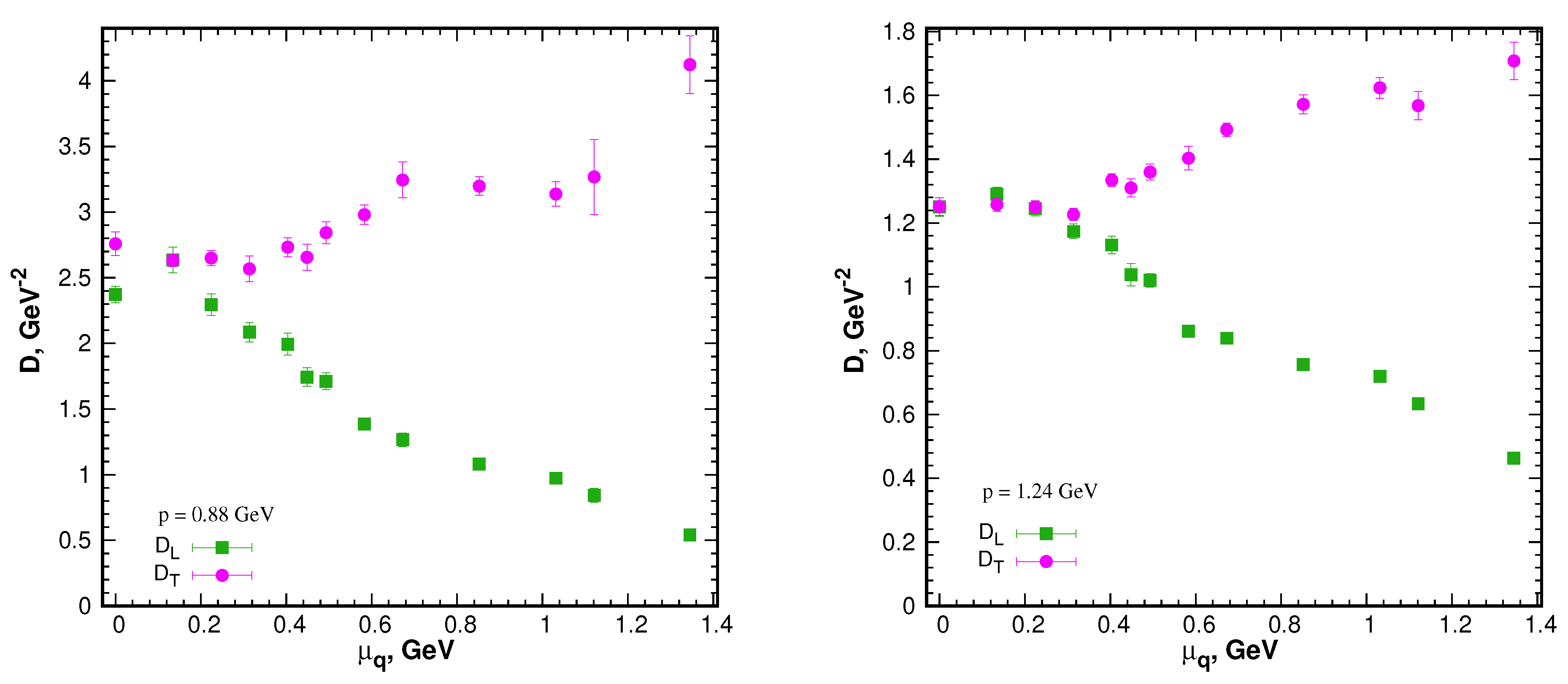
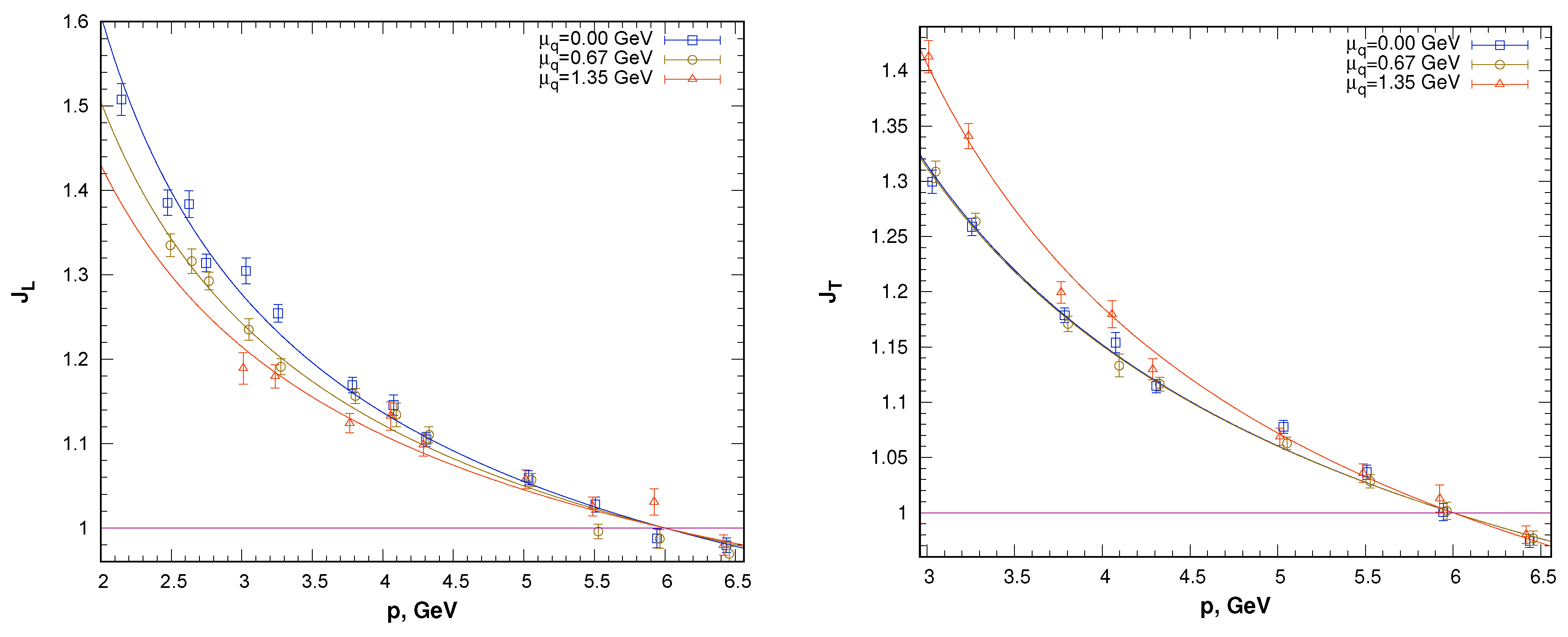
4. Perturbative Behavior at High Momenta and Chemical Potentials
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kogut, J.B.; Stephanov, M.A.; Toublan, D.; Verbaarschot, J.J.M.; Zhitnitsky, A. QCD—Like theories at finite baryon density. Nucl. Phys. B 2000, 582, 477. [Google Scholar] [CrossRef]
- Splittorff, K.; Toublan, D.; Verbaarschot, J.J.M. Diquark condensate in QCD with two colors at next-to-leading order. Nucl. Phys. B 2002, 620, 290. [Google Scholar] [CrossRef]
- Kanazawa, T.; Wettig, T.; Yamamoto, N. Chiral Lagrangian and spectral sum rules for dense two-color QCD. JHEP 2009, 908, 003. [Google Scholar] [CrossRef]
- Brauner, T.; Fukushima, K.; Hidaka, Y. Two-color quark matter: U(1)(A) restoration, superfluidity, and quarkyonic phase. Phys. Rev. D 2009, 80, 074035, Erratum: [Phys. Rev. D 2010, 81, 119904]. [Google Scholar] [CrossRef]
- Sun, G.f.; He, L.; Zhuang, P. BEC-BCS crossover in the Nambu-Jona-Lasinio model of QCD. Phys. Rev. D 2007, 75, 096004. [Google Scholar] [CrossRef]
- He, L. Nambu-Jona-Lasinio model description of weakly interacting Bose condensate and BEC-BCS crossover in dense QCD-like theories. Phys. Rev. D 2010, 82, 096003. [Google Scholar] [CrossRef]
- Strodthoff, N.; Schaefer, B.J.; von Smekal, L. Quark-meson-diquark model for two-color QCD. Phys. Rev. D 2012, 85, 074007. [Google Scholar] [CrossRef]
- Strodthoff, N.; von Smekal, L. Polyakov-Quark-Meson-Diquark Model for two-color QCD. Phys. Lett. B 2014, 731, 350. [Google Scholar] [CrossRef]
- Vanderheyden, B.; Jackson, A.D. Random matrix study of the phase structure of QCD with two colors. Phys. Rev. D 2001, 64, 074016. [Google Scholar] [CrossRef]
- Kanazawa, T.; Wettig, T.; Yamamoto, N. Singular values of the Dirac operator in dense QCD-like theories. JHEP 2011, 1112, 007. [Google Scholar] [CrossRef]
- Hands, S.; Kogut, J.B.; Lombardo, M.P.; Morrison, S.E. Symmetries and spectrum of SU(2) lattice gauge theory at finite chemical potential. Nucl. Phys. B 1999, 558, 327. [Google Scholar] [CrossRef]
- Kogut, J.B.; Sinclair, D.K.; Hands, S.J.; Morrison, S.E. Two color QCD at nonzero quark number density. Phys. Rev. D 2001, 64, 094505. [Google Scholar] [CrossRef]
- Kogut, J.B.; Toublan, D.; Sinclair, D.K. Diquark condensation at nonzero chemical potential and temperature. Phys. Lett. B 2001, 514, 77. [Google Scholar] [CrossRef][Green Version]
- Kogut, J.B.; Toublan, D.; Sinclair, D.K. The Phase diagram of four flavor SU(2) lattice gauge theory at nonzero chemical potential and temperature. Nucl. Phys. B 2002, 642, 181. [Google Scholar] [CrossRef][Green Version]
- Braguta, V.V.; Ilgenfritz, E.; Kotov, A.Y.; Molochkov, A.V.; Nikolaev, A.A. Study of the phase diagram of dense two-color QCD within lattice simulation. Phys. Rev. D 2016, 94, 114510. [Google Scholar] [CrossRef]
- Bornyakov, V.G.; Braguta, V.V.; Ilgenfritz, E.-M.; Kotov, A.Y.; Molochkov, A.V.; Nikolaev, A.A. Observation of deconfinement in a cold dense quark medium. JHEP 2018, 1803, 161. [Google Scholar] [CrossRef]
- Astrakhantsev, N.Y.; Bornyakov, V.G.; Braguta, V.V.; Ilgenfritz, E.; Kotov, A.Y.; Nikolaev, A.A.; Rothkopf, A. Lattice study of static quark-antiquark interactions in dense quark matter. JHEP 2019, 1905, 171. [Google Scholar] [CrossRef]
- Wilhelm, J.; Holicki, L.; Smith, D.; Wellegehausen, B.; von Smekal, L. Continuum Goldstone spectrum of two-color QCD at finite density with staggered quarks. Phys. Rev. D 2019, 100, 114507. [Google Scholar] [CrossRef]
- Nakamura, A. Quarks and Gluons at Finite Temperature and Density. Phys. Lett. 1984, 149B, 391. [Google Scholar] [CrossRef]
- Hands, S.; Kim, S.; Skullerud, J.I. Deconfinement in dense 2-color QCD. Eur. Phys. J. C 2006, 48, 193. [Google Scholar] [CrossRef]
- Hands, S.; Kim, S.; Skullerud, J.I. A Quarkyonic Phase in Dense Two Color Matter? Phys. Rev. D 2010, 81, 091502. [Google Scholar] [CrossRef]
- Hands, S.; Kenny, P.; Kim, S.; Skullerud, J.I. Lattice Study of Dense Matter with Two Colors and Four Flavors. Eur. Phys. J. A 2011, 47, 60. [Google Scholar] [CrossRef][Green Version]
- Cotter, S.; Giudice, P.; Hands, S.; Skullerud, J.I. Towards the phase diagram of dense two-color matter. Phys. Rev. D 2013, 87, 034507. [Google Scholar] [CrossRef]
- Boz, T.; Hajizadeh, O.; Maas, A.; Skullerud, J.I. Finite-density gauge correlation functions in QC2D. Phys. Rev. D 2019, 99, 074514. [Google Scholar] [CrossRef]
- Maris, P.; Roberts, C.D. Dyson-Schwinger equations: A Tool for hadron physics. Int. J. Mod. Phys. 2003, E12, 297–365. [Google Scholar] [CrossRef]
- Fischer, C.S. Infrared properties of QCD from Dyson-Schwinger equations. J. Phys. 2006, G32, R253–R291. [Google Scholar] [CrossRef]
- Eichmann, G.; Sanchis-Alepuz, H.; Williams, R.; Alkofer, R.; Fischer, C.S. Baryons as relativistic three-quark bound states. Prog. Part. Nucl. Phys. 2016, 91, 1–100. [Google Scholar] [CrossRef]
- Biernat, E.P.; Gross, F.; Peña, M.T.A.; Leitão, S. Quark mass function from a one-gluon-exchange-type interaction in Minkowski space. Phys. Rev. 2018, D98, 114033. [Google Scholar] [CrossRef]
- Boz, T.; Cotter, S.; Fister, L.; Mehta, D.; Skullerud, J.-I. Phase transitions and gluodynamics in 2-colour matter at high density. Eur. Phys. J. 2013, 87, 1303–3223. [Google Scholar] [CrossRef]
- Hajizadeh, O.; Boz, T.; Maas, A.; Skullerud, J.-I. Gluon and ghost correlation functions of 2-color QCD at finite density. EPJ Web Conf. 2018, 175, 07012. [Google Scholar] [CrossRef]
- Weisz, P. Continuum Limit Improved Lattice Action for Pure Yang-Mills Theory. 1. Nucl. Phys. B 1983, 212, 1. [Google Scholar] [CrossRef]
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; DeTar, C.; Ding, H.T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; et al. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Mandula, J.E.; Ogilvie, M. The Gluon Is Massive: A Lattice Calculation of the Gluon Propagator in the Landau Gauge. Phys. Lett. 1987, B185, 127. [Google Scholar] [CrossRef]
- Bornyakov, V.G.; Mitrjushkin, V.K.; Muller-Preussker, M. SU(2) lattice gluon propagator: Continuum limit, finite-volume effects and infrared mass scale m(IR). Phys. Rev. D 2010, 81, 054503. [Google Scholar] [CrossRef]
- Kapusta, J.I.; Gale, C. Finite-Temperature Field Theory: Principles and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Bornyakov, V.G.; Mitrjushkin, V.K. SU(2) lattice gluon propagators at finite temperatures in the deep infrared region and Gribov copy effects. Phys. Rev. D 2011, 84, 094503. [Google Scholar] [CrossRef]
- Dudal, D.; Oliveira, O.; Silva, P.J. High precision statistical Landau gauge lattice gluon propagator computation vs. the Gribov–Zwanziger approach. Ann. Phys. 2018, 397, 351. [Google Scholar] [CrossRef]
- Linde, A.D. Infrared Problem in Thermodynamics of the Yang-Mills Gas. Phys. Lett. 1980, 96B, 289. [Google Scholar] [CrossRef]
- Maas, A. Describing gauge bosons at zero and finite temperature. Phys. Rep. 2013, 524, 203. [Google Scholar] [CrossRef]
- Bornyakov, V.G.; Mitrjushkin, V.K.; Muller-Preussker, M. Infrared Behavior and Gribov Ambiguity in SU(2) Lattice Gauge Theory. arXiv 2009, arXiv:0812.2761. [Google Scholar]
- Bogolubsky, I.L.; Bornyakov, V.G.; Burgio, G.; Ilgenfritz, E.M.; Muller-Preussker, M.; Mitrjushkin, V.K. Improved Landau gauge fixing and the suppression of finite-volume effects of the lattice gluon propagator. Phys. Rev. D 2008, 77, 014504, Erratum: [Phys. Rev. D 2008, 77, 039902]. [Google Scholar] [CrossRef]
- Bornyakov, V.G.; Mitrjushkin, V.K. Lattice QCD gluon propagators near transition temperature. Int. J. Mod. Phys. 2012, A27, 1250050. [Google Scholar] [CrossRef]
- Son, D.T. Superconductivity by long range color magnetic interaction in high density quark matter. Phys. Rev. 1999, D59, 094019. [Google Scholar] [CrossRef]
- Politzer, H.D. Asymptotic Freedom: An Approach to Strong Interactions. Phys. Rep. 1974, 14, 129. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bornyakov, V.; Kotov, A.; Nikolaev, A.; Rogalyov, R. Gluon Propagators in QC2D at High Baryon Density. Particles 2020, 3, 308-319. https://doi.org/10.3390/particles3020023
Bornyakov V, Kotov A, Nikolaev A, Rogalyov R. Gluon Propagators in QC2D at High Baryon Density. Particles. 2020; 3(2):308-319. https://doi.org/10.3390/particles3020023
Chicago/Turabian StyleBornyakov, Vitaly, Andrey Kotov, Aleksandr Nikolaev, and Roman Rogalyov. 2020. "Gluon Propagators in QC2D at High Baryon Density" Particles 3, no. 2: 308-319. https://doi.org/10.3390/particles3020023
APA StyleBornyakov, V., Kotov, A., Nikolaev, A., & Rogalyov, R. (2020). Gluon Propagators in QC2D at High Baryon Density. Particles, 3(2), 308-319. https://doi.org/10.3390/particles3020023




