Heavy Baryon Spectroscopy in the Relativistic Quark Model

Abstract

Masses of heavy baryons are calculated in the framework of the relativistic quark-diquark picture and QCD. The obtained results are in good agreement with available experimental data including recent measurements by the LHCb Collaboration. Possible quantum numbers of excited heavy baryon states are discussed.

1. Introduction

Recently, significant experimental progress has been achieved in studying heavy baryon spectroscopy. Many new heavy baryon states have been observed. The main contribution was made by the LHCb Collaboration. Thus, last year the amplitude analysis of the decay ${\Lambda }_b^0\to D^{0}p{\pi }^{-}$ was performed in the region of the phase space containing $D^{0}p$ resonant contributions which revealed three ${\Lambda }_c$ excited states and allowed precise measurement of their masses and decay widths [1]—the ${\Lambda }_c{\left(2880\right)}^{+}$ with the preferred spin $J=5/2$;—the new state ${\Lambda }_c{\left(2860\right)}^{+}$ with quantum numbers $J^P=3/2^{+}$, its parity was measured relative to that of the ${\Lambda }_c{\left(2880\right)}^{+}$;—the ${\Lambda }_c{\left(2940\right)}^{+}$ with the most likely spin-parity assignment $J^P=3/2^{-}$, but other solutions with spins from $1/2$ to $7/2$ were not excluded. Then five new, narrow excited ${\Omega }_c$ states decaying to ${\Xi }_c^{+}{K}^{-}$ were observed [2]—the ${\Omega }_c{\left(3000\right)}^0$, ${\Omega }_c{\left(3050\right)}^0$, ${\Omega }_c{\left(3066\right)}^0$, ${\Omega }_c{\left(3090\right)}^0$, and ${\Omega }_c{\left(3119\right)}^0$. These states were later confirmed by Belle [3]. Soon the discovery of the long-awaited doubly charmed baryon ${\Xi }_{cc}^{++}$ was reported [4,5]. In 2018, the new ${\Xi }_b{\left(6227\right)}^{-}$ resonance was observed as a peak in both the ${\Lambda }_b^0{K}^{-}$ and ${\Xi }_b^0{\pi }^{-}$ invariant mass spectra [6]. The first observation of two structures $\Sigma {\left(6097\right)}^{\pm }$, consistent with resonances in the final states ${\Lambda }_b^0{\pi }^{-}$ and ${\Lambda }_b^0{\pi }^{+}$ was reported by the LHCb [7] and two new resonances ${\Lambda }_b\left(6146\right)$ and ${\Lambda }_b\left(6152\right)$ were found in the ${\Lambda }_b^0{\pi }^{+}{\pi }^{-}$ system [8].

In this paper, we compare these new data with the predictions of the relativistic quark-diquark model of heavy baryons [9,10,11,12].

2. Relativistic Quark-Diquark Model of Heavy Baryons

Our approach is based on the relativistic quark-diquark picture and the quasipotential equation. The interaction of two quarks in a diquark and the quark-diquark interaction in a baryon are described by the diquark wave function ${\Psi }_d$ of the bound quark-quark state and by the baryon wave function ${\Psi }_B$ of the bound quark-diquark state respectively. These wave functions satisfy the relativistic quasipotential equation of the Schrödinger type [9,10]

$$\left(\frac{b^2\left(M\right)}{2{\mu }_R}-\frac{{\mathbf{p}}^2}{2{\mu }_R}\right){\Psi }_{d,B}\left(\mathbf{p}\right)=\int \frac{d^{3}q}{{\left(2\pi \right)}^3}V(\mathbf{p},\mathbf{q};M){\Psi }_{d,B}\left(\mathbf{q}\right),$$

(1)

where ${\mu }_R$ is the relativistic reduced mass, $b^2\left(M\right)$ is the center-of-mass relative momentum squared on the mass shell, $\mathbf{p},\mathbf{q}$ are the off-mass-shell relative momenta, and M is the bound state mass (diquark or baryon).

The kernel $V(\mathbf{p},\mathbf{q};M)$ in Equation (1) is the quasipotential operator of the quark-quark or quark-diquark interaction, which is constructed with the help of the off-mass-shell scattering amplitude, projected onto the positive energy states. We assume that the effective interaction is the sum of the usual one-gluon exchange term and the mixture of long-range vector and scalar linear confining potentials, where the vector confining potential contains the Pauli term. The vertex of the diquark-gluon interaction takes into account the diquark internal structure and effectively smears the Coulomb-like interaction. The corresponding form factor is expressed as an overlap integral of the diquark wave functions. Explicit expressions for the quasipotentials of the quark-quark interaction in a diquark and quark-diquark interaction in a baryon can be found in Reference [11]. All parameters of the model were fixed previously from considerations of meson properties and are kept fixed in the baryon spectrum calculations.

The quark-diquark picture of heavy baryons reduces a very complicated relativistic three-body problem to a significantly simpler two step two-body calculation. First we determine the properties of diquarks. We consider a diquark to be a composite $\left(q{q}^{\prime }\right)$ system. Thus diquark in our approach is not a point-like object. Its interaction with gluons is smeared by the form factor expressed through the overlap integral of diquark wave functions. These form factors enter the diquark-gluon interaction and effectively take diquark structure into account [11,12]. Note that the ground state diquark composed from quarks with different flavours can be both in scalar and axial vector state, while the ground state diquarks composed from quarks of the same flavour can be only in the axial vector state due to the Pauli principle. Solving the quasipotential equation numerically we calculate the masses, determine the diquark wave functions and use them for evaluation of the diquark form factors. Only ground-state scalar and axial vector diquarks are considered for heavy baryons. While both ground-state as well as orbital and radial excitations of heavy diquarks are necessary for doubly heavy baryons, since the lowest excitations of such baryons originate from the excitations of the doubly heavy diquark.

Next we calculate the masses of heavy baryons in the quark–diquark picture [11,12]. The heavy baryon is considered as a bound state of a heavy-quark and light-diquark. All excitations are assumed to occur between heavy quark and light diquark. On the other hand, the doubly heavy baryon is considered as a bound state of a light-quark and heavy-diquark. Both excitations in the quark-diquark system and excitations of the heavy diquark are taken into account. It is important to note that such approach predicts significantly less excited states of baryons compared to a genuine three-quark picture. We do not expand the potential of the quark–diquark interaction either in $p/m_{q,Q}$ or in $p/m_d$ and treat both diquark and quark fully relativistically.

3. Masses of Heavy Baryons

The calculated masses of heavy baryons are given in Table 1, Table 2, Table 3, Table 4 and Table 5. In the first column we show the baryon total isospin I, spin J and parity P. The second column lists the quark-diquark state. The next three columns refer to the charm and the last three columns to the bottom baryons. There we first give our prediction for the mass, then available experimental data [13]—baryon status and measured mass. For the status of the state we use the Particle Data Group (PDG) [13] star notations. With the number of the stars it ranges from * meaning “Evidence of existence is poor”, to **** meaning “Existence is certain, and properties are at least fairly explored”. The combined experimental error values are taken form PDGLive. The charm and bottom baryon states recently discovered by the LHCb Collaboration [1,2,4,5,6,7] are marked as new.

Table 1. Masses of the ${\Lambda }_Q$ ($Q=c,b$) heavy baryons (in MeV).

		$\mathit{Q}=\mathit{c}$			$\mathit{Q}=\mathit{b}$
$\mathit{I}\left({\mathit{J}}^{\mathit{P}}\right)$	$\mathit{Qd}$ State	M	Status	${\mathit{M}}^{\mathbf{exp}}$	M	Status	${\mathit{M}}^{\mathbf{exp}}$
$0\left({\frac{1}{2}}^{+}\right)$	$1S$	2286	****	2286.46(14)	5620	***	5619.51(23)
	$2S$	2769	*	2766.6(2.4)?	6089
	$3S$	3130			6455
	$4S$	3437			6756
	$5S$	3715			7015
	$6S$	3973			7256
$0\left({\frac{1}{2}}^{-}\right)$	$1P$	2598	***	2592.25(28)	5930	***	5912.11(26)
	$2P$	2983	***	2944.8${(}_{1.5}^{1.4})$?	6326
	$3P$	3303			6645
	$4P$	3588			6917
	$5P$	3852			7157
$0\left({\frac{3}{2}}^{-}\right)$	$1P$	2627	***	2628.1(6)	5942	***	5919.81(23)
	$2P$	3005			6333
	$3P$	3322			6651
	$4P$	3606			6922
	$5P$	3869			7171
$0\left({\frac{3}{2}}^{+}\right)$	$1D$	2874	new	2856.1${(}_{6.0}^{2.3})$	6190	new	6146.17(43)
	$2D$	3189			6526
	$3D$	3480			6811
	$4D$	3747			7060
$0\left({\frac{5}{2}}^{+}\right)$	$1D$	2880	***	2881.75(35)	6196	new	6152.51(38)
	$2D$	3209			6531
	$3D$	3500			6814
	$4D$	3767			7063
$0\left({\frac{5}{2}}^{-}\right)$	$1F$	3097			6408
	$2F$	3375			6705
	$3F$	3646			6964
	$4F$	3900			7196
$0\left({\frac{7}{2}}^{-}\right)$	$1F$	3078			6411
	$2F$	3393			6708
	$3F$	3667			6966
	$4F$	3922			7197
$0\left({\frac{7}{2}}^{+}\right)$	$1G$	3270			6598
	$2G$	3546			6867
$0\left({\frac{9}{2}}^{+}\right)$	$1G$	3284			6599
	$2G$	3564			6868
$0\left({\frac{9}{2}}^{-}\right)$	$1H$	3444			6767
$0\left({\frac{11}{2}}^{-}\right)$	$1H$	3460			6766

Table 2. Masses of the ${\Sigma }_Q$ ($Q=c,b$) heavy baryons (in MeV).

		$\mathit{Q}=\mathit{c}$			$\mathit{Q}=\mathit{b}$
$\mathit{I}\left({\mathit{J}}^{\mathit{P}}\right)$	$\mathit{Qd}$ State	M	Status	${\mathit{M}}^{\mathbf{exp}}$	M	Status	${\mathit{M}}^{\mathbf{exp}}$
$1\left({\frac{1}{2}}^{+}\right)$	$1S$	2443	****	2453.76(18)	5808	***	5807.8(2.7)
	$2S$	2901			6213
	$3S$	3271			6575
	$4S$	3581			6869
	$5S$	3861			7124
$1\left({\frac{3}{2}}^{+}\right)$	$1S$	2519	***	2518.0(5)	5834	***	5829.0(3.4)
	$2S$	2936	***	2939.3${(}_{1.5}^{1.4})$?	6226
	$3S$	3293			6583
	$4S$	3598			6876
	$5S$	3873			7129
$1\left({\frac{1}{2}}^{-}\right)$	$1P$	2799	***	2802(${}_7^4$)	6101
	$2P$	3172			6440
	$3P$	3488			6756
	$4P$	3770			7024
	$1P$	2713			6095
	$2P$	3125			6430
	$3P$	3455			6742
	$4P$	3743			7008
$1\left({\frac{3}{2}}^{-}\right)$	$1P$	2798	***	2802(${}_7^4$)	6096	new	6095.8(1.8)
	$2P$	3172			6430
	$3P$	3486			6742
	$4P$	3768			7009
	$1P$	2773	*	2766.6(2.4)?	6087
	$2P$	3151			6423
	$3P$	3469			6736
	$4P$	3753			7003
$1\left({\frac{5}{2}}^{-}\right)$	$1P$	2789			6084
	$2P$	3161			6421
	$3P$	3475			6732
	$4P$	3757			6999
$1\left({\frac{1}{2}}^{+}\right)$	$1D$	3041			6311
	$2D$	3370			6636
$1\left({\frac{3}{2}}^{+}\right)$	$1D$	3043			6326
	$2D$	3366			6647
	$1D$	3040			6285
	$2D$	3364			6612
$1\left({\frac{5}{2}}^{+}\right)$	$1D$	3038			6284
	$2D$	3365			6612
	$1D$	3023			6270
	$2D$	3349			6598
$1\left({\frac{7}{2}}^{+}\right)$	$1D$	3013			6260
	$2D$	3342			6590

Table 3. Masses of the ${\Xi }_Q$ ($Q=c,b$) heavy baryons with the scalar diquark (in MeV).

		$\mathit{Q}=\mathit{c}$			$\mathit{Q}=\mathit{b}$
$\mathit{I}\left({\mathit{J}}^{\mathit{P}}\right)$	$\mathit{Qd}$ State	M	Status	${\mathit{M}}^{\mathbf{exp}}$	M	Status	${\mathit{M}}^{\mathbf{exp}}$
$\frac{1}{2}\left({\frac{1}{2}}^{+}\right)$	$1S$	2476	***	2470.88${(}_{80}^{34})$	5803	***	5790.5(2.7)
	$2S$	2959			6266
	$3S$	3323			6601
	$4S$	3632			6913
	$5S$	3909			7165
$\frac{1}{2}\left({\frac{1}{2}}^{-}\right)$	$1P$	2792	***	2792.8(1.2)	6120
	$2P$	3179			6496
	$3P$	3500			6805
	$4P$	3785			7068
	$5P$	4048			7302
$\frac{1}{2}\left({\frac{3}{2}}^{-}\right)$	$1P$	2819	***	2820.22(32)	6130
	$2P$	3201			6502
	$3P$	3519			6810
	$4P$	3804			7073
	$5P$	4066			7306
$\frac{1}{2}\left({\frac{3}{2}}^{+}\right)$	$1D$	3059	***	3055.9(0.4)	6366
	$2D$	3388			6690
	$3D$	3678			6966
	$4D$	3945			7208
$\frac{1}{2}\left({\frac{5}{2}}^{+}\right)$	$1D$	3076	*	3079.9(1.4)	6373
	$2D$	3407			6696
	$3D$	3699			6970
	$4D$	3965			7212

Table 4. Masses of the ${\Xi }_Q$ ($Q=c,b$) heavy baryons with the axial vector diquark (in MeV).

		$\mathit{Q}=\mathit{c}$			$\mathit{Q}=\mathit{b}$
$\mathit{I}\left({\mathit{J}}^{\mathit{P}}\right)$	$\mathit{Qd}$ State	M	Status	${\mathit{M}}^{\mathbf{exp}}$	M	Status	${\mathit{M}}^{\mathbf{exp}}$
$\frac{1}{2}\left({\frac{1}{2}}^{+}\right)$	$1S$	2579	***	2577.9(2.9)	5936	***	5935.02(5)
	$2S$	2983		2971.4(3.3)	6329
	$3S$	3377			6687
	$4S$	3695			6978
	$5S$	3978			7229
$\frac{1}{2}\left({\frac{3}{2}}^{+}\right)$	$1S$	2649	***	2645.9(0.5)	5963	***	5955.33(13)
	$2S$	3026			6342
	$3S$	3396			6695
	$4S$	3709			6984
	$5S$	3989			7234
$\frac{1}{2}\left({\frac{1}{2}}^{-}\right)$	$1P$	2936	*	2931(6)	6233
	$2P$	3313			6611
	$3P$	3630			6915
	$4P$	3912			7174
	$1P$	2854			6227	new	6226.9(2.1)
	$2P$	3267			6604
	$3P$	3598			6906
	$4P$	3887			7164
$\frac{1}{2}\left({\frac{3}{2}}^{-}\right)$	$1P$	2935	*	2931(6)	6234
	$2P$	3311			6605
	$3P$	3628			6905
	$4P$	3911			7163
	$1P$	2912			6224	new	6226.9(2.1)
	$2P$	3293			6598
	$3P$	3613			6900
	$4P$	3898			7159
$\frac{1}{2}\left({\frac{5}{2}}^{-}\right)$	$1P$	2929	*	2931(6)	6226	new	6226.9(2.1)
	$2P$	3303			6596
	$3P$	3619			6897
	$4P$	3902			7156
$\frac{1}{2}\left({\frac{1}{2}}^{+}\right)$	$1D$	3163			6447
$\frac{1}{2}\left({\frac{1}{2}}^{+}\right)$	$2D$	3505			6767
$\frac{1}{2}\left({\frac{3}{2}}^{+}\right)$	$1D$	3167			6459
$\frac{1}{2}\left({\frac{3}{2}}^{+}\right)$	$2D$	3506			6775
	$1D$	3160			6431
$\frac{1}{2}\left({\frac{5}{2}}^{+}\right)$	$1D$	3166			6432
$\frac{1}{2}\left({\frac{5}{2}}^{+}\right)$	$2D$	3504			6751
	$1D$	3153			6420
$\frac{1}{2}\left({\frac{5}{2}}^{+}\right)$	$2D$	3493			6740
$\frac{1}{2}\left({\frac{7}{2}}^{+}\right)$	$1D$	3147	*	3122.9(1.3)	6414
$\frac{1}{2}\left({\frac{7}{2}}^{+}\right)$	$2D$	3486			6736

Table 5. Masses of the ${\Omega }_Q$ ($Q=c,b$) heavy baryons (in MeV).

		$\mathit{Q}=\mathit{c}$			$\mathit{Q}=\mathit{b}$
$\mathit{I}\left({\mathit{J}}^{\mathit{P}}\right)$	$\mathit{Qd}$ State	M	Status	${\mathit{M}}^{\mathbf{exp}}$	M	Status	${\mathit{M}}^{\mathbf{exp}}$
$0\left({\frac{1}{2}}^{+}\right)$	$1S$	2698	***	2695.2(1.7)	6064	***	6046.4(1.9)
	$2S$	3088	new	3090.2${(}_8^7)$	6450
	$3S$	3489			6804
	$4S$	3814			7091
	$5S$	4102			7338
$0\left({\frac{3}{2}}^{+}\right)$	$1S$	2768	***	2765.9(2.0)	6088
	$2S$	3123	new	3119.1${(}_{1.1}^{1.0})$	6461
	$3S$	3510			6811
	$4S$	3830			7096
	$5S$	4114			7343
$0\left({\frac{1}{2}}^{-}\right)$	$1P$	3055			6339
	$2P$	3435			6710
	$3P$	3754			7009
	$4P$	4037			7265
	$1P$	2966			6330
	$2P$	3384			6706
	$3P$	3717			7003
	$4P$	4009			7257
$0\left({\frac{3}{2}}^{-}\right)$	$1P$	3054	new	3065.6${(}_7^6)$	6340
	$2P$	3433			6705
	$3P$	3752			7002
	$4P$	4036			7258
	$1P$	3029	new	3000.4${(}_6^4)$	6331
	$2P$	3415			6699
	$3P$	3737			6998
	$4P$	4023			7250
$0\left({\frac{5}{2}}^{-}\right)$	$1P$	3051	new	3050.2${(}_5^4)$	6334
	$2P$	3427			6700
	$3P$	3744			6996
	$4P$	4028			7251
$0\left({\frac{1}{2}}^{+}\right)$	$1D$	3287			6540
$0\left({\frac{1}{2}}^{+}\right)$	$2D$	3623			6857
$0\left({\frac{3}{2}}^{+}\right)$	$1D$	3298			6549
$0\left({\frac{3}{2}}^{+}\right)$	$2D$	3627			6863
	$1D$	3282			6530
$0\left({\frac{3}{2}}^{+}\right)$	$2D$	3613			6846
$0\left({\frac{5}{2}}^{+}\right)$	$1D$	3297			6529
$0\left({\frac{5}{2}}^{+}\right)$	$2D$	3626			6846
	$1D$	3286			6520
$0\left({\frac{5}{2}}^{+}\right)$	$2D$	3614			6837
$0\left({\frac{7}{2}}^{+}\right)$	$1D$	3283			6517
$0\left({\frac{7}{2}}^{+}\right)$	$2D$	3611			6834
$0\left({\frac{3}{2}}^{-}\right)$	$1F$	3533			6763

Note that the orbitally excited states of heavy baryons (${\Sigma }_Q,{\Xi }_Q,{\Omega }_Q$) containing the axial vector diquark and having the same total angular momentum J and parity P but different light diquark total momentum $\mathbf{j}=\mathbf{L}+{\mathbf{S}}_d$ mix due to the presence of the spin-orbit (${\mathbf{LS}}_Q$) and tensor interactions [11]. Two mixed states for each $J=L\pm \frac{1}{2}$ and $P={(-1)}^L$ emerge. Thus there are two $nP$ states for $J^P={\frac{1}{2}}^{-}$ and for $J^P={\frac{3}{2}}^{-}$, two states $nD$ for $J^P={\frac{3}{2}}^{+}$ and for $J^P={\frac{5}{2}}^{+}$ in Table 2, Table 4 and Table 5.

From Table 1 and Table 2 we see that the ${\Lambda }_c\left(2765\right)$ (or ${\Sigma }_c\left(2765\right)$), if it is indeed the ${\Lambda }_c$ state, can be interpreted in our model as the first radial ($2S$) excitation of the ${\Lambda }_c$. If instead it is the ${\Sigma }_c$ state, then it can be identified as its first orbital excitation ($1P$) with $J^P={\frac{3}{2}}^{-}$ (see Table 2). The ${\Lambda }_c\left(2880\right)$ baryon corresponds to the second orbital excitation ($1D$) with $J^P={\frac{5}{2}}^{+}$ in accord with the LHCb analysis [1]. The other charmed baryon, denoted as ${\Lambda }_c\left(2940\right)$, probably has $I=0$, since it was discovered in the $p{D}^0$ mass spectrum and not observed in $p{D}^{+}$ channel, but $I=1$ is not ruled out [13]. If it is really the ${\Lambda }_c$ state, then it could be both an orbitally and radially excited ($2P$) state with $J^P={\frac{1}{2}}^{-}$, whose mass is predicted to be about 40 MeV heavier. A better agreement with experiment (within few MeV) is achieved, if the ${\Lambda }_c\left(2940\right)$ is interpreted as the first radial excitation ($2S$) of the ${\Sigma }_c$ with $J^P={\frac{3}{2}}^{+}$. The ${\Sigma }_c\left(2800\right)$ can be identified with one of the first orbital ($1P$) excitations of the ${\Sigma }_c$ with $J^P={\frac{1}{2}}^{-}$ or ${\frac{3}{2}}^{-}$ which have very close masses compatible with experimental value within errors (see Table 2). The new state ${\Lambda }_c\left(2860\right)$ with quantum numbers ${\frac{3}{2}}^{+}$ [1] can be well interpreted as second orbital excitation ($1D$ state). In the bottom sector the ${\Lambda }_b\left(5912\right)$ and ${\Lambda }_b\left(5920\right)$ correspond to the first orbitally excited ($1P$) states with $J^P={\frac{1}{2}}^{-}$ and ${\frac{3}{2}}^{-}$, respectively. The new ${\Sigma }_b\left(6097\right)$ state [7] can be the first orbital excitation ($1P$) with quantum numbers $J^P={\frac{3}{2}}^{-}$, while ${\Lambda }_b\left(6146\right)$ and ${\Lambda }_b\left(6152\right)$ can be $1D$ states with $J^P={\frac{3}{2}}^{+}$ and $J^P={\frac{5}{2}}^{+}$, respectively.

In the ${\Xi }_Q$ baryon sector, as we see from Table 3 and Table 4, the ${\Xi }_c\left(2790\right)$ and ${\Xi }_c\left(2815\right)$ can be assigned to the first orbital ($1P$) excitations of the ${\Xi }_c$ containing a scalar diquark with $J^P={\frac{1}{2}}^{-}$ and $J^P={\frac{3}{2}}^{-}$, respectively. On the other hand, the charmed baryon ${\Xi }_c\left(2930\right)$ can be considered as either the $J^P={\frac{1}{2}}^{-}$, $J^P={\frac{3}{2}}^{-}$ or $J^P={\frac{5}{2}}^{-}$ state (all these states are predicted to have close masses) corresponding to the first orbital ($1P$) excitations of the ${\Xi }_c^{\prime }$ with an axial vector diquark. While the ${\Xi }_c\left(2980\right)$ can be viewed as the first radial ($2S$) excitation with $J^P={\frac{1}{2}}^{+}$ of the ${\Xi }_c^{\prime }$. The ${\Xi }_c\left(3055\right)$ and ${\Xi }_c\left(3080\right)$ baryons can be interpreted as a second orbital ($1D$) excitations of the ${\Xi }_c$ containing a scalar diquark with $J^P={\frac{3}{2}}^{+}$ and $J^P={\frac{5}{2}}^{+}$, and the ${\Xi }_c\left(3123\right)$ can be viewed as the corresponding ($1D$) excitation of the ${\Xi }_c^{\prime }$ with $J^P={\frac{7}{2}}^{+}$. The recently observed excited bottom baryon ${\Xi }_b{\left(6227\right)}^{-}$ [6] can be one of the first radially excited states ($1P$) of the ${\Xi }_b^{\prime }$ baryon with the axial vector diquark and quantum numbers $J^P={\frac{1}{2}}^{-}$, ${\frac{3}{2}}^{-}$, ${\frac{5}{2}}^{-}$ which are predicted to have very close masses.

Masses of the ${\Omega }_c$ and ${\Omega }_b$ baryons are given in Table 5. The ground state ($1S$) masses were predicted [9,10] before experimental discovery and agree well with measured values. Recently the LHCb observed [2] five new, narrow excited ${\Omega }_c$ are also in accord with our predictions. Three lighter states ${\Omega }_c{\left(3000\right)}^0$, ${\Omega }_c{\left(3050\right)}^0$ and ${\Omega }_c{\left(3066\right)}^0$ are well described as first orbital ($1P$) excitations with $J^P=$ ${\frac{3}{2}}^{-}$, ${\frac{5}{2}}^{-}$ and ${\frac{3}{2}}^{-}$, respectively. These states are expected to be narrow. The remaining $1P$ states with ${\frac{1}{2}}^{-}$ are expected to be broad and thus can escape detection. The small peak in the low end of ${\Xi }_c^{+}{K}^{-}$ mass distribution (see Figure 1) can correspond to ${\frac{1}{2}}^{-}$ state with the predicted mass 2966 MeV (see Table 5). The remaining two heavier states ${\Omega }_c{\left(3090\right)}^0$ and ${\Omega }_c{\left(3119\right)}^0$ are naturally described as first radial ($2S$) excitations with quantum numbers ${\frac{1}{2}}^{+}$ and ${\frac{3}{2}}^{+}$, respectively. Their predicted masses coincide with the measured ones within a few MeV. The proposed assignment of spins and parities of excited ${\Omega }_c$ states observed by the LHCb Collaboration is given in Figure 1. In Table 6 we compare different quark model (QM), QCD sum rules (QCD SR), lattice QCD predictions and available experimental data for the masses of the ${\Omega }_c$ states.

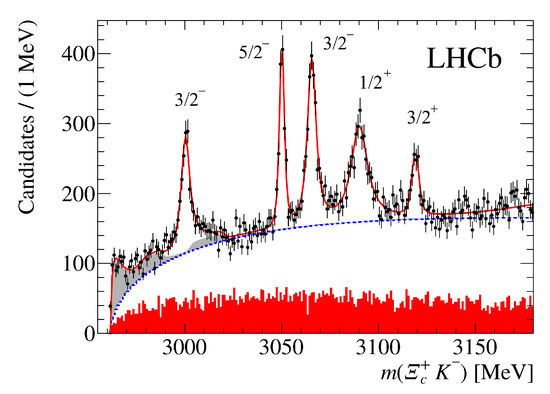
Figure 1. Proposed assignment of spins and parities of excited ${\Omega }_c$ states observed by LHCb Collaboration.

Table 6. Comparison of theoretical predictions for the masses of the ${\Omega }_c$ states (in MeV).

State	Our [11]	[14]	[15]	[16]	[17]	[18]	Experiment.
$\mathit{nL},{\mathit{J}}^{\mathit{P}}$	RQM	QM	QM	Lattice	Lattice	QCD SR	PDG+LHCb
$1S,{\frac{1}{2}}^{+}$	2698	2718	2695	2648(28)	$2695\left(28\right)$	$2685\left(123\right)$	$2695.2\left(1.7\right)$
$2S,{\frac{1}{2}}^{+}$	3088	3152	3100	3294(73)		$3066\left(138\right)$	3090.2${(}_8^7)$
$1S,{\frac{3}{2}}^{+}$	2768	2776	2767	2709(32)	$2781\left(25\right)$	$2769\left(89\right)$	$2765.9\left(2.0\right)$
$2S,{\frac{3}{2}}^{+}$	3123	3190	3126	3355(92)		$3119\left(114\right)$	3119.1${(}_{1.1}^{1.0})$
$1P,{\frac{1}{2}}^{-}$	2966	2977	3028	2995(46)	$3015\left(45\right)$
$1P,{\frac{1}{2}}^{-}$	3055	2990	3011
$1P,{\frac{3}{2}}^{-}$	3054	2986	2976	3016(69)			3065.6${(}_7^6)$
$1P,{\frac{3}{2}}^{-}$	3029	2994	2993				3000.4${(}_6^4)$
$1P,{\frac{5}{2}}^{-}$	3051	3014	2947				3050.2${(}_5^4)$

4. Doubly Heavy Baryons

Mass spectra of doubly heavy baryons were calculated in the light-quark–heavy-diquark picture in Reference [12]. The light quark was treated completely relativistically, while the expansion in the inverse heavy quark mass was used. Table 7 shows the ${\Xi }_{cc}$ mass spectrum. Excitaions inside doubly heavy diquark and light-quark–heavy-diquark bound systems are taken into account. We use the notations $\left(n_{d}L{n}_{q}l\right)J^P$, where we first show the radial quantum number of the diquark ($n_d=1,2,3\cdots$) and its orbital momentum by a capital letter ($L=S,P,D\cdots$), then the radial quantum number of the light quark ($n_q=1,2,3\cdots$) and its orbital momentum by a lowercase letter ($l=s,p,d\cdots$), and at the end the total angular momentum J and parity P of the baryon. In Table 8 we compare different theoretical predictions for the ground state masses of the doubly heavy baryons. Our prediction (2002) for the mass of the ${\Xi }_{cc}$ baryon [12] excellently agrees with its mass recently measured (2017) by the LHCb Collaboration [4,5]:

$$M^{\exp }\left({\Xi }_{cc}^{++}\right)=3621.40\pm 0.55\pm 0.23\pm 0.30\mathrm{MeV}.$$

Table 7. Mass spectrum of ${\Xi }_{cc}$ baryons (in MeV).

State	Mass		State	Mass
$\left({\mathit{n}}_{\mathit{d}}{\mathit{Ln}}_{\mathit{q}}\mathit{l}\right){\mathit{J}}^{\mathit{P}}$	Our	[19]	$\left({\mathit{n}}_{\mathit{d}}{\mathit{Ln}}_{\mathit{q}}\mathit{l}\right){\mathit{J}}^{\mathit{P}}$	Our	[19]
$\left(1S1s\right){\frac{1}{2}}^{+}$	3620	3478	$\left(1P1s\right){\frac{1}{2}}^{-}$	3838	3702
$\left(1S1s\right){\frac{3}{2}}^{+}$	3727	3610	$\left(1P1s\right){\frac{3}{2}}^{-}$	3959	3834
$\left(1S1p\right){\frac{1}{2}}^{-}$	4053	3927	$\left(2S1s\right){\frac{1}{2}}^{+}$	3910	3812
$\left(1S1p\right){\frac{3}{2}}^{-}$	4101	4039	$\left(2S1s\right){\frac{3}{2}}^{+}$	4027	3944
$\left(1S1p\right){\frac{1}{2}}^{\prime -}$	4136	4052	$\left(2P1s\right){\frac{1}{2}}^{-}$	4085	3972
$\left(1S1p\right){\frac{5}{2}}^{-}$	4155	4047	$\left(2P1s\right){\frac{3}{2}}^{-}$	4197	4104
$\left(1S1p\right){\frac{3}{2}}^{\prime -}$	4196	4034	$\left(3S1s\right){\frac{1}{2}}^{+}$	4154	4072

Table 8. Mass spectrum of ground states of doubly heavy baryons (in MeV). $\left\{QQ\right\}$ denotes the diquark in the axial vector state and $\left[QQ\right]$ denotes diquark in the scalar state.

Baryon	Quark	${\mathit{J}}^{\mathit{P}}$	Our	[19]	[20]	[21]	[22]	[14]	[23]
	Content		[12]
${\Xi }_{cc}$	$\left\{cc\right\}q$	${\frac{1}{2}}^{+}$	3620	3478	3660	3690	3510	3676	3627(12)
${\Xi }_{cc}^{*}$	$\left\{cc\right\}q$	${\frac{3}{2}}^{+}$	3727	3610	3740		3548	3753	3690(12)
${\Omega }_{cc}$	$\left\{cc\right\}s$	${\frac{1}{2}}^{+}$	3778	3590	3740	3860	3719	3815
${\Omega }_{cc}^{*}$	$\left\{cc\right\}s$	${\frac{3}{2}}^{+}$	3872	3690	3826		3746	3876
${\Xi }_{bb}$	$\left\{bb\right\}q$	${\frac{1}{2}}^{+}$	10202	10093	10340	10160	10130	10340	10162(12)
${\Xi }_{bb}^{*}$	$\left\{bb\right\}q$	${\frac{3}{2}}^{+}$	10237	10133	10370		10144	10367	10184(12)
${\Omega }_{bb}$	$\left\{bb\right\}s$	${\frac{1}{2}}^{+}$	10359	10180	10370	10340	10422	10454
${\Omega }_{bb}^{*}$	$\left\{bb\right\}s$	${\frac{3}{2}}^{+}$	10389	10200	10400		10432	10486
${\Xi }_{cb}$	$\left\{cb\right\}q$	${\frac{1}{2}}^{+}$	6933	6820	7040	6960	6792	7011	6914(13)
${\Xi }_{cb}^{\prime }$	$\left[cb\right]q$	${\frac{1}{2}}^{+}$	6963	6850	6990		6825	7047	6933(12)
${\Xi }_{cb}^{*}$	$\left\{cb\right\}q$	${\frac{3}{2}}^{+}$	6980	6900	7060		6827	7074	6969(14)
${\Omega }_{cb}$	$\left\{cb\right\}s$	${\frac{1}{2}}^{+}$	7088	6910	7090	7130	6999	7136
${\Omega }_{cb}^{\prime }$	$\left[cb\right]s$	${\frac{1}{2}}^{+}$	7116	6930	7060		7022	7165
${\Omega }_{cb}^{*}$	$\left\{cb\right\}s$	${\frac{3}{2}}^{+}$	7130	6990	7120		7024	7187

5. Conclusions

Recent observations of excited charm and bottom baryons confirm predictions of the relativistic quark–diquark model of heavy baryons [9,10,11]. The new state ${\Lambda }_c\left(2860\right)$ is in accordance with the predicted $1D$- state with $J^P={\frac{3}{2}}^{+}$. The experimentally preferred quantum numbers $J^P={\frac{5}{2}}^{+}$ of ${\Lambda }_c\left(2880\right)$ agree with our assignment of this state to $1D$- state with $J^P={\frac{5}{2}}^{+}$. The ${\Lambda }_b\left(5912\right)$ and ${\Lambda }_b\left(5920\right)$ are well described as the first orbitally excited ($1P$) states with $J^P={\frac{1}{2}}^{-}$ and ${\frac{3}{2}}^{-}$, respectively. The new ${\Sigma }_b\left(6097\right)$ state can be the first orbital excitation ($1P$) with quantum numbers $J^P={\frac{3}{2}}^{-}$. The recently observed excited bottom baryon ${\Xi }_b{\left(6227\right)}^{-}$ can be one of the first radially excited states ($1P$) of the ${\Xi }_b^{\prime }$ baryon with the axial vector diquark and quantum numbers $J^P={\frac{1}{2}}^{-}$, ${\frac{3}{2}}^{-}$, ${\frac{5}{2}}^{-}$ which are predicted to have very close masses. Observation of five new narrow ${\Omega }_c$ states in the mass range 3000-3200 MeV agrees with our prediction of orbitally excited $1P$-states and radially excited $2S$-states in this mass region: ${\Omega }_c\left(3000\right)$, ${\Omega }_c\left(3066\right)$, ${\Omega }_c\left(3050\right)$ can be $1P$-states with $J^P={\frac{3}{2}}^{-},{\frac{3}{2}}^{-},{\frac{5}{2}}^{-}$ while ${\Omega }_c\left(3090\right)$ and ${\Omega }_c\left(3119\right)$ states are most likely the first radially excited $2S$ states with $J^P={\frac{1}{2}}^{+},{\frac{3}{2}}^{+}$.

In the doubly heavy baryon sector, the mass of the recently observed ${\Xi }_{cc}^{++}$ baryon is in excellent agreement with our prediction made more than 15 years ago [12]. Masses of ground state doubly charm baryons are predicted to be in 3.5–3.9 GeV range. Masses of ground state doubly bottom baryons are predicted to be in the 10.1–10.5 GeV range. Masses of ground state bottom-charm baryons are predicted to be in the 6.8–7.2 GeV range. Rich spectra of narrow excited states below the strong decay thresholds are expected. We strongly encourage experimenters to search for new heavy baryons and especially for doubly heavy baryons.