Abstract
Semileptonic and rare semileptonic decays of heavy baryons are studied in the framework of the relativistic quark model based on the quark-diquark picture, quasipotential approach, and quantum chromodynamics (QCD). The form factors parametrizing the matrix elements of the weak transitions are calculated in the whole accessible kinematical range with the comprehensive account of the relativistic effects. The obtained results for the branching ratios and other observables agree well with the available experimental data.
1. Introduction
In recent years significant experimental progress has been achieved in studying decays of heavy baryons. Many decay channels of these baryons were observed and new more precise data are expected in near future, since heavy baryons are copiously produced at the Large Hadron Collider LHC. Weak decays of heavy baryons can serve as an additional source for the determination of the Cabbibo-Kobayashi-Maskawa (CKM) matrix elements. Such decays can be also used to verify the lepton flavour universality, indications of which violation were reported recently in the semileptonic B meson decays.
Here we review our study of the bottom and charm baryon decays in the framework of the relativistic quark model based on the quark-diquark picture and the quasipotential approach [1,2,3,4,5,6,7]. Heavy baryons are considered to be the heavy-quark–light-diquark bound states. Such approximation reduces very complicated relativistic three-body problem to the subsequent solution of two more simple two-body problems. Firstly, diquark is considered to be a bound state of two quarks. Secondly, baryon is considered to be the bound state of a quark and diquark. It is important to remember that the diquark inside a baryon is composed of two quarks. Thus, it is not a point-like object and its interaction with gluons is smeared by the form factor which can be expressed through the overlap integral of diquark wave functions. It is also important to account for the relativistic nature of light and heavy quarks and diquarks and thus treat them fully relativistically.
To calculate weak decay rates of heavy baryons it is necessary to determine the form factors which parametrize the matrix elements of the weak current between initial and final baryon states. On the basis of the relativistic quark model the explicit expressions for the decay form factors were obtained in terms of the overlap integrals over the baryon wave functions which are known from their mass spectrum calculations [8,9]. All relativistic effects including contributions of the intermediate negative-energy states and wave function transformations from the rest to the moving reference frame were systematically taken into account. The obtained formulas are valid in the whole accessible range of the momentum transfer squared and do not require additional model assumptions. The convenient analytic expressions which accurately reproduce the dependence of form factors are given. The calculated form factors are used for obtaining predictions for the differential and total decay rates and different asymmetry parameters. Good agreement of theoretical results with experimental data is found.
2. Relativistic Quark Model
In the relativistic quark model based on the quark-diquark picture and the quasipotential approach the interaction of two quarks in a diquark and the quark-diquark interaction in a baryon are described by the diquark wave function of the bound quark-quark state and by the baryon wave function of the bound quark-diquark state, which satisfy the relativistic quasipotential equation of the Schrödinger type [10]
where the relativistic reduced mass and the center-of-mass system relative momentum squared on mass shell are
and M is the bound state mass (diquark or baryon), are the masses of quarks ( and ) which form the diquark or of the diquark (d) and quark (q) which form the baryon (B), and is their relative momentum.
The quasipotentials of the quark-quark or quark-diquark interaction are constructed with the help of the QCD-motivated off-mass-shell scattering amplitude, projected onto the positive energy states. The effective quark interaction is taken to be the sum of the usual one-gluon exchange term and the mixture of long-range vector and scalar linear confining potentials with the mixing coefficient . It is also assumed that the vector confining potential contains not only the Dirac term but the Pauli term, thus introducing the anomalous chromomagnetic quark moment . The explicit expressions for the quasipotentials are given in Ref. [1].
In the nonrelativistic limit the usual Cornell-like potential is reproduced
where the QCD running coupling constant with freezing is given by
is the number of flavors, and the background mass GeV, MeV.
All parameters of the model were fixed previously from calculations of meson and baryon properties [1,10]. The constituent quark masses GeV, GeV, GeV and the parameters of the linear potential GeV and GeV have the usual values of quark models. The value of the mixing coefficient of vector and scalar confining potentials and the universal Pauli interaction constant [10]. Please note that the long-range chromomagnetic contribution to the potential, which is proportional to , vanishes for the chosen value of .
The matrix element of weak current between initial and final baryon states in the considered approach is given by [1]
where is the two-particle vertex function that receives relativistic contributions both from the impulse approximation diagram (see Figure 1 of Ref. [1])
and from the diagrams with the intermediate negative-energy states which are the consequence of the projection onto the positive-energy states in the quasipotential approach (see Figure 2 of Ref. [1])
where
and ; ; ;
The wave function of the moving baryon is connected with the rest-frame wave function by the transformation
where – Wigner rotation, and is the Lorentz boost from the baryon rest frame to a moving one. The rotation matrix of heavy quark spin is given by
while the rotation matrices of diquark with spin are as follows: for scalar diquark and for axial vector diquark.
3. Semileptonic Decay form Factors
The schematic diagram of the semileptonic decay of a heavy baryon ( and ) in quark-diquark picture is shown in Figure 1. The heavy quark Q undergoes the weak transition, while the light diquark d acts as a spectator.
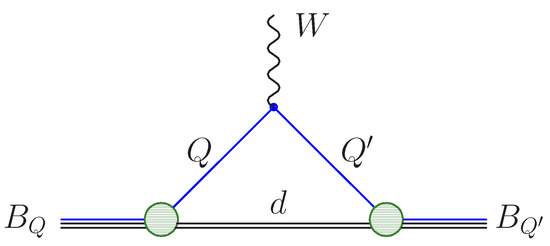
Figure 1.
The schematic diagram of the weak decay of a heavy baryon. The W boson produces the lepton pair . Green circles denote the baryon wave functions, the blue line corresponds to the heavy quarks Q and in the initial and final baryon , respectively.
The hadronic matrix elements for the semileptonic decays of baryons with scalar diquark () are parameterized in terms of six invariant form factors
where M and are masses and Dirac spinors of the baryons.
Using Equation (4) for the decay matrix element of the weak current the form factors are expressed as overlap integrals of baryon wave functions. (The spin-flavour structure of the wave functions of the members of the light baryon octet in the quark-diquark model is given in Ref. [11].) Contribution both of leading and subleading order vertex functions as well as relativistic transformation of the baryon wave function form the rest to moving reference frame are taken into account. The explicit expressions are given in Ref. [1]. Substituting in these expressions the baryon wave functions, found in calculation of their mass spectra, we obtain the values of the decay form factors and determine their dependence on in the whole kinematical region. As an example in Figure 2 we plot form factors for the transitions. The values of form factors at and as well as accurate analytic approximation of numerical results for form factors in the accessible range are given in Refs. [1,2,3,4].
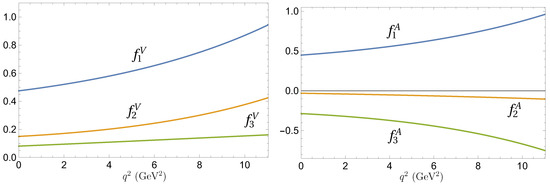
Figure 2.
Form factors of the weak transitions parameterizing vector (left) and axial vector (right) weak currents.
4. Semileptonic Decays
Using the obtained form factors and helicity formalism we calculate the total and differential semileptonic decays of heavy baryons as well as other important observables.
4.1. Bottom Baryon Decays
The semileptonic differential decay rates of the baryon are plotted in Figure 3. In Table 1 we compare our predictions in the framework of the relativistic quark model (RQM) for the total semileptonic decay rates of bottom baryons with the results of other theoretical approaches [12,13,14,15,16,17,18,19,20,21] and available experimental data from Particle Data Group (PDG) [22]. The most comprehensive results for different decay parameters were previously obtained in the covariant confined quark model (CCQM) [12,13,14,15], with which we find the general agreement. The semirelativistic quark model (SRQM) is used in Ref. [16], while effective Lagrangian approach (ELA) with form factors calculated on the lattice [21] is employed in Ref. [17]. The authors of Refs. [18,19] made calculations in the light-front quark model (LFQM) and in QCD light-cone sum (LCSR) rules, respectively. Calculations in the framework of QCD sum rules (QCDSR) in full theory are given in Ref. [20]. The only experimental data are available for the branching ratio of the decay (). All theoretical predictions agree well with data within error bars. However, note that lattice calculations [21] give somewhat lower predictions for the branching ratios normalized by the square of the corresponding CKM matrix element for transitions but give higher results for transitions than other approaches.
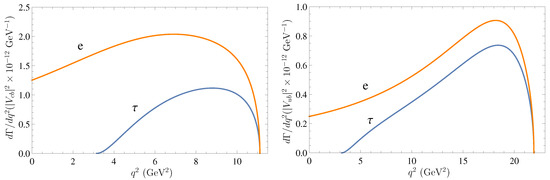
Figure 3.
Predictions for the differential decay rates of the (left) and (right) semileptonic decays.

Table 1.
Comparison of theoretical predictions for baryon semileptonic decays with experimental data.
At present, the tension between predictions of the Standard Model and experimental data in the B meson sector is observed for the ratio of branching fractions of semileptonic B decays to mesons involving and muon or electron. Therefore it is very important to search for the similar decays in baryon sector. We can define the following ratios of the baryon branching fractions
Our predictions for these ratios are given in Table 2 in comparison with calculations [17] based on lattice values of weak decay form factors [21]. Results of predictions for are in good agreement, while our value is slightly lower than the estimate in Ref. [17]. Please note that lattice determination of form factors is done in the region of small recoils of the final baryon and then their values are extrapolated to the whole kinematical region, which is broad especially for the heavy-to-light decay. In our model we explicitly determine the form factor dependence in the whole kinematical range without extrapolations.

Table 2.
Comparison of theoretical predictions for the ratios of the decay rates with experimental data.
The LHCb collaboration [23] measured the ratio of the heavy-to-heavy and heavy-to-light semileptonic decays in the limited interval of . Such measurement is very important since it allows for the first time to extract the ratio of CKM matrix elements from the baryon decays and compare it to the corresponding ratio determined from B and meson decays. Our prediction for the ratio in comparison with lattice result [21] and experimental value is given in Table 2. From this table we see that our value of the coefficient in front of is significantly lower than lattice one. This is the result of the above mentioned deviation of our (and other quark model calculations) from lattice predictions for normalized by the square of CKM matrix element value for heavy-to-heavy and heavy-to-light semileptonic decays. This deviation even increases in the ratio.
Comparing our result for with experimental data we find
in good agreement with the experimental ratio of these matrix elements extracted from inclusive decays
and with the corresponding ratio found in our previous analysis of exclusive semileptonic B and meson decays [, ]
4.2. Charm Baryon Decays
In Figure 4 we plot the differential decay rates for and () semileptonic decays. In Table 3 we compare our results for various semileptonic decay observables with the recent predictions of other theoretical approaches [13,14,15,16,24,25] and available experimental data [22]. The most detailed predictions are given in the framework of the covariant confined quark model [13,14,15]. The authors present the values not only of decay rates and branching fractions but also of different asymmetries and polarization parameters. We find good agreement with their results. The semirelativistic quark model is used in Ref. [16]. Different versions of QCD light-cone sum rules (LCSR) are employed in Refs. [24,25]. We compare theoretical predictions with experimental values given in PDG [22], which are available for the branching fractions of decays. All theoretical predictions reasonably agree with data. For the decay no data are available at present. Most of the theoretical predictions [13,14,15,16,24], except the light cone QCD sum rule approach [25], give close values for the branching fractions .
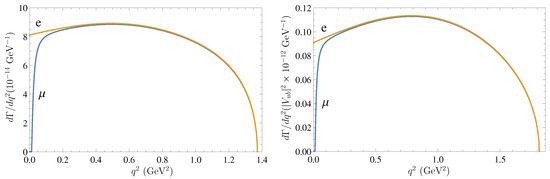
Figure 4.
Differential decay rates of the (left) and (right) semileptonic decays.

Table 3.
Theoretical predictions for the baryon semileptonic decays and experimental data.
Theoretical predictions [26,27,28,29] for the semileptonic decay branching fractions are compared in Table 4. The light-front quark model is used for the weak decay form factor and branching fraction calculations in Ref. [26]. The predictions of Refs. [27,28] are based on the application of the SU(3) flavor symmetry, while the light-cone QCD sum rules are employed in Ref. [29]. The experimental branching fractions are obtained by multiplying values [22] for the ratios and by the recently measured by the Belle Collaboration branching fractions [30] and [31]. We find reasonable agreement of our predictions for the CKM favored decays with the results of Refs. [26,27,28] and experimental data, while the light-cone QCD sum rule values for branching fractions are substantially higher and disagree with data by more than a factor of 2 for the decay. Please note that the ratio [22] combined with the Belle data [30,31] leads to the semi-inclusive branching fraction in good agreement with our result. There is no data yet for the CKM suppressed decays and theoretical evaluations differ substantially. Our prediction is about a factor of 6 larger than the light-cone quark model value [26] and a factor of 3 larger than the SU(3) flavor symmetry result [28]. The difference for the with Ref. [26] originates from larger values of form factors predicted by our model.

Table 4.
Comparison of theoretical predictions for the semileptonic decay branching fractions (in %) with available experimental data.
We can combine our predictions for the semileptonic baryon decays with our analysis of the semileptonic decays to test the flavor symmetry. Under the exact symmetry the following relations should hold [26,27]
In Table 5 we test these relations for the ratios , where the corresponding CKM matrix element is used. In the first column we give the semileptonic decay process. In the second column we present predictions of our model. The third column contains the flavor symmetry result using relations (10) and as an input, while the last column gives the relative difference in %. From this table we see that the flavor is broken for the charmed baryon semileptonic decays especially for where its breaking is about 20–35%. This is the consequence of the larger mass of the s quark in comparison with the quarks and the employed quark-diquark picture of baryons.

Table 5.
Predictions for the ratios in ps ()
5. Rare Semileptonic Baryon Decays
The effective Hamiltonian for the rare transitions is given by
where is the Fermi constant, are CKM matrix elements, are the Wilson coefficients. are the standard model operators:
and the only operators with a tree-level non-vanishing matrix element in :
Then the matrix element of the transition amplitude between baryon states has the following form
where
() are expressed through the form factors and the Wilson coefficients.
The matrix elements of the flavour changing neutral current for the rare baryon decays are parametrized by the following set of invariant form factors
where and are Dirac spinors, . We need to calculate four additional form factors and which parametrize matrix element of tensor and axial tensor current matrix elements. The form factors of the rare weak transition are plotted in Figure 5 [5].
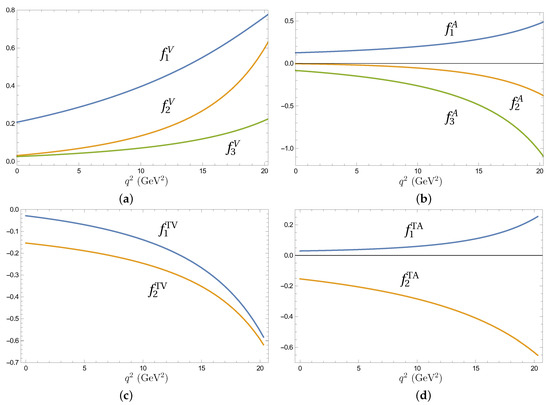
Figure 5.
Form factors of the rare weak transition parameterizing vector (a), axial vector (b), tensor (c) and axial tensor (d) weak currents.
The effective Wilson coefficient contains additional pertubative and long-distance contributions
The perturbative part is equal to
where
The long-distance (nonperturbative) contributions are assumed to originate from the resonances () and have a usual Breit-Wigner structure:
We include contributions of the vector charmonium states: , , , , and , with their masses (), leptonic [] and total () decay widths taken from PDG [22].
The lepton angle differential decay distribution is given by
where is the angle between the baryon and the positively charged lepton in the dilepton rest frame. The lepton forward-backward asymmetry is defined by [13,14,15]
and is the fraction of longitudinally polarized dileptons.
The hadron angle differential distribution of the decay is given by
where is the angle between the proton and the baryon in the rest frame. is the hadron forward-backward asymmetry. The other useful observable is the combined hadron-lepton forward-backward asymmetry . It is proportional to the coefficient in front of the term in the threefold joint angular decay distribution for the decay of the unpolarized [13,14,15].
In Figure 6, Figure 7, Figure 8 and Figure 9 we plot our predictions [5] for the differential branching ratios , lepton and hadron forward-backward asymmetries as well as the fraction of longitudinally polarized dileptons for rare decays and in comparison with available experimental data [32,33]. By solid (dashed) lines we plot theoretical results obtained without (with) inclusion of the long-distance contributions to the Wilson coefficients coming from the charmonium resonances. Experimental data for the decay from the LHCb [32] and CDF [33] Collaborations are plotted by dots with solid and dashed error bars, respectively.
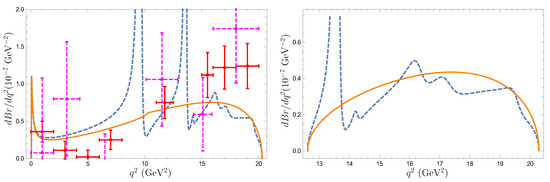
Figure 6.
Predictions for the differential branching ratios for the (left) and (right) rare decays. Results without (orange solid curves) and with (dashed blue curves) long-distance contributions are plotted. Available experimental data from LHCb [32] are given by red dots with solid error bars, CDF [33] data are given by magenta dots with dashed error bars.
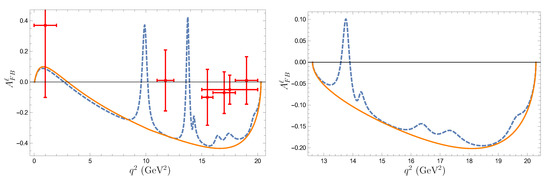
Figure 7.
Predictions for the lepton forward-backward asymmetries in the (left) and (right) rare decays. Notations are the same as in Figure 6.
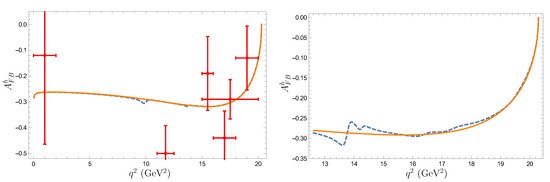
Figure 8.
Predictions for the hadron forward-backward asymmetries in the (left) and (right) rare decays. Notations are the same as in Figure 6.
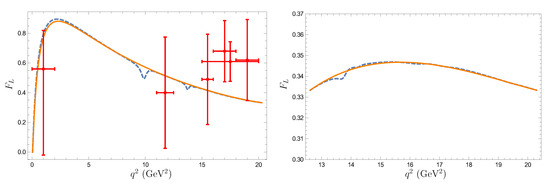
Figure 9.
Prediction for the fraction of longitudinally polarized dileptons in the (left) and (right) rare decays. Notations are the same as in Figure 6.
In Table 6 we compare different theoretical predictions [13,14,15,34,35,36,37,38] for the total branching fractions of rare semileptonic decays with available experimental data [22]. The presented values include results of the relativistic and nonrelativistic quark model calculations [13,14,15,36,37] as well as evaluations based on various versions of the light-cone QCD sum rules [34,35,38]. At present, experimental data are available for decay only. The values obtained in our model and Refs. [13,14,15,36,37] agree well with data, while other results are significantly larger. From Table 6 we also see that predictions for the rare decay vary significantly. Our results [5,6,7] are close to those from quark models Refs. [13,14,15,37]. On the other hand, the light-cone QCD sum rules [34,35] predict significantly larger values while the quark model [36] gives a significantly lower value. Thus experimental measurement of the rare decay branching fraction can help to discriminate between theoretical approaches. In this table we also include our predictions for the rare semileptonic decay rates.

Table 6.
Comparison of theoretical predictions for baryon rare decay branching fractions () with available experimental data.
6. Rare Radiative Baryon Decay
The exclusive rare radiative decay rate for the emission of a real photon () is given by
Our predictions for the branching fraction are given in Table 7 in comparison with other theoretical values [13,14,15,35,38,39,40] and the experimental data [41]. Our result [5,6] is consistent with the values from Refs. [35,39], but about a factor of 2 larger than the prediction of the covariant constituent quark model [13,14,15]. The result of the light-cone QCD sum rule study [38] is about an order of magnitude lower, while the value obtained within three-point QCD sum rules in the heavy quark limit [40] is more than a factor 3 larger than other theoretical predictions. Very recently the LHCb Collaboration [41] measured the decay branching fraction . It is in nice agreement with our prediction and the results of [13,14,15,35,39], but is significantly different form [38,40].

Table 7.
Comparison of theoretical predictions for the rare radiative decay branching fraction () with available experimental data.
7. Conclusions
We studied the semileptonic decays of heavy baryons in the framework of the relativistic quark-diquark picture. All calculations were done with the comprehensive account of the relativistic effects without application heavy quark expansion. All parameters of the model were fixed in previous considerations of meson and baryon properties. The wave functions of baryons were taken from their mass spectra calculations. It was found that obtained results agree well with available experimental data and some theoretical predictions.
Author Contributions
Investigation, R.N.F. and V.O.G., Writing—original draft, R.N.F. and V.O.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Higher Education of Russian Federation.
Acknowledgments
The authors are grateful to D. Ebert and M. Ivanov for valuable discussions. We thank the organizers of the Helmholtz International Summer School “Quantum Field Theory at the Limits: From Strong Fields to Heavy Quarks” for the invitation to participate in such a pleasant and productive meeting.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Faustov, R.N.; Galkin, V.O. Semileptonic decays of Λb baryons in the relativistic quark model. Phys. Rev. D 2016, 94, 073008. [Google Scholar] [CrossRef]
- Faustov, R.N.; Galkin, V.O. Relativistic description of the Ξb baryon semileptonic decays. Phys. Rev. D 2018, 98, 093006. [Google Scholar] [CrossRef]
- Faustov, R.N.; Galkin, V.O. Semileptonic decays of Λc baryons in the relativistic quark model. Eur. Phys. J. C 2016, 76, 628. [Google Scholar] [CrossRef]
- Faustov, R.N.; Galkin, V.O. Semileptonic Ξc baryon decays in the relativistic quark model. Eur. Phys. J. C 2019, 79, 695. [Google Scholar] [CrossRef]
- Faustov, R.N.; Galkin, V.O. Rare Λb → Λl+l− and Λb → Λγ decays in the relativistic quark model. Phys. Rev. D 2017, 96, 053006. [Google Scholar] [CrossRef]
- Faustov, R.N.; Galkin, V.O. Rare Λb → nl+l− decays in the relativistic quark-diquark picture. Mod. Phys. Lett. A 2017, 32, 1750125. [Google Scholar] [CrossRef]
- Faustov, R.N.; Galkin, V.O. Rare Λc → pℓ+ℓ− decay in the relativistic quark model. Eur. Phys. J. C 2018, 78, 527. [Google Scholar] [CrossRef]
- Ebert, D.; Faustov, R.N.; Galkin, V.O. Spectroscopy and Regge trajectories of heavy baryons in the relativistic quark-diquark picture. Phys. Rev. D 2011, 84, 014025. [Google Scholar] [CrossRef]
- Faustov, R.N.; Galkin, V.O. Strange baryon spectroscopy in the relativistic quark model. Phys. Rev. D 2015, 92, 054005. [Google Scholar] [CrossRef]
- Ebert, D.; Faustov, R.N.; Galkin, V.O. Properties of heavy quarkonia and Bc mesons in the relativistic quark model. Phys. Rev. D 2003, 67, 014027. [Google Scholar] [CrossRef]
- Lichtenberg, D.B.; Tassie, L.J.; Keleman, P.J. Quark-Diquark Model of Baryons and SU (6). Phys. Rev. 1968, 167, 1535. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E.; Santorelli, P.; Habyl, N. Semileptonic decay in the covariant confined quark model. Phys. Rev. D 2015, 91, 074001. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E.; Santorelli, P. Heavy-to-light semileptonic decays of Λb and Λc baryons in the covariant confined quark model. Phys. Rev. D 2014, 90, 114033. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E.; Santorelli, P. Semileptonic decays (ℓ = e,μ) in the covariant quark model and comparison with the new absolute branching fraction measurements of Belle and BESIII. Phys. Rev. D 2016, 93, 034008. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E.; Santorelli, P. Rare baryon decays Λb → Λl+l− (l = e,μ,τ) and Λb → Λγ: differential and total rates, lepton- and hadron-side forward-backward asymmetries. Phys. Rev. D 2013, 87, 074031. [Google Scholar] [CrossRef]
- Pervin, M.; Roberts, W.; Capstick, S. Semileptonic decays of heavy lambda baryons in a quark model. Phys. Rev. C 2005, 72, 035201. [Google Scholar] [CrossRef]
- Dutta, R. Phenomenology of Ξb → Ξc τ ν decays. Phys. Rev. D 2018, 97, 073004. [Google Scholar] [CrossRef]
- Ke, H.W.; Li, X.Q.; Wei, Z.T. Diquarks and Λb → Λc weak decays. Phys. Rev. D 2008, 77, 014020. [Google Scholar] [CrossRef]
- Khodjamirian, A.; Klein, C.; Mannel, T.; Wang, Y.M. Form Factors and Strong Couplings of Heavy Baryons from QCD Light-Cone Sum Rules. J. High Energy Phys. 2011, 1109, 106. [Google Scholar] [CrossRef]
- Azizi, K.; Süngü, J.Y. Semileptonic Transition in Full QCD. Phys. Rev. D 2018, 97, 074007. [Google Scholar] [CrossRef]
- Detmold, W.; Lehner, C.; Meinel, S. and form factors from lattice QCD with relativistic heavy quarks. Phys. Rev. D 2015, 92, 034503. [Google Scholar] [CrossRef]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of particle physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Determination of the quark coupling strength |Vub| using baryonic decays. Nature Phys. 2015, 11, 743. [Google Scholar]
- Liu, Y.L.; Huang, M.Q.; Wang, D.W. Improved analysis on the semi-leptonic decay Λc → Λl+ν from QCD light-cone sum rules. Phys. Rev. D 2009, 80, 074011. [Google Scholar] [CrossRef]
- Azizi, K.; Bayar, M.; Sarac, Y.; Sundu, H. Semileptonic Λb,c to Nucleon Transitions in Full QCD at Light Cone. Phys. Rev. D 2009, 80, 096007. [Google Scholar] [CrossRef]
- Zhao, Z.X. Weak decays of heavy baryons in the light-front approach. Chin. Phys. C 2018, 42, 093101. [Google Scholar] [CrossRef]
- Geng, C.Q.; Hsiao, Y.K.; Liu, C.W.; Tsai, T.H. Antitriplet charmed baryon decays with SU(3) flavor symmetry. Phys. Rev. D 2018, 97, 073006. [Google Scholar] [CrossRef]
- Geng, C.Q.; Liu, C.W.; Tsai, T.H.; Yeh, S.W. Semileptonic decays of anti-triplet charmed baryons. Phys. Lett. B 2019, 792, 214. [Google Scholar] [CrossRef]
- Azizi, K.; Sarac, Y.; Sundu, H. Light cone QCD sum rules study of the semileptonic heavy ΞQ and transitions to Ξ and Σ baryons. Eur. Phys. J. A 2012, 48, 2. [Google Scholar] [CrossRef]
- Li, Y.B.; Shen, C.P.; Yuan, C.Z.; Adachi, I.; Aihara, H.; Al Said, S.; Asner, D.M.; Aushev, T.; Ayad, R.; Badhrees, I.; et al. First Measurements of Absolute Branching Fractions of the Baryon at Belle. Phys. Rev. Lett. 2019, 122, 082001. [Google Scholar] [CrossRef]
- Li, Y.B.; Shen, C.P.; Adachi, I.; Ahn, J.K.; Aihara, H.; Al Said, S.; Asner, D.M.; Atmacan, H.; Aushev, T.; Ayad, R.; et al. First measurements of absolute branching fractions of the baryon at Belle. Phys. Rev. D 2019, 100, 031101. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Differential branching fraction and angular analysis of decays. J. High Energy Phys. 2015, 1506, 115. [Google Scholar] [CrossRef]
- Aaltonen, T.; Alvarez Gonzalezv, B.; Amerio, S.; Amidei, D.; Anastassov, A.; Annovi, A.; Antos, J.; Apollinari, G.; Appel, J.A.; Apresyan, A.; et al. Observation of the Baryonic Flavor-Changing Neutral Current Decay Λb → Λμ+μ−. Phys. Rev. Lett. 2011, 107, 201802. [Google Scholar] [CrossRef] [PubMed]
- Aliev, T.M.; Azizi, K.; Savci, M. Analysis of the Λb → Λℓ+ℓ− decay in QCD. Phys. Rev. D 2010, 81, 056006. [Google Scholar] [CrossRef]
- Wang, Y.M.; Li, Y.; Lu, C.D. Rare Decays of Λb → Λ + γ and Λb → Λ + l+l− in the Light-cone Sum Rules. Eur. Phys. J. C 2009, 59, 861. [Google Scholar] [CrossRef][Green Version]
- Liu, Y.; Liu, L.-L.; Guo, X.-H. Study of Λb → Λl+l− and decays in the Bethe-Salpeter equation approach. arXiv 2015, arXiv:1503.06907. [Google Scholar]
- Mott, L.; Roberts, W. Lepton polarization asymmetries for FCNC decays of the Λb baryon. Int. J. Mod. Phys. A 2015, 30, 1550172. [Google Scholar] [CrossRef]
- Gan, L.F.; Liu, Y.L.; Chen, W.B.; Huang, M.Q. Improved Light-cone QCD Sum Rule Analysis Of The Rare Decays Λb → Λγ And Λb → Λl+l−. Commun. Theor. Phys. 2012, 58, 872. [Google Scholar] [CrossRef][Green Version]
- Mannel, T.; Wang, Y.M. Heavy-to-light baryonic form factors at large recoil. J. High Energy Phys. 2011, 1112, 067. [Google Scholar] [CrossRef]
- Colangelo, P.; De Fazio, F.; Ferrandes, R.; Pham, T.N. FCNC Bs and Λb transitions: Standard model versus a single universal extra dimension scenario. Phys. Rev. D 2008, 77, 055019. [Google Scholar] [CrossRef]
- Aaij, R.; Abellán Beteta, C.; Adeva, B.; Adinolfi, M.; Aidala, A.C.; Ajaltouni, Z.; Akar, S.; Albicocco, P.; Albrecht, J.; Alessio, F.; et al. First Observation of the Radiative Decay . Phys. Rev. Lett. 2019, 123, 031801. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).