D
*
Polarization as an Additional Constraint on New Physics in the b → cτ
ν
¯
τ Transition
Abstract
1. Introduction
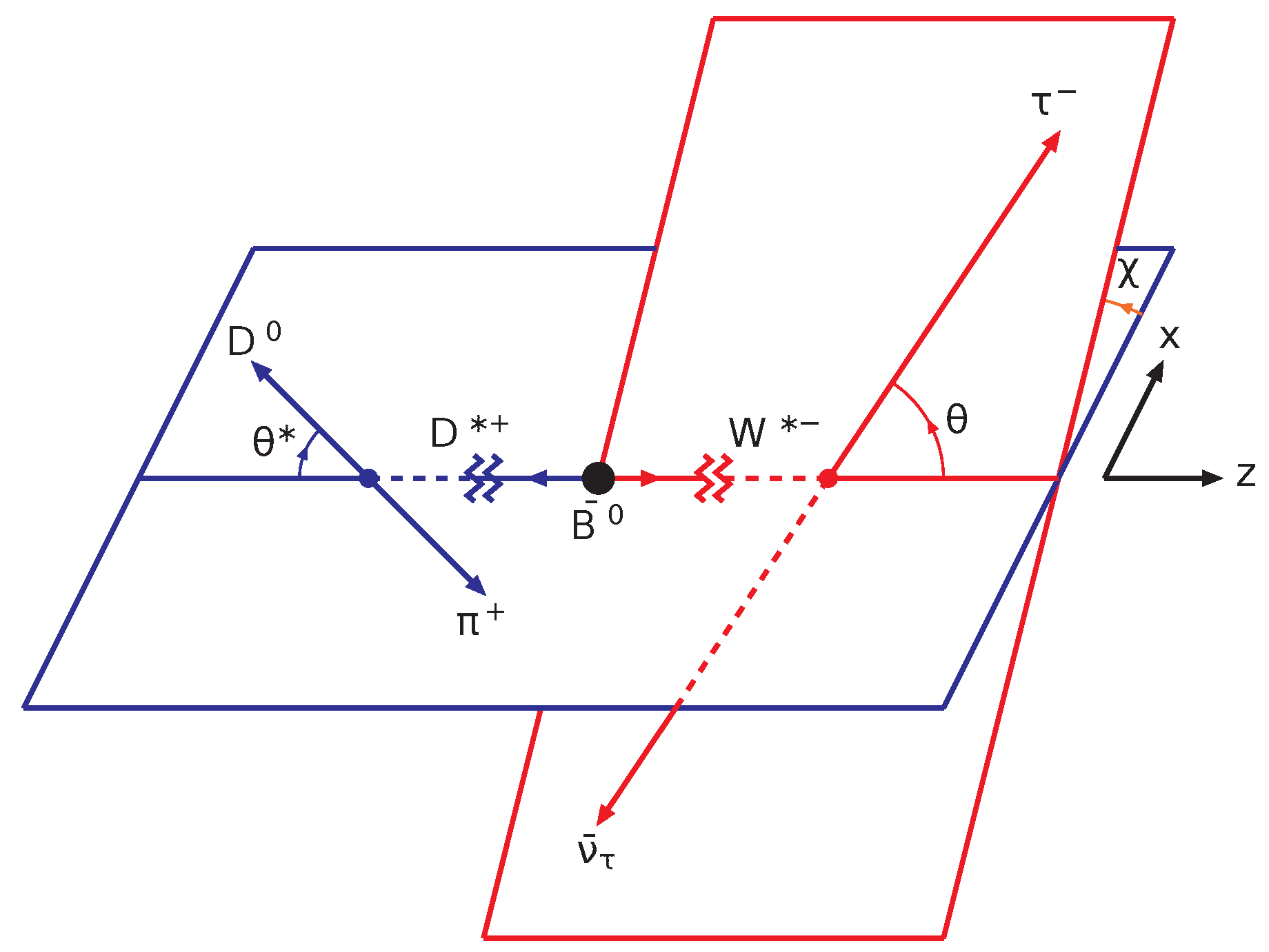
2. Theoretical Framework
3. Form Factors in the Covariant Constituent Quark Model
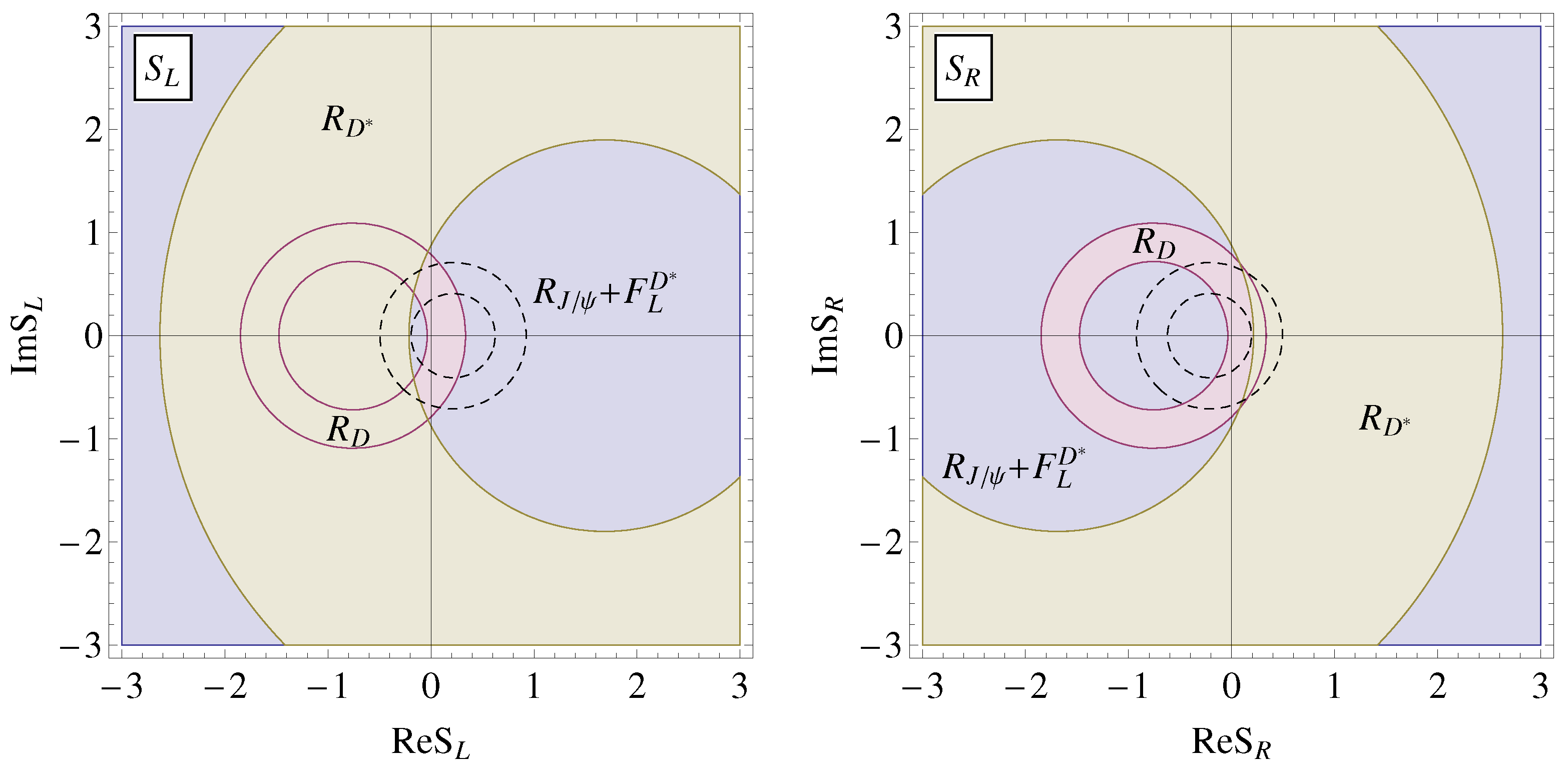
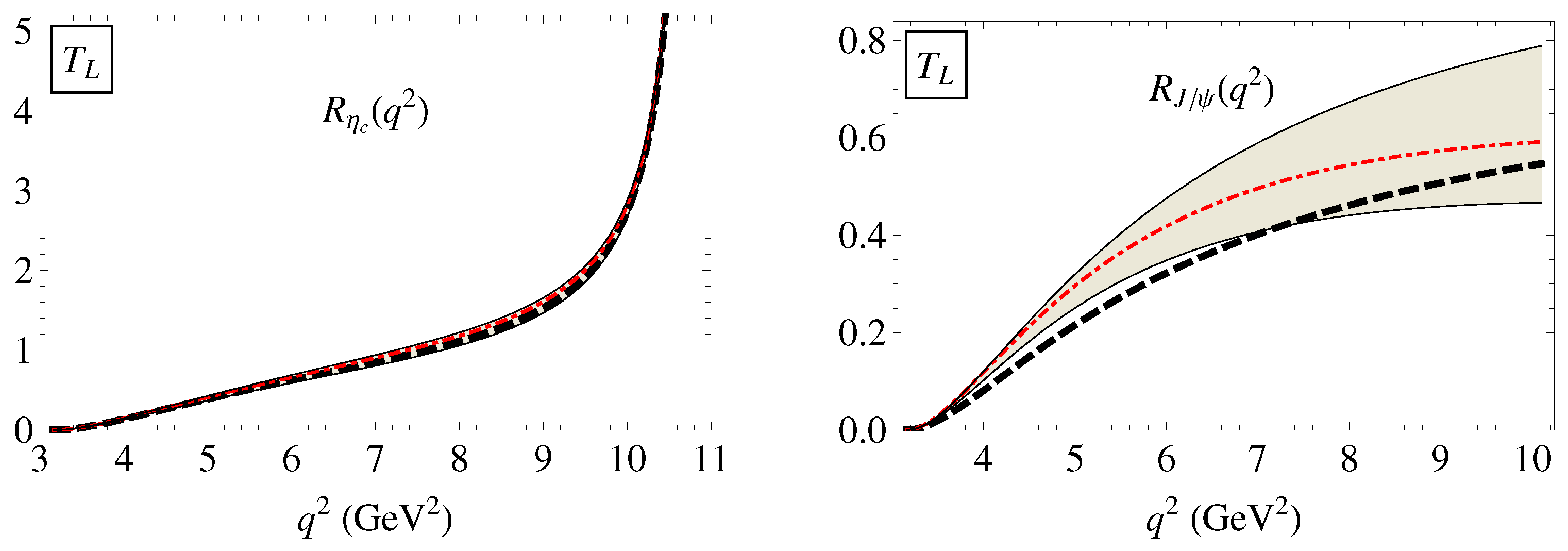
4. Numerical Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ciezarek, G.; Sevilla, M.F.; Hamilton, B.; Kowalewski, R.; Kuhr, T.; Lüth, V.; Sato, Y. A Challenge to Lepton Universality in B Meson Decays. Nature 2017, 546, 227. [Google Scholar] [CrossRef] [PubMed]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Garra Tico, J.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; et al. Evidence for an excess of decays. Phys. Rev. Lett. 2012, 109, 101802. [Google Scholar] [CrossRef] [PubMed]
- Lees, J.P.; Poireau, V.; Tisserand, V.; Grauges, E.; Palano, A.; Eigen, G.; Stugu, B.; Brown, D.N.; Kerth, L.T.; Kolomensky, Y.G.; et al. Measurement of an Excess of Decays and Implications for Charged Higgs Bosons. Phys. Rev. D 2013, 88, 072012. [Google Scholar] [CrossRef]
- Huschle, M.; Kuhr, T.; Heck, M.; Goldenzweig, P.; Abdesselam, A.; Adachi, I.; Adamczyk, K.; Aihara, H.; Al Said, S.; Arinstein, K.; et al. Measurement of the branching ratio of relative to decays with hadronic tagging at Belle. Phys. Rev. D 2015, 92, 072014. [Google Scholar] [CrossRef]
- Sato, Y.; Iijima, T.; Adamczyk, K.; Aihara, H.; Asner, D.M.; Atmacan, H.; Aushev, T.; Ayad, R.; Aziz, T.; Babu, V.; et al. Measurement of the branching ratio of relative to decays with a semileptonic tagging method. Phys. Rev. D 2016, 94, 072007. [Google Scholar] [CrossRef]
- Hirose, S.; Iijima, T.; Adachi, I.; Adamczyk, K.; Aihara, H.; Al Said, S.; Asner, D.M.; Atmacan, H.; Aulchenko, V.; Aushev, T.; et al. Measurement of the τ lepton polarization and R(D*) in the decay . Phys. Rev. Lett. 2017, 118, 211801. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Affolder, A.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Ali, S.; et al. Measurement of the ratio of branching fractions . Phys. Rev. Lett. 2015, 115, 111803, Erratum: Phys. Rev. Lett. 2015, 115, 159901. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Alfonso Albero, A.; Ali, S.; et al. Measurement of the ratio of the B0 → D*−τ+ντ and B0 → D*−μ+νμ branching fractions using three-prong τ-lepton decays. Phys. Rev. Lett. 2018, 120, 171802. [Google Scholar] [CrossRef]
- Amhis, Y.; Banerjee, S.; Ben-Haim, E.; Bernlochner, F.; Bozek, A.; Bozzi, C.; Chrza̧szcz, M.; Dingfelder, J.; Duell, S.; Gersabeck, M.; et al. Averages of b-hadron, c-hadron, and τ-lepton properties as of summer 2016. Eur. Phys. J. C 2017, 77, 895. [Google Scholar] [CrossRef]
- Abdesselam, A.; Adachi, I.; Adamczyk, K.; Ahn, J.K.; Aihara, H.; Al Said, S.; Arinstein, K.; Arita, Y.; Asner, D.M.; Atmacan, H.; et al. Measurement of (D) and (D*) with a semileptonic tagging method. arXiv 2019, arXiv:1904.08794. [Google Scholar]
- Bigi, D.; Gambino, P. Revisiting B → Dℓν. Phys. Rev. D 2016, 94, 094008. [Google Scholar] [CrossRef]
- Bernlochner, F.U.; Ligeti, Z.; Papucci, M.; Robinson, D.J. Combined analysis of semileptonic B decays to D and D*: R(D(*)), |Vcb|, and new physics. Phys. Rev. D 2017, 95, 115008, Erratum: Phys. Rev. D 2018, 97, 059902. [Google Scholar]
- Bigi, D.; Gambino, P.; Schacht, S. R(D*), |Vcb|, and the Heavy Quark Symmetry relations between form factors. J. High Energy Phys. 2017, 11, 061. [Google Scholar] [CrossRef]
- Jaiswal, S.; Nandi, S.; Patra, S.K. Extraction of |Vcb| from B → D(*)ℓνℓ and the Standard Model predictions of R(D(*)). J. High Energy Phys. 2017, 12, 060. [Google Scholar] [CrossRef]
- Bifani, S.; Descotes-Genon, S.; Romero Vidal, A.; Schune, M.H. Review of Lepton Universality tests in B decays. J. Phys. G 2019, 46, 023001. [Google Scholar] [CrossRef]
- Aaij, R.; Adeva, B.; Adinolfi, M.; Ajaltouni, Z.; Akar, S.; Albrecht, J.; Alessio, F.; Alexander, M.; Alfonso Albero, A.; Ali, S.; et al. Measurement of the ratio of branching fractions ( → J/ψτ+ντ)/( → J/ψμ+νμ). Phys. Rev. Lett. 2018, 120, 121801. [Google Scholar] [CrossRef] [PubMed]
- Cohen, T.D.; Lamm, H.; Lebed, R.F. Model-independent bounds on R(J/ψ). J. High Energy Phys. 2018, 09, 168. [Google Scholar] [CrossRef]
- Leljak, D.; Melíc, B.; Patra, M. On lepton flavour universality in semileptonic Bc → ηc, J/ψ decays. J. High Energy Phys. 2019, 05, 094. [Google Scholar] [CrossRef]
- Murphy, C.W.; Soni, A. Model-Independent Determination of → ηcℓ+ν Form Factors. Phys. Rev. D 2018, 98, 094026. [Google Scholar] [CrossRef]
- Angelescu, A.; Bečirević, D.; Faroughy, D.A.; Sumensari, O. Closing the window on single leptoquark solutions to the B-physics anomalies. J. High Energy Phys. 2018, 10, 183. [Google Scholar] [CrossRef]
- Yan, H.; Yang, Y.D.; Yuan, X.B. Phenomenology of b → cτ decays in a scalar leptoquark model. Chin. Phys. C 2019, 43, 083105. [Google Scholar] [CrossRef]
- Bansal, S.; Capdevilla, R.M.; Kolda, C. Constraining the minimal flavor violating leptoquark explanation of the RD(*) anomaly. Phys. Rev. D 2019, 99, 035047. [Google Scholar] [CrossRef]
- Li, S.P.; Li, X.Q.; Yang, Y.D.; Zhang, X. RD(*), RK(*) and neutrino mass in the 2HDM-III with right-handed neutrinos. J. High Energy Phys. 2018, 09, 149. [Google Scholar] [CrossRef]
- Marzo, C.; Marzola, L.; Raidal, M. Common explanation to the RK(*), RD(*) and ϵ′/ϵ anomalies in a 3HDM+νR and connections to neutrino physics. Phys. Rev. D 2019, 100, 055031. [Google Scholar] [CrossRef]
- Greljo, A.; Robinson, D.J.; Shakya, B.; Zupan, J. R(D(*)) from and right-handed neutrinos. J. High Energy Phys. 2018, 09, 169. [Google Scholar] [CrossRef]
- Gómez, J.D.; Quintero, N.; Rojas, E. Charged current b → cττ anomalies in a general boson scenario. Phys. Rev. D 2019, 100, 093003. [Google Scholar] [CrossRef]
- Fajfer, S.; Kamenik, J.F.; Nišandžić, I. On the B → D*ττ Sensitivity to New Physics. Phys. Rev. D 2012, 85, 094025. [Google Scholar] [CrossRef]
- Datta, A.; Duraisamy, M.; Ghosh, D. Diagnosing New Physics in b → cτντ decays in the light of the recent BaBar result. Phys. Rev. D 2012, 86, 034027. [Google Scholar] [CrossRef]
- Tanaka, M.; Watanabe, R. New physics in the weak interaction of → D(*)τ. Phys. Rev. D 2013, 87, 034028. [Google Scholar] [CrossRef]
- Biancofiore, P.; Colangelo, P.; De Fazio, F. On the anomalous enhancement observed in B → D(*)ττ decays. Phys. Rev. D 2013, 87, 074010. [Google Scholar] [CrossRef]
- Dutta, R.; Bhol, A.; Giri, A.K. Effective theory approach to new physics in b → u and b → c leptonic and semileptonic decays. Phys. Rev. D 2013, 88, 114023. [Google Scholar] [CrossRef]
- Murgui, C.; Peñuelas, A.; Jung, M.; Pich, A. Global fit to b → cτν transitions. J. High Energy Phys. 2019, 09, 103. [Google Scholar] [CrossRef]
- Kim, C.S.; Park, S.C.; Sahoo, D. Angular distribution as an effective probe of new physics in semihadronic three-body meson decays. Phys. Rev. D 2019, 100, 015005. [Google Scholar] [CrossRef]
- Hu, Q.Y.; Li, X.Q.; Yang, Y.D. b → cτν transitions in the standard model effective field theory. Eur. Phys. J. C 2019, 79, 264. [Google Scholar] [CrossRef]
- Asadi, P.; Shih, D. Maximizing the Impact of New Physics in b → cτν Anomalies. Phys. Rev. D 2019, 100, 115013. [Google Scholar] [CrossRef]
- Blanke, M.; Crivellin, A.; Kitahara, T.; Moscati, M.; Nierste, U.; Nišandžić, I. Addendum to“Impact of polarization observables and Bc → τν on new physics explanations of the b → cτν anomaly”. Phys. Rev. D 2019, 100, 035035. [Google Scholar] [CrossRef]
- Shi, R.X.; Geng, L.S.; Grinstein, B.; Jäger, S.; Camalich, J.M. Revisiting the new-physics interpretation of the b → cτν data. J. High Energy Phys. 2019, 12, 065. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Körner, J.G.; Tran, C.T. Analyzing new physics in the decays 0 → D(*)τ−τ with form factors obtained from the covariant quark model. Phys. Rev. D 2016, 94, 094028. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Körner, J.G.; Tran, C.T. Probing new physics in 0 → D(*)τ−τ using the longitudinal, transverse, and normal polarization components of the tau lepton. Phys. Rev. D 2017, 95, 036021. [Google Scholar] [CrossRef]
- Tran, C.T.; Ivanov, M.A.; Körner, J.G.; Santorelli, P. Implications of new physics in the decays Bc → (J/ψ, ηc)τν. Phys. Rev. D 2018, 97, 054014. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E.; Santorelli, P.; Tran, C.T. Analyzing lepton flavor universality in the decays Λb → (±,−)+ℓℓ. Phys. Rev. D 2018, 98, 053003. [Google Scholar] [CrossRef]
- Alok, A.K.; Kumar, D.; Kumbhakar, S.; Sankar, S.U. D* polarization as a probe to discriminate new physics in → D*τ. Phys. Rev. D 2017, 95, 115038. [Google Scholar] [CrossRef]
- Huang, Z.R.; Li, Y.; Lu, C.D.; Paracha, M.A.; Wang, C. Footprints of New Physics in b → cτν Transitions. Phys. Rev. D 2018, 98, 095018. [Google Scholar] [CrossRef]
- Iguro, S.; Kitahara, T.; Omura, Y.; Watanabe, R.; Yamamoto, K. D* polarization vs. RD(*) anomalies in the leptoquark models. J. High Energy Phys. 2019, 02, 194. [Google Scholar] [CrossRef]
- Abdesselam, A.; Adachi, I.; Adamczyk, K.; Ahn, J.K.; Aihara, H.; Al Said, S.; Arinstein, K.; Arita, Y.; Asner, D.M.; Atmacan, H.; et al. Measurement of the D*− polarization in the decay B0 → D*−τ+ντ. arXiv 2019, arXiv:1903.03102. [Google Scholar]
- Ivanov, M.A.; Körner, J.G.; Tran, C.T. Exclusive decays B → ℓ− and B → D(*)ℓ− in the covariant quark model. Phys. Rev. D 2015, 92, 114022. [Google Scholar] [CrossRef]
- Goldberger, W.D. Semileptonic B decays as a probe of new physics. arXiv 1999, arXiv:hep-ph/9902311. [Google Scholar]
- Buchmuller, W.; Wyler, D. Effective Lagrangian Analysis of New Interactions and Flavor Conservation. Nucl. Phys. B 1986, 268, 621. [Google Scholar] [CrossRef]
- Grzadkowski, B.; Iskrzynski, M.; Misiak, M.; Rosiek, J. Dimension-Six Terms in the Standard Model Lagrangian. J. High Energy Phys. 2010, 10, 085. [Google Scholar] [CrossRef]
- Hill, D.; John, M.; Ke, W.; Poluektov, A. Model-independent method for measuring the angular coefficients of B0 → D*−τ+ντ decays. J. High Energy Phys. 2019, 11, 133. [Google Scholar] [CrossRef]
- Branz, T.; Faessler, A.; Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E. Relativistic constituent quark model with infrared confinement. Phys. Rev. D 2010, 81, 034010. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Körner, J.G.; Kovalenko, S.G.; Santorelli, P.; Saidullaeva, G.G. Form factors for semileptonic, nonleptonic and rare B(Bs) meson decays. Phys. Rev. D 2012, 85, 034004. [Google Scholar] [CrossRef]
- Dubnička, S.; Dubničková, A.Z.; Ivanov, M.A.; Liptaj, A.; Santorelli, P.; Tran, C.T. Study of Bs → ℓ+ℓ−γ decays in covariant quark model. Phys. Rev. D 2019, 99, 014042. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E. Novel ideas in nonleptonic decays of double heavy baryons. Particles 2019, 2, 339. [Google Scholar] [CrossRef]
- Gutsche, T.; Ivanov, M.A.; Körner, J.G.; Lyubovitskij, V.E.; Santorelli, P.; Habyl, N. Semileptonic decay Λb → Λc + τ− + τ in the covariant confined quark model. Phys. Rev. D 2015, 91, 074001, Erratum: Phys. Rev. D 2015, 91, 119907. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Tran, C.T. Exclusive decays J/ψ → ℓ+νℓ in a covariant constituent quark model with infrared confinement. Phys. Rev. D 2015, 92, 074030. [Google Scholar] [CrossRef]
- Soni, N.R.; Ivanov, M.A.; Körner, J.G.; Pandya, J.N.; Santorelli, P.; Tran, C.T. Semileptonic D(s)-meson decays in the light of recent data. Phys. Rev. D 2018, 98, 114031. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Körner, J.G.; Pandya, J.N.; Santorelli, P.; Soni, N.R.; Tran, C.T. Exclusive semileptonic decays of D and Ds mesons in the covariant confining quark model. Front. Phys. (Beijing) 2019, 14, 64401. [Google Scholar] [CrossRef]
- Akeroyd, A.G.; Chen, C.H. Constraint on the branching ratio of Bc → τ from LEP1 and consequences for R(D(*)) anomaly. Phys. Rev. D 2017, 96, 075011. [Google Scholar] [CrossRef]
- Ivanov, M.A.; Körner, J.G.; Tran, C.T. Looking for new physics in leptonic and semileptonic decays of B-meson. Phys. Part. Nucl. Lett. 2017, 14, 669. [Google Scholar] [CrossRef]
- Alonso, R.; Grinstein, B.; Camalich, J.M. Lifetime of Constrains Explanations for Anomalies in B → D(*)τν. Phys. Rev. Lett. 2017, 118, 081802. [Google Scholar] [CrossRef]



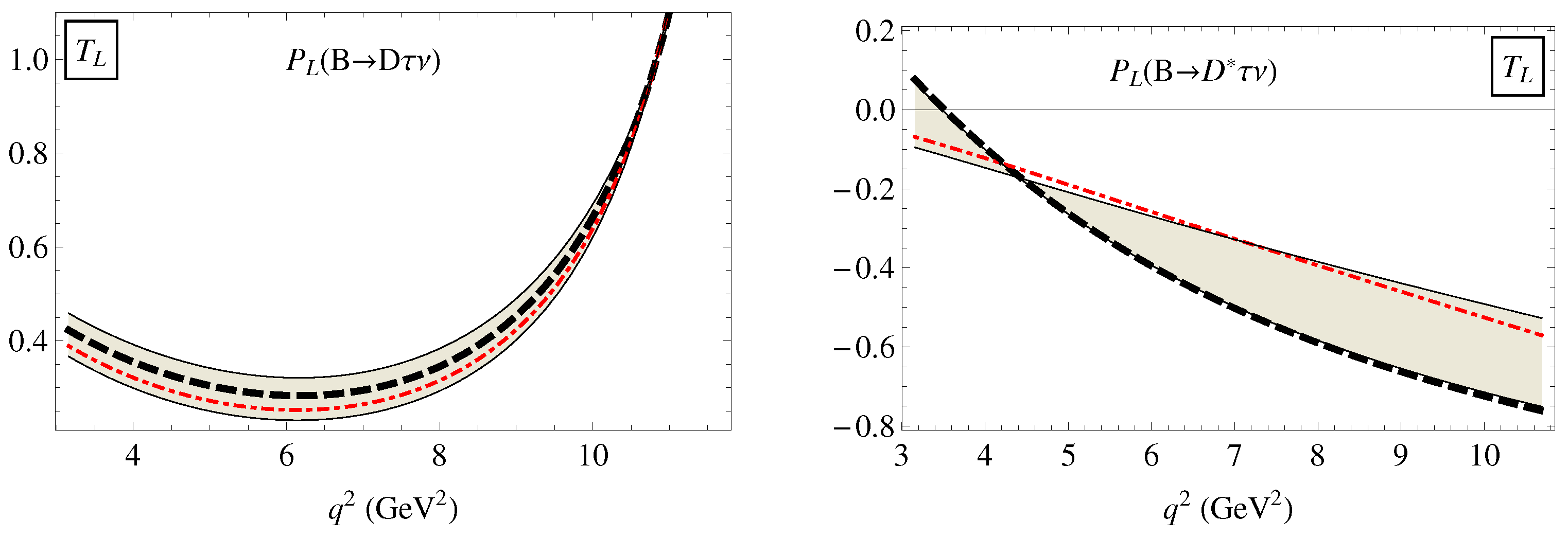
| V | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.62 | 0.67 | 0.77 | 0.73 | 0.79 | 0.80 | 0.77 | ||||||
| 0.34 | 0.87 | 0.89 | 0.90 | 0.87 | 1.23 | 0.90 | 0.88 | 0.75 | 0.77 | 0.22 | 0.76 | |
| 0.06 | 0.07 | 0.08 | 0.06 | 0.33 | 0.07 | 0.07 | 0.04 | 0.05 | 0.04 | |||
| 1.91 | 0.99 | 1.15 | 1.10 | 1.14 | 0.89 | 1.11 |
| V | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.65 | 0.55 | 0.78 | 0.56 | 0.75 | 0.69 | 0.93 | ||||||
| 1.19 | 1.68 | 1.85 | 1.82 | 1.84 | 2.16 | 1.86 | 1.91 | 1.31 | 1.25 | 0.68 | 1.30 | |
| 0.17 | 0.70 | 0.91 | 0.86 | 0.91 | 1.33 | 0.93 | 1.00 | 0.33 | 0.25 | 0.31 | ||
| 2.34 | 0.89 | 1.33 | 0.96 | 1.12 | 0.86 | 1.40 |
| SM | ||
| SM | ||||
| Best-fit | ||||
| Experiment | [6] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanov, M.A.; Körner, J.G.; Santorelli, P.; Tran, C.-T.
Ivanov MA, Körner JG, Santorelli P, Tran C-T.
Ivanov, Mikhail A., Jürgen G. Körner, Pietro Santorelli, and Chien-Thang Tran.
2020. "
Ivanov, M. A., Körner, J. G., Santorelli, P., & Tran, C.-T.
(2020).





