Nonperturbative Kinetic Description of Electron-Hole Excitations in Graphene in a Time Dependent Electric Field of Arbitrary Polarization
Abstract
1. Introduction
2. Kinetic Equation
2.1. The Low-Energy Approximation
2.2. Order Parameter
3. Observables
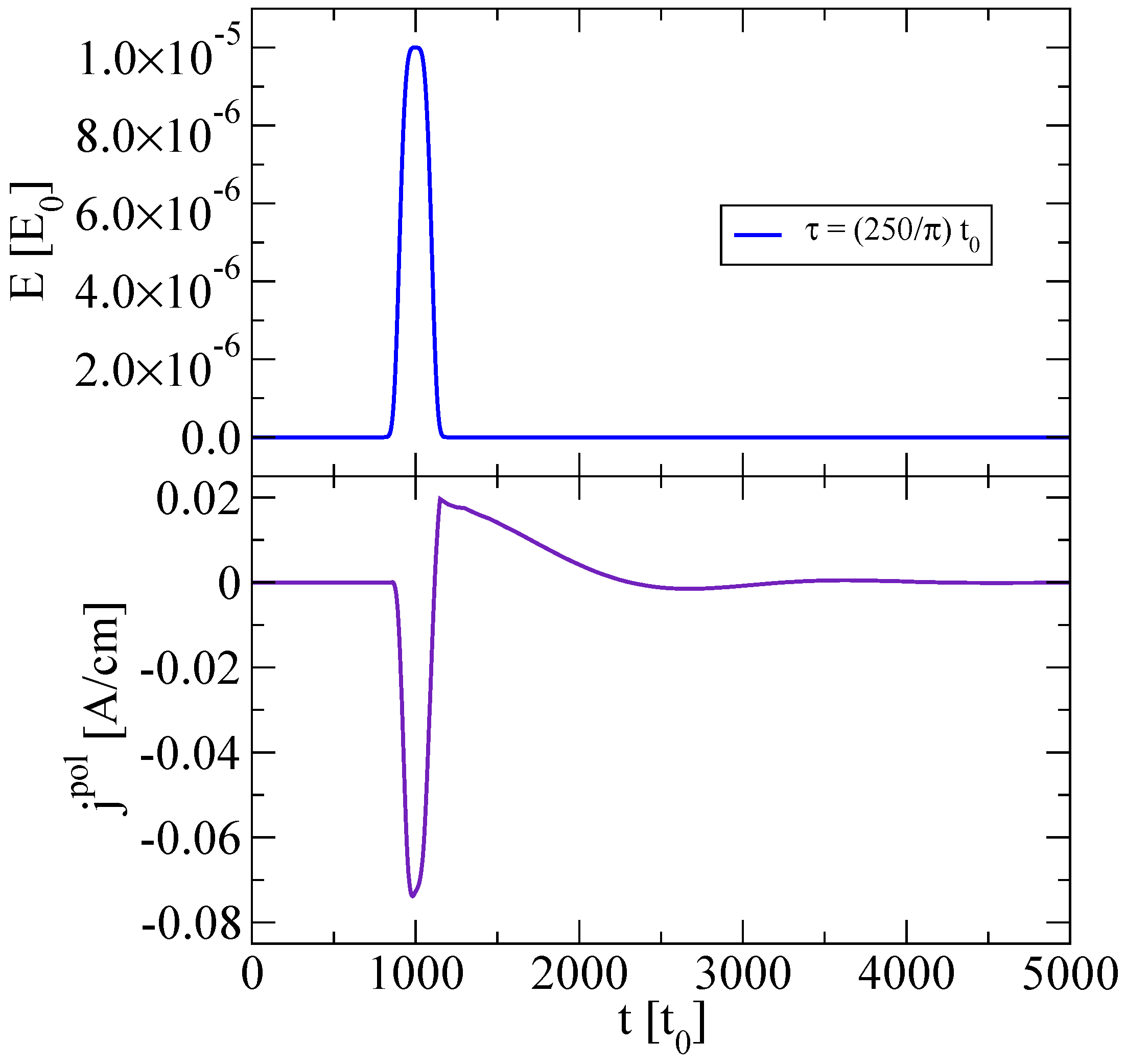
4. Residual Currents
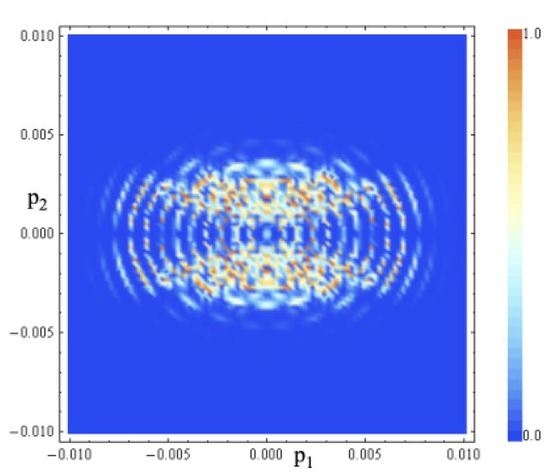
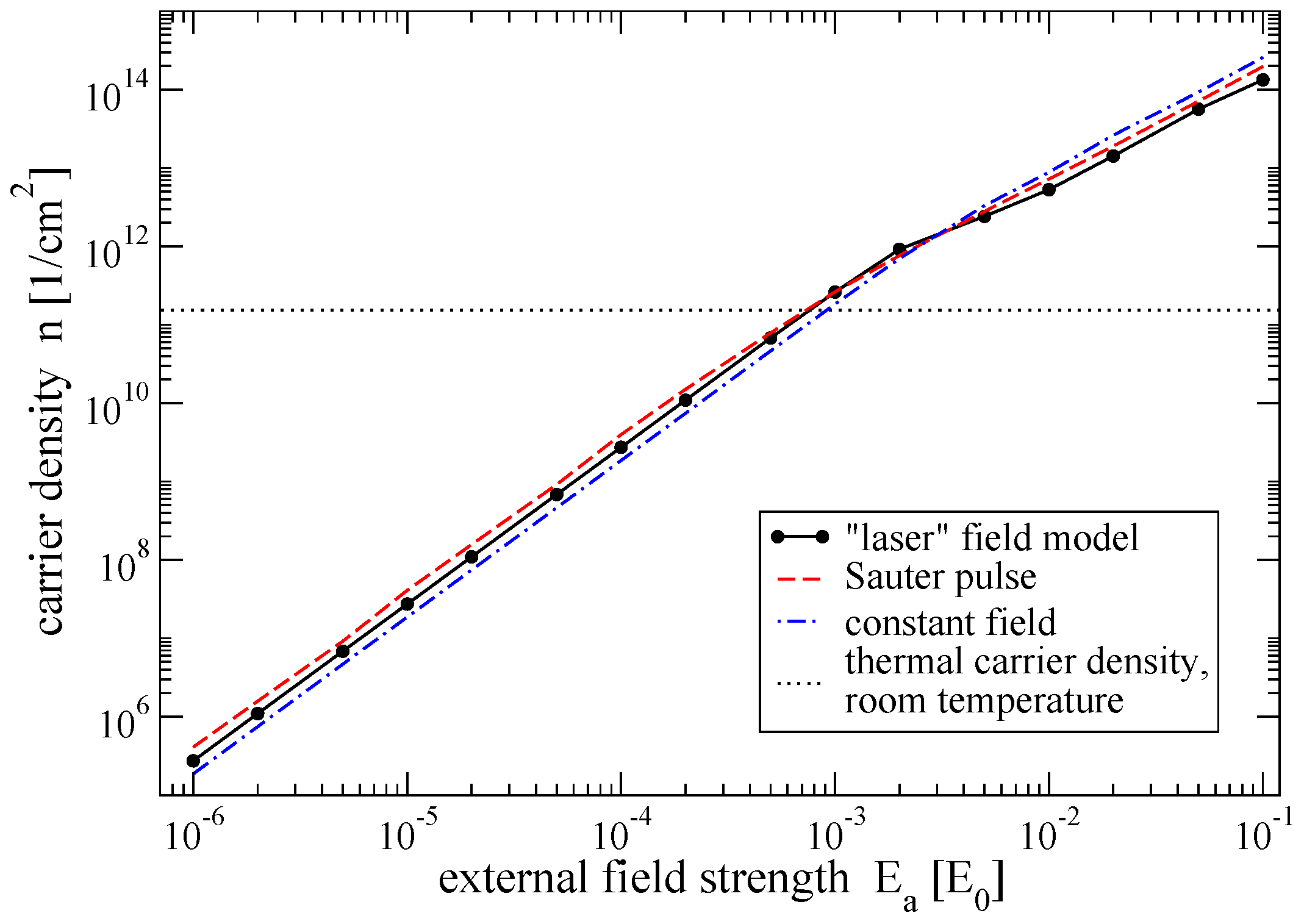
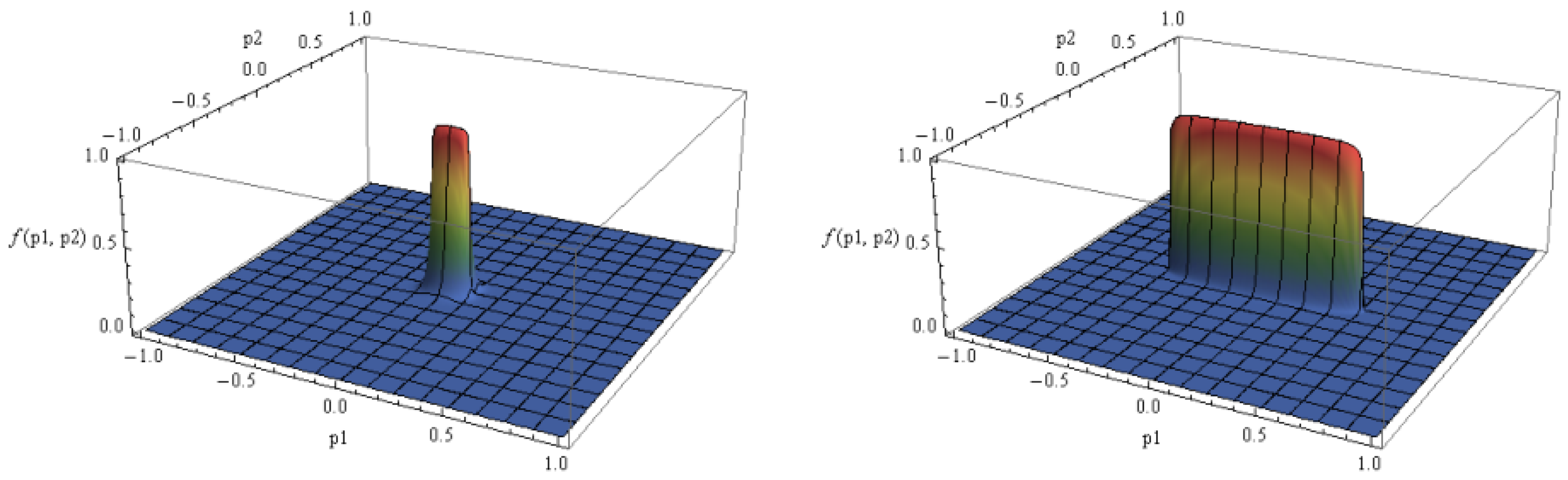
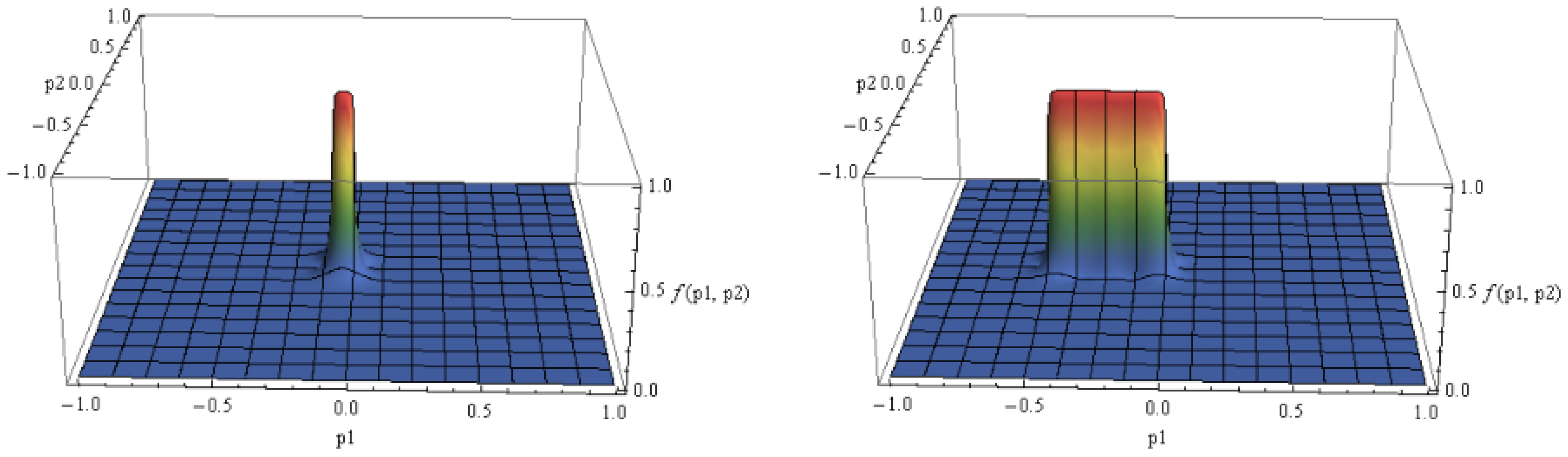
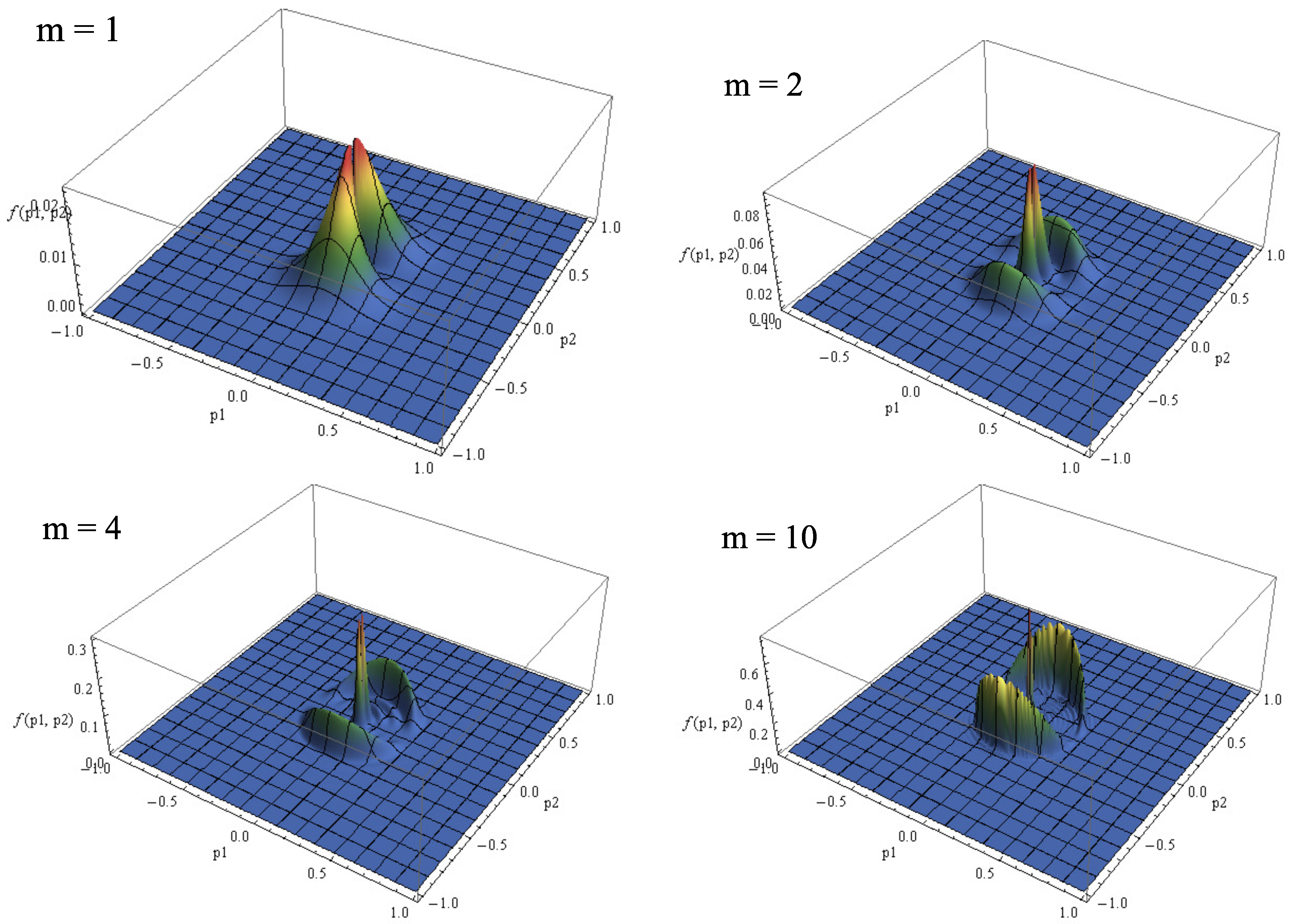
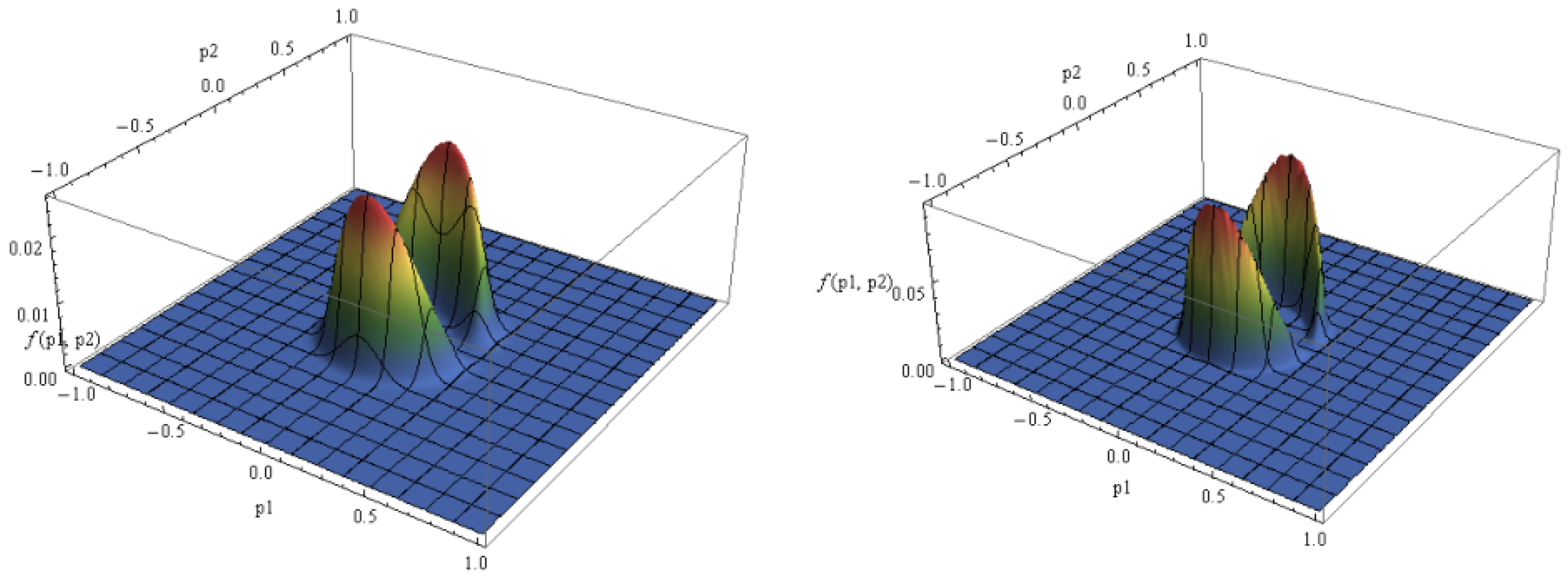
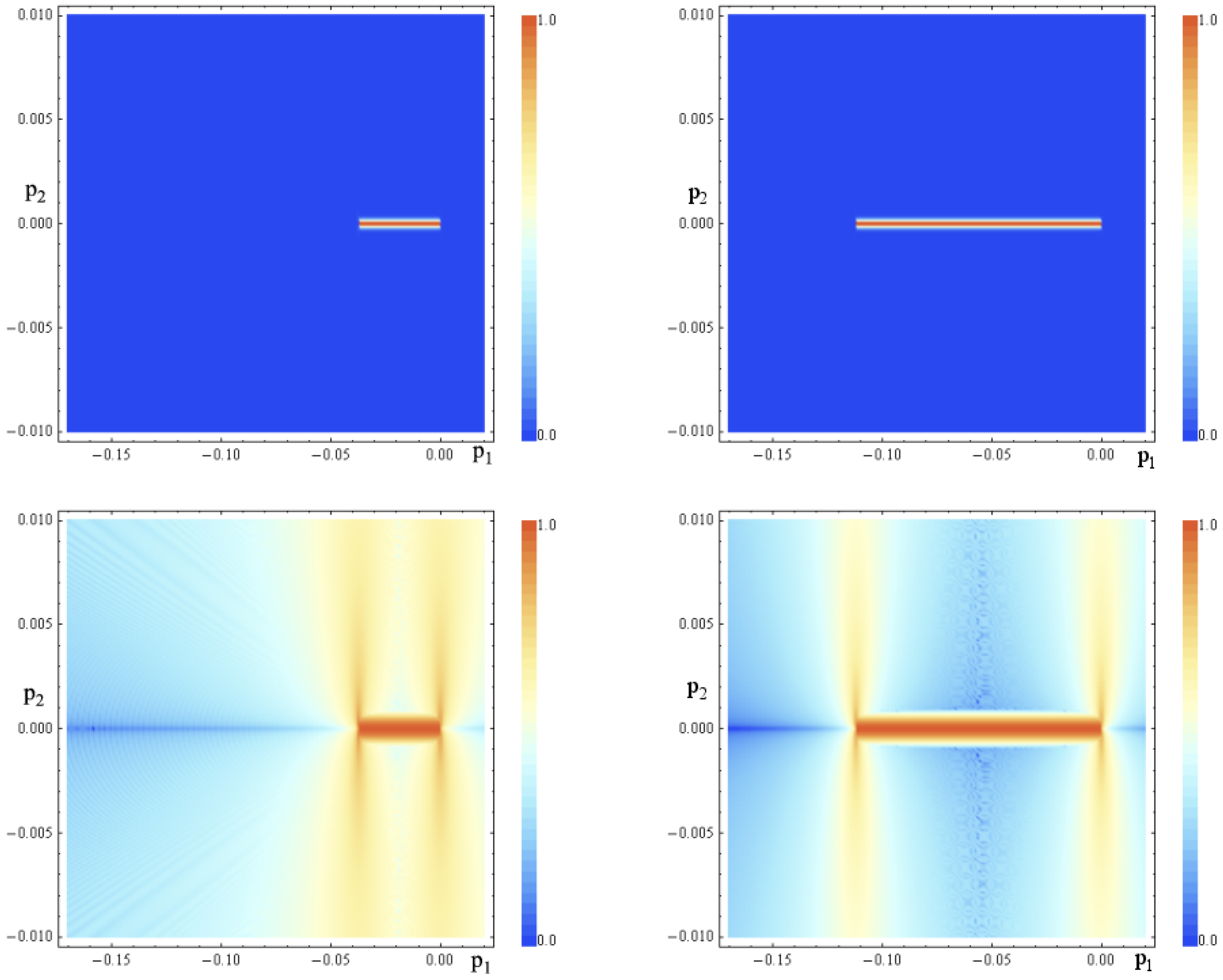
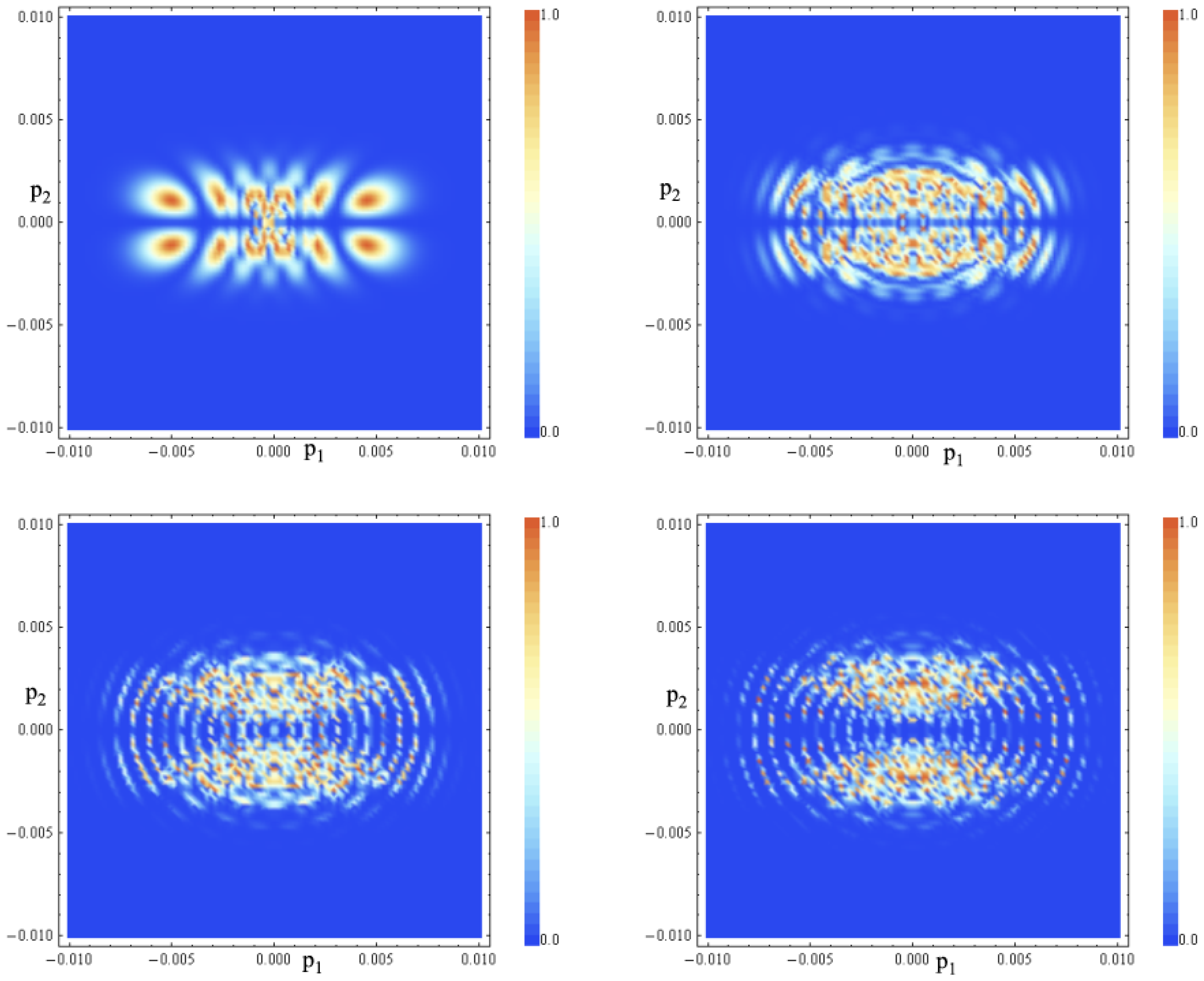
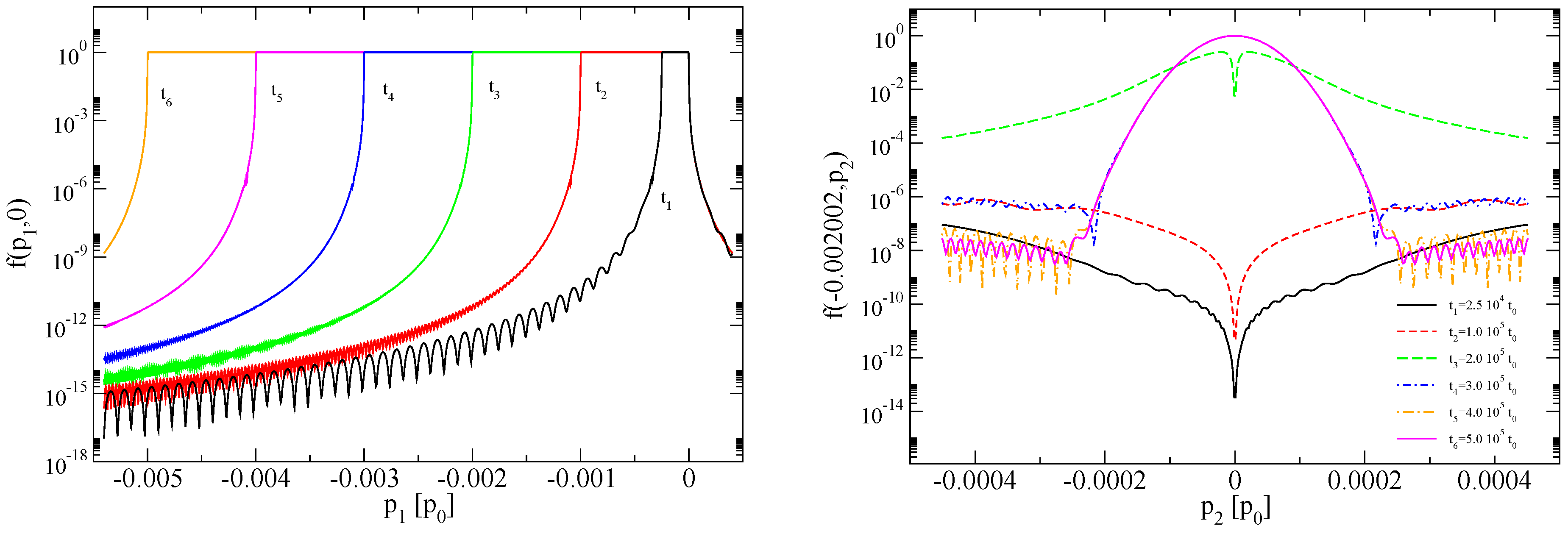
5. Numerical Analysis
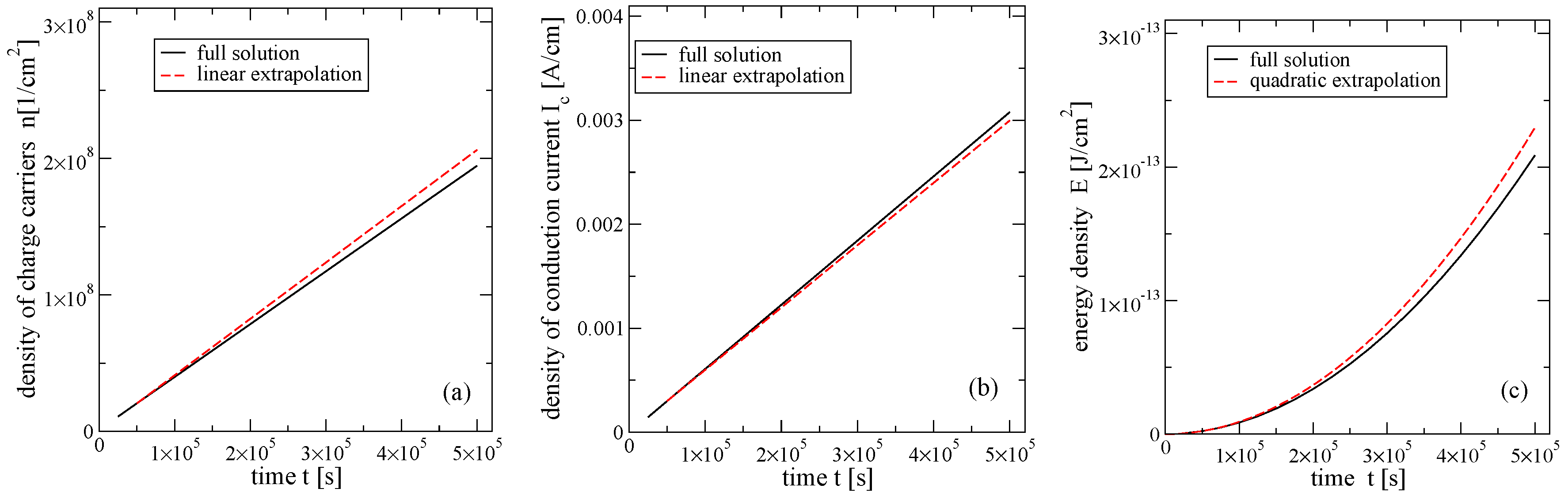
6. Graphene as Active Medium
7. Tight Binding Model
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Perturbation Theory
References
- Oka, T. Nonlinear doublon production in a Mott insulator: Landau-Dykhne method applied to an integrable model. Phys. Rev. 2012, B86, 075148. [Google Scholar] [CrossRef]
- Yokomizo, N. Radiation from electrons in graphene in strong electric field. Ann. Phys. 2014, 351, 166. [Google Scholar] [CrossRef][Green Version]
- Kao, H.C.; Lewkowicz, M.; Rosenstein, B. Ballistic transport, chiral anomaly and emergence of the neutral electron - hole plasma in graphene. Phys. Rev. 2010, B82, 035406. [Google Scholar] [CrossRef]
- Schwinger, J.S. On gauge invariance and vacuum polarization. Phys. Rev. 1951, 82, 664. [Google Scholar] [CrossRef]
- Fradkin, E.S.; Gitman, D.M.; Shvartsman, S.M. Quantum Electrodynamics with Unstable Vacuum; Springer: Berlin, Germany, 1991. [Google Scholar]
- Grib, A.A.; Mamaev, S.G.; Mostepanenko, V.M. Vacuum Quantum Effects in Strong External Fields; Friedmann Laboratory Publishing: St. Petersburg, Russia, 1994. [Google Scholar]
- Schmidt, S.M.; Blaschke, D.; Röpke, G.; Smolyansky, S.A.; Prozorkevich, A.V.; Toneev, V.D. A Quantum kinetic equation for particle production in the Schwinger mechanism. Int. J. Mod. Phys. 1998, E7, 709. [Google Scholar] [CrossRef]
- Blaschke, D.B.; Prozorkevich, A.V.; Röpke, G.; Roberts, C.D.; Schmidt, S.M.; Shkirmanov, D.S.; Smolyansky, S.A. Dynamical Schwinger effect and high-intensity lasers. realising nonperturbative QED. Eur. Phys. J. 2009, D55, 341. [Google Scholar] [CrossRef]
- Otto, A.; Nousch, T.; Seipt, D.; Kämpfer, B.; Blaschke, D.; Panferov, A.D.; Smolyansky, S.A.; Titov, A.I. Pair production by Schwinger and Breit? Wheeler processes in bi-frequent fields. J. Plasma Phys. 2016, 82, 655820301. [Google Scholar] [CrossRef]
- Blaschke, D.; Smolyansky, S.A.; Panferov, A.D.; Juchnowski, L. Particle Production in Strong Time-dependent Fields. In Proceedings of the Helmholtz International Summer School on Quantum Field Theory at the Limits: From Strong Fields to Heavy Quarks, Dubna, Russia, 18–30 July 2016. [Google Scholar]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. AC conductivity of graphene: from tight-binding model to 2+1-dimensional quantum electrodynamics. Int. J. Mod. Phys. 2007, B21, 4611. [Google Scholar] [CrossRef]
- Gavrilov, S.P.; Gitman, D.M.; Yokomizo, N. Dirac fermions in strong electric field and quantum transport in graphene. Phys. Rev. 2012, D86, 125022. [Google Scholar] [CrossRef]
- Klemchitskaya, G.L.; Mostepanenko, V.M. Creation of quasiparticles in graphene by a time-dependent electric field. Phys. Rev. 2013, D87, 125011. [Google Scholar] [CrossRef]
- Dora, B.; Moessner, R. Nonlinear electric transport in graphene: Quantum quench dynamics and the Schwinger mechanism. Phys. Rev. 2010, B81, 165431. [Google Scholar] [CrossRef]
- Smolyansky, S.A.; Panferov, A.D.; Blaschke, D.; Juchnowski, L.; Kämpfer, B.; Otto, A. Vacuum particle- antiparticle creation in strong fields as a field induced phase transition. Russ. Phys. J. 2017, 59, 1731–1738. [Google Scholar] [CrossRef]
- Fedotov, A.M.; Dmitriev, V.V.; Panferov, A.D.; Smolyansky, S.A. Spin Effects in Schwinger Pair Production: Quantum Kinetics vs. Imaginary Time. In Proceedings of the the 27th Annual International Laser Physics Workshop (LPHYS’18), Nottingham, UK, 16–20 July 2018. [Google Scholar]
- Kluger, Y.; Mottola, E.; Eisenberg, J.M. The Quantum Vlasov equation and its Markov limit. Phys. Rev. 1998, D58, 125015. [Google Scholar] [CrossRef]
- Bialynicky-Birula, I.; Gornicki, P.; Rafelski, J. Phase space structure of the Dirac vacuum. Phys. Rev. 1991, D44, 1825. [Google Scholar] [CrossRef]
- Pervushin, V.N.; Skokov, V.V. Kinetic description of fermion production in the oscillator representation. Acta Phys. Polon. 2006, B37, 2587. [Google Scholar]
- Filatov, A.V.; Prozorkevich, A.V.; Smolyansky, S.A. Pair creation by electromagnetic wave in a collisionless plasma. Proc. SPIE Int. Soc. Opt. Eng. 2006, 6165, 616509. [Google Scholar]
- Filatov, A.V.; Smolyansky, S.A.; Tarakanov, A.V. Kinetics of parton-antiparton plasma vacuum creation in the time—Dependent chromo—Electric fields of arbitrary polarization. arXiv, 2009; arXiv:0901.0522. [Google Scholar]
- Zeldovich, Y.B.; Starobinsky, A.A. Rate of particle production in gravitational fields. JETP Lett. 1977, 26, 252. [Google Scholar]
- Schmidt, S.M.; Blaschke, D.; Röpke, G.; Prozorkevich, A.V.; Smolyansky, S.A.; Toneev, V.D. NonMarkovian effects in strong field pair creation. Phys. Rev. 1999, D59, 094005. [Google Scholar]
- Beneventano, C.J.; Giacconi, P.; Santangelo, E.M.; Soldati, R. Planar QED at finite temperature and density: Hall conductivity, Berry’s phases and minimal conductivity of graphene. J. Phys. A Math. Theor. 2009, 42, 275401. [Google Scholar] [CrossRef]
- Bloch, J.C.; Mizerny, V.A.; Prozorkevich, A.V.; Roberts, C.D.; Schmidt, S.M.; Smolyansky, S.A.; Vinnik, D.V. Pair creation: Back reactions and damping. Phys. Rev. 1999, D60, 1160011. [Google Scholar] [CrossRef]
- Martin, P.; Schwinger, J. Theory of many particle systems. 1. Phys. Rev. 1959, 115, 1342. [Google Scholar] [CrossRef]
- Hebenstreit, F.; Alkofer, R.; Dunne, G.; Gies, H. Momentum signatures for Schwinger pair production in short laser pulses with sub-cycle structure. Phys. Rev. Lett. 2009, 102, 150404. [Google Scholar] [CrossRef]
- Fillion-Gourdeau, F.; MacLean, S. Time-dependent pair creation and the Schwinger mechanism in graphene. Phys. Rev. 2015, B92, 035401. [Google Scholar] [CrossRef]
- Zubkov, M.A. Schwinger pair creation in multilayer graphene. JETP Lett. 2012, 95, 476. [Google Scholar] [CrossRef]
- Panferov, A.; Smolyansky, S.; Blaschke, D.; Gevorgyan, N. Comparing two different descriptions of the I-V characteristic of graphene: theory and experiment. EPJ Web Conf. 2019, 204, 06008. [Google Scholar] [CrossRef]
- Vandecasteele, N.; Barreiro, A.; Lazzeri, M.; Bachtold, A.; Mauri, F. Current-voltage characteristics of graphene devices: Interplay between Zener-Klein tunneling and defects. Phys. Rev. 2010, B82, 045416. [Google Scholar] [CrossRef]
- Blaschke, D.B.; Kämpfer, B.; Schmidt, S.M.; Panferov, A.D.; Prozorkevich, A.V.; Smolyansky, S.A. Properties of the electron-positron plasma created from a vacuum in a strong laser field: Quasiparticle excitations. Phys. Rev. 2013, D88, 045017. [Google Scholar] [CrossRef]
- Vajna, S.; Dora, B.; Moessner, R. Nonequilibrium transport and statistics of Schwinger pair production in Weyl semimetals. Phys. Rev. 2015, B92, 085122. [Google Scholar] [CrossRef]
- Ludwig, A.W.W.; Fisher, M.P.A.; Shankar, R.; Grinstein, G. Integer quantum Hall transition: An alternative approach and exact results. Phys. Rev. 1994, B50, 7526. [Google Scholar] [CrossRef]
- Ziegler, K. Robust Transport Properties in Graphene. Phys. Rev. Lett. 2006, 97, 266802. [Google Scholar] [CrossRef]
- Ziegler, K. Minimal conductivity of graphene: Nonuniversal values from the Kubo formula. Phys. Rev. 2007, B75, 233407. [Google Scholar] [CrossRef]
- Ryu, S.; Mudry, C.; Furusaki, A.; Ludwig, A.W.W. Landauer conductance and twisted boundary conditions for Dirac fermions in two space dimensions. Phys. Rev. 2007, B75, 205344. [Google Scholar] [CrossRef]
- Cserti, J. Minimal longitudinal dc conductivity of perfect bilayer graphene. Phys. Rev. 2007, B75, 033405. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smolyansky, S.A.; Panferov, A.D.; Blaschke, D.B.; Gevorgyan, N.T. Nonperturbative Kinetic Description of Electron-Hole Excitations in Graphene in a Time Dependent Electric Field of Arbitrary Polarization. Particles 2019, 2, 208-230. https://doi.org/10.3390/particles2020015
Smolyansky SA, Panferov AD, Blaschke DB, Gevorgyan NT. Nonperturbative Kinetic Description of Electron-Hole Excitations in Graphene in a Time Dependent Electric Field of Arbitrary Polarization. Particles. 2019; 2(2):208-230. https://doi.org/10.3390/particles2020015
Chicago/Turabian StyleSmolyansky, Stanislav A., Anatolii D. Panferov, David B. Blaschke, and Narine T. Gevorgyan. 2019. "Nonperturbative Kinetic Description of Electron-Hole Excitations in Graphene in a Time Dependent Electric Field of Arbitrary Polarization" Particles 2, no. 2: 208-230. https://doi.org/10.3390/particles2020015
APA StyleSmolyansky, S. A., Panferov, A. D., Blaschke, D. B., & Gevorgyan, N. T. (2019). Nonperturbative Kinetic Description of Electron-Hole Excitations in Graphene in a Time Dependent Electric Field of Arbitrary Polarization. Particles, 2(2), 208-230. https://doi.org/10.3390/particles2020015