Seismic Assessment of an Existing Precast Reinforced Concrete Industrial Hall Based on the Full-Scale Tests of Joints—A Case Study

Abstract

Construction of precast reinforced concrete (PRC) industrial halls in seismically active areas has been increasing in recent decades. As connections are one of the most sensitive and vulnerable zones of PRC structures, there is a need to pay special attention to their investigation and modeling in seismic analysis. Knowing that each PRC system is specific and unique, this study aims to evaluate the actual seismic performances of PRC industrial halls built in the AMONT system, which represent a significant portion of the existing industrial building stock in Italy, the Balkans, and Turkey. As there is a lack of published research data on its specific joints, the results of the quasi-static full-scale experiments carried out up to failure on the models of four characteristic connections are presented. Since the implementation of nonlinear dynamic analysis in everyday engineering practice can be demanding, a simplified model of the structure considering the effects of the connections’ stiffness is proposed in this paper. The differences in the roof top displacements between the proposed model and the model with the rigid joints of the analyzed frames are in the range from 16.53% to 66.93%. The values of inter-story drift ratios are larger by 10–100% when the real stiffness of connections is considered, which is above the limit value provided by standard EN 1998-1. These results confirm the necessity of considering the nonlinear behavior and stiffness of connections in precast frame structures when determining displacements, which is particularly important for the verification of the serviceability limit state of structures in seismic regions.

1. Introduction

The industrialization of certain regions in the world has caused a sharp increase in the construction of industrial halls, whereby the most common types are precast reinforced concrete (PRC) structures, even in seismically active areas, due to the known advantages such as increased speed of construction, improved quality control due to the member-fabrication environment, and reduced site formwork and labor. It is particularly important to recognize that in the design phase, industrial halls have to be treated completely separately from other building-type structures. Structural systems of industrial halls differ from other building structures because floor heights are significantly higher, and spans of main roof beams and floor beams are larger than those of ordinary buildings. Due to the large dimensions of industrial halls, almost all prefabricated elements are large in size and weight. Some halls, especially two-storey and multi-storey ones, can be designed for large payloads, and so in the event of an earthquake, due to the large mass, seismic forces of considerable intensity can be generated, which can cause damage or total collapse of buildings. All of those differences, and differences typical for implementation of precast reinforced concrete construction systems, highly contribute to the existence of very different characteristics of dynamic structural response and resulting damage and failure modes under moderate and strong earthquake ground motions.

Although the total number of industrial structures located in earthquake-prone areas is usually limited, their failure may lead to severe social and economic consequences. Past earthquakes clearly demonstrated the vulnerability of precast reinforced concrete (PRC) industrial buildings when seismic resistance was not adequately considered. For instance, during the 1976 Friuli earthquakes in Italy, a large number of industrial buildings suffered extensive damage or collapse due to the absence of seismic design provisions in the adopted PRC systems [1]. Similarly, the 2012 Emilia-Romagna earthquake revealed deficiencies related to inadequate seismic design and construction details of PRC structures, whereas properly designed and detailed buildings generally exhibited satisfactory performance, as reported by post-earthquake investigations [2]. Turkey is one of the most seismically active regions with short earthquake return periods. In recent decades, destructive earthquakes such as the 2020 Elazığ-Sivrice and 2023 Kahramanmaraş events caused significant casualties and structural damage. In PRC industrial halls, the damage was largely due to design and construction inadequacies, and deficiencies in critical joints, particularly hinged column-to-rafter and column-to-foundation connections [3]. Similarly, Japan, prone to frequent earthquakes, reinforced its seismic evaluation and retrofit legislation after the 1995 Kobe earthquake, leading to improved performance of existing RC buildings, as confirmed during the 2011 Tohoku and 2016 Kumamoto earthquakes [4]. These and other past earthquakes [5,6,7,8,9,10] highlight the need for thorough experimental, numerical, and analytical studies to enhance seismic performance of industrial structures.

Extensive research conducted since the 1980s has led to the development of precast concrete structural systems and detailing solutions suitable for application in regions of high seismic hazard. A comprehensive review of these advances, including code developments and practical applications, is presented in [11], where it was concluded that the use of precast concrete in seismic regions is feasible and can provide satisfactory seismic performance when appropriately designed.

Stability and seismic performance of precast reinforced concrete (PRC) structural systems largely depend on the behavior of their connections, which have been identified as the most vulnerable components based on damage observations from past earthquakes. Consequently, significant experimental and numerical research has been devoted to the study of PRC connections.

These studies have consistently shown that connections in precast structures exhibit semi-rigid behavior rather than idealized pinned or fully rigid behavior. The influence of connection rigidity on the seismic response of precast concrete frames has been investigated within the framework of the European COST C1 project and by several authors who emphasized the need to consider connection rigidity as a design parameter [12,13]. Experimental investigations, including full-scale tests, further contributed to the characterization and modeling of beam-to-column connections in precast concrete structures [14]. Analytical studies on the behavior of precast reinforced concrete (PRC) beam-to-column connections have led to the development of various modeling approaches, including section-based methods and analytical models for predicting shear resistance and nonlinear response under seismic excitation [15,16,17]. These studies highlighted significant differences in seismic response between precast and monolithic RC frames, emphasizing the need for nonlinear models specifically tailored for precast systems.

In parallel, extensive experimental research has been conducted on PRC connections, involving both full-scale and scaled specimens, with the aim of improving connection design and calibrating numerical models [18,19,20]. Based on these experimental results, numerous numerical models have been developed to simulate different types of beam-to-column and slab–beam–column connections, including dowel, hybrid, and mechanical solutions [21,22,23,24,25,26,27,28,29,30,31,32].

Despite these advances, investigations focusing on the seismic performance of entire precast concrete frame structures explicitly incorporating realistic connection behavior remain relatively limited. Experimental studies on multi-story precast frames subjected to quasi-static cyclic loading demonstrated the significant influence of connection behavior on the global seismic response [33,34,35].

Several authors have addressed the numerical analysis of entire precast reinforced concrete (PRC) structures to investigate their seismic behavior. Comparative studies between precast and monolithic RC frames, and parametric analyses focusing on different modeling assumptions for precast systems, have been reported [36,37]. Numerical investigations of industrial single-story PRC buildings considering variations in structural configuration and seismic hazard levels have also been performed according to the current design codes [38]. Industrial precast reinforced concrete (PRC) buildings have specific characteristics that require careful consideration in seismic assessment. Several studies evaluated the influence of different modeling assumptions, including beam-to-column connections, roof-to-beam connections, system mass, and cladding, on both local and global seismic response [39,40,41]. One important conclusion from Fischinger et al. [21] highlights that minor differences in connection details can significantly alter structural behavior, and that experimental verification and inelastic analyses are essential for large-series prefabricated buildings in seismically active zones.

Existing PRC industrial buildings, especially those constructed before modern seismic design knowledge, have been the subject of a few vulnerability studies. Bosio et al. [42,43] investigated single-story PRC buildings in Italy to assess probabilistic seismic vulnerability and the effect of modeling choices on risk and retrofit requirements. Similarly, Batalha et al. [44] analyzed six Portuguese PRC buildings with common beam-to-column connections (pure friction and mechanical dowels), evaluating both local and global response under nonlinear static and dynamic analyses.

The main research objective of this study is to show how the outcomes from full-scale experiments of connections affect the structural analysis results and design procedures. The importance of experimental data for the creation of a reliable numerical model for dynamic analysis of a system with semi-rigid connections, such as PRC industrial halls, is pointed out. The description and results of the quasi-static full-scale experiments carried out up to failure on the models of four characteristic connections of the existing industrial building are presented. These results confirm the necessity of considering the nonlinear behavior and stiffness of connections in precast frame structures when determining displacements, which is particularly important for the verification of the serviceability limit state of structures in seismic regions. The simplified approach for taking into account stiffness reduction due to nonlinear behavior of element connections is proposed in the paper and applied for seismic behavior assessment of the case study structure. This approach is also applicable for seismic risk assessment of existing industrial halls and commercial buildings constructed in the considered structural system, and for other PCR systems which are produced industrially in large series and which are designed for seismically active regions.

2. Case Study

The prototype of the hall (Figure 1) for the purpose of the numerical research was constructed according to the AMONT System (Morava Krušce) in Niš, Serbia. It was chosen considering that full-size tests of its connections had been previously conducted [45,46], but the recorded integral original results have not been presented or published in detail to date. Using unique, full-scale experimental test results, even if conducted nearly 30 years ago, is highly valuable today because of its direct applicability. Since the structural system has not changed, these results represent the “true” behavior of the current building stock in the Balkans, Italy, and Turkey. The results obtained from the conducted extensive experimental full-scale testing of the selected characteristic structural joints are highly important for advanced nonlinear modeling of this specific PRC system. Accurate modeling based on original tests allows engineers to design targeted retrofitting solutions where the original joints are most vulnerable.

The existing hall is a spacious two-storey frame structure, and it is intended for storage of electrical materials and home appliances. The building was designed according to the previous Serbian (former Yugoslav) code for the VIII seismic zone according to the MCS scale, which can approximately correspond to the peak acceleration of PGA = 0.20 g, but no direct dynamic analyses were performed. Only standard static analyses of the action of defined seismic forces for the transverse and longitudinal directions of the structure were performed. Therefore, this building was a suitable prototype for the realization of specific research for various seismic actions. In this way, and especially since the full-size tests of its connections were performed on the basis of which the results applied in this analysis were obtained, it was possible to give a much more accurate assessment of the structural system behavior and draw relevant conclusions about the degree of seismic resistance of the system in the zones of different seismic intensity.

The facility was built in 1986. An on-site inspection of the building revealed that the building exhibited no noticeable structural or non-structural damage. The general conclusion was that the behavior of the facility during the previous service period was satisfactory. This indicates the fact that the quality of the installed materials and the quality of the prefabricated elements as a whole are at a satisfactory level.

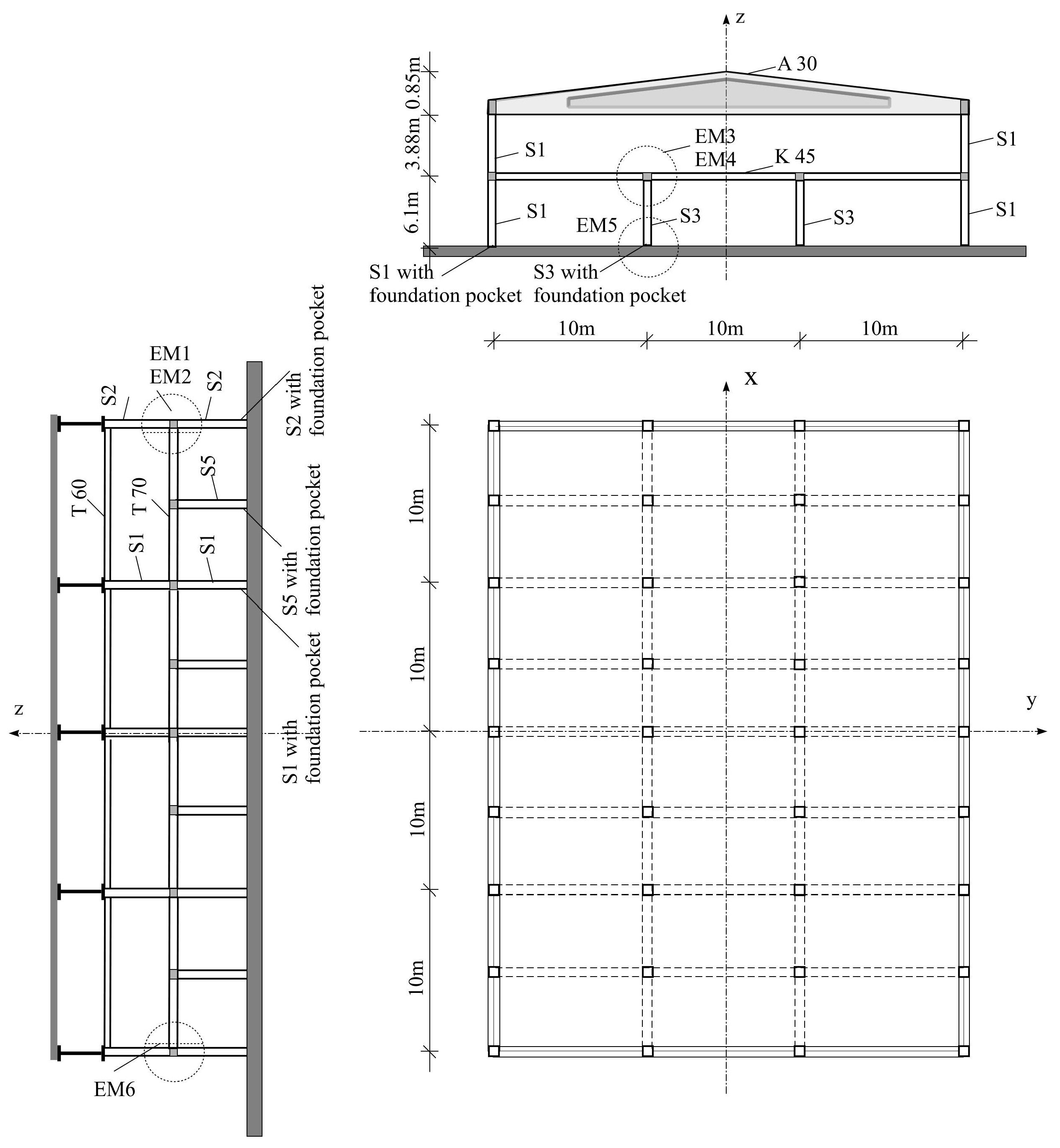
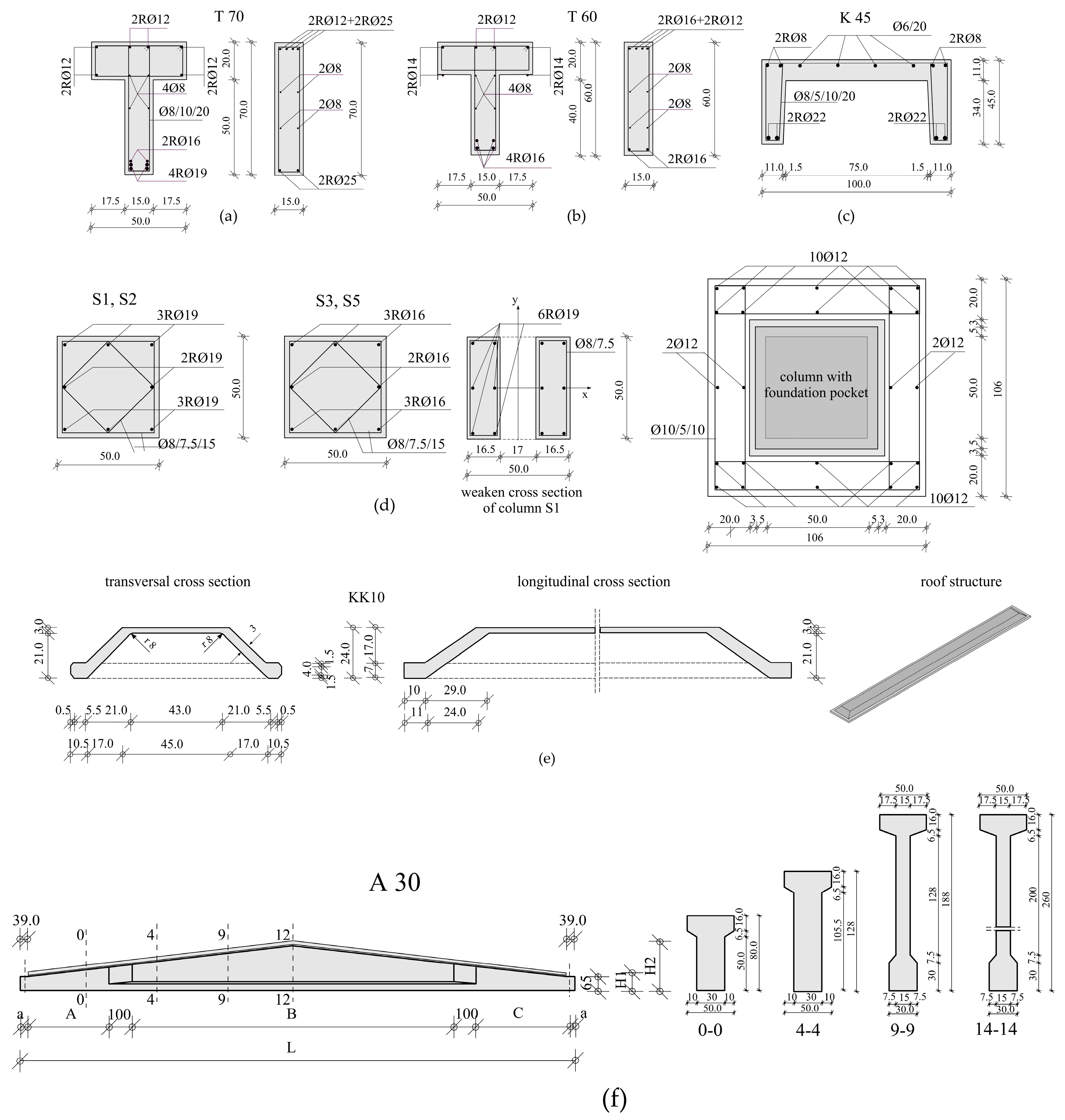
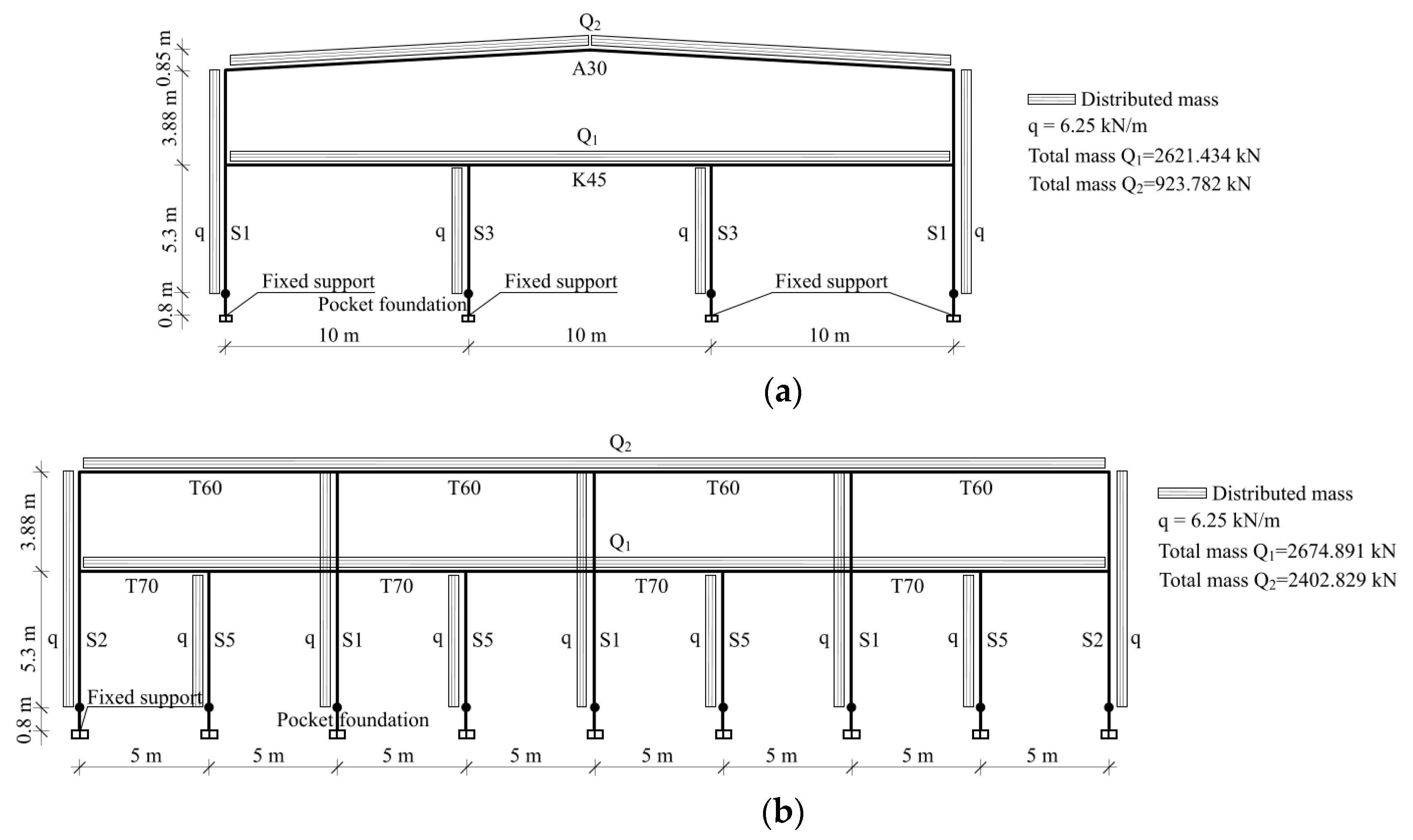
2.1. Structure Description

The basic structural system of the building, whose layout and cross-sections are shown in Figure 2, consists of the prefabricated structural elements shown in Figure 3. The real joints of the prototype hall, constructed according to the AMONT System, are represented in Figure 4.

The structure consists of precast columns, floor beams, floor structure, and roof beams.

The main roof beams carry the roof elements. They are designed as beams of variable height, with a two-sided slope of the upper edge of about 12°, designated as A-30 (Figure 2 and Figure 3f). The main roof beams are made of concrete class C40 (C40 stands for the 40 MPa concrete compressive strength obtained experimentally on the cube specimens with an edge size of 200 mm). The main roof girders A-30 are adhesively pre-stressed with a span of 30.0 m, with an I-shaped cross-section at the point of support, which gradually forms into a T-shaped cross-section with a height of 80 cm, while in the middle of the span, its height is 260 cm. In addition to the reinforcement cables, 7 rows of 7 cables 7ϕ3 arranged in the lower zone of the beam, it is also reinforced by the non-structural reinforcement 6 Rϕ16 at the beam flange, 4 Rϕ16 at the bottom flange of the beam, and 22 Rϕ16 in the beam web. Secondary girders on the roof level (connecting girders) extend in the longitudinal direction of the building. They are designed as T-60 (designation stands for “T” cross-section and cross-section height) of constant height and span of 10.0 m (Figure 2 and Figure 3b), and made of concrete class C30.

The floor structure is made of trapezoidal elements designated as K45 (Figure 2 and Figure 3c), made of C40 concrete.

The main girders of the floor carry the floor slabs. These girders extend in the longitudinal direction of the object. They are of constant height, span 5 m, and are designed as T-90 in the central part and as T-70 (Figure 2 and Figure 3a) around the perimeter of the structure. The secondary girders of the floor extend in the transverse direction only around the perimeter of the building and are designed as T-40, constant height, and span of 10.0 m. The floor girders are made of concrete class C30.

All columns are prefabricated, square cross-section 50/50 cm, fixed in foundation pockets, and made of concrete class C30.

The building is entirely founded on the foundation footings. The peripheral parapet walls were constructed on the foundation beams designed for this purpose. The building is on the façade, enclosed by prefabricated façade corrugated elements.

Connection of precast elements is completed by anchors, welding, and grouting with small-sized aggregate concrete. This procedure is known as the wet procedure.

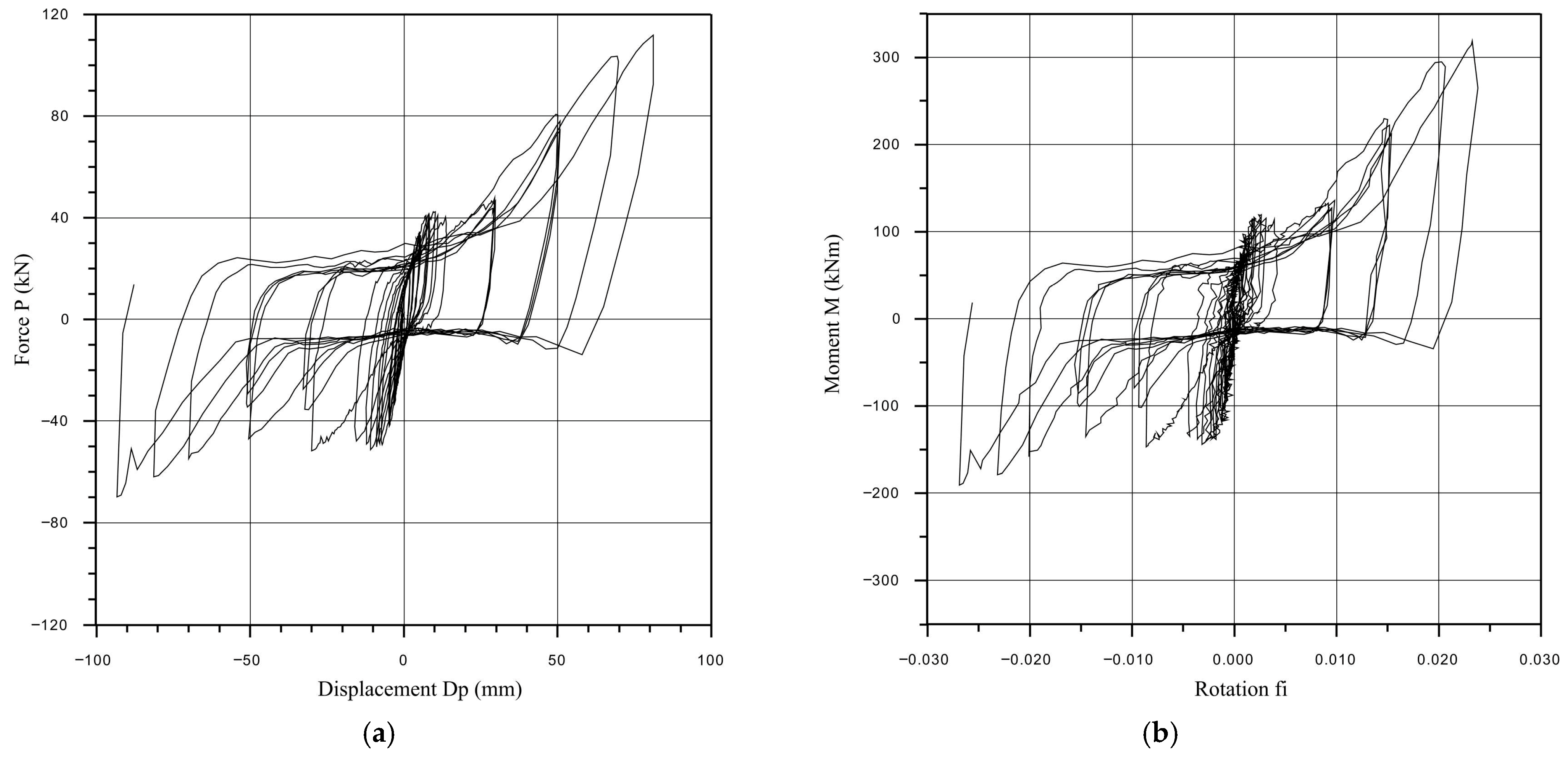
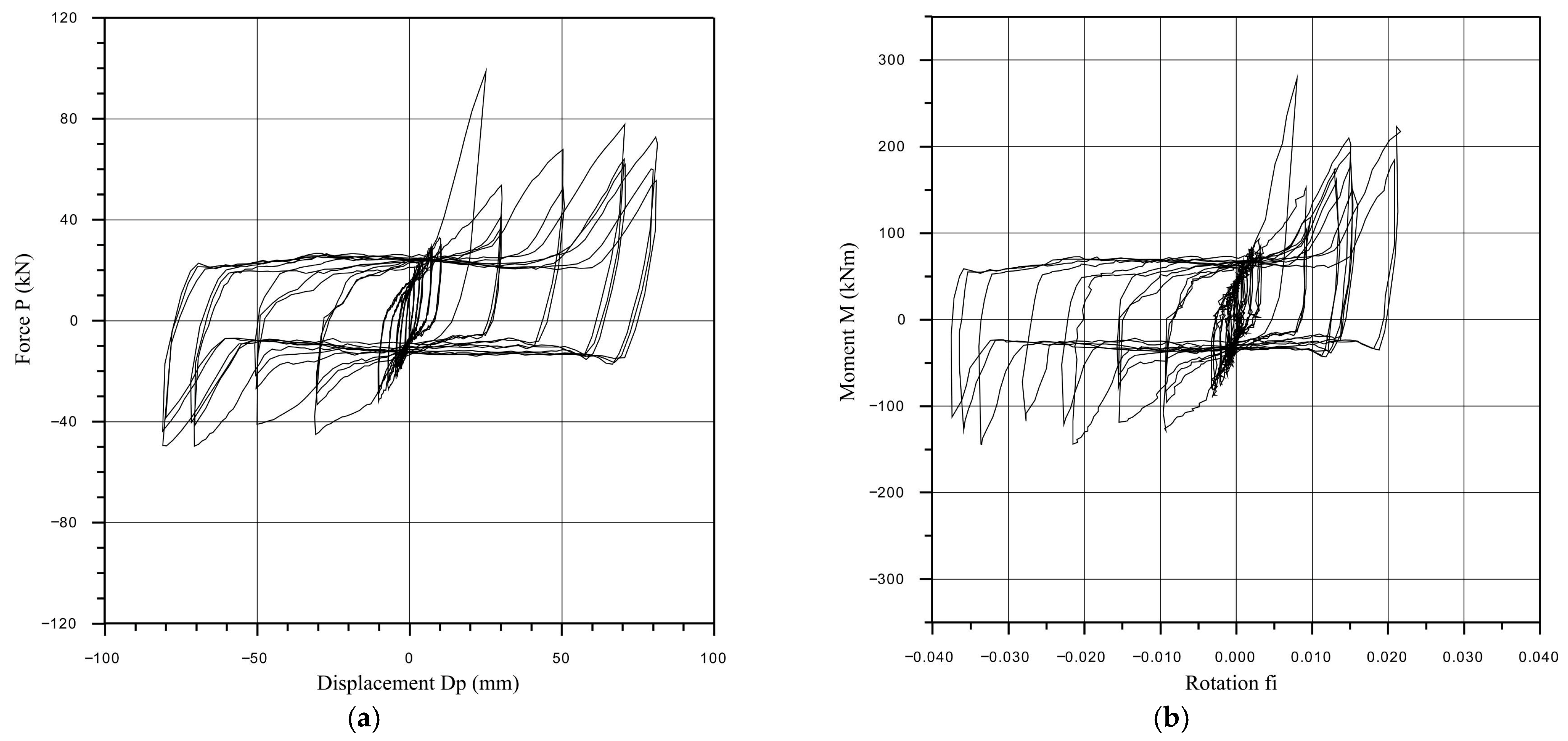
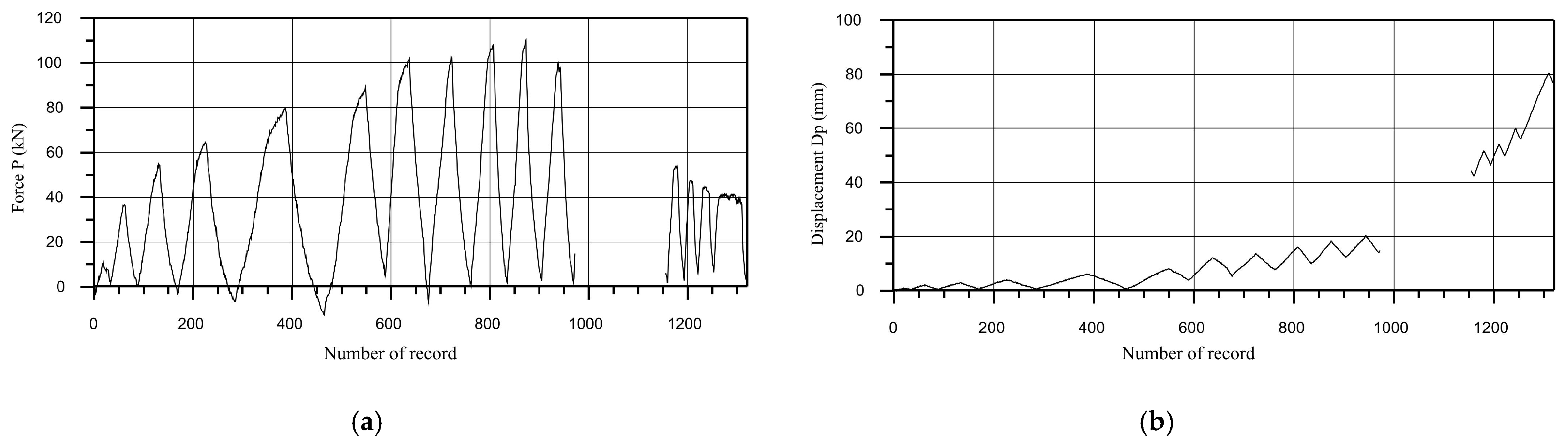
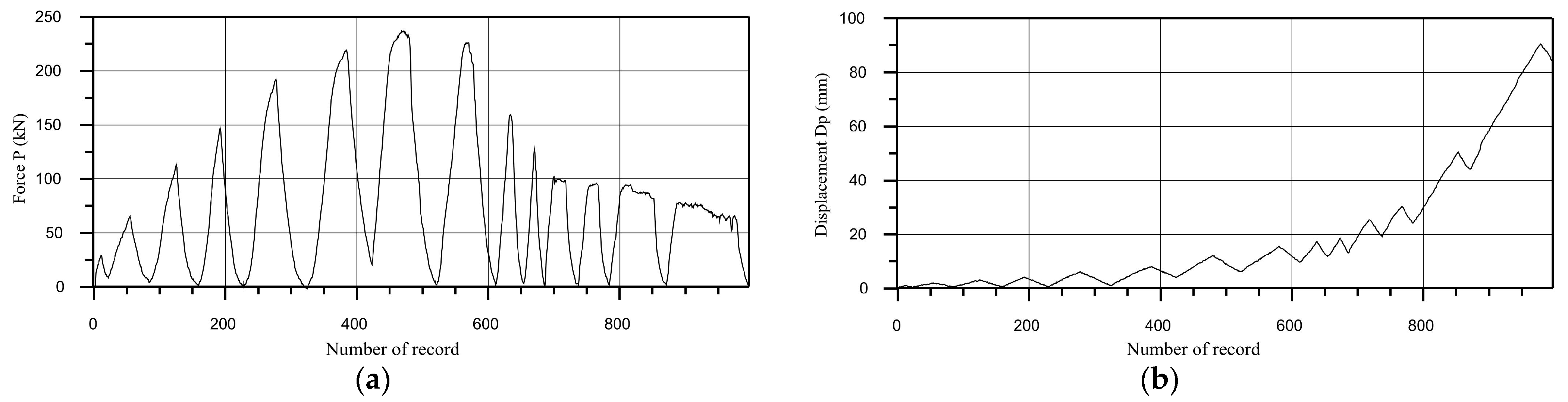
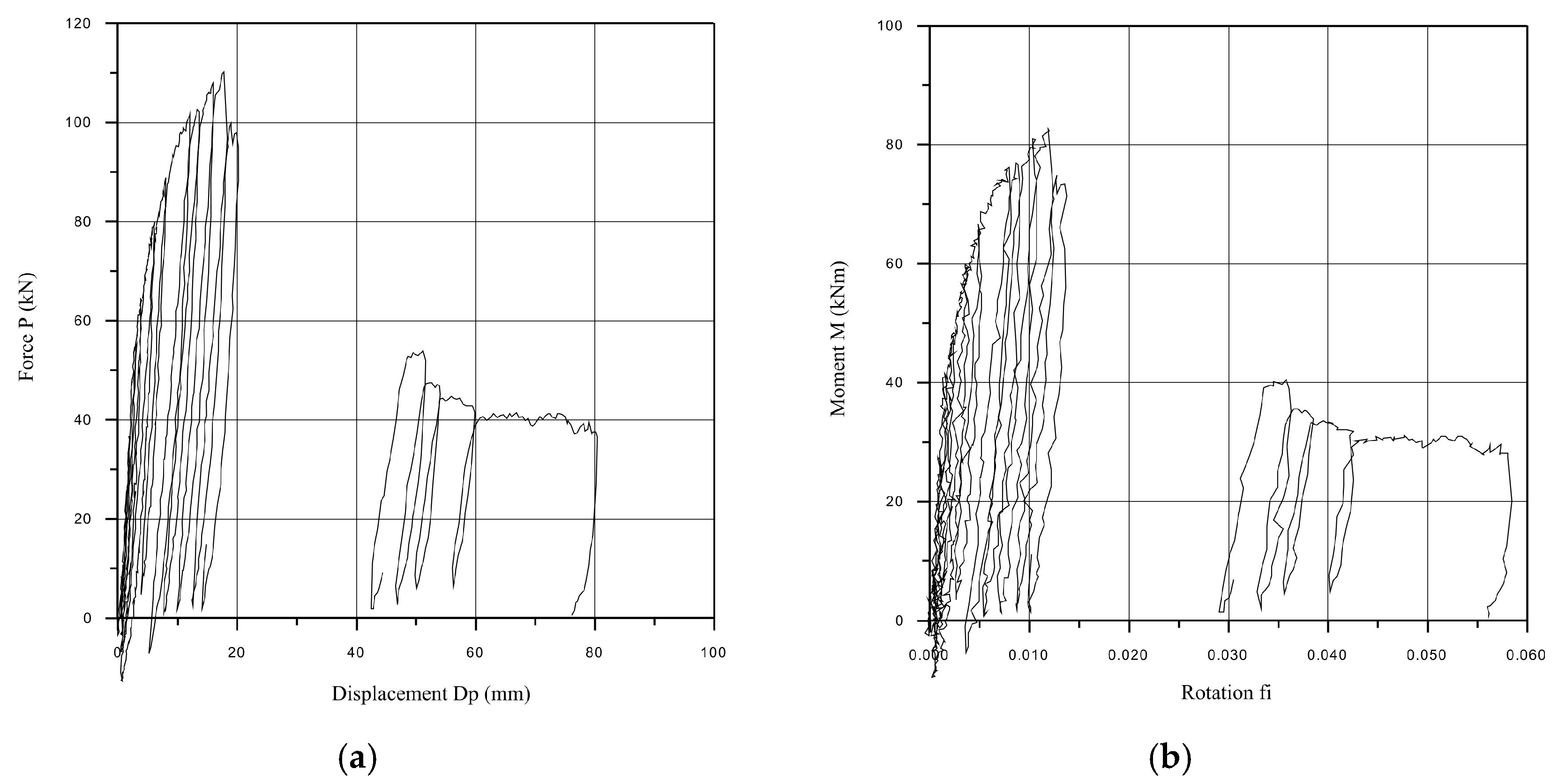
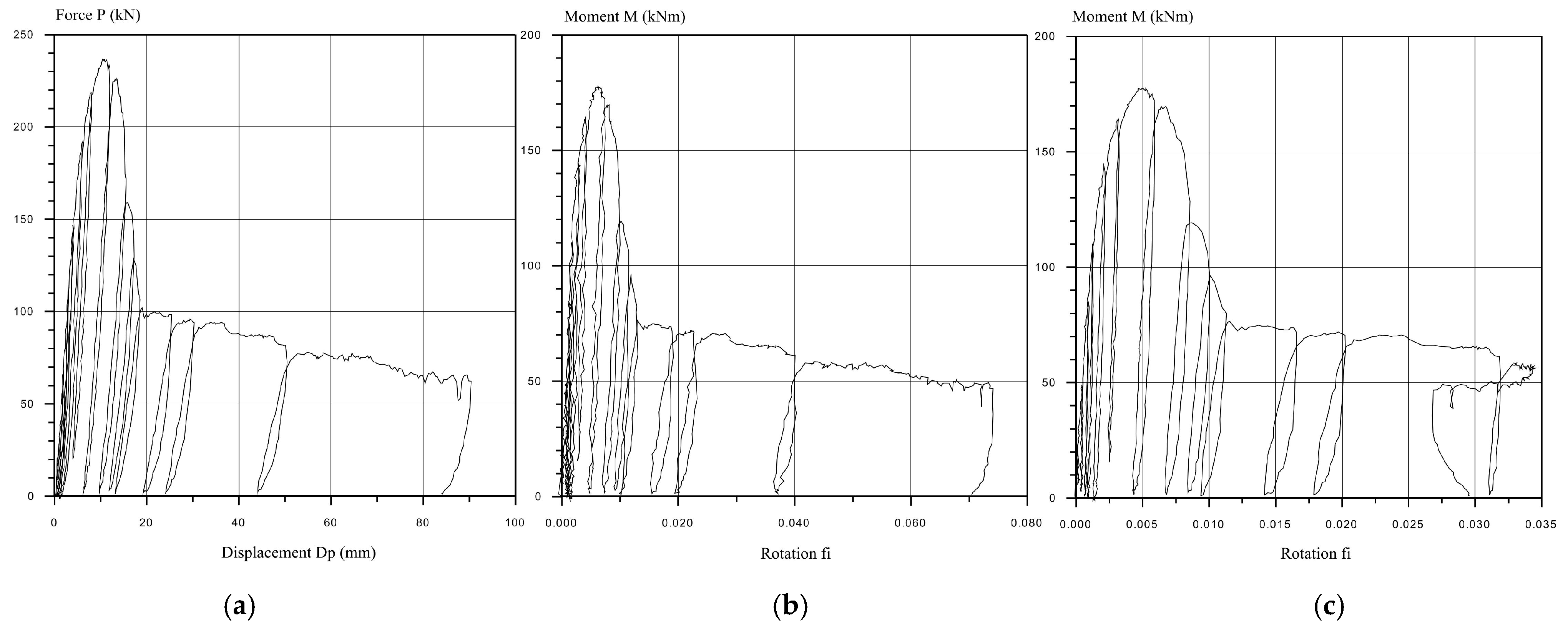
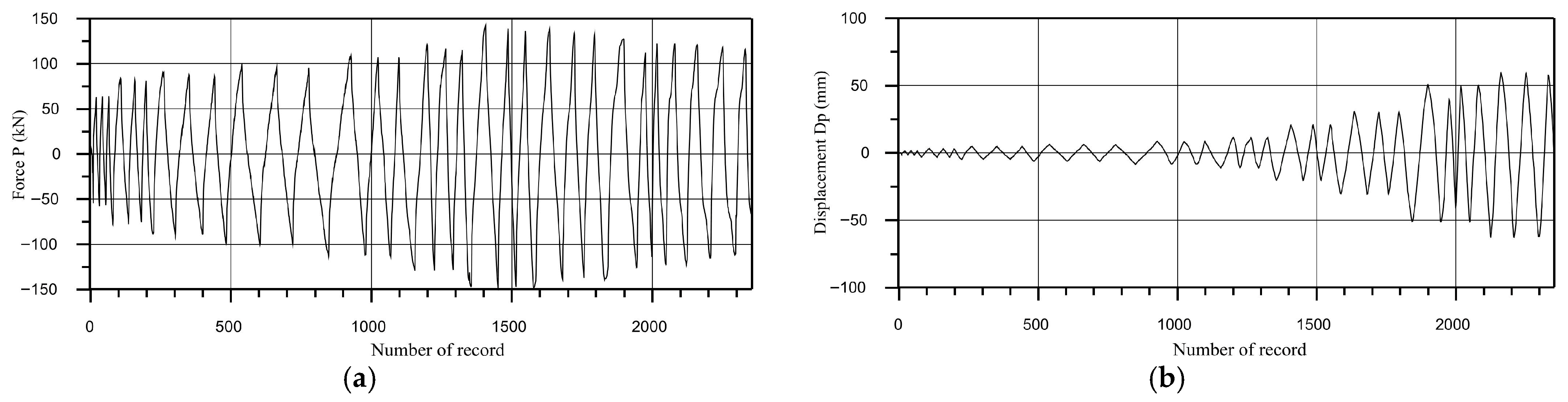
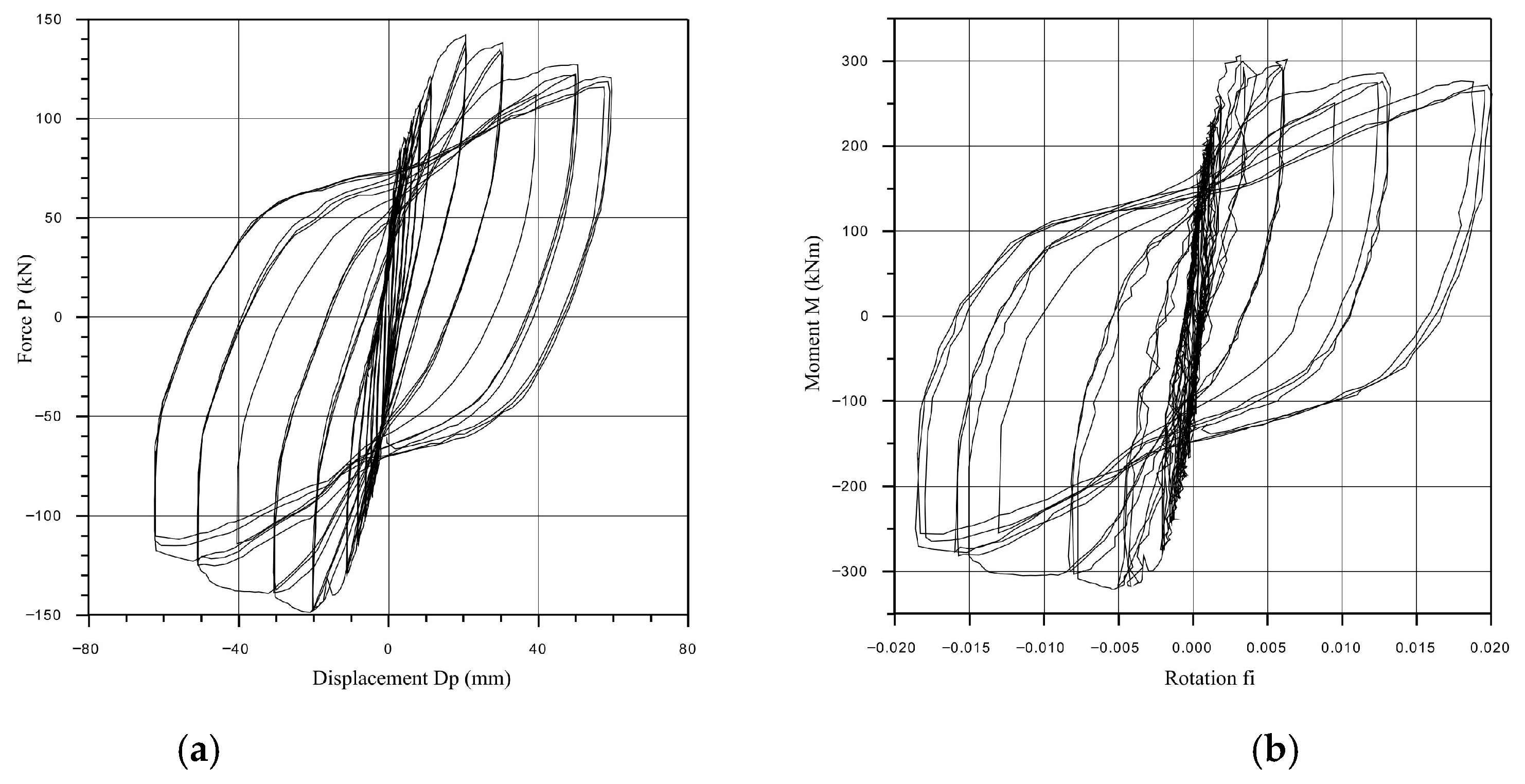
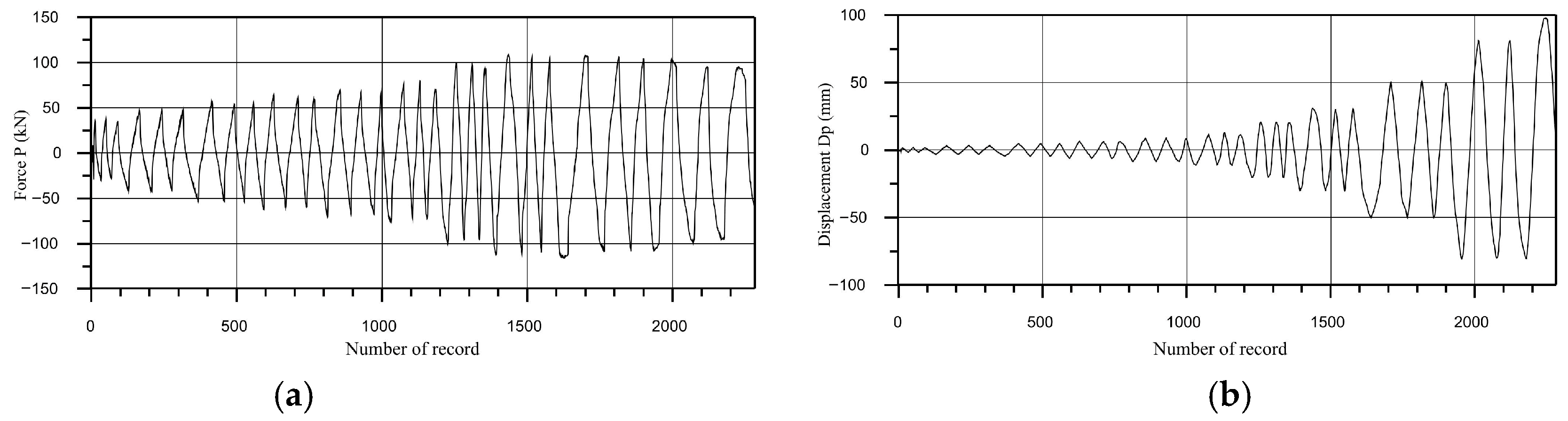
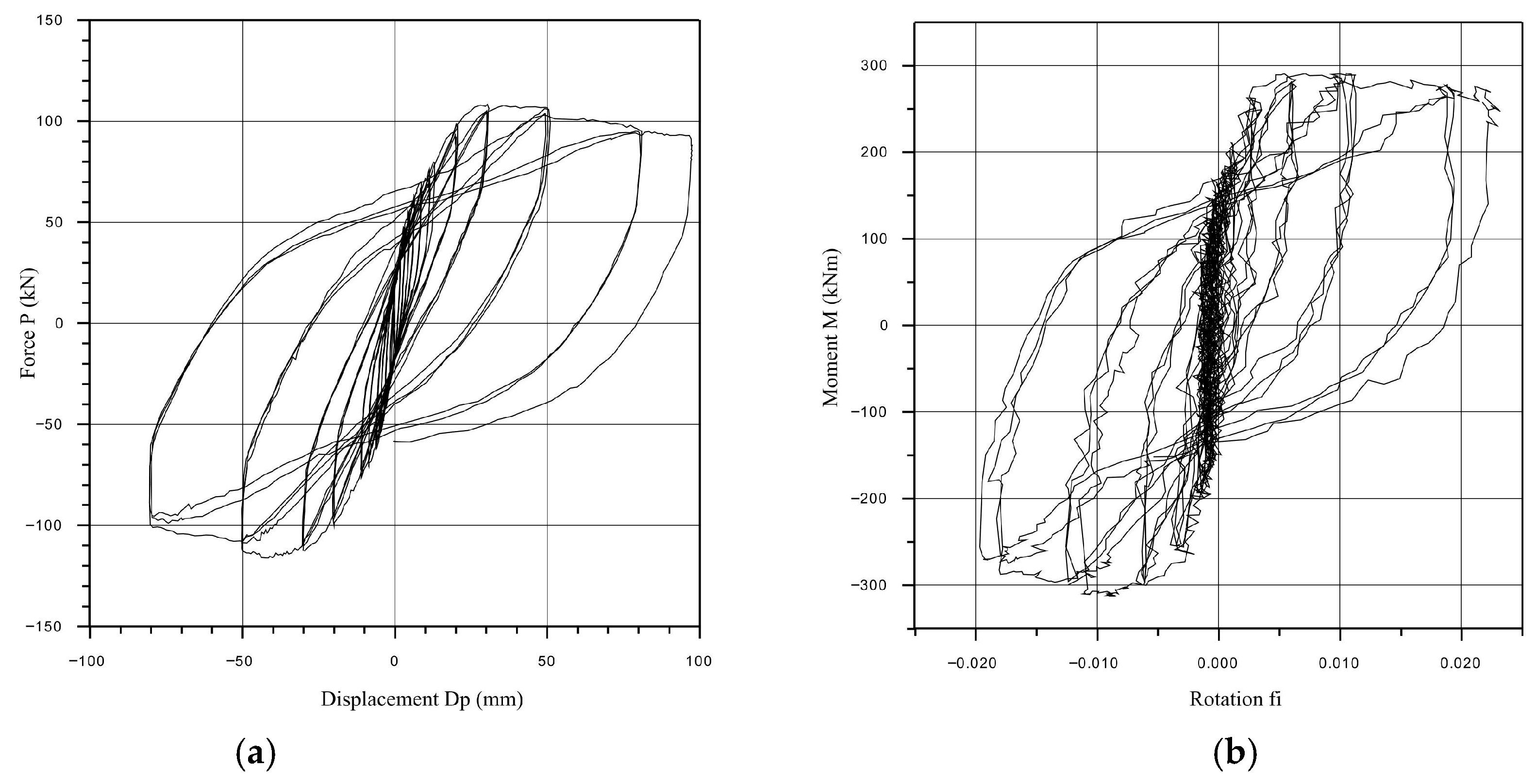
2.2. Quasi-Static Tests of the Full-Scale Models of Connections up to Failure

Experimental laboratory investigation of bearing capacity and deformability of chosen connections was conducted at the Institute for Earthquake Engineering and Engineering Seismology (IZIIS) in Skopje, Macedonia [45]. The essential aim of this investigation was attesting of static and dynamic stability of the most significant and typical modulus of a hall program of the considered precast RC structural system AMONT, developed in company Morava Krušce, Serbia.

In the case of the presented research, optimization of the experimental program was made so that models of the characteristic structural fragments were tested, instead of testing all structural elements and their connections, upon which it was possible to draw very useful conclusions about the integral system behavior. The results of these tests were used in numerical analysis, which is the focus of this paper.

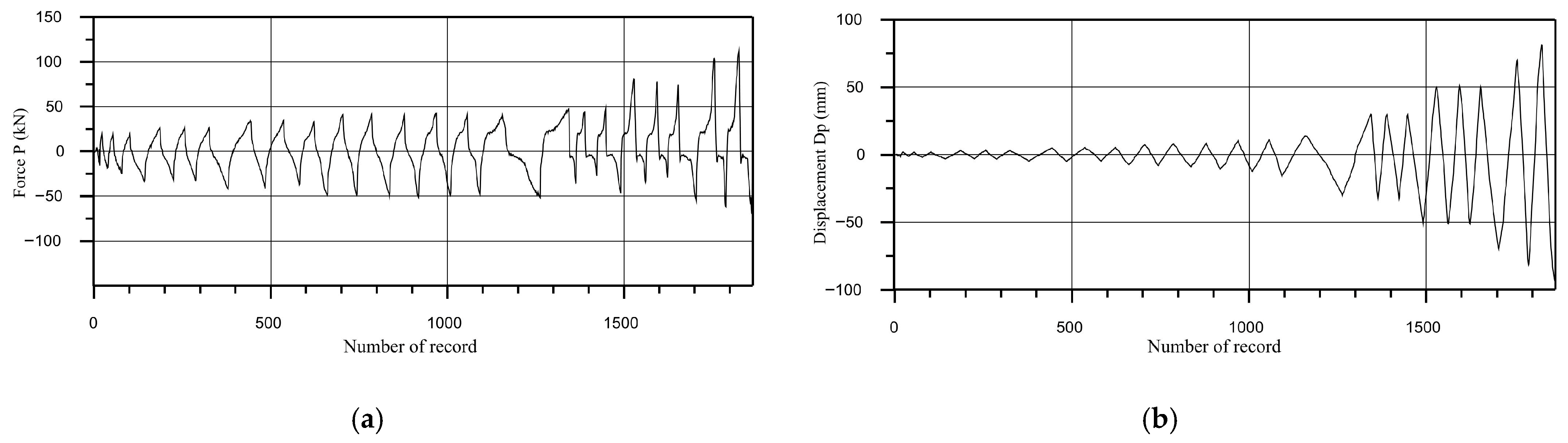
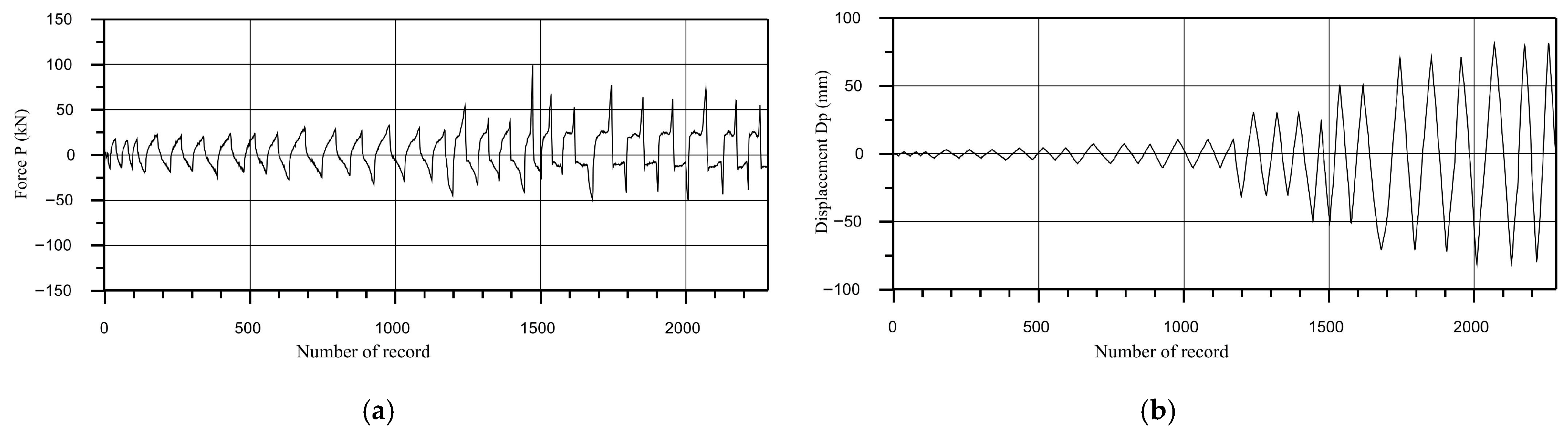
2.2.1. Procedure of Quasi-Static Tests

All models were internally instrumented and constructed in the company’s facilities in Krušce, Serbia, and transported to the Institute (IZIIS) in Skopje to the laboratory for dynamic tests. The elements and joints were designed according to the project documentation of the existing building.

One or two horizontal pistons (servo actuators) with a capability of a maximum input force of 1500 kN or 1000 kN were used for loading input, depending on the experimental model. Displacement measuring instruments (LVDTs) with different ranges were placed at characteristic points, marked on experimental models in advance. The force that is applied in servo actuators and displacement of the piston were measured during the tests. It is worth mentioning that lateral displacement in quasi-static tests was applied in a series of three cycles with the same maximum amplitude, with the maximum amplitude in each series being greater than that of the previous one, which is in accordance with the widely adopted testing procedure. The lateral displacement amplitude was increased until a significant nonlinear response of the connections was observed.

The whole process of programmed cyclic displacement was controlled and conducted by use of a linear potentiometer. Data processing was carried out by specific software. Data processing and analysis enable review of the hysteresis nonlinear relation force-deformation, hysteresis nonlinear relation moment–rotation for characteristic cross-sections, stiffness degradation, propagation and spreading of cracks, and capacity of connection ductility in conditions of cyclic loading up to failure, which is particularly significant to prove the reliability of the system in seismic regions.

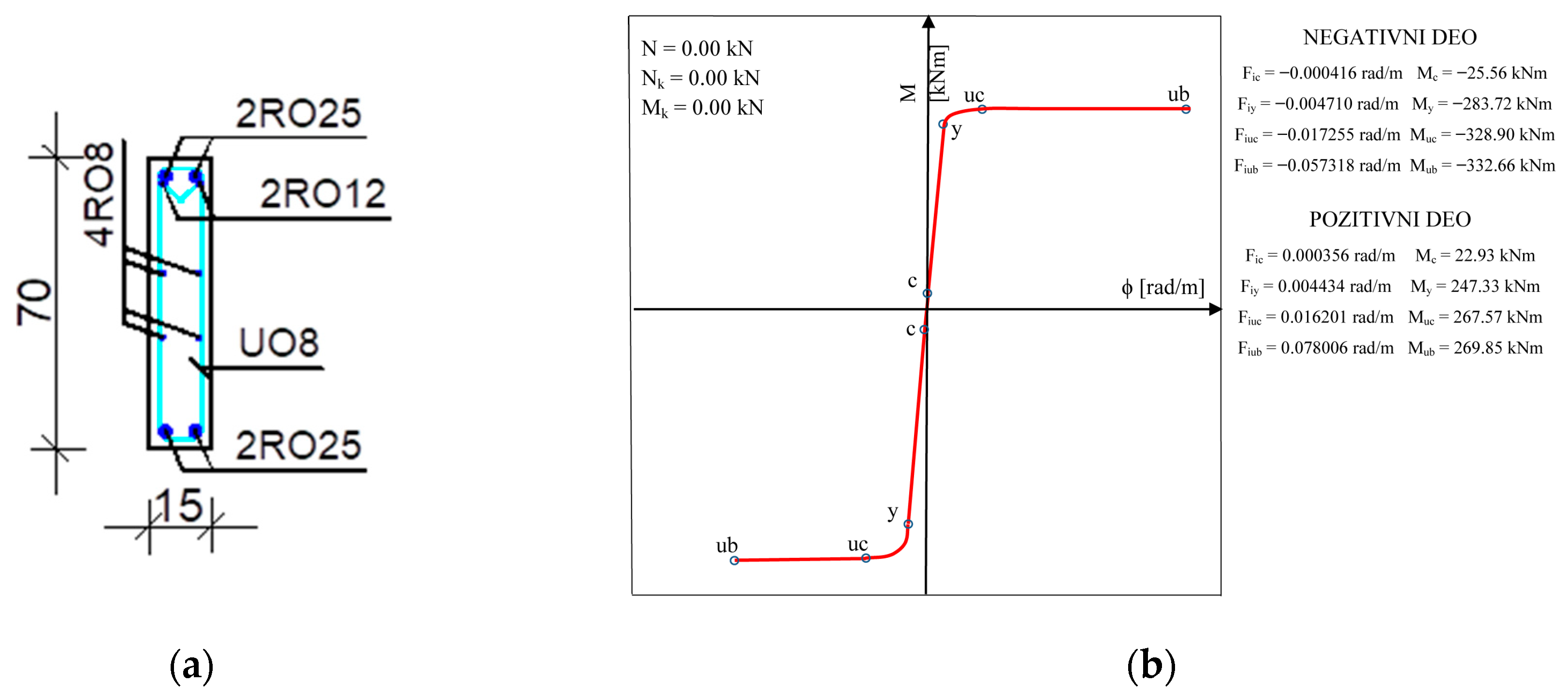
2.2.2. Corner Column to Girder of Floor Structure Connection

Experimental examination of the characteristics of the nonlinear behavior of the connection of the floor beam to the corner column was performed on two full-size physical models designated as experimental model-1 (EM-1) and experimental model-2 (EM-2), as shown in Figure 5. These two identical models, among other things, make it possible to determine the actual level of potential variation in the quality of construction of a prefabricated semi-rigid connection. Part of the prefabricated column, 50 × 50 cm, is supported by two metal brackets and fastened with bolts that ensure complete restraint. In two existing orthogonal openings, two floor beams were fitted: one short (for simulation) and one long. The goal of the experiment was to determine the effective degree of restraint of the longer T-70 standard beam, which has a tenon inserted into the opening of the corner column. This connection was joined by the standard procedure of grouting using cement mortar implemented by the contractor. The testing of the T-70 beam restraint degree was performed under the simultaneous action of constant axial force and cyclic transversal force guided along the cyclic displacement record with various amplitudes to failure. The level of axial force was defined, and the way and sequence of applied transversal cyclic displacements are shown in Figure 6 and Figure 7. Initially an axial force of N = 75 kN was applied by a stronger servo actuator with the purpose of compensating for the effect of the gravity load lateral to the considered connection. Subsequently, cyclic displacements were applied using a smaller servo actuator. The amplitude of displacement at the end of the beam T-70 was successively monotonously increased by this actuator, up to failure of the connection. Displacement was applied in a series of three full cycles with the same maximum amplitude, while the maximum amplitude was increased in each subsequent series.

In this way, the force intensity for each displacement value was registered, and the hysteresis force–displacement dependence was obtained. The applied instrumentation for the critical transverse direction enabled the registration of rotations at each amount of force. Thus, using the known force, the value of the bending moment was obtained, and so the (M-ϕ) real hysteresis dependences of the moment-curves were generated, which have a great importance in the formulation of the model for simulation of the real behavior of semi-rigid connections. The form of these dependences is very similar to the obtained hysteresis force–displacement dependences.

Cyclic force P-displacement diagram of the end of the beam and moment–rotation diagram of the connection column to beam for models EM1 and EM2 are shown in Figure 8 and Figure 9, respectively.

2.2.3. Floor Structure to Floor Beam Connection

Providing of data about bearing capacity and deformability of the connection of floor structure elements K-45 with the floor beam, i.e., about transmission of negative moments at the point of support above the floor beam T-70, was carried out using almost two identical models, EM-3 and EM-4, as shown in Figure 10. The difference between these two models is in the amount of montage reinforcement placed in the continuity layer. In the model EM-3, only one reinforcement mesh, Q-131, and in the model EM-4, two such meshes were embedded. In addition, the side contact of the head of beam T-70 was grouted with ribs of floor elements K-45 in the model EM-4. The level of rigidity of this connection was observed when the construction was finished.

Composition of the EM-3 and EM-4 models of the connection floor element to the floor beam was tested up to failure as well. Cyclic displacement of the rib of the beam (Figure 11 and Figure 12) simulated the influence of negative moment with gradually increasing intensity at the support of two floor elements from neighboring bays.

Cyclic force P-displacement diagram of the rib of the girder T-70 and moment–rotation diagram of the floor element K-45 at the support on the beam T-70 (models EM-3 and EM-4) are shown in Figure 13 and Figure 14, respectively.

2.2.4. Column to Foundation Connection

The connection of a precast RC column 50/50 cm to the foundation pocket was investigated using the model EM-5, as shown in Figure 15. Static vertical axial force and transverse increasing cyclic force up to failure were applied as loading.

Testing of the model EM-5 was performed so that at first the axial force N = 385 kN was applied by stronger servo actuator with the purpose of simulating an expected gravity load in the considered cross-section of the column during exploitation, and then displacement amplitude of the column end was increased successively monotonously using smaller servo actuator, up to nonlinear behavior of the connection and the column, as shown in Figure 16.

Cyclic force–displacement diagram of the column end and moment–rotation diagram of the column at its connection to the foundation pocket are shown in Figure 17. It can be concluded that this type of connection shows stable hysteretic behavior up to failure. There is no significant degradation during the repeated loading cycles with the same amplitude, but the connection stiffness degradation occurs at higher load levels due to the concrete cracking and crushing (especially of the concrete cover). The hysteresis shows satisfying ductile behavior of the connection (energy dissipation), with a clear pinching effect characteristic of the RC joints.

2.2.5. Corner Column to Beam Connection

Test of the model EM-6 was performed to find out data about bearing capacity and deformations of the weakened column at the connection point with the floor beam, as shown in Figure 18, up to failure. Loading was a vertical static axial force at the second-story level and an increasing lateral cyclic force up to failure of the connection.

Testing of the model EM-6 was performed according to the prepared loading program. The axial force N = 285 kN was applied at first by a stronger servo actuator with the purpose of simulating an expected gravity load in the considered cross-section of the column during exploitation. Then displacement amplitude of the column end was increased successively monotonously using a smaller servo actuator, up to deeply nonlinear behavior of the connection and the column, as shown in Figure 19.

Cyclic force–displacement diagram of the column end and moment–rotation diagram of the column at its connection with the floor girder are shown in Figure 20. Similarly to the connection EM5, this connection has stable hysteretic and ductile behavior up to failure, with the stiffness degradation at higher load levels and pinching of hysteresis. It can be concluded that the weakened column at the connection point with the floor beam provides adequate nonlinear behavior for the application in the seismic-prone regions.

2.2.6. Frame Beam to the Column Connection

For the direct dynamic analysis of the considered industrial precast structure, it is necessary to define the moment–rotation relationship for the connection of the frame beam T70 with the column. The experimental testing of this connection has not been conducted. Therefore, the theoretical moment–rotation diagram, as shown in Figure 21, is defined using the dedicated computer program SECAP (Section Capacity) developed at IZIIS. The calculation is based on the fiber model, in which the section is discretized into a finite number of fibers. Each fiber is represented by a stress–strain relationship based on the material characteristics in its tributary area. Based on the plane sections assumption (Bernoulli hypothesis), and the equilibrium of section forces, the moment–rotation relationship of the section is defined through the characteristic discrete points. Considering that the flange of the beam is cut off at the connection, the geometric characteristics and reinforcement of the cross-section’s rib are used in the theoretical analysis, along with material characteristics of the concrete class C30, compressive strength on cubic specimen 30 MPa and modulus of elasticity 31.5 GPa, and reinforcement yield stress of 400 MPa and modulus of elasticity 210 GPa.

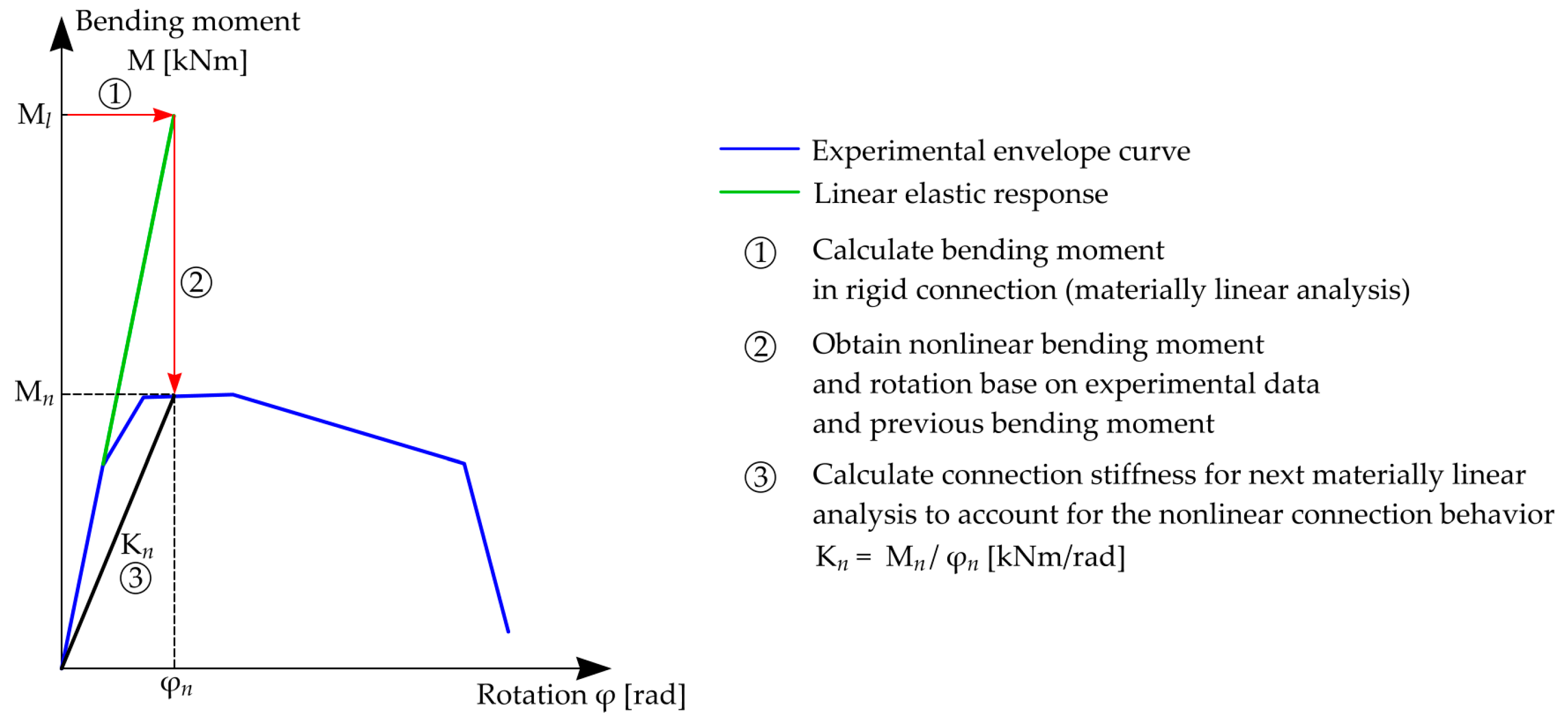
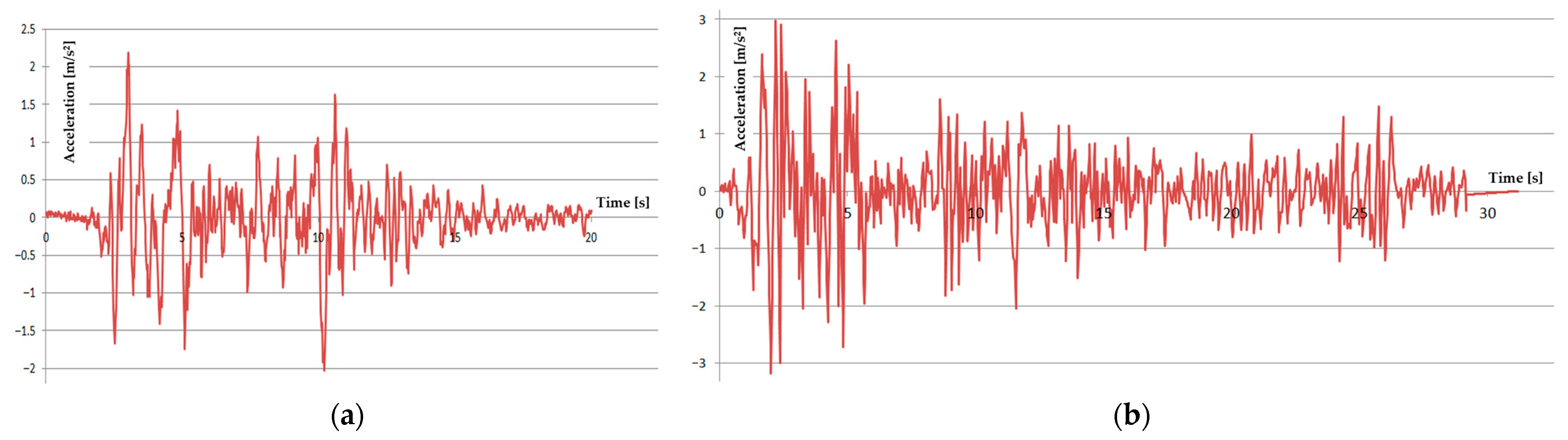
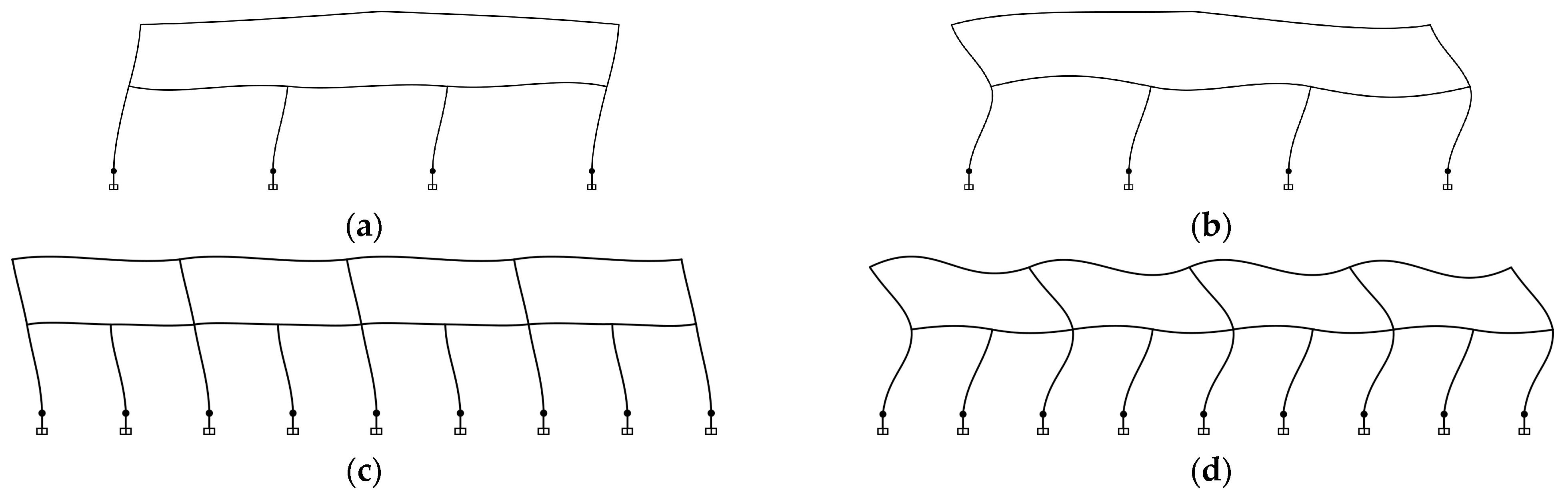
3. Modeling of the Structure and Numerical Analysis

The seismic response of a structure can be obtained based on the nonlinear direct dynamic analysis, introducing the experimentally and theoretically obtained moment–rotation (M-ϕ) relationships of precast concrete frame connections. On the other hand, the implementation of nonlinear dynamic analysis in everyday engineering practice can be demanding [47,48]. Therefore, the aim is to propose a simplified model of the structure in order to calculate the roof top displacement considering the effects of the connections’ stiffness.

The proposed simplified approach, applicable in engineering practice, consists of two steps: The first step involves materially linear and geometrically nonlinear dynamic analysis in order to obtain bending moments in the vicinity of the frame connections. Further, the obtained bending moments using materially linear analyses are combined with the experimentally/theoretically defined moment–rotation relationships to calculate stiffness change in the connections. This proposed approach is schematically presented in Figure 22. The second step involves materially linear and geometrically nonlinear dynamic analysis with defined stiffness of the connections according to the previous step. The main goal is to obtain displacements of the structure using materially linear analysis instead of nonlinear direct time history analysis. Although standard provisions [49,50,51,52] require that possible response degradation of connections should be taken into account, there are no, or at least, there are limited instructions for the determination of connection stiffness and resistance. Therefore, this proposed approach represents an attempt to provide a simplified but valid model that considers connection stiffnesses based on experimental and/or theoretical moment–rotation relationships, making it practical for everyday engineering.

The described procedure was conducted on a model consisting of two orthogonal planar frames, since the structure considered in this study meets the requirements prescribed for such an approach in EC8 [49], under the action of two real earthquake records with characteristic frequency–amplitude content. The following seismic excitations (ground-acceleration time history records) were selected, as shown in Figure 23: (1) Montenegro earthquake of 15 April, 1979 (N–S component), Ulcinj–Albatros station; (2) El Centro earthquake of May 18, 1940 (S00E component). Namely, El Centro is adopted worldwide as a benchmark in nonlinear seismic analysis, while Ulcinj–Albatros accelerogram represents a significant earthquake record for the Balkan region, where the considered precast structure is used. Therefore, these two earthquake records are adopted in the analysis. Considering that the significant nonlinear deformations do not occur at lower levels of ground acceleration, the analyses are performed by scaling the records to the level of maximum peak ground acceleration of 0.4 g (g stands for the gravitational acceleration g = 9.81 m/s²).

The finite element analysis was performed using the software ETABS 22, suitable for dynamic analysis using direct integration of equations of motion in the time domain, including material and geometric nonlinearities [53]. The geometry of the model was evaluated in accordance with the geometry of the building (Figure 2 and Figure 3), where the models of the transverse and longitudinal frames are presented in Figure 24. The columns and beams were modeled by 1D beam finite elements (FE). The mesh sensitivity analysis was performed for both frames for different FE lengths: 0.25 m, 0.50 m, and 1.00 m. Considering that the roof top displacements are almost identical for different mesh sizes, the FE length of 0.5 m was adopted. Concrete is modeled as an isotropic linear elastic material, whereby the Poisson’s ratio is 0.20 and modulus of elasticity is 31.5 GPa and 34 GPa for concrete classes C30 and C40, respectively. At the foundation level, appropriate fixed supports are defined in the model.

The geometric nonlinearity was included using P-Δ and the large displacement method built into the software (equilibrium equations are formulated in the deformed configuration of the structure at each load step). Nonlinear dynamic analysis was conducted with a time increment of 0.01 s, which corresponded to the discrete values of applied accelerograms. The calculation includes the damping of 5% defined by the Rayleigh model using vibration periods of the first two modes for each frame, as shown in Figure 25. The integration of the dynamic equations is performed by the implicit Hilber–Hughes–Taylor method, where the integration parameters are α = 0, β = 0.25, and γ = 0.5 [53,54].

Based on the bending moments in the different connection joints obtained from the materially linear dynamic analysis on the models with rigid joints, the connection’s stiffness was calculated according to the proposed procedure (see Figure 22). Such calculated connection stiffnesses, shown in

Table 1. Stiffness of the analyzed connections for the transverse frame.

Connection Type	Ulcinj–Albatros
	Ml [kNm]	Mn [kNm]	φn [rad]	Kn [kNm/rad]
EM4	764.20	162.74	0.002732	59,568.08
EM5 (end columns)	1249.52	300.00	0.003250	92,307.69
EM5 (middle columns)	972.61	300.00	0.002530	118,577.10
EM6	881.53	233.60	0.000626	373,282.20
Connection type	El Centro
	Ml [kNm]	Mn [kNm]	φn [rad]	Kn [kNm/rad]
EM4	864.37	167.31	0.003090	54,145.63
EM5 (end columns)	1489.64	300.00	0.003879	77,339.52
EM5 (middle columns)	1098.40	300.00	0.002857	105,005.30
EM6	1020.24	243.49	0.000724	336,172.86

and

Table 2. Stiffness of the analyzed connections for the longitudinal frame.

Connection Type	Ulcinj–Albatros
	Ml [kNm]	Mn [kNm]	φn [rad]	Kn [kNm/rad]
EM4 (end connections)	1164.64	130.12	0.002309	56,358.28
EM4 (middle connections)	934.20	116.07	0.001851	62,696.48
EM5 (end columns)	1046.71	300.00	0.002722	11,021.31
EM5 (middle columns)	1278.12	300.00	0.003324	9025.27
EM6	671.13	306.93	0.011155	27,515.02
Connection type	El Centro
	Ml [kNm]	Mn [kNm]	φn [rad]	Kn [kNm/rad]
EM4 (end connections)	1294.08	145.51	0.002566	56,711.36
EM4 (middle connections)	1033.05	122.10	0.002048	59,630.79
EM5 (end columns)	1232.91	300.00	0.003207	93,545.37
EM5 (middle columns)	1475.09	300.00	0.003837	78,186.08
T70	693.82	308.29	0.011532	26,733.44

, were used in the second model as frame elements end releases stiffness in order to obtain the roof top displacements and inter-story drift ratios at the time of maximum roof top displacement of the analyzed frames under the considered earthquake acceleration records (

Table 3. Transverse frame—comparison of the roof top displacements obtained by the proposed method and nonlinear direct dynamic analysis.

Earthquake	Rigid Connect. (1)	Proposed Model (2)	Nonlinear Dynamics (3)	(3)/(2)	(2)/(1)
Ulcinj–Albatros	0.0901 m	0.1504 m	0.1539 m	1.0233	1.6693
El Centro	0.1099 m	0.1287 m	0.1242 m	0.9650	1.1711

and

Table 4. Longitudinal frame—comparison of the roof top displacements obtained by the proposed method and nonlinear direct dynamic analysis.

Earthquake	Rigid Connect. (1)	Proposed Model (2)	Nonlinear Dynamics (3)	(3)/(2)	(2)/(1)
Ulcinj–Albatros	0.0787 m	0.1137 m	0.1168 m	1.0273	1.4447
El Centro	0.0877 m	0.1022 m	0.0931 m	0.9109	1.1653

).

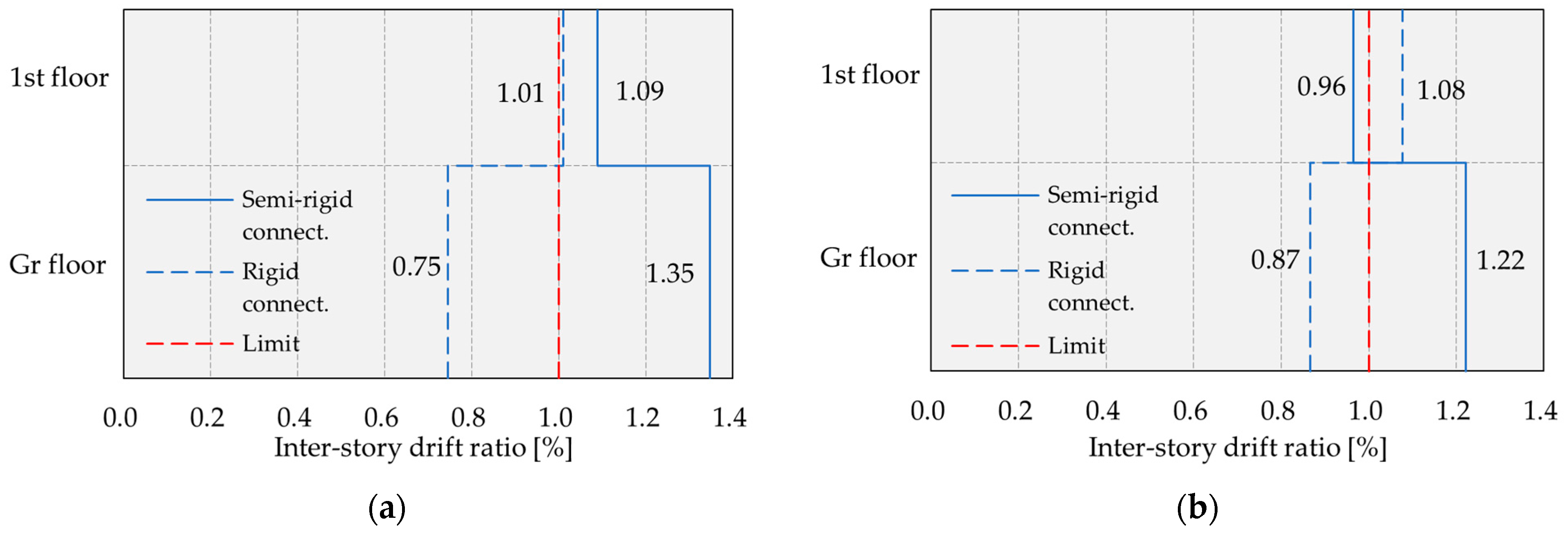
4. Results and Discussion

Behavior of the experimental models EM-1 and EM-2 has shown that the connection between the corner column and floor beam possesses great rotation capacity. The yielding phase occurs due to significant displacements ranging from ±30 to ±40 mm. In the final phase, the structural connection shows a tendency to harden. Failure occurs when the tenon begins to separate from the beam, as shown in Figure 5c. This connection was tested by applying a relatively small axial pressure force, and therefore, the registered hysteresis dependence is valid for such conditions in practice. The beam is to be treated as a partially fixed element with nonlinear bearing characteristics of the connection. Taking such behavior of this connection into consideration, there is a real danger of bond slippage of the tenon from the column during a strong earthquake due to out-of-phase vibrations. Therefore, it is necessary to provide a real simulation of its experimentally proven nonlinear characteristics in all further analytical considerations.

A certain level of rigidity of connection of floor structure elements K-45 with the girder, labeled as EM-3 and EM-4, is achieved by a reinforced finishing concrete layer. Such a structural solution enables transmission of negative moments. Nonlinear characteristics of this connection are presented as half-hysteretic relations: force–displacement and moment–rotation. After reaching the limit bearing force, for each subsequent loading and unloading cycle, there is a sudden drop in the bearing force. After decreasing, the load-bearing limit force of this connection remains at the level of about 1/3 of the maximum registered load-bearing limit force, that is, until the occurrence of brittle fracture.

Test of the model EM-5 shows that the foundation is very favorable and it does not experience any damage. Column inclination occurs above the pocket foundation with corresponding propagation of plastic hinge, which is favorable. Nonlinear hysteretic relations for the critical cross-section of the column in the form of force–displacement and moment–rotation, as shown in Figure 17, show very stable nonlinear characteristics and a high level of ductility, which is very favorable for the integral structural system.

The test results of model EM-6 show that a successful structural solution (with adequate reinforcing of the reduced cross-section of the column by longitudinal bars) is created at the point of the weakened column, which enables very stable behavior of this connection. Characteristics of the nonlinear behavior of the weakened and full cross-sections of the column are very close, i.e., deviation is almost negligible, which confirms the quality of this connection.

The validation of the proposed approach for the calculation of the displacements using material linear direct dynamic analysis and reduced stiffness calculated based on the bending moments on the frame with rigid joints, and experimentally/theoretically defined moment–rotation relationships of connections is conducted comparing the results with the materially nonlinear direct dynamic analysis of the same frames (previous research, Ref. [55]). The nonlinear direct dynamic analysis was conducted using the finite element method and the program NORA 2005 [56]. The material nonlinearity was simulated by applying a dense subdivision of the elements into a series of closely spaced cross-sections whose constitutive relations were represented by M–φ.

Comparing the roof top displacements obtained by the proposed approach and nonlinear direct dynamic analysis, shown in Table 3 and Table 4, it can be concluded that the proposed model provides reliable results considering that the differences are in the range of 2.33–8.91%. Accordingly, the proposed model has been validated for application in everyday engineering practice, being significantly simpler to implement compared to direct dynamic analysis, in cases where experimental data on connection capacity or theoretical relationships are available.

The differences in the roof top displacements of the analyzed frames under the considered earthquake excitations between the proposed model and the model with the rigid joints, shown in Table 3 and Table 4, are in the range from 16.53% to 66.93%. These results confirm the necessity of considering the nonlinear behavior and stiffness of connections in precast frame structures when determining displacements, which is particularly important for the verification of the serviceability limit state of structures in seismic regions.

The inter-story drift ratios at time of maximum roof top displacement calculated using the proposed model are analyzed and compared with the case of rigid connections, as well (Figure 26 and Figure 27). It can be concluded that connection stiffness significantly influences the seismic response of precast frame structures. Namely, under the Ulcinj–Albatros earthquake, the inter-story drift ratio at the ground floor for the case of semi-rigid connections is larger for approx. 100% and 80% compared to the case of rigid connections for transverse and longitudinal frames, respectively. On the first floor, inter-story drift ratios are larger for approx. 25% and 10%. It should be mentioned that the maximum inter-story drift ratio is larger at the first floor in the case of rigid connections, while it is larger at the ground floor in the case of semi-rigid connections. Furthermore, the inter-story drift ratios are compared with the limit value according to the standard EN 1998-1 [49] for buildings in which non-structural elements are fixed so that they do not interfere with structural deformations (1%). For almost all the analyzed cases of frames with rigid connections, drifts are slightly lower or slightly higher than the limit value. On the other hand, in cases of frames with semi-rigid connections, reals stiffnesses, drifts are significantly larger than the limit value, which confirms the necessity of considering the nonlinear behavior and stiffness of connections in precast frame structures, especially for the seismic vulnerability of existing structures.

The obtained results regarding the roof top displacements and inter-story drift ratios are fully in accordance with previous research. Ingle et al. [36] analyzed the seismic response of a 10-story precast concrete building frame with 12 types of modeling of the beam–column joints under seven earthquake records. They concluded that the peak top displacements are significantly larger (from approx. 10% to 200% regarding the connection modeling type) compared to the case of a monolithic frame. Comparable results are reported in [57] as well. Song et al. [17] analyzed an eight-story two-bay frame with six different variants of the connections and compared the results with the monolithic counterpart and concluded that under strong seismic excitation, the response differences between precast frames and the RC frame were significant (approx. 10–30% regarding the inter-story drift ratios), so it is worthwhile to appropriately incorporate connections behavior and stiffness in precast frames seismic analysis.

5. Conclusions

Based on the experimental research of the precast frame element connection capacity of one characteristic industrial hall chosen as the case study and the proposed numerical analysis for seismic response regarding structural displacements, the following conclusions can be drawn:

• All the experimentally tested connection overlays showed satisfying nonlinear behavior with certain specifics regarding failure. The connection of the floor beam to the corner column is prone to the bond slippage of the tenon from the column during a strong earthquake. The connection of the floor element with the floor beam is characterized by a reduction in the resistance up to 60% after the load-bearing limit force, which can be characterized as brittle fracture. The column–foundation connection and the weakened column–floor beam connection showed stable nonlinear hysteretic behavior with slight stiffness degradation after reaching the ultimate load-bearing capacity, which can be accepted as favorable in the seismic-prone regions.
• These results confirm the necessity of considering the nonlinear behavior and stiffness of connections in precast frame structures when determining displacements, which is particularly important for the verification of the serviceability limit state of structures in seismic regions.
• The simplified approach for taking into account stiffness reduction due to nonlinear behavior of element connections is proposed in the paper.
• The proposed model is validated considering that the roof top displacements differ in the range of 2.33–8.91% compared to nonlinear direct dynamic analysis results.
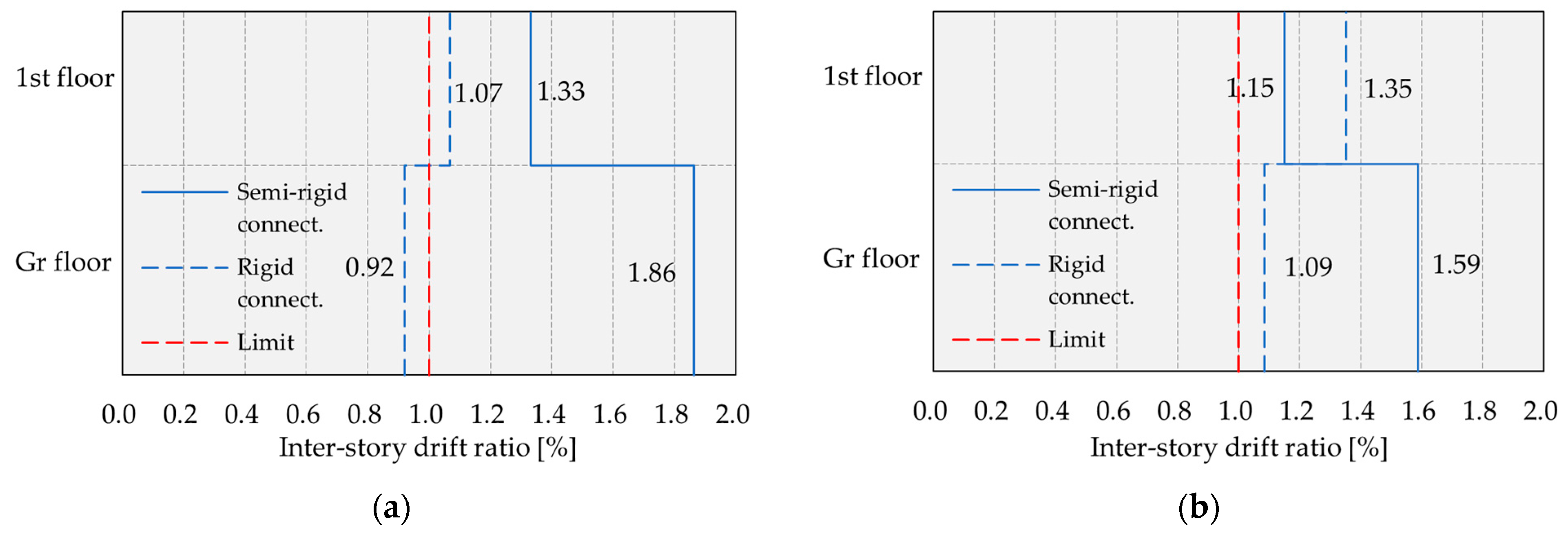
• Roof top displacements of the considered structure are larger by 16.53–66.93% when the stiffness of the connections is taken into account, compared to the case where the connections are treated as rigid. In the case of inter-story drift ratios, the values are larger by 10–100%, highlighting that inter-story drift ratios are larger than the limit value provided by standard EN 1998-1 when the real stiffnesses of connections are considered. This is especially important from the aspect of the serviceability limit state of structures in seismic regions.
• The simplified approach and proposed modeling of the connections are applicable for seismic risk assessment of existing industrial halls and commercial buildings constructed in the considered structural system, and for other PCR systems which are produced industrially in large series and which are designed in zones of seismic activity VIII or IX.