Vibration Mitigation Through Rail Track Design for Structures Built Directly Above a Double-Deck Railway Depot
Abstract
1. Introduction
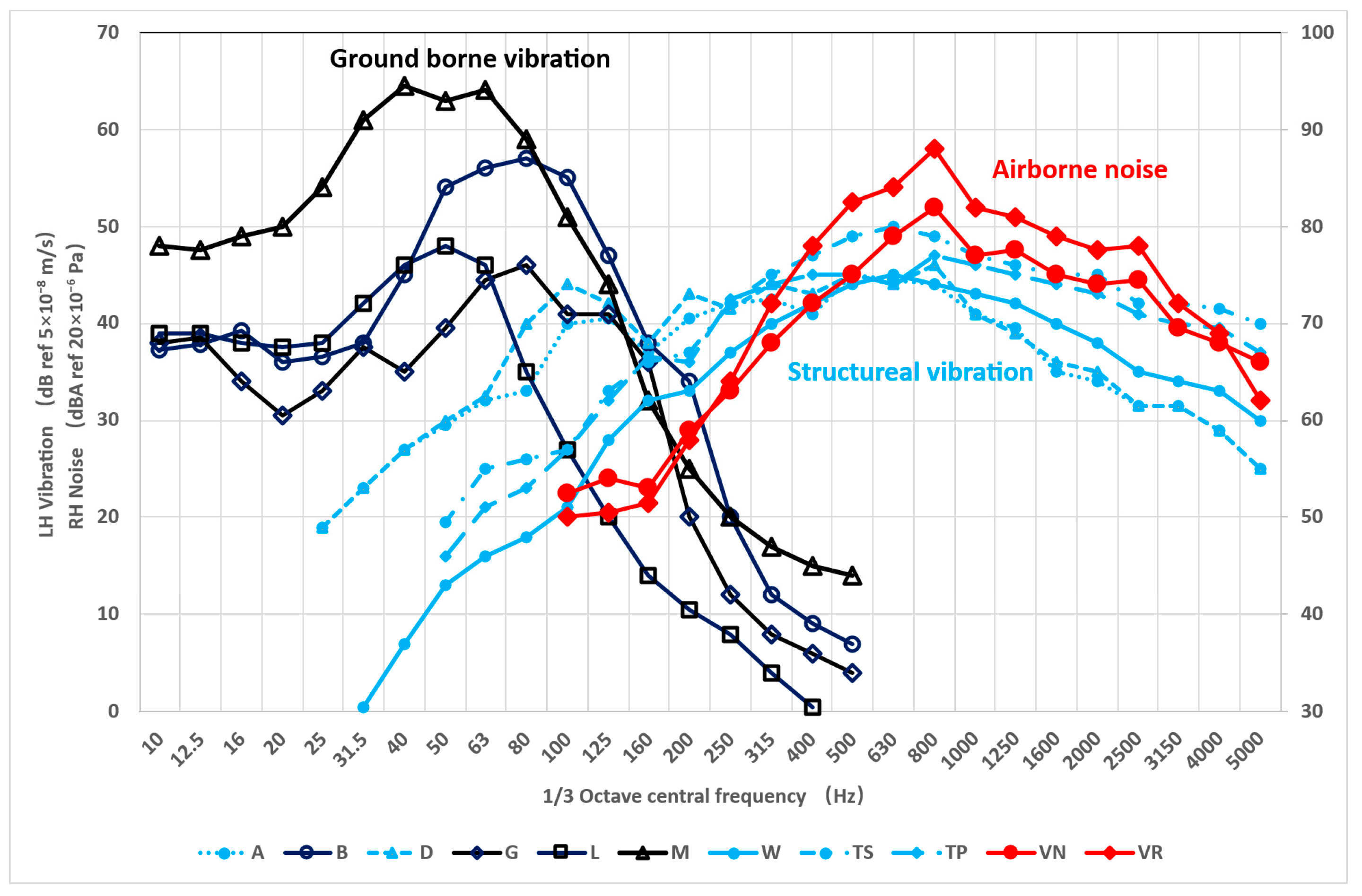
1.1. Noise and Vibration from the Metro System
1.2. Transit-Oriented-Development (TOD)
- The track layout at railway depots is far more complex, with a large number of small-radius curves, rail switches, and rail joints, leading to significant impact load and more frequent and severe vibration excitation.
- The operation modes at a typical railway depot of the metro system are significantly different from that on main lines. For instance, the majority of activities at the depot are undertaken during night-time hours or very early in the morning with low background noise; the operation hours at the depot also impose more stringent noise and vibration limits.
- Different train activities at the depot feature a wide range of train speeds, varying from 5 to 10 km/h in the inspection and maintenance warehouse; around 15–20 km/h at the throat zone (amongst the metro-line operators and relevant stakeholders in China, the throat zone is loosely defined as the area where tracks merge and diverge through rail switches between the main line and the railway depot); and up-to 60 km/h on the test track.
2. Research Methodology
2.1. The Double-Deck Railway Depot
- The construction, verification, and validation of the computational model: a 2.5D Finite Element (FE) model was developed using Ansys software 2020 R2 [36]. The vibration level on the “16 m plate”, as per Figure 2a, was compared against field measurement collected from the depot roof plate at a similar depot, to validate the FE model.
- Using the validated FE model, vibration contribution of trains running on the upper-and lower-decks of the depot was evaluated, to support the design of rail track-forms on both decks.
- A parametric study was then undertaken wherein the vibration attenuation effect of using different combinations of track-forms at the throat zone with complex track geometry was examined, providing useful information for the design of vibration mitigation measures at source.
- After the completion of the construction of the depot, numerically computed vibration levels in rooms of the two-storey office building were compared to site measurement at corresponding sensitive receivers.
2.2. The Numerical Model
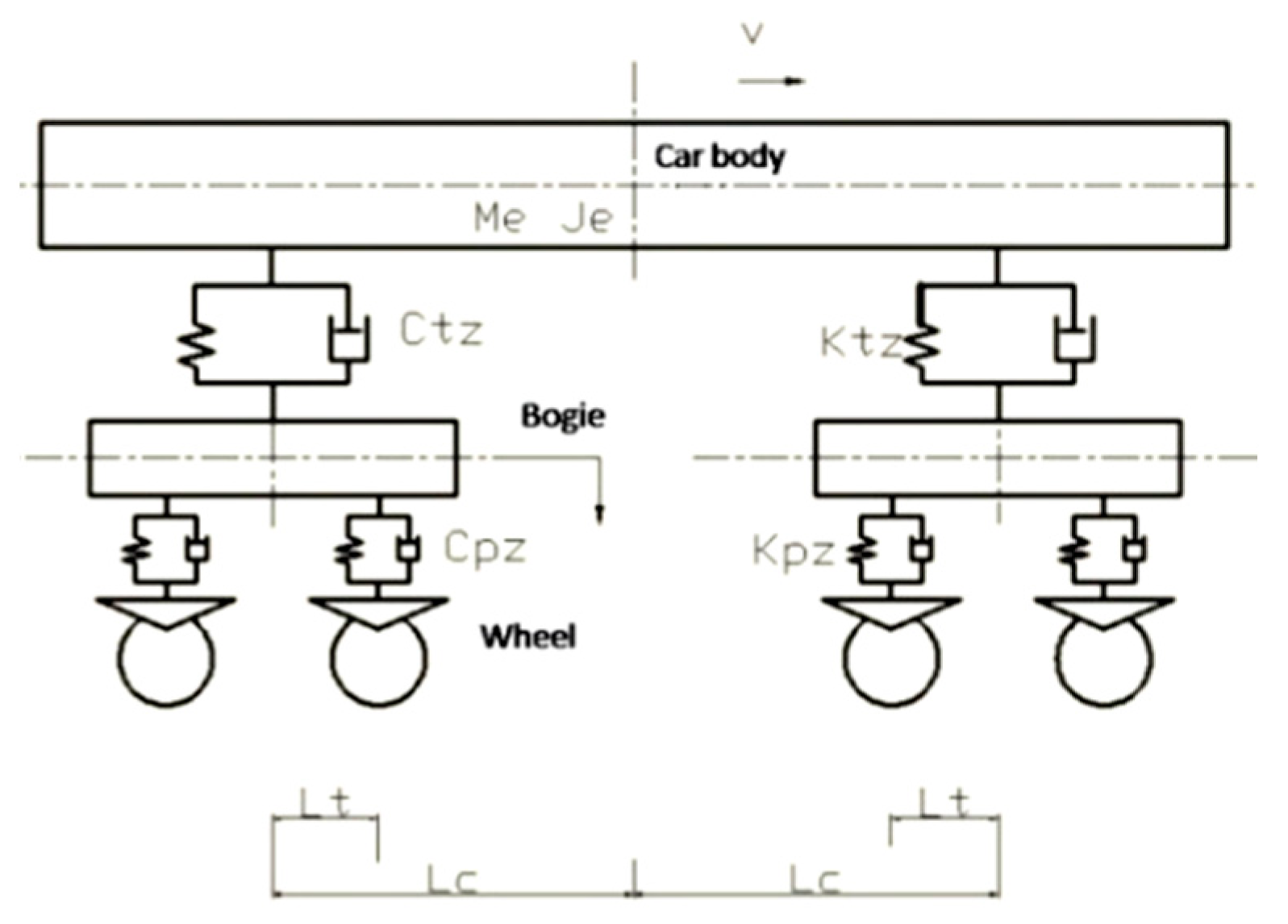
2.2.1. The Rail Track Model
2.2.2. The Foundation Model
2.2.3. The Building Model
- (1)
- The building in consideration is of simple rectangle shape, without curvature or any complex shape.
- (2)
- Structural columns within the office building are evenly distributed along the train running direction, which means periodical boundary conditions is applicable.
- (3)
- The “track-tunnel-ground” excitation source originates from the interaction between the “train-track” system. Since the train has a finite length, only the effect of one train’s length is considered herein. The finite train excitation source is assumed to be an infinite line source. The conditions assumed, here, are that the influence of the train’s length on the effects beyond a certain distance within the frequency range of interest can be considered negligible for a given observation point, e.g., a building. For example, the contribution of far-field excitation beyond 50 m to the near-field response of vibrations above 20 Hz can be considered negligible.
- (4)
- The frequency range of interests is between 1 Hz and 80 Hz, as per compliance standard; and the actual frequency range of interests from the majority of train-vehicle excitations and responses in the metro system is between 20 Hz and 80 Hz, which means short wavelength excitation at the wheel-rail coupled interface, which contributes the most energy in wheel-rail induce vibration, is dissipated through the transmission paths from the source to the receiver at the TOD.
- (5)
- The ground-borne vibration decay rate due to railway excitation is some 0.5 dB/m to 1.5 dB/m, i.e., around 10 dB attenuation with the source and receiver 10 m apart, which means that the truncation is irrelevant as long as the computational grid is large enough.
- The main parameters in the building model are:
- (1)
- Equivalent mass: The equivalent total mass of key structural elements such as beams, columns, slabs, and walls per unit length is equivalent to the actual total mass of the building per unit length. This is achieved by using the equivalent material density.
- (2)
- Equivalent stiffness: The equivalent stiffness of the 2.5D building per unit length is the same as the actual stiffness of the key structural elements of the building, specifically the equivalent Young’s modulus E and cross-sectional moment of inertia I.
- (3)
- Equivalent damping: Different physical material damping coefficients are used for various sections within a building structure. The damping parameters in 2.5D FE and 3D FE models are identical in this case.
2.2.4. Excitation Force from Wheel-Rail Interaction
2.2.5. Input of the Numerical Model
2.2.6. Boundary Conditions
2.2.7. Validation of the Numerical Model
3. A Parametric Study of the Vibration Mitigation Effects of Track-Forms
3.1. Track-Forms and Properties
3.2. Vibration Contributions from Trains Running on the Upper- and Lower-Deck
- (a)
- Test train running on the upper-deck only (TUD);
- (b)
- Test train running on the lower-deck only (TLD);
- (c)
- Test trains running on both the upper- and lower-decks simultaneously (TBD).
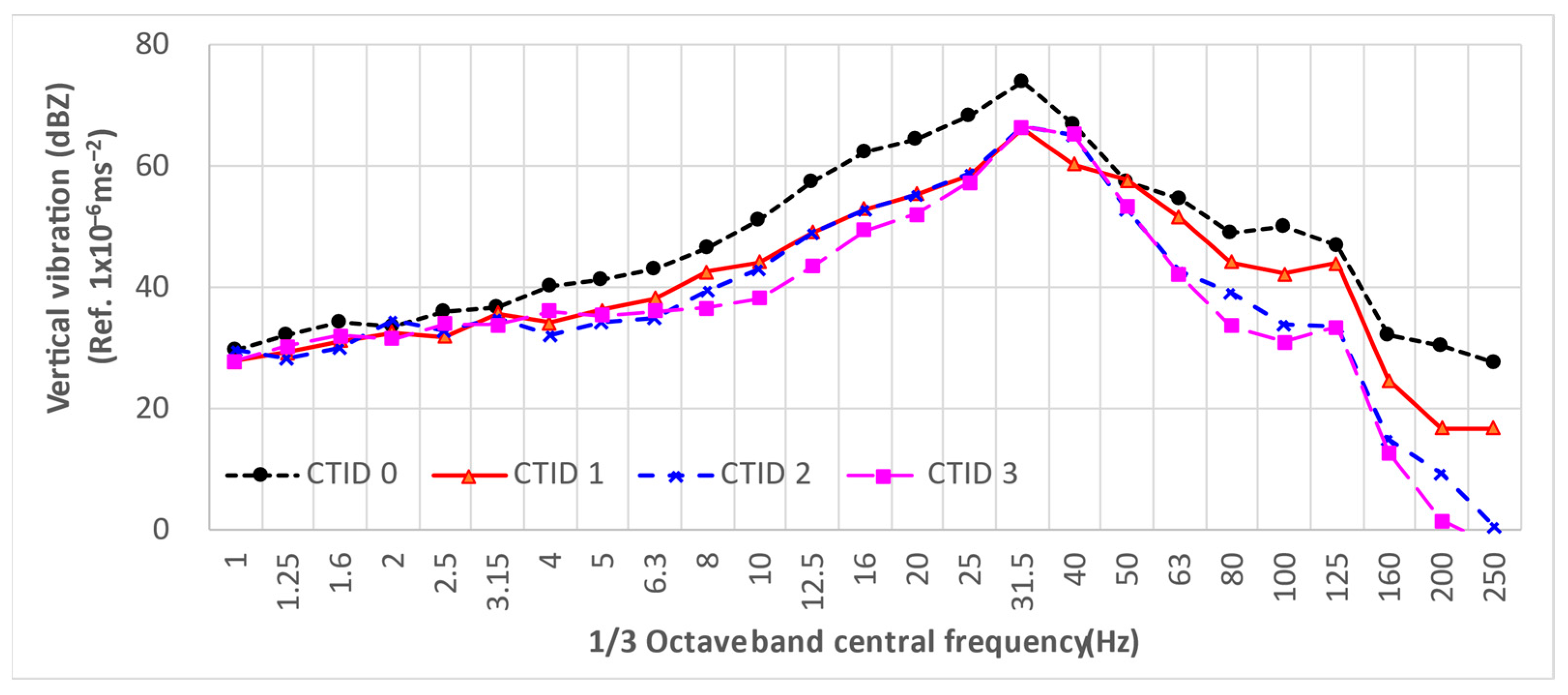
3.3. Vibraton Attenuation at Sensitive Receivers
3.4. Validation of the Computation
4. Conclusions
- Evaluate vibration contribution from trains running simultaneously on the upper- and lower-deck of a double-deck metro-line depot; this output gives an indication for the design of rail track-forms on the upper- and lower-deck.
- Examine receiver-end ground-borne vibration of using different track-forms representing different vibration mitigation measures at the source.
- Comparison of numerical simulation results and site measurements.
- Outputs from the 2.5D FE model in the study have been successfully validated against site measurements from a similar metro-line depot. Therefore, the model is adequate for the prediction of vibration transmission from the railway depot to the TOD built above the depot.
- It has been found that when trains run simultaneously on the upper- and lower-deck of the railway depot, vibration impacts from the train-track interaction on the lower-deck contributes no more than 1 dB, thus can be considered negligible.
- Compared to the reference track-form, using ballast track with vibration isolation mat on the upper-deck may provide up to 8 dB vibration insertion loss, whereas Steel Spring Floating Slab Track (SSFST) provides a similar level of vibration attenuation, i.e., no more than 1 dB difference. Ballast track with isolation mat is therefore a cost-effective option considering its lower capital cost.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TOD | Transit oriented development |
| PSD | Power spectral density |
| PCB | PCB accelerometers |
| SSFST | Steel spring floating slab track |
| TUD | Test train running on the upper-deck only |
| TLD | Test train running on the lower-deck only |
| TBD | Test trains running on both the upper- and lower-decks simultaneously |
References
- Thompson, D. Railway Noise and Vibration: Mechanisms, Modelling and Means of Control, 1st ed.; Elsevier Science: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Cox, S.J.; Wang, A.; Adedipe, A. Survey of Metro Excitation Frequencies and Coincidence of Different Modes. In Noise and Vibration Mitigation for Rail Transportation Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 78–85. [Google Scholar] [CrossRef]
- ISO 2631-1:1997; Mechanical Vibration and Shock—Evaluation of Human Exposure to Whole-Body Vibration—Part 1: General Requirements. International Organization for Standardization: Geneva, Switzerland, 1997.
- Degrande, G.; Schevenels, M.; Chatterjee, P.; Van de Velde, W.; Hölscher, P.; Hopman, V.; Wang, A.; Dadkah, N. Vibrations due to a test train at variable speeds in a deep bored tunnel embedded in London clay. J. Sound Vib. 2006, 293, 626–644. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Ground-Borne Noise and Vibration in Buildings Caused by Rail Transit; Transportation Research Board: Washington, DC, USA, 2010. [Google Scholar] [CrossRef]
- Sanayei, M.; Maurya, P.; Moore, J.A. Measurement of building foundation and ground-borne vibrations due to surface trains and subways. Eng. Struct. 2013, 53, 102–111. [Google Scholar] [CrossRef]
- Cao, Z.; Guo, T.; Zhang, Z.; Li, A. Measurement and analysis of vibrations in a residential building constructed on an elevated metro depot. Measurement 2018, 125, 394–405. [Google Scholar] [CrossRef]
- Kurzweil, L.G. Ground-borne noise and vibration from underground rail systems. J. Sound Vib. 1979, 66, 363–370. [Google Scholar] [CrossRef]
- Ouakka, S.; Verlinden, O.; Kouroussis, G. Railway ground vibration and mitigation measures: Benchmarking of best practices. Railw. Eng. Sci. 2022, 30, 1–22. [Google Scholar] [CrossRef]
- Esmaeili, 19M.; Mosayebi, S.A.; Zakeri, J.A. Ground-Borne Vibrations Caused by Unsupported Railway Sleepers in Ballasted Tracks. Procedia Eng. 2017, 199, 2645–2650. [Google Scholar] [CrossRef]
- Lurcock, D.E.J.; Thompson, D.J.; Bewes, O.G. Groundborne Railway Noise and Vibration in Buildings: Results of a Structural and Acoustic Parametric Study. In Noise and Vibration Mitigation for Rail Transportation Systems; Springer: Cham, Switzerland, 2018; pp. 193–204. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, Z.; Liu, T.; Lou, P.; Song, X. Comparison of 2D and 3D prediction models for environmental vibration induced by underground railway with two types of tracks. Comput. Geotech. 2015, 68, 169–183. [Google Scholar] [CrossRef]
- Suhairy, S. Prediction of Ground Vibration from Railways; Chalmers University of Technology: Gothenburg, Sweden, 2000. [Google Scholar]
- Eadie, D.T.; Santoro, M. Top-of-rail friction control for curve noise mitigation and corrugation rate reduction. J. Sound Vib. 2006, 293, 747–757. [Google Scholar] [CrossRef]
- Eadie, D.T.; Kalousek, J.; Chiddick, K.C. The role of high positive friction (HPF) modifier in the control of short pitch corrugations and related phenomena. Wear 2002, 253, 185–192. [Google Scholar] [CrossRef]
- Eadie, D.T.; Santoro, M.; Oldknow, K.; Oka, Y. Field studies of the effect of friction modifiers on short pitch corrugation generation in curves. Wear 2008, 265, 1212–1221. [Google Scholar] [CrossRef]
- Torstensson, P.T.; Pieringer, A.; Nielsen, J.C.O. Simulation of rail roughness growth on small radius curves using a non-Hertzian and non-steady wheel-rail contact model. Wear 2014, 314, 241–253. [Google Scholar] [CrossRef]
- Torstensson, P.T.; Schilke, M. Rail corrugation growth on small radius curves-Measurements and validation of a numerical prediction model. Wear 2013, 303, 381–396. [Google Scholar] [CrossRef]
- Wu, T.X. Parametric excitation of wheel/track system and its effects on rail corrugation. Wear 2008, 265, 1176–1182. [Google Scholar] [CrossRef]
- Jin, X.S.; Wen, Z.F.; Wang, K.Y.; Zhou, Z.R.; Liu, Q.Y.; Li, C.H. Three-dimensional train-track model for study of rail corrugation. J. Sound Vib. 2006, 293, 830–855. [Google Scholar] [CrossRef]
- Jin, X.; Wen, Z.; Zhang, W.; Shen, Z. Numerical simulation of rail corrugation on a curved track. Comput. Struct. 2005, 83, 2052–2065. [Google Scholar] [CrossRef]
- Moreno, A.G.; Aguilar, J.J.R.; Lopez, J.A.M. Towards the numerical ground-borne vibrations predictive models as a design tool for railway lines: A starting point THE. Transp. Res. Procedia 2021, 58, 363–369. [Google Scholar] [CrossRef]
- Arcos, R.; Soares, P.J.; Costa, P.A.; Godinho, L. An experimental/numerical hybrid methodology for the prediction of railway-induced ground-borne vibration on buildings to be constructed close to existing railway infrastructures: Numerical validation and parametric study. Soil Dyn. Earthq. Eng. 2021, 150, 106888. [Google Scholar] [CrossRef]
- Jean, P.; Guigou-Carter, C. Reducing ground borne noise due to railways: A practical application. Appl. Acoust. 2021, 178, 108011. [Google Scholar] [CrossRef]
- Colaço, A.; Costa, P.A.; Amado-Mendes, P.; Calçada, R. Vibrations induced by railway traffic in buildings: Experimental validation of a sub-structuring methodology based on 2.5D FEM-MFS and 3D FEM. Eng. Struct. 2021, 240, 112381. [Google Scholar] [CrossRef]
- U. Health and Safety Executive, How Do I Reduce Noise? n.d. Available online: https://www.hse.gov.uk/Noise/Reducenoise.Htm (accessed on 13 November 2025).
- U.S. Department of Labor. Occupational Safety and Health Administration, Occupational Noise Exposure. Available online: https://www.osha.gov/Noise/Exposure-Controls (accessed on 13 November 2025).
- The National People’s Congress of the People’s Republic of China. Law of the People’s Republic of China on the Prevention and Control of Noise Pollution. 2021. Available online: http://en.npc.gov.cn.cdurl.cn/2022-10/08/c_817695.htm (accessed on 13 November 2025).
- Tao, Z.; Wang, Y.; Sanayei, M.; Moore, J.A.; Zou, C. Experimental study of train-induced vibration in over-track buildings in a metro depot. Eng. Struct. 2019, 198, 109473. [Google Scholar] [CrossRef]
- Zou, C.; Wang, Y.; Zhang, X.; Tao, Z. Vibration isolation of over-track buildings in a metro depot by using trackside wave barriers. J. Build. Eng. 2020, 30, 101270. [Google Scholar] [CrossRef]
- GB 10070-1988; Standard of Environmental Vibration in Urban Area. Ministry of Ecology and Environment of People’s Republic of China: Beijing, China, 1988.
- GB 3096-2008; Environmental Quality Standard for Noise. Ministry of Ecology and Environment of the People’s Republic of China: Beijing, China, 2008.
- GB 55016-2021; General Code for Building Environment. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2021.
- GB 12348-2008; Emission Standard for Industrial Enterprises Noise at Boundary. Ministry of Ecology and Environment of the People’s Republic of China: Beijing, China, 2008.
- JGJ/T 170-2009; Standard for Limit and Measuring Method of Building Vibration and Secondary Noise Caused by Urban Rail Transit. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2009.
- ANSYS Mechanical APD 2020 R2, Synopsys, 2020. Available online: www.ansys.com (accessed on 15 September 2025).
- Li, H.; Thompson, D.; Squicciarini, G. A 2.5D acoustic finite element method applied to railway acoustics. Appl. Acoust. 2021, 182, 108270. [Google Scholar] [CrossRef]
- Yaseri, A.; Bazyar, M.H.; Javady, S. 2.5D coupled FEM-SBFEM analysis of ground vibrations induced by train movement. Soil Dyn. Earthq. Eng. 2018, 104, 307–318. [Google Scholar] [CrossRef]
- Amado-Mendes, P.; Costa, P.A.; Godinho, L.M.C.; Lopes, P. 2.5D MFS-FEM model for the prediction of vibrations due to underground railway traffic. Eng. Struct. 2015, 104, 141–154. [Google Scholar] [CrossRef]
- Yang, Y.B.; Liu, S.J.; Chen, W.; Tan, Q.; Wu, Y.T. Half-space response to trains moving along curved paths by 2.5D finite/infinite element approach. Soil Dyn. Earthq. Eng. 2021, 145, 106740. [Google Scholar] [CrossRef]
- Yang, Y.B.; Liu, S.J.; Li, Q.M.; Ge, P.B. Stress waves in half-space due to moving train loads by 2.5D finite/infinite element approach. Soil Dyn. Earthq. Eng. 2019, 125, 105714. [Google Scholar] [CrossRef]
- Connolly, D.P.; Galvín, P.; Olivier, B.; Romero, A.; Kouroussis, G. A 2.5D time-frequency domain model for railway induced soil-building vibration due to railway defects. Soil Dyn. Earthq. Eng. 2019, 120, 332–344. [Google Scholar] [CrossRef]
- Costa, P.A.; Calçada, R.; Cardoso, A.S. Track–ground vibrations induced by railway traffic: In-situ measurements and validation of a 2.5D FEM-BEM model. Soil Dyn. Earthq. Eng. 2012, 32, 111–128. [Google Scholar] [CrossRef]
- Ghangale, D.; Arcos, R.; Clot, A.; Cayero, J.; Romeu, J. A methodology based on 2.5D FEM-BEM for the evaluation of the vibration energy flow radiated by underground railway infrastructures. Tunn. Undergr. Space Technol. 2020, 101, 103392. [Google Scholar] [CrossRef]
- Jin, Q.; Thompson, D.J.; Lurcock, D.E.J.; Toward, M.G.R.; Ntotsios, E. A 2.5D finite element and boundary element model for the ground vibration from trains in tunnels and validation using measurement data. J. Sound Vib. 2018, 422, 373–389. [Google Scholar] [CrossRef]
- Tabib, M.; Rasheed, A.; Siddiqui, M.S.; Kvamsdal, T. A full-scale 3D Vs 2.5D Vs 2D analysis of flow pattern and forces for an industrial-scale 5MW NREL reference wind-turbine. Energy Procedia 2017, 137, 477–486. [Google Scholar] [CrossRef]
- U.S. Department of Transportation. U.S. Manual for High-Speed Ground Transportation Noise and Vibration Impact Assessment; Federal Railroad Administration; U.S. Department of Transportation: Washington, DC, USA, 2005.
- ISO 3095:2025; Railway Applications—Acoustics—Measurement of Noise Emitted by Railbound Vehicles. International Organization for Standardization: Geneva, Switzerland, 2025.
- RailMeasurement, Corrugation Analysis Trolley (CAT). Available online: https://www.railmeasurement.com/ (accessed on 21 August 2024).
- GB 10071-1988; Measurement Method of Environmental Vibration of Urban Area. Ministry of Ecology and Environment of the People’s Republic of China: Beijing, China, 1988.








| Category of Standard | Name of Standard | Limit | ||
|---|---|---|---|---|
| Residential Buildings | Educational Facilities (Including Schools and Nurseries) | Office and Mixes | ||
| Vibration | GB 10070-88 <Standard of environmental vibration in urban area> [31] | Category I: Daytime 70 dB; Night-time 67 dB | Category I: Daytime 70 dB; Night-time 67 dB | Category II: Daytime 75 dB; Night-time 72 dB |
| Environmental noise | GB 3096-2008 <Environmental quality standard for noise> [32] | Category II: Daytime 60 dB (A); Night-time 50 dB (A) | Category II: Daytime 60 dB (A); Night-time 50 dB (A) | Category II: Daytime 60 dB (A); Night-time 50 dB (A) |
| Room interior noise | GB 55016-2021 <General code for building environment> [33] | Category ‘Sleeping’: Daytime40 dB (A); Night-time 30 dB (A); Category ‘Living’: 45 dB (A) | Category ‘Education’: 45 dB (A) | Category ‘Office’: 45 dB (A) |
| Industrial enterprises noise at boundary | GB 12348-2008 <Emission standard for industrial enterprises noise at boundary> [34] | Category 2: Daytime 60 dBA (A); Night-time 50 dB (A) | ||
| Vibration and structure-borne noise | JGJ/T 170-2009 <Standard for limit and measuring method of building vibration and secondary noise caused by urban rail transit> [35] | Vibration: Category 2: Daytime 70 dB; Night-time 67 dB | Vibration: Category 2: Daytime 70 dB; Night-time 67 dB | Vibration: Category 2: Daytime 70 dB; Night-time 67 dB |
| Structure-borne noise: Category 2: Daytime 41 dB (A); Night-time 38 dB (A) | Structure-borne noise: Category 2: Daytime 41 dB (A); Night-time 38 dB (A) | Structure-borne noise: Category 2: Daytime 41 dB (A); Night-time 38 dB (A) | ||
| ID | Name of Parts of the Train Vehicle | Material Property | Unit | Quantity |
|---|---|---|---|---|
| 1 | Axle load | Without passengers | kg | 11,000 |
| 2 | Full load | kg | 16,000 | |
| 3 | Car body | Mass (without passengers) | kg | 23,000 |
| 4 | Mass (full load) | kg | 48,000 | |
| 5 | Length | m | 24.4 | |
| 6 | Primary suspension | Vertical Stiffness KV | N/m | 1.229 × 106 |
| 7 | Lateral Stiffness KL | N/m | 1.542 × 106 | |
| 8 | Vertical Damping CV | N·s/m | 1.229 × 103 | |
| 9 | Lateral Damping CL | N·s/m | 1.542 × 103 | |
| 10 | Secondary suspension | Vertical Stiffness KV | N/m | 0.227 × 106 |
| 11 | Lateral Stiffness KL | N/m | 0.118 × 106 | |
| 12 | Vertical Damping CV | N·s/m | 0.227 × 103 | |
| 13 | Lateral Damping CL | N·s/m | 0.118 × 103 | |
| 14 | Bogie | Mass (Motor) | kg | 4600 |
| 15 | Mass (Trailer) | kg | 2800 | |
| 16 | Distance between bogie centres (2Lc) | m | 15.7 | |
| 17 | Wheelset | Unsprung mass (Motor) | kg | 1590 |
| 18 | Unsprung mass (Trailer) | kg | 1140 |
| ID | Item | Young’s Modulus (GPa) | Poisson’s Ratio | Density (kg·m−3) | Damping Ratio |
|---|---|---|---|---|---|
| 1 | 50 kg/m rail | 206 | 0.3 | 7850 | 0.005 |
| 2 | Concrete slab | 34.5 | 0.2 | 2500 | 0.05 |
| 3 | Resilient mat | 3 × 10−3 | 0.45 | 2.25 × 10−1 | 0.075 |
| 4 | Standard rail fasteners | 7.35 × 10−3 | 0.45 | 1000 | 0.05 |
| 5 | Resilient rail fasteners | 2.83 × 10−3 | 0.45 | 1000 | 0.075 |
| 6 | Ballast | 1 × 10−8 | 0.35 | 1800 | 0.05 |
| 7 | Steel Spring | 3.83 × 10−3 | 0.3 | 1000 | 0.001 |
| 8 | Ground | 1 × 10−1 | 0.25 | 1500 | 0.25 |
| ID | Item | Young’s Modulus (GPa) | Poisson’s Ratio | Density (kg·m−3) | Damping Ratio |
|---|---|---|---|---|---|
| 1 | Depot plates (0 m, 9 m, and 16 m plates) | 34.5 | 0.2 | 2700 | 0.05 |
| 2 | Depot structural columns | 82.8 × 10−3 | 0.2 | 85 | 0.05 |
| 3 | Building walls | 33 | 0.2 | 2700 | 0.05 |
| 4 | Building floor slabs | 33 | 0.2 | 2700 | 0.05 |
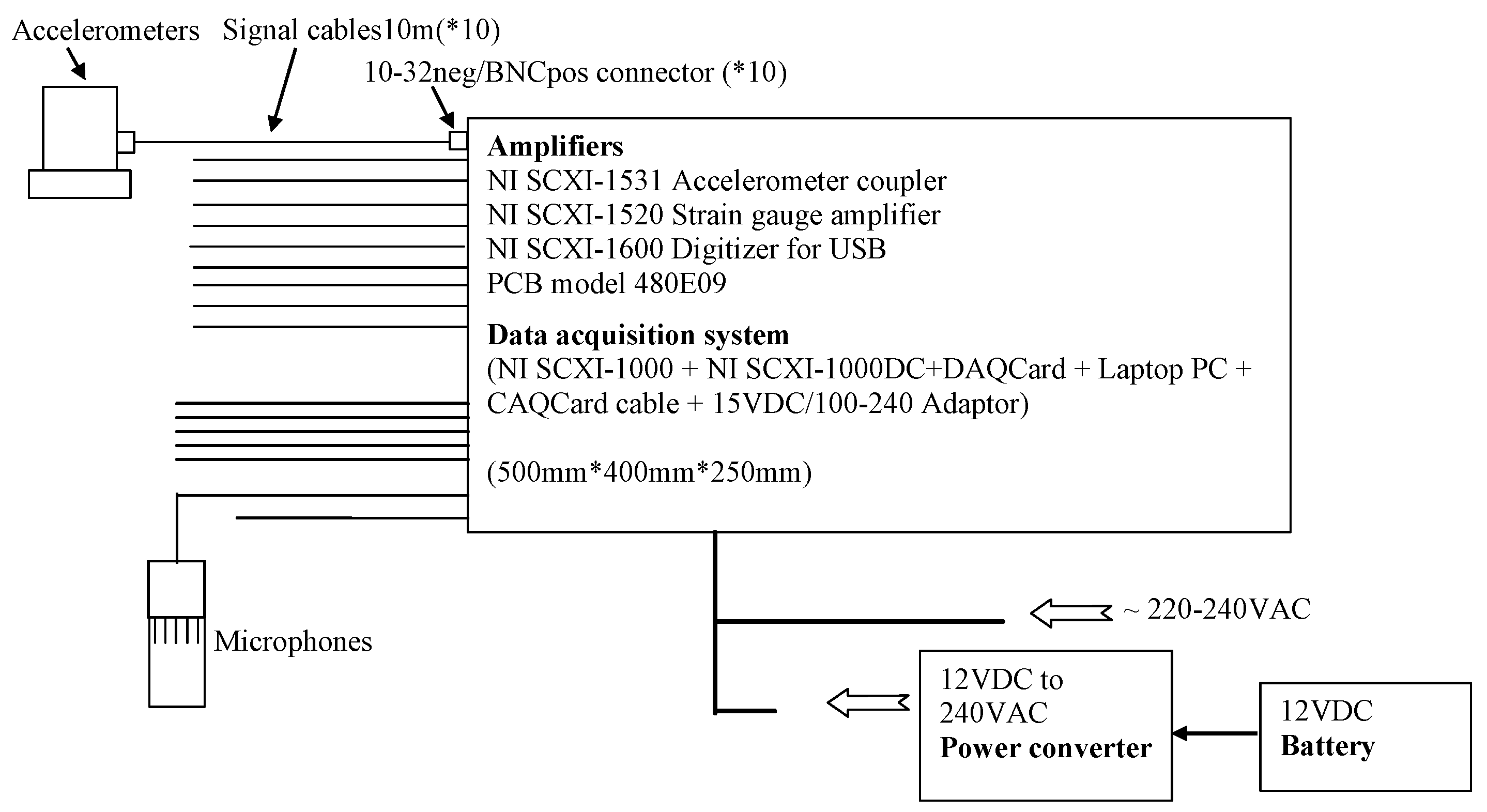
| Sensor ID | Measurement Location | Measurement Range | Sensitivity | Frequency Range |
|---|---|---|---|---|
| A1–A4 | Rails | ±500 g pk | (±10%) 10 mV/g | (±5%) 0.5 to 10,000 Hz |
| A7–A10 | On the ground and at the columns at the source level (Figure 8a) | ±5 g pk | (±5%) 1000 mV/g | (±5%) 0.5 to 2000 Hz |
| A11–A15 | On the ground of the depot roof plate (Figure 8b) | ±0.5 g pk | (±10%) 10,000 mV/g | (±5%) 0.15 to 1000 Hz |
| Track ID | Track-form | Formation | Key Parameters |
|---|---|---|---|
| A | Slab track | Standard rail fasteners + concrete sleepers + concrete slab | Reference track-form with no resilient component, under the traffic of an empty type A train vehicle; |
| B | Ballast track | Standard rail fasteners + concrete sleepers + ballast track-bed | Sleeper dynamic displacement with reference to the ground-level = 0.5 mm; Sleeper equivalent static stiffness = 30 kN/mm; |
| C | Ballast track with under-mat | Standard rail fasteners + concrete sleepers + ballast track-bed + ballast mat | Track-bed dynamic displacement with reference to the ground-level = 1.0 mm; |
| D | Slab track with resilient rail fasteners | Resilient rail fasteners + concrete slab | Rail dynamic displacement with reference to the sleeper-level = 1.0 mm; Resilient fastener equivalent static stiffness = 15 kN/mm; |
| E | Steel Spring Floating-Slab-Track (SSFST) | Standard rail fasteners + Steel Spring Floating-Slab-Track | Slab dynamic displacement with reference to the ground-level = 2.0 mm; |
| Combo-Track ID | Upper-Deck | Lower-Deck | Track ID |
|---|---|---|---|
| 0 | Slab track | Slab track | A + A |
| 1 | Ballast track with mat | Slab track with resilient rail fasteners | C + D |
| 2 | SSFST | Slab track with resilient rail fasteners | E + D |
| 3 | SSFST | Ballast track with mat | E + C |
| Combination of Track-Forms | Total Vertical Vibration Level (LdBZ Ref. 1 × 10−6 ms−2) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Computation Point A | Computation Point B | Computation Point C | ||||||||||||
| Combo-Track ID | Upper-Deck | Lower-Deck | TUD | TLD | TBD | TBD-TUD | TUD | TLD | TBD | TBD-TUD | TUD | TLD | TBD | TBD-TUD |
| 0 | Slab track | Slab track | 71.5 | 62.7 | 72.0 | 0.5 | 72.3 | 61.8 | 72.6 | 0.3 | 68.7 | 59.7 | 69.2 | 0.5 |
| 1 | Ballast track with mat | Slab track with resilient rail fasteners | 66.5 | 57.2 | 67.0 | 0.5 | 68.3 | 56.4 | 68.6 | 0.3 | 62.2 | 54.5 | 62.9 | 0.7 |
| 2 | SSFST | Slab track with resilient rail fasteners | 65.7 | 57.2 | 66.3 | 0.6 | 66.3 | 56.4 | 66.7 | 0.4 | 61.7 | 54.5 | 62.4 | 0.7 |
| 3 | SSFST | Ballast track with mat | 65.7 | 58.2 | 66.4 | 0.7 | 66.3 | 54.1 | 66.5 | 0.2 | 61.7 | 50.8 | 62.0 | 0.3 |
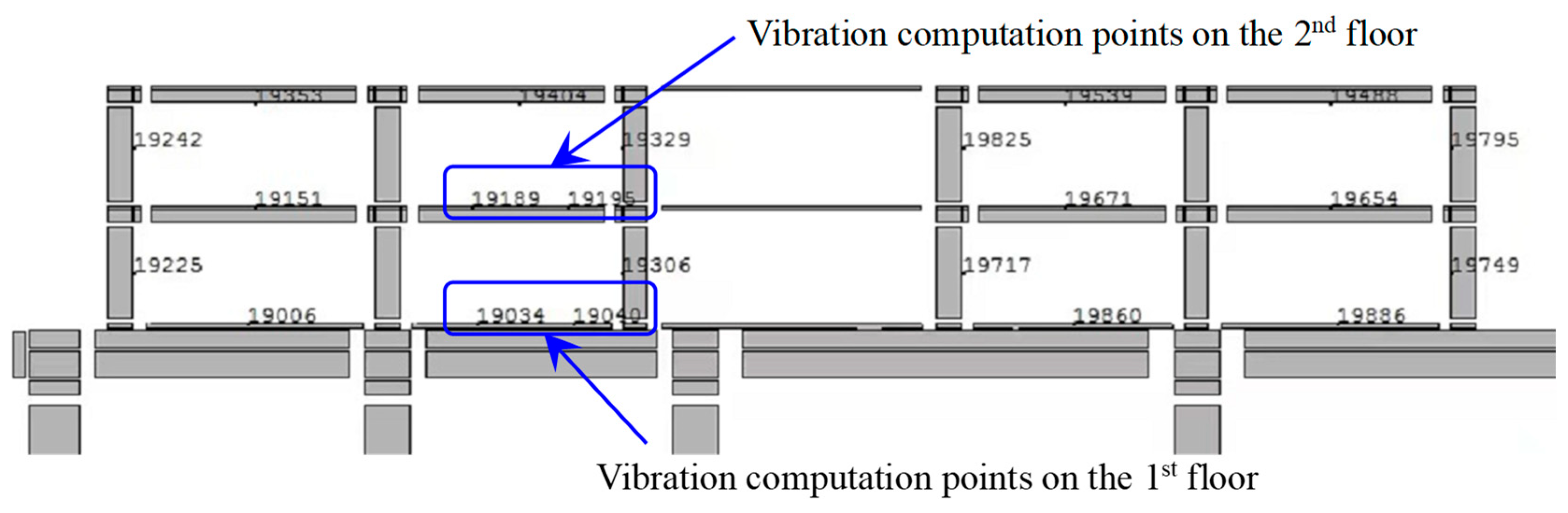
| Combination of Track-Forms | Total Vertical Vibration Level (LdBZ) (Ref. 1 × 10−6 ms−2) | Vibration Attenuation (LdBZ) (Ref. 1 × 10−6 ms−2) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Through Transmission Path | In the Building | |||||||||||||
| CTID | Upper-Deck | Lower-Deck | Ground | Columns | 1st Floor | 2nd Floor | 1st Floor | 2nd Floor | ||||||
| A | B | C | 19034 | 19040 | 19189 | 19195 | 19034 | 19040 | 19189 | 19195 | ||||
| 0 | Slab track | Slab track | 72.0 | 72.6 | 69.2 | 76.3 | 73.7 | 77.5 | 77.7 | - | - | - | - | |
| 1 | Ballast track with mat | Slab track with vibration isolation fasteners | 67.0 | 68.6 | 62.9 | 68.7 | 66.2 | 69.2 | 69.6 | −7.6 | −7.5 | −8.3 | −8.1 | |
| 2 | SSFST | Slab track with vibration isolation fasteners | 66.3 | 66.7 | 62.4 | 69.7 | 66.5 | 69.7 | 70.1 | −6.6 | −7.2 | −7.8 | −7.6 | |
| 3 | SSFST | Ballast track with mat | 66.4 | 66.5 | 62 | 69.4 | 65.8 | 69 | 69.4 | −6.9 | −7.9 | −8.5 | −8.3 | |
| Location | Total Vertical Vibration Level (LdBZ Ref 1 × 10−6 ms−2) | ||||
|---|---|---|---|---|---|
| Numerical Simulation | Site Measurement | % Difference | |||
| Southbound | Northbound | Average | |||
| Point A (0m plate 7.5 m ground) | 65.7 | 77.4 | 70.4 | 73.9 | 12% |
| Point B (0 m plate column) | 66.3 | 60.4 | 52.9 | 56.7 | 15% |
| Point C (9 m plate column) | 61.7 | 65.3 | 61.3 | 63.3 | 3% |
| 2nd floor office room | 69.7 | 64.5 | 58.6 | 61.6 | 12% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, X.P.; Wang, A.; Huang, H. Vibration Mitigation Through Rail Track Design for Structures Built Directly Above a Double-Deck Railway Depot. Vibration 2025, 8, 79. https://doi.org/10.3390/vibration8040079
Gu XP, Wang A, Huang H. Vibration Mitigation Through Rail Track Design for Structures Built Directly Above a Double-Deck Railway Depot. Vibration. 2025; 8(4):79. https://doi.org/10.3390/vibration8040079
Chicago/Turabian StyleGu, Xiaohan Phrain, Anbin Wang, and Hongdong Huang. 2025. "Vibration Mitigation Through Rail Track Design for Structures Built Directly Above a Double-Deck Railway Depot" Vibration 8, no. 4: 79. https://doi.org/10.3390/vibration8040079
APA StyleGu, X. P., Wang, A., & Huang, H. (2025). Vibration Mitigation Through Rail Track Design for Structures Built Directly Above a Double-Deck Railway Depot. Vibration, 8(4), 79. https://doi.org/10.3390/vibration8040079








