The Effect of Wave Signature on the Voltage Output of an Oscillating Water Column
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
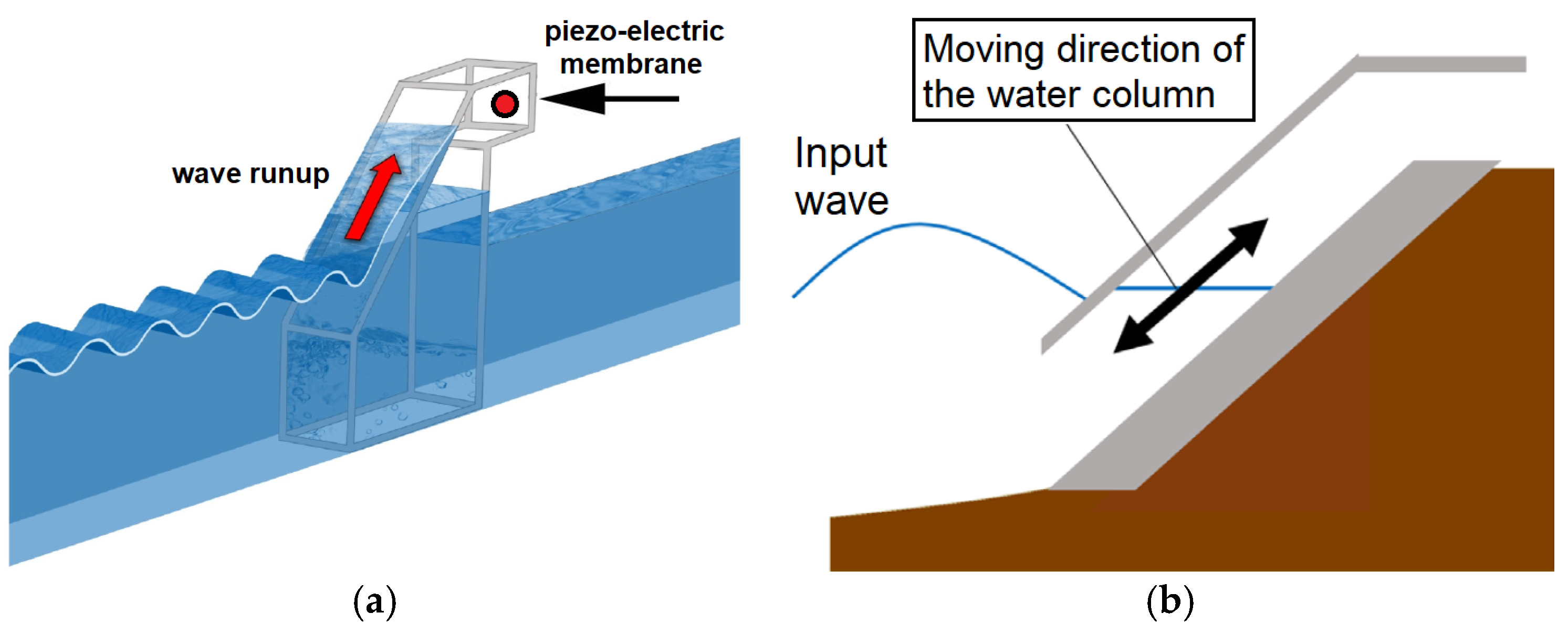
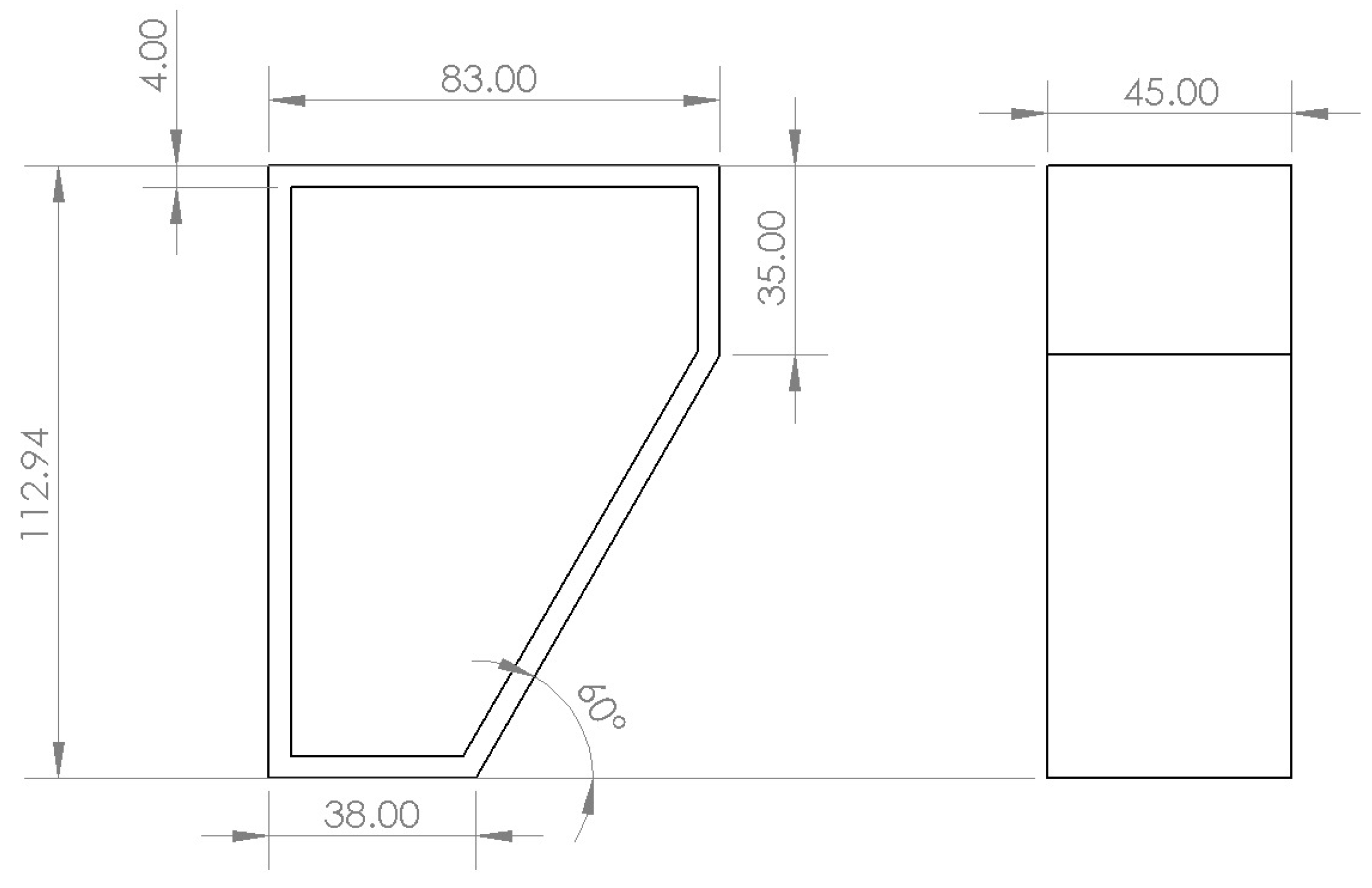
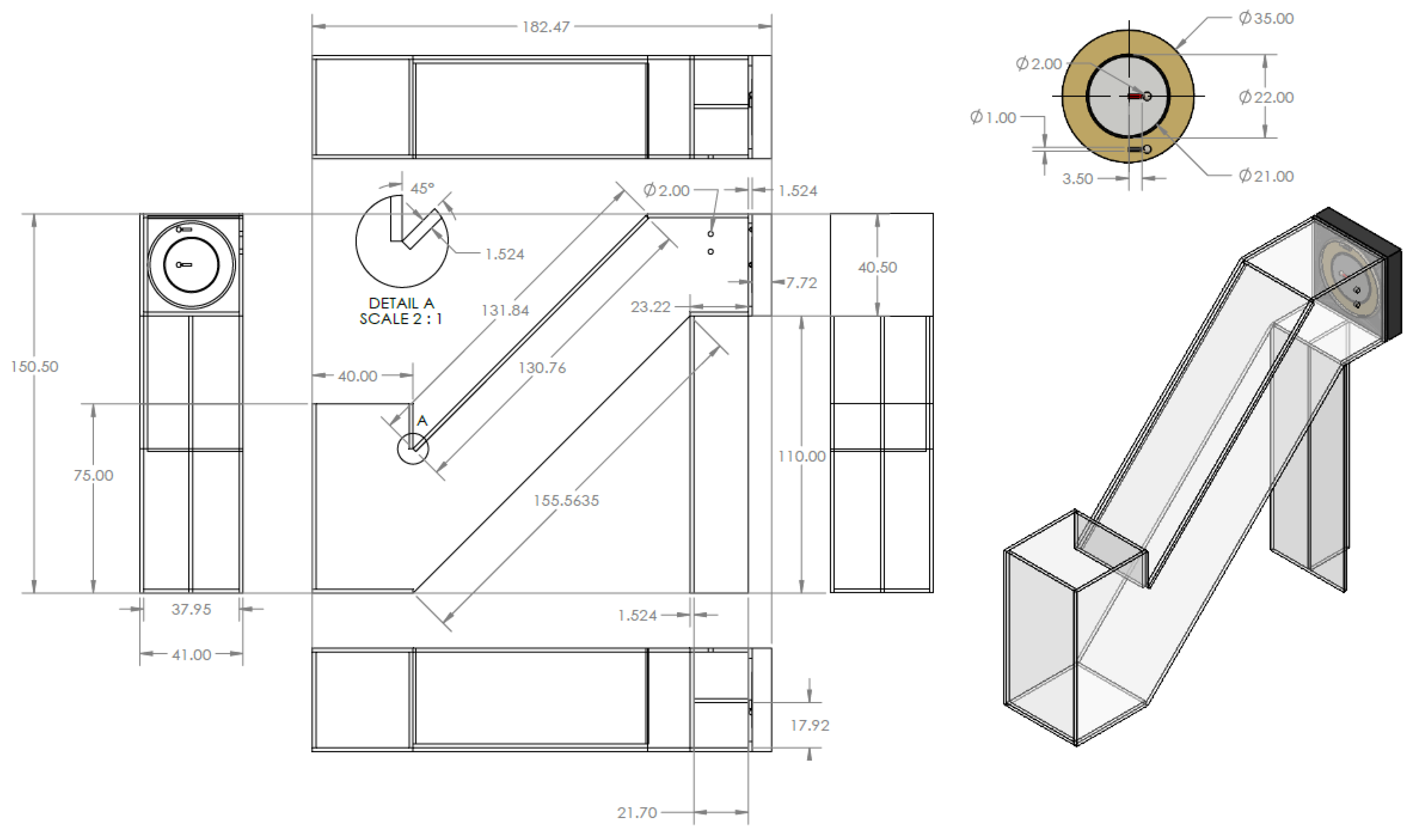
3.1. Laboratory-Scale Oscillating Water Column
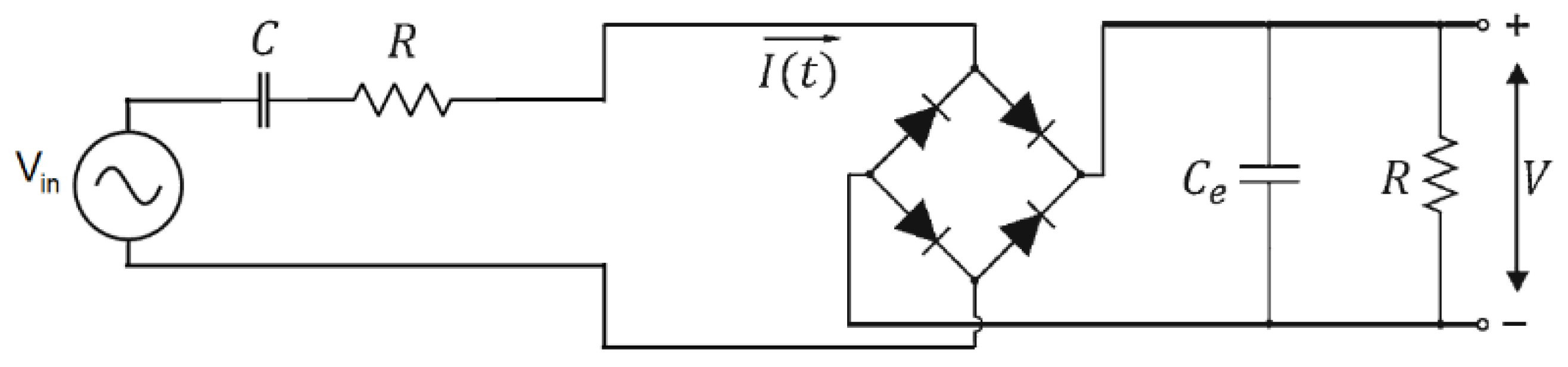
3.2. Experimental Method
4. Results
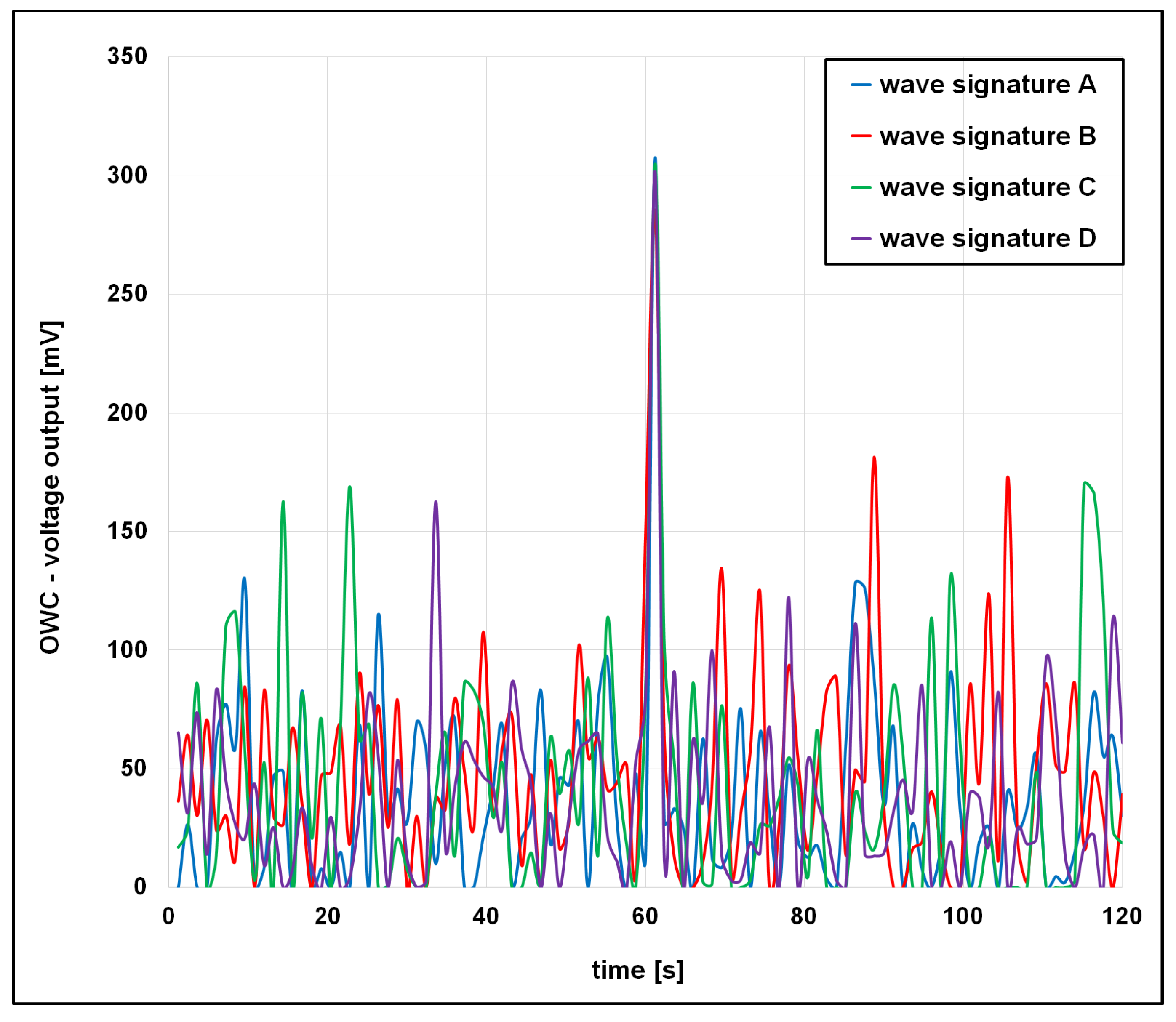
4.1. Analysis of Wave Signature
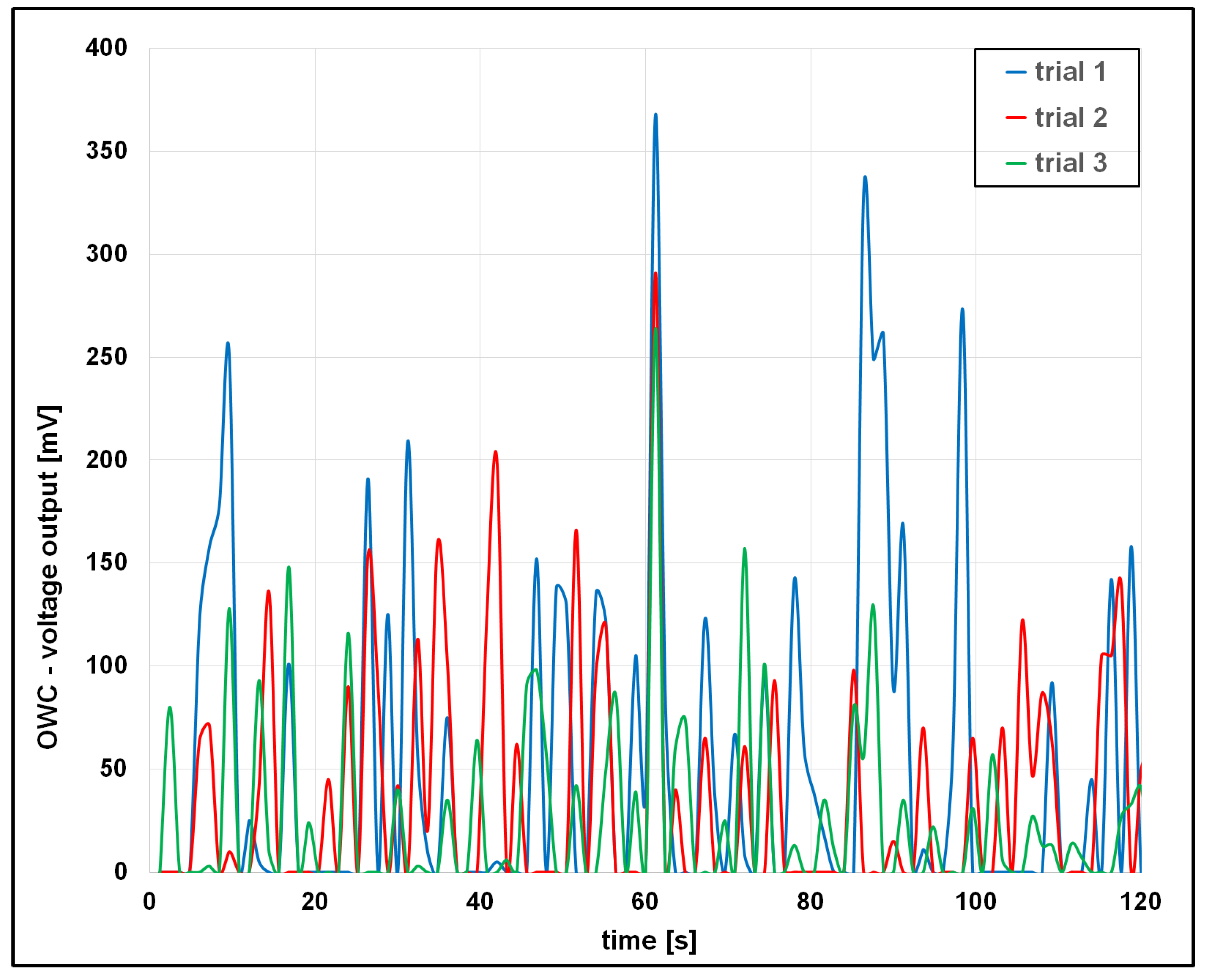
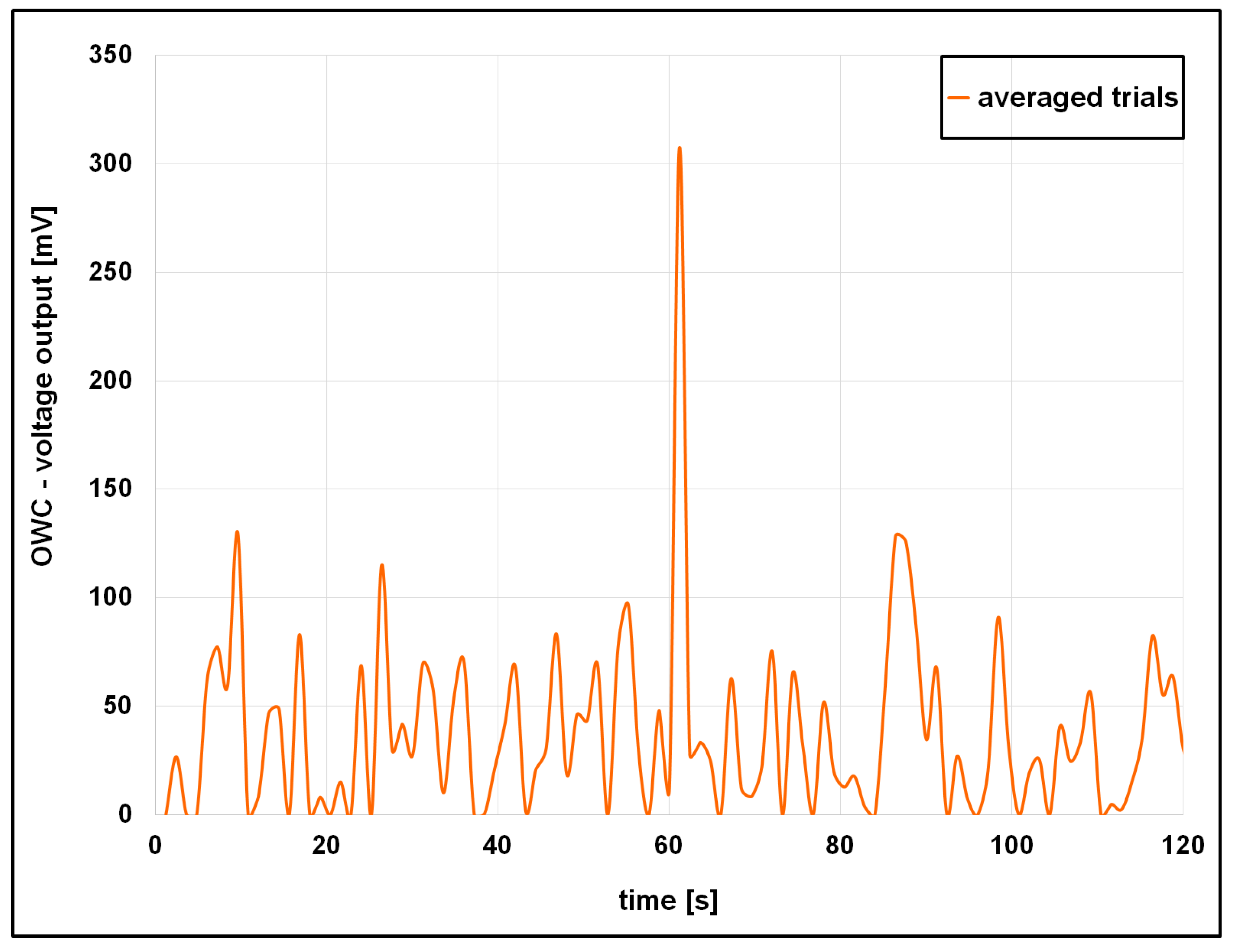
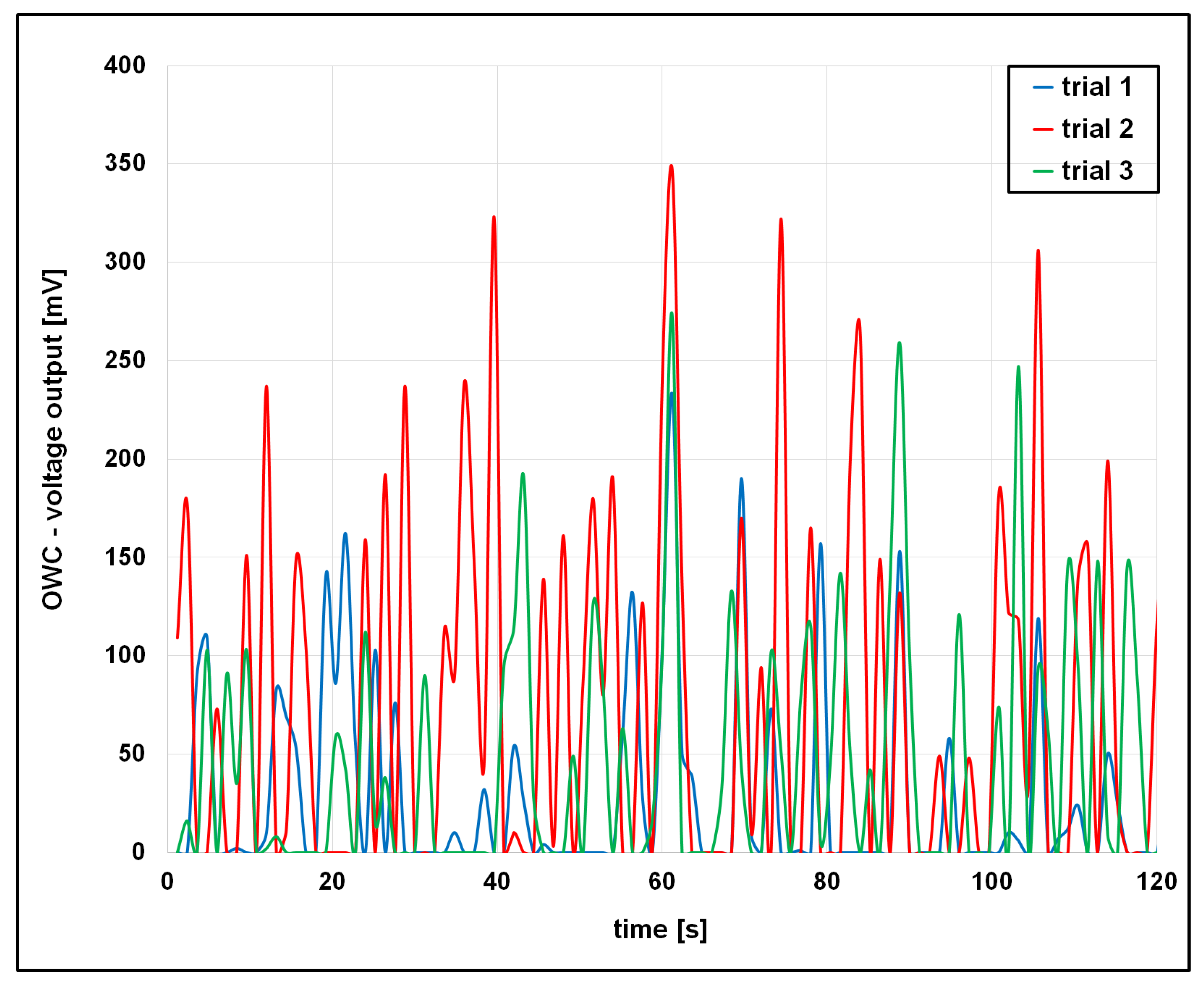
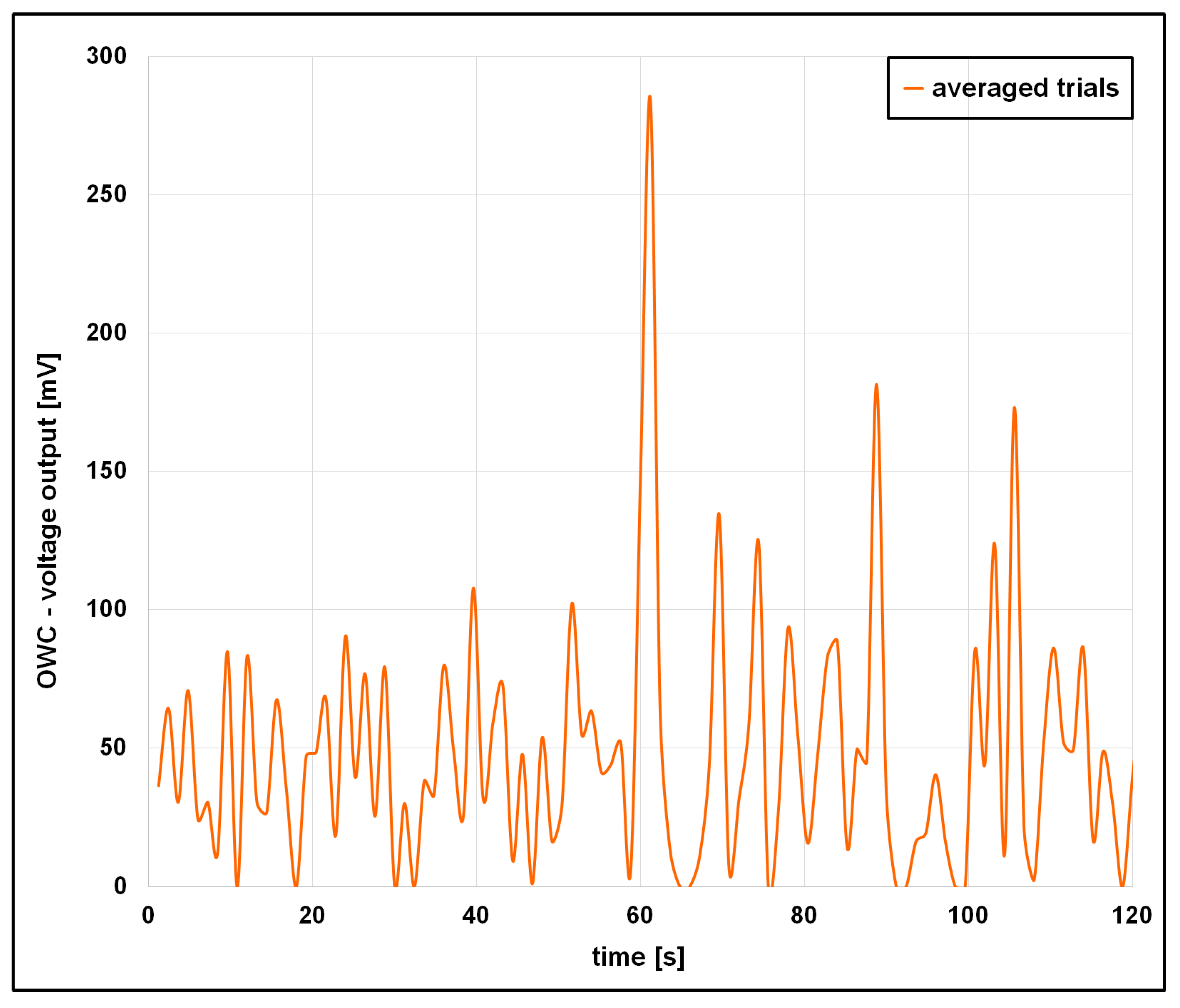
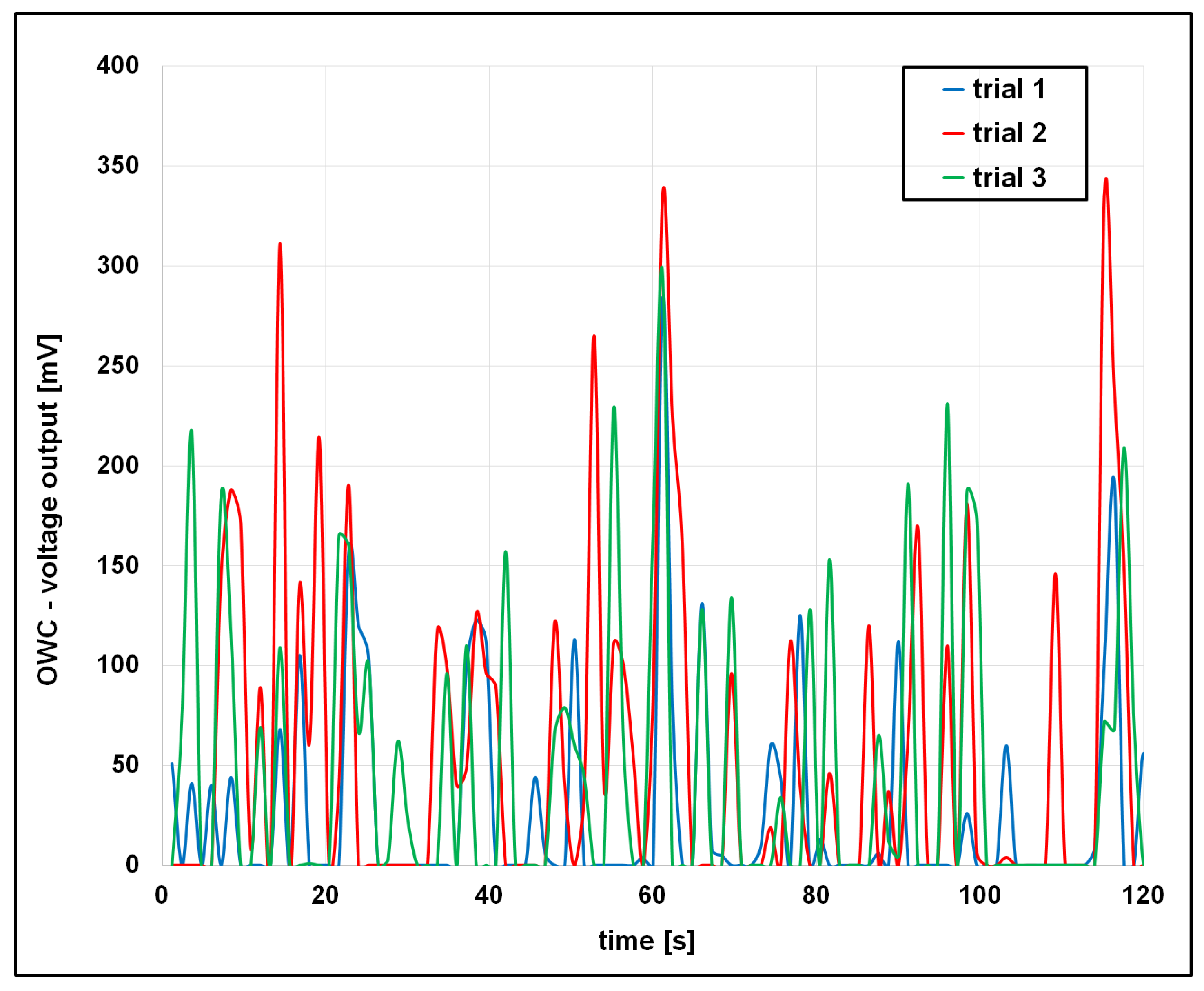
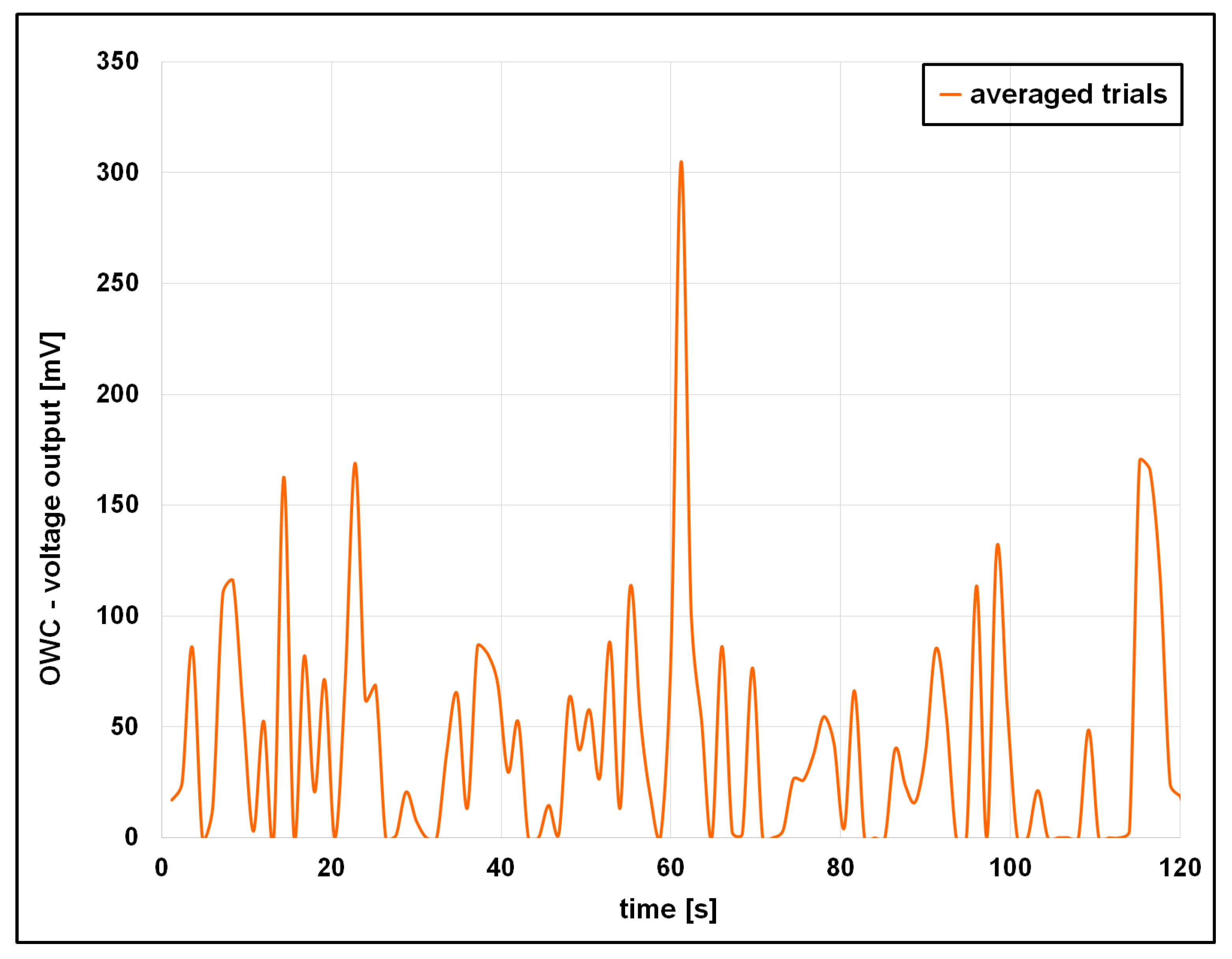
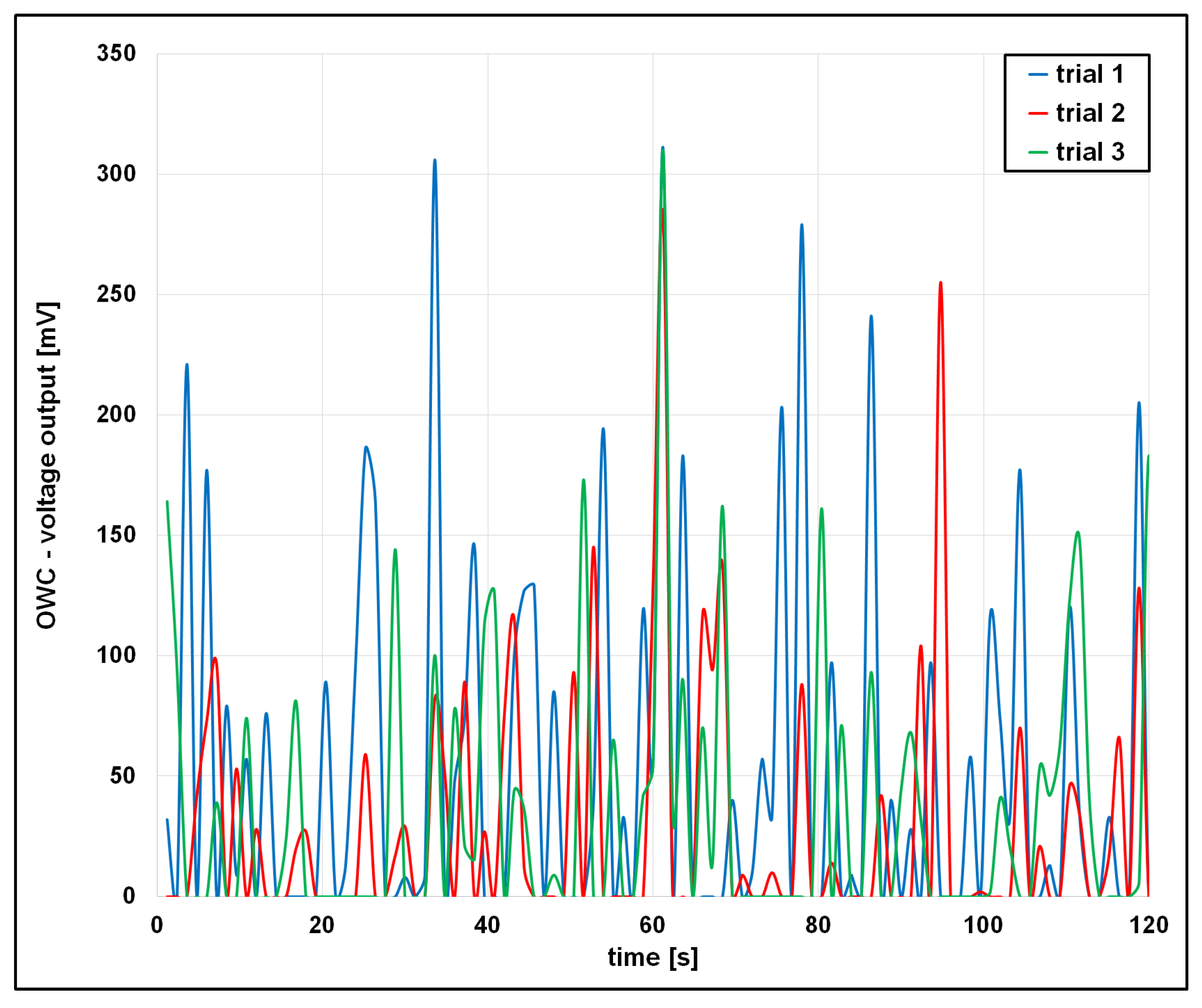
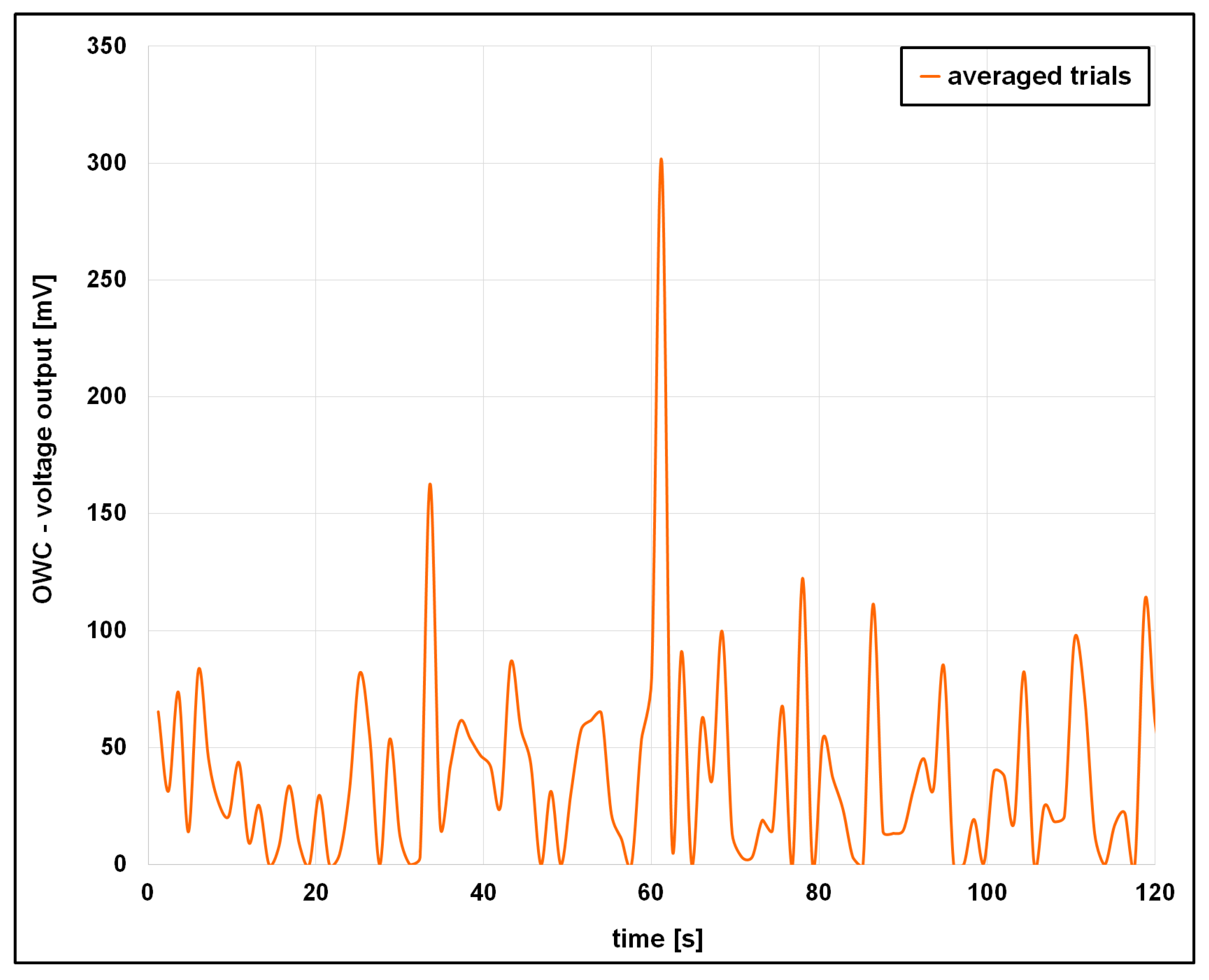
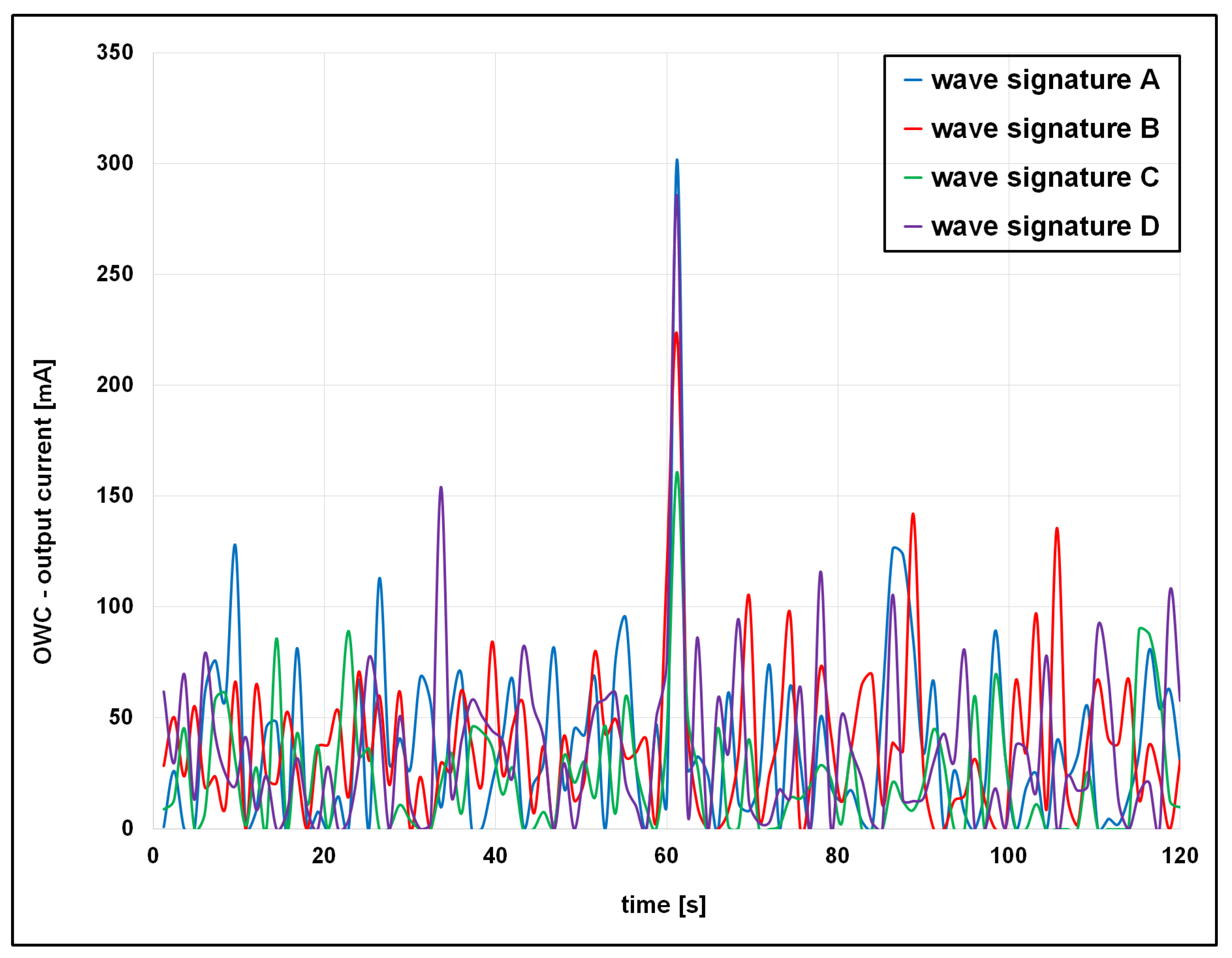
4.2. Analysis of the OWC Voltage Output
5. Discussion
5.1. Influence of Wave Signature Characteristics on OWC Response
5.2. Nonlinearities in the OWC System
- Wave asymmetry and steep slopes introduced rapid transitions in hydrodynamic loading, affecting water column motion.
- Air compressibility within the OWC chamber contributed to phase lags and damping, altering pressure propagation and energy conversion timing.
- Wave–structure interactions, particularly wave impact on the OWC front wall and slamming loads, result in energy dissipation.
5.3. Air Compressibility and Compression Number Analysis
5.4. Secondary Voltage Peaks and Bidirectional Energy Capture
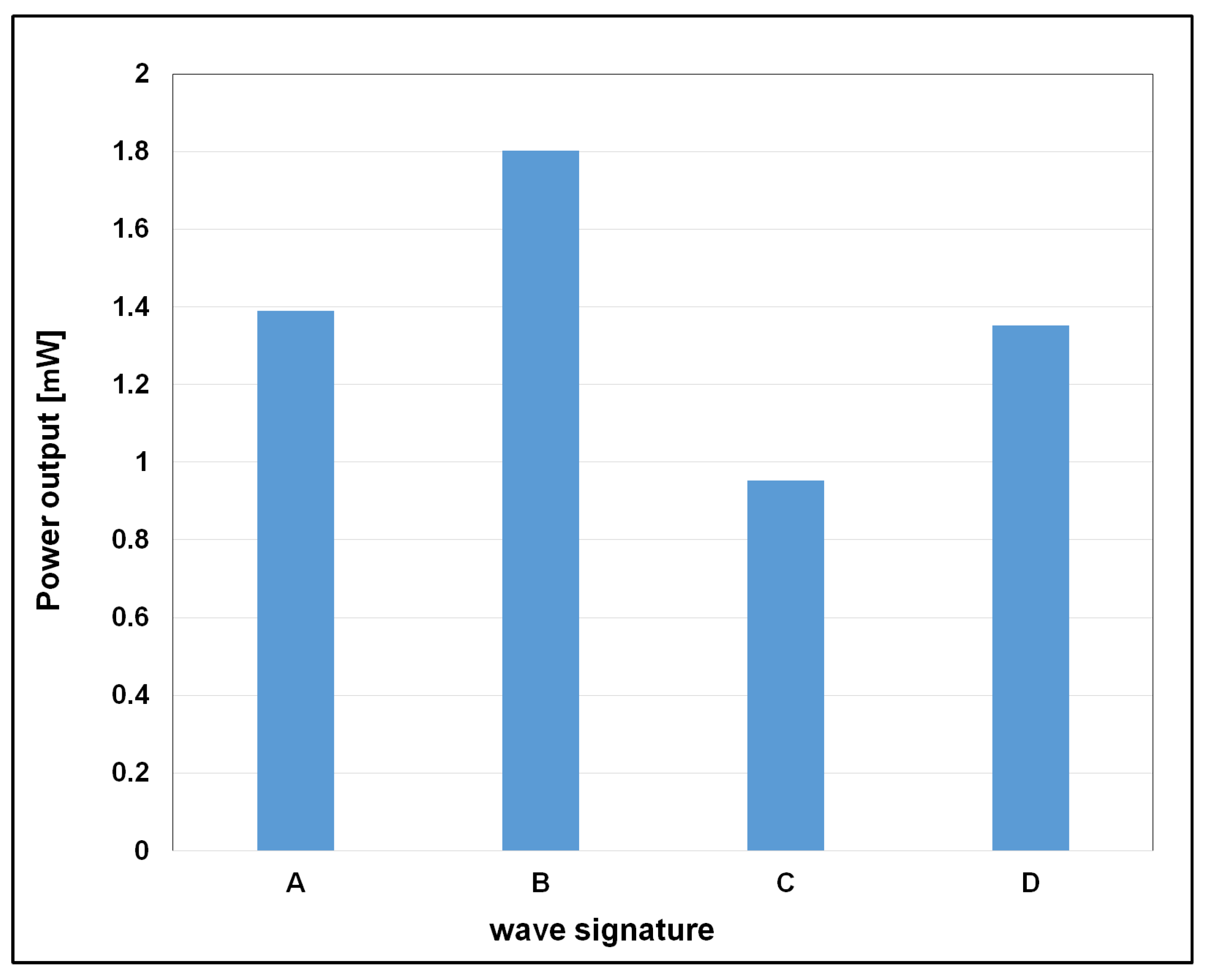
5.5. Energy Output Behavior and Design Implications
- Wave profile tuning is essential; optimal energy capture may occur under moderate wave conditions rather than extreme wave heights.
- Chamber design should account for compressibility-induced phase shifts, enabling better synchronization between wave forcing and pressure buildup.
- Structural resilience to hydrodynamic-induced loads must be considered to avoid performance degradation under highly nonlinear wave conditions.
- Energy recovery from decompression cycles could be harnessed with bidirectional turbines or adaptive damping systems.
5.6. Uncertainty Analysis
5.7. Summary of Key Findings
- The voltage output of an OWC system is highly sensitive to wave signature characteristics, including amplitude, steepness, and frequency.
- Nonlinear system behavior is driven by interactions among the water column, compressible air, and incident wave, with air compressibility playing a significant but not singular role.
- The compression number Ω, ranging between 0.437 and 0.513, confirms the compressible nature of the airflow in all tested cases.
- Secondary voltage peaks, arising from air decompression, suggest that both phases of water motion contribute to energy generation.
- Wave signature C yielded the highest voltage and energy output, while signature D, despite larger amplitudes, underperformed due to increased turbulence and energy losses.
- OWC design should prioritize not only wave height but also control of nonlinear dynamics and air–water phase interactions.
- The trials exhibited variability in results, indicating the presence of experimental uncertainty despite consistent procedures.
- This study identified several sources of uncertainty: (i) dynamic wave conditions (amplitude and period fluctuations), (ii) complex, nonlinear wave–structure interactions in OWC systems, and (iii) scale effects.
- The observed variability aligns with previous studies, which reported 15–30% variation even under standardized experimental conditions, underscoring a common challenge in hydrodynamic testing [20].
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aderinto, T.; Li, H. Review on power performance and efficiency of wave energy converters. Energies 2019, 12, 4329. [Google Scholar]
- Altunkaynak, A.; Çelik, A. A novel Geno-Nonlinear formula for oscillating water column efficiency estimation. Energy 2022, 241, 122513. [Google Scholar]
- Amini, E.; Golbaz, D.; Asadi, R.; Nasiri, M.; Ceylan, O.; Nezhad, M.M.; Neshat, M. A comparative study of metaheuristic algorithms for wave energy converter power take-off optimization: A case study for Eastern Australia. J. Mar. Sci. Eng. 2021, 9, 490. [Google Scholar]
- Brendmo, A. Linear modelling of oscillating water columns including viscous loss. Appl. Ocean Res. 1997, 18, 65–75. [Google Scholar] [CrossRef]
- Çelik, A.; Altunkaynak, A. An in depth experimental investigation into effects of incident wave characteristics front wall opening and PTO damping on the water column displacement and air differential pressure in an OWC chamber. Energy 2021, 230, 120–827. [Google Scholar]
- Çelik, A.; Altunkaynak, A. Determination of hydrodynamic parameters of a fixed OWC by performing experimental and numerical free decay tests. Ocean Eng. 2020, 204, 106827. [Google Scholar]
- Falcao, A.F.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Falcao, A.F.O.; Henriques, J.C.C. Oscillating water column wave energy convertors and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar]
- Falcao, A.F.O.; Henriques, J.C.C. Model-Prototype similarity of oscillating-water-column wave energy converters. Int. J. Marine Energy 2014, 6, 18–34. [Google Scholar] [CrossRef]
- Falcao, A.F.O.; Henriques, J.C.C. The spring-like air compressibility effect in oscillating- water-column wave energy converters: Review and analyses. Renew. Sustain. Energy Rev. 2019, 112, 483–498. [Google Scholar] [CrossRef]
- Hsieh, M.; Lin, I.; Dorrell, D.G.; Hsieh, M.; Lin, C. Development of a wave energy converter using a two chamber oscillating water column. IEEE Trans. Sustain. Energy 2012, 3, 482–497. [Google Scholar]
- Kinoshita, T.; Masuda, K.; Miyajima, S.; Kato, W. Research on the system simulation for a fixed, O.W.C. type wave energy absorber. J. Soc. Nav. Archit. Jpn. 1984, 156, 255–263. [Google Scholar] [CrossRef] [PubMed]
- Lopez, I.; Castro, A.; Iglesias, G. Hydrodynamic performance of an Oscillating Water Column wave energy converter by means of particle imaging velocimetry. Energy 2015, 83, 89–103. [Google Scholar] [CrossRef]
- Mandev, M.B.; Altunkaynak, A.; Çelik, A. Enhancing wave energy harvesting: Performance analysis of a dual chamber oscillating water column. Energy 2024, 290, 130191. [Google Scholar] [CrossRef]
- Mitsumasa, I.; Takeaki, M.; Hiroshi, S.; Makoto, I. Effect of inclination on oscillation characteristics of an oscillating water column wave energy converter. Ocean. Eng. 2016, 116, 226–235. [Google Scholar]
- Mora, A.; Bautista, E.; Mendez, F. Influence of a tapered and slender wave collector on the increment of the efficiency of an oscillating water column wave-energy converter. Ocean Eng. 2017, 129, 20–30. [Google Scholar] [CrossRef]
- Ning, D.; Wang, R.; Zhang, C. Numerical simulation of a dual-chamber oscillating water column wave energy converter. Sustainability 2017, 9, 1599. [Google Scholar] [CrossRef]
- Ning, D.; Wang, R.; Chen, L.; Sun, K. Experimental investigation of a land-based dual chamber OWC wave energy converter. Renew. Sustain. Energy Rev. 2019, 105, 48–60. [Google Scholar] [CrossRef]
- Payne, G.S.; Taylor, J.R.M.; Bruce, T.; Parkin, P. Assessment of boundary- element method for modelling a free-floating sloped wave energy device. Part 1: Numerical modelling. Ocean Eng. 2008, 35, 333–341. [Google Scholar] [CrossRef][Green Version]
- Orphin, J. Uncertainty in Hydrodynamic Model Test Experiments of Wave Energy Coverters. Ph.D. Thesis, University of Tasmania, Dynnyrne, Australia, 2020. [Google Scholar] [CrossRef]
- Sheng, W. Wave energy conversion and hydrodynamics modelling technologies: A review. Renew. Sustain. Energy Rev. 2019, 109, 482–498. [Google Scholar] [CrossRef]
- Sheng, W.; Alcorn, R.; Lewis, T. Physical modelling of wave energy converters. Ocean Eng. 2014, 84, 29–36. [Google Scholar] [CrossRef]
- Suzuki, M. Numerical methods to predict characteristics of oscillating water column for terminator-type wave energy converter. Int. J. Offshore Polar Eng. 2005, 15, 5381. [Google Scholar]
- Vicinanza, D.; Di Lauro, E.; Contestabile, P.; Gisonni, C.; Lara, J.L.; Losada, I.J. Review of innovative harbor breakwaters for wave-energy conversion. J. Waterw. Port Coast Ocean Eng. 2019, 145, 3119001. [Google Scholar] [CrossRef]
- Viviano, A.; Naty, S.; Foti, E. Scale effects in physical modelling of a generalized OWC. Ocean Eng. 2018, 162, 248–258. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, Q.-P.; Greaves, D. Air-water two phase flow modelling of hydrodynamic performance of an oscillating water column device. Renew. Energy 2012, 41, 159–170. [Google Scholar] [CrossRef]
- Zhou, Y.; Ning, D.; Chen, L.; Iglesias, G. Nonlinear hydrodynamic modeling of an offshore stationary multi-oscillating water column platform. Ocean Eng. 2021, 227, 108–919. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y. Performance enhancement for a dual-chamber OWC conceived from side wall effects in narrow flumes. Ocean Eng. 2022, 247, 110552. [Google Scholar] [CrossRef]
- Dimakopoulos, A.S.; Cooker, M.J.; Bruce, T. The influence of scale on the air flow and pressure in the modelling of Oscillating Water Column Wave Energy Converters. Int. J. Mar. Energy 2017, 19, 272–291. [Google Scholar] [CrossRef]
- Mia, M.R.; Zhao, M.; Wu, H.; Palmer, H. Numerical simulation of a stationary offshore multi-chamber OWC wave energy converter. Ocean Eng. 2022, 265, 112546. [Google Scholar] [CrossRef]
- Rezanejad, K.; Gadelho, J.; Xu, S.; Soares, C.G. Guedes Soares, Experimental investigation on the hydrodynamic performance of a new type floating Oscillating Water Column device with dual-chambers. Ocean Eng. 2021, 234, 109307. [Google Scholar] [CrossRef]
- Boccotti, P. Comparison between a U-OWC and a conventional OWC. Ocean Eng. 2007, 34, 799–805. [Google Scholar] [CrossRef]
- Ning, D.; Zhou, Y.; Zhang, C. Hydrodynamic modeling of a novel dual-chamber OWC wave energy converter. Appl. Ocean. Res. 2018, 78, 180–191. [Google Scholar] [CrossRef]
- Samak, M.M.; Elgamal, H.; Elmekawy, A.M.N. Nagib Elmekawy, The contribution of L-shaped front wall in the improvement of the oscillating water column wave energy converter performance. Energy 2021, 226, 120421. [Google Scholar] [CrossRef]
- Qu, M.; Yu, D.; Xu, Z.; Gao, Z. The effect of the elliptical front wall on energy conversion performance of the offshore OWC chamber: A numerical study. Energy 2022, 255, 124428. [Google Scholar] [CrossRef]
- Yamaç, H.I.; Koca, A. Shore type effect on onshore wave energy converter performance. Ocean Eng. 2019, 190, 106494. [Google Scholar] [CrossRef]
- Hayati, M.; Nikseresht, A.H.; Haghighi, A.T. Sequential optimization of the geometrical parameters of an OWC device based on the specific wave characteristics. Renew. Energy 2020, 161, 386–394. [Google Scholar] [CrossRef]
- Guo, B.; Ning, D.; Wang, R.; Ding, B. Hydrodynamics of an oscillating water column WEC—Breakwater integrated system with a pitching front-wall. Renew. Energy 2021, 176, 67–80. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Deng, Z. Wave power extraction for an oscillating water column device consisting of a surging front and back lip-wall: An analytical study. Renew. Energy 2022, 184, 100–114. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y. Wave power extraction analysis for an oscillating water column device with various surging lip-walls. Ocean Eng. 2021, 220, 108483. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, C.; Wang, P.; Higuera, P.; Wang, R. Hydrodynamic performance of an offshore-stationary OWC device with a horizontal bottom plate: Experimental and numerical study. Energy 2019, 187, 115941. [Google Scholar] [CrossRef]
- Hasanabad, M.G. Free Surface Modeling in OWC Chamber with Parabolic Side Walls Using 3D BEM. AIP Conf. Proc. 2015, 1648, 770005. [Google Scholar]
- Mia, M.R.; Zhao, M.; Wu, H.; Munir, A. Numerical investigation of offshore oscillating water column devices. Renew. Energy 2022, 191, 380–393. [Google Scholar] [CrossRef]
- Malmo, O.; Reitan, A. Wave-power absorption by an oscillating water column in a reflecting wall. Appl. Ocean. Res. 1986, 8, 842–848. [Google Scholar] [CrossRef]
- Rezanejad, K.; Bhattacharjee, J.; Guedes Soares, C. Analytical and numerical study of dual-chamber oscillating water columns on stepped bottom. Renew. Energy 2015, 75, 272–282. [Google Scholar] [CrossRef]
- Rashidi, S.; Nikseresht, A.H. Numerical investigation of the response of the hybrid wave energy converter including oscillating water column and horizontal floating cylinder to irregular waves. Energy 2024, 301, 131717. [Google Scholar] [CrossRef]
- Felice, A.; Malara, G.; Romolo, A.; Vannucchi, V. Monitoring of the REWEC3 full scale model for the energy conversion from the motion of sea waves. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC), Nantes, France, 6–11 September 2015. [Google Scholar]
- Boccotti, P. On a new wave energy absorber. Ocean Eng. 2007, 34, 772–779. [Google Scholar] [CrossRef]
- Henriques, C.; Gato, L.; Falcão, A. Dynamics and optimization of the U-OWC (U-shaped oscillating water column) wave energy converter. Renew. Energy 2012, 39, 371–379. [Google Scholar]
- Moretti, G.; Tognarelli, M.; Vicinanza, D. CFD analysis of air chamber dynamics in U-shaped OWC seawalls. Appl. Ocean Res. 2020, 96, 102006. [Google Scholar]
- Setoguchi, T.; Santhakumar, S.; Maeda, H.; Takao, M.; Kaneko, K. A review of impulse turbines for wave energy conversion. Renew. Energy 2001, 23, 261–271. [Google Scholar] [CrossRef]
- Takahashi, S.; Utsunomiya, T.; Hotta, H. Development of wave energy converter combined with breakwater. In Proceedings of the International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992; pp. 2902–2915. [Google Scholar]
- Vicinanza, D.; Contestabile, P.; Ferrante, V. Wave energy potential in the north-west of Sardinia (Italy). Renew. Energy 2014, 50, 506–521. [Google Scholar] [CrossRef]
- Whittaker, T.; Raghunathan, S. The Wells air turbine: A review. Int. J. Ambient Energy 1996, 17, 81–92. [Google Scholar]
- Mandev, M.B.; Altunkaynak, A. Cylindrical frontwall entrance geometry optimization of an oscillating water column for utmost hydrodynamic performance. Energy 2023, 280, 128147. [Google Scholar] [CrossRef]
- Li, Y.; Liu, S.; Xu, C.; Li, D.; Shi, H. Experimental study on the cylindrical oscillating water column device. Ocean Eng. 2022, 246, 110523. [Google Scholar] [CrossRef]
- Mia, M.R.; Zhao, M.; Wu, H.; Munir, A. Numerical investigation of scaling effect in two-dimensional oscillating water column wave energy devices for harvesting wave energy. Renew. Energy 2021, 178, 1381–1397. [Google Scholar] [CrossRef]
- Moretti, G.; Malara, G.; Scialo, A.; Daniele, L.; Romolo, A.; Vertechy, R.; Fontana, M.; Arena, F. Modelling and field testing of a breakwater-integrated U-OWC wave energy converter with dielectric elastomer generator. Renew. Energy 2020, 146, 628–642. [Google Scholar] [CrossRef]
- Ahmed, R.; Hasan, M.N.; Rahman, M.T.; Lee, S.; Kim, H.S. Recent advances in piezoelectric energy harvesting technologies for biomedical applications. Micromachines 2023, 14, 345. [Google Scholar]
- Pradhan, A.; Chen, Z.; Pan, C. Recent advances in flexible piezoelectric energy harvesters for self-powered wearable devices. Adv. Compos. Hybrid. Mater. 2025, 8, 123–138. [Google Scholar]
- Yao, Y.; Li, H.; Wang, J.; Xu, Y. Design and performance of flexible piezoelectric energy harvesters for wearable electronics. Nano Energy 2023, 110, 107456. [Google Scholar]
- Naqvi, A.; Ali, A.; Altabey, W.A.; Kouritem, S.A. Energy Harvesting from Fluid Flow Using Piezoelectric Materials: A Review. Energies 2022, 15, 7424. [Google Scholar] [CrossRef]
- Baghbani Kordmahale, S.; Do, J.; Chang, K.-A.; Kameoka, J. A Hybrid Structure of Piezoelectric Fibers and Soft Materials as a Smart Floatable Open-Water Wave Energy Converter. Micromachines 2021, 12, 1269. [Google Scholar] [CrossRef]
- Du, X.; Chen, H.; Li, C.; Li, Z.; Wang, W.; Guo, D.; Yu, H.; Wang, J.; Tang, L. Wake galloping piezoelectric-electromagnetic hybrid ocean wave energy harvesting with oscillating water column. Appl. Energy 2024, 353, 122081. [Google Scholar] [CrossRef]
- Li, X.; Sui, Y.; Meng, Y.; Zhang, X.; Khayyer, A.; He, M.; Liang, D. Theory for plunger-type wavemakers to generate second-order Stokes waves and Smoothed Particle Hydrodynamics verification. Appl. Ocean. Res. 2024, 153, 104244. [Google Scholar] [CrossRef]
- Boccotti, P.; Filianoti, P.; Fiamma, V.; Arena, F. Caisson breakwaters embodying an OWC with a small opening—Part II: A small-scale field experiment. Ocean Eng. 2007, 34, 820–841. [Google Scholar] [CrossRef]
- Orphin, J.; Schmitt, P.; Nader, J.; Penesis, I. Experimental investigation into laboratory effects of an OWC wave energy converter. Renew. Energy 2022, 186, 250–263. [Google Scholar] [CrossRef]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers & Scientists, Advanced Series on Ocean Engineering—Volume 2; World Scientific Publishing Company: Singapore, 1991. [Google Scholar]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters, 1st ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Lowell, S.; McPhee, J.; Irani, R.A. Plunger-type wave makers with flow: Sensitivity analysis and experimental validation. Appl. Ocean Res. 2022, 121, 103065. [Google Scholar] [CrossRef]
- Çelik, A.; Altunkaynak, A. Experimental investigations on the performance of a fixed-oscillating water column type wave energy converter. Energy 2019, 188, 116071. [Google Scholar] [CrossRef]
- Mandev, M.B.; Çelik, A.A.; Altunkaynak, A. Maximizing oscillating water column efficiency: The impact of vertical plate and guide vane. Energy 2024, 308, 132901. [Google Scholar] [CrossRef]
- Raj, D.D.; Sundar, V.; Sannasiraj, S.A. Enhancement of hydrodynamic performance of an Oscillating Water Column with harbor walls. Renew. Energy 2019, 132, 142–156. [Google Scholar]
- Xu, C.; Liu, Z.; Tang, G. Experimental study of the hydrodynamic performance of a U-oscillating water column wave energy converter. Ocean Eng. 2022, 265, 112598. [Google Scholar] [CrossRef]
- Zhu, G.; Samuel, J.; Zheng, S.; Hughes, J.; Simmonds, D.; Greaves, D. Numerical investigation on the hydrodynamic performance of a 2D U-shaped Oscillating Water Column wave energy converter. Energy 2023, 274, 127357. [Google Scholar] [CrossRef]
- Orphin, J.; Nader, J.; Penesis, I. Uncertainty analysis of a WEC model test experiment. Renew. Energy 2021, 168, 216–233. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Deng, Z.A. A novel dual-chamber oscillating water column system with dual lip-wall pitching motions for wave energy conversion. Energy 2022, 246, 123319. [Google Scholar] [CrossRef]




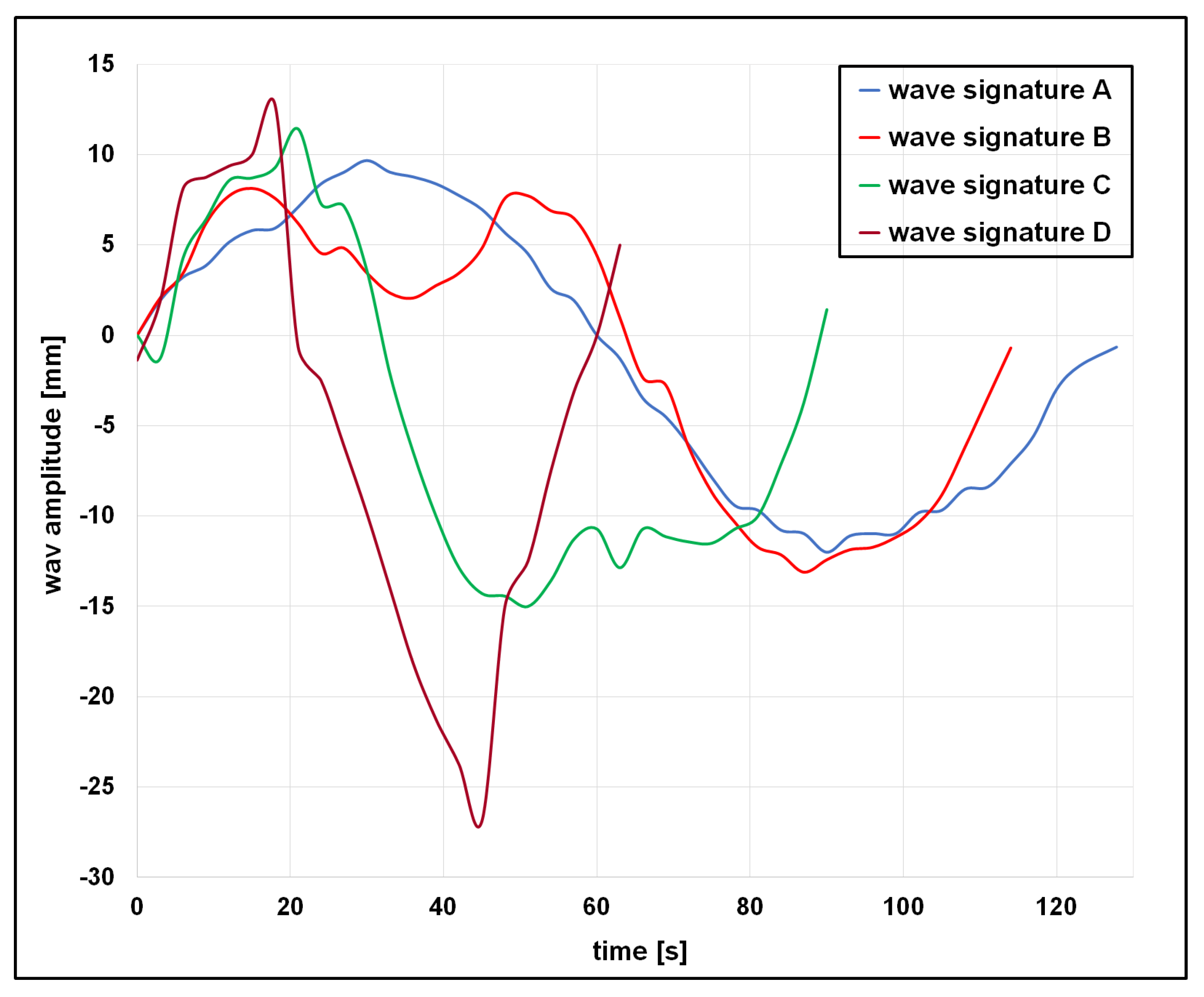
| Wave Signature | Encounter Times (s) | ||
|---|---|---|---|
| Crest | Trough | Time Span (s) | |
| A | 30 s | 90 s | 60 s |
| B | 31.5 s | 51 s | 19.5 s |
| C | 10.5 s | 27 s | 16.5 s |
| D | 9 s | 27 s | 18 s |
| Wave Signature | Wave Period (T) |
|---|---|
| A | 126 s |
| B | 105 s |
| C | 84 s |
| D | 54 s |
| Wave Signature | Wave Steepness | |
|---|---|---|
| Descending | Ascending | |
| A | −87.36° | 86.83° |
| B | −88.54° | 87.92° |
| C | −89.20° | 87.27° |
| D | −89.35° | 89.46° |
| Wave Signature | Wave Power Density (W/m) |
|---|---|
| A | 0.1 |
| B | 0.069 |
| C | 0.0886 |
| D | 0.0673 |
| Trial Number | ||||
|---|---|---|---|---|
| A | B | C | D | |
| 1 | 3.72 | 3.89 | 4.23 | 4.93 |
| 2 | 4.83 | 4.17 | 5.12 | 5.82 |
| 3 | 4.27 | 4.34 | 4.82 | 6.12 |
| Wave Signature | W |
|---|---|
| A | 0.461 |
| B | 0.513 |
| C | 0.437 |
| D | 0.453 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilie, M. The Effect of Wave Signature on the Voltage Output of an Oscillating Water Column. Vibration 2025, 8, 54. https://doi.org/10.3390/vibration8030054
Ilie M. The Effect of Wave Signature on the Voltage Output of an Oscillating Water Column. Vibration. 2025; 8(3):54. https://doi.org/10.3390/vibration8030054
Chicago/Turabian StyleIlie, Marcel. 2025. "The Effect of Wave Signature on the Voltage Output of an Oscillating Water Column" Vibration 8, no. 3: 54. https://doi.org/10.3390/vibration8030054
APA StyleIlie, M. (2025). The Effect of Wave Signature on the Voltage Output of an Oscillating Water Column. Vibration, 8(3), 54. https://doi.org/10.3390/vibration8030054





