Prediction of Local Vibration Analysis for Ship Stiffened Panel Structure Using Artificial Neural Network Algorithm
Abstract
1. Introduction
2. Local Vibration Analysis of Ship Stiffened Panel
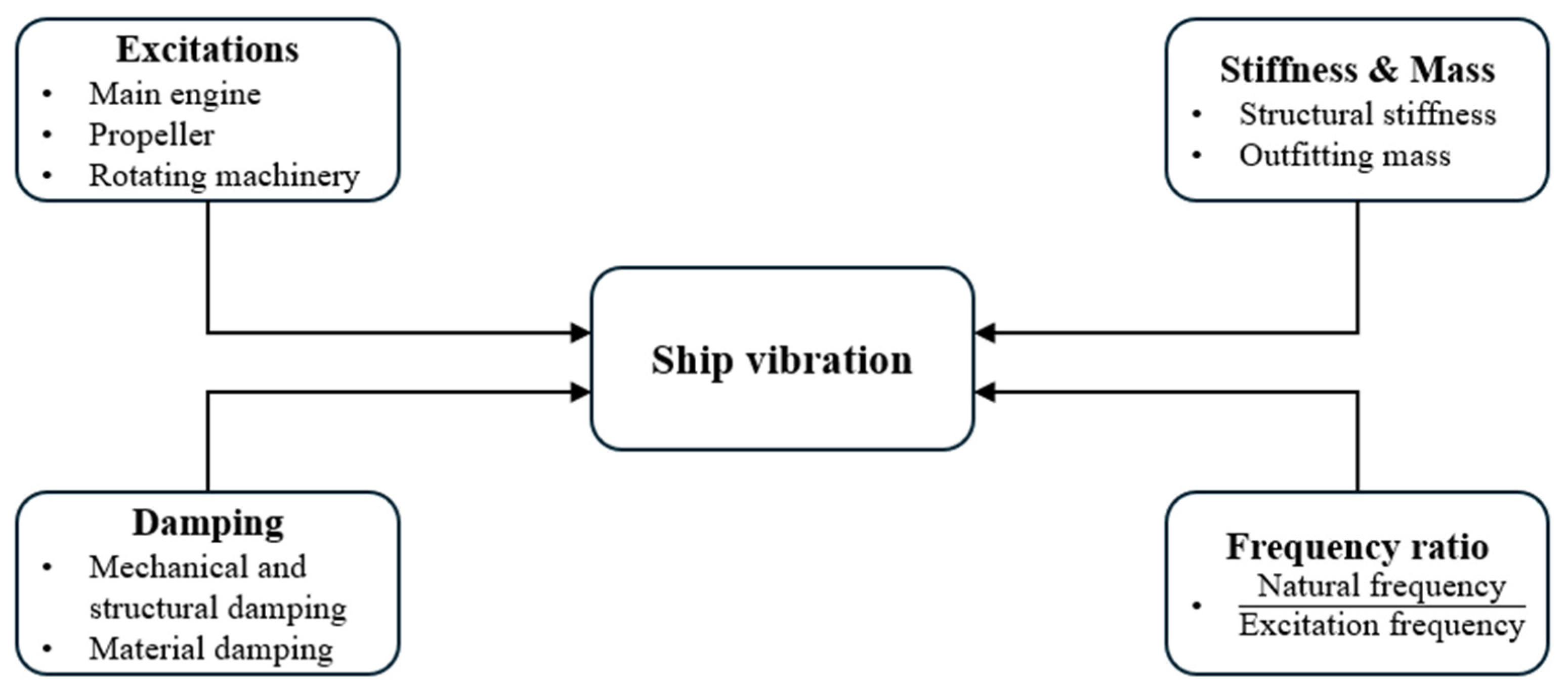
2.1. Local Vibration of Ship Structure
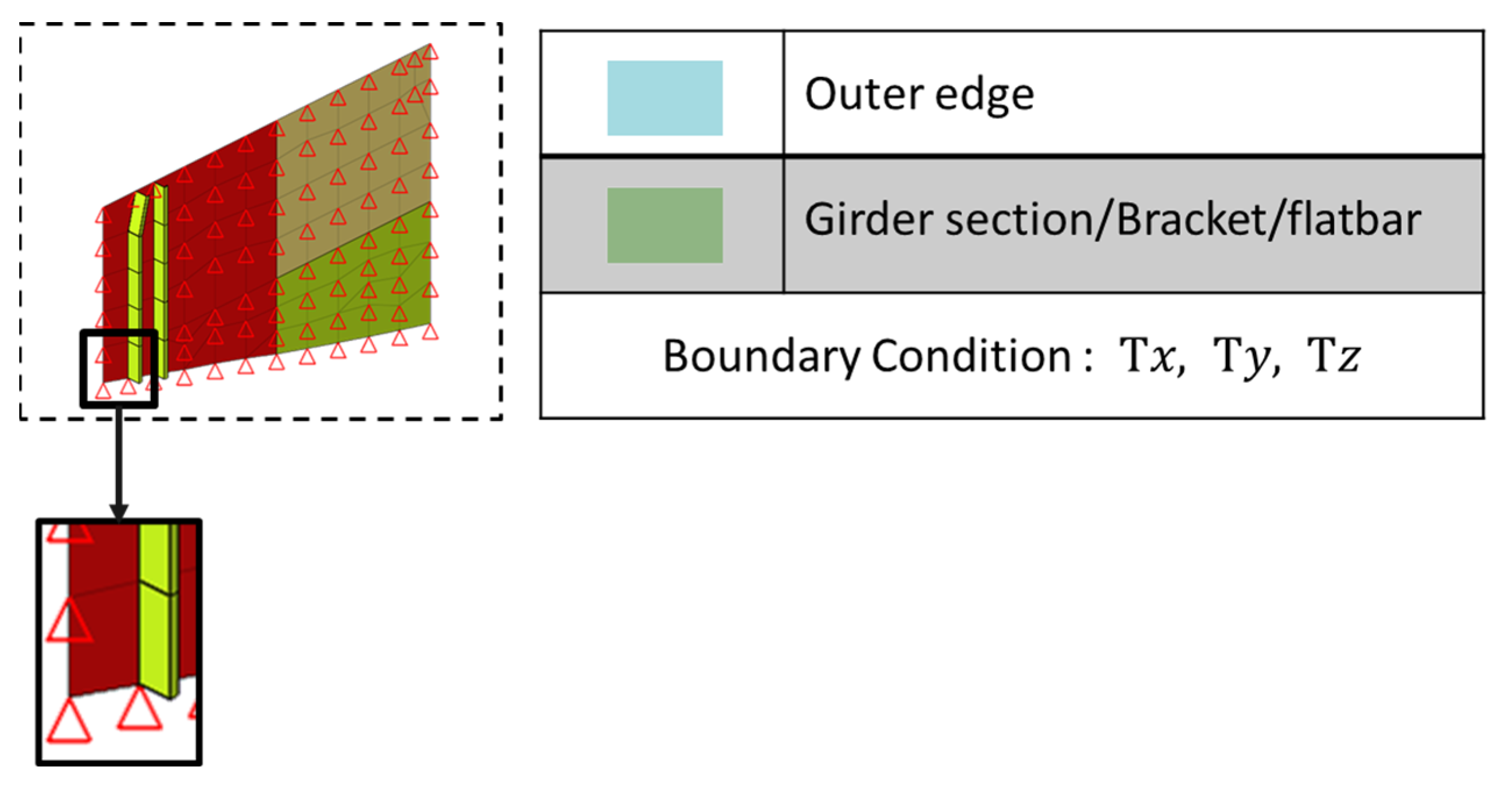
2.2. Local Vibration Analysis of Stiffened Panel
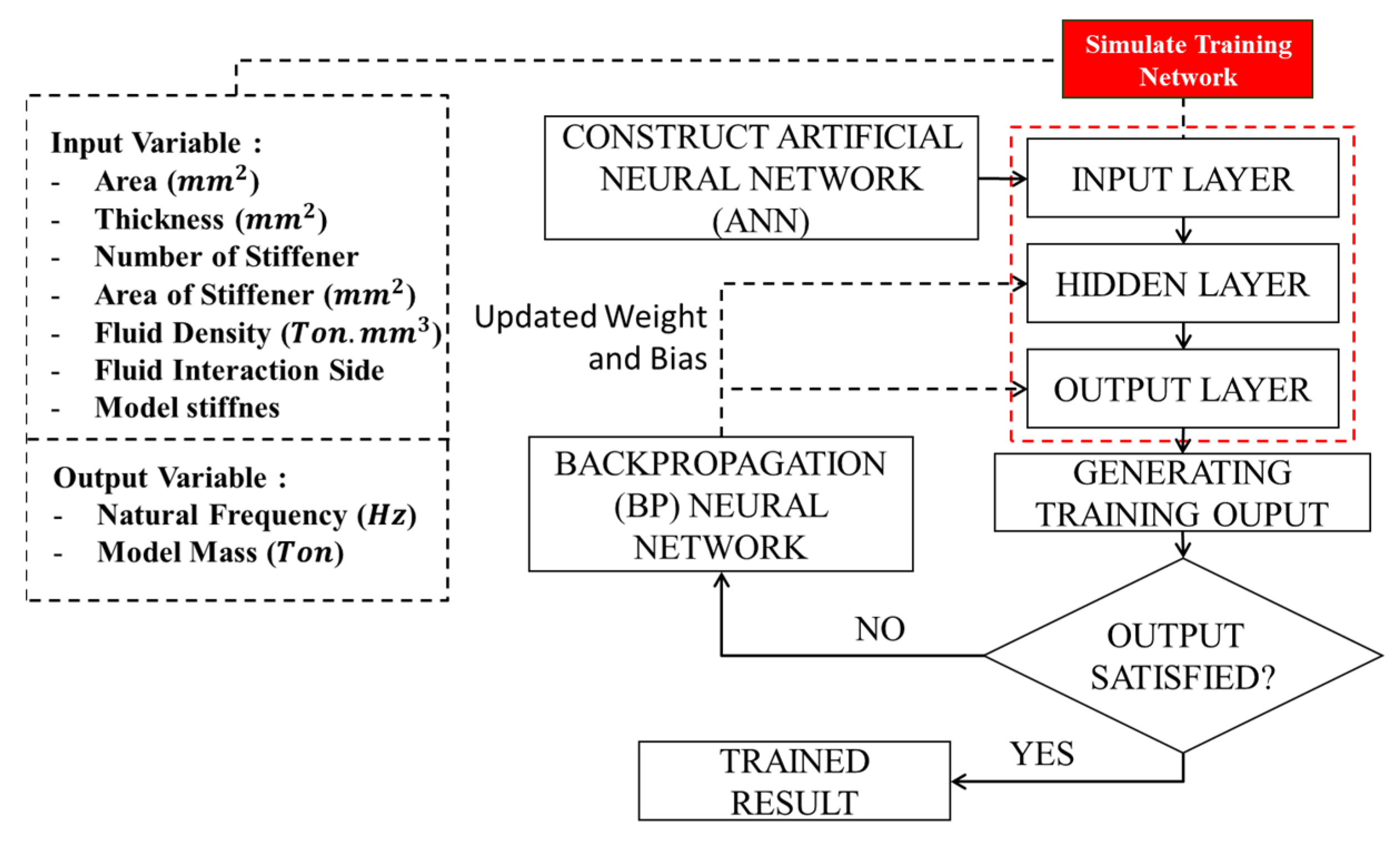
3. ANN Model Generation
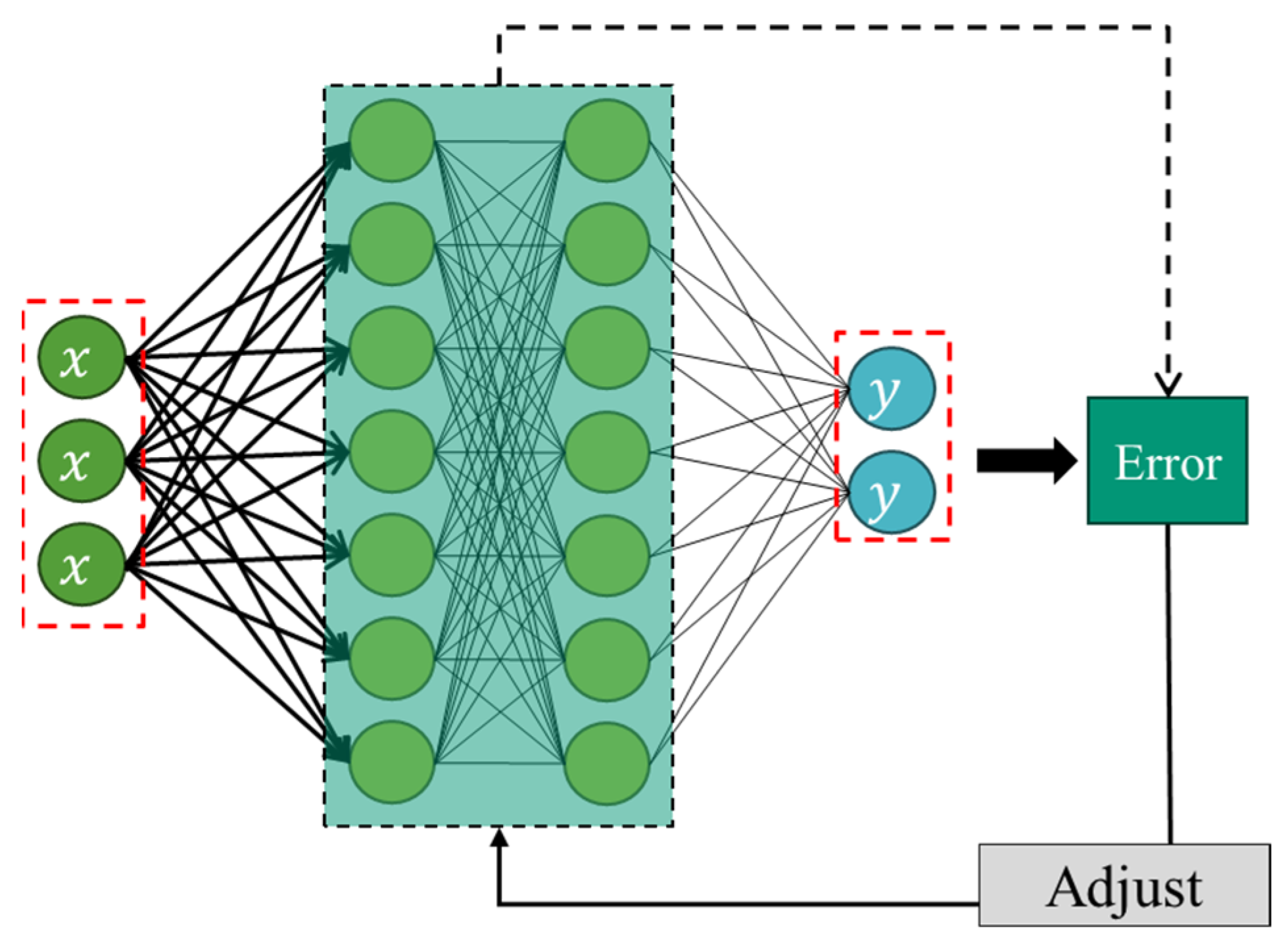
3.1. Theoretical Background
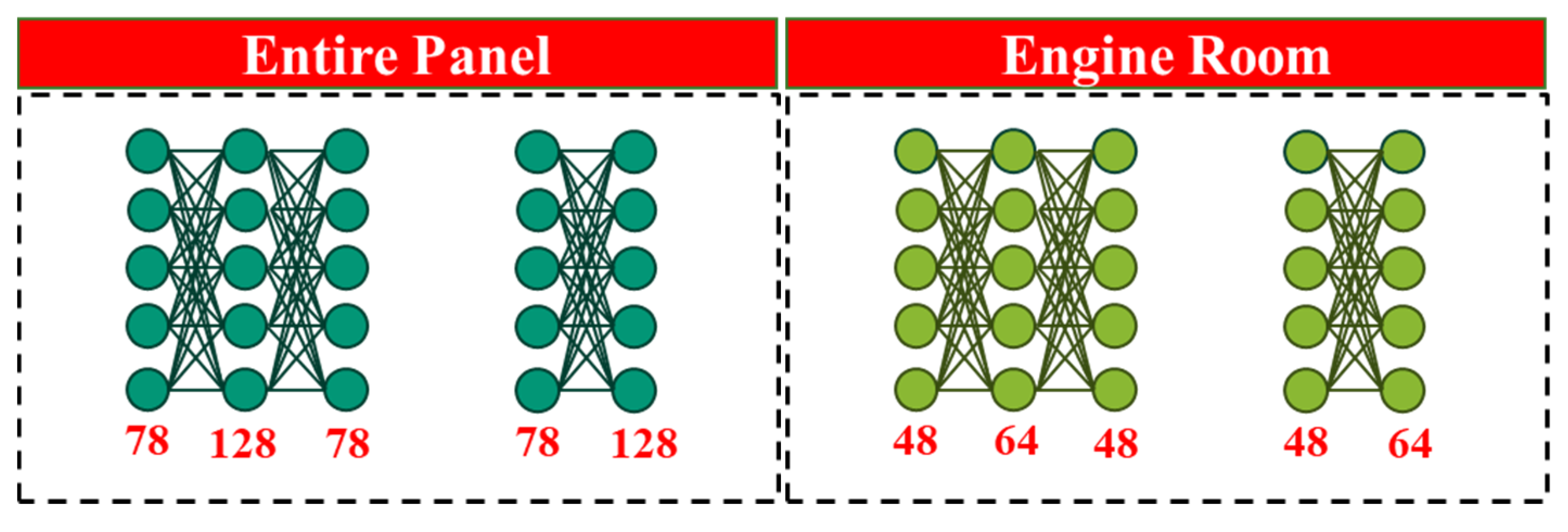
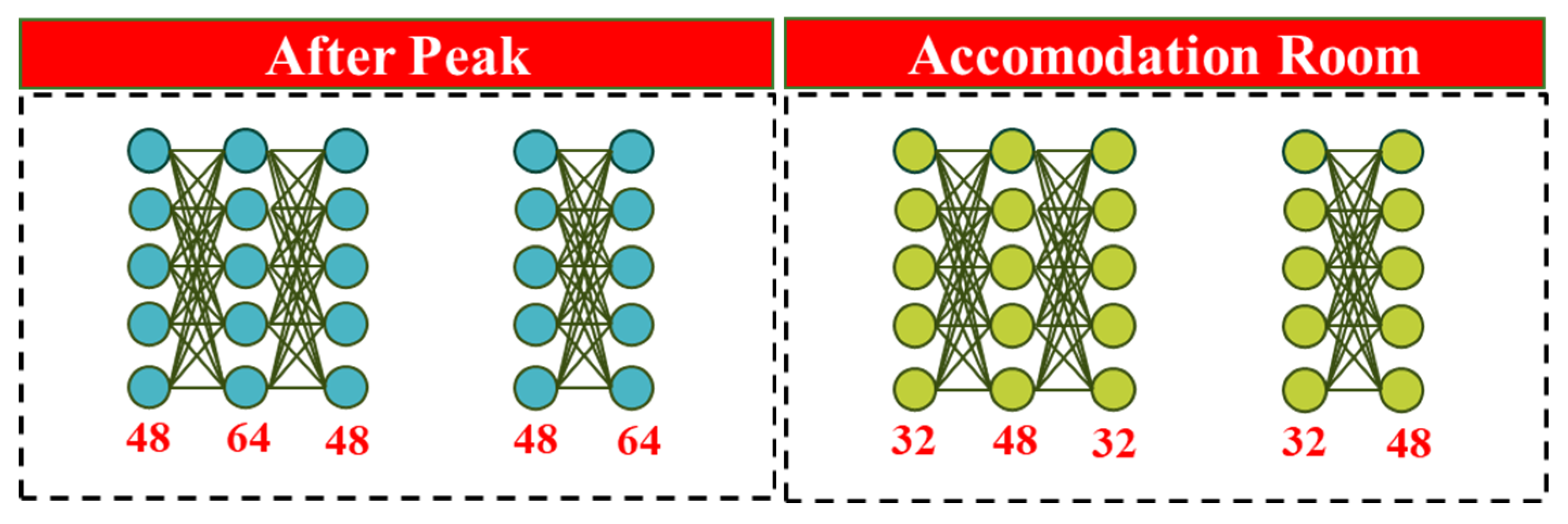
3.2. ANN Model Setting
4. Results and Discussion
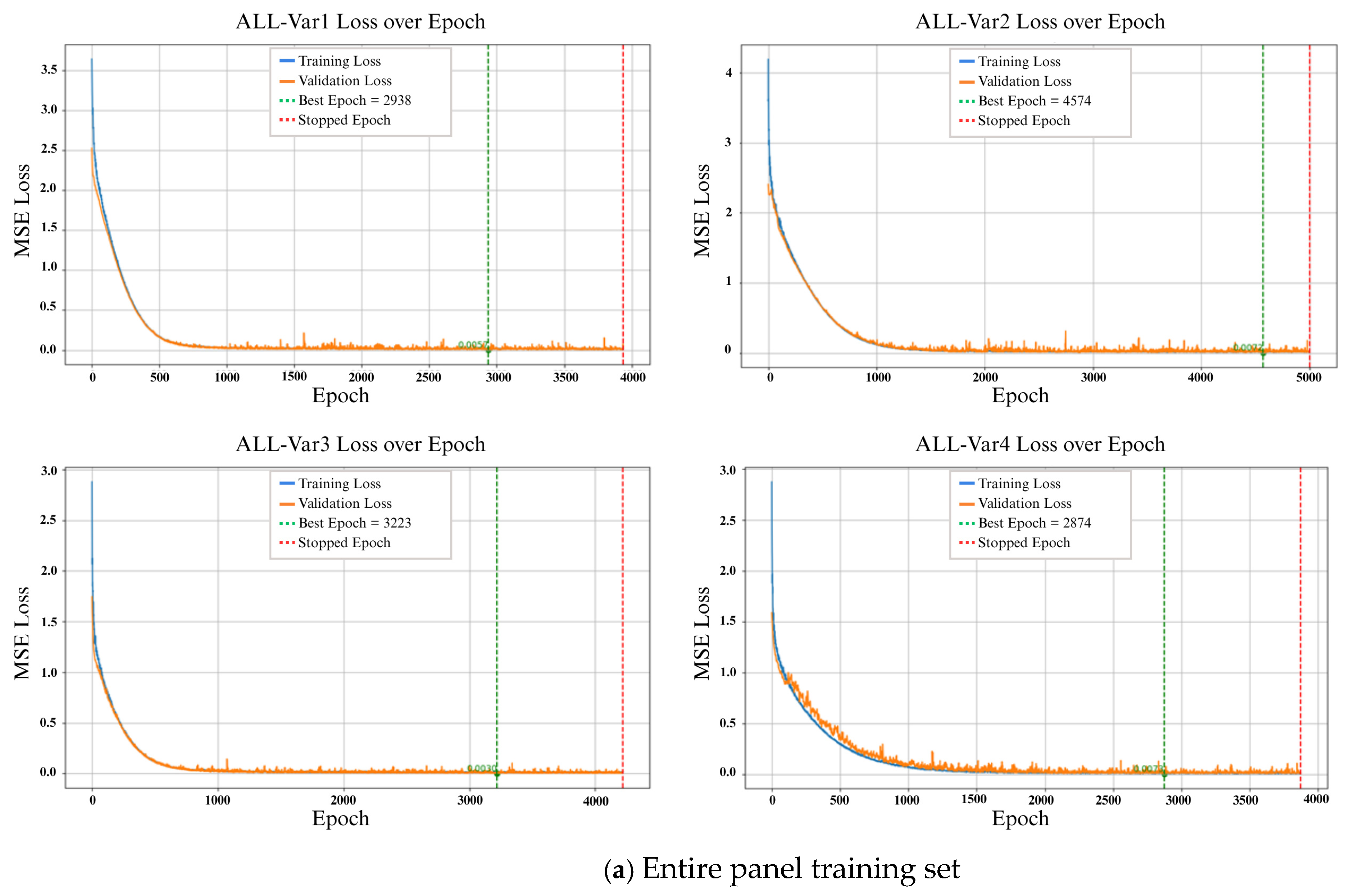
4.1. Training Loss
4.2. Output Prediction Performance
4.3. Summary
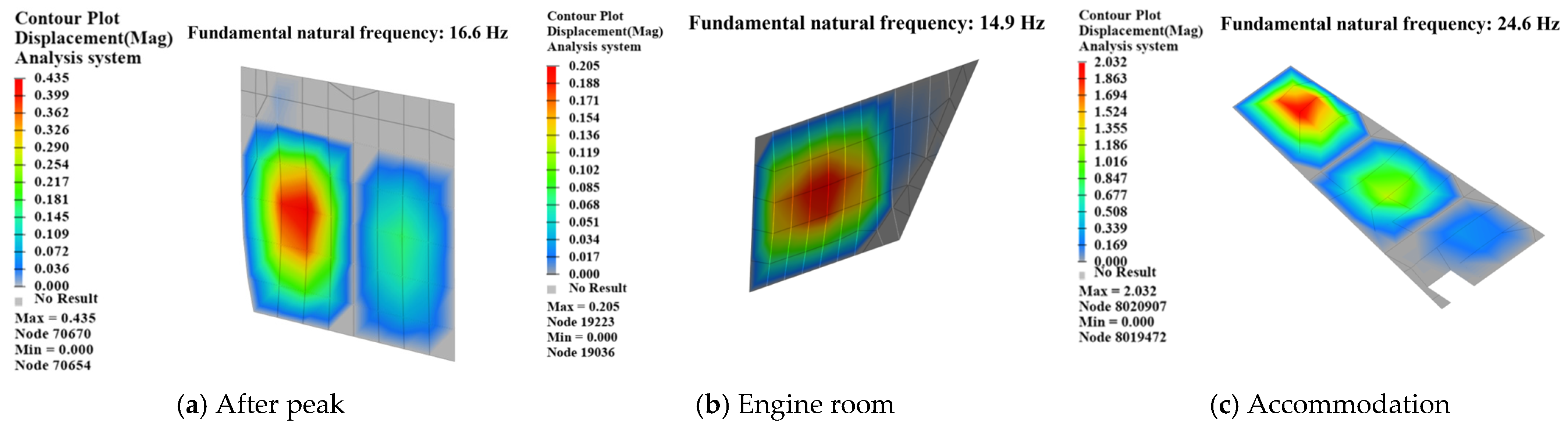
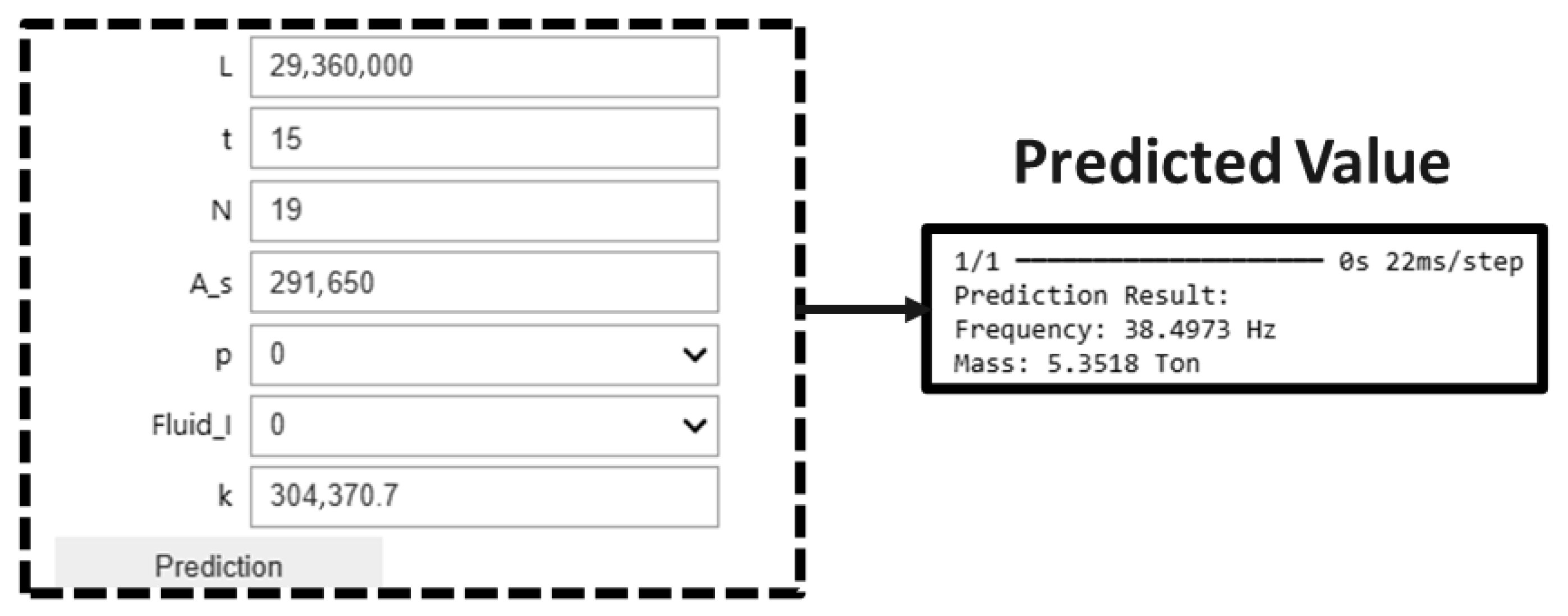
4.4. Case Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEA | Finite Element Analysis |
| MLP | Multilayer Perceptron |
| SL | Supervised Learning |
| BPNN | Back Propagation Neural Network |
| FEINN | Finite Element Informed Neural Network |
| ALL-Var1 | Entire Panel Variation 1 |
| ALL-Var2 | Entire Panel Variation 2 |
| ALL-Var3 | Entire Panel Variation 3 |
| ALL-Var4 | Entire Panel Variation 4 |
| ER-Var1 | Engine Room Variation 1 |
| ER-Var2 | Engine Room Variation 2 |
| ER-Var3 | Engine Room Variation 3 |
| ER-Var4 | Engine Room Variation 4 |
| AE-Var1 | After Peak Variation 1 |
| AE-Var2 | After Peak Variation 2 |
| AE-Var3 | After Peak Variation 3 |
| AE-Var4 | After Peak Variation 4 |
| ACC-Var1 | Accommodation Room Variation 1 |
| ACC-Var2 | Accommodation Room Variation 2 |
| ACC-Var3 | Accommodation Room Variation 3 |
| ACC-Var4 | Accommodation Room Variation 4 |
References
- Yang, Y.; Zhang, Z.; Zhao, J.; Zhang, B.; Zhang, L.; Hu, Q.; Sun, J. Research on Ship Resistance Prediction Using Machine Learning with Different Samples. J. Mar. Sci. Eng. 2024, 12, 556. [Google Scholar] [CrossRef]
- Li, W.; Zhang, D.; Shi, X. Establishment of a flow-induced vibration power database based on deep neural network machine learning method. Ocean. Eng. 2023, 285, 115463. [Google Scholar] [CrossRef]
- Mottaghian, F.; Taheri, F. Machine learning/finite element analysis—A collaborative approach for predicting the axial impact response of adhesively bonded joints with unique sandwich composite adherends. Compos. Sci. Technol. 2023, 242, 110162. [Google Scholar] [CrossRef]
- Lu, Y.; Luo, Q.; Liao, Y.; Xu, W. Vortex-induced vibration fatigue damage prediction method for flexible cylinders based on RBF neural network. Ocean. Eng. 2022, 254, 111344. [Google Scholar] [CrossRef]
- Hajializadeh, F.; Ince, A. Integration of artificial neural network with finite element analysis for residual stress prediction of direct metal deposition process. Mater. Today Commun. 2021, 27, 102197. [Google Scholar] [CrossRef]
- Duan, C.; Zhang, S. Prediction of fully plastic J-integral for weld centerline surface crack considering strength mismatch based on 3D finite element analyses and artificial neural network. Int. J. Nav. Archit. Ocean. Eng. 2020, 12, 354–366. [Google Scholar] [CrossRef]
- Han, H. Psycho-acoustic evaluation of the indoor noise in cabins of a naval vessel using a back-propagation neural network algorithm. Int. J. Nav. Archit. Ocean. Eng. 2012, 4, 374–385. [Google Scholar] [CrossRef][Green Version]
- Le-Duc, T.; Nguyen-Xuan, H.; Lee, J. A finite-element-informed neural network for parametric simulation in structural mechanics. Finite Elem. Anal. Des. 2023, 217, 103904. [Google Scholar] [CrossRef]
- Xiong, W.; Long, X.; Bordas, S.P.; Jiang, C. The deep finite element method: A deep learning framework integrating the physics-informed neural networks with the finite element method. Comput. Methods Appl. Mech. Eng. 2024, 436, 117681. [Google Scholar] [CrossRef]
- Zhang, N.; Xu, K.; Yin, Z.-Y.; Li, K.-Q. Transfer learning-enhanced finite element-integrated neural networks. Int. J. Mech. Sci. 2025, 290, 110075. [Google Scholar] [CrossRef]
- Yang, J.; Chen, Z.; Zhou, J. Enhanced soft Monte Carlo simulation coupled with support vector regression for high-dimensional reliability analysis. Proc. Inst. Civ. Eng.-Transp. 2025, 178, 128–141. [Google Scholar]
- Zhou, X.; Zhang, Y.; Deng, C.; Sun, C. Physics-guided neural networks for multiaxial fatigue life prediction under irregular loading. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2022, 380, 20220395. [Google Scholar]
- Meng, D.; Nie, P.; Yang, S.; Su, X.; Liao, C. Reliability analysis of wind turbine gearboxes: Past, progress and future prospects. Int. J. Struct. Integr. 2025, 16, 4–38. [Google Scholar] [CrossRef]
- Ban, I.; Lim, C.; Kim, G.; Choi, S.; Shin, S. A Data-Driven DNN model to predict the ultimate strength of a ship’s bottom structure. J. Mar. Sci. Eng. 2024, 12, 1328. [Google Scholar] [CrossRef]
- Cepowski, T. Utilizing artificial neural network ensembles for ship design optimization to reduce added wave resistance and CO2 emissions. Energies 2024, 17, 5326. [Google Scholar] [CrossRef]
- Hwang, H.E.; Cho, Y.S.; Hwang, S.C.; Kim, S.B. Optimal tire design using machine learning and Bayesian optimization. J. Korean Inst. Ind. Eng. 2022, 48, 433–440. [Google Scholar] [CrossRef]
- Martić, I.; Degiuli, N.; Majetić, D.; Farkas, A. Artificial neural network model for the evaluation of added resistance of container ships in head waves. J. Mar. Sci. Eng. 2021, 9, 826. [Google Scholar] [CrossRef]
- Radojčić, D.V.; Morabito, M.G.; Simić, A.P.; Zgradić, A.B. Modeling with Regression Analysis and Artificial Neural Networks the Resistance and Trim of Series 50 Experiments with V-Bottom Motorboats. J. Ship Prod. Des. 2014, 30, 153–174. [Google Scholar] [CrossRef]
- Santos, A.B.D.; Vasconcelos, H.M.; Domingues, T.M.R.M.; Sousa, P.J.S.C.P.; Dias, S.; Lopes, R.F.F.; Parente, M.L.P.; Tomé, M.; Cavadas, A.M.S.; Moreira, P.M.G.P. Predictive analysis of structural damage in submerged structures: A case study approach using machine learning. Fluids 2025, 10, 10. [Google Scholar] [CrossRef]
- American Bureau of Shipping (ABS). Guidance Notes on Ship Vibration; American Bureau of Shipping: New York, NY, USA, 2006. [Google Scholar]
- Det Norske Veritas (DNV). Rules for Classification of Ships—Vibration Class; Det Norske Veritas: Oslo, Norway, 2011. [Google Scholar]
- ISO 20283-5:2016; Mechanical Vibration—Measurement of Vibration on Ships. International Organization for Standardization (ISO): Geneva, Switzerland, 2016.
- Korean Register of Shipping (KR). Control of Ship Vibration and Noise; Korean Register of Shipping: Seoul, Republic of Korea, 2018. [Google Scholar]
- Lloyd’s Register (LR). Guidance Notes—General Overview of Ship Structural Vibration Problems; Lloyd’s Register: London, UK, 2015. [Google Scholar]
- American Bureau of Shipping (ABS). Insights into Ship Vibration Analysis; American Bureau of Shipping: New York, NY, USA, 2022. [Google Scholar]
- Altair Engineering. HyperMesh User Guide; Altair Engineering Inc.: Troy, MI, USA, 2023. [Google Scholar]
- MSC Software Corporation. MSC NASTRAN 2022.1 Reference Manual; Hexagon AB: Stockholm, Sweden, 2022. [Google Scholar]
- International Maritime Organization. MARPOL Consolidated Edition 2022; IMO Publishing: London, UK, 2023. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Microsoft. Visual Studio Code Documentation; Microsoft: Washington, DC, USA, 2024. [Google Scholar]
- Python Software Foundation. The Python Language Reference, Version 3.12; Python Software Foundation: Beaverton, OR, USA, 2024.
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
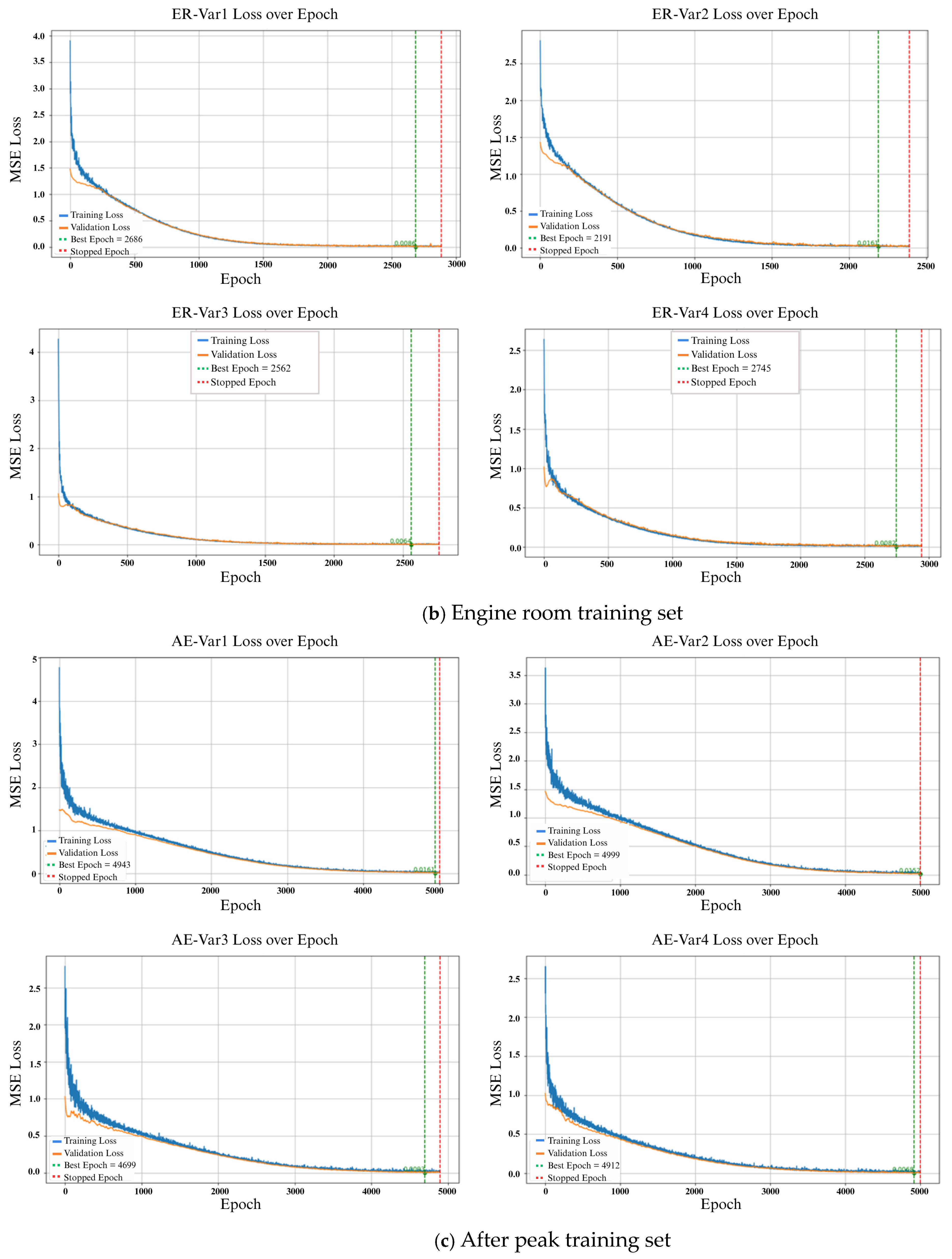
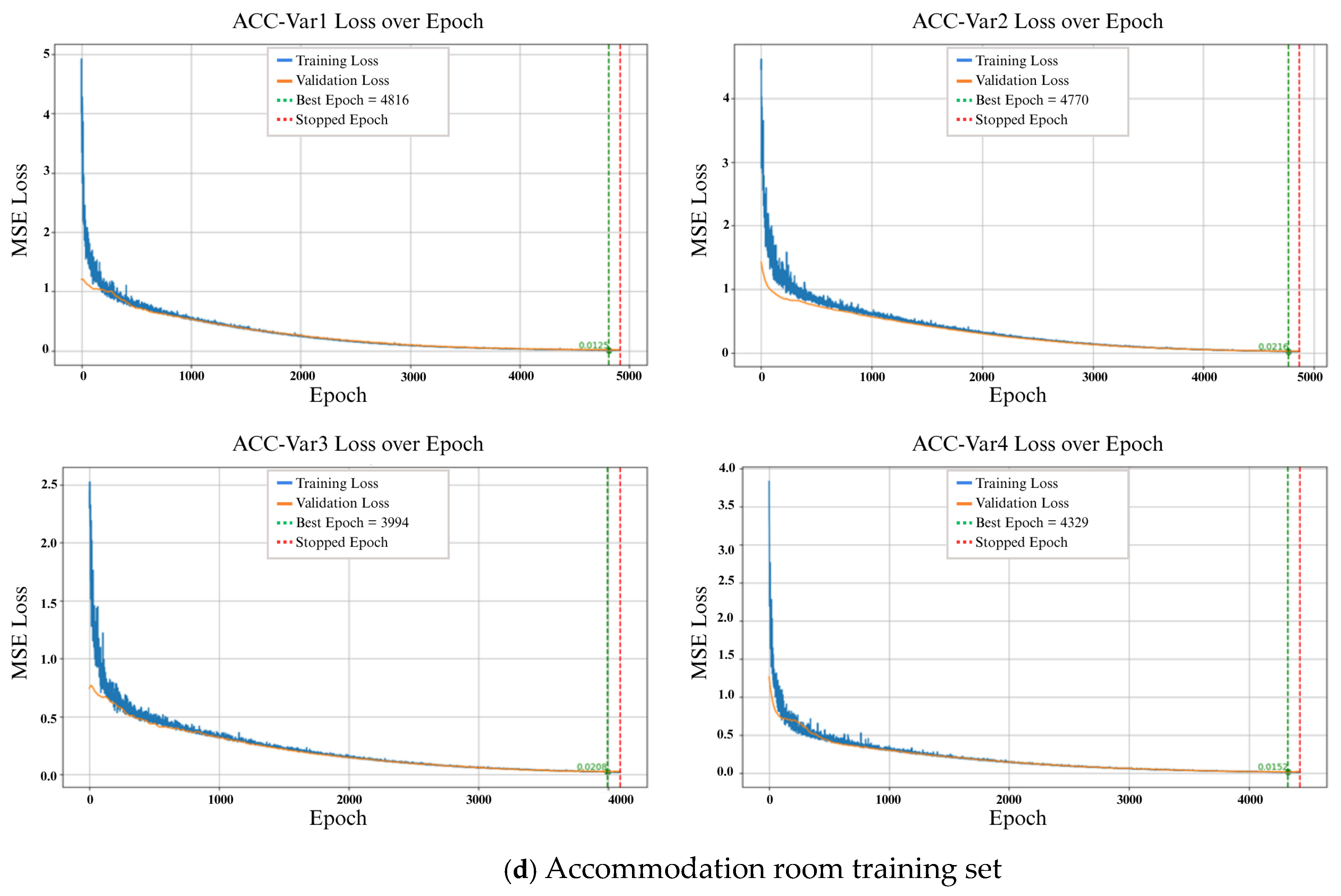
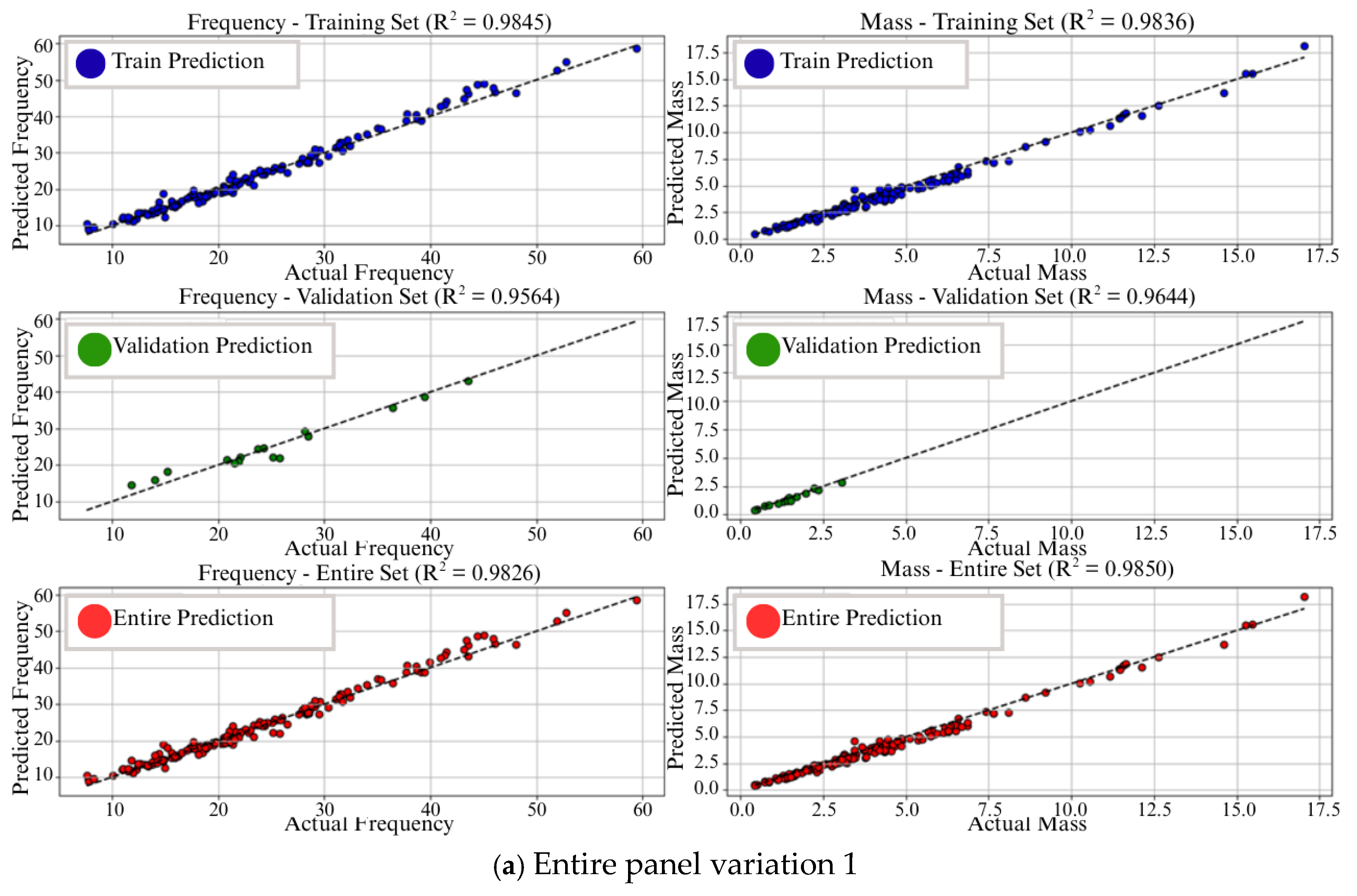
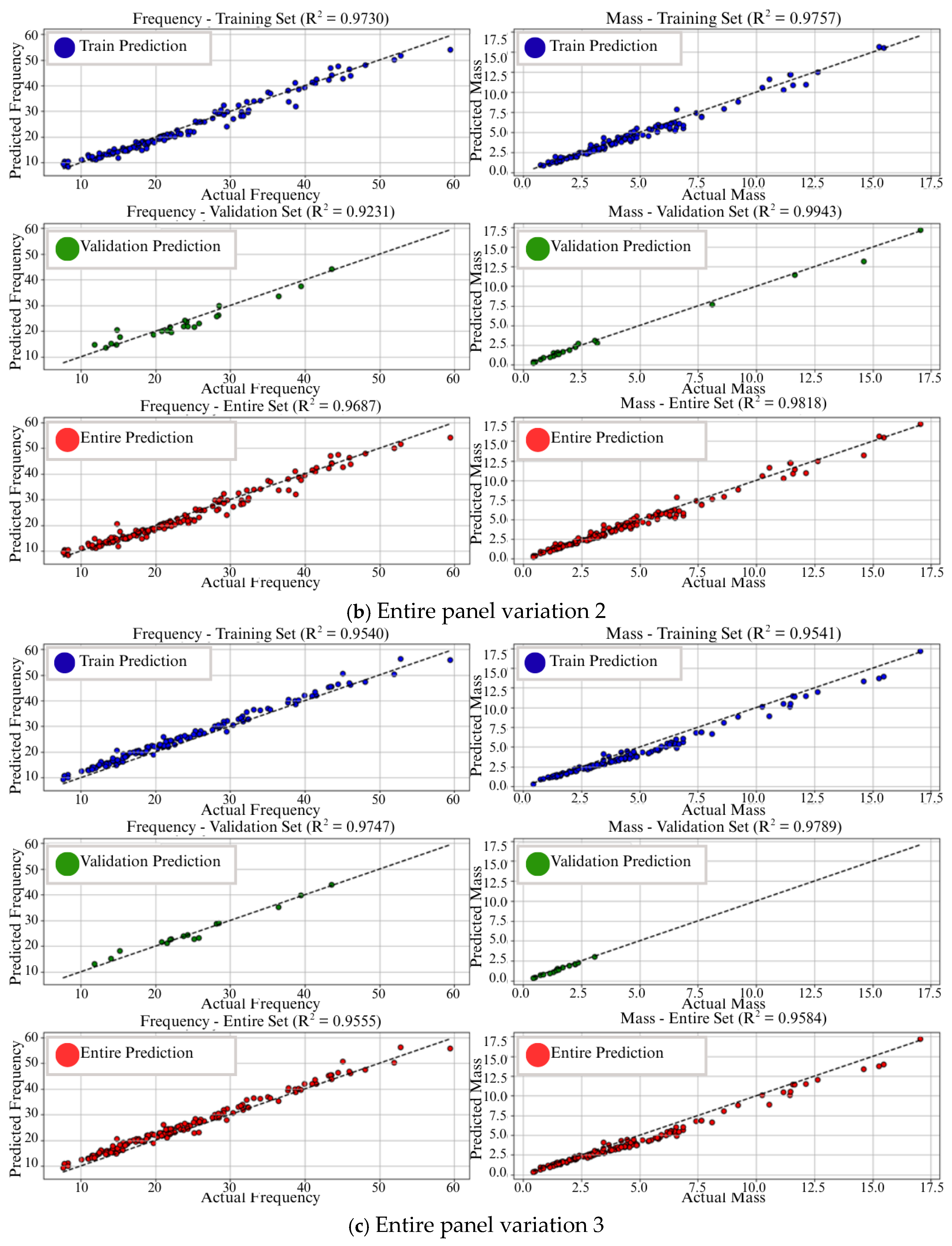
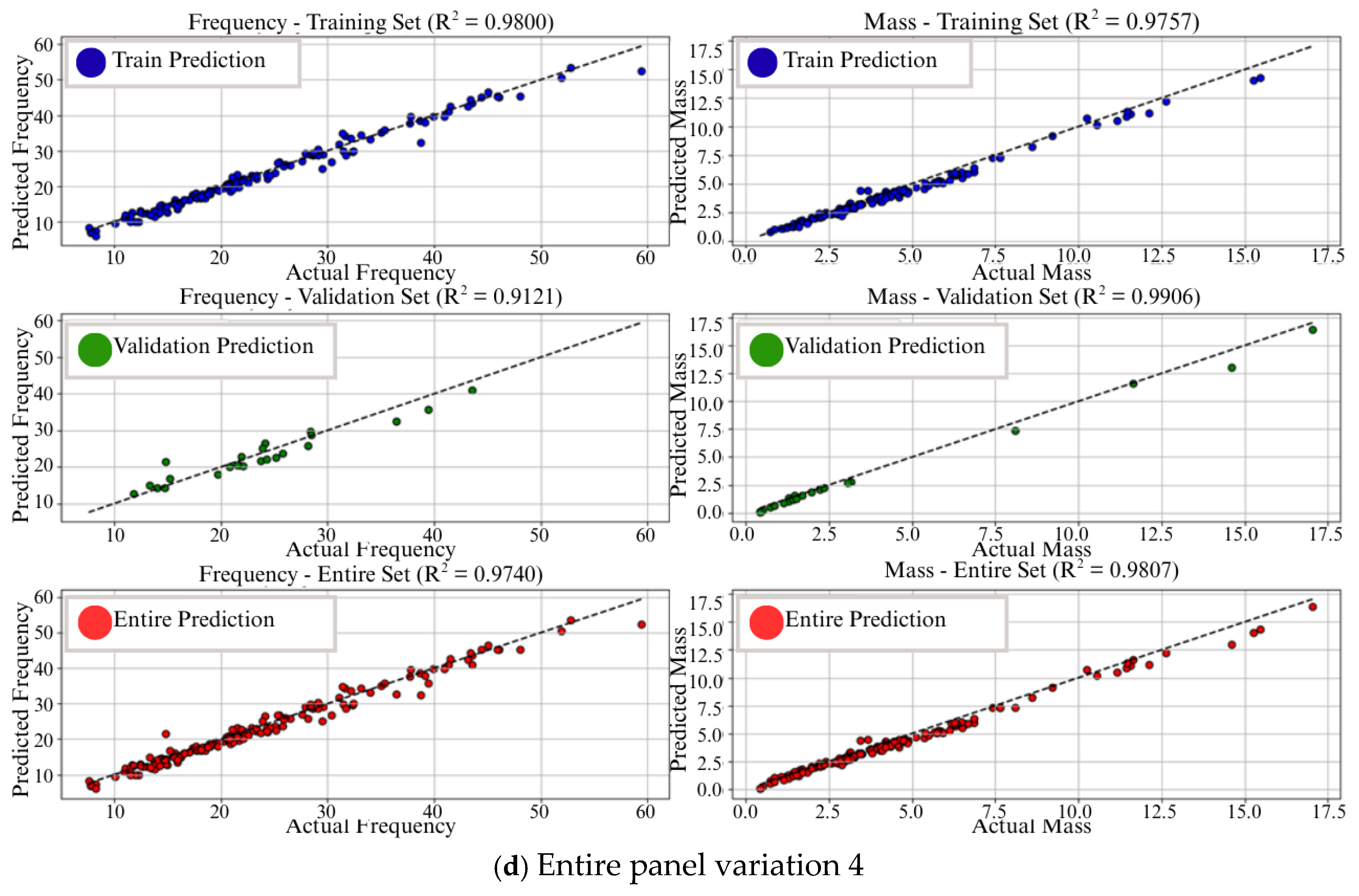
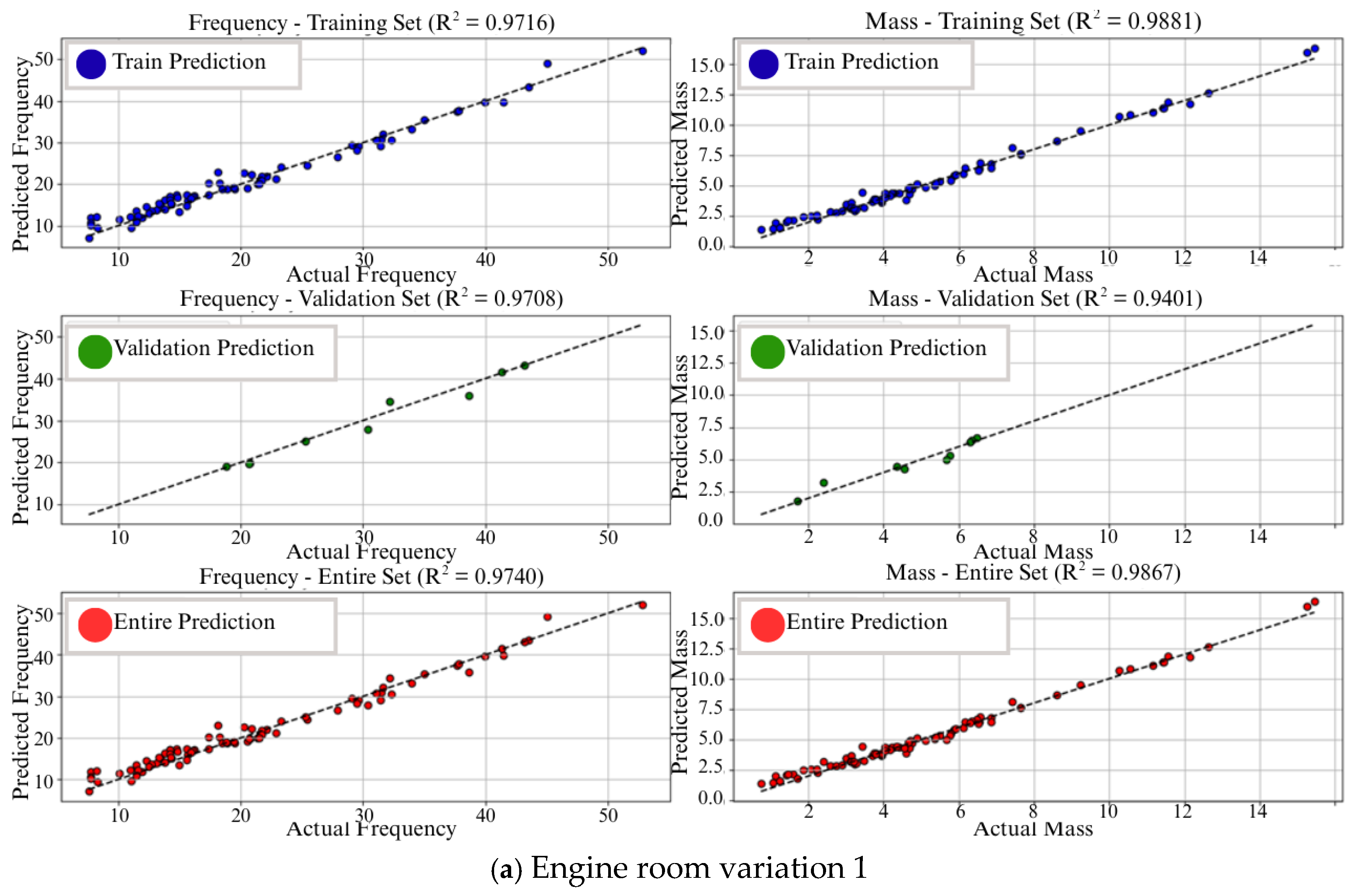
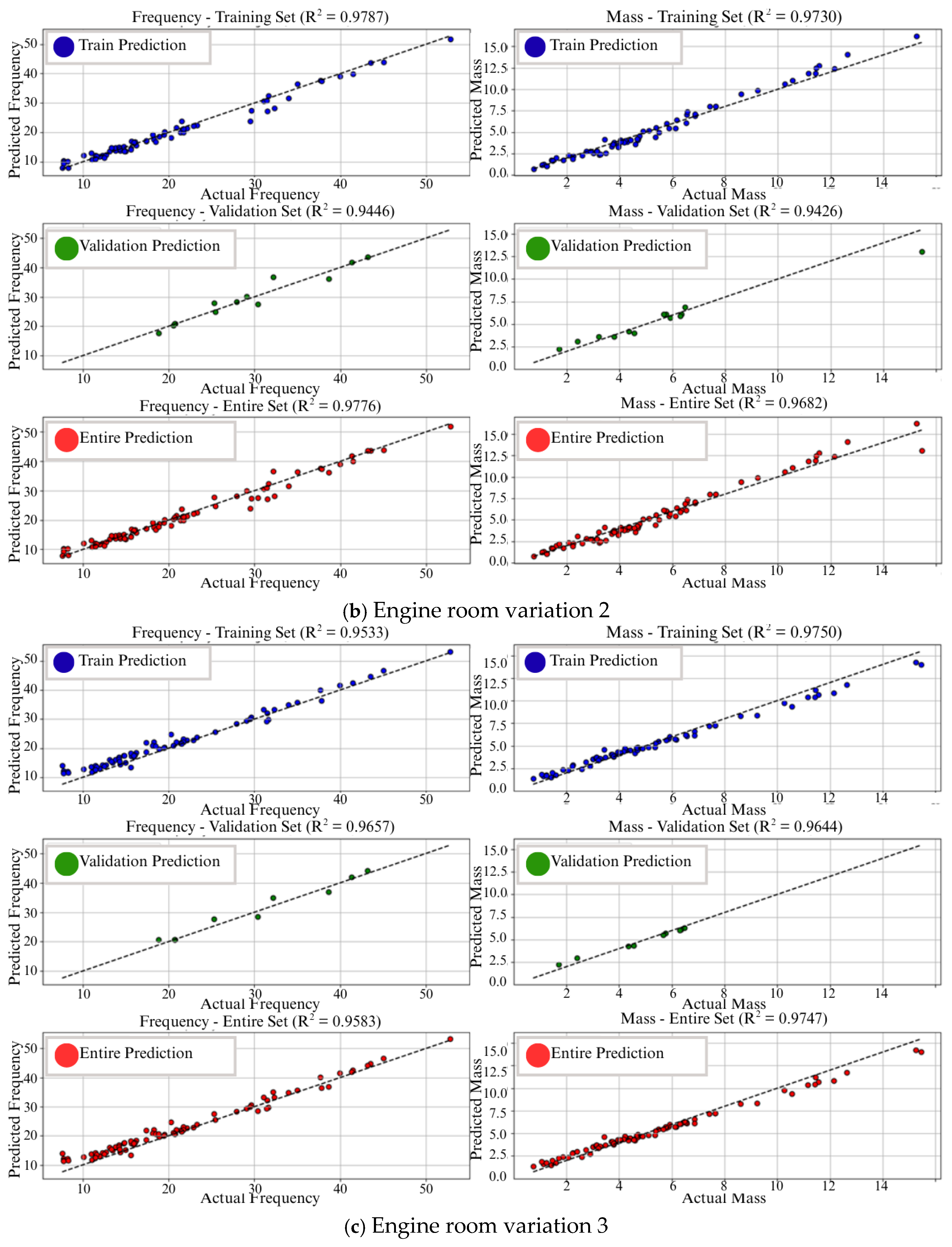
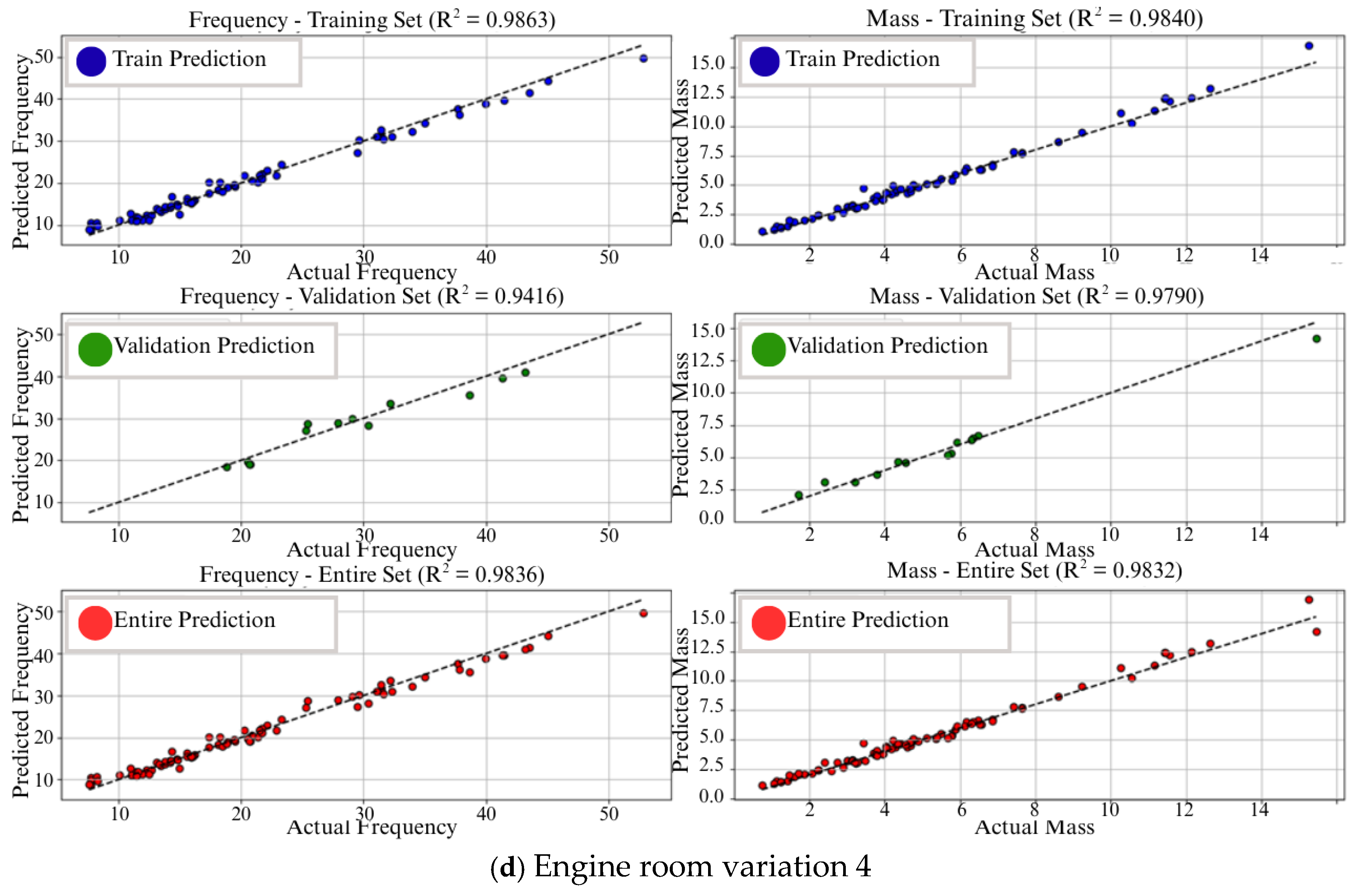
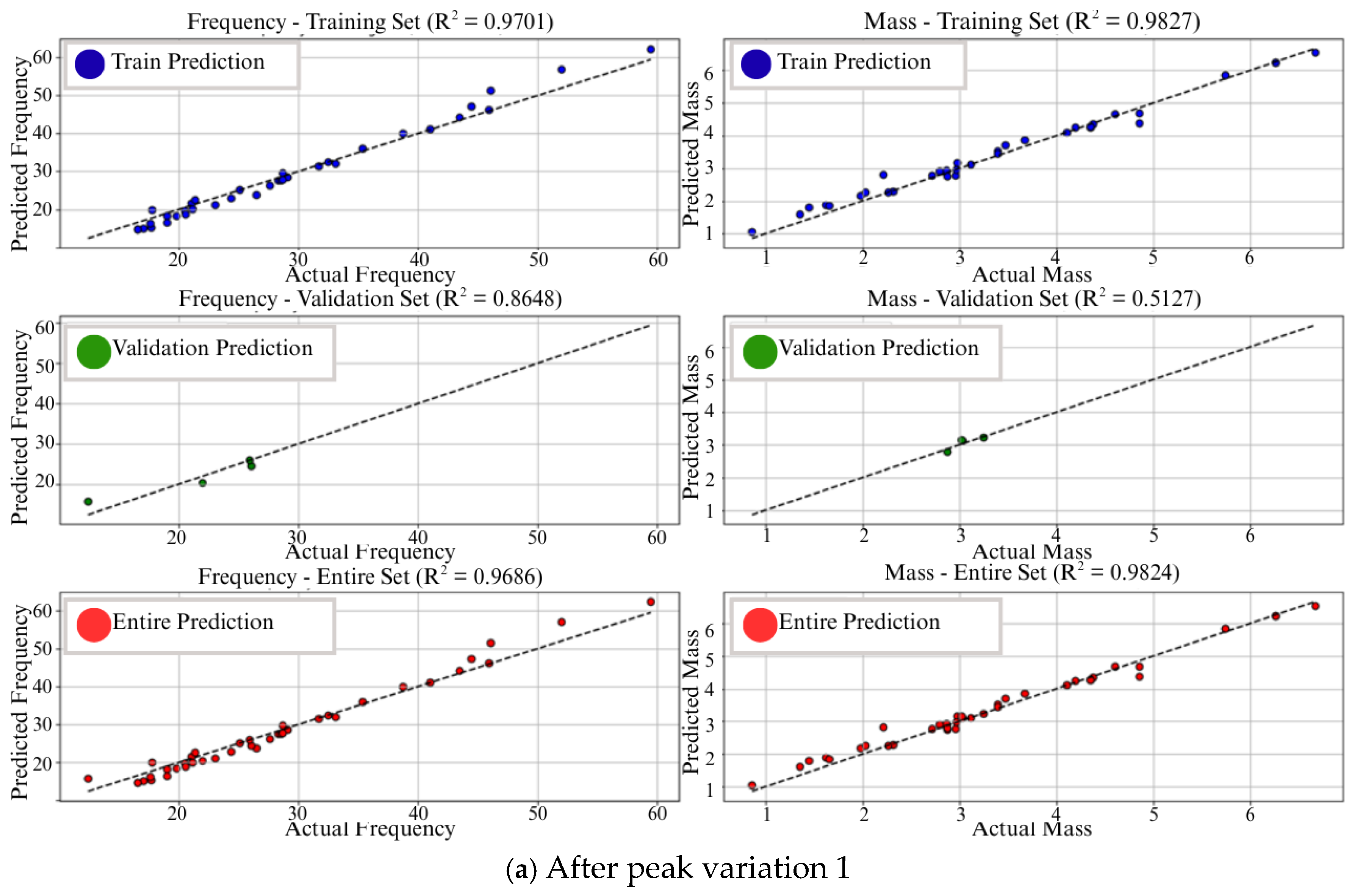
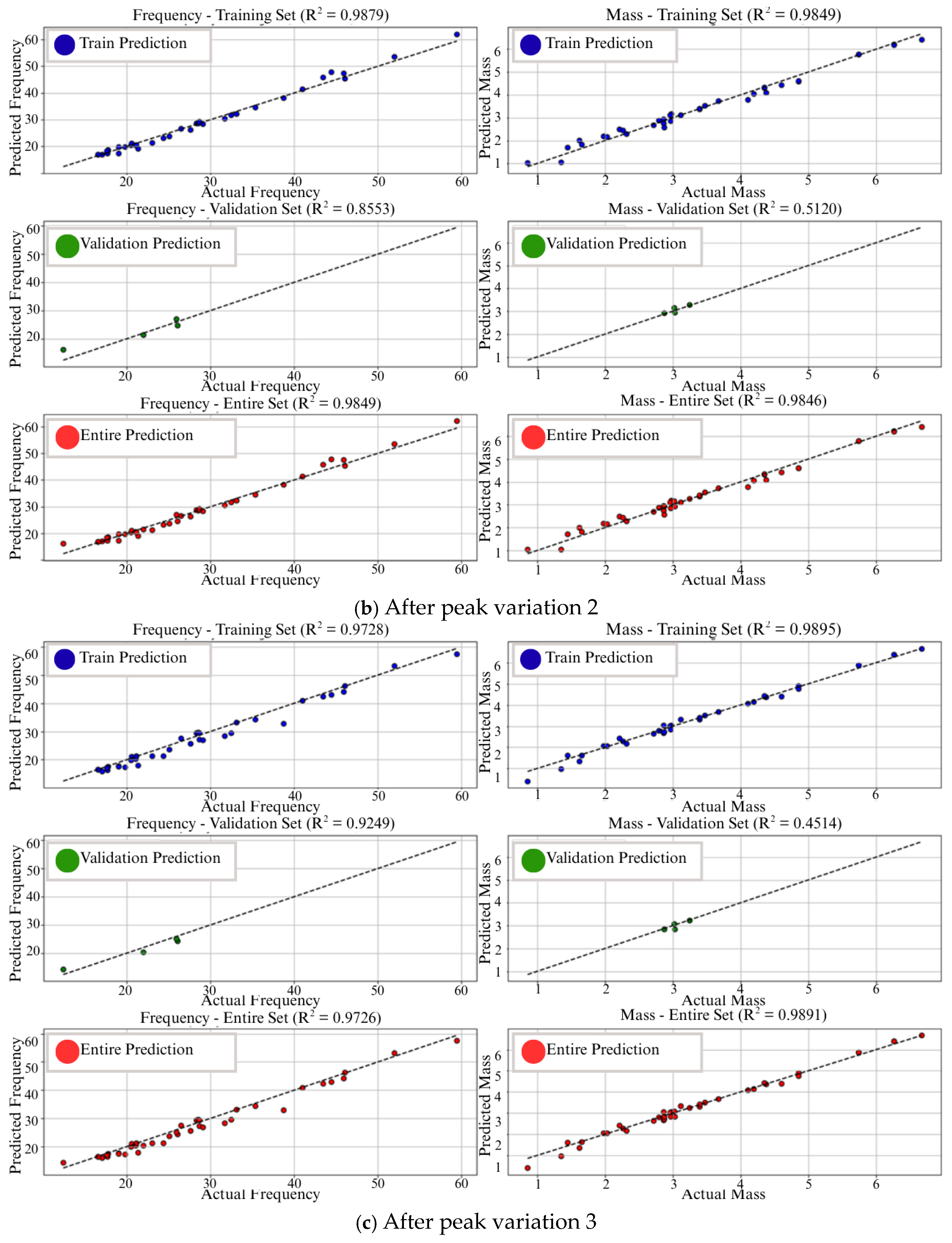
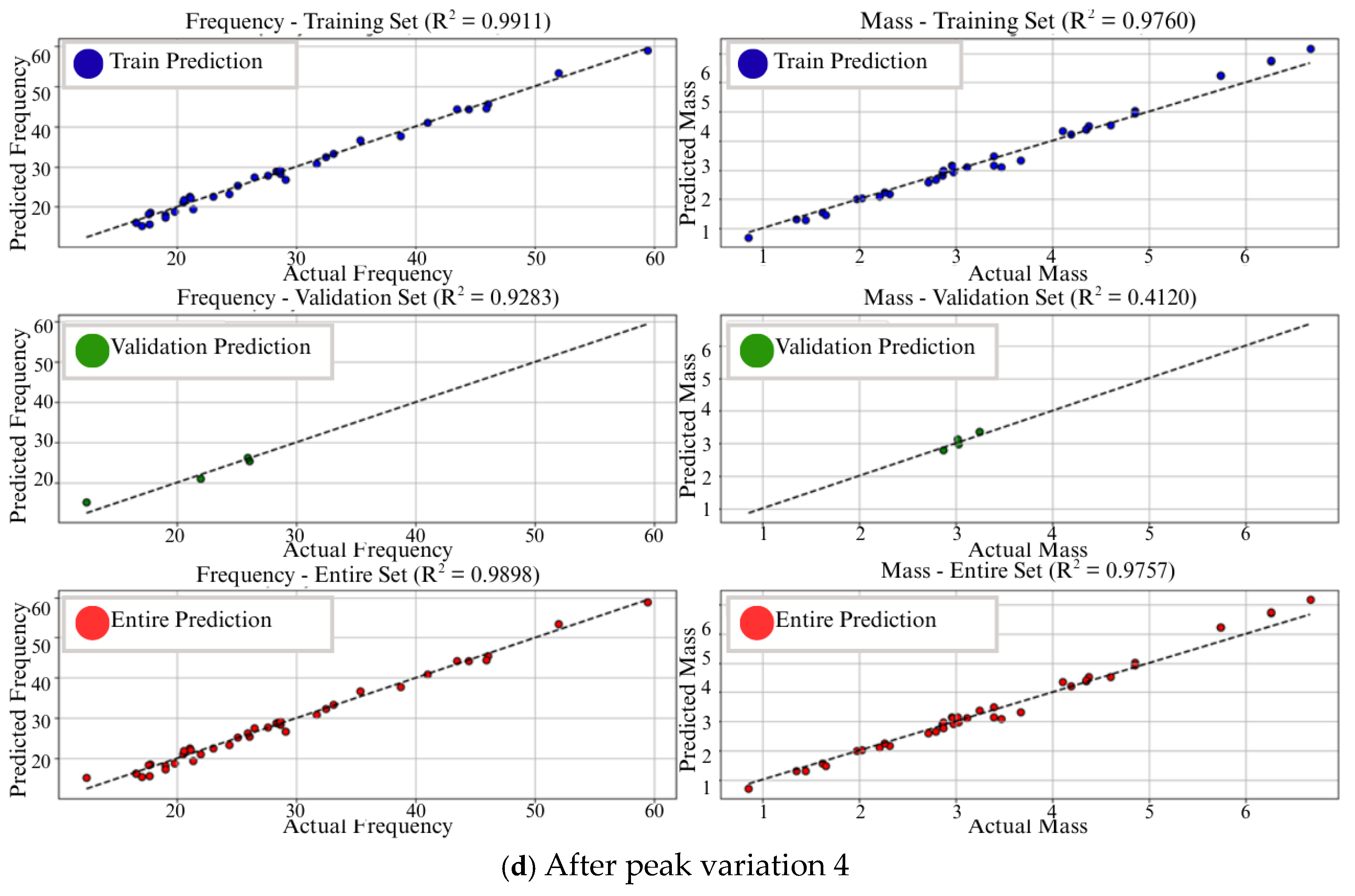
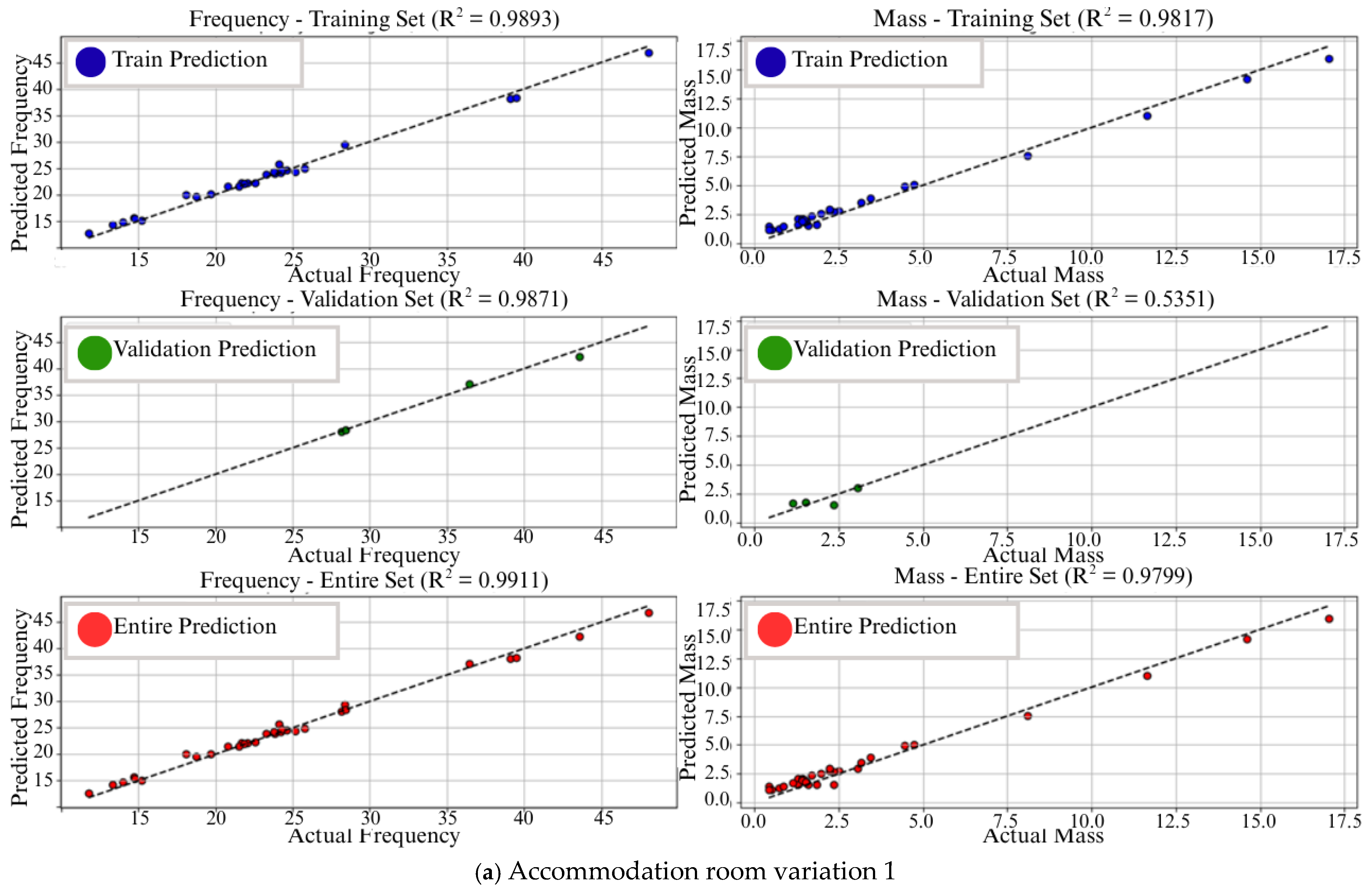
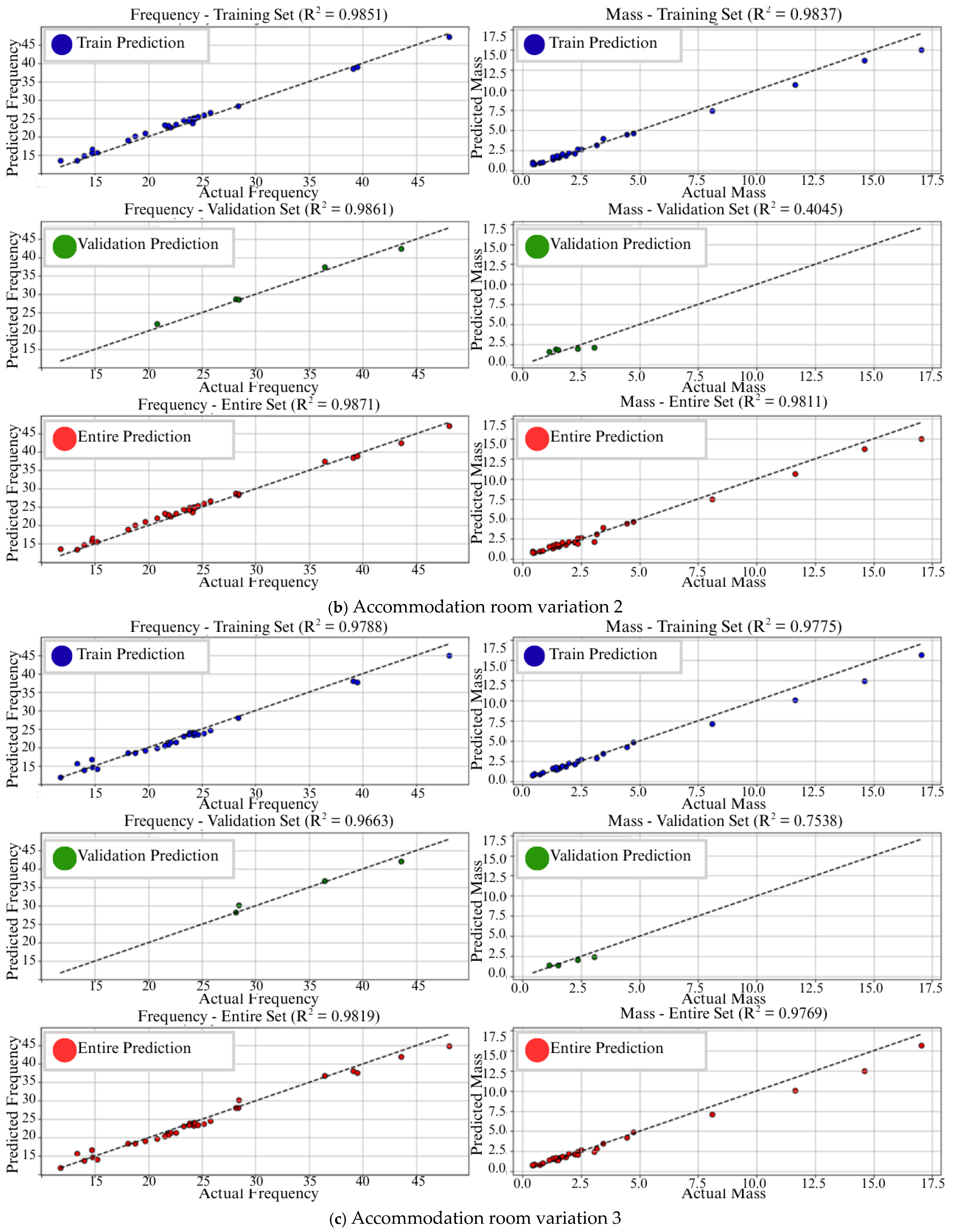
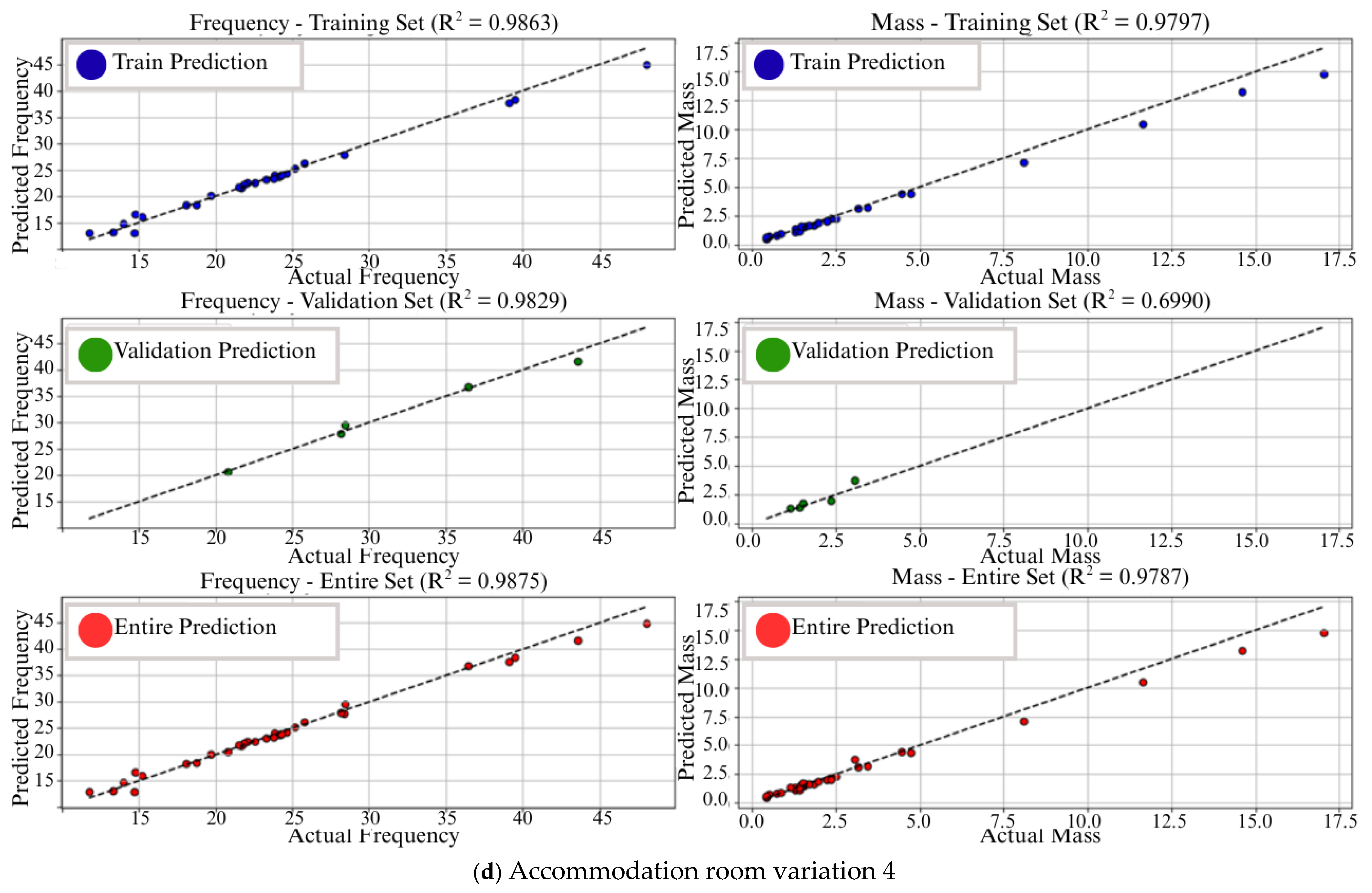
| Section | Number of Panel |
|---|---|
| Engine Room | 84 |
| After Peak | 40 |
| Accommodation Room | 32 |
| Fluid Type | Density () |
|---|---|
| Fresh water | 1.000 × 10−9 |
| Sea water | 1.025 × 10−9 |
| Urea | 1.335 × 10−9 |
| Heavy fuel oil | 9.910 × 10−10 |
| Low-sulfur marine gas oil | 8.900 × 10−10 |
| System oil | 9.200 × 10−10 |
| Cylinder oil | 9.600 × 10−10 |
| Low base number cylinder oil | 9.200 × 10−10 |
| No. | Variation | Training Set | Hidden Layers | Validation Split |
|---|---|---|---|---|
| 1 | ALL-Var1 | Entire Panel | 3 Hidden Layers | 10% |
| 2 | ALL-Var3 | Entire Panel | 3 Hidden Layers | 15% |
| 3 | ALL-Var3 | Entire Panel | 2 Hidden Layers | 10% |
| 4 | ALL-Var4 | Entire Panel | 2 Hidden Layers | 15% |
| 5 | ER-Var1 | Engine Room | 3 Hidden Layers | 10% |
| 6 | ER-Var3 | Engine Room | 3 Hidden Layers | 15% |
| 7 | ER-Var3 | Engine Room | 2 Hidden Layers | 10% |
| 8 | ER-Var4 | Engine Room | 2 Hidden Layers | 15% |
| 9 | AE-Var1 | After Peak | 3 Hidden Layers | 10% |
| 10 | AE-Var3 | After Peak | 3 Hidden Layers | 15% |
| 11 | AE-Var3 | After Peak | 2 Hidden Layers | 10% |
| 12 | AE-Var4 | After Peak | 2 Hidden Layers | 15% |
| 13 | ACC-Var1 | Accommodation | 3 Hidden Layers | 10% |
| 14 | ACC-Var3 | Accommodation | 3 Hidden Layers | 15% |
| 15 | ACC-Var3 | Accommodation | 2 Hidden Layers | 10% |
| 16 | ACC-Var4 | Accommodation | 2 Hidden Layers | 15% |
| No. | Variation | Frequency Accuracy | Mass Accuracy | Prediction Gap | Model Fitting | |||
|---|---|---|---|---|---|---|---|---|
| Train | Val. | Train | Val. | Freq. | Mass | |||
| 1 | ALL-Var1 | 98% | 95% | 98% | 96% | 3% | 2% | fit |
| 2 | ALL-Var3 | 97% | 92% | 97% | 99% | 5% | 2% | |
| 3 | ALL-Var3 | 95% | 97% | 95% | 97% | 2% | 2% | |
| 4 | ALL-Var4 | 98% | 91% | 97% | 99% | 7% | 2% | |
| 5 | ER-Var1 | 97% | 97% | 98% | 94% | 0% | 4% | |
| 6 | ER-Var3 | 97% | 94% | 97% | 94% | 3% | 3% | |
| 7 | ER-Var3 | 95% | 96% | 97% | 96% | 1% | 1% | |
| 8 | ER-Var4 | 98% | 94% | 98% | 97% | 4% | 1% | |
| 9 | AE-Var1 | 97% | 86% | 98% | 51% | 11% | 47% | overfit |
| 10 | AE-Var3 | 98% | 85% | 98% | 51% | 12% | 47% | |
| 11 | AE-Var3 | 97% | 92% | 98% | 45% | 5% | 53% | |
| 12 | AE-Var4 | 99% | 92% | 97% | 41% | 7% | 56% | |
| 13 | ACC-Var1 | 98% | 98% | 98% | 53% | 0% | 45% | |
| 14 | ACC-Var3 | 98% | 98% | 98% | 40% | 0% | 58% | |
| 15 | ACC-Var3 | 97% | 96% | 97% | 75% | 1% | 22% | |
| 16 | ACC-Var4 | 98% | 98% | 97% | 69% | 0% | 28% | |
| Panel | Frequency | Mass | Panel | Frequency | Mass | ||||
|---|---|---|---|---|---|---|---|---|---|
| No. | Act. | Pred. | Act. | Pred. | No. | Act. | Pred. | Act. | Pred. |
| 1 | 21.6 | 20.1 | 3.0 | 2.7 | 79 | 38.6 | 41.1 | 2.4 | 2.4 |
| 2 | 21.6 | 20.1 | 3.0 | 2.7 | 80 | 20.8 | 20.3 | 6.4 | 6.1 |
| 3 | 10.1 | 11.2 | 4.6 | 3.9 | 81 | 32.2 | 33.8 | 4.6 | 4.1 |
| 4 | 11.0 | 13.1 | 3.2 | 2.9 | 82 | 41.3 | 40.9 | 5.7 | 5.7 |
| 5 | 13.5 | 13.3 | 4.7 | 4.4 | 83 | 25.3 | 26.3 | 4.3 | 4.1 |
| 6 | 18.3 | 18.4 | 1.2 | 1.3 | 84 | 20.6 | 20.3 | 6.3 | 6.0 |
| 7 | 34.0 | 34.2 | 1.6 | 1.4 | 85 | 17.0 | 16.1 | 6.3 | 5.4 |
| 8 | 31.5 | 29.8 | 1.4 | 1.2 | 86 | 17.7 | 16.8 | 6.3 | 5.6 |
| 9 | 15.7 | 14.8 | 5.4 | 4.6 | 87 | 21.1 | 20.7 | 3.5 | 2.9 |
| 10 | 29.6 | 29.8 | 2.1 | 1.9 | 88 | 23.0 | 21.3 | 3.0 | 2.8 |
| 11 | 14.9 | 11.9 | 3.4 | 4.4 | 89 | 28.6 | 29.4 | 3.0 | 2.7 |
| 12 | 14.4 | 15.4 | 2.6 | 2.4 | 90 | 20.5 | 19.3 | 3.4 | 3.1 |
| 13 | 21.4 | 20.5 | 10.3 | 10.6 | 91 | 25.1 | 22.1 | 2.2 | 2.2 |
| 14 | 31.1 | 32.5 | 2.7 | 2.4 | 92 | 16.6 | 15.5 | 5.7 | 5.0 |
| 15 | 22.1 | 21.1 | 3.1 | 2.8 | 93 | 16.6 | 15.5 | 5.7 | 5.0 |
| 16 | 14.8 | 14.2 | 3.1 | 3.2 | 94 | 19.0 | 17.6 | 2.9 | 2.7 |
| 17 | 14.2 | 13.8 | 3.1 | 3.3 | 95 | 38.7 | 32.0 | 0.9 | 0.9 |
| 18 | 14.2 | 13.8 | 3.1 | 3.3 | 96 | 19.0 | 18.2 | 6.7 | 6.1 |
| 19 | 29.5 | 24.1 | 1.1 | 1.1 | 97 | 41.0 | 41.4 | 4.4 | 4.5 |
| 20 | 32.3 | 29.7 | 1.5 | 1.3 | 98 | 24.3 | 20.9 | 2.0 | 1.9 |
| 21 | 18.1 | 18.1 | 1.1 | 1.3 | 99 | 28.3 | 29.2 | 4.3 | 4.2 |
| 22 | 12.3 | 12.2 | 4.3 | 4.1 | 100 | 44.4 | 47.6 | 3.0 | 3.1 |
| 23 | 16.2 | 14.7 | 6.2 | 6.0 | 101 | 28.5 | 29.2 | 4.3 | 4.3 |
| 24 | 13.8 | 13.3 | 3.7 | 3.7 | 102 | 46.1 | 43.8 | 4.9 | 5.5 |
| 25 | 20.9 | 19.5 | 2.2 | 2.1 | 103 | 21.4 | 19.7 | 1.6 | 1.5 |
| 26 | 21.7 | 19.9 | 1.9 | 1.7 | 104 | 33.1 | 34.0 | 4.9 | 4.3 |
| 27 | 21.7 | 21.0 | 5.5 | 5.3 | 105 | 35.3 | 37.0 | 2.3 | 2.0 |
| 28 | 11.9 | 11.2 | 4.2 | 4.3 | 106 | 59.4 | 54.1 | 1.4 | 1.9 |
| 29 | 19.5 | 18.7 | 6.1 | 5.8 | 107 | 29.1 | 28.7 | 2.3 | 2.0 |
| 30 | 13.8 | 14.5 | 3.3 | 2.9 | 108 | 21.1 | 18.8 | 3.7 | 3.9 |
| 31 | 20.2 | 19.2 | 0.7 | 0.9 | 109 | 27.6 | 27.4 | 2.8 | 2.6 |
| 32 | 15.6 | 15.8 | 2.9 | 2.7 | 110 | 17.7 | 17.4 | 2.0 | 1.9 |
| 33 | 13.1 | 13.3 | 3.5 | 3.1 | 111 | 32.4 | 30.6 | 1.7 | 1.5 |
| 34 | 7.7 | 10.5 | 4.0 | 3.8 | 112 | 31.7 | 28.3 | 1.4 | 1.4 |
| 35 | 23.3 | 21.2 | 2.2 | 2.0 | 113 | 43.4 | 47.0 | 2.9 | 3.0 |
| 36 | 14.2 | 13.4 | 4.2 | 4.1 | 114 | 26.5 | 25.9 | 4.6 | 5.0 |
| 37 | 16.1 | 14.8 | 4.8 | 4.7 | 115 | 28.7 | 30.6 | 3.4 | 3.2 |
| 38 | 7.8 | 9.9 | 4.7 | 4.2 | 116 | 45.9 | 46.4 | 4.1 | 4.2 |
| 39 | 11.5 | 11.5 | 5.1 | 4.7 | 117 | 17.6 | 17.7 | 2.7 | 2.3 |
| 40 | 12.7 | 12.1 | 6.8 | 5.5 | 118 | 20.6 | 20.0 | 4.2 | 3.8 |
| 41 | 17.4 | 18.1 | 1.2 | 1.3 | 119 | 52.0 | 50.1 | 2.9 | 3.4 |
| 42 | 35.0 | 37.4 | 3.8 | 3.4 | 120 | 19.8 | 18.0 | 3.1 | 3.0 |
| 43 | 8.2 | 10.6 | 4.0 | 3.8 | 121 | 26.0 | 26.0 | 2.9 | 2.5 |
| 44 | 13.3 | 13.3 | 3.8 | 3.7 | 122 | 12.4 | 13.7 | 3.0 | 2.7 |
| 45 | 7.7 | 9.0 | 6.5 | 5.6 | 123 | 22.0 | 20.4 | 3.2 | 3.0 |
| 46 | 17.4 | 15.9 | 3.9 | 3.5 | 124 | 25.9 | 26.0 | 3.0 | 2.8 |
| 47 | 11.6 | 11.8 | 6.9 | 5.8 | 125 | 22.6 | 20.3 | 1.5 | 1.5 |
| 48 | 7.6 | 9.5 | 11.6 | 10.9 | 126 | 18.1 | 14.8 | 4.4 | 4.6 |
| 49 | 12.5 | 11.9 | 9.2 | 8.8 | 127 | 18.8 | 15.6 | 3.4 | 3.7 |
| 50 | 18.9 | 17.9 | 4.7 | 4.2 | 128 | 24.2 | 22.3 | 2.5 | 2.4 |
| 51 | 43.5 | 44.2 | 4.9 | 4.8 | 129 | 23.3 | 21.2 | 4.7 | 5.2 |
| 52 | 19.4 | 18.4 | 4.7 | 4.2 | 130 | 24.6 | 22.3 | 2.3 | 2.3 |
| 53 | 15.6 | 15.1 | 7.6 | 7.0 | 131 | 48.1 | 48.0 | 1.6 | 1.9 |
| 54 | 37.7 | 38.1 | 5.4 | 5.5 | 132 | 39.1 | 38.7 | 1.9 | 1.8 |
| 55 | 22.9 | 22.7 | 5.9 | 5.7 | 133 | 13.3 | 13.7 | 11.6 | 11.4 |
| 56 | 14.9 | 14.2 | 7.6 | 6.9 | 134 | 28.4 | 26.4 | 8.1 | 7.7 |
| 57 | 21.5 | 21.1 | 12.6 | 12.5 | 135 | 24.1 | 23.7 | 14.6 | 13.2 |
| 58 | 40.0 | 39.4 | 5.8 | 6.0 | 136 | 23.9 | 24.1 | 3.2 | 2.8 |
| 59 | 45.1 | 42.7 | 10.6 | 11.6 | 137 | 14.7 | 14.8 | 17.0 | 17.2 |
| 60 | 11.0 | 12.3 | 12.1 | 10.9 | 138 | 14.8 | 20.6 | 0.4 | 0.4 |
| 61 | 52.8 | 51.7 | 6.6 | 7.8 | 139 | 19.7 | 18.6 | 1.3 | 1.5 |
| 62 | 14.3 | 13.9 | 6.5 | 5.2 | 140 | 21.7 | 20.3 | 1.5 | 1.4 |
| 63. | 41.5 | 42.5 | 4.0 | 4.4 | 141 | 23.8 | 21.9 | 2.0 | 1.9 |
| 64. | 11.5 | 12.4 | 11.1 | 10.3 | 142 | 15.2 | 17.7 | 1.4 | 1.4 |
| 65 | 37.8 | 33.8 | 11.4 | 12.2 | 143 | 24.3 | 21.8 | 1.7 | 1.6 |
| 66 | 31.6 | 28.8 | 11.5 | 12.3 | 144 | 39.5 | 37.6 | 1.3 | 1.1 |
| 67 | 15.9 | 14.7 | 4.0 | 4.0 | 145 | 14.0 | 15.2 | 2.2 | 2.3 |
| 68 | 18.5 | 17.2 | 7.4 | 7.4 | 146 | 22.1 | 19.7 | 1.5 | 1.6 |
| 69 | 31.4 | 28.2 | 15.3 | 15.7 | 147 | 11.8 | 14.7 | 2.2 | 2.3 |
| 70 | 15.9 | 14.8 | 4.4 | 4.3 | 148 | 21.9 | 21.8 | 0.5 | 0.4 |
| 71 | 8.3 | 8.4 | 8.6 | 7.9 | 149 | 25.2 | 21.6 | 0.7 | 0.7 |
| 72 | 20.5 | 20.1 | 5.9 | 5.7 | 150 | 21.5 | 20.2 | 0.8 | 0.9 |
| 73 | 25.4 | 25.8 | 15.5 | 15.5 | 151 | 25.8 | 23.0 | 0.4 | 0.2 |
| 74 | 29.1 | 32.3 | 3.2 | 2.8 | 152 | 20.8 | 20.0 | 1.4 | 1.4 |
| 75 | 27.9 | 29.9 | 3.8 | 3.6 | 153 | 28.2 | 25.9 | 1.5 | 1.4 |
| 76 | 30.4 | 27.2 | 1.7 | 1.8 | 154 | 28.4 | 29.9 | 3.1 | 3.1 |
| 77 | 18.9 | 17.0 | 6.5 | 6.3 | 155 | 36.5 | 33.6 | 1.1 | 1.0 |
| 78 | 43.1 | 42.3 | 5.8 | 6.0 | 156 | 43.6 | 44.2 | 2.3 | 2.7 |
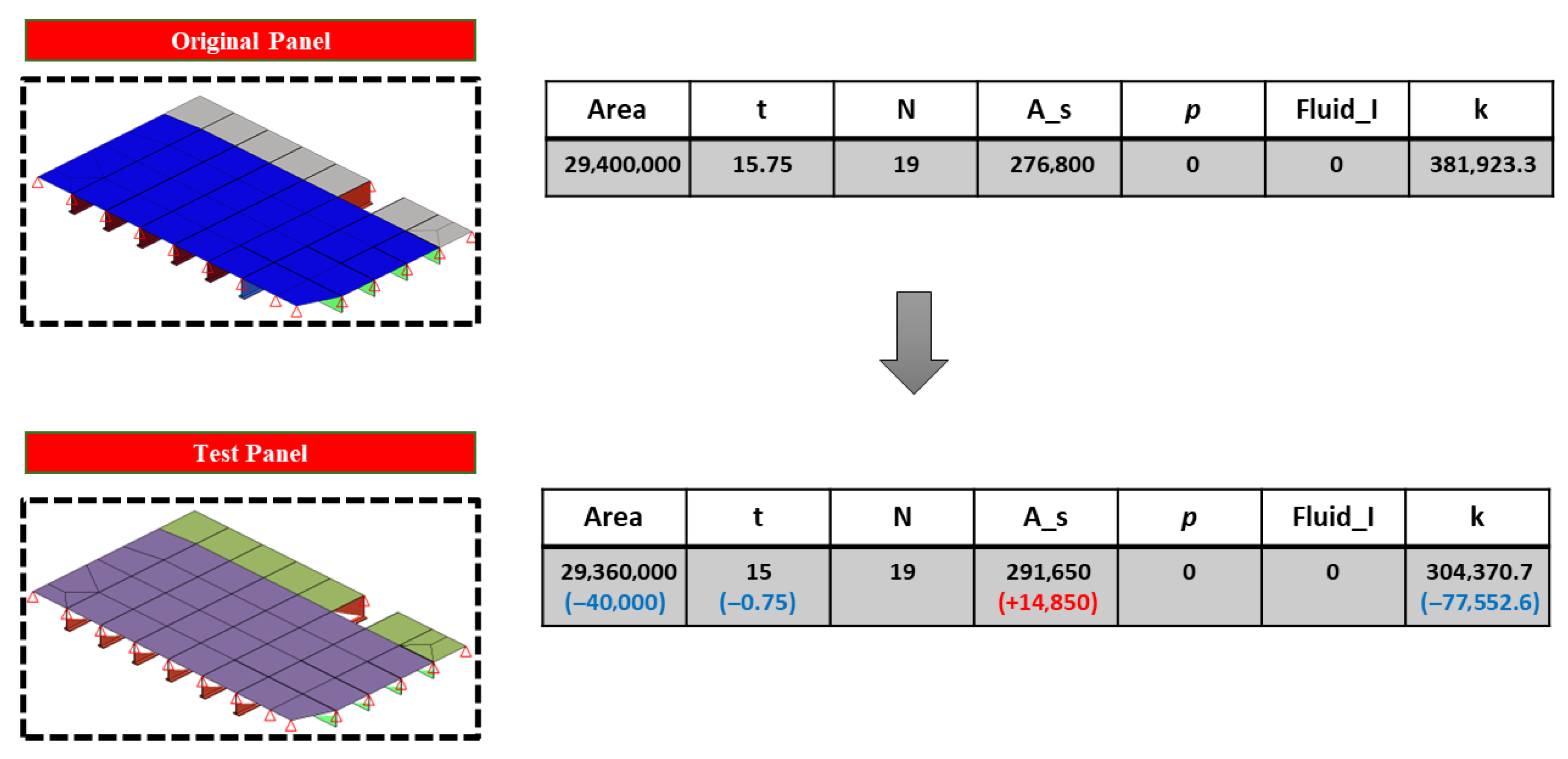
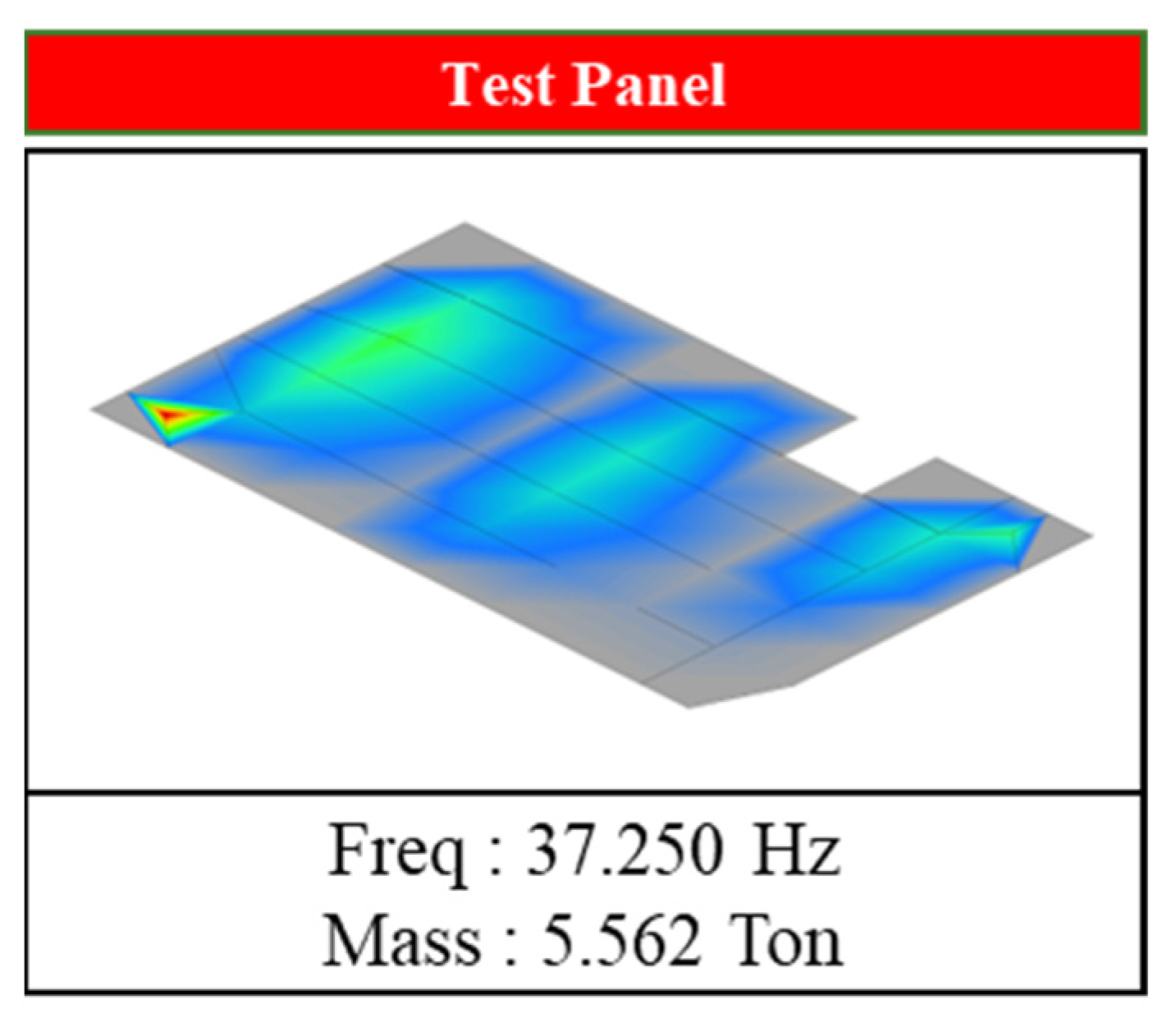
| Panel Type | Frequency | Mass | Margin | Accuracy | ||||
|---|---|---|---|---|---|---|---|---|
| Act. | Pred. | Act. | Pred. | Freq. | Mass | Freq. | Mass | |
| Original panel | 41.3 | 40.9 | 5.7 | 5.7 | 0.97% | 0% | 99.03% | 100% |
| Test panel | 37.3 | 38.5 | 5.6 | 5.4 | 3.22% | 3.57% | 96.78% | 96.48% |
| ALL-Var1 (validation set accuracy) | 95% | 96% | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pynasti, M.R.; Song, C.-Y. Prediction of Local Vibration Analysis for Ship Stiffened Panel Structure Using Artificial Neural Network Algorithm. Vibration 2025, 8, 52. https://doi.org/10.3390/vibration8030052
Pynasti MR, Song C-Y. Prediction of Local Vibration Analysis for Ship Stiffened Panel Structure Using Artificial Neural Network Algorithm. Vibration. 2025; 8(3):52. https://doi.org/10.3390/vibration8030052
Chicago/Turabian StylePynasti, Mahardika Rizki, and Chang-Yong Song. 2025. "Prediction of Local Vibration Analysis for Ship Stiffened Panel Structure Using Artificial Neural Network Algorithm" Vibration 8, no. 3: 52. https://doi.org/10.3390/vibration8030052
APA StylePynasti, M. R., & Song, C.-Y. (2025). Prediction of Local Vibration Analysis for Ship Stiffened Panel Structure Using Artificial Neural Network Algorithm. Vibration, 8(3), 52. https://doi.org/10.3390/vibration8030052







