Linearly Perturbed Frequency Equation, New Frequency Formula, and a Linearized Galerkin Method for Nonlinear Vibrational Oscillators
Abstract
1. Introduction
- A new frequency–amplitude formula is addressed, which improves an ancient Chinese mathematics method and advocates a modification of He’s formula. The new frequency formula obtained from the new relationship is more accurate than He’s frequency–amplitude formula when the parameter involved in the new formula is obtained by minimizing the absolute error of the periodicity condition.
- A linearly perturbed frequency equation by adding a linear term in the original frequency equation is proposed, which can be used to obtain a more accurate value of the frequency by properly setting the perturbed parameter.
- A novel integral type frequency–amplitude formula is derived, which involves a weight function; through a few lines of computations, the approximate value of the true frequency can be well estimated.
- A simple method is developed by linearizing the residual Galerkin method (LRGM), which is combined with the new frequency–amplitude formula as a hybrid method to generate the higher-order periodic solution of the nonlinear oscillator and its frequency with high accuracy.
2. He’s Frequency–Amplitude Formula
3. A New Frequency-Amplitude Formula
4. Applications of the New Formula to Compute the Frequency
4.1. Duffing Oscillator
4.2. Micken’s Oscillator
4.3. Tapered Beam’s Oscillator
5. An Integral Formulation and Its Applications
5.1. Integral-Type Frequency–Amplitude Formula
5.2. Applications of the Integral Formula
6. The Theory of a New Algebraic Equation
7. Linearized Residual Galerkin Method
8. The Applications of Theorem 3 and LRGM
8.1. A Nonlinear Oscillator with Irrational Restoring Force
8.2. A Nonconservative Nonlinear Oscillator
8.3. A Cubic-Quintic Duffing Nonlinear Oscillator
8.4. The Helmholtz–Duffing Nonlinear Oscillator
9. Higher-Order Periodic Solutions of Duffing Oscillator
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ismail, G.M.; Cveticanin, L. Higher order Hamiltonian approach for solving doubly clamped beam type N/MEMS subjected to the van der Waals attraction. Chin. J. Phys. 2021, 72, 69–77. [Google Scholar]
- Rehman, S.; Hussain, A.; Rahman, J.U.; Anjum, N.; Munir, T. Modified Laplace based variational iteration method for the mechanical vibrations and its applications. Acta Mech. Autom. 2022, 16, 98–102. [Google Scholar]
- Tang, W.; Anjum, N.; He, J.-H. Variational iteration method for the nanobeams-based N/MEMS system. MethodsX 2023, 11, 102465. [Google Scholar]
- Lu, J. Global residue harmonic balance method for strongly nonlinear oscillator with cubic and harmonic restoring force. J. Low Freq. Noise Vib. Active Control 2022, 41, 1402–1410. [Google Scholar]
- Wang, S.; Zhang, Y.; Guo, W.; Pi, T.; Li, X. Vibration analysis of nonlinear damping systems by the discrete incremental harmonic balance method. Nonlinear Dyn. 2023, 111, 2009–2028. [Google Scholar]
- Liu, C.S.; Kuo, C.L.; Chang, C.W. Linearized harmonic balance method for seeking the periodic vibrations of second and third orders nonlinear oscillators. Mathematics 2025, 13, 162. [Google Scholar] [CrossRef]
- Molla, M.; Sharif, N. Energy balance method for solving nonlinear oscillators with non-rational restoring force. Appl. Math. Sci. 2023, 17, 689–700. [Google Scholar]
- He, J.H.; Jiao, M.L.; Gepreel, K.A.; Khan, Y. Homotopy perturbation method for strongly nonlinear oscillators. Math. Comput. Simul. 2023, 204, 243–258. [Google Scholar]
- Ismail, G.M.; Abul-Ez, M.; Zayed, M.; Farea, N.M. Analytical accurate solutions of nonlinear oscillator systems via coupled homotopy-variational approach. Alex. Eng. J. 2022, 61, 5051–5058. [Google Scholar]
- Ismail, G.M.; El-Moshneb, M.M.; Zayed, M. Analytical technique for solving strongly nonlinear oscillator differential equations. Alex. Eng. J. 2023, 74, 547–557. [Google Scholar]
- Roy, Y.; Maiti, D.K. General approach on the best fitted linear operator and basis function for homotopy methods and application to strongly nonlinear oscillators. Math. Comput. Simul. 2024, 220, 44–64. [Google Scholar] [CrossRef]
- Mohammadian, M. Application of He’s new frequency-amplitude formulation for the nonlinear oscillators by introducing a new trend for determining the location points. Chin. J. Phys. 2024, 89, 1024–1040. [Google Scholar] [CrossRef]
- Ismail, G.M.; Kamel, A.; Alsarrani, A. Approximate analytical solutions to nonlinear oscillations via semi-analytical method. Alex. Eng. J. 2024, 98, 97–102. [Google Scholar] [CrossRef]
- He, J.H. Comment on He’s frequency formulation for nonlinear oscillators. Eur. J. Phys. 2008, 29, L19–L22. [Google Scholar] [CrossRef]
- He, J.H.; Garcia, A. The simplest amplitude-period formula for non-conservative oscillators. Rep. Mech. Eng. 2021, 2, 143–148. [Google Scholar] [CrossRef]
- Akbarzade, M.; Khan, Y. Dynamic model of large amplitude non-linear oscillations arising in the structural engineering: Analytical solutions. Math. Comput. Model. 2012, 55, 480–489. [Google Scholar] [CrossRef]
- Cai, X.C.; Liu, J.F. Application of the modified frequency formulation to a nonlinear oscillator. Comput. Math. Appl. 2011, 61, 2237–2240. [Google Scholar] [CrossRef]
- He, J.H. Amplitude-frequency relationship for conservative nonlinear oscillators with odd nonlinearities. Int. J. Appl. Comput. Math. 2017, 3, 1557–1560. [Google Scholar] [CrossRef]
- Ren, Z.F.; Hu, G.F. He’s frequency-amplitude formulation with average residuals for nonlinear oscillators. J. Low Freq. Noise Vib. Active Control 2018, 38, 1050–1059. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Y.P. Residual calculation in He’s frequency-amplitude formulation. J. Low Freq. Noise Vib. Active Control 2021, 40, 1040–1047. [Google Scholar] [CrossRef]
- Tian, D.; Liu, Z. Period/frequency estimation of a nonlinear oscillator. J. Low Freq. Noise Vib. Active Control 2019, 38, 1629–1634. [Google Scholar]
- He, C.H.; Wang, J.H.; Yao, S. A complement to period/frequency estimation of a nonlinear oscillator. J. Low Freq. Noise Vib. Active Control 2019, 38, 992–995. [Google Scholar]
- El-Dib, Y.O. A review of the frequency-amplitude formula for nonlinear oscillators and its advancements. J. Low Freq. Noise Vib. Active Control 2024, 43, 1032–1064. [Google Scholar]
- He, J.H. Ancient Chinese algorithm: The Ying Buzu Shu (method od surplus and deficiency) vs. Newton iteration method. Appl. Math. Mech. 2002, 23, 1407–1412. [Google Scholar]
- He, C.H. An introduction to an ancient Chinese algorithm and its modification. Int. J. Numer. Meth. Heat Fluid Flow 2016, 26, 2486–2491. [Google Scholar]
- Liu, Y.Q.; He, J.H. On relationship between two ancient Chinese algorithms and their application to flash evaporation. Results Phys. 2017, 7, 320–322. [Google Scholar]
- Liu, C.S.; Chang, C.W. Updating to optimal parametric values by memory-dependent methods: Fractional type iterative schemes for solving nonlinear equations. Mathematics 2024, 12, 1032. [Google Scholar]
- He, C.H.; He, J.H. Double trials method for nonlinear problems arising in heat transfer. Therm. Sci. Suppl. 2011, 15, S153–S155. [Google Scholar]
- Krasnosel’skii, M.A.; Vainikko, G.M.; Zabreiko, P.P.; Rutitcki, J.B.; Stecenko, V.J. Approximated Solutions of Operator Equations; Walters–Noordhoff: Groningen, The Netherlands, 1972. [Google Scholar]
- Fatoorehchi, H.; Abolghasemi, H.; Rach, R. A new parametric algorithm for isothermal flash calculations by the Adomian decomposition of Michaelis-Menten type nonlinearities. Fluid Phase Equilib. 2015, 395, 44–50. [Google Scholar] [CrossRef]
- He, J.H. Some asymptotic methods for strongly nonlinear equations. Int. J. Modern Phy. B 2006, 20, 1141–1199. [Google Scholar] [CrossRef]
- Geng, L.; Cai, X.C. He’s frequency formulation for nonlinear oscillators. Eur. J. Phys. 2007, 28, 923–931. [Google Scholar]
- Ren, Z.F.; Gui, W.K. He’s frequency formulation for nonlinear oscillators using a golden mean location. Comput. Math. Appl. 2011, 61, 1987–1990. [Google Scholar]
- Mickens, R.E. Investigation of the properties of the period for the nonlinear oscillator x¨+(1+x˙2)x=0. J. Sound Vib. 2006, 292, 1031–1035. [Google Scholar]
- Liu, C.S.; Chang, C.W. A novel perturbation method to approximate the solution of nonlinear ordinary differential equation after being linearized to the Mathieu equation. Mech. Syst. Signal Process. 2022, 178, 109261. [Google Scholar]
- He, J.H. Modified Lindstedt-Poincare methods for some strongly nonlinear oscillations Part I: Expansion of a constant. Int. J. Non-Linear Mech. 2002, 37, 309–314. [Google Scholar]
- Shou, D.H. The homotopy perturbation method for nonlinear oscillators. Comput. Math. Appl. 2009, 58, 2456–2459. [Google Scholar]
- Zhao, L. He’s frequency-amplitude formulation for nonlinear oscillators with an irrational force. Comput. Math. Appl. 2009, 58, 2477–2479. [Google Scholar]
- Ren, Z.F.; Wu, J.B. He’s frequency-amplitude formulation for nonlinear oscillator with damping. J. Low Freq. Noise Vib. Active Control 2019, 38, 1045–1049. [Google Scholar]
- Yao, S.W.; Cheng, Z.B. The homotopy perturbation method for a nonlinear oscillator with a damping. J. Low Freq. Noise Vib. Active Control 2019, 38, 1110–1112. [Google Scholar]
- Ma, H. Simplified Hamiltonian-based frequency-amplitude formulation for nonlinear vibration systems. Facta Univ. Ser. Mech. Eng. 2022, 20, 445–455. [Google Scholar]
- He, J.H.; Hou, W.F.; Qie, N.; Gepreel, A.K.; Shirazi, A.H.; Sedighi, H.M. Hamiltonian-based frequency-amplitude formulation for nonlinear oscillators. Facta-Univ.-Ser. Mech. Eng. 2021, 19, 199–208. [Google Scholar] [CrossRef]
- El-Dib, Y.O. Insightful and comprehensive formularization of frequency–amplitude formula for strong or singular nonlinear oscillators. J. Low Freq. Noise Vib. Active Control 2023, 42, 89–109. [Google Scholar] [CrossRef]
- El-Dib, Y.O.; Alyousef, H.A. Successive approximate solutions for nonlinear oscillation and improvement of the solution accuracy with efficient non-perturbative technique. J. Low Freq. Noise Vib. Active Control 2023, 42, 1296–1311. [Google Scholar] [CrossRef]
- Leung, A.Y.T.; Guo, Z. Homotopy perturbation for conservative Helmholtz-Duffing oscillators. J. Sound Vib. 2009, 325, 287–296. [Google Scholar] [CrossRef]
- Askari, H.; Saadatnia, Z.; Younesian, D.; Yildirim, A.; Kalami-Yazdi, M. Approximate periodic solutions for the Helmholtz–Duffing equation. Comput. Math. Appl. 2011, 62, 3894–3901. [Google Scholar] [CrossRef]

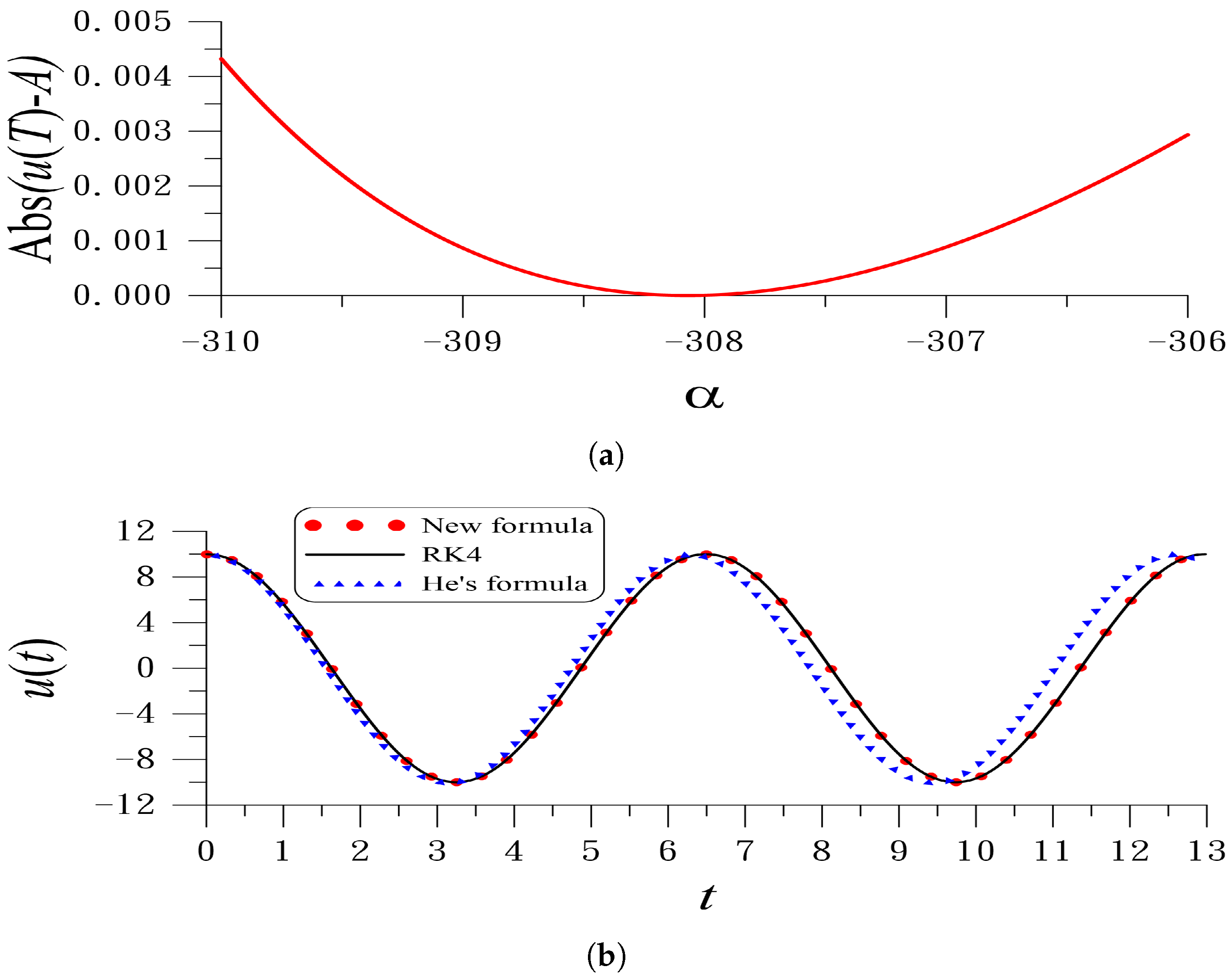
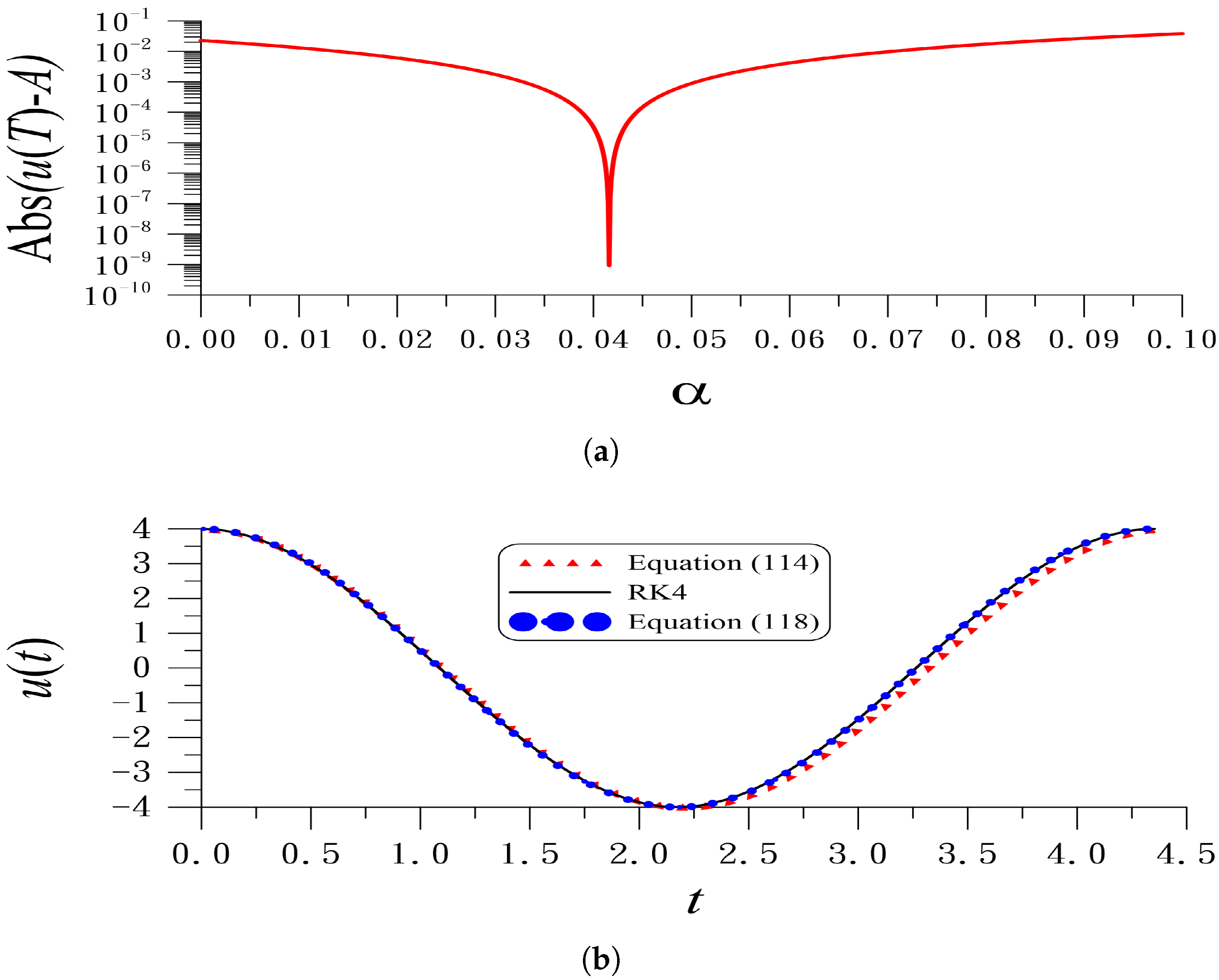
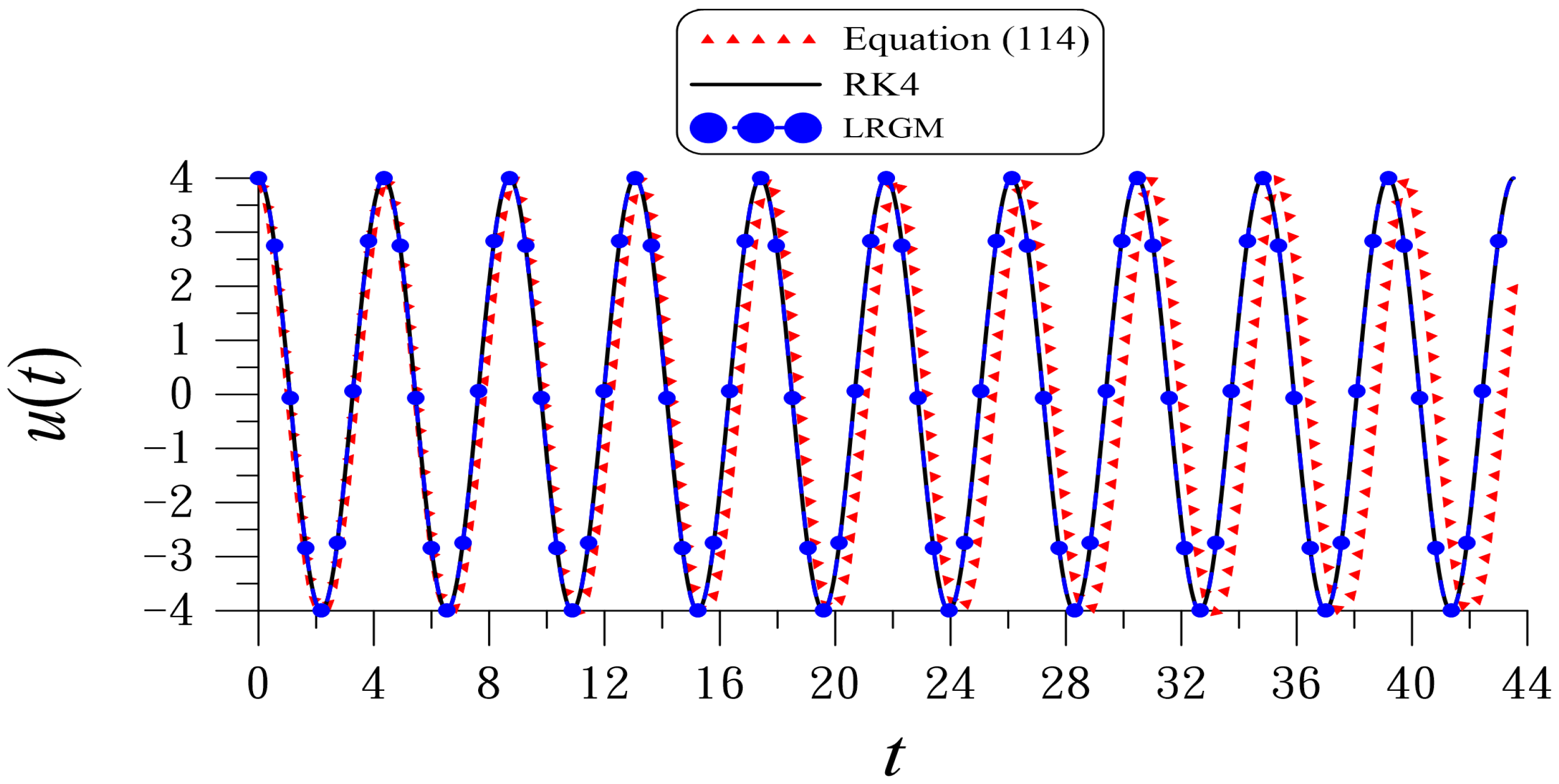

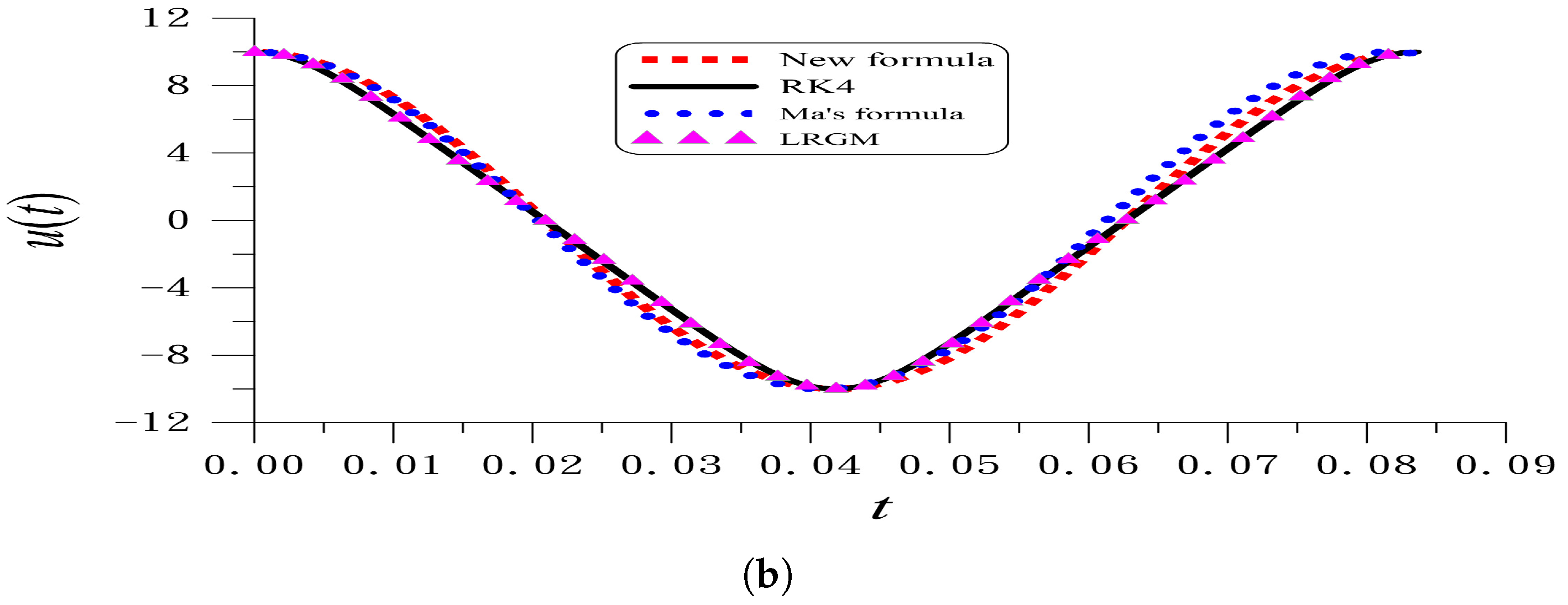

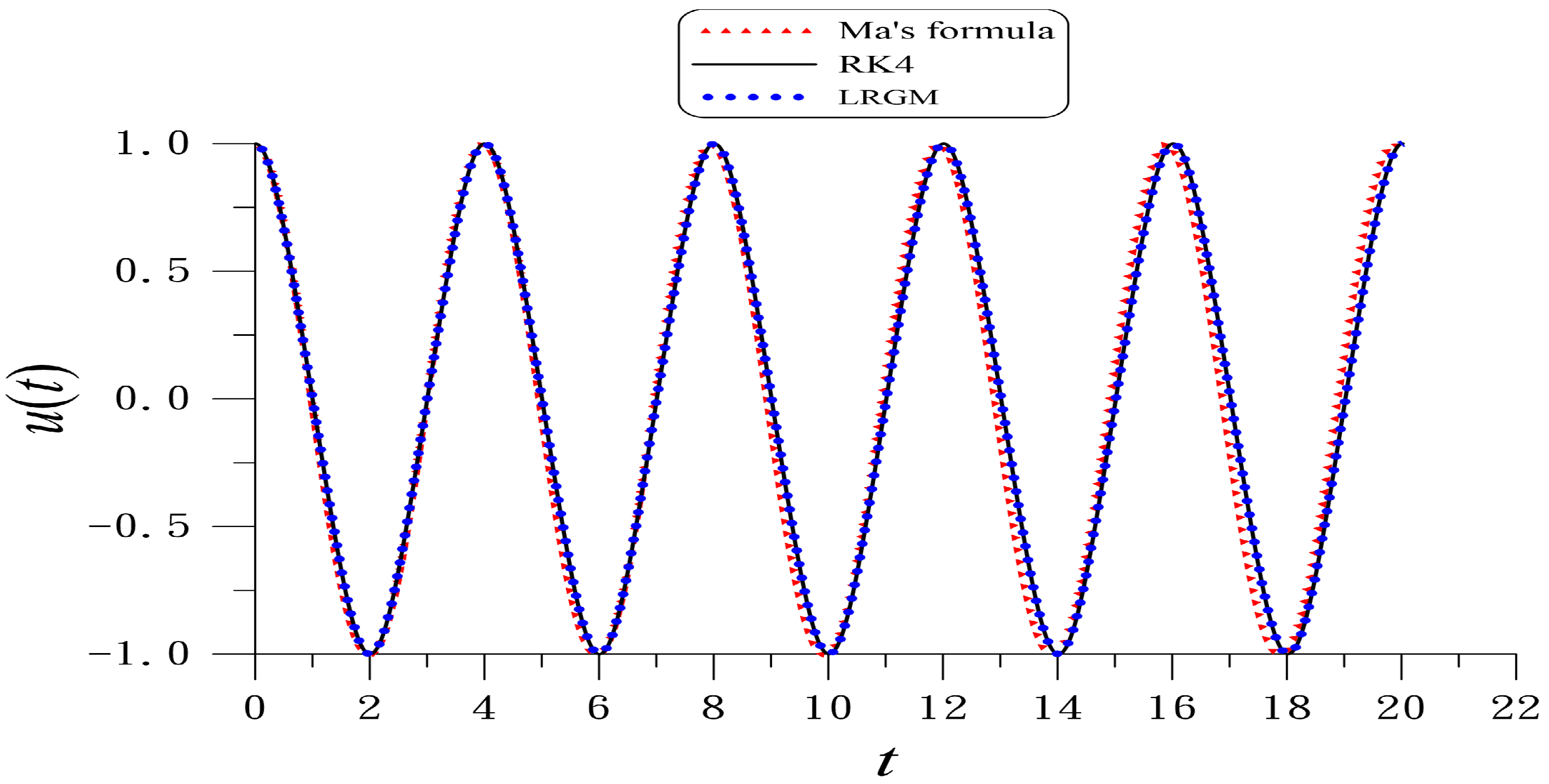
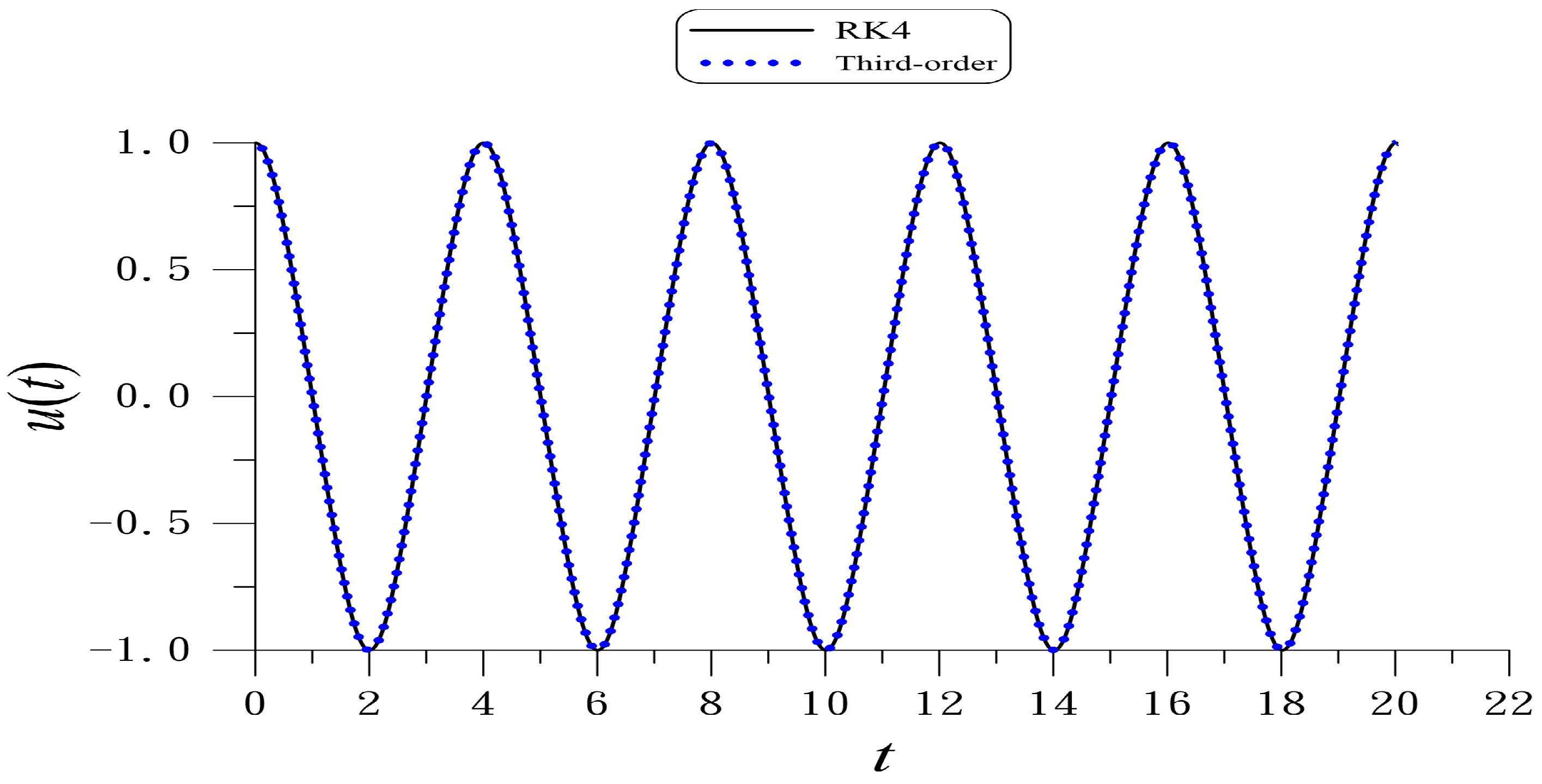
| k | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Equation (18) | |||||
| Equation (19) |
| A | 0.5 | 1 | 3 | 5 | 10 |
|---|---|---|---|---|---|
| Equation (28) | 1.1726039 | 1.5811388 | 3.8078866 | 6.2048368 | 12.288206 |
| Exact | 1.1707815 | 1.5691058 | 3.7365995 | 6.0772487 | 12.024950 |
| Equation (29) | 1.1707820 | 1.5690951 | 3.7365875 | 6.0772426 | 12.024907 |
| A | 0.5 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 2.86 | 0.744 | 0.4559 | 0.354 | 0.17816 | |
| Equation (34) | 1.0307764 | 1.3701069 | 1.4142136 | 1.8027756 | 2.2360680 |
| Exact | 1.0373540 | 1.1432943 | 1.6845799 | 2.7120276 | 3.8624997 |
| Equation (35) | 1.0373541 | 1.1432958 | 1.6846060 | 2.7120994 | 3.8626185 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.-S.; Tsai, C.-C.; Chang, C.-W. Linearly Perturbed Frequency Equation, New Frequency Formula, and a Linearized Galerkin Method for Nonlinear Vibrational Oscillators. Vibration 2025, 8, 16. https://doi.org/10.3390/vibration8020016
Liu C-S, Tsai C-C, Chang C-W. Linearly Perturbed Frequency Equation, New Frequency Formula, and a Linearized Galerkin Method for Nonlinear Vibrational Oscillators. Vibration. 2025; 8(2):16. https://doi.org/10.3390/vibration8020016
Chicago/Turabian StyleLiu, Chein-Shan, Chia-Cheng Tsai, and Chih-Wen Chang. 2025. "Linearly Perturbed Frequency Equation, New Frequency Formula, and a Linearized Galerkin Method for Nonlinear Vibrational Oscillators" Vibration 8, no. 2: 16. https://doi.org/10.3390/vibration8020016
APA StyleLiu, C.-S., Tsai, C.-C., & Chang, C.-W. (2025). Linearly Perturbed Frequency Equation, New Frequency Formula, and a Linearized Galerkin Method for Nonlinear Vibrational Oscillators. Vibration, 8(2), 16. https://doi.org/10.3390/vibration8020016







