User-Friendly Tool for Expedited Ground Vibration Assessment Induced by Impact Pile Driving
Abstract
1. Introduction
2. Development of the User-Friendly Prediction Tool
2.1. Database Generation
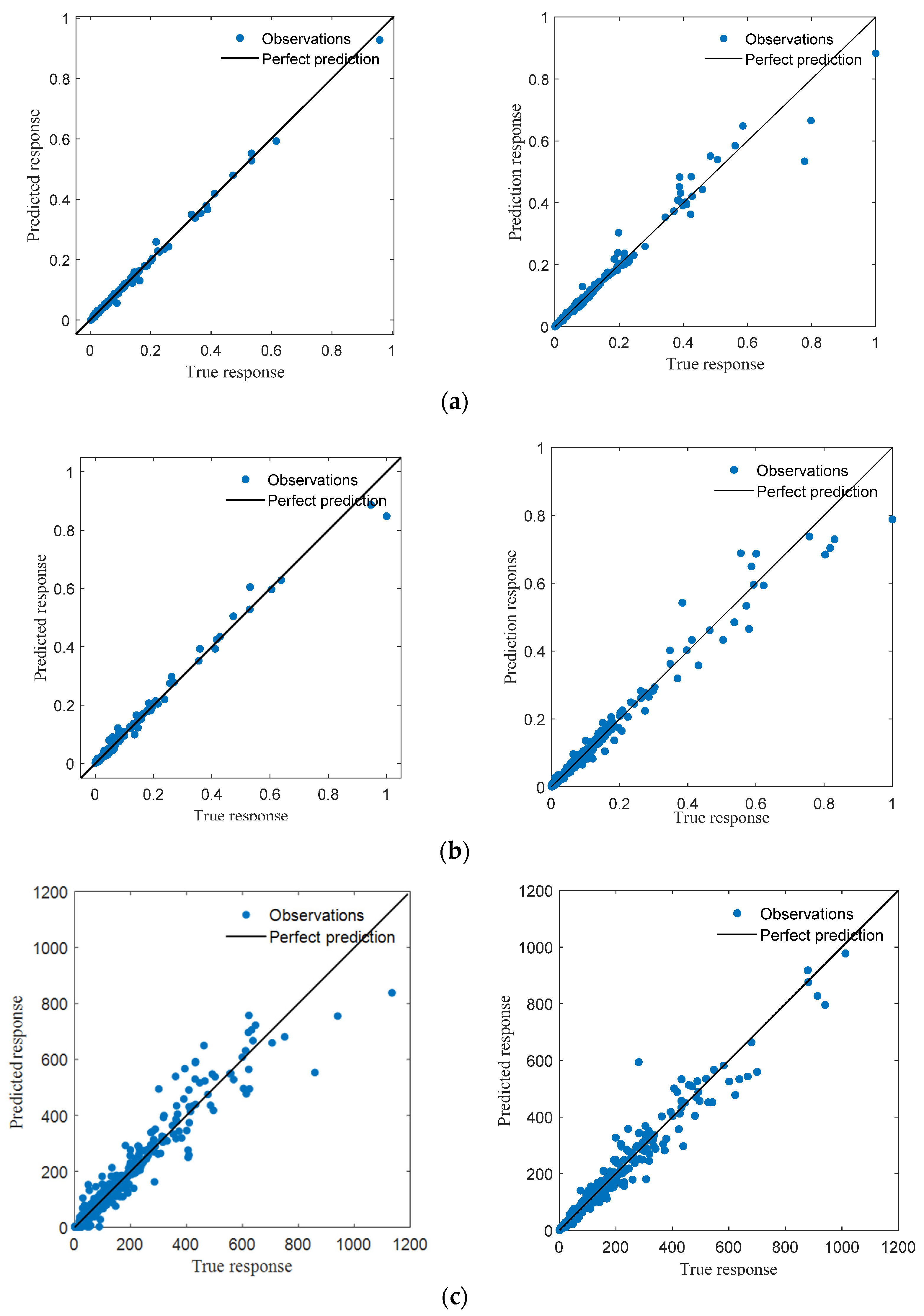
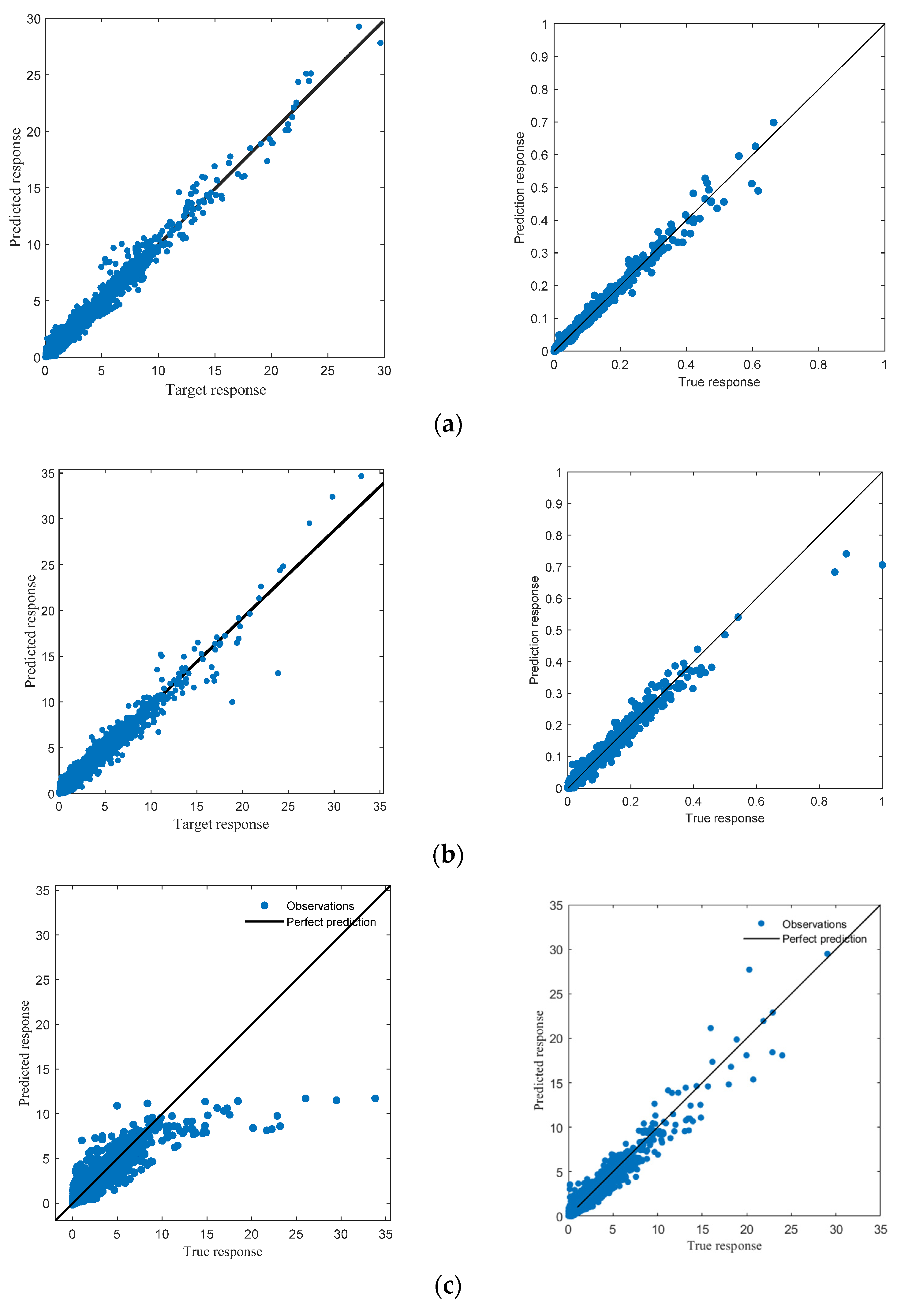
2.2. Machine Learning Model
2.3. User-Friendly Graphical Interface
3. Experimental Validation
4. Conclusions
Author Contributions
Funding

Data Availability Statement
Conflicts of Interest
References
- Rausche, F.; Beim, J. Analyzing and Interpreting Dynamic Measurements Taken During Vibratory Pile Driving; GRL Engineers Technical Report; Testing and Design Methods for Deep Foundations: Kanazawa, Japan, 2012; pp. 123–131. [Google Scholar]
- Deckner, F.; Guillemet, C.; Viking, K.; Hintze, S. Instrumentation system for ground vibration analysis during sheet pile driving. Geotech. Test. J. 2015, 38, 893–905. [Google Scholar]
- Deckner, F.; Viking, K.; Hintze, S. Wave Patterns in the Ground: Case Studies Related to Vibratory Sheet Pile Driving. Geotech. Geol. Eng. 2017, 35, 2863–2878. [Google Scholar] [CrossRef]
- Cleary, J.C.; Steward, E.J. Analysis of Ground Vibrations Induced by Pile Driving and a Comparison of Vibration Prediction Methods. DFI J. J. Deep Found. Inst. 2017, 10, 125–134. [Google Scholar]
- Bayındır, C. Effects of ground water table and ground inclination on train induced ground-borne vibrations. TWMS J. Appl. Eng. Math. 2019, 9, 735–746. [Google Scholar]
- Bayındır, C.; Namlı, B. Efficient Sensing of Von KáRmáN Vortices Using Compressive Sensing. Comput. Fluids 2021, 226, 104975. [Google Scholar] [CrossRef]
- Bayındır, C.; Alan, A.R. Efficient sensing of ground-borne vibrations induced by pile driving using compressive sampling. TWMS J. Appl. Eng. Math. 2022, 12, 24–33. [Google Scholar]
- Madheswaran, C.; Sundaravadivelu, R.; Boominathan, A.; Natarajan, K. Response of ground during pile driving. J. Inst. Eng. (India) Part CV Civ. Eng. Div. 2005, 86, 22–27. [Google Scholar]
- Attewell, P.B.; Selby, A.R.; O’Donnell, L. Estimation of ground vibration from driven piling based on statistical analyses of recorded data. Geotech. Geol. Eng. 1992, 10, 41–59. [Google Scholar] [CrossRef]
- Federal Railroad Administration (FTA). Department of Transportation Federal Transit Administration; Federal Railroad Administration: Washington, DC, USA, 2018. [Google Scholar]
- Colaço, A.; Ferreira, M.; Alves Costa, P.A. Empirical, experimental and numerical prediction of ground-borne vibrations induced by impact pile driving. Vibration 2023, 5, 80–95. [Google Scholar] [CrossRef]
- Serdaroglu, M. Nonlinear Analysis of Pile Driving and Ground Vibrations in Saturated Cohesive Soils Using the Finite Element Method. Ph.D. Thesis, University of Iowa, Iowa City, IA, USA, 2010. [Google Scholar]
- Masoumi, H.; Degrande, G.; Lombaert, G. Prediction of free field vibrations due to pile driving using a dynamic soil–structure interaction formulation. Soil Dyn. Earthq. Eng. 2007, 27, 126–143. [Google Scholar]
- Masoumi, H.; François, S.; Degrande, G. A non-linear coupled finite element–boundary element model for the prediction of vibrations due to vibratory and impact pile driving. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 245–274. [Google Scholar] [CrossRef]
- Khoubani, A.; Ahmadi, M. Numerical study of ground vibration due to impact pile driving. Proc. Inst. Civ. Eng.-Geotech. Eng. 2014, 167, 28–39. [Google Scholar] [CrossRef]
- Rooz, A.; Hamidi, A. A numerical model for continuous impact pile driving using ale adaptive mesh method. Soil Dyn. Earthq. Eng. 2019, 118, 134–143. [Google Scholar] [CrossRef]
- Singh, T.N.; Singh, V. An intelligent approach to prediction and control ground vibration in mines. Geotech. Geol. Eng. 2005, 23, 249–262. [Google Scholar] [CrossRef]
- Hung, C.; Ni, S. Using multiple neural networks to estimate the screening effect of surface waves by in-filled trenches. Comput. Geotech. 2007, 34, 397–409. [Google Scholar] [CrossRef]
- Monjezi, M.; Ghafurikalajahi, M.; Bahrami, A. Prediction of blast-induced ground vibration using artificial neural networks. Tunn. Undergr. Space Technol. 2011, 26, 46–50. [Google Scholar] [CrossRef]
- Connolly, D.; Kouroussis, G.; Giannopoulos, A.; Verlinden, O.; Woodward, P.K.; Forde, M.C. Assessment of railway vibrations using an efficient scoping model. Soil Dyn. Earthq. Eng. 2014, 58, 37–47. [Google Scholar]
- Colaço, A.; Alves Costa, P.; Mont’Alverne Parente, C.; Silva Cardoso, A. Ground-borne noise and vibrations in buildings induced by pile driving: An integrated approach. Appl. Acoust. 2021, 179, 108059. [Google Scholar]
- Abouelmaty, A.M.; Colaço, A.; Fares, A.; Ramos, A.; Alves Costa, P.A. Integrating Machine Learning Techniques for Ground Vibration Prediction in Pile Driving Activities. Comput. Geotech. 2024, 176, 106784. [Google Scholar] [CrossRef]
- Colaço, A.; Abouelmaty, A.M.; Alves Costa, P.A. Ground-borne vibrations induced by impact pile driving: Experimental assessment and mitigation measures. Earthq. Eng. Eng. Vib. 2023, 22, 105–115. [Google Scholar] [CrossRef]



| Item | Unit | Homo. Soil | Single Layer on a Half-Space | Two Layers on a Half-Space | |||
|---|---|---|---|---|---|---|---|
| Max | Min | Max | Min | Max | Min | ||
| 1st level | |||||||
| Shear wave velocity | m/s | 200 | 60 | 200 | 60 | 200 | 60 |
| Layer thickness | m | Inf. | 15 | 4 | 15 | 4 | |
| Damping ratio | - | 0.02 | 0.08 | 0.02 | 0.08 | 0.02 | 0.08 |
| Poisson’s ratio | - | 0.49 | 0.25 | 0.49 | 0.25 | 0.49 | 0.25 |
| 2nd level | |||||||
| Shear wave velocity | m/s | N/A * | 800 | 200 | 800 | 200 | |
| Layer thickness | m | N/A | Inf. | 6 | 3 | ||
| Damping ratio | - | N/A | 0.04 | 0.02 | 0.02 | 0.04 | |
| Poisson’s ratio | - | N/A | 0.49 | 0.25 | 0.49 | 0.25 | |
| 3rd level | |||||||
| Shear wave velocity | m/s | N/A | N/A | 800 | 600 | ||
| Layer thickness | m | N/A | N/A | Inf. | |||
| Damping ratio | - | N/A | N/A | 0.02 | |||
| Poisson’s ratio | - | N/A | N/A | 0.3 | |||
| Set | Unit | Case Scenario Number | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| Training | % | 40 | 50 | 55 | 60 | 70 | 45 | 40 |
| Validation | % | 30 | 20 | 20 | 30 | 20 | 25 | 25 |
| Testing | % | 30 | 30 | 25 | 20 | 10 | 30 | 35 |
| Soil Profile | Training Model | Normalized RMSE × 10−3 (R2) | |||||
|---|---|---|---|---|---|---|---|
| Training Set | Testing Set | Validation Set | |||||
| PPV | Freq. | PPV | Freq. | PPV | Freq. | ||
| Homo. soil | ANNS | 0.030 (0.996) | 3.0 (0.992) | 0.028 (0.996) | 2.7 (0.992) | 0.027 (0.993) | 2.9 (0.99) |
| XGBoost | 0.5 (0.97) | 0.007 (0.95) | 0.5 (0.97) | 0.004 (0.97) | 0.4 (0.966) | 0.004 (0.97) | |
| Single layer on a half-space | ANNS | 0.042 (0.994) | 2.8 (0.989) | 0.042 (0.994) | 2.8 (0.985) | 0.044 (0.995) | 2.9 (0.99) |
| XGBoost | 0.76 (0.98) | 0.006 (0.97) | 0.7 (0.97) | 0.007 (0.97) | 0.65 (0.97) | 0.007 (0.97) | |
| Two layers on a half-space | ANNS | 0.048 (0.93) | 4.0 (0.88) | 0.048 (0.92) | 3.8 (0.88) | 0.042 (0.93) | 3.6 (0.88) |
| XGBoost | 0.035 (0.94) | 0.017 (0.94) | 0.034 (0.95) | 0.015 (0.94) | 0.039 (0.93) | 0.013 (0.95) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abouelmaty, A.M.; Colaço, A.; Alves Costa, P. User-Friendly Tool for Expedited Ground Vibration Assessment Induced by Impact Pile Driving. Vibration 2025, 8, 17. https://doi.org/10.3390/vibration8020017
Abouelmaty AM, Colaço A, Alves Costa P. User-Friendly Tool for Expedited Ground Vibration Assessment Induced by Impact Pile Driving. Vibration. 2025; 8(2):17. https://doi.org/10.3390/vibration8020017
Chicago/Turabian StyleAbouelmaty, Ahmed M., Aires Colaço, and Pedro Alves Costa. 2025. "User-Friendly Tool for Expedited Ground Vibration Assessment Induced by Impact Pile Driving" Vibration 8, no. 2: 17. https://doi.org/10.3390/vibration8020017
APA StyleAbouelmaty, A. M., Colaço, A., & Alves Costa, P. (2025). User-Friendly Tool for Expedited Ground Vibration Assessment Induced by Impact Pile Driving. Vibration, 8(2), 17. https://doi.org/10.3390/vibration8020017









