Analytical Study of Nonlinear Flexural Vibration of a Beam with Geometric, Material and Combined Nonlinearities

Abstract

This article explores the nonlinear vibration of beams with different types of nonlinearities. The beam vibration was modeled using Hamilton’s principle, and the equation of motion was solved using method of multiple time scales. Three models were developed assuming (a) geometric nonlinearity, (b) material nonlinearity and (c) combined geometric and material nonlinearity. The material nonlinearity also included both third and fourth nonlinear elasticity terms. The frequency response equation of these models were further evaluated quantitatively and qualitatively. The models capture the hardening effect, i.e., increase in resonant frequency as a function of forcing amplitude for geometric nonlinearity, and the softening effect, i.e., decrease in resonant frequency for material nonlinearity. The model is applied on the first three bending modes of the cantilever beam. The effect of the fourth-order material nonlinearity was smaller compared to the third-order term in the first mode, whereas it is significantly larger in second and third mode. The combined nonlinearity models shows a discontinuous frequency shift, which was resolved by utilizing a set of transition assumptions. This results in a smooth transition between the material and geometric zones in amplitude. These parametric models allow us to fine tune the nonlinear response of the system by changing the physical properties such as geometry, linear and nonlinear elastic properties.

1. Introduction

The vibration of beams has been a problem of interest in several disciplines. A consolidated theory of beam vibration was given by Lord Rayleigh in their two-volume treatise on acoustics [1,2]. There are several modes of beam vibration such as longitudinal, torsional, flexural and coupled modes depending the boundary condition. Isolating and understanding the vibration modes has been very important in several disciplines across physics and engineering applications. Understanding the nonlinear behavior of structures is significant for a variety of different applications including nonlinear resonant ultrasound spectroscopy [3], SHM, defect detection [4] and vibrational analysis where amplitude dependence is of interest [5]. Traditional analysis includes small amplitude vibrations, which satisfy the linear assumptions in the governing equations, i.e., linearity in strain-displacement, and stress–strain relationships. However, there are several modern engineering problems where the vibration amplitudes are much larger resulting in nonlinear vibration. There are several bodies of work which have explored nonlinear beam vibration using different types of nonlinearities [6,7,8,9,10]. Modeling vibration of a beam requires defining the constitutive equations such as strain, strain displacement and the stress–strain relationship.

There are four common sources of nonlinearity in a vibrating beam: (1) geometric nonlinearity, i.e., nonlinearity in the strain-displacement relationship, (2) material nonlinearity, i.e., nonlinearity in the stress–strain relationship, (3) combined geometric and material nonlinearity, and (4) physical nonlinearity arising from cracks and defects in the solid. Sources 1 through 3 are termed as classical sources of nonlinearity, while the nonlinearity arising from cracks and defects is termed as nonclassical nonlinearity [11,12,13,14,15]. Of the classical sources, there is abundant literature on geometric nonlinearity of beams since this applies to cases of thin beams which can undergo large deformations, such as thin composite beams, microelectromechanical systems (MEMS), etc. [5,9,16,17,18,19,20,21,22,23,24,25,26,27,28]. This geometric nonlinearity has also been studied using numerical methods [29,30]. Similarly, material nonlinearity has also been studied in great detail for highly nonlinear materials such as rubber [31,32]. Materials which exhibit weak nonlinearity relative to rubber have also been studied using a Taylor series expansion of strain energy density [33,34]. Using a continuum approximation, several researchers have presented nonlinear elastic models including Birch [35], Murnaghan [36], Seeger and Buck, Thurston [37], Brugger [38], Wallace [39] and several others. Nonlinearity in beam vibration often leads to a shift in resonant frequency as forcing amplitude changes. This shift, observed as softening due to material nonlinearity and hardening due to geometric nonlinearity, has been extensively investigated in the existing literature [5,16,35,37]. While certain studies have examined the combined effects on composite beams featuring a thin PZT layer [40] attached to a solid metallic structure, wherein softening nonlinearity arises from the elastic constant of piezoelectric material rather than the higher-order material nonlinearity of the base solid, there remains a notable gap in the literature concerning nonlinear beam vibration incorporating both higher-order material and geometric nonlinearities.

Several of the existing studies [41] use mathematical formulations which can simulate a physical system. Typically, these models are further fitted to experimental data to obtain a set of fitting coefficients which are used to define the system’s response. From an engineering and physical point of view, parameterization of these models is very important, since it can lead to the development of inverse problems which can further be used to back-calculate important physical properties and not just extract coefficients. While a mathematical model helps in the generalization of the problem, the parameterization helps in direct application to engineering structures. Therefore, the objective of the present work is to develop closed-form solutions for nonlinear beam vibration using a first principle’s approach starting with the constitutive equations. This allows one to frame a parametric model where the coefficients of the resulting equations can be related to physical parameters such as stiffness, density and beam dimensions. The models developed here will use coefficients which can be calculated, and the unknown coefficients can be directly inverted using experimental results in future work. Previously, the authors had developed models based on geometric nonlinearity [34] and second-order material nonlinearity [3] and validated with experiments. The present work extends this to a higher-order material nonlinearity model including elastic constants up to fourth order and a combined geometric and material nonlinearity model, both of which have not been explored in the literature. The material nonlinearity has been studied in detail using both third- and fourth-order elastic constants derived from the strain energy density formulation. The effect of the nonlinear contributions towards the nonlinear response of the beam was observed for the first three bending modes. For the sake of completeness and coherency, all four models have been consolidated in the present article. Previous research on dynamics with material nonlinearity investigates highly nonlinear materials like rubber which can have very complicated stress–strain relationships. However, materials with weak nonlinearity such as metals, plastics, etc., are mostly modeled using a Taylor series approximation of the strain density function. The present study will explore classical nonlinear sources and omit the non-classical case partly due to its complexity and since it has been dealt with elsewhere [42,43]. However, the results from the classical model highlight the necessity to develop a deeper understanding of the non-classical models.

This article is structured into theoretical models of nonlinear beam vibration, results and the discussion. The geometric, material nonlinearity and combined nonlinearity models are presented in model sections. The frequency response equations capture the nonlinear shift of the resonant frequency as a function of the forcing amplitude. Nonlinearity of a cantilever beam is investigated using the first three bending modes. The models capture the well-known softening and hardening nonlinearity that have been reported in the literature. Additionally, the combined nonlinearity was captured using two models, which show a continuous and discontinuous transition between the material and geometric nonlinear zones.

2. Models

2.1. Geometric Nonlinearity

The present model follows the classical laminated plate theory (CLPT). According to the Kirchhoff hypothesis, the displacements are given as follows:

$$\begin{array}{c}w(x,y,z,t)=w_0(x,y,t)\end{array}$$

(1)

where t is the time, and $u_0$ and $w_0$ are the in-plane and transverse mid-plane displacements. The von Kármán-type nonlinear strain-displacement relationship is given by

$${\epsilon }_{xx}=\frac{\partial u_0}{\partial x}+\frac{1}{2}{\left(\frac{\partial w_0}{\partial x}\right)}^2-z\frac{{\partial }^2{w}_0}{\partial x^2}$$

(2)

Assuming the solid to be viscoelastic, a linear elastic stress–strain relationship together with the Kelvin–Voigt damping term for the viscoelastic contribution is given by

$$\sigma =E\epsilon +\eta \dot{\epsilon }$$

(3)

where E is the Young’s modulus which can be written as the stiffness matrix, $\eta$ is the Kelvin–Voigt damping term which controls the strain rate. Equation (3) can be written as follows:

$$\sigma ={\sigma }_e+{\sigma }_v$$

(4)

where ${\sigma }_e$ is the elastic component of the stress–strain response, and ${\sigma }_v$ is the viscoelastic component.

By using the extended Hamilton’s principle,

$$\delta {\int }_0^T(K-\mathrm{\Pi }+W)dt=0$$

(5)

where K is the kinetic energy, $\mathrm{\Pi }$ is the potential energy, and W is the work carried out by non-conservative forces. The potential energy can be rewritten as $\mathrm{\Pi }=U+V$, where U is the elastic strain energy, and V is the potential energy change from conservative external forces. Writing out each term separately,

$$\begin{array}{c}\delta U={\int \int \int }_v\left({\sigma }_e\delta {ϵ}_{xx}\right)dzdxdy\end{array}$$

(6a)

$$\begin{array}{c}\delta V=-{\int \int \int }_v\left(F\delta w(x,y)\right)dzdxdy\end{array}$$

(6b)

$$\begin{array}{c}\delta K={\int \int \int }_v{\rho }_0[\left({\dot{u}}_0-z\frac{\partial {\dot{w}}_0)}{\partial x}\right)\left(\delta {\dot{u}}_0-z\frac{\partial \delta {\dot{w}}_0)}{\partial x}\right)+{\dot{w}}_0\delta {\dot{w}}_0]dzdxdy\end{array}$$

(6c)

$$\begin{array}{c}\partial W=-{\int \int \int }_v\left({\sigma }_v\delta {ϵ}_{xx}\right)dzdxdy\end{array}$$

(6d)

$${\int }_0^T{\int \int \int }_v({\sigma }_e+{\sigma }_v)\delta {ϵ}_{xx}-\left(F\delta w_0\right)-{\rho }_0\left[\left(\dot{u_0}-z\frac{\partial \dot{w_0}}{\partial x}\right)\left(\delta \dot{u_0}-z\frac{\partial \delta \dot{w_0}}{\partial x}\right)+\dot{w_0}\delta \dot{w_0}\right]dzdxdydt=0$$

(7)

Using Equation (4), the elastic and viscous stress can be rewritten, and Equation (7) can be solved for a 1D cantilever beam as shown in Figure 1 to obtain the following equations of motion:

$$(\partial N_{xx})/\partial x=I_0\frac{{\partial }^2{u}_0}{\partial t^2}$$

(8)

$$\frac{\partial }{\partial }\left(N_{xx}\frac{\partial w_0}{\partial x}\right)+\frac{{\partial }^2{M}_{xx}}{\partial x^2}+F=I_0\frac{{\partial }^2{w}_0}{\partial t^2}$$

(9)

where $N_{xx}$ and $M_{xx}$ are the force and moment resultants, and $I_0$ is the mass moment of inertia. These are given by

$$N_{xx}={\int }_{-h⁄2}^{h⁄2}{\sigma }_{xx}dz$$

(10)

$$M_{xx}={\int }_{-h⁄2}^{h⁄2}{\sigma }_{xx}zdz$$

(11)

$$I{M}_{xx}={\int }_{-h⁄2}^{h⁄2}{\rho }_{0}zdz$$

(12)

Figure 1. Schematic of 1D cantilever beam with nonlinear flexural vibrations.

Rewriting the nonlinear strain relationship in simpler notations,

$${ϵ}_{xx}=u_0^{\prime }+\frac{1}{2}{\left(w_0^{\prime }\right)}^2-w_0^{″}$$

(13)

where the term $u_0^{\prime }$ corresponds to a partial differential of $u_0$ with respect to x.

Substituting Equations (13) and (3) into (10) and (11) gives

$$N_{xx}=A\left(u_0^{\prime }+\frac{1}{2}{\left(w_0^{\prime }\right)}^2\right)-B{w}_0^{″}+{\mu }_1\left({\dot{u}}_0^{\prime }+w_0^{\prime }{\dot{w_0}}^{″}\right)-{\mu }_2{\dot{w_0}}^{″}$$

(14)

$$M_{xx}=B\left(u_0^{\prime }+\frac{1}{2}{\left(w_0^{\prime }\right)}^2\right)-D{w}_0^{″}+{\mu }_2\left({\dot{u_0}}^{\prime }+w_0^{\prime }{\dot{w_0}}^{″}\right)-{\mu }_3{\dot{w_0}}^{″}$$

(15)

where

$$(A,B,D)={\int }_{-h/2}^{h/2}{C}_{11}(1,z,z^2)dz$$

(16)

$$({\mu }_1,{\mu }_2,{\mu }_3)={\int }_{-h⁄2}^{h⁄2}\eta (1,z,z^2)dz$$

(17)

For the nonlinear vibration analysis, the transverse displacement is expressed as

$$w(x,t)=q\left(t\right)p\left(x\right)$$

(18)

where $q\left(t\right)$ corresponds to the temporal function, and $p\left(x\right)$ corresponds to the spatial function or linear vibration mode shape. Substituting Equation (18) into force and moment resultant equations, i.e., Equations (16) and (17) and re-substituting those into the equation of motion, Equation (9), we can obtain the following nonlinear equation:

$$\ddot{q}+\left({\omega }^2\right)q+\left(\gamma \right)q^3+\left(\delta \right)q^{2}q+\left(\alpha \right)\dot{q}=F$$

(19)

where

$$\begin{array}{c}{\omega }^2=\frac{D}{\lambda }{\int }_0^{L}p{p}^{IV}dx\end{array}$$

(20)

$$\begin{array}{c}\gamma =\frac{A}{2\lambda }{\int }_0^{L}p{p}^{″}dx{\int }_0^L{\left(p^{\prime }\right)}^{2}dx\end{array}$$

(21)

$$\begin{array}{c}\delta =\frac{\mu }{2\lambda }{\int }_0^{L}p{p}^{″}dx{\int }_0^L{\left(p^{\prime }\right)}^{2}dx\end{array}$$

(22)

$$\begin{array}{c}\alpha =\frac{{\mu }^{″}}{\lambda }{\int }_0^{L}p{p}^{IV}dx\end{array}$$

(23)

$$\begin{array}{c}\lambda =I_0{\int }_0^L\left(p^2\right)dx\end{array}$$

(24)

Let us restrict to the case of cantilever beam vibration; hence, the boundary conditions are given by

$$w\left(0\right),w^{\prime }\left(0\right),w^{″}\left(L\right),w^{‴}\left(L\right),=0$$

(25)

Equation (21) represents the linear frequency, Equation (22) is the nonlinear parameter arising from geometrical nonlinearity, and Equations (23) and (24) represent damping terms arising from the Kelvin–Voigt model. The nonlinear equation can be solved by various perturbation techniques, but in this work, the method of multiple time scales (MTS) [44] has been used. Two time scales are introduced which give rise to

$$q(t,ϵ)=q_0(T_0,T_1)+ϵq_1(T_0,T_1)+\dots$$

(26)

where $T_0=t$ and $T_1=ϵt$. This leads to the transformation of the derivatives of the time scales

$$\frac{d}{dt}=D_0+ϵD_1;\frac{d^2}{d{t}^2}=D_0^2+2ϵD_0{D}_1+\dots$$

(27)

This approach assumes small displacements along with small nonlinearity. It also assumes that the nonlinearity, excitation and damping are all on the same scale $ϵ$. Hence, with external harmonic excitation, the nonlinear equation is given by

$$\ddot{q}+\left({\omega }^2\right)q+ϵ\left(\gamma \right)q^3+ϵ\left(\delta \right)q^{2}q+ϵ\left(\alpha \right)\dot{q}=ϵFsin\left(\mathrm{\Omega }t\right)$$

(28)

Substituting Equations (26) and (27) into (28) and separating the coefficients of ${ϵ}_0$ and ${ϵ}_1$ terms,

$$\begin{array}{c}{D}_0^2{q}_0+{\omega }^2{q}_0=0\end{array}$$

(29)

$$\begin{array}{c}2D_0{D}_1{q}_0+D_0^2{q}_1+{\omega }^2{q}_1+\gamma q_0^3+D_0\delta q_0^3+\alpha q_0{D}_0=Fsin\left(\mathrm{\Omega }t\right)\end{array}$$

(30)

The general solution of Equation (30) is given by

$$q_0=\left(A\left(T_1\right)e^{\left(i\beta T_0\right)}+\overline{A}\left(T_1\right)e^{(-i\beta T_0)}\right)$$

(31)

The overall transverse displacement of the beam is given by Equations (31) and (18), subjected to the boundary conditions, Equation (25). This gives the mode shape of the beam:

$$p\left(x\right)=\frac{1}{\sqrt{L}}\left\{cosh\left(\frac{r_{n}x}{L}\right)-cos\left(\frac{r_{n}x}{L}\right)+R_i\left(sinh\left(\frac{r_{n}x}{L}\right)-sin\left(\frac{r_{n}x}{L}\right)\right)\right\}$$

(32)

where $r_n$ is the nth root of the characteristic equation $(1+cos(r\left)cosh\right(r)=0$), and $R_i$ is given by

$$R_i=\frac{cos\left(r_n\right)+cosh\left(r_n\right)}{sin\left(r_n\right)+sinh\left(r_n\right)}$$

(33)

Substituting Equation (31) into (30) and isolating the secular terms $\left(e^{\left(i\beta T_0\right)}\right)$ which must vanish leads us to

$$2A^{\prime }\left(i\beta \right)+3A^2\overline{A}+3A^2\overline{A}-\delta \left(i\beta \right)+\alpha A\left(i\beta \right)=F/2e^{\left(i\omega T_0\right)}$$

(34)

We introduce a detuning parameter “$\tau$” defined as follows:

$$\mathrm{\Omega }=\omega +ϵ\tau$$

(35)

We express A in polar form and introduce a new parameter $\phi$ as follows:

$$\phi =\tau T_1-\omega \varphi$$

(36)

$$A=\frac{1}{2}a{e}^{i\varphi }$$

(37)

Substituting Equations (35)–(37) into (34) and separating the real and imaginary parts,

$$a^{\prime }=\frac{1}{2\omega }Fsin\left(\phi \right)-\frac{3}{8}{a}^3\delta -\frac{1}{2}\alpha a$$

(38)

$$a{\phi }^{\prime }=\frac{1}{2\omega }Fcos\left(\phi \right)-\frac{3a^3}{8\omega }\gamma +a\tau$$

(39)

At steady state, the terms $a^{\prime }$ and $a{\phi }^{\prime }$ will vanish. Hence by squaring and adding Equations (38) and (39), the frequency response equation can be obtained as follows:

$${\left(\frac{3}{8}{a}^3\delta +\frac{1}{2}\alpha a\right)}^2+{\left(a\tau -\frac{3a^3}{8\omega }\gamma \right)}^2=\frac{F^2}{4{\omega }^2}$$

(40)

2.2. Material Nonlinearity

The nonlinearity that manifests in the stress–strain relationship of a material is termed as material nonlinearity. Weakly nonlinear materials have been traditionally described in the area of condensed matter physics using a Taylor’s series expansion of the strain energy density. This results in a polynomial expansion of the stress–strain relationship with the higher -order nonlinear terms controlling the nonlinearity. The present study ia limited to third-order and fourth-order strain terms which have been previously described from the first-principles approach as given below:

$${\sigma }_{ij}=C_{ijkl}{\epsilon }_{kl}+M_{ijklmn}{\epsilon }_{kl}{\epsilon }_{mn}+K_{ijklmnpq}{\epsilon }_{kl}{\epsilon }_{mn}{\epsilon }_{pq}...$$

(41)

2.2.1. Third-Order Elasticity

The displacements of the beam can once again be defined according to the Kirchhoff hypothesis:

$$\begin{array}{c}u(x,y,z,t)=u_0(x,y,t)-z\frac{\partial w_0}{\partial x}\end{array}$$

(42a)

$$\begin{array}{c}w(x,y,z,t)=w_0(x,y,t)\end{array}$$

(42b)

A linear strain-displacement relationship can be described by the von Kármán strains:

$${\epsilon }_{xx}=\frac{\partial u_0}{\partial x}-z\frac{{\partial }^2{w}_0}{\partial x^2}$$

(43)

This form of strain-displacement relationship is a reduction in the nonlinear von Kármán strains, with the nonlinear contribution being neglected. The only other equation that has to be defined is the stress–strain relationship. A formulation that is well described in the literature is given by

$${\sigma }_{ij}=C_{ijkl}{\epsilon }_{kl}+M_{ijklmn}{\epsilon }_{kl}{\epsilon }_{mn}$$

(44)

where $C_{ijkl}$ is the linear stiffness of the material, otherwise known as the second-order elastic constants (SOEC), and $M_{ijklmn}$ is given by

$$M_{ijklmn}=C_{ijklmn}+C_{ijln}{\delta }_{km}+C_{jnkl}{\delta }_{im}+C_{j}lmn{\delta }_{ik}$$

(45)

where $C_{ijkl}$ is the third-order elastic constants. Using Voigt notation, these constants can be rewritten as $C_{ijkl}\to C_{ij}$ and $C_{ijklmn}\to C_{ijk}$. Since this is a one-dimensional beam model, the constants can be written as

$$M=3C_{11}+C_{111}$$

(46)

Using Hamilton’s principle as shown earlier, the equations of motions can be obtained. The in-plane force and moment resultants can now be defined as

$$N_{xx}=A{u}_0^{\prime }+B{w}_0^{″}+M_1{\left(u_0^{\prime }\right)}^2+M_3{\left(w_0^{″}\right)}^2-2M_2{u}_0^{\prime }{w}_0^{″}$$

(47)

$$M_{xx}=B{u}_0^{\prime }+D{w}_0^{″}+M_2{\left(u_0^{\prime }\right)}^2+M_4{\left(w_0^{″}\right)}^2-2M_3{u}_0^{\prime }{w}_0^{″}$$

(48)

where,

$$(M_1,M_2,M_3,M_4)={\int }_{-h⁄2}^{h⁄2}M(1,z,z^2,z^3)dz$$

(49)

Expressing the transverse displacement as two separate variables as before, and introducing a damping term ${\alpha }^{\prime }$ for the purpose of completeness, the equation of motion can be written as

$$\ddot{q}+\left({\omega }^2\right)q+\left(\mathrm{\Gamma }\right)q^3+(\Delta )q^{2}q+\left(\alpha \right)\dot{q}=F$$

(50)

where

$$\begin{array}{c}\mathrm{\Gamma }=\frac{M_3}{\lambda }{\int }_0^{L}p{\left(p^{″}\right)}^{3}dx\end{array}$$

(51)

$$\begin{array}{c}\Delta =\frac{M_3}{\lambda }{\int }_0^{L}p\left(p^{″}{p}^{IV}dx+p^{‴}\right)-\frac{B}{\lambda }{\int }_0^L{\left(p^{″}\right)}^{2}dx\end{array}$$

(52)

Solving Equation (50) using MTS as before, the frequency response equation can be obtained as

$${\left(\frac{a\alpha }{2}\right)}^2+{\left(a\tau -\frac{3a^3}{8\omega }\mathrm{\Gamma }\right)}^2=\frac{F^2}{4{\omega }^2}$$

(53)

2.2.2. Fourth-Order Elasticity

The stress–strain relationship defined in Equation (44) is expanded to include the fourth-order elastic constant [45]:

$${\sigma }_{ij}=C_{ijkl}{\epsilon }_{kl}+M_{ijklmn}{\epsilon }_{kl}{\epsilon }_{mn}+K_{ijklmnpq}{\epsilon }_{kl}{\epsilon }_{mn}{\epsilon }_{pq}$$

(54)

where $C_{ijkl}$ is the linear stiffness of the material, otherwise known as the second-order elastic constants (SOECs), $M_{ijklmn}$ is a combination of second- and third-order elastic constants, and $K_{ijklmnpq}$ is a combination of second-, third- and fourth-order elastic constants. For a one-dimensional beam model, the third-order constant can be written as

The fourth-order constant is given by

$$K=\frac{3}{2}{C}_{11}+3C_{111}+\frac{1}{2}{C}_{1111}$$

(55)

Using Hamilton’s principle as shown in Section 2.1, the equations of motions can be obtained. The in-plane force and moment resultants can now be defined as follows:

$$\begin{array}{c}{N}_{xx}=B{w}_0^{″}+M_3{\left(w_0^{″}\right)}^2-K_1{\left(w_0^{″}\right)}^3\end{array}$$

(56)

$$\begin{array}{c}{M}_{xx}=D{w}_0^{″}+M_4{\left(w_0^{″}\right)}^2-K_2{\left(w_0^{″}\right)}^3\end{array}$$

(57)

where

$$(K_1,K_2)={\int }_{-h⁄2}^{h⁄2}K(z^3,z^4)dz$$

(58)

Expressing the transverse displacement as two separate variables as before, and introducing a damping term ${\alpha }^{\prime }$ for the purpose of completeness, the equation of motion can be written as

$$\ddot{q}+\left({\omega }^2\right)q+\left(\mathrm{\Lambda }\right)q^2+\left(\mathrm{\Theta }\right)q^3+\left(\mathrm{\Phi }\right)q^{4}q+\left(\alpha \right)\dot{q}=F$$

(59)

where

$$\begin{array}{c}\mathrm{\Lambda }=\frac{M_4}{\lambda }{\int }_0^{L}p\left(p^{″}{p}^{IV}+{\left(p^{‴}\right)}^2\right)dx+\frac{B}{\lambda }{\int }_0^L{\left(p^{‴}\right)}^{2}dx\end{array}$$

(60)

$$\begin{array}{c}\mathrm{\Theta }=\frac{M_4}{\lambda }{\int }_0^{L}p{\left(p^{″}\right)}^{3}dx+\frac{K_2}{\lambda }{\int }_0^L\left(6p{p}^{″}{\left(p^{‴}\right)}^2+3{\left(p^{″}\right)}^2{p}^{IV}\right)dx\end{array}$$

(61)

$$\begin{array}{c}\mathrm{\Phi }=\frac{K_1}{\lambda }{\int }_0^{L}p{\left(p^{″}\right)}^{4}dx\end{array}$$

(62)

Solving Equation (59) using MTS, the frequency response equation can be obtained as follows:

$${\left(\frac{a\alpha }{2}\right)}^2+{\left(a\tau -\frac{3a^3}{8\omega }\mathrm{\Theta }\right)}^2=\frac{F^2}{4{\omega }^2}$$

(63)

2.3. Combined Geometric and Material Nonlinearity

To simulate the combined effect of geometric and material nonlinearity, a nonlinear strain-displacement relationship described by the von Kármán strains is used along with third-order stress–strain relationship. The strain-displacement relationship is given by

$$\begin{array}{c}{N}_{xx}=\frac{A}{2}{\left(w_0^{\prime }\right)}^2-B{w}_0^{″}+\frac{M_1}{4}{\left(w_0^{\prime }\right)}^4+M_3{\left(w_0^{″}\right)}^2-M_2{\left(w_0^{\prime }\right)}^2{w}_0^{″}\end{array}$$

(64)

$$\begin{array}{c}{M}_{xx}=\frac{B}{2}{\left(w_0^{\prime }\right)}^2-D{w}_0^{″}+\frac{M_2}{4}{\left(w_0^{\prime }\right)}^4+M_4{\left(w_0^{″}\right)}^2-M_3{\left(w_0^{\prime }\right)}^2{w}_0^{″}\end{array}$$

(65)

Expressing the transverse displacement as two separate variables as before, and introducing a damping term ${\alpha }^{\prime }$ for the purpose of completeness, the equation of motion can be written as

$$\ddot{q}+\left({\omega }^2\right)q+\left(\mathrm{{\rm Y}}\right)q^2+\left(\mathrm{\Xi }\right)q^3+\left(\mathrm{\Psi }\right)q^4+\left(\chi \right)q^5+\left(\alpha \right)\dot{q}=F$$

(66)

where

$$\begin{array}{c}{\omega }^2=\frac{D}{\lambda }{\int }_0^{L}p{p}^{IV}dx\end{array}$$

(67)

$$\begin{array}{c}\mathrm{{\rm Y}}=\frac{B}{\lambda }{\int }_0^{L}p{\left(p^{″}\right)}^{2}dx-\frac{B}{\lambda }{\int }_0^{L}p\left(p^{\prime }{p}^{‴}+{\left(p^{″}\right)}^2\right)dx-\frac{M_4}{\lambda }{\int }_0^{L}p{p}^{IV}dx\end{array}$$

(68)

$$\begin{array}{c}\mathrm{\Xi }=\underset{{\mathrm{\Xi }}_{Material}}{\underbrace{\frac{M_3}{\lambda }{\int }_0^{L}p{\left(p^{″}\right)}^3}}-\underset{{\mathrm{\Xi }}_{Coupled}}{\underbrace{\frac{M_3}{\lambda }{\int }_0^{L}p\left(2{\left(p^{″}\right)}^3+{\left(p^{\prime }\right)}^2{p}^{IV}+6p^{\prime }{p}^{″}{p}^{‴}\right)dx}}\hfill \\ \hfill +\underset{{\mathrm{\Xi }}_{Geometric}}{\underbrace{\frac{A}{2\lambda }{\int }_0^{L}p{p}^{″}dx{\int }_0^L{\left(p^{\prime }\right)}^{2}dx}}\end{array}$$

(69)

$$\begin{array}{c}\mathrm{\Psi }=\frac{M_2}{\lambda }{\int }_0^{L}3p{\left(p^{″}\right)}^2{p}^{\prime }+p{p}^{‴}{\left(p^{\prime }\right)}^2+p{\left(p^{\prime }\right)}^2{\left(p^{″}\right)}^{2}dx\end{array}$$

(70)

$$\begin{array}{c}\chi =\frac{M_1}{4\lambda }{\int }_0^{L}p{\left(p^{\prime }\right)}^4{p}^{″}dx\end{array}$$

(71)

Solving Equation (66) using MTS, the frequency response equation can be obtained as

$${\left(\frac{a\alpha }{2}\right)}^2+{\left(a\tau -\frac{3a^3}{8\omega }\mathrm{\Xi }+\frac{5a^5}{16\omega }\chi \right)}^2=\frac{F^2}{4{\omega }^2}$$

(72)

3. Results and Discussions

3.1. Model Evaluation

The developed models allow us to develop the frequency vs. magnitude resonance curves. However, for a more quantitative comparison between the models, the nonlinear frequency shift, i.e., the frequency at peak amplitude, was calculated as a function of the applied force. The flowchart shown in Figure 2 outlines the algorithm to calculate the change in frequency shift with the applied force. By incorporating respective boundary conditions and nonlinearities, we established the relationships between the beam amplitude (a), applied force (F) and detuning parameter ($\tau$) as Equations (40), (53), (63) and (72) using the developed models. Here, the detuning parameter $\tau$ is defined as $f-\omega$, where f represents the frequency of the applied force. Subsequently, the applied force and detuning parameter were initialized as $F_{min}$ and ${\tau }_{min}$. For a given set of geometric and material properties, the vibration amplitude (a) of the beam was solved for all applied force and detuning parameters within the ranges ($F_{min},F_{max}$) and (${\tau }_{min},{\tau }_{max}$) by incrementing $F^{+},{\tau }^{+}$. The output is a set of frequency-response curves as shown in Figure 2. For each frequency-response curve applied force, the frequency corresponding to the maximum amplitude was identified, representing the resonant frequency of the beam under that force. Finally, the nonlinear frequency shift, defined as the difference between the resonant and natural frequencies, was plotted against the applied force. The developed models were evaluated for a cantilever beam with specified geometric and material properties, detailed in Table 1, considering the first three bending modes of the beam by substituting $r_n=$ 1.875, 4.694, and 7.855 in Equation (33). The subsequent sections illustrate the impact of the applied force on the nonlinear frequency shift resulting from various nonlinearities. In the case of a linear beam, where nonlinearity is absent, there is no frequency shift in the resonant frequency. Therefore, the resonant frequency becomes independent of the forcing amplitude.

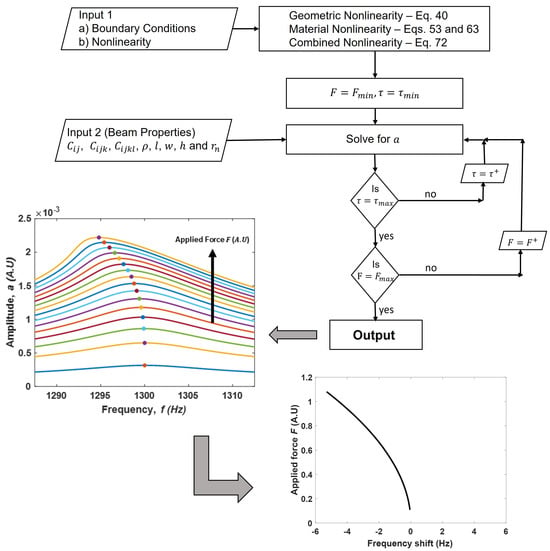
Figure 2. Flowchart to calculate the nonlinear resonant frequency shift as a function of applied force for a vibrating beam.

Table 1. Descriptions and values of parameters used in the model. The values for parameters correspond to iron.

Symbol	Description	Value
${\rho }_0$	Material Density	$7850\mathrm{kg}{\mathrm{m}}^{-3}$
$C_{11}$ (E)	Second Order Elastic Constant	$205\mathrm{GPa}$
M	Third Order Elastic Constant	$-2425\mathrm{GPa}$
K	Fourth Order Elastic Constant	$1530\mathrm{GPa}$
G	Shear Modulus	$80\mathrm{GPa}$
$\eta$	Damping Coefficient	$0.0007\mathrm{Pa}\mathrm{s}$
L	Length of beam	$76.2\mathrm{mm}$
W	Width of beam	$12.7\mathrm{mm}$
H	Thickness of beam	$7.29\mathrm{mm}$

3.2. Geometric Nonlinearity

Equation (40) provides the relationship between the frequency shift ($\tau$) and applied force (F). In this case, the coefficient of cubic nonlinearity in Equation (19) is positive, resulting in a rightward shift in resonant frequency for all the three modes as shown in Figure 3. This hardening or stiffening effect is consistent with previously reported models, numerical techniques and experiments in the literature [5,27,30,40].

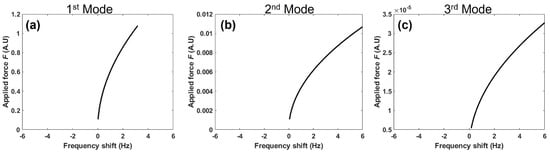
Figure 3. Nonlinear shift in resonant frequency with change in applied force for a beam with only geometric nonlinearity observed in (a) 1st mode, (b) 2nd mode and (c) 3rd mode.

3.3. Material Nonlinearity

The impact of third- and fourth-order material nonlinearity on the shift in resonant frequency can be visualized by using Equations (53) and (63) in Figure 4, demonstrating the phenomenon across the first three bending modes. The material nonlinearity here results in a leftward shift in resonant frequency which is consistent with the existing literature [3,14,34,46]. As shown in Table 2, the cubic nonlinearity coefficient in both cases are negative for all the three modes, but the difference between coefficients for two cases are significantly higher in the second and third mode. The effect of this difference is clearly shown in terms of the frequency shift in Figure 4. Interestingly, for the first mode (Figure 4a), the effect of fourth-order material constant is nearly insignificant, but for the second and third modes, the addition of fourth-order material nonlinearity showed a significant difference in the frequency shift as shown in Figure 4b,c. As the third- and fourth-order values exhibit opposite signs, the fourth-order nonlinearity counteracts the softening effect induced by the third-order material nonlinearity. This phenomenon intensifies in higher-order modes, as shown in Figure 4.

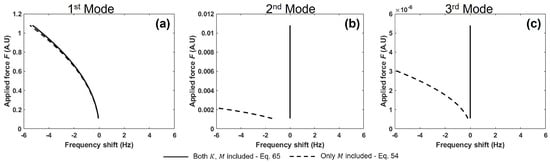
Figure 4. Change in resonant frequency shift with change in applied force in the beam with third-order ($K=0$) and fourth−order ($K\ne 0$) material nonlinearity observed in (a) 1st mode, (b) 2nd mode and (c) 3rd mode.

Table 2. Coefficients of cubic nonlinearity.

Parameters	Nonlinearity	1st Mode	2nd Mode	3rd Mode
$\gamma$	Geometric	$1.59\times {10}^{21}$	$1.21\times {10}^{27}$	$1.01\times {10}^{33}$
$\mathrm{\Gamma }$	Third order material	$-2.76\times {10}^{21}$	$-2.76\times {10}^{28}$	$-1.15\times {10}^{35}$
$\mathrm{\Theta }$	Fourth order material	$-2.65\times {10}^{21}$	$-1.33\times {10}^{26}$	$-9.41\times {10}^{31}$
${\mathrm{\Xi }}_{Material}$	Combined (material)	$-2.76\times {10}^{21}$	_	_
${\mathrm{\Xi }}_{Geometric}$	Combined (geometric)	$1.59\times {10}^{21}$	_	_
${\mathrm{\Xi }}_{Coupled}$	Combined (coupled)	$1.90\times {10}^{22}$	_	_
$\chi$	Combined	$1.53\times {10}^{22}$	_	_

3.4. Combined Nonlinearity

Geometric nonlinearity requires large amplitude vibrations. Therefore, with the increased amplitude of vibration, we can hypothesize that the material nonlinearity will be dominant at the low amplitude range, and it will transition into geometric nonlinearity, when the deformations are sufficiently large. From Equation (69), we can see that the material, geometric and a coupled term determines the eventual nonlinear frequency shift. The first model assumes that beam displacement a and forcing function F are related to each other through some function. This assumption allows us to define regions where the three terms in the coupled equation will manifest.

Model 1: We modify Equation (69) as

$$\begin{array}{cc}\hfill \mathrm{\Xi }& =A\left({\mathrm{\Xi }}_{Material}\right)+B\left({\mathrm{\Xi }}_{Geometric}\right)+C\left({\mathrm{\Xi }}_{Coupled}\right)\hfill \\ \hfill A& =1,B=0,C=0if-1<H\left(a\right)<0\hfill \\ \hfill A& =1,B=0,C=F\left(a\right)if0\le H\left(a\right)<1\hfill \\ \hfill A& =0,B=1,C=0ifH\left(a\right)\ge 0\hfill \end{array}$$

(73)

Here, $H\left(a\right)$ is a function of beam deflection (a) which ranges from −1 to 1 with an increase in a as shown in Figure 5. We assume that $H\left(a\right)$ is a hyperbolic tangent function, $Tanh$.

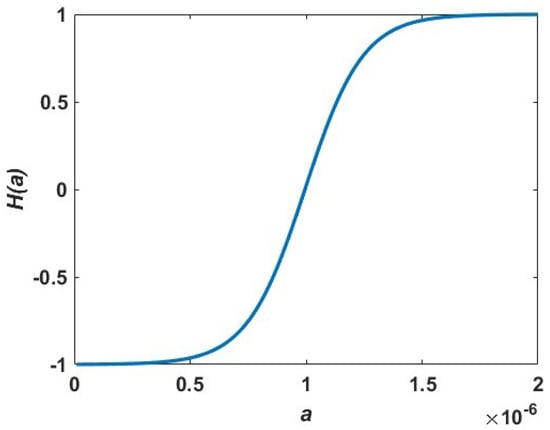
Figure 5. $H\left(a\right)$ with change in beam deflection (a).

By using Equations (72) and (73), the effect of combined nonlinearity on the frequency shift of the first mode is observed in Figure 6. In Figure 6, the various types of nonlinearity influencing the frequency shift are portrayed through three distinct color-coded zones, each denoting material, coupled and geometric nonlinearity, respectively. At lower amplitudes, the material nonlinearity results in a leftward shift and with the increase in applied force, the geometric and coupled effects begin to dominate, and hence, the nonlinear frequency shifts rightward. The green region of the force is where the coupled term manifests. As can be noted in Table 2, the coupled term is an order of magnitude larger than the geometric term, which results in a higher rightward shift comparatively. However, with the increase in applied force, it can be noted that the geometric nonlinearity is lower and hence results in a sharp discontinuity. This discontinuous behavior seems erratic and abnormal for physical systems.

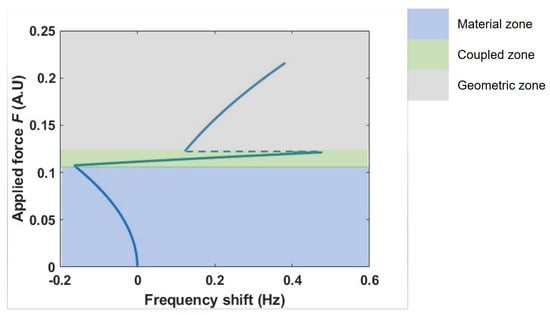
Figure 6. Change in resonant frequency shift with change in applied force in the beam with material and geometric nonlinearity using Model 1.

Model 2: To rectify the discontinuity, we introduce a different set of conditions given by

$$\begin{array}{cc}\hfill \mathrm{\Xi }& =A\left({\mathrm{\Xi }}_{Material}\right)+C\left({\mathrm{\Xi }}_{Coupled}\right)\hfill \\ \hfill A& =1,C=0if-1<H\left(a\right)<0\hfill \\ \hfill A& =1,C=H\left(a\right)ifH\left(a\right)\ge 0\hfill \\ \hfill \mathrm{\Xi }& ={\mathrm{\Xi }}_{Geometric}if{\mathrm{\Xi }}_{Material}+H\left(a\right){\mathrm{\Xi }}_{Coupled}\ge {\mathrm{\Xi }}_{Geometric}\hfill \end{array}$$

(74)

By using Equations (72) and (74), the effect of coupled nonlinearity on the nonlinear frequency shift can be observed in Figure 7. Model 2 is able to generate a more continuous behavior, wherein the leftward frequency shift due to material nonlinearity will transition smoothly into a rightward shift into the geometric nonlinearity zone. This combined shifting behavior has not been reported in the literature.

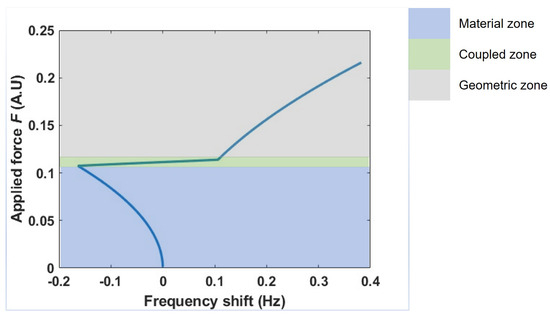
Figure 7. Change in resonant frequency shift with change in applied force in the beam with material and geometric nonlinearity using Model 2.

4. Conclusions

The theoretical models developed here show the different nonlinear behavior resulting from geometric, material and combined nonlinearity of a cantilever beam vibration. The results indicate that in a nonlinear beam with cantilever boundary conditions, geometric nonlinearity induces a hardening effect: as the forcing amplitude increases, the resonant frequency of the beam rises. Conversely, material nonlinearity induces a softening effect: as the forcing amplitude increases, the resonant frequency decreases. When both nonlinearities are combined, the resonant frequency initially decreases due to material nonlinearity, and then increases due to geometric nonlinearity as the amplitude further increases. In the combined case, the model developed here is capable of capturing the transition of the nonlinear effect from softening to hardening (left to right) as a function of the applied load. Since the contribution of geometric and material nonlinearity depends on the beam deflection, a function $H\left(a\right)$ was assumed to be the hyperbolic tangent and was used to regulate the cubic nonlinearity coefficient. While this assumption may not be valid for all cases, the purpose of using it was simply to demonstrate a transition between the material and geometric regions. Future studies will need to focus on determining the $H\left(a\right)$ empirically by fitting these models on experiments.