Evaluating Contact-Less Sensing and Fault Diagnosis Characteristics in Vibrating Thin Cantilever Beams with a MetGlas^® 2826MB Ribbon

Abstract

The contact-less sensing and fault diagnosis characteristics induced by fixing short Metglas^® 2826MB ribbons onto the surface of thin cantilever polymer beams are examined and statistically evaluated in this study. Excitation of the beam’s free end generates magnetic flux from the vibrating ribbon (fixed near the clamp side), which, via a coil suspended above the ribbon surface, is recorded as voltage with an oscilloscope. Cost-efficient design and operation are key objectives of this setup since only conventional equipment (coil, oscilloscope) is used, whereas filtering, amplification and similar circuits are absent. A statistical framework for extending past findings on the relationship between spectral changes in voltage and fault occurrence is introduced. Currently, different levels of beam excitation (within a frequency range) are shown to result in statistically different voltage spectral changes (frequency shifts). The principle is also valid for loads (faults) of different magnitudes and/or locations on the beam for a given excitation. Testing with either various beam excitation frequencies or different loads (magnitude/locations) at a given excitation demonstrates that voltage spectral changes are statistically mapped onto excitation levels or occurrences of distinct faults (loads). Thus, conventional beams may cost-efficiently acquire contact-less sensing and fault diagnosis capabilities using limited hardware/equipment.

1. Introduction

The use of magnetoelastic materials in the design and production of contact-less sensors owes much to their characteristic property of exhibiting shape changes under external magnetic fields. Conversely, these materials also emit magnetic flux when suffering shape deformation due to external loading, with flux dynamics related to those of the imposed loading [1,2,3,4,5]. Then, if magnetoelastic strips are, for instance, clamped on both sides and subjected to variable magnetic fields, the resulting shape changes will cause the strip to vibrate. The dynamics of such vibration depend on the external variable magnetic field, the strip dimensions and its mass distribution. Thus, the accumulation on the strip surface of substances such as biological agents [6], air pollutants [7], volatile organic compounds [8], H₂O [9] or H₂O₂ [10], which bind to suitable surface coating, will change its mass distribution and consequently its vibration characteristics (resonant frequencies). Hence, shifted resonant frequencies indicate a significant concentration of substances on it and, accordingly, the environment. This is the operational principle of magnetoelastic (magnetostrictive) sensors, which allow for monitoring dangerous substances in hostile environments without requiring human presence on the field since the strip vibration signal can obviously be remotely recorded and assessed.

Two main classes of sensor setups can be distinguished based on whether the magnetoelastic element is driven to resonance via electrical excitation used specifically for this purpose, or whether it is simply vibrating because it receives mechanical excitation from its environment. The first class involves setups such as those presented in the previous paragraph, where an interrogation coil (excited by a suitable electrical signal) is used to provide the magnetoelastic material with the magnetic flux required to drive it to resonance. Then, another coil placed above the vibrating ribbon or film (usually referred to as the reception coil) picks up the emitted flux in a contact-less manner and transforms it into an electrical signal (voltage). The latter is then monitored for frequency shifts indicating the accumulation of substances. This two-coil setup is referred to as active and was reviewed among others in [5]. The active setup is quite sensitive to mass accumulation on the magnetoelastic element’s surface, especially if the latter is selected based on its Young’s modulus and ∆E effect characteristics [11], its length-to-width ratio [11,12,13] or even its shape, with hourglass [14] or rhomboid forms [15,16] being more efficient.

The second class of sensor setups involves those not requiring interrogation coils to provide excitation to the magnetoelastic element since the latter is part of vibrating mechanical structures (or machines with rotating parts) and, hence, vibrates due to its normal operation. Then, the vibrating magnetoelastic element produces magnetic flux, which is picked up by a reception coil in a contact-less manner. Analyzing the signal’s spectral characteristics draws conclusions on the dynamics of the magnetoelastic part and, obviously, of the underlying mechanical structure [17,18,19,2021]. This one-coil-only setup is referred to as the passive setup and was also reviewed in [5]. Note that, sometimes, setups involving magnetoelastic elements that are fixed as parts of a vibrating structure, with the intention of estimating spectral characteristics of the underlying structure, do use two coils but with the interrogation coil fed by DC. This is completed in order to induce bias to the magnetic flux produced by the magnetoelastic element and seemingly achieve better efficiency [22,23]. Due to the presence of the interrogation coil, such setups should really be included in the class of active setups. This remark also illustrates the fact that the magnetic flux produced by the passive setups is notably weaker than that of the active ones, but the operational costs are lower, and the associated electrical or electronic circuits are far simpler. Even though signals obtained with passive setups are noisy, faults/failures that influence the dynamics of the underlying structure (or machinery) are, indeed, detectable in the recorded voltage. In [17,19,20], it was shown that specific resonant frequencies of the structure’s dynamics, which were estimated using Finite Element Analysis, are present in the recorded voltage’s spectral characteristics. Using a passive setup, fault diagnosis was achieved in polymer slabs with magnetoelastic ribbons integrated with 3D printing during slab manufacturing [17]. Fault diagnosis was also achieved for structures composed by bolting together such slabs, and specifically, for indicating loose connections between structural members [18]. Interestingly, this study demonstrated that although only one slab with integrated magnetoelastic material was used in the structure, more than one loose connection could be detected. Again, cracks were diagnosed in metal cantilever beams involving magnetoelastic ribbons fixed on their surface [19] or metal rotating beams [21]. Most importantly, passive setups were proven adequate for obtaining sensing and diagnostic results both for short/sturdy and for long, thin/flexible polymer cantilever beams (see [24] and references therein). Pure sensing properties were also extensively evaluated for metal cantilever beams [20] and for plastic beams (in terms of bending frequencies) [23], although, strictly speaking, these works involved an interrogation coil inducing bias into the magnetic flux produced.

The current work aims at obtaining a novel two-fold extension of the preliminary results presented in [24]. First, the previously established sensing ability of the setup is consolidated with a statistical evaluation of the mapping between the level of excitation of the beam and the resulting frequency shifts in the recorded voltage signal. Hence, sensing capabilities are obtained because the vibration level provided to the beam may now be deduced by monitoring frequency shifting patterns in the voltage signal, with the uncertainty in the process quantified. Second, the fault diagnosis capabilities already shown in [24] are statistically consolidated: A mapping of complex-plane areas (containing poles linked to shifted voltage frequencies) onto faults (loads) of specific magnitude and position affecting the beam is statistically established, so that the risk of wrong diagnosis is quantified. As already explained, the setup involves a thin, flexible cantilever beam clamped on one end and supported by an exciter on the opposite end. The latter provides excitation as specified with a waveform generator. The magnetoelastic element (short ribbon of Metglas^® 2826MB) is attached at the clamped end (in contrast to [19,20,21]), with a low-cost reception coil suspended above the ribbon surface. The raw voltage induced in a contact-less manner is recorded using a conventional oscilloscope, without circuits for preliminary conditioning/filtering or amplification. Thus, the objective of obtaining sensing and diagnostic capabilities out of a low complexity (in terms of hardware and operation) setup, by investing in the optimization of the algorithmic framework used, is possible: It is shown that although the beam is only excited at the free end, the sensing of the beam excitation level and diagnosis of different structural changes (magnitude/position on the beam) are both achievable. By virtue of the current results, conventional long, flexible beams equipped with magnetoelastic elements may be used: (i) either for deducing the level of excitation (due to external forces, for instance) suffered by the beam (or any structure connected to it) or (ii) for detecting and localizing faults (loads) of different magnitude affecting the beam for a given level of excitation.

2. Materials and Methods

The experimental setup is essentially that which was used in [24] and consists of a long, thin and flexible beam (with a length of 425 mm, width of 25 mm and thickness equal to 1 mm), an exciter (SMARTSHAKER^TM K2004E01), a 25 mm long ribbon of Metglas^® 2826MB magnetoelastic material and a low-cost Vishay IWAS reception coil (normally used for wireless charging). The beam is 3D-printed in FDM (fused deposition modeling) mode with a PET-G filament and is used in a cantilever arrangement with one end clamped, as presented in Figure 1. The opposite (free) end is fixed to the exciter rod, thereby receiving the vibration of the user-defined profile. For this purpose, an external waveform generator (SIGLENT SDG 5122) is connected to the exciter. The magnetoelastic ribbon is fixed on the beam surface near the clamp with glue, whereas the reception coil is fixed 5 mm above the ribbon, thus bearing no contact with it. The distance of 5 mm was selected from sensitivity tests, as described in [24]. Magnetic flux created by the vibrating (along with the beam) ribbon induces voltage in the reception coil circuit, which is recorded with a digital oscilloscope. Based on the analysis of the recorded voltage’s spectral characteristics, sensing and fault diagnosis results may be obtained. Especially in terms of fault diagnosis, this approach based on using only one signal is representative of real-life applications (bridges, flexible structures and so on), because the excitation signal is often unavailable (or hard to measure) with only the structure’s response signal being available.

2.1. Methodology for the Evaluation of the Sensing Characteristics of the Setup

The sensing principle of the proposed passive setup was previously examined in [24] using a first series of tests with voltage recorded while the beam was at rest and a second one with the beam excited with a triangular force at 160 Hz. Triangular waveforms were used instead of pure sinusoids or pulses because they correspond better to real sources of vibrations such as those created by machine-reciprocating parts [18]. Comparison of the two series of recorded voltage signals led to two conclusions. First, the time histories of both voltage series were almost identical, as expected for passive setups [18]. Second, the spectral characteristics of the voltage with the beam under excitation were different than those from the voltage recorded with the beam at rest. Dominant frequencies at 1300–1370 Hz showed consistent shifting with the beam under excitation, as presented in Figure 2b,c in [24].

Based on this result, the current study systematically examines the link between the shifting of dominant frequencies in the recorded voltage and the excitation levels provided to the beam. For this purpose (see also Section 3.1), the excitation level is set to as low as 10 Hz for the first series of tests, and keeps increasing for each test series, until reaching a value of 160 Hz. For each test series (and, hence, excitation level), frequency bands with higher contributions to the voltage frequency content (those corresponding to prominent peaks in Fourier plots) are designated. In each such band, the values of dominant frequency peaks form relevant groups, one per test series. Then, statistically comparing two (or more) of these groups (in the considered band) corresponds to statistically evaluating whether the respective beam excitation levels cause similar shifting patterns in the recorded voltage’s spectral characteristics. Demonstrating that different excitation levels ultimately result in statistically not similar groups of dominant frequency values in the considered band means that there exists a mapping between beam excitation levels and frequency shifts in the recorded voltage signal. Then, conversely, one may use this mapping to estimate the level of beam excitation based on the dominant frequency shifting pattern exhibited.

Statistical evaluation of the similarity in two or more groups (intervals) of data may be formulated as a problem of deciding whether the data in both groups come from similar distributions or not. In the current case, a hypothesis-testing problem may be formulated as follows:

H₀: Frequency values in both (or all) groups follow a similar distribution.
H₁: Frequency values in both (or all) groups follow different distributions.

(1)

with H₀ referred to as the null hypothesis and H₁ as the alternative hypothesis. Note that there is no available information on whether the data in the previously mentioned groups follow a normal distribution; hence, non-parametric statistical tests must be used to choose between the null and alternative hypotheses in (1) at a given risk level α (usually equal to 0.05). The latter is the probability of rejecting H₀ even though it is true. Such non-parametric statistical tests include the Kolmogorov–Smirnov two-sample test and the Kruskal–Wallis test [25,26]. As its name suggests, the Kolmogorov–Smirnov two-sample test is designed to address a hypothesis problem such as that in (1), when comparisons between only two groups are considered. The null hypothesis is accepted (or rejected) based on the distance between the empirical distributions of data for each group estimated using the associated data. On the other hand, the Kruskal–Wallis test may be used for two or more groups of data [25,26,27] and provides an answer to the question of whether data in the groups under consideration follow similar statistical distributions. If these distributions have similar shapes, then the Kruskal–Wallis test accepts (or rejects) the null hypothesis based on whether the medians of all groups are sufficiently (in some statistical sense) close [25]. Furthermore, the Kruskal–Wallis test may be used with groups containing 5 or 6 data values, as shown in cases presented in [25,26], respectively. These characteristics motivated the choice of the Kruskal–Wallis test to address the hypothesis testing problem (1), which will be presented later (Section 3.1). The Kruskal–Wallis test is coded in most software packages like SPSS^® or MATLAB^®, with the relevant routines using data provided to instantly compute the probability value (referred to as the p-value), which evaluates the evidence against the null hypothesis. A lower p-value indicates more important evidence against accepting the null hypothesis. As will be explained in Section 3.1 and Section 3.2, the p-value may offer valuable information for quantifying the uncertainty (risk) involved when deciding on whether two or more frequency groups feature significant similarities: in other words, whether these groups potentially overlap in part or not.

2.2. Methodology for Evaluating Fault Diagnosis Characteristics of the Setup

The principle of fault diagnosis was also examined in [24] using several series of tests with faults affecting the beam. These were simulated as loads of two different magnitudes (EUR 1 cent designated with the suffix –1C or a bolt fixed with its nut on the beam designated with –BN) potentially placed on the beam at three positions (A, B or C—see Figure 1).

Table 1. Test configurations (scenarios) presenting load magnitudes and positions on the beam.

Fault Case (Test Scenario)	Load Used	Load Mass (g)	Load Position (From Free End)
N-1C	No load	0	n/a
A-1C	EUR 1 cent	2.3	A (35 mm)
B-1C	EUR 1 cent	2.3	B (185 mm)
C-1C	EUR 1 cent	2.3	C (360 mm)
N-BN	No load	0	n/a
A-BN	Bolt + nut	6	A (35 mm)
B-BN	Bolt + nut	6	B (185 mm)
C-BN	Bolt + nut	6	C (360 mm)

presents the fault cases (also referred to as test scenarios) and their characteristics. For each series of tests, one load was placed at one position throughout the series with voltage recorded as usual. The series also involved tests without load on the beam (designated with the prefix N). For each fault case, a prefix other than N designated the load position—so it should be A, B or C. The associated voltage signals were recorded and analyzed, the bands of dominant frequencies were inspected and the patterns of the dominant peak shifting according to the load, its magnitude and its position on the beam were studied. Once the impact of load position and magnitude was validated in specific frequency bands, a model-based fault diagnosis procedure was defined and applied to all signals (obtained from testing according to the test scenarios in Table 1), with the following steps:

• The voltage signal considered was filtered and subsampled (details are given in Section 3.2 in [24]);
• Discrete-time stochastic AutoRegressive (AR) time-series representations were identified on the signal resulting from step 1 (thus modeling its spectral characteristics), and the discrete-time AR poles corresponding to specific bands of the dominant frequencies were computed and plotted on the z-plane;
• Using the AR poles from step 2, the corresponding continuous-time poles were computed and plotted on the s-plane, thus enabling the calculation of the natural frequencies ω_n and damping ratios ζ for the considered bands of dominant frequencies.

The reader is referred to [24] for specific details on signal filtering, identification of AR representations and their optimization for enhancing fault detectability. The application of the 3-step procedure allowed for mapping areas of the s-plane onto each one of the test scenarios in Table 1. According to this mapping, the majority of poles from each test scenario would only be located inside their proper s-plane area, meaning that fault occurrence, localization and magnitude estimation were in principle achievable.

The current study addresses the remaining part of the problem, namely, the demonstration that each s-plane area (which contains mostly poles resulting from one of the specific fault scenarios in Table 1) may be statistically distinguishable from other neighboring areas with a specific level of confidence. This is crucial because, as described in [24] (and alluded to in the previous paragraph), it is hard to delimitate (pole) areas in the s-plane corresponding to specific faults without using some kind of statistical inference to estimate the level of accuracy of this process. In other terms, the risk of erroneously classifying poles with respect to the fault case they result from should be quantified. For instance, ref. [24] shows that in a few isolated cases, the poles from the signals corresponding to N-1C faults were in the s-plane areas designating A-1C faults. Again, an isolated case of poles from the signals corresponding to A-1C faults inside the area designating the poles from B-1C fault scenarios may also be found in [24]. Obviously, such isolated cases do not cast doubt on the principle that fault diagnosis is, indeed, achievable using this setup. Nonetheless, it is important to quantify the risk of overlapping s-plane areas potentially leading to wrong decisions when attempting to detect and isolate specific faults.

Interestingly, the current study also demonstrates that results similar to those obtained in continuous time (s-plane areas) may also be achievable in discrete time (z-plane areas). This could lead to simplifying the previously presented 3-step procedure in terms of fault detection/classification, if the calculation of natural frequencies ω_n and damping ratios ζ for the considered bands of dominant frequencies is not needed. This fact is particularly promising because in [24], no conclusive (or even indicative) evidence of z-plane pole areas being able to be mapped onto fault cases (test scenarios) was found.

For these purposes, the following statistical hypothesis problem may be formulated:

H₀: Pole locations inside the considered groups follow a similar distribution.
H₁: Pole locations inside the considered groups follow different distributions.

(2)

where H₀ is the null hypothesis potentially corresponding to (neighboring) s- or z-plane areas with significant overlapping and H₁ is the alternative hypothesis designating substantially separable areas at a given risk level. As with the frequency data used to evaluate the setup sensing characteristics, there is no available knowledge of pole locations following a normal distribution. Then, non-parametric statistical tests should be used to decide between the null and alternative hypotheses in (2) at a given risk level α (usually equal to 0.05 or 5%), which is the probability of the examined pole areas not being considered as overlapping (or, in other terms, that H₀ is rejected) even though they are. The Kruskal–Wallis test may again be used to solve the hypothesis testing problem (2), as will be presented later (Section 3.2).

3. Results and Discussion

The proposed setup is evaluated in the current section with extended testing and statistical evaluation of results using the methodology presented in Section 2. Sensing characteristics are assessed in Section 3.1 by statistically evaluating the mapping between excitation frequency levels and experimentally obtained shifts in the voltage signal’s dominant frequency peaks inside the principal frequency bands. The fault diagnosis characteristics are assessed in Section 3.2 by statistically evaluating the connection between the recorded signal’s AR pole locations in the s-plane or z-plane and the occurrence of specific faults (type, magnitude and location as in Table 1).

3.1. Results of the Statistical Evaluation of Sensing Characteristics

The testing procedure involved six experiments for each excitation level, as presented in

Table 2. Excitation in Hz provided to the beam for each test series and the number of experiments.

Excitation Frequency (Hz)	Test Series	Number of Experiments
0	s0	6
10	s1	6
40	s2	6
55	s3	6
70	s4	6
85	s5	6
100	s6	6
115	s7	6
130	s8	6
145	s9	6
160	s10	6

. The reception coil was placed at a distance of 5 mm above the ribbon, following the relevant testing performed in [24], to define an optimal value for that distance. As seen in Table 2, the beam was excited with frequencies starting at 10 Hz for the first series of six experiments and finishing at 160 Hz for the last series. In general, at each test series, the excitation level increased by 15 Hz with respect to the previous one. The only exception to this rule regarded the test series with the beam excited at 25 Hz, which presented very similar results to those obtained when the beam was under an excitation of 10 Hz (see also the relevant comment later on) and was therefore omitted. Note also that a test series of six experiments with the beam at rest, namely, series zero, was included for comparison purposes. The voltage signals were recorded and examined with respect to their frequency content. 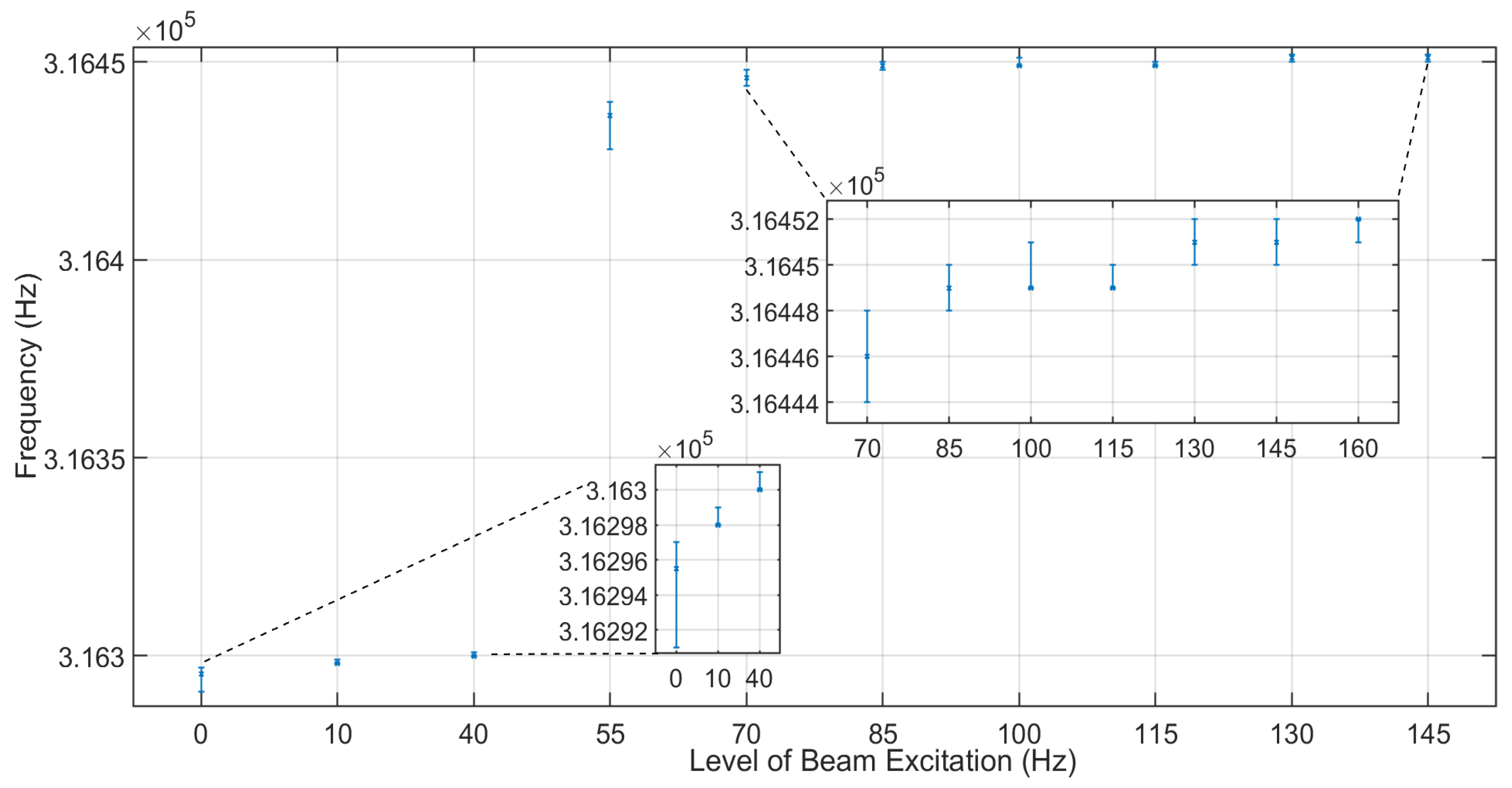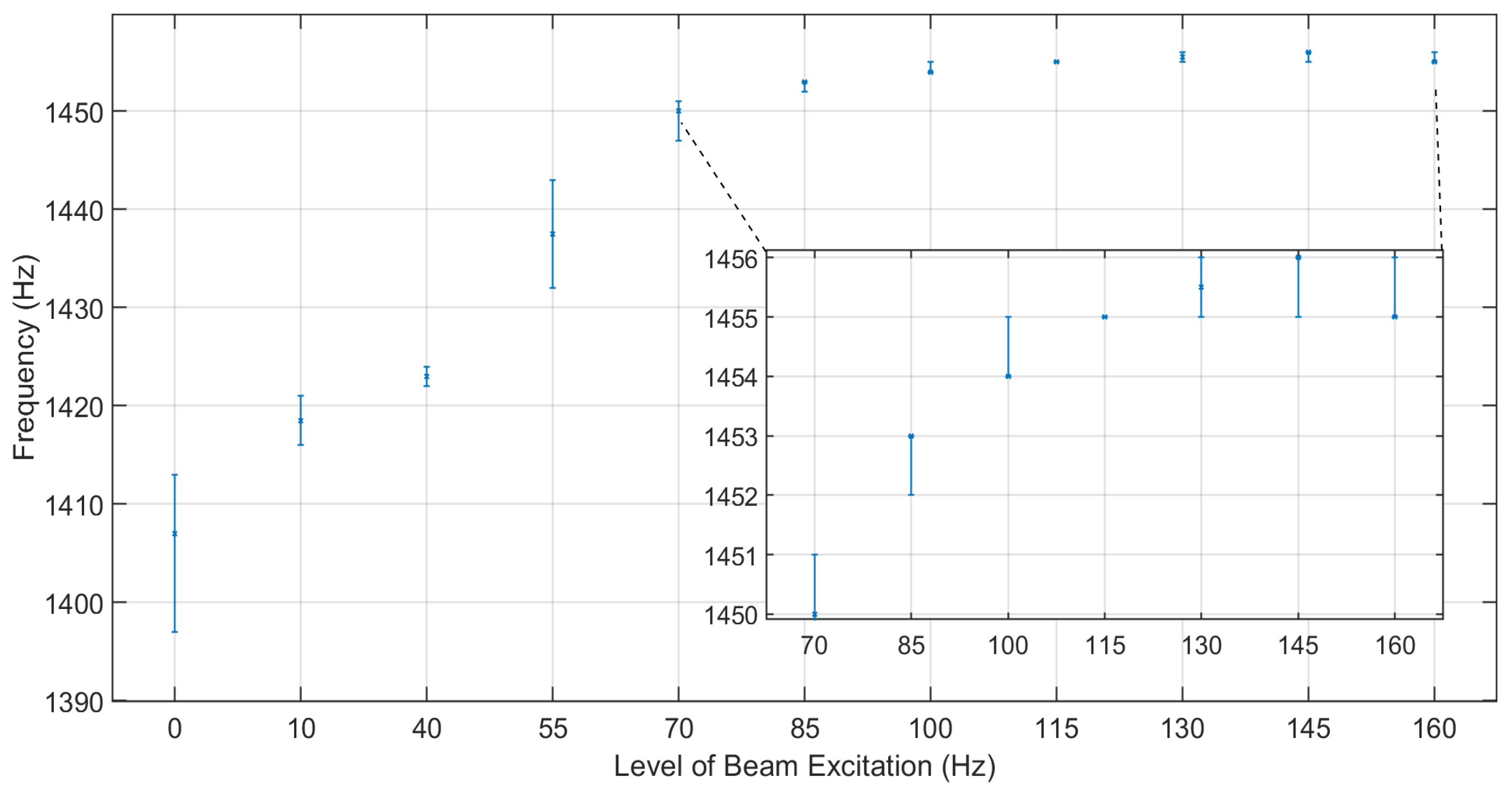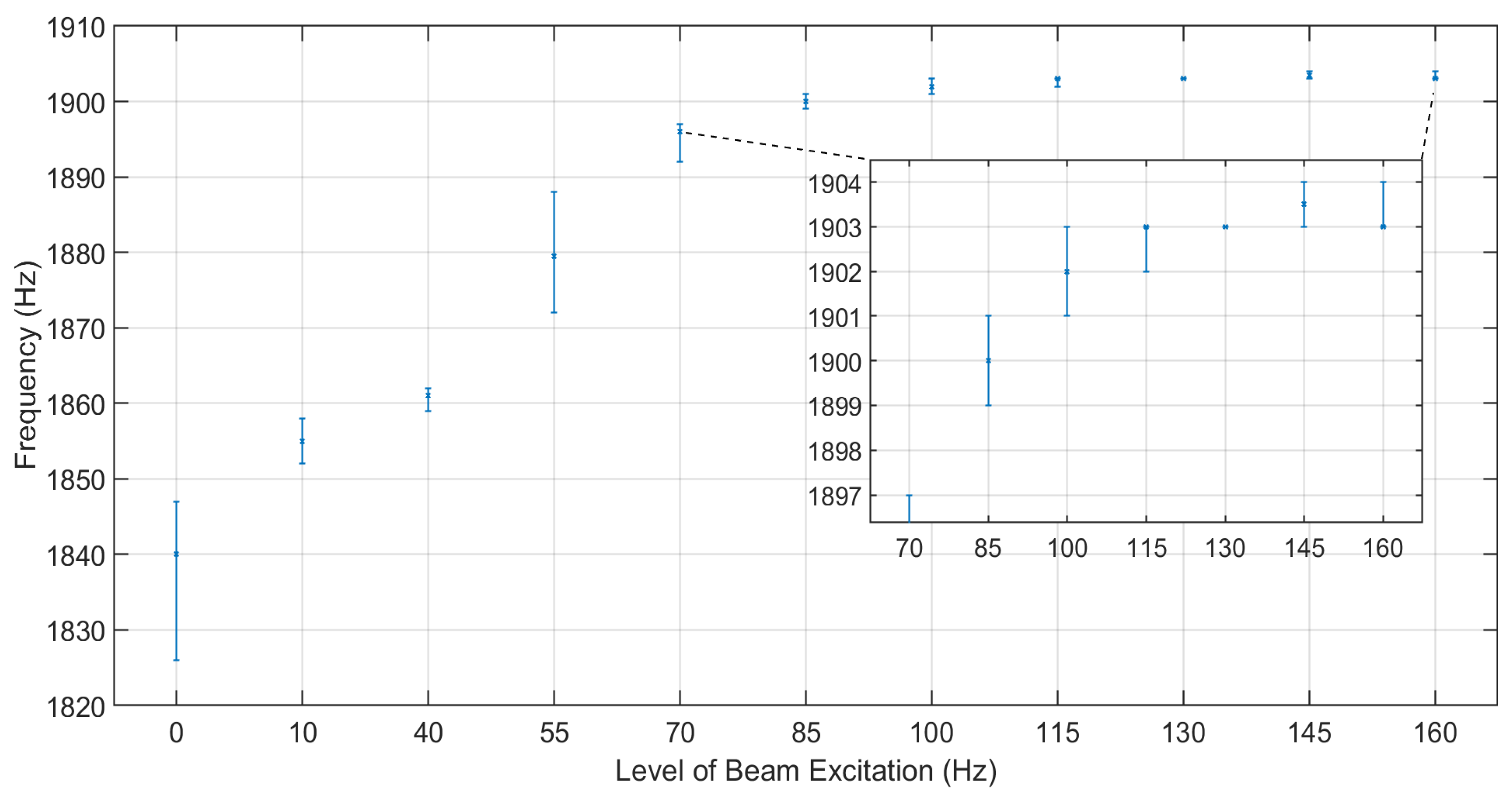In Figure 2, the Fourier plot of one representative signal from each test series shows that the bands of the dominant frequencies are consistently situated (in a decreasing order of magnitude) around 316 KHz, 1400 Hz, 1800 Hz and 2100 Hz. For each of these four frequency bands, the values of the dominant peaks are collected for each test series (six values per series), and the respective groups are plotted (in the form of error bars) in Figure 3, Figure 4, Figure 5 and Figure 6.

An initial remark is related to the groups resulting from the excitations at 10 Hz and 40 Hz, whose upper and lower values, respectively, are very close in all four frequency bands. This is indicative of the fact that an intermediate excitation level at 25 Hz was, indeed, not necessary since its group exhibited considerable overlapping neighboring groups. Then, it is easily noted that all groups up to 100 Hz feature an increasing trend with no apparent overlapping in frequency bands around 1400, 1800 and 2100 Hz. This, in turn, means that by focusing on the band around 1400 Hz and examining the frequency groups shown in Figure 4, Figure 5 and Figure 6, a one-to-one mapping may be established between the beam excitation levels and the respective frequency peak groups. Hence, if a (voltage) signal’s frequency peak around, for instance, 1400 Hz is available, then one may deduce the excitation level of the beam simply using the previously mentioned mapping, provided that this level does not exceed 100 Hz.

This mapping becomes less consistent for excitation levels above 100 Hz, with Figure 4 suggesting that the levels of 100 Hz are distinguishable from those of 115 Hz in the 1400 Hz band, or that the levels of 115 Hz are distinguishable from those of 130 Hz in the 316 KHz band (Figure 3). In any case, a measure of the probability that two or more frequency groups are mutually distinguishable in each frequency band is required. For this purpose, the Kruskal–Wallis test is used between all possible pairs of groups to solve the hypothesis testing problem (1). The results, in terms of p-values, are given in

Table 3. p-values for the comparison of two groups with the Kruskal–Wallis test in the band of 316 KHz.

Excitation	0 Hz	10 Hz	40 Hz	55 Hz	70 Hz	85 Hz	100 Hz	115 Hz	130 Hz	145 Hz	160 Hz
0 Hz	N/A	0.0032	0.0032	0.0038	0.0036	0.0036	0.0032	0.0032	0.0036	0.0036	0.0032
10 Hz	0.0032	N/A	0.0027	0.0032	0.0031	0.0031	0.0028	0.0027	0.0031	0.0031	0.0027
40 Hz	0.0032	0.0027	N/A	0.0032	0.0031	0.0031	0.0028	0.0027	0.0031	0.0031	0.0027
55 Hz	0.0038	0.0032	0.0032	N/A	0.0037	0.0037	0.0033	0.0032	0.0037	0.0037	0.0032
70 Hz	0.0036	0.0031	0.0031	0.0037	N/A	0.0086	0.0032	0.0031	0.0036	0.0036	0.0031
85 Hz	0.0036	0.0031	0.0031	0.0037	0.0086	N/A	0.3880	0.4844	0.0086	0.0086	0.0031
100 Hz	0.0032	0.0028	0.0028	0.0033	0.0032	0.3880	N/A	0.8474	0.0203	0.0203	0.0045
115 Hz	0.0032	0.0027	0.0027	0.0032	0.0031	0.4844	0.8474	N/A	0.0077	0.0077	0.0027
130 Hz	0.0036	0.0031	0.0031	0.0037	0.0036	0.0086	0.0203	0.0077	N/A	1.0000	0.1620
145 Hz	0.0036	0.0031	0.0031	0.0037	0.0036	0.0086	0.0203	0.0077	1.0000	N/A	0.1620
160 Hz	0.0032	0.0027	0.0027	0.0032	0.0031	0.0031	0.0045	0.0027	0.1620	0.1620	N/A

,

Table 4. p-values for the comparison of two groups with the Kruskal–Wallis test in the band of 1400 Hz.

Excitation	0 Hz	10 Hz	40 Hz	55 Hz	70 Hz	85 Hz	100 Hz	115 Hz	130 Hz	145 Hz	160 Hz
0 Hz	N/A	0.0038	0.0036	0.0037	0.0036	0.0032	0.0032	0.0020	0.0033	0.0027	0.0032
10 Hz	0.0038	N/A	0.0037	0.0038	0.0037	0.0032	0.0032	0.0021	0.0034	0.0028	0.0032
40 Hz	0.0036	0.0037	N/A	0.0036	0.0036	0.0031	0.0031	0.0020	0.0033	0.0026	0.0031
55 Hz	0.0037	0.0038	0.0036	N/A	0.0036	0.0032	0.0032	0.0020	0.0033	0.0027	0.0032
70 Hz	0.0036	0.0037	0.0036	0.0036	N/A	0.0031	0.0031	0.0020	0.0033	0.0026	0.0031
85 Hz	0.0032	0.0032	0.0031	0.0032	0.0031	N/A	0.0027	0.0017	0.0029	0.0023	0.0027
100 Hz	0.0032	0.0032	0.0031	0.0032	0.0031	0.0027	N/A	0.0190	0.0105	0.0037	0.0144
115 Hz	0.0020	0.0021	0.0020	0.0020	0.0020	0.0017	0.0190	N/A	0.0555	0.0051	0.1380
130 Hz	0.0033	0.0034	0.0033	0.0033	0.0033	0.0029	0.0105	0.0555	N/A	0.2410	0.5751
145 Hz	0.0027	0.0028	0.0026	0.0027	0.0026	0.0023	0.0037	0.0051	0.2410	N/A	0.0926
160 Hz	0.0032	0.0032	0.0031	0.0032	0.0031	0.0027	0.0144	0.1380	0.5751	0.0926	N/A

,

Table 5. p-values for the comparison of two groups with the Kruskal–Wallis test in the band of 1800 Hz.

Excitation	0 Hz	10 Hz	40 Hz	55 Hz	70 Hz	85 Hz	100 Hz	115 Hz	130 Hz	145 Hz	160 Hz
0 Hz	N/A	0.0037	0.0036	0.0038	0.0036	0.0036	0.0035	0.0032	0.0020	0.0033	0.0027
10 Hz	0.0037	N/A	0.0036	0.0038	0.0036	0.0036	0.0035	0.0032	0.0020	0.0033	0.0027
40 Hz	0.0036	0.0036	N/A	0.0037	0.0036	0.0036	0.0035	0.0031	0.0020	0.0033	0.0026
55 Hz	0.0038	0.0038	0.0037	N/A	0.0037	0.0037	0.0036	0.0032	0.0021	0.0034	0.0028
70 Hz	0.0036	0.0036	0.0036	0.0037	N/A	0.0036	0.0035	0.0031	0.0020	0.0033	0.0026
85 Hz	0.0036	0.0036	0.0036	0.0037	0.0036	N/A	0.0084	0.0031	0.0020	0.0033	0.0026
100 Hz	0.0035	0.0035	0.0035	0.0036	0.0035	0.0084	N/A	0.0570	0.0068	0.0062	0.0074
115 Hz	0.0032	0.0032	0.0031	0.0032	0.0031	0.0031	0.0570	N/A	0.1380	0.0303	0.0917
130 Hz	0.0020	0.0020	0.0020	0.0021	0.0020	0.0020	0.0068	0.1380	N/A	0.0555	0.3173
145 Hz	0.0033	0.0033	0.0033	0.0034	0.0033	0.0033	0.0062	0.0303	0.0555	N/A	0.2410
160 Hz	0.0027	0.0027	0.0026	0.0028	0.0026	0.0026	0.0074	0.0917	0.3173	0.2410	N/A

and

Table 6. p-values for the comparison of two groups with the Kruskal–Wallis test in the band of 2100 Hz.

Excitation	0 Hz	10 Hz	40 Hz	55 Hz	70 Hz	85 Hz	100 Hz	115 Hz	130 Hz	145 Hz	160 Hz
0 Hz	N/A	0.0037	0.0036	0.0038	0.0036	0.0035	0.0037	0.0033	0.0020	0.0032	0.0020
10 Hz	0.0037	N/A	0.0036	0.0038	0.0036	0.0035	0.0037	0.0033	0.0020	0.0032	0.0020
40 Hz	0.0036	0.0036	N/A	0.0038	0.0036	0.0035	0.0036	0.0033	0.0020	0.0031	0.0020
55 Hz	0.0038	0.0038	0.0038	N/A	0.0038	0.0036	0.0038	0.0035	0.0021	0.0033	0.0021
70 Hz	0.0036	0.0036	0.0036	0.0038	N/A	0.0035	0.0036	0.0033	0.0020	0.0031	0.0020
85 Hz	0.0035	0.0035	0.0035	0.0036	0.0035	N/A	0.0068	0.0032	0.0019	0.0030	0.0019
100 Hz	0.0037	0.0037	0.0036	0.0038	0.0036	0.0068	N/A	0.0750	0.0071	0.0051	0.0071
115 Hz	0.0033	0.0033	0.0033	0.0035	0.0033	0.0032	0.0750	N/A	0.0555	0.0105	0.0555
130 Hz	0.0020	0.0020	0.0020	0.0021	0.0020	0.0019	0.0071	0.0555	N/A	0.0190	1
145 Hz	0.0032	0.0032	0.0031	0.0033	0.0031	0.0030	0.0051	0.0105	0.0190	N/A	0.0190
160 Hz	0.0020	0.0020	0.0020	0.0021	0.0020	0.0019	0.0071	0.0555	1	0.0190	N/A

for the frequency bands at 316 KHz, 1400 Hz, 1800 Hz and 2100 Hz, respectively.

In these tables, the intersecting cell of the i-th line and the j-th column presents the p-value obtained using the Kruskal–Wallis test for the groups indicated in the respective line and column. Standard (non-shaded) cells correspond to cases where H₀ (groups with a similar distribution of data) is rejected in favor of H₁ (groups with a different distribution of data) at a risk level equal to α = 0.05, as explained in Section 2.1. In such cases, the two groups considered are mutually distinguishable at the indicated risk level, meaning that the previously mentioned mapping is valid, again, at the indicated risk level. On the other hand, the shaded cells correspond to cases where H₀ (groups with a similar distribution of data) is accepted for the pair of groups under consideration, at a risk level equal to α = 0.05. Then, the two considered excitation frequencies would result in significantly overlapping groups of frequency peaks in the band of interest, meaning that no exclusive one-to-one mapping is possible. An examination of Table 3, Table 4, Table 5 and Table 6 basically validates the conclusions drawn by visual inspection of (the corresponding) Figure 3, Figure 4, Figure 5 and Figure 6. The frequency band around 1400 Hz provides statistically non-overlapping groups at a risk level of 0.05 (Table 4) for beam excitation frequencies up to 115 Hz. Then, the excitation levels of 115 Hz and 130 Hz create overlapping groups (at a risk level of 0.05), since the p-value computed with the Kruskal–Wallis test is 0.055 (see the intersection between the ninth line and the tenth column), or just larger than 0.05, which leads to accepting the null hypothesis. At the same time, p-values just larger than the risk level indicate a statistical tendency of being close to rejecting H₀. In other words, even though the 1400 Hz band does not actually allow for distinguishing between the excitation levels of 115 and 130 Hz, it would be relevant to look at other frequency bands for the null hypothesis being rejected when comparing the groups associated with the levels of 115 and 130 Hz. The band at 316 KHz offers this possibility since the p-value (related to comparing groups created by the excitation levels of 115 Hz and 130 Hz—Table 3) computed with the Kruskal–Wallis test is 0.0077 (see the intersection between the ninth line and the tenth column). However, in the band around 316 KHz, all groups created by the excitation levels above 130 Hz are statistically similar, as indicated by a p-value of the Kruskal–Wallis test statistic equal to 0.2738 > 0.05 when comparing all three groups corresponding to the excitation levels of 130, 145 and 160 Hz. Then, distinguishing between the excitation levels of 115 and 130 Hz in the 316 KHz band may only be achieved in conjunction with p-values from the band around 2100 Hz in Table 6. The latter indicates that the group resulting from the beam excited at 130 Hz cannot be mistaken for that associated with the excitation of 145 Hz at the considered risk level of 0.05. Thus, frequency peak groups resulting from excitation levels up to 145 Hz may be distinguished in a one-to-one comparison using the proposed setup and methodology. Figure 3, Figure 4, Figure 5 and Figure 6 and Table 3, Table 4, Table 5 and Table 6 suggest that a meaningful solution for distinguishing groups associated with excitation levels up to 145 Hz from a group associated with the excitation levels of 160 Hz is not available in all four bands considered.

A final remark regards these results with respect to the passive excitation principle used in this setup. Using mechanical excitation for the beam (and, hence, the magnetoelastic ribbon) without, for instance, some form of DC bias from a second coil [20,23] mainly allows for inducing sensing capabilities in standard conventional beams in a cost-effective manner. On the other hand, the recorded signal is quite noisy, meaning that more (and surely non-trivial) algorithmic effort has to be invested in rejecting noise effects and obtaining results on higher-order modes of vibrations and/or larger beam deflections.

3.2. Results of the Statistical Evaluation of Fault Diagnosis Characteristics

The testing procedure involved six experiments per fault case (or test scenario as referred to) in Table 1. The 48 voltage signals resulting from the testing were also used in [24] along with the three-step procedure outlined in Section 2.2, to deliver initially the discrete-time AR poles inside the bands of the dominant frequencies (around 1350–1400 Hz in this case) and then their corresponding continuous-time counterparts. 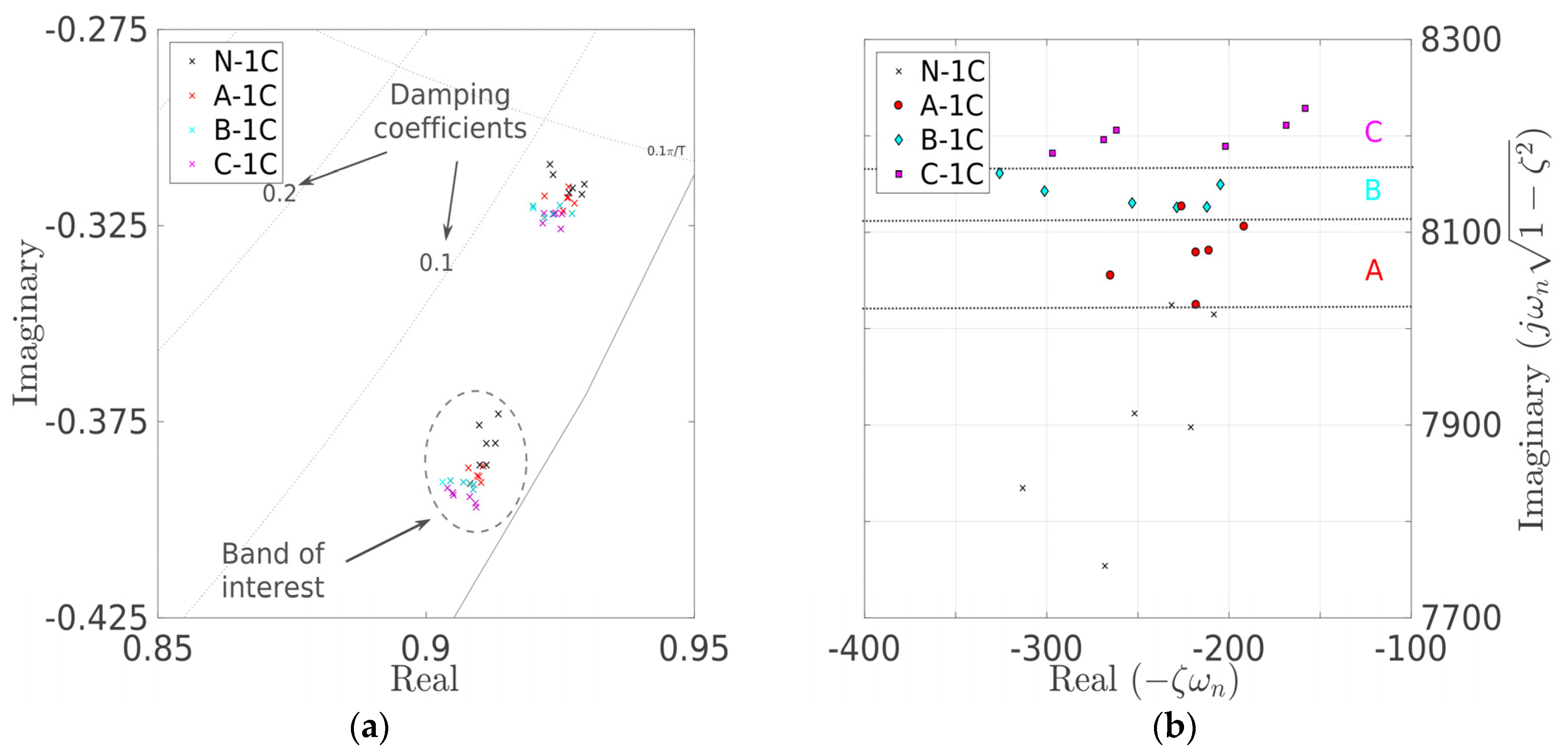This yielded the pole areas in Figure 7a,b at the z-plane and the s-plane, respectively, for the –1C fault cases. 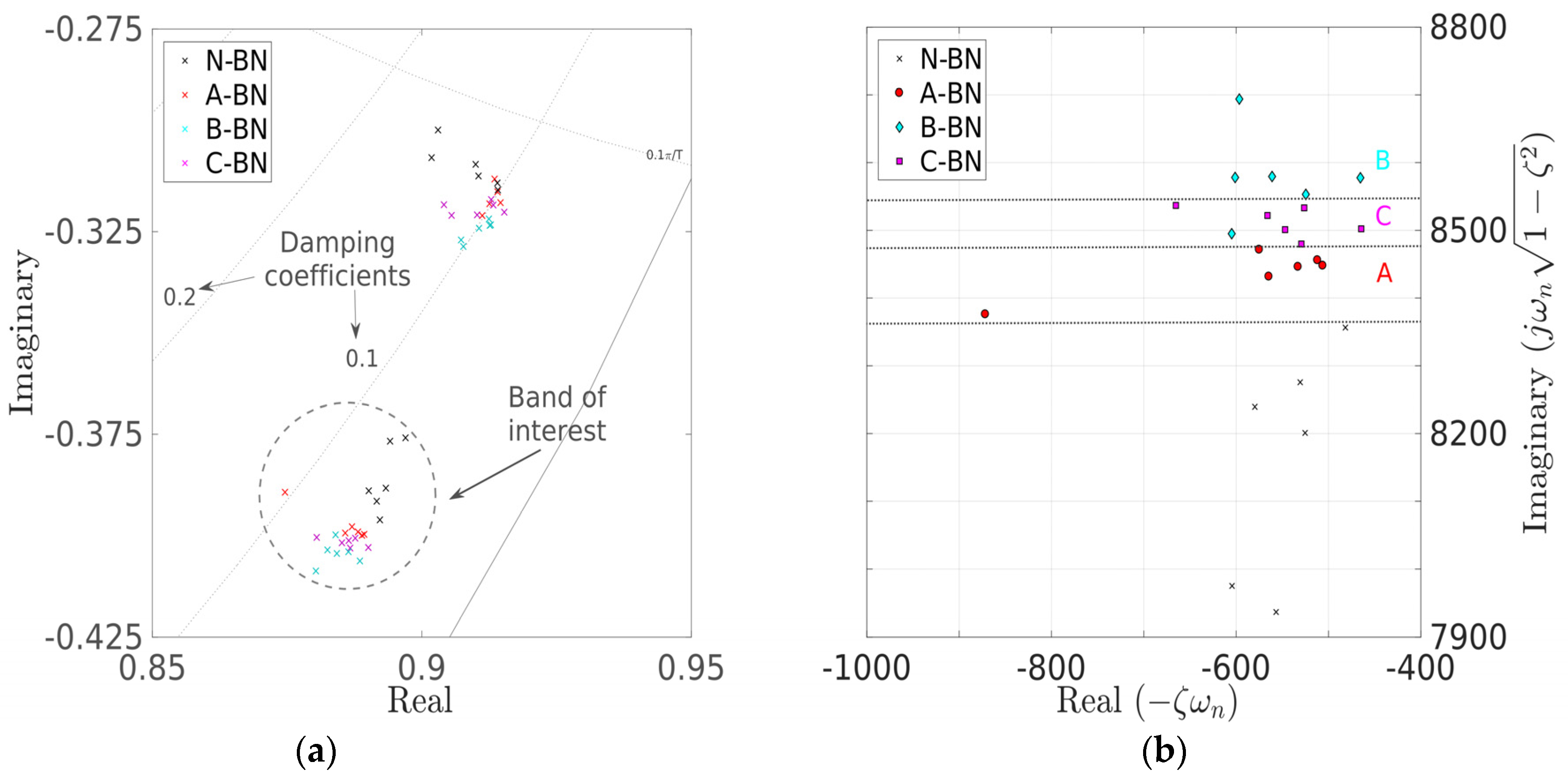Figure 8a,b presents the pole areas at the z-plane and the s-plane, respectively, for the –BN fault cases. From these figures, it seems quite hard to visually distinguish groups of poles corresponding to specific pole scenarios in discrete time (z-plane), whereas it is relatively easier to distinguish these groups in continuous time (s-plane). But even when the s-plane is considered, poles corresponding to the N-1C beam configuration may be found in the area involving poles corresponding to the A-1C-affected beam (Figure 7b). In other words, the corresponding pole groups seem to effectively (although slightly) overlap. The same is obvious for the A-1C and B-1C poles, as well as the poles from the B-BN- and C-BN-affected beams (Figure 8b). Hence, although, in principle, –1C or –BN faults of all magnitudes and positions on the beam may be distinguished from each other, a statistical assessment of (overlapping) pole groups would be desirable. This assessment would quantify the inherent uncertainty when fault diagnosis (detection, isolation and magnitude estimation) is carried out by examining regions where these pole groups are located on the s-plane.

The statistical assessment of whether the regions of continuous-time pole groups corresponding to fault cases (test scenarios) are distinguishable between them may be carried out by formulating the statistical hypothesis problem (2), as described in Section 2.2. The Kruskal–Wallis test is again used for pairs of pole groups and addresses the hypothesis testing problem at a risk level α equal to 0.05. Only imaginary parts of the poles for each group are considered as pole coordinates since pole regions are delimited with respect to their imaginary part in Figure 7b and Figure 8b. The detection of fault occurrence for fault types –1C and –BN is examined by forming

Table 7. p-values for the comparison of two groups in the s-plane with the Kruskal–Wallis test for the fault detection and localization of –1C cases.

Fault Case	N-1C	A-1C	B-1C	C-1C
N-1C	N/A	0.0039	0.0039	0.0039
A-1C	0.0039	N/A	0.0104	0.0039
B-1C	0.0039	0.0104	N/A	0.0039
C-1C	0.0039	0.0039	0.0039	N/A

and

Table 8. p-values for the comparison of two groups in the s-plane with the Kruskal–Wallis test for the fault detection and localization of –BN cases.

Fault Case	N-BN	A-BN	B-BN	C-BN
N-BN	N/A	0.0039	0.0039	0.0039
A-BN	0.0039	N/A	0.0039	0.0039
B-BN	0.0039	0.0039	N/A	0.0374
C-BN	0.0039	0.0039	0.0374	N/A

, respectively. The intersecting cell of the i-th line and the j-th column presents the p-value obtained using the Kruskal–Wallis test for the fault cases indicated in the respective line and column. The shaded cells correspond to significantly overlapping groups of poles.

In Table 7, H₀ is systematically rejected for any comparison of N-1C against the A, B or C-1C fault cases, at α = 0.05, since in all such cases, the p-value is lower than α. In other words, the (imaginary parts of the) poles from the N-1C configuration do not follow a similar distribution as those from the A, B or C-1C configurations at α = 0.05, and faults may be systematically detected. Again, in Table 7, H₀ is systematically rejected for any comparison of N-1C against the A, B or C-1C fault cases at α = 0.05. Hence, all –1C fault cases have different impacts on the pole (imaginary) locations, meaning that all –1C faults may be identified. Note, however, that the p-value for comparing the A-1C and B-1C configurations is notably higher (see the intersection between the third line and the fourth column), although smaller than α = 0.05. This is related to the overlap between the two groups, as seen in Figure 7b, which was commented upon earlier on. The same conclusions in terms of detection and identification may be drawn for the –BN configurations with a careful examination of Table 8. Again, comparing the B-BN and C-BN configurations results in a higher-than-usual p-value (although again smaller than α = 0.05), which is related to the slight overlap of groups designating the B-BN and C-BN fault cases in Figure 8b. Lastly,

Table 9. p-values for the comparison of two groups in the s-plane with the Kruskal–Wallis test for fault localization and magnitude estimation between the –1C (small fault) and –BN (large fault) cases.

Fault Case	A-1C	B-1C	C-1C	A-BN	B-BN	C-BN
A-1C	N/A	0.0104	0.0039	0.0039	0.0039	0.0039
B-1C	0.0104	N/A	0.0039	0.0039	0.0039	0.0039
C-1C	0.0036	0.0036	N/A	0.0038	0.0036	0.0035
A-BN	0.0038	0.0038	0.0038	N/A	0.0038	0.0036
B-BN	0.0036	0.0036	0.0036	0.0038	N/A	0.0035
C-BN	0.0035	0.0035	0.0035	0.0036	0.0035	N/A

allows for addressing the issue of distinguishing between the fault configurations –1C (small fault magnitude) and –BN (large fault magnitude), as defined in Table 1. Again, the shaded cells correspond to significantly overlapping groups of poles. In general, the p-values are always smaller than α = 0.05, meaning that H₀ is systematically rejected at the risk level α = 0.05 for all comparisons between the –1C and –BN configurations. Then, no –BN fault may be mistaken for a –1C fault at the designated risk level. Obviously, these results are valid for cases of a single fault (load) occurrence at a time.

Note that formulating the statistical hypothesis problem (2), as described in Section 2.2, proved again to be highly beneficial for discrete-time pole groups in the z-plane. As noted before, in [24], it was hard to delimit specific z-plane pole areas associated with the fault cases of Table 1 using a simple visual inspection. In the current study, the Kruskal–Wallis test is again used for pairs of discrete-time pole groups (see Figure 7a and Figure 8a) in order to address the hypothesis testing problem at a risk level α equal to 0.05. For each such pole, its angle of rotation with respect to the origin is considered, and specifically, the ratio of its imaginary over its real part (effectively corresponding to the tangent of that angle). The detection of fault occurrence for the fault types –1C and –BN is examined by forming

Table 10. p-values for the comparison of two groups in the z-plane with the Kruskal–Wallis test for the fault detection and localization of –1C cases.

Fault Case	N-1C	A-1C	B-1C	C-1C
N-1C	N/A	0.0163	0.0039	0.0039
A-1C	0.0163	N/A	0.0065	0.0039
B-1C	0.0039	0.0065	N/A	0.0374
C-1C	0.0039	0.0039	0.0374	N/A

and

Table 11. p-values for the comparison of two groups in the z-plane with the Kruskal–Wallis test for the fault detection and localization of –BN cases.

Fault Case	N-ΒΝ	A-ΒΝ	B-ΒΝ	C-ΒΝ
N-BN	N/A	0.0039	0.0039	0.0039
A-BN	0.0039	N/A	0.0039	0.0039
B-BN	0.0039	0.0039	N/A	0.0374
C-BN	0.0039	0.0039	0.0374	N/A

, respectively. As in the continuous-time case, the intersecting cell of the i-th line and the j-th column presents the p-value obtained using the Kruskal–Wallis test for the fault cases indicated in the respective line and column. The shaded cells correspond to significantly overlapping groups of poles. The results are equivalent to those obtained for the s-plane pole groups, with H₀ systematically rejected for any comparison of N-1C against the A, B or C-1C fault cases, at α = 0.05, as shown in Table 10.

The same comments hold for results presented in Table 11, with H₀ systematically rejected for any comparison of N-BN against the A, B or C-BN fault cases, at α = 0.05. Again, one may distinguish between the s –1C (small fault) and –BN (large fault) configurations in Table 1 using rotation angles of the discrete-time poles in the z-plane to form

Table 12. p-values for the comparison of two groups in the z-plane with the Kruskal–Wallis test for fault localization and magnitude estimation between the –1C (small load) and –BN (big load) cases.

Fault Case	A-1C	B-1C	C-1C	A-BN	B-BN	C-BN
A-1C	N/A	0.0065	0.0039	0.0039	0.0039	0.0039
B-1C	0.0065	N/A	0.0374	0.0039	0.0039	0.0039
C-1C	0.0039	0.0374	N/A	0.0039	0.0039	0.0039
A-BN	0.0039	0.0039	0.0039	N/A	0.0039	0.0039
B-BN	0.0039	0.0039	0.0039	0.0039	N/A	0.0374
C-BN	0.0039	0.0039	0.0039	0.0039	0.0374	N/A

. As in the continuous-time case, the p-values are always smaller than α = 0.05, meaning that H₀ is systematically rejected at the risk level α = 0.05 for all comparisons between the –1C and –BN configurations. Then, no –BN fault may be mistaken for a –1C fault at the designated risk level, even using discrete-time AR poles. As in the continuous-time case, these results are valid for cases of a single fault (load) occurrence at a time.

A remark may at this point be made on having relatively few data values in each group when the comparisons between two or more groups are carried out using the Kruskal–Wallis test. As noted in Section 2, the Kruskal–Wallis test may be used with groups of five or more data values each [25,26,27], with relevant examples in [25], ch. 8, and in [26], ch. 25. It is clear that in the current study, this condition is fulfilled. Nonetheless, it would be advisable to use more data values per group since this would render the Kruskal–Wallis test more powerful. Currently, the test is more conservative rather than powerful in the sense that it is more reluctant to reject the null hypothesis H₀ at the designated risk level. This, in turn, means that the results presented both for sensing and for fault diagnosis purposes are rather conservative. In terms of evaluating sensing characteristics, for instance, if more data per group were available, then comparisons between certain groups at the band around 1400 Hz (which indicated overlapping groups due to the p-values being marginally higher than α = 0.05) could yield results toward rejecting H₀, thus enabling a distinction between the groups considered.

A final remark is related to these sensing and fault diagnosis results being obtained for a long, thin and flexible beam. The same basic setup with a model-based algorithmic framework was applied to shorter, thicker and quite more rigid polymer beams in the previous works [17] and (in part) [18], with similarly successful fault diagnosis results. Nonetheless, sensing properties were not comprehensively evaluated in these studies since they both aimed at obtaining fault diagnosis results. Moreover, no experiments with steel structures have been carried out yet. Specifically, for such cases, the applicability of the proposed setup and algorithmic analysis in terms of sensing and fault diagnosis has yet to be tested, even though the currently obtained results are promising.

4. Conclusions

A thin cantilever polymer beam with a short Metglas^® 2826MB ribbon attached to its surface was statistically evaluated in terms of contact-less sensing and fault diagnosis characteristics. The vibration of the beam’s free end creates the emission of magnetic flux by the Metglas^® ribbon (fixed on the opposite end), which induces a voltage in a coil suspended over the film. This voltage is, hence, obtained in a contact-less manner and is recorded with an oscilloscope. The voltage signal analysis showed that shifting of the dominant frequencies may result either from changes in the excitation frequency provided to the beam or from faults (loads) of various magnitudes and positions on the beam when the latter vibrates at a given frequency. A statistical framework based on the formulation of statistical hypothesis problems was introduced to evaluate such frequency-shifting characteristics, which led to two main results. First, a mapping between the vibration frequency level of the beam and the resulting frequency shifts observed in the recorded voltage was statistically established. Hence, sensing properties were obtained because the vibration level of the beam may be deduced by monitoring frequency shifting patterns in the voltage signal, with the uncertainty in the process quantified. Second, s-plane or z-plane areas containing poles corresponding to shifted frequencies of the voltage signal (modeled as per Section 2.2) were statistically linked to faults (loads) of specific magnitude and position affecting the beam. Hence, fault diagnosis properties were obtained because the occurrence, magnitude and position of faults (loads) on the beam may be deduced by checking the s-plane or z-plane pole locations, with the uncertainty in the process quantified. Future work will involve validating the setup’s sensing and fault diagnosis performance for low excitation frequency and/or high beam deflection and/or cases of multiple fault occurrence. It would be equally useful to evaluate the impact of integrating multiple sensing sets (ribbon and coils) on the beam.