Using Wearable Accelerometers to Develop a Vertical Ground Reaction Force Prediction Model during Running: A Sensitivity Study
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Materials
2.3. Protocol
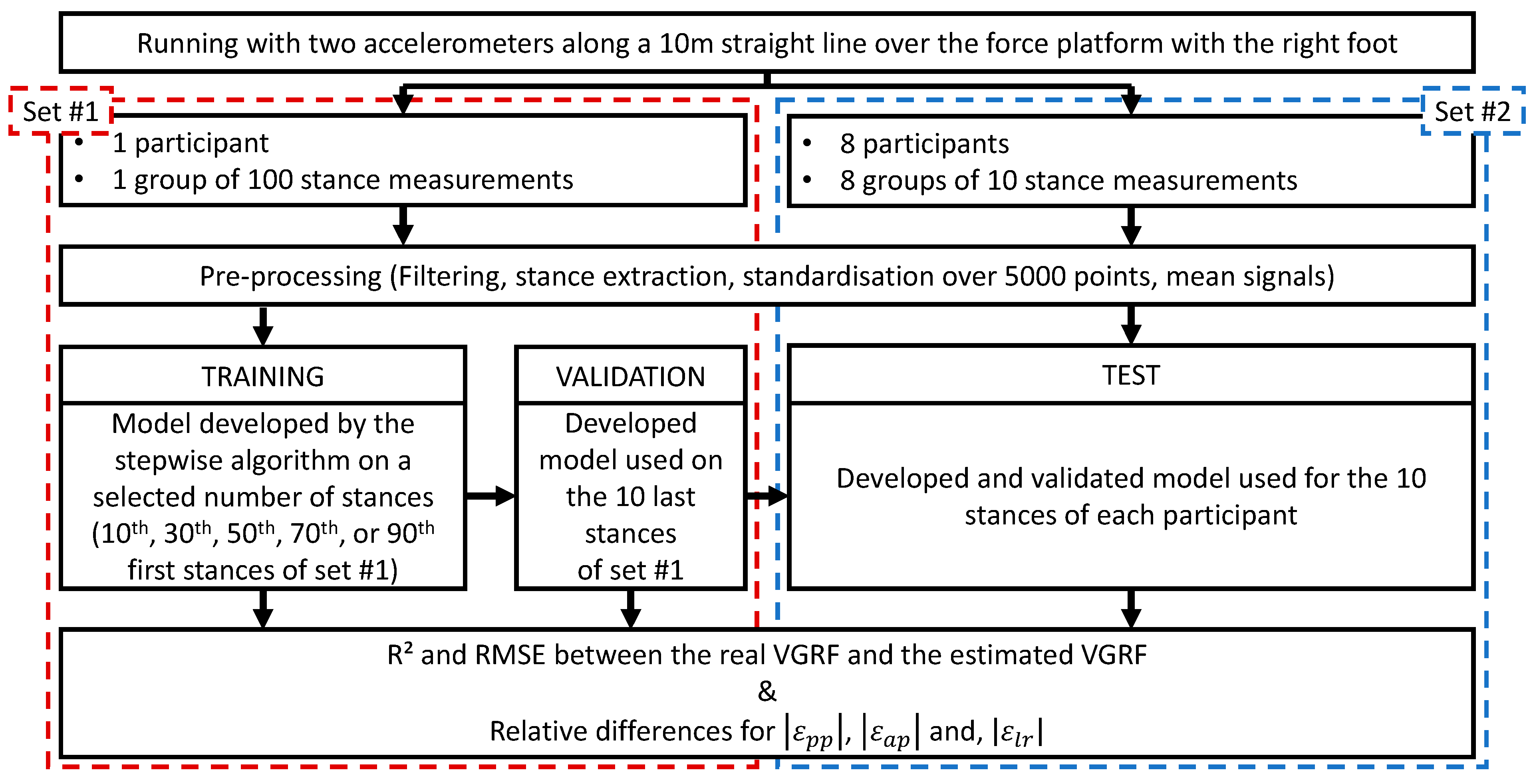
2.4. Data Management
2.5. Pre-Processing
2.6. Model Development
2.7. Statistics and Model Validation
3. Results
3.1. General Results
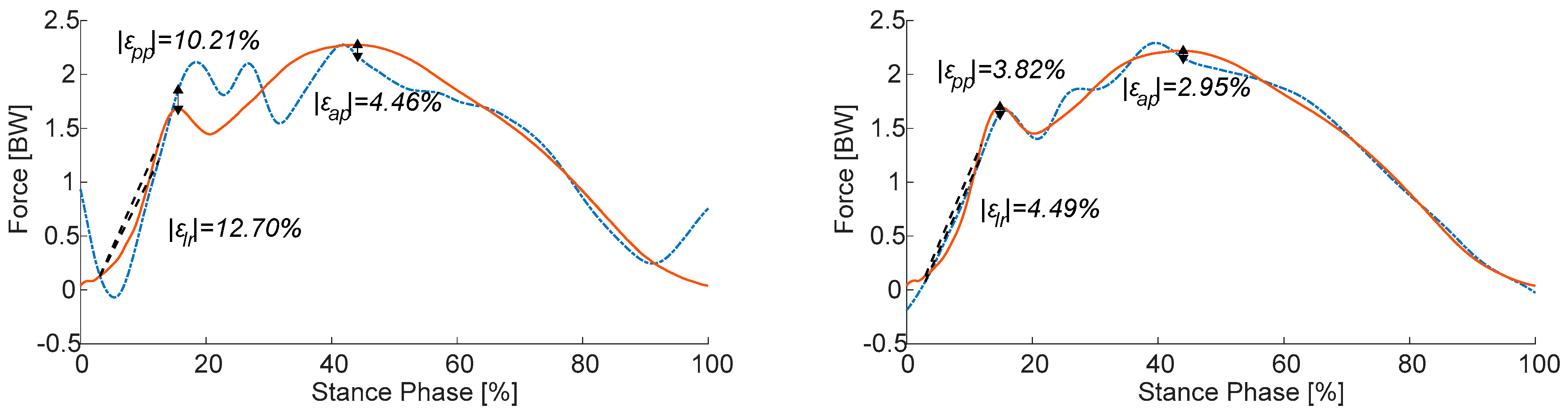
3.2. Training Phase
3.3. Validation Phase
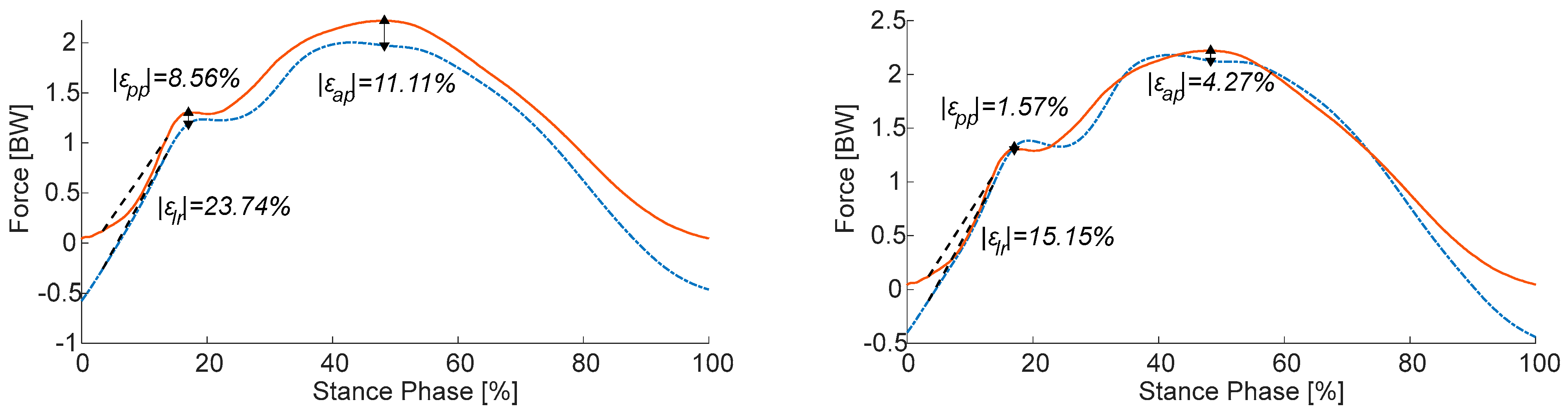
3.4. Test Phase
4. Discussion
4.1. Training and Validation Phases
4.2. Sensitivity to Cut-Off Frequency Conditions and Size of Training Dataset
4.3. Test Phase
4.4. Personalized Model
4.5. Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Cut-Off Freq. (Hz) | Stance # | Training | Validation | ||||||||
| R2 | RMSE (BW) | (%) | (%) | (%) | R2 | RMSE (BW) | (%) | (%) | (%) | ||
| 5 | 10 | 0.987 | 0.08 | 10.95 | 1.71 | 18.08 | 0.712 | 0.48 | 72.31 | 11.39 | 49.41 |
| 30 | 0.985 | 0.09 | 14.14 | 1.79 | 8.33 | 0.970 | 0.23 | 21.39 | 15.45 | 2.80 | |
| 50 | 0.988 | 0.08 | 12.50 | 0.87 | 9.26 | 0.979 | 0.15 | 4.86 | 7.19 | 3.51 | |
| 70 | 0.989 | 0.08 | 11.99 | 0.44 | 8.95 | 0.971 | 0.13 | 1.51 | 1.29 | 1.15 | |
| 90 | 0.989 | 0.08 | 12.02 | 0.68 | 9.51 | 0.967 | 0.14 | 1.17 | 0.17 | 5.90 | |
| 10 | 10 | 0.983 | 0.10 | 6.41 | 1.15 | 15.39 | 0.658 | 0.52 | 96.81 | 13.87 | 115.70 |
| 30 | 0.988 | 0.08 | 11.33 | 1.75 | 7.20 | 0.931 | 0.25 | 35.87 | 11.64 | 21.07 | |
| 50 | 0.989 | 0.08 | 11.02 | 0.53 | 8.79 | 0.975 | 0.13 | 11.18 | 2.80 | 0.95 | |
| 70 | 0.990 | 0.07 | 10.39 | 0.70 | 7.23 | 0.968 | 0.14 | 2.71 | 0.61 | 0.85 | |
| 90 | 0.990 | 0.07 | 10.23 | 0.46 | 7.33 | 0.963 | 0.14 | 1.51 | 2.11 | 1.89 | |
| 15 | 10 | 0.970 | 0.13 | 1.18 | 1.34 | 13.09 | 0.548 | 0.59 | 114.19 | 15.68 | 176.38 |
| 30 | 0.990 | 0.07 | 7.77 | 2.20 | 5.83 | 0.900 | 0.28 | 42.23 | 11.68 | 41.68 | |
| 50 | 0.991 | 0.07 | 8.98 | 0.11 | 8.01 | 0.960 | 0.16 | 15.23 | 1.59 | 10.51 | |
| 70 | 0.990 | 0.07 | 8.21 | 2.44 | 5.08 | 0.956 | 0.16 | 2.84 | 1.01 | 1.40 | |
| 90 | 0.990 | 0.07 | 7.80 | 2.20 | 4.71 | 0.951 | 0.17 | 0.26 | 2.48 | 1.54 | |
| 20 | 10 | 0.952 | 0.16 | 2.71 | 1.72 | 11.73 | 0.425 | 0.68 | 128.22 | 17.94 | 221.23 |
| 30 | 0.990 | 0.07 | 3.82 | 2.95 | 4.49 | 0.873 | 0.31 | 45.99 | 12.14 | 60.70 | |
| 50 | 0.992 | 0.07 | 6.57 | 0.96 | 7.11 | 0.935 | 0.20 | 19.38 | 1.21 | 22.37 | |
| 70 | 0.989 | 0.08 | 5.63 | 4.46 | 3.09 | 0.934 | 0.20 | 3.50 | 0.84 | 6.60 | |
| 90 | 0.989 | 0.08 | 4.94 | 4.22 | 2.40 | 0.932 | 0.20 | 0.45 | 2.24 | 4.28 | |
| 25 | 10 | 0.934 | 0.19 | 5.49 | 2.12 | 11.21 | 0.323 | 0.77 | 140.79 | 20.08 | 254.36 |
| 30 | 0.986 | 0.08 | 0.21 | 3.87 | 3.62 | 0.847 | 0.33 | 48.22 | 12.40 | 77.05 | |
| 50 | 0.992 | 0.06 | 4.00 | 1.90 | 6.38 | 0.904 | 0.25 | 23.38 | 1.26 | 34.40 | |
| 70 | 0.986 | 0.09 | 2.91 | 6.49 | 1.72 | 0.908 | 0.24 | 4.63 | 0.35 | 13.38 | |
| 90 | 0.985 | 0.09 | 1.94 | 6.24 | 0.96 | 0.909 | 0.23 | 0.54 | 1.71 | 9.09 | |
| 30 | 10 | 0.917 | 0.21 | 7.38 | 2.54 | 11.25 | 0.249 | 0.85 | 152.24 | 21.94 | 279.08 |
| 30 | 0.981 | 0.10 | 4.15 | 4.88 | 3.38 | 0.822 | 0.35 | 49.39 | 12.33 | 90.66 | |
| 50 | 0.992 | 0.07 | 1.42 | 2.87 | 5.98 | 0.869 | 0.29 | 26.95 | 1.48 | 45.47 | |
| 70 | 0.982 | 0.10 | 0.21 | 8.38 | 1.12 | 0.879 | 0.28 | 5.98 | 0.22 | 20.70 | |
| 90 | 0.981 | 0.10 | 0.97 | 8.10 | 0.50 | 0.885 | 0.26 | 0.20 | 1.18 | 14.97 | |
| 35 | 10 | 0.903 | 0.23 | 8.63 | 3.00 | 11.56 | 0.196 | 0.93 | 162.60 | 23.51 | 297.54 |
| 30 | 0.973 | 0.12 | 7.86 | 5.92 | 3.75 | 0.799 | 0.36 | 49.82 | 11.95 | 101.73 | |
| 50 | 0.990 | 0.07 | 1.08 | 3.81 | 5.94 | 0.835 | 0.33 | 29.96 | 1.73 | 55.14 | |
| 70 | 0.978 | 0.11 | 2.33 | 10.06 | 1.22 | 0.851 | 0.31 | 7.34 | 0.71 | 27.85 | |
| 90 | 0.975 | 0.11 | 3.64 | 9.75 | 0.90 | 0.863 | 0.29 | 0.39 | 0.78 | 21.16 | |
| 40 | 10 | 0.891 | 0.24 | 9.44 | 3.48 | 11.97 | 0.159 | 0.99 | 171.86 | 24.83 | 311.26 |
| 30 | 0.964 | 0.14 | 11.27 | 6.96 | 4.61 | 0.778 | 0.38 | 49.74 | 11.32 | 110.54 | |
| 50 | 0.989 | 0.08 | 3.44 | 4.72 | 6.25 | 0.803 | 0.37 | 32.40 | 1.92 | 63.30 | |
| 70 | 0.974 | 0.12 | 4.66 | 11.52 | 1.87 | 0.825 | 0.34 | 8.58 | 1.05 | 34.47 | |
| 90 | 0.970 | 0.13 | 6.01 | 11.18 | 1.93 | 0.842 | 0.31 | 1.04 | 0.56 | 27.18 | |
| 45 | 10 | 0.880 | 0.26 | 9.93 | 3.97 | 12.36 | 0.134 | 1.04 | 180.03 | 25.94 | 321.39 |
| 30 | 0.954 | 0.16 | 14.33 | 7.95 | 5.81 | 0.759 | 0.39 | 49.33 | 10.51 | 117.43 | |
| 50 | 0.986 | 0.08 | 5.61 | 5.55 | 6.83 | 0.775 | 0.39 | 34.31 | 2.02 | 70.07 | |
| 70 | 0.969 | 0.13 | 6.76 | 12.77 | 2.91 | 0.802 | 0.36 | 9.67 | 1.24 | 40.39 | |
| 90 | 0.964 | 0.14 | 8.07 | 12.40 | 3.38 | 0.824 | 0.32 | 1.69 | 0.50 | 32.77 | |
| 50 | 10 | 0.872 | 0.27 | 10.21 | 4.46 | 12.70 | 0.115 | 1.08 | 187.19 | 26.88 | 328.78 |
| 30 | 0.943 | 0.17 | 17.03 | 8.87 | 7.25 | 0.742 | 0.40 | 48.74 | 9.60 | 122.75 | |
| 50 | 0.984 | 0.09 | 7.59 | 6.32 | 7.62 | 0.750 | 0.42 | 35.79 | 2.04 | 75.61 | |
| 70 | 0.965 | 0.14 | 8.61 | 13.85 | 4.20 | 0.782 | 0.38 | 10.57 | 1.29 | 45.60 | |
| 90 | 0.959 | 0.15 | 9.83 | 13.44 | 5.06 | 0.808 | 0.34 | 2.27 | 0.58 | 37.82 | |
References
- Lieberman, D.E.; Venkadesan, M.; Werbel, W.A.; Daoud, A.I.; Dandrea, S.; Davis, I.S.; Mangeni, R.O.; Pitsiladis, Y. Foot Strike Patterns and Collision Forces in Habitually Barefoot versus Shod Runners. Nature 2010, 463, 531–535. [Google Scholar] [CrossRef]
- Weyand, P.G.; Sternlight, D.B.; Bellizzi, M.J.; Wright, S. Faster Top Running Speeds Are Achieved with Greater Ground Forces Not More Rapid Leg Movements. J. Appl. Physiol. 2000, 89, 1991–1999. [Google Scholar] [CrossRef]
- Zadpoor, A.A.; Nikooyan, A.A. The Relationship between Lower-Extremity Stress Fractures and the Ground Reaction Force: A Systematic Review. Clin. Biomech. 2011, 26, 23–28. [Google Scholar] [CrossRef]
- Milner, C.E.; Ferber, R.; Pollard, C.D.; Hamill, J.; Davis, I.S. Biomechanical Factors Associated with Tibial Stress Fracture in Female Runners. Med. Sci. Sports Exerc. 2006, 38, 323–328. [Google Scholar] [CrossRef]
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends Supporting the In-Field Use of Wearable Inertial Sensors for Sport Performance Evaluation: A Systematic Review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef]
- Pouliot-Laforte, A.; Veilleux, L.N.; Rauch, F.; Lemay, M. Validity of an Accelerometer as a Vertical Ground Reaction Force Measuring Device in Healthy Children and Adolescents and in Children and Adolescents with Osteogenesis Imperfecta Type I. J. Musculoskelet. Neuronal Interact. 2014, 14, 155–161. [Google Scholar]
- Elvin, N.G.; Elvin, A.A.; Arnoczky, S.P. Correlation between Ground Reaction Force and Tibial Acceleration in Vertical Jumping. J. Appl. Biomech. 2007, 23, 180–189. [Google Scholar] [CrossRef]
- Neugebauer, J.M.; Hawkins, D.A.; Beckett, L. Estimating Youth Locomotion Ground Reaction Forces Using an Accelerometer-Based Activity Monitor. PLoS ONE 2012, 7, e48182. [Google Scholar] [CrossRef]
- Howard, R.; Conway, R.; Harrison, A.J. Estimation of Force during Vertical Jumps Using Body Fixed Accelerometers. In Proceedings of the 25th IET Irish Signals & Systems Conference 2014 and 2014 China-Ireland International Conference on Information and Communities Technologies (ISSC 2014/CIICT 2014), Limerick, Ireland, 26–27 June 2014; Volume 2014, pp. 102–107. [Google Scholar]
- Raper, D.P.; Witchalls, J.; Philips, E.J.; Knight, E.; Drew, M.K.; Waddington, G. Use of a Tibial Accelerometer to Measure Ground Reaction Force in Running: A Reliability and Validity Comparison with Force Plates. J. Sci. Med. Sport 2018, 21, 84–88. [Google Scholar] [CrossRef]
- Henning, E.M.; Lafortune, M.A. Relationships between Ground Reaction Force and Tibial Bone Acceleration Parameters. J. Appl. Biomech. 1997, 7, 303–309. [Google Scholar] [CrossRef]
- Ancillao, A.; Tedesco, S.; Barton, J.; O’Flynn, B. Indirect Measurement of Ground Reaction Forces and Moments by Means of Wearable Inertial Sensors: A Systematic Review. Sensors 2018, 18, 2564. [Google Scholar] [CrossRef] [PubMed]
- Wundersitz, D.W.T.; Netto, K.J.; Aisbett, B.; Gastin, P.B. Validity of an Upper-Body-Mounted Accelerometer to Measure Peak Vertical and Resultant Force during Running and Change-of-Direction Tasks. Sports Biomech. 2013, 12, 403–412. [Google Scholar] [CrossRef] [PubMed]
- Gurchiek, R.D.; McGinnis, R.S.; Needle, A.R.; McBride, J.M.; van Werkhoven, H. The Use of a Single Inertial Sensor to Estimate 3-Dimensional Ground Reaction Force during Accelerative Running Tasks. J. Biomech. 2017, 61, 263–268. [Google Scholar] [CrossRef]
- Cavagna, G.A. Force Platforms as Ergometers. J. Appl. Physiol. 1985, 39, 174–179. [Google Scholar] [CrossRef] [PubMed]
- Blickhan, R. The Spring-Mass Model for Running and Hopping. J. Biomech. 1989, 22, 1217–1227. [Google Scholar] [CrossRef]
- Morin, J.-B.; Dalleau, G.; Kyröläinen, H.; Jeannin, T.; Belli, A. A Simple Method for Measuring Stiffness during Running. J. Appl. Biomech. 2005, 21, 167–180. [Google Scholar] [CrossRef]
- Nedergaard, N.J.; Verheul, J.; Drust, B.; Etchells, T.; Lisboa, P.; Robinson, M.A.; Vanrenterghem, J. The Feasibility of Predicting Ground Reaction Forces during Running from a Trunk Accelerometry Driven Mass-Spring-Damper Model. PeerJ 2018, 6, e6105. [Google Scholar] [CrossRef]
- Derie, R.; Robberechts, P.; Van den Berghe, P.; Gerlo, J.; De Clercq, D.; Segers, V.; Davis, J. Tibial Acceleration-Based Prediction of Maximal Vertical Loading Rate During Overground Running: A Machine Learning Approach. Front. Bioeng. Biotechnol. 2020, 8, 33. [Google Scholar] [CrossRef]
- Ngoh, K.J.-H.; Gouwanda, D.; Gopalai, A.A.; Chong, Y.Z. Estimation of Vertical Ground Reaction Force during Running Using Neural Network Model and Uniaxial Accelerometer. J. Biomech. 2018, 76, 269–273. [Google Scholar] [CrossRef]
- Neugebauer, J.M.; Collins, K.H.; Hawkins, D.A. Ground Reaction Force Estimates from ActiGraph GT3X+ Hip Accelerations. PLoS ONE 2014, 9, e99023. [Google Scholar] [CrossRef]
- Seeley, M.K.; Evans-Pickett, A.; Collins, G.Q.; Tracy, J.B.; Tuttle, N.J.; Rosquist, P.G.; Merrell, A.J.; Christensen, W.F.; Fullwood, D.T.; Bowden, A.E. Predicting Vertical Ground Reaction Force during Running Using Novel Piezoresponsive Sensors and Accelerometry. J. Sports Sci. 2020, 38, 1844–1858. [Google Scholar] [CrossRef] [PubMed]
- Thiel, D.V.; Shepherd, J.; Espinosa, H.G.; Kenny, M.; Fischer, K.; Worsey, M.; Matsuo, A.; Wada, T. Predicting Ground Reaction Forces in Sprint Running Using a Shank Mounted Inertial Measurement Unit. Proceedings 2018, 2, 199. [Google Scholar] [CrossRef]
- Lariviere, O.; Provot, T.; Valdes-Tamayo, L.; Bourgain, M.; Chadefaux, D. Force Pattern and Acceleration Waveform Repeatability of Amateur Runners. Proceedings 2020, 49, 136. [Google Scholar] [CrossRef]
- Gruber, A.H.; Edwards, W.B.; Hamill, J.; Derrick, T.R.; Boyer, K.A. A Comparison of the Ground Reaction Force Frequency Content during Rearfoot and Non-Rearfoot Running Patterns. Gait Posture 2017, 56, 54–59. [Google Scholar] [CrossRef] [PubMed]
- Hunter, J.P.; Marshall, R.N.; McNair, P.J. Relationships between Ground Reaction Force Impulse and Kinematics of Sprint-Running Acceleration. J. Appl. Biomech. 2005, 21, 31–43. [Google Scholar] [CrossRef]
- Benson, L.C.; Clermont, C.A.; Watari, R.; Exley, T.; Ferber, R. Automated Accelerometer-Based Gait Event Detection during Multiple Running Conditions. Sensors 2019, 19, 1483. [Google Scholar] [CrossRef]
- Mo, S.; Chow, D.H.K. Accuracy of Three Methods in Gait Event Detection during Overground Running. Gait Posture 2018, 59, 93–98. [Google Scholar] [CrossRef]
- Hopkins, W.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive Statistics for Studies in Sports Medicine and Exercise Science. Med. Sci. Sports Exerc. 2009, 41, 3–12. [Google Scholar] [CrossRef]
- Verheul, J.; Nedergaard, N.J.; Pogson, M.; Lisboa, P.; Gregson, W.; Vanrenterghem, J.; Robinson, M.A. Biomechanical Loading during Running: Can a Two Mass-Spring-Damper Model Be Used to Evaluate Ground Reaction Forces for High-Intensity Tasks? Sports Biomech. 2019, 20, 571–582. [Google Scholar] [CrossRef]
- Ueda, T.; Hobara, H.; Kobayashi, Y.; Heldoorn, T.A.; Mochimaru, M.; Mizoguchi, H. Comparison of 3 Methods for Computing Loading Rate during Running. Int. J. Sports Med. 2016, 37, 1087–1090. [Google Scholar] [CrossRef]
- Huang, Y.; Xia, H.; Chen, G.; Cheng, S.; Cheung, R.T.H.; Shull, P.B. Foot strike pattern, step rate, and trunk posture combined gait modifications to reduce impact loading during running. J. Biomech. 2019, 86, 102–109. [Google Scholar] [CrossRef]
- Provot, T.; Chiementin, X.; Bolaers, F.; Murer, S. Effect of Running Speed on Temporal and Frequency Indicators from Wearable MEMS Accelerometers. Sports Biomech. 2021, 20, 831–843. [Google Scholar] [CrossRef]
- Komaris, D.S.; Pérez-Valero, E.; Jordan, L.; Barton, J.; Hennessy, L.; O’flynn, B.; Tedesco, S. Predicting Three-Dimensional Ground Reaction Forces in Running by Using Artificial Neural Networks and Lower Body Kinematics. IEEE Access 2019, 7, 156779–156786. [Google Scholar] [CrossRef]
- Johnson, W.R.; Mian, A.; Robinson, M.A.; Verheul, J.; Lloyd, D.G.; Alderson, J.A. Multidimensional Ground Reaction Forces and Moments from Wearable Sensor Accelerations via Deep Learning. IEEE Trans. Biomed. Eng. 2020, 68, 289–297. [Google Scholar] [CrossRef]
- Van Hooren, B.; Fuller, J.T.; Buckley, J.D.; Miller, J.R.; Sewell, K.; Rao, G.; Barton, C.; Bishop, C.; Willy, R.W. Is Motorized Treadmill Running Biomechanically Comparable to Overground Running? A Systematic Review and Meta-Analysis of Cross-over Studies. Sports Med. 2019, 50, 785–813. [Google Scholar] [CrossRef]
- Keller, T.; Weisberger, A.; Ray, J.; Hasan, S.; Shiavi, R.; Spengler, D. Relationship between Vertical Ground Reaction Force and Speed during Walking, Slow Jogging, and Running. Clin. Biomech. 1996, 11, 253–259. [Google Scholar] [CrossRef] [PubMed]
- Lafortune, M.A. Three-Dimensional Acceleration of the Tibia during Walking and Running. J. Biomech. 1991, 24, 877–886. [Google Scholar] [CrossRef]
- Alcantara, R.S.; Edwards, W.B.; Millet, G.Y.; Grabowski, A.M. Predicting Continuous Ground Reaction Forces from Accelerometers during Uphill and Downhill Running: A Recurrent Neural Network Solution. PeerJ 2022, 10, e12752. [Google Scholar] [CrossRef]
- Purcell, B.; Channells, J.; James, D.; Barrett, R. Use of Accelerometers for Detecting Foot-Ground Contact Time during Running. In BioMEMS and Nanotechnology II, Proceedings of the Microelectronics, MEMS, and Nanotechnology, Brisbane, Australia, 11–14 December 2005; Nicolau, D.V., Ed.; SPIE: Bellingham, WA, USA, 2006; Volume 6036, p. 603615. [Google Scholar]
- Chew, D.-K.; Ngoh, K.J.-H.; Gouwanda, D.; Gopalai, A.A. Estimating Running Spatial and Temporal Parameters Using an Inertial Sensor. Sport. Eng. 2018, 21, 115–122. [Google Scholar] [CrossRef]
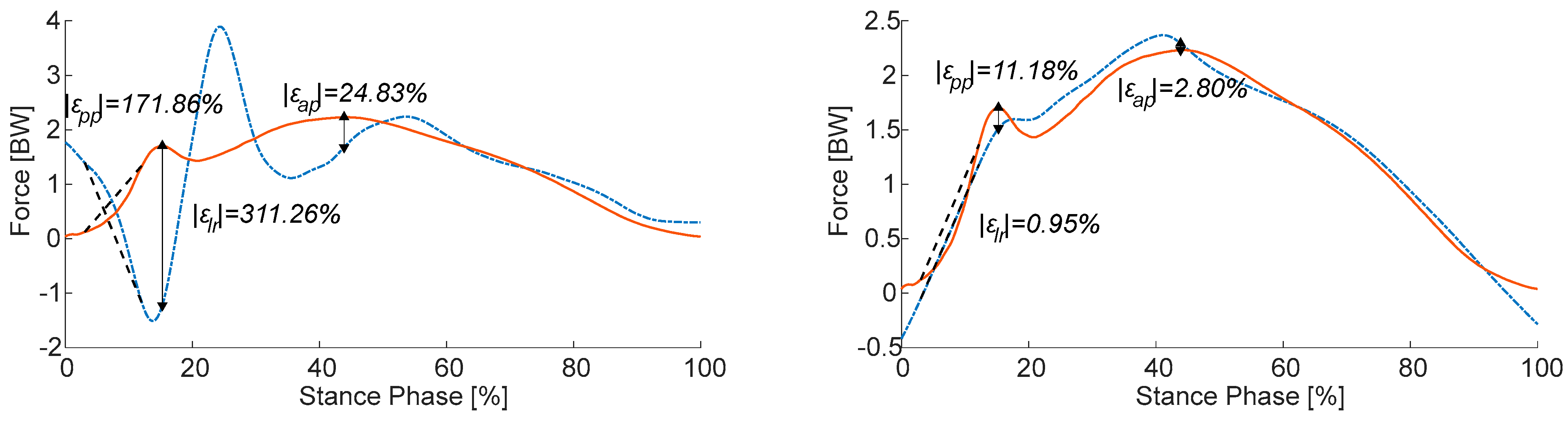
| Participant # | Mean | Standard Deviation |
|---|---|---|
| 1 | 3.19 | 0.11 |
| 2 | 3.13 | 0.25 |
| 3 | 2.78 | 0.03 |
| 4 | 3.08 | 0.06 |
| 5 | 2.75 | 0.06 |
| 6 | 2.83 | 0.06 |
| 7 | 3.39 | 0.19 |
| 8 | 3.11 | 0.06 |
| Number of Stances | Cut-Off Frequency (Hz) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
| 10 | 0.987 | 0.983 | 0.970 | 0.952 | 0.934 | 0.917 | 0.903 | 0.891 | 0.880 | 0.872 |
| 30 | 0.985 | 0.988 | 0.990 | 0.990 | 0.986 | 0.981 | 0.973 | 0.964 | 0.954 | 0.943 |
| 50 | 0.988 | 0.989 | 0.991 | 0.992 | 0.992 | 0.992 | 0.990 | 0.989 | 0.986 | 0.984 |
| 70 | 0.989 | 0.990 | 0.990 | 0.989 | 0.986 | 0.982 | 0.978 | 0.974 | 0.969 | 0.965 |
| 90 | 0.989 | 0.990 | 0.990 | 0.989 | 0.985 | 0.981 | 0.975 | 0.970 | 0.964 | 0.959 |
| Number of Stances | Cut-Off Frequency (Hz) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
| 10 | 0.712 | 0.658 | 0.548 | 0.425 | 0.323 | 0.249 | 0.196 | 0.159 | 0.134 | 0.115 |
| 30 | 0.970 | 0.931 | 0.900 | 0.873 | 0.847 | 0.822 | 0.799 | 0.778 | 0.759 | 0.742 |
| 50 | 0.979 | 0.975 | 0.960 | 0.935 | 0.904 | 0.869 | 0.835 | 0.803 | 0.775 | 0.750 |
| 70 | 0.971 | 0.968 | 0.956 | 0.934 | 0.908 | 0.879 | 0.851 | 0.825 | 0.802 | 0.782 |
| 90 | 0.967 | 0.963 | 0.951 | 0.932 | 0.909 | 0.885 | 0.863 | 0.842 | 0.824 | 0.808 |
| Participant # | R2 | RMSE (BW) | (%) | (%) | (%) |
|---|---|---|---|---|---|
| 1 | 0.924 | 0.45 | 30.77 | 32.42 | 40.90 |
| 2 | 0.661 | 0.45 | 47.25 | 23.62 | 56.36 |
| 3 | 0.742 | 0.84 | 33.26 | 43.95 | 3.64 |
| 4 | 0.985 | 0.17 | 1.57 | 4.27 | 15.15 |
| 5 | 0.793 | 0.36 | 51.20 | 12.81 | 25.42 |
| 6 | 0.900 | 0.42 | 26.30 | 33.21 | 28.59 |
| 7 | 0.340 | 0.74 | 68.45 | 23.80 | 21.77 |
| 8 | 0.411 | 0.75 | 60.16 | 23.15 | 55.65 |
| Participant # | R2 | RMSE (BW) | (%) | (%) | (%) |
|---|---|---|---|---|---|
| 1 | 0.957 ± 0.016 | 0.45 ± 0.08 | 18.32 ± 7.36 | 24.33 ± 7.09 | 34.94 ± 2.75 |
| 2 | 0.749 ± 0.136 | 0.41 ± 0.10 | 21.28 ± 15.36 | 18.91 ± 6.15 | 48.78 ± 5.94 |
| 3 | 0.785 ± 0.055 | 1.02 ± 0.28 | 25.45 ± 7.07 | 58.77 ± 19.22 | 14.74 ± 10.46 |
| 4 | 0.947 ± 0.036 | 0.45 ± 0.29 | 21.96 ± 19.39 | 21.96 ± 18.04 | 20.09 ± 9.81 |
| 5 | 0.898 ± 0.062 | 0.43 ± 0.15 | 51.41 ± 11.74 | 12.06 ± 7.84 | 13.25 ± 7.49 |
| 6 | 0.807 ± 0.084 | 0.48 ± 0.08 | 10.49 ± 7.83 | 29.83 ± 5.97 | 15.35 ± 6.85 |
| 7 | 0.294 ± 0.111 | 0.88 ± 0.23 | 77.05 ± 15.64 | 28.43 ± 6.83 | 23.43 ± 5.36 |
| 8 | 0.574 ± 0.111 | 0.63 ± 0.08 | 56.87 ± 4.23 | 16.09 ± 4.75 | 49.69 ± 3.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Provot, T.; Choupani, S.; Bourgain, M.; Valdes-Tamayo, L.; Chadefaux, D. Using Wearable Accelerometers to Develop a Vertical Ground Reaction Force Prediction Model during Running: A Sensitivity Study. Vibration 2023, 6, 680-694. https://doi.org/10.3390/vibration6030042
Provot T, Choupani S, Bourgain M, Valdes-Tamayo L, Chadefaux D. Using Wearable Accelerometers to Develop a Vertical Ground Reaction Force Prediction Model during Running: A Sensitivity Study. Vibration. 2023; 6(3):680-694. https://doi.org/10.3390/vibration6030042
Chicago/Turabian StyleProvot, Thomas, Samaneh Choupani, Maxime Bourgain, Laura Valdes-Tamayo, and Delphine Chadefaux. 2023. "Using Wearable Accelerometers to Develop a Vertical Ground Reaction Force Prediction Model during Running: A Sensitivity Study" Vibration 6, no. 3: 680-694. https://doi.org/10.3390/vibration6030042
APA StyleProvot, T., Choupani, S., Bourgain, M., Valdes-Tamayo, L., & Chadefaux, D. (2023). Using Wearable Accelerometers to Develop a Vertical Ground Reaction Force Prediction Model during Running: A Sensitivity Study. Vibration, 6(3), 680-694. https://doi.org/10.3390/vibration6030042






