Investigation on the Rotordynamic Characteristics of Turbopumps with Angular Contact Ball Bearings
Abstract
:1. Introduction
2. Stiffness Theoretical Model of Angular Contact Ball Bearing
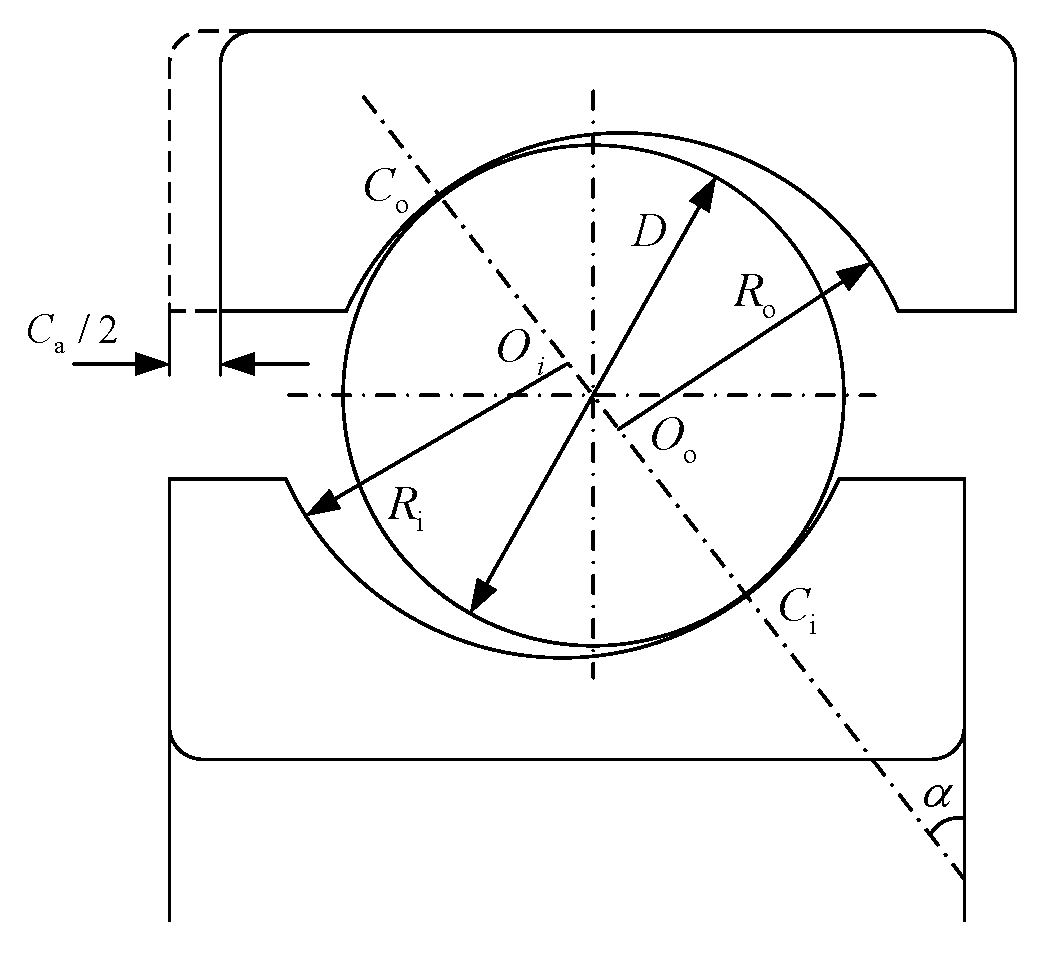
2.1. Clearance and Contact Angle
2.2. Stiffness Theoretical Model of Ball Bearing
2.3. Dynamic Model of Rotor System
- (1)
- The radial stiffness and angular stiffness of the angular contact ball bearing were calculated, according to the inner ring speed at the nth time of the current speed.
- (2)
- Based on Equation (13), and the equivalent stiffness obtained from the above previous step, the vibration response at (n + 1)th will be obtained.
- (3)
- Compare the vibration response of the nth and (n + 1)th. If it is less than the threshold value, the iteration exits. Otherwise, the response of (n + 2)th was defined as the mean value of the vibration response at nth and (n + 1)th, and the iterative solution was continued.
3. Dynamical Response of the Turbopump Rotor System
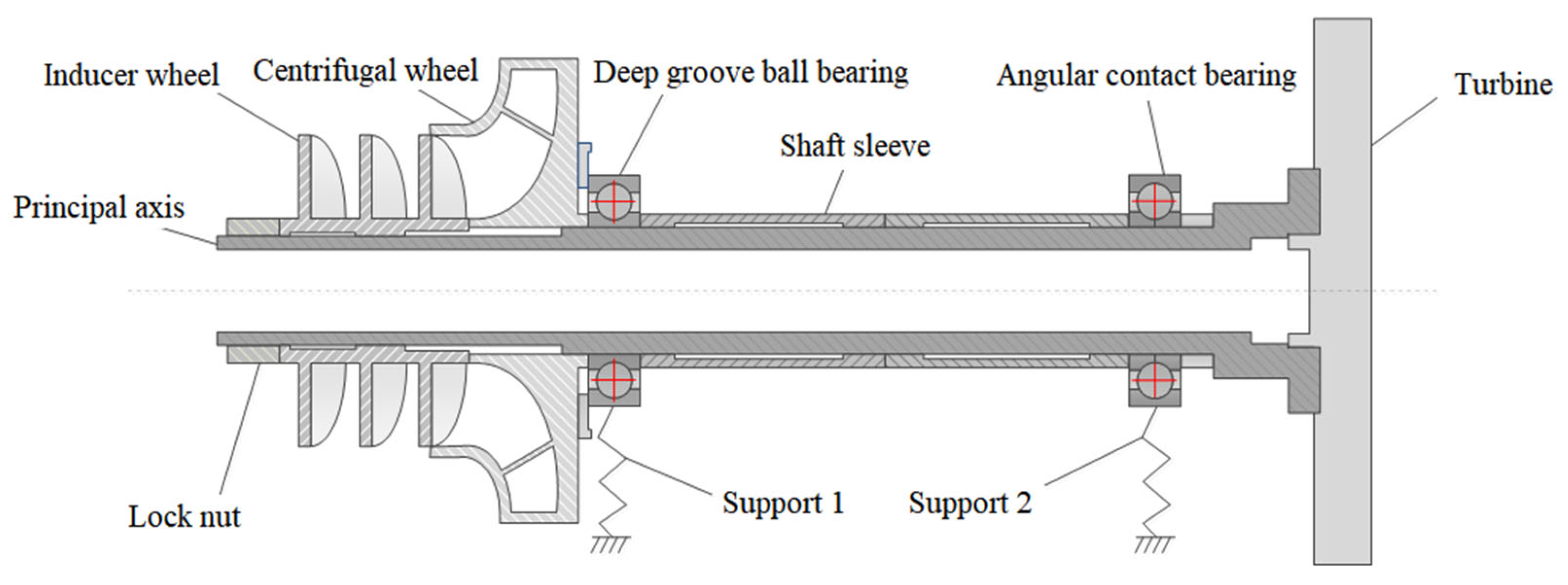
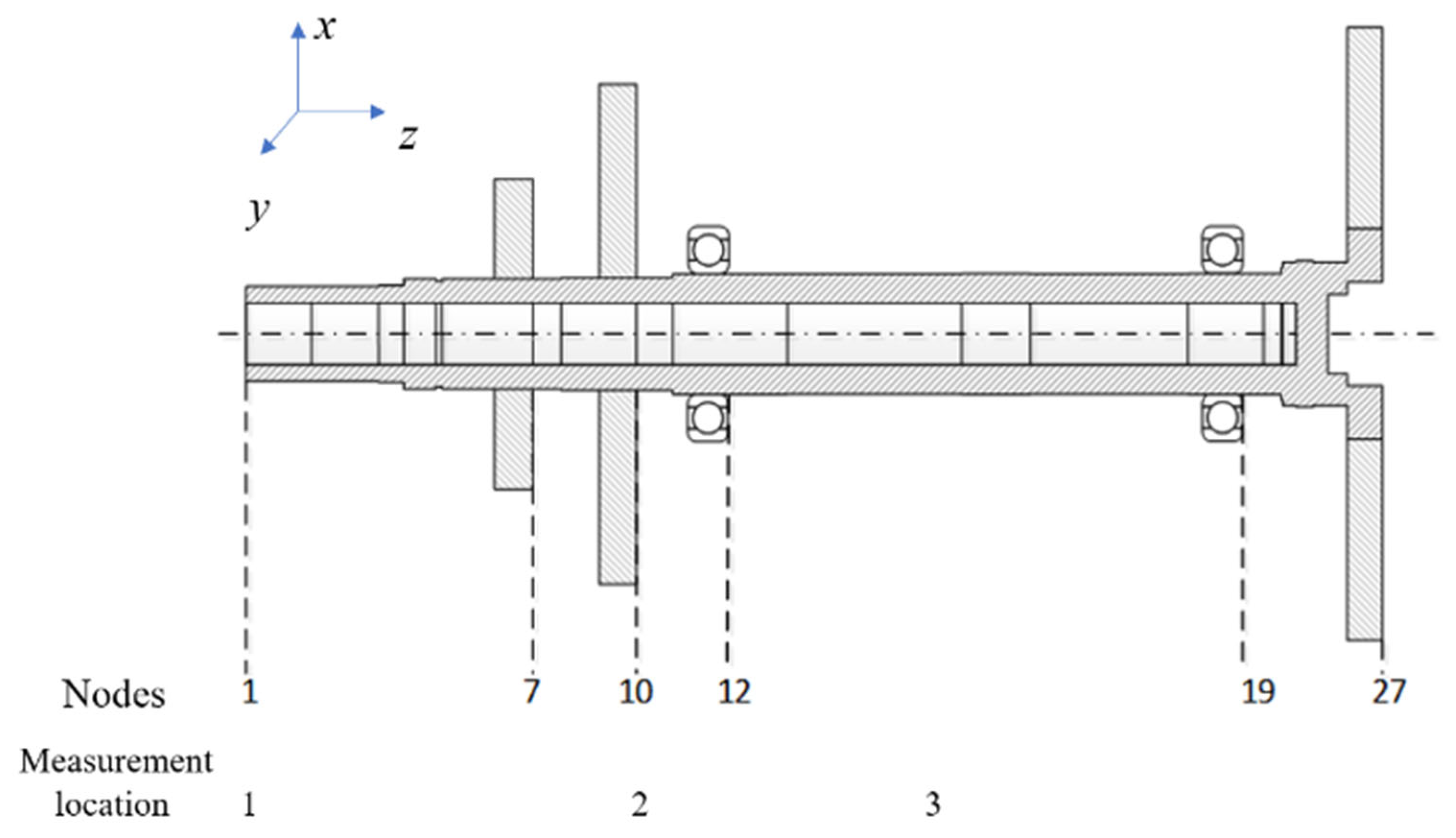
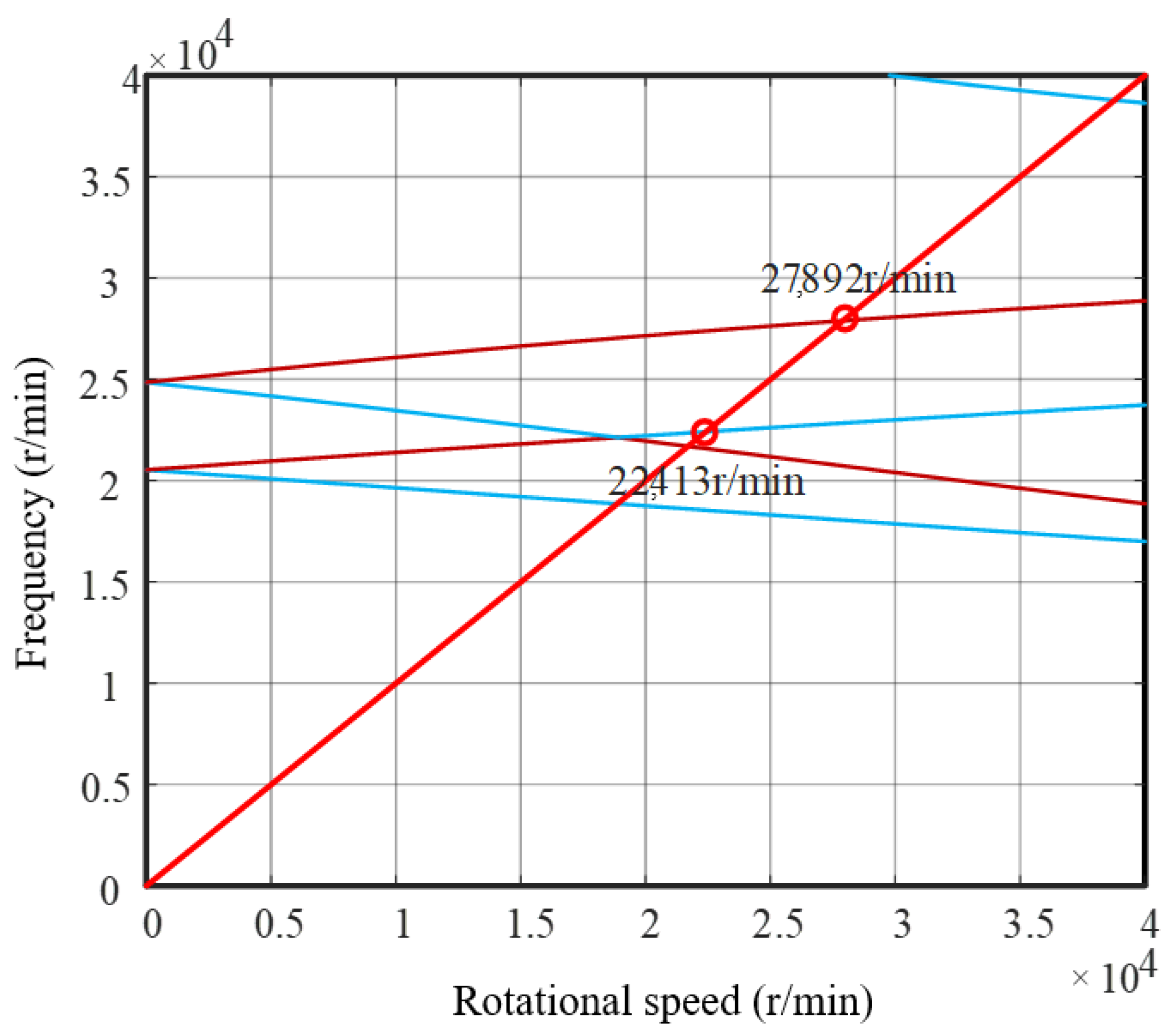
3.1. Structure and Modal Analysis
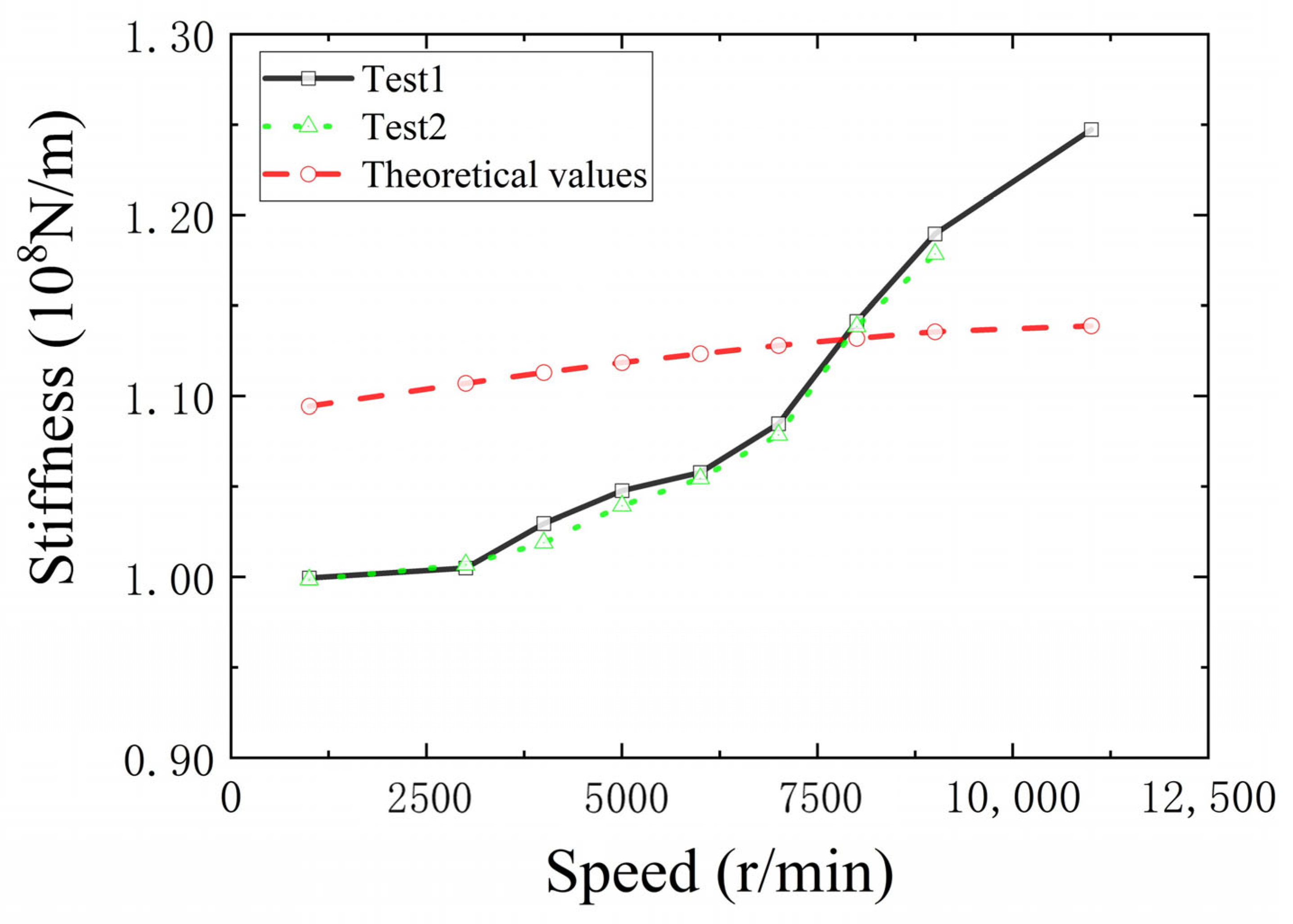
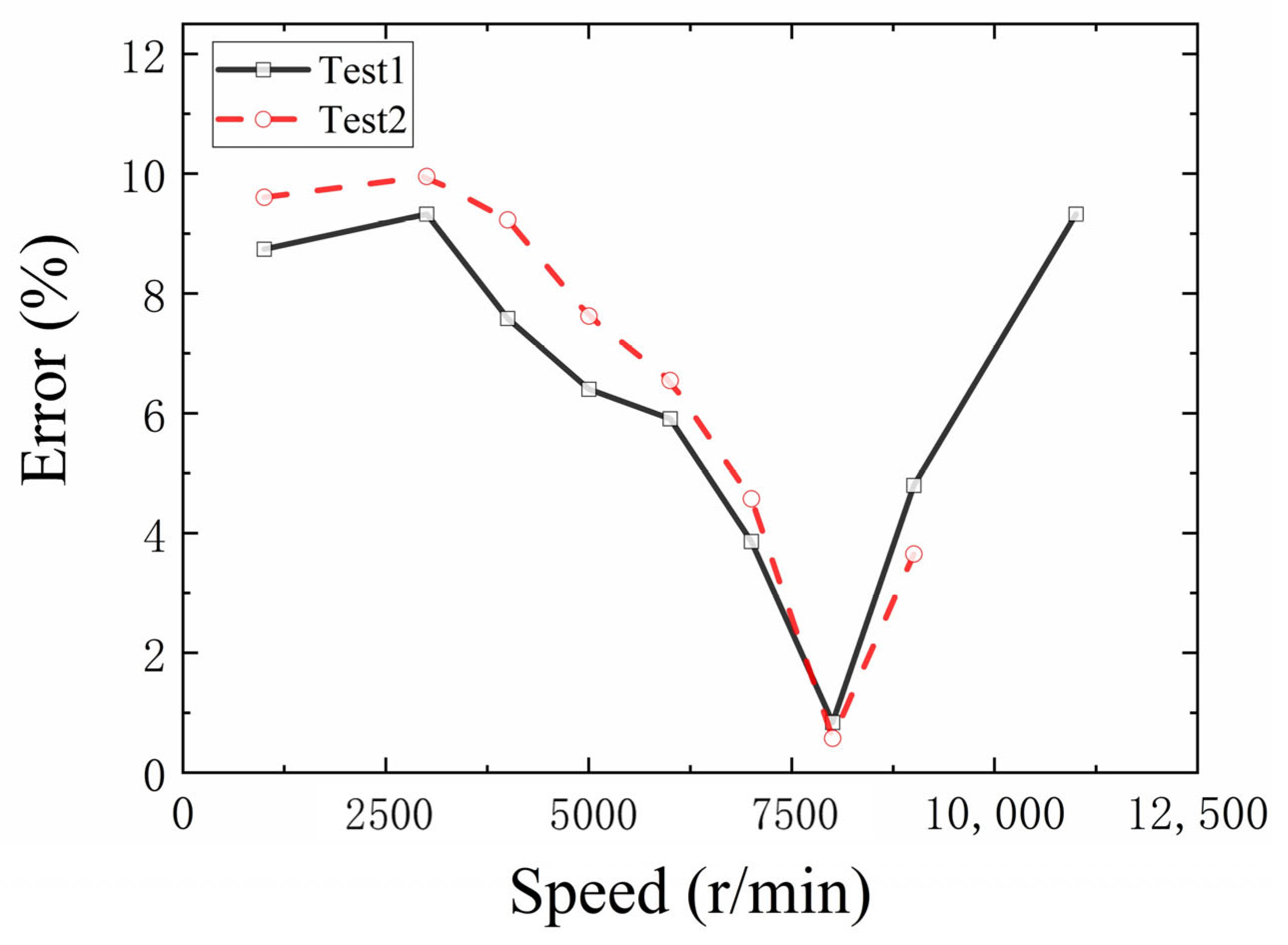
3.2. Stiffness Model Verification of Angular Contact Ball Bearing
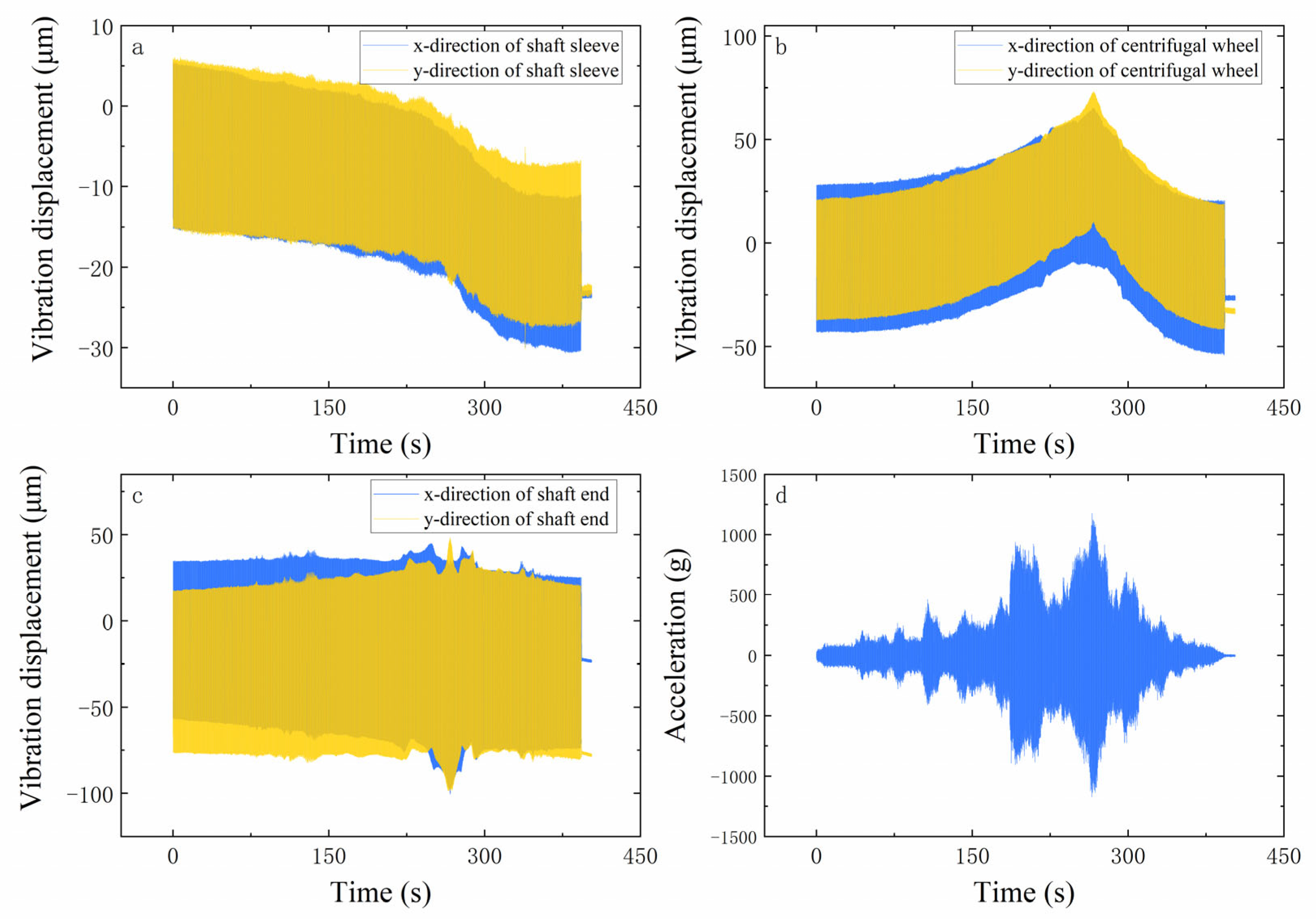
4. Results and Discussion of Turbopump Rotor Tests
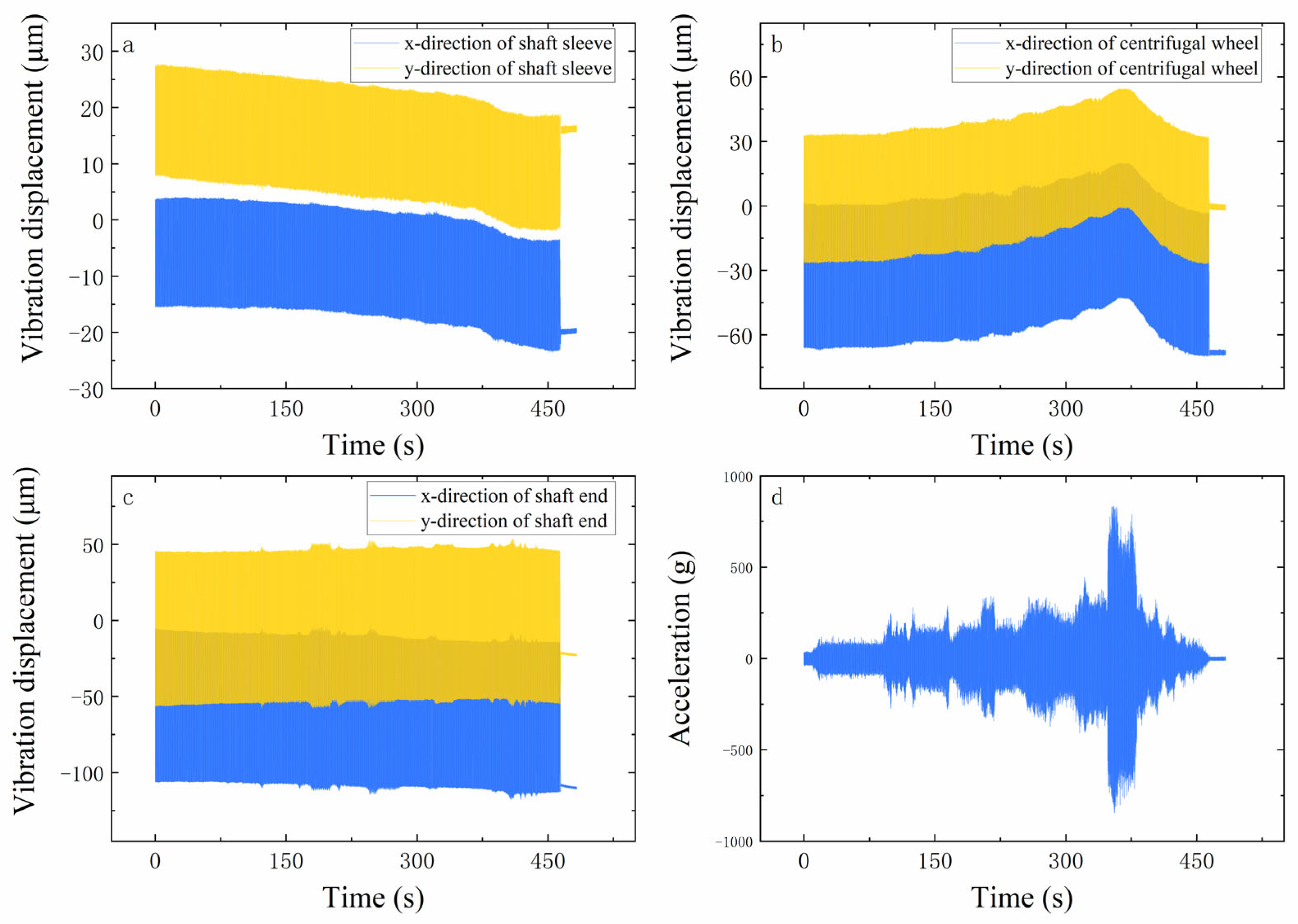
4.1. Turbopump Rotor Test System
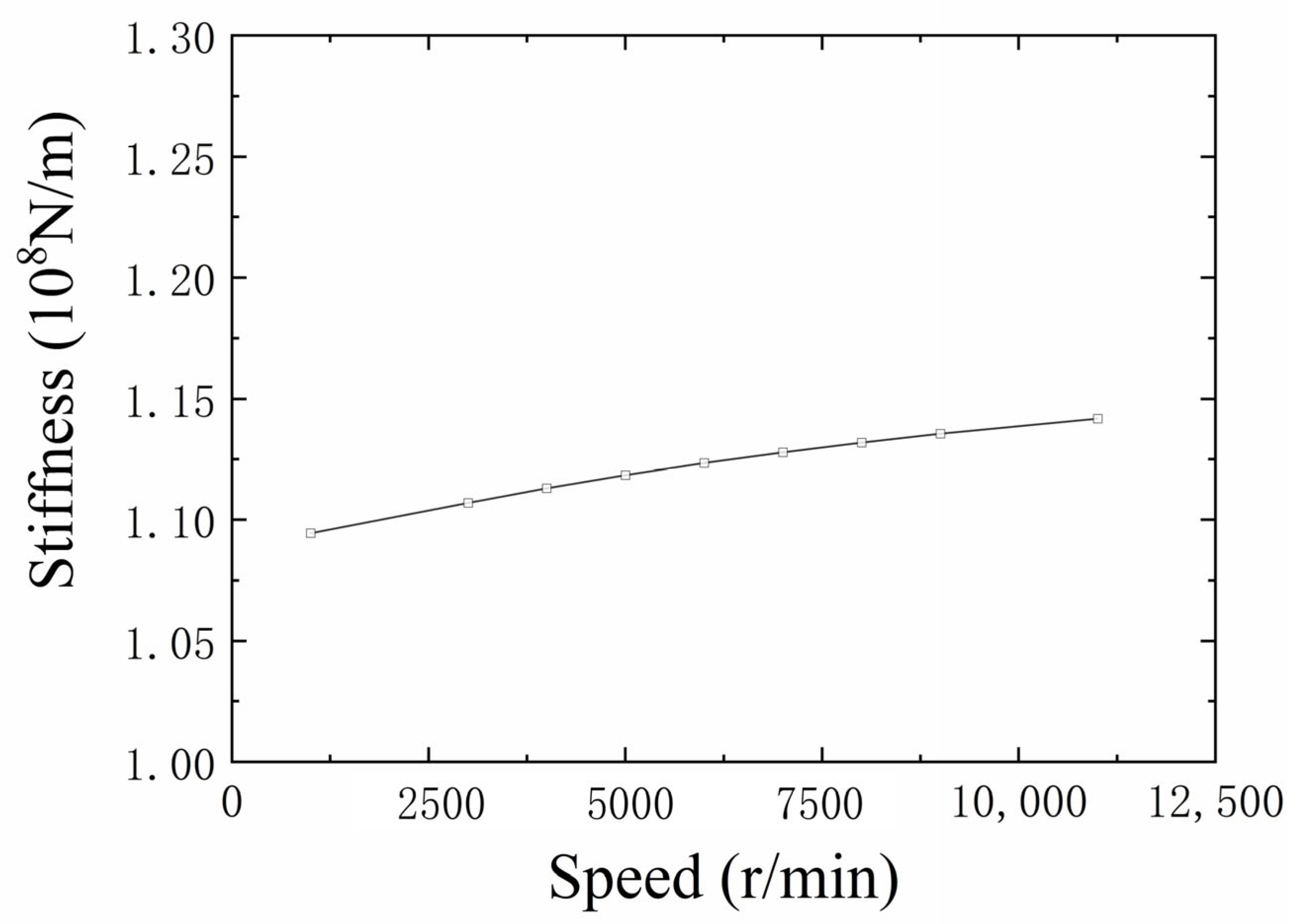
4.2. Stiffness Theoretical Model Verification
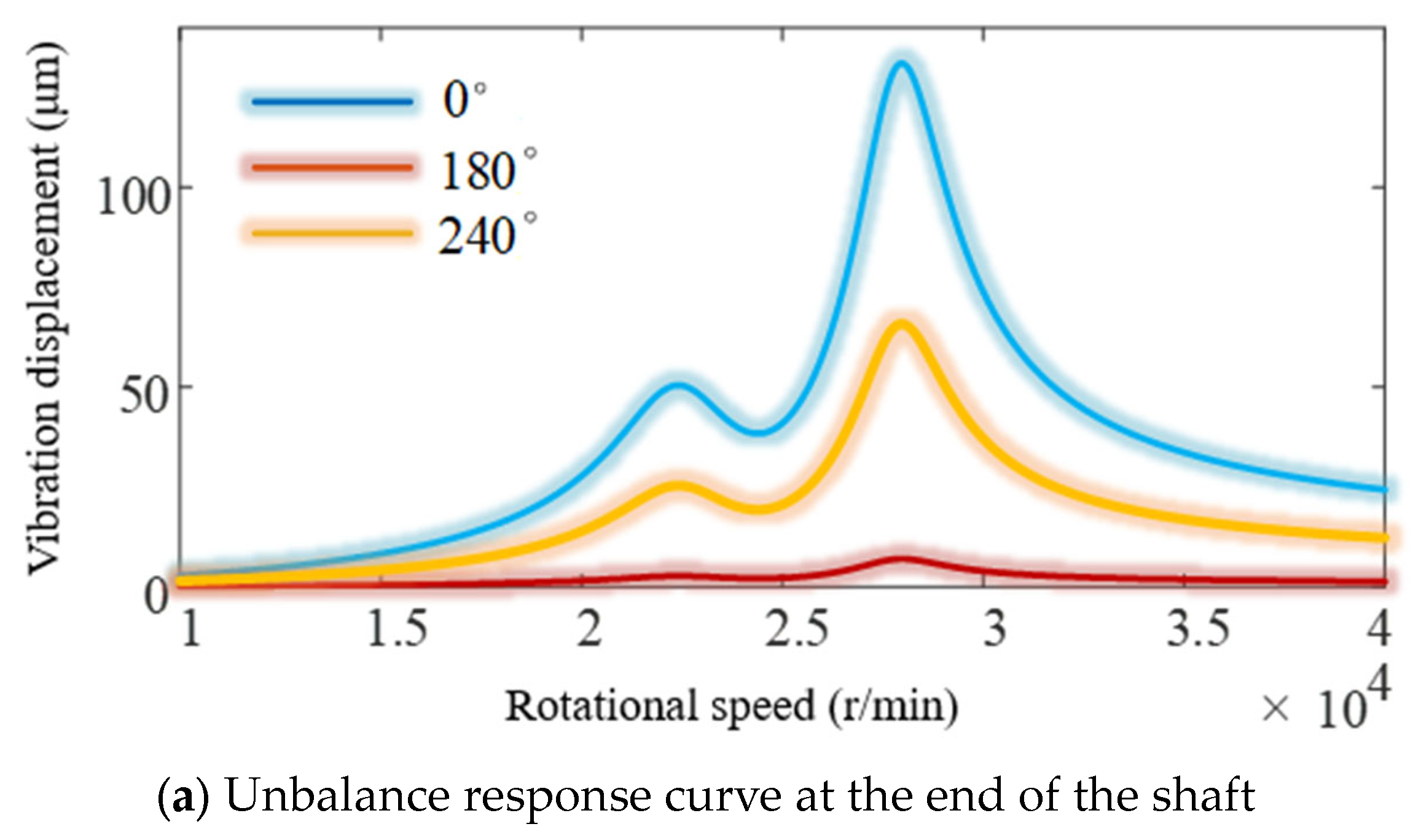
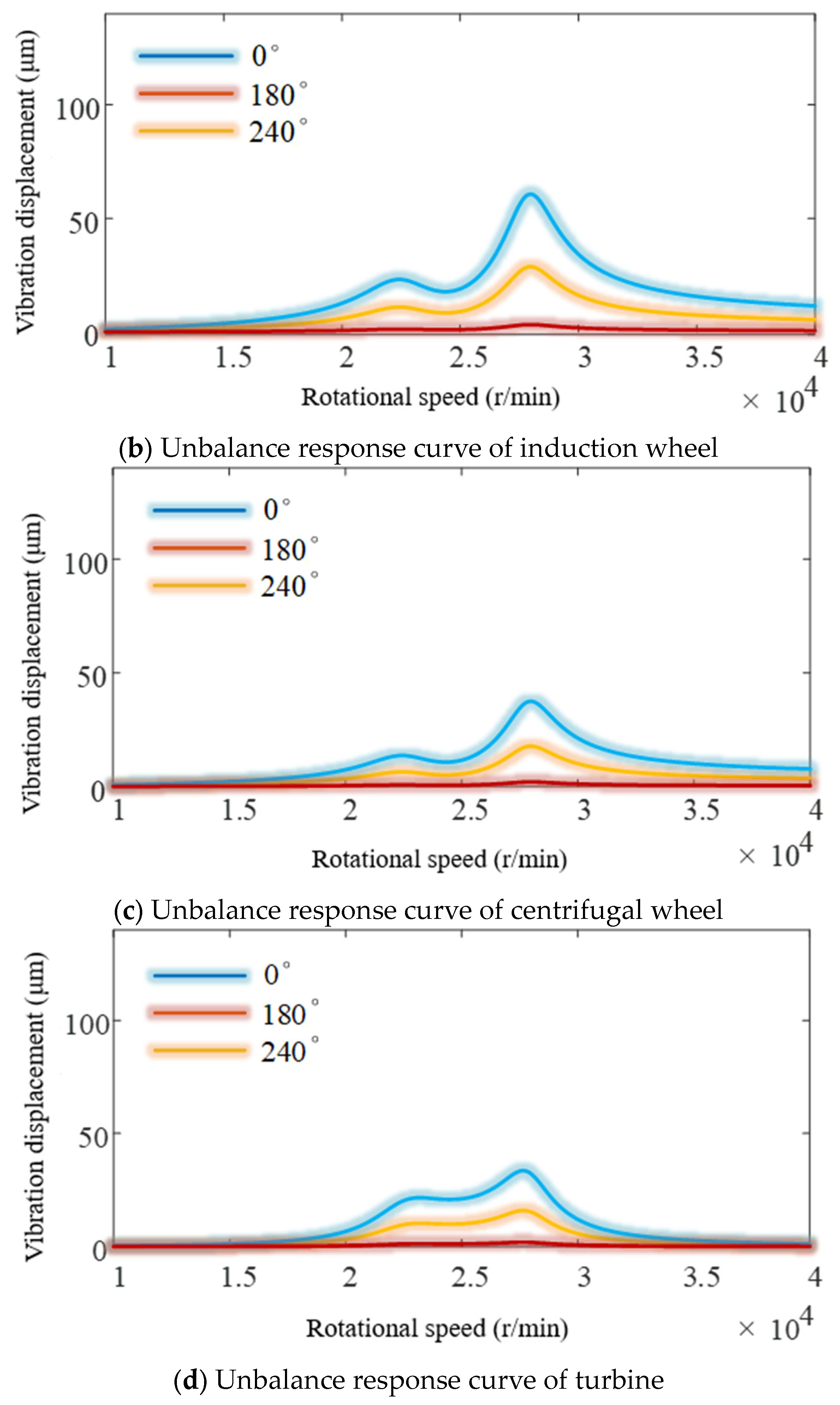
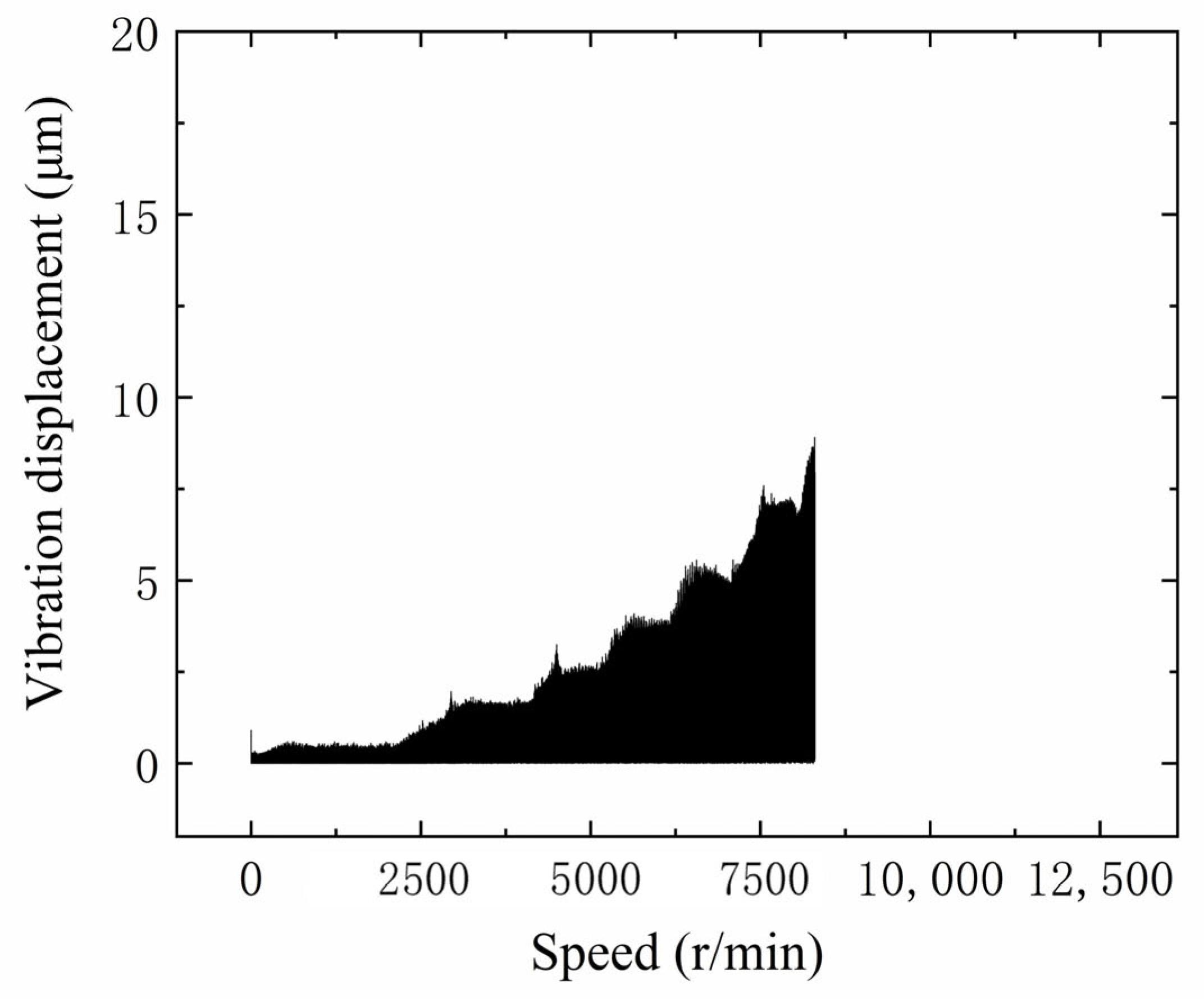
4.3. The Influence of Stiffness on Unbalance Response
5. Conclusions
- (1)
- A theoretical model for the angular contact ball bearings stiffness considering speed, structure and assembly parameters was developed. Then, a dynamic model of the rotor system was also developed. The dynamics of the turbopump rotor system were also calculated. The effects of component position, fit state and axial force on the unbalance response were elucidated. It was found that the shaft end was more sensitive to the unbalance response. It was shown that the unbalance response was an important factor affecting the service performance.
- (2)
- In order to verify the accuracy of the stiffness model and the dynamics model, a turbopump rotor test system with angular contact ball bearings was designed. Unbalance response tests were also carried out. The tests found that the dynamic characteristics were consistent with the theoretical analysis, while the axial force reduced the unbalanced response of the rotor. It was shown that the developed model of the stiffness is accurate with the dynamics of the rotor system. This provides support for the dynamics design of a turbopump with angular contact ball bearings.
- (3)
- As the stiffness of angular contact ball bearings cannot be measured directly, a stiffness discrimination model was introduced. The dynamic increase in the bearing stiffness was found in the test. The variation law and mechanism of the stiffness were revealed. It was verified that the stiffness prediction error was less than 10%. This provides important support for the design of turbopump rotors.
- (4)
- The unbalanced response of the turbopump rotor at dynamic stiffness was significantly lower compared to the fixed values. This is in better agreement with the actual test results. So, the effect of dynamic stiffness on the dynamic response of the turbopump was elucidated.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| contact angle | |
| βj | attitude angle |
| β | eccentricity phase |
| ε | mass eccentricity |
| C | clearance |
| damping matrix | |
| D | rolling body diameter |
| inner diameter of the bearing | |
| inner diameter of the shaft | |
| The diameter of the bottom of the raceway of the inner ring | |
| inner diameter of the bearing inner ring | |
| the diameter of the inner ring raceway groove bottom | |
| E | elastic modulus |
| centrifugal force | |
| moment of inertia | |
| K | stiffnesses |
| K | Stiffnesses matrix |
| gyroscopic torque matrix | |
| gyroscopic moment | |
| mass matrix | |
| m | unbalanced mass |
| n | the number of iteration steps |
| material density | |
| R | raceway curvature radius |
| X | The distance between the raceway and the ball center |
| O | curvature center |
| Q | contact load of the inner and outer ring raceway |
| unbalanced force vector | |
| the inner ring rotation velocity | |
| Angular velocity of ball revolution | |
| Rotor speed | |
| f | The ratio of the radius of curvature to the rolling element diameter |
| hollow shaft mating diameter | |
| Poisson’s ratio | |
| The distribution coefficients of the raceway friction torque | |
| end stress of the inner ring | |
| displacement vector | |
| displacement | |
| angular displacement | |
| Z | Number of balls |
| subscript | |
| i | inner ring |
| o | outer ring |
| b | bearings |
| s | shafts |
| a | axial |
| r | Radial |
| α | Angular |
| j | The ball number |
| subscript | |
| ‘ | The location after deformation |
| s | rotor system |
References
- Childs, D.W. The Space Shuttle Main Engine High-Pressure Fuel Turbopump Rotordynamic Instability Problem. J. Eng. Power 1978, 100, 48–57. [Google Scholar] [CrossRef]
- Jeon, S.M.; Kwak, H.D.; Yoon, S.H.; Kim, J. Rotordynamic analysis of a turbopump with the casing structural flexibility. J. Propuls. Power 2008, 24, 433–436. [Google Scholar] [CrossRef]
- Zakeralhoseini, S.; Schiffmann, J. Design, computational and experimental investigation of a small-scale turbopump for organic Rankine cycle systems. Energy Convers. Manag. 2023, 287, 117073. [Google Scholar] [CrossRef]
- Li, W. Research on the Fault Mechanism and Diagnosis Technology of Liquid Rocket Engine Turbopump; Beijing University of Chemical Technology: Beijing, China, 2020. [Google Scholar]
- Apollonio, A.; Anderlini, A.; Valentini, D.; Pace, G.; Pasini, A.; Salvetti, M.V.; d’Agostino, L. Concurrent theoretical, experimental and numerical analyses of mixed-flow turbopump design. Aerosp. Sci. Technol. 2022, 123, 107459. [Google Scholar] [CrossRef]
- Zhao, L.; Liao, M.; Hong, L.; Lei, X.; Li, M.; Wang, S.; Hou, L.; Shao, Z. Analysis of engine vibration response under sudden addition unbalance. J. Aerosp. Power 2022, 37, 12. [Google Scholar]
- Wensing, J.A. On the Dynamics of Ball Bearings; University of Twente: Enschede, The Netherlands, 1998. [Google Scholar]
- Du, D.; Li, B. A review of key technologies for structural dynamics design of liquid rocket motors. J. Aeronaut. 2023, 444, 27554. [Google Scholar]
- Yan, Z. Reliability and Dynamic Stiffness Analysis of Aero-Engine Bearings; Xi’an Technological University: Xi’an, China, 2017. [Google Scholar]
- Yin, Y. Stiffness Study of Engine Magazine Structure with Bolted Coupling; Dalian University of Technology: Dalian, China, 2016. [Google Scholar]
- Li, Q. Study on the Effect of Support Stiffness on the Critical Speed of Rotor System; Shenyang Aerospace University: Shenyang, China, 2014. [Google Scholar]
- Jiang, Y.; Shi, B.; Zhang, T.; Chen, J.; Bai, G. Stiffness Characteristic of Co-Rotating/Counter-Rotating Inter-Shaft Bearing with Different Supporting Structures. J. Propuls. Technol. 2022, 43, 1–12. [Google Scholar]
- Ding, Z. Finite element analysis of dynamic stiffness of a type of aero-engine front support. J. Chang. Aeronaut. Vocat. Tech. Coll. 2014, 14, 5. [Google Scholar]
- Ri, C.; Namgung, H.; Zhang, Z.; Zhang, Z.; Chae, C.; Ri, K.; Ho, P.; Zhang, R. Comprehensive stiffness analysis of the cylindrical roller bearing for aircraft engines considering the radial clearance. Aircr. Eng. Aerosp. Technol. 2023, 95, 62–72. [Google Scholar] [CrossRef]
- Jeon, S.M.; Kwak, H.D.; Yoon, S.H.; Kim, J. Rotordynamic analysis of a high thrust liquid rocket engine fuel (Kerosene) turbopump. Aerosp. Sci. Technol. 2013, 26, 169–175. [Google Scholar] [CrossRef]
- Outirba, B.; Hendrick, P. Influence of geometrical parameters on the performance of brush seals for aero-engines bearing chambers. In Proceedings of the Asme Turbo Expo: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; pp. 23–27. [Google Scholar]
- Hong, J.; Wang, H.; Xiao, D.; Chen, P. Effects of Dnamic Stiffness of Rotor Bearing on Rotordynam in Characteristics. Aeroengine 2008, 34, 23–27. [Google Scholar]
- Du, J.; Li, M.; Wang, Y.; Jiang, X. Effects of Vibration of Supporting Structure on Dynamic Characteristics of a Turbopump Rotor. J. Propuls. Technol. 2023, 44, 1–12. [Google Scholar]
- Jiang, Y.; Liao, M.; Chen, J.; Zeng, Y.; Shi, B.; Hong, L. Support Stiffness Dependent on Aero-engine Bearing Assembly Conditions. J. Vib. Meas. Diagn. 2020, 40, 348–354+421. [Google Scholar]
- Lu, P.; Liao, M.; Li, M. Dynamic Stiffness Test and Its Application in Analysis of Unbalance Response of Rotors. Noise Vib. Control 2014, 34, 207–211. [Google Scholar]
- Qiao, L. Stiffness Characteristics Analysis and Experimental Research of the Special-Shaped Bearing for Elastic Support Structure; Dalian University of Technology: Dalian, China, 2018. [Google Scholar]
- Zhao, W. Research on the Whole Engine Vibration Modeling and Validation of Aero-Engine Considering the Dynamic Stiffness of the Tested Casing Bearing; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2012. [Google Scholar]
- Junzo, O. Design and Calculation of Ball Bearing; China Machine Press: Beijing, China, 2003. [Google Scholar]
- Bu, C.; Xia, B.; Lian, Y.; Zeng, H. Simulation of hertz transient contact/impact of flexible bodies. J. Earth Sci. 2012, 23, 225–232. [Google Scholar] [CrossRef]
- Harris, T.A.; Kotzalas, M.N. Rolling Bearing Analysis-2 Volume Set; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Liao, M. Aero-Engine Rotor Dynamics; Xi’an Northwestern Polytechnical University Press: Xi’an, China, 2006. [Google Scholar]
- Rao, J.S. Rotor Dynamics; New Age International: Daryaganj, India, 1996. [Google Scholar]


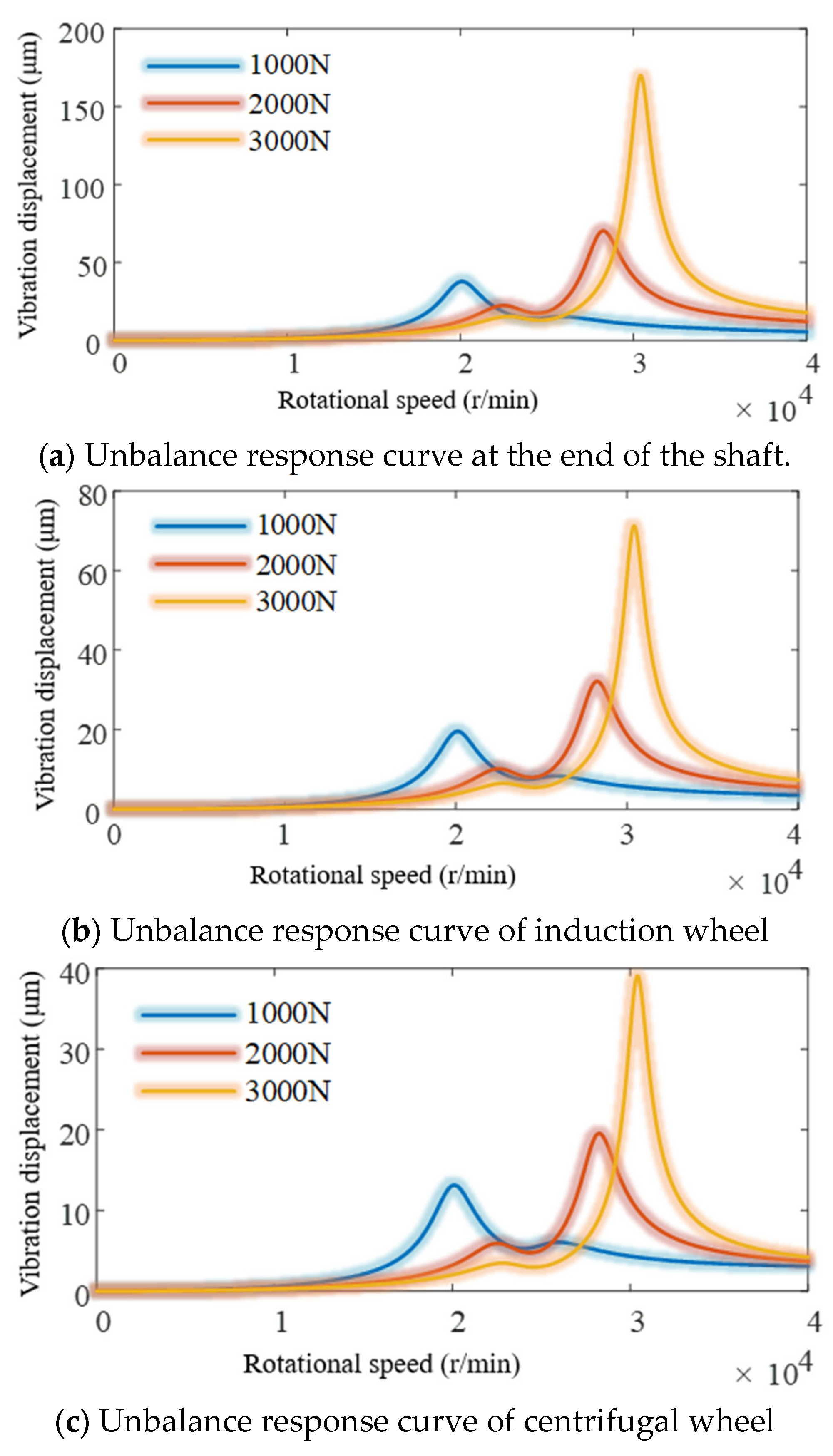
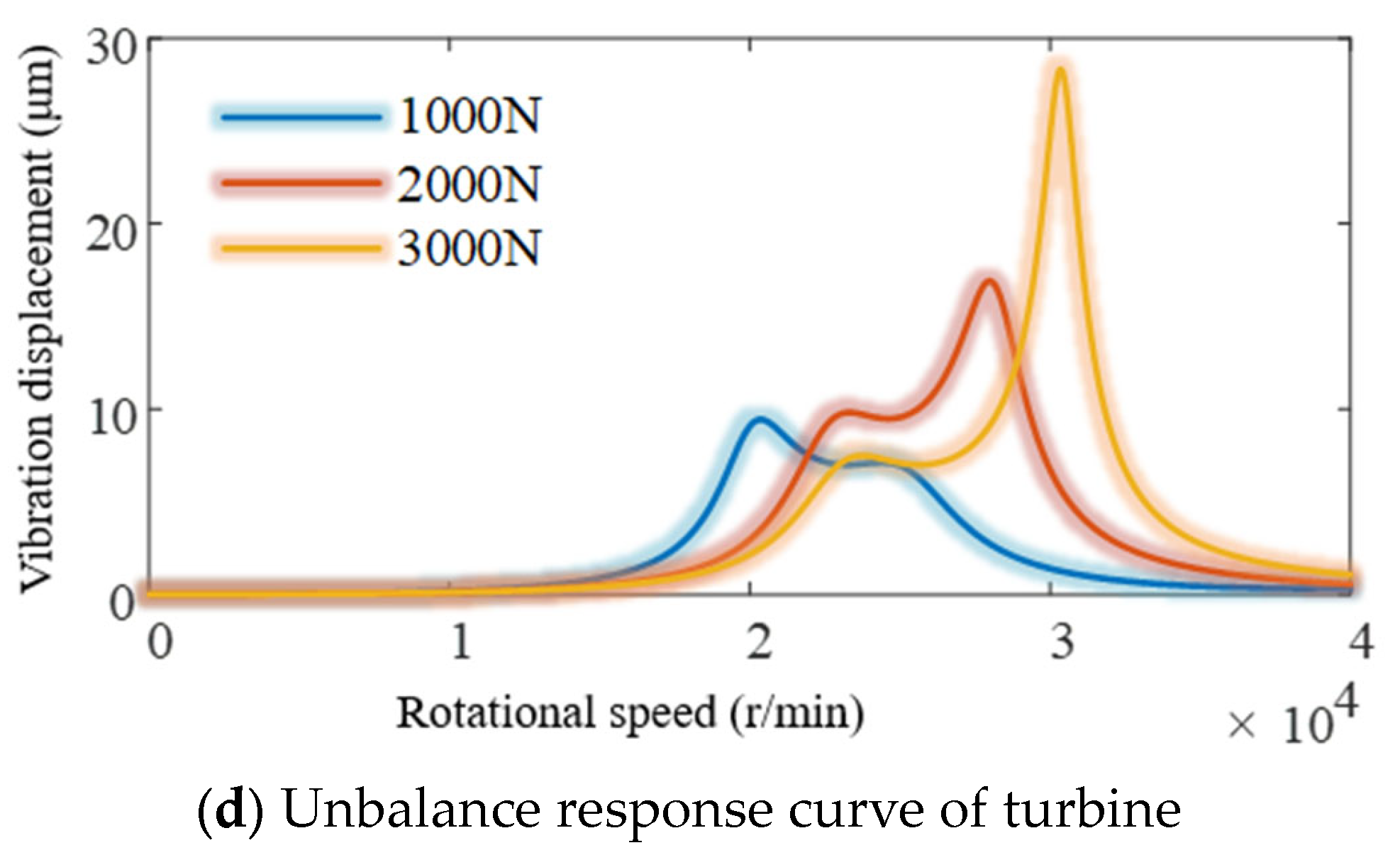
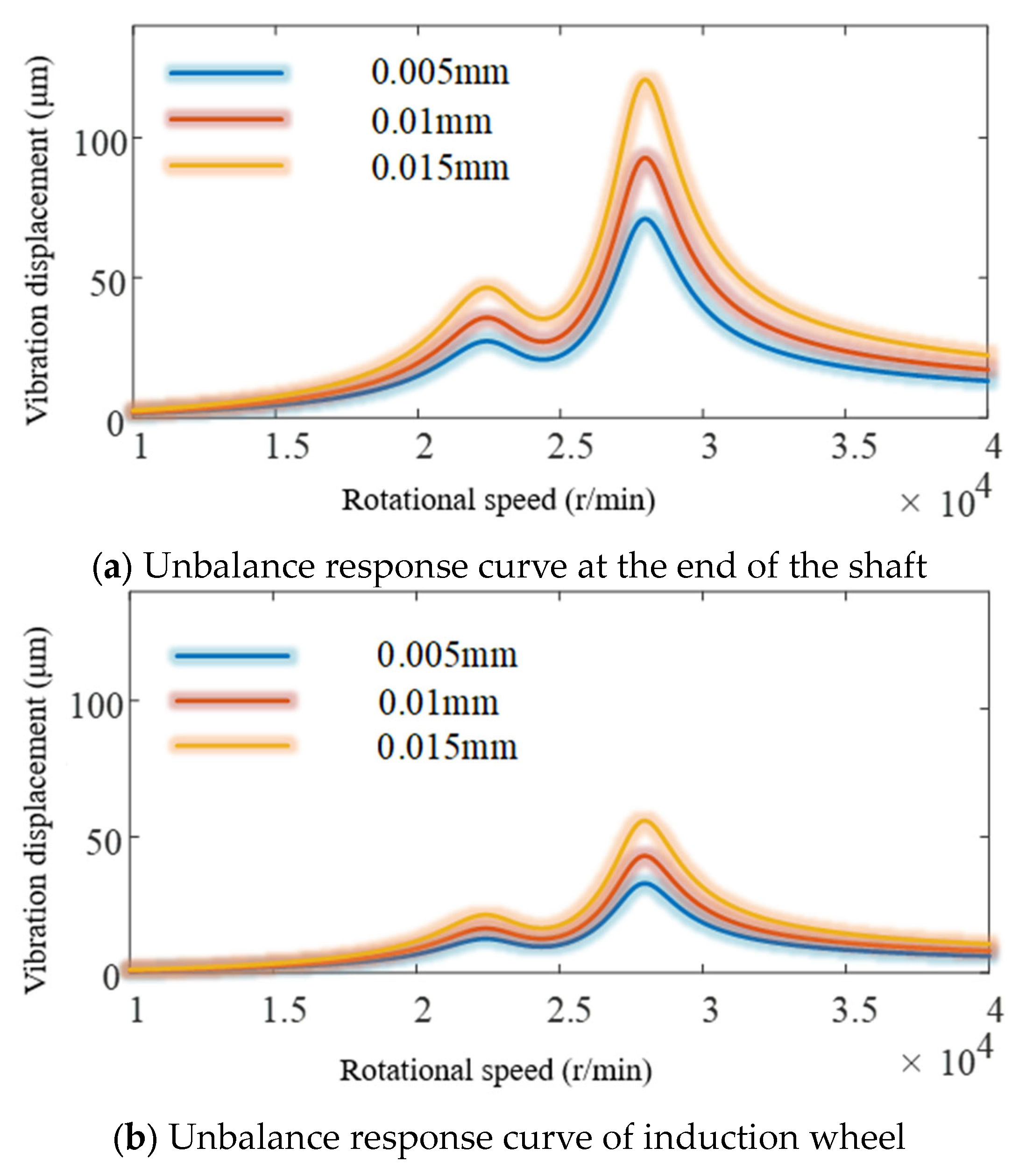
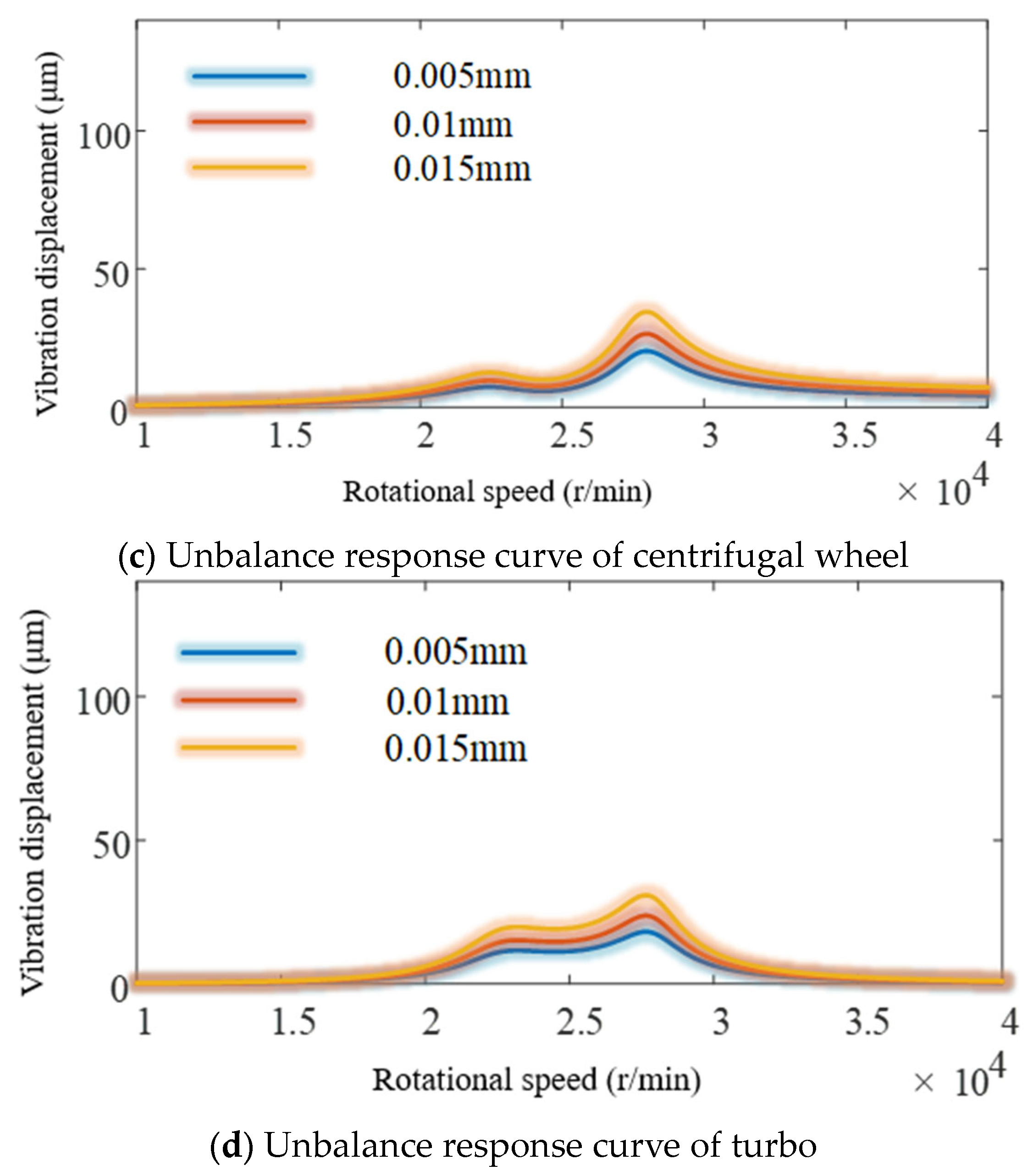



| Project | Inducer Wheel | Centrifugal Wheel | Turbine |
|---|---|---|---|
| Radial moment of inertia/kg·m2 | 0.006842 | 0.02731 | 0.03904 |
| Polar moment of inertia/kg·m2 | 0.00899 | 0.05027 | 0.07707 |
| Quality/kg | 3.025 | 6.978 | 8.86 |
| Node number | 7 | 10 | 27 |
| Position | Measure of Inequality (g·cm) | |
|---|---|---|
| Quality | Phase | |
| Inducer wheel | 12.4 | 0 |
| Centrifugal wheel | 7.4 | 0 |
| Turbine | 7.4 | 0 |
| Density g/cm3 | Modulus of Elasticity GPa | Poisson’s Ratio | Number of Balls | Inside Diameter mm | Outside Diameter mm | Ball Diametermm |
|---|---|---|---|---|---|---|
| 7.75 | 200 | 0.29 | 10 | 70 | 125 | 17.46 |
| Group | Amplitude/g·mm | Phase/° |
|---|---|---|
| Test 1 | 43.365 | 60 |
| Test 2 | 270.81 | 240 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Xu, K.; Gao, Y.; Jin, L. Investigation on the Rotordynamic Characteristics of Turbopumps with Angular Contact Ball Bearings. Vibration 2023, 6, 659-679. https://doi.org/10.3390/vibration6030041
Su Y, Xu K, Gao Y, Jin L. Investigation on the Rotordynamic Characteristics of Turbopumps with Angular Contact Ball Bearings. Vibration. 2023; 6(3):659-679. https://doi.org/10.3390/vibration6030041
Chicago/Turabian StyleSu, Yue, Kaifu Xu, Yongqiang Gao, and Lu Jin. 2023. "Investigation on the Rotordynamic Characteristics of Turbopumps with Angular Contact Ball Bearings" Vibration 6, no. 3: 659-679. https://doi.org/10.3390/vibration6030041
APA StyleSu, Y., Xu, K., Gao, Y., & Jin, L. (2023). Investigation on the Rotordynamic Characteristics of Turbopumps with Angular Contact Ball Bearings. Vibration, 6(3), 659-679. https://doi.org/10.3390/vibration6030041




