Vertical Transient Response Analysis of a Cracked Jeffcott Rotor Based on Improved Empirical Mode Decomposition
Abstract
1. Introduction
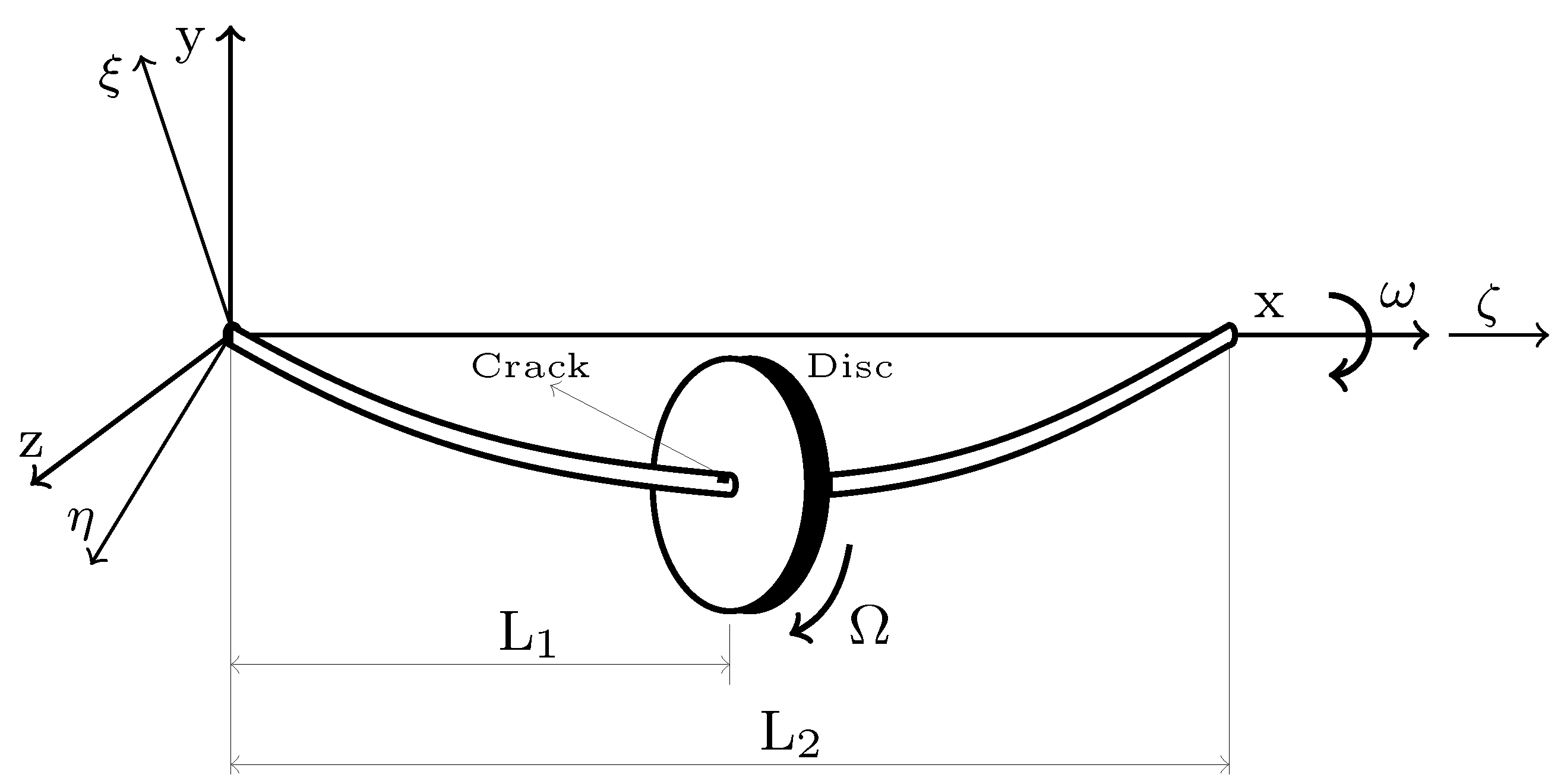
2. Jeffcott Rotor and Crack Modeling
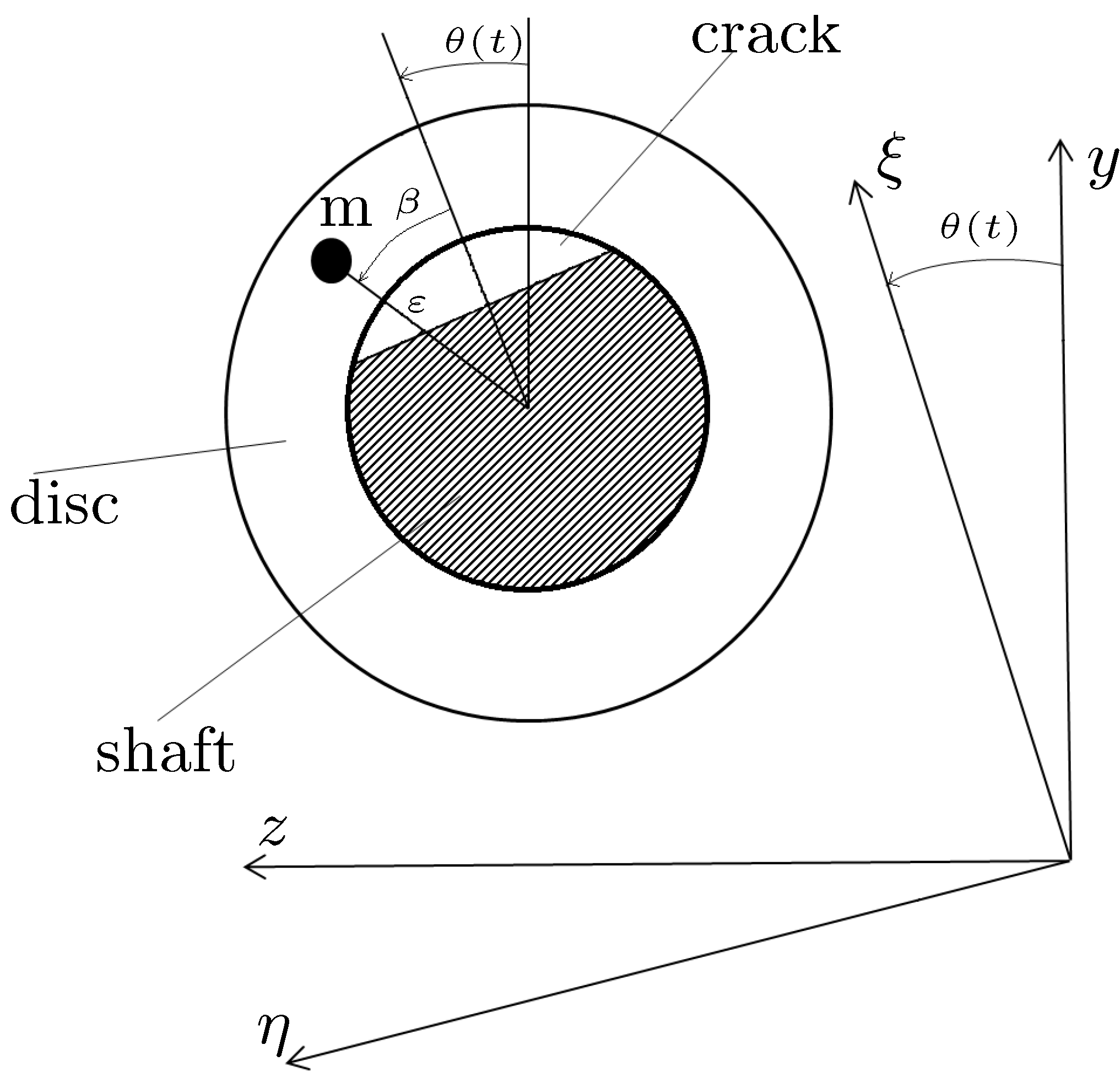
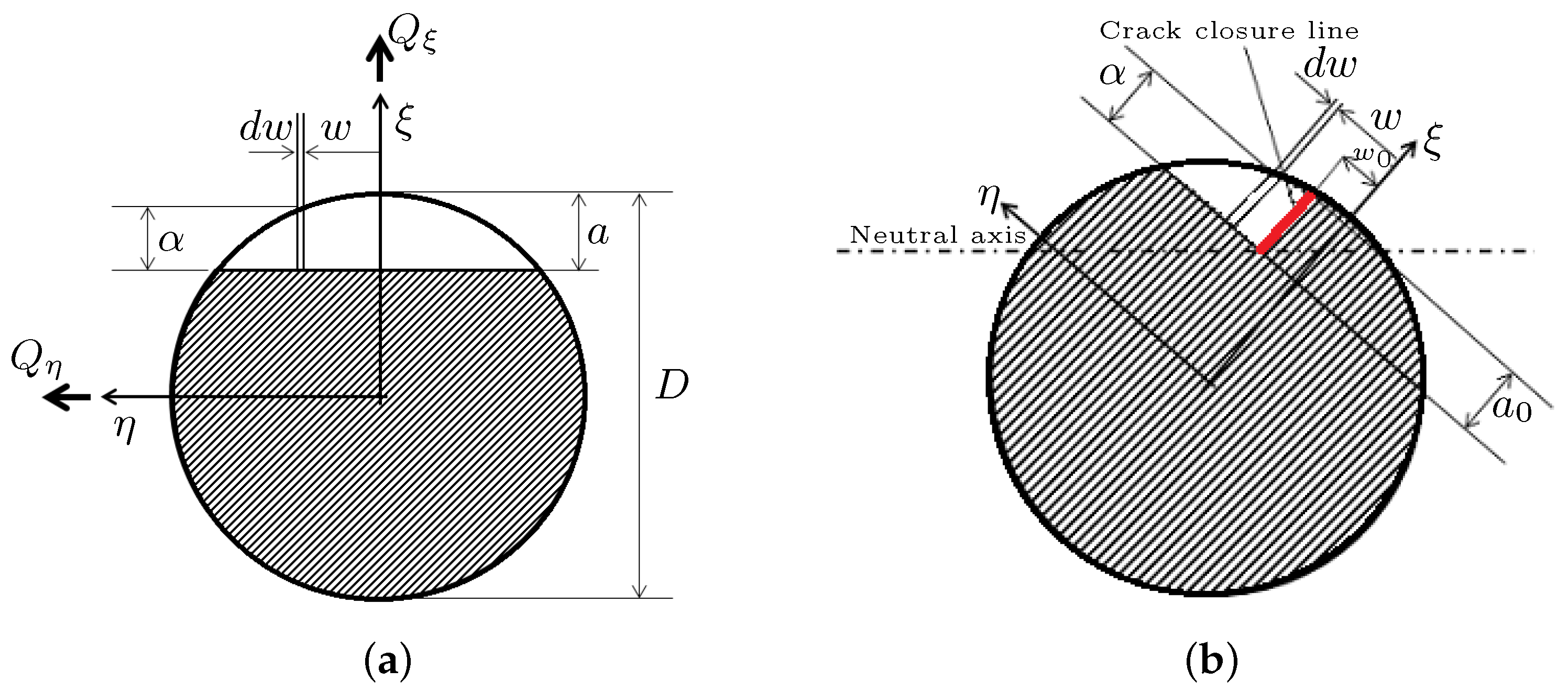
2.1. Crack Modeling
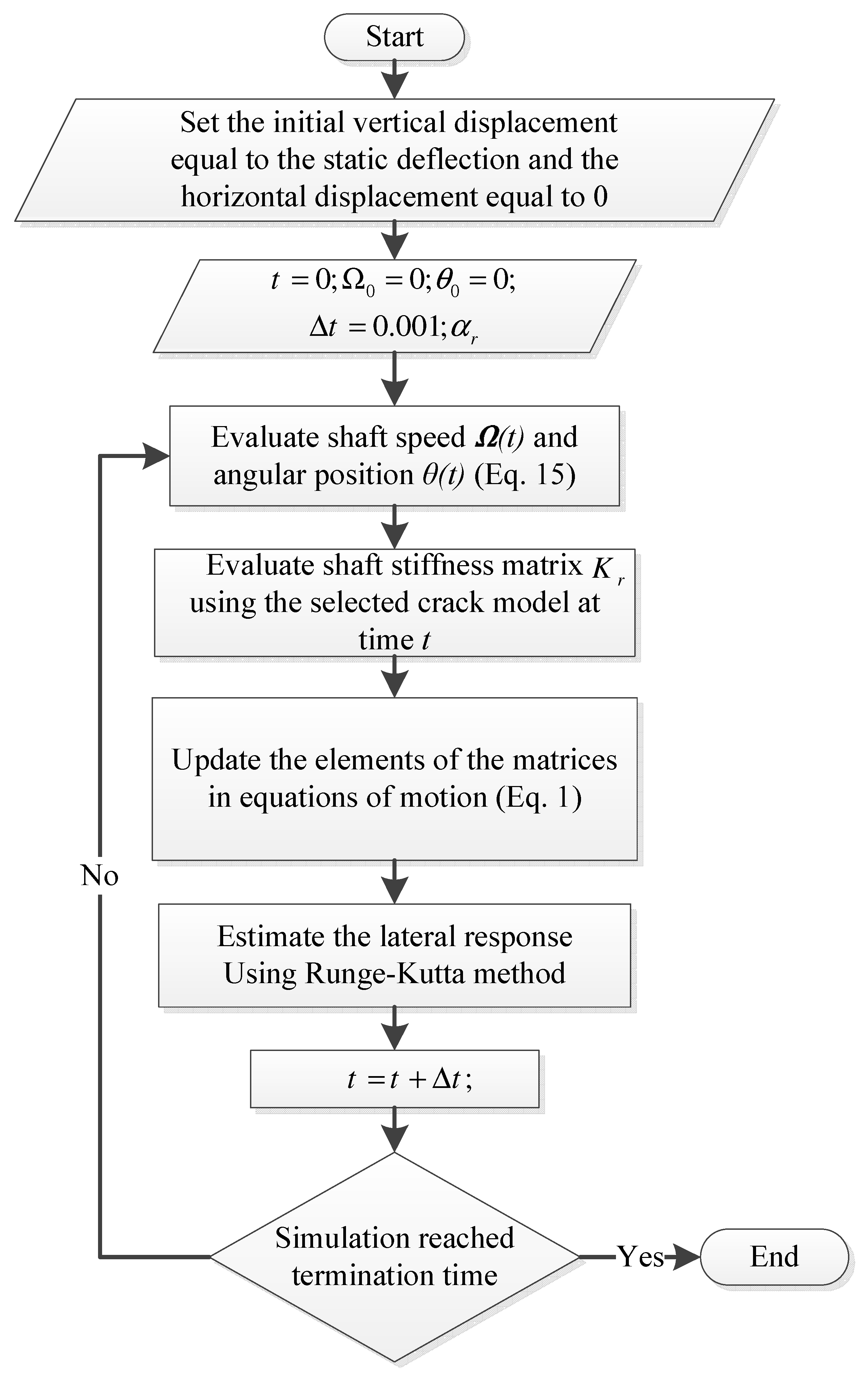
2.2. Method of Solution
3. Time–Frequency Analysis
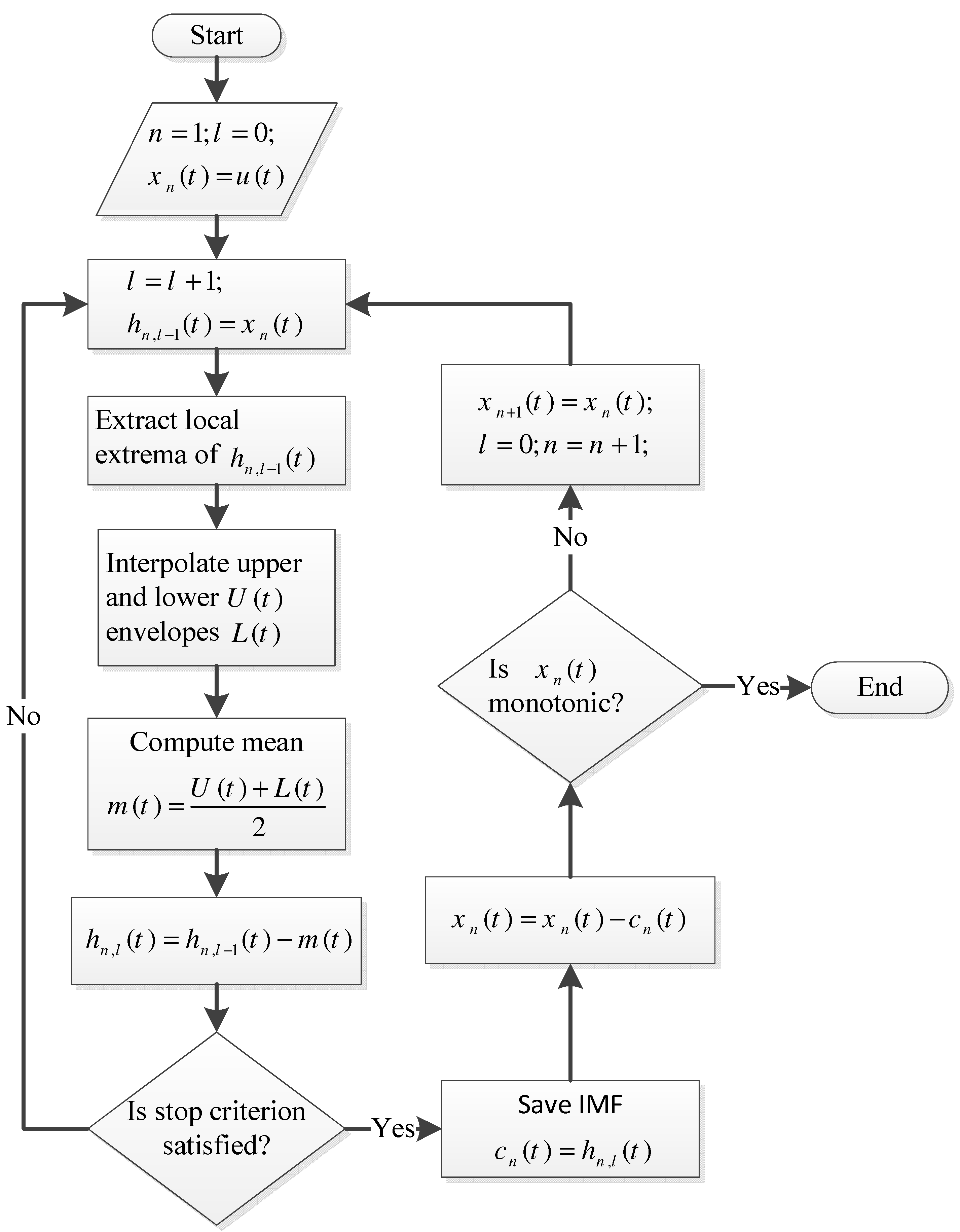
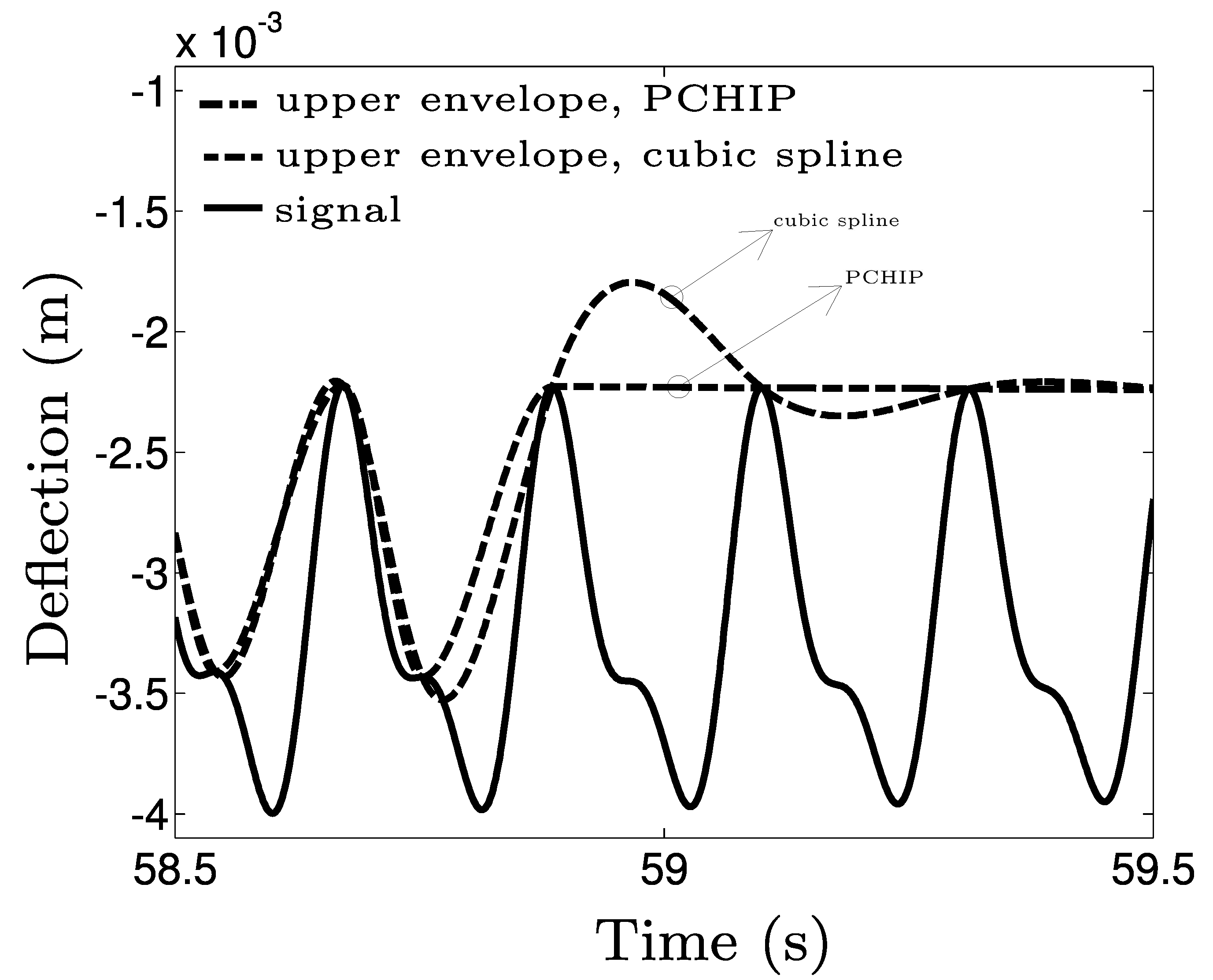
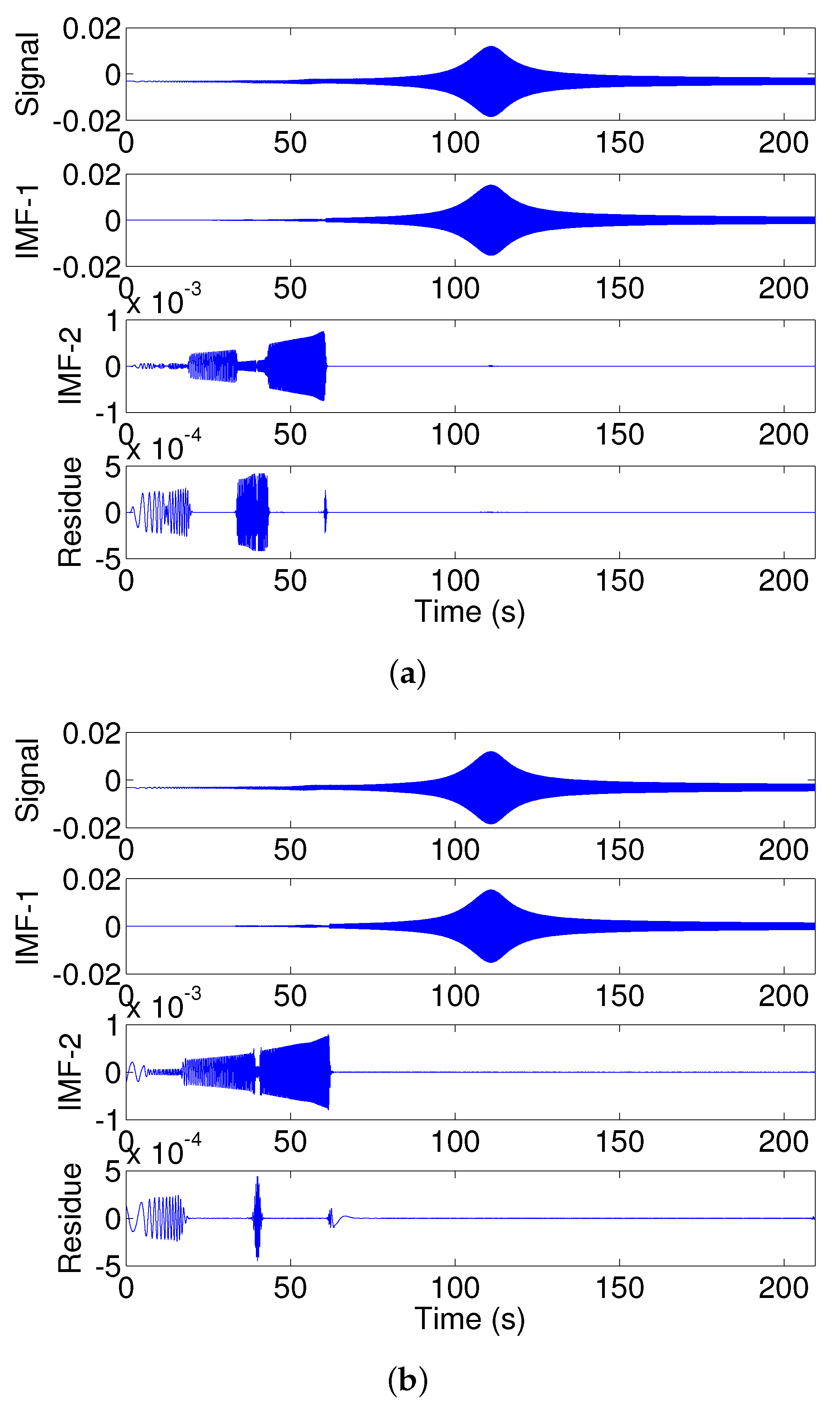
Empirical Mode Decomposition (EMD)
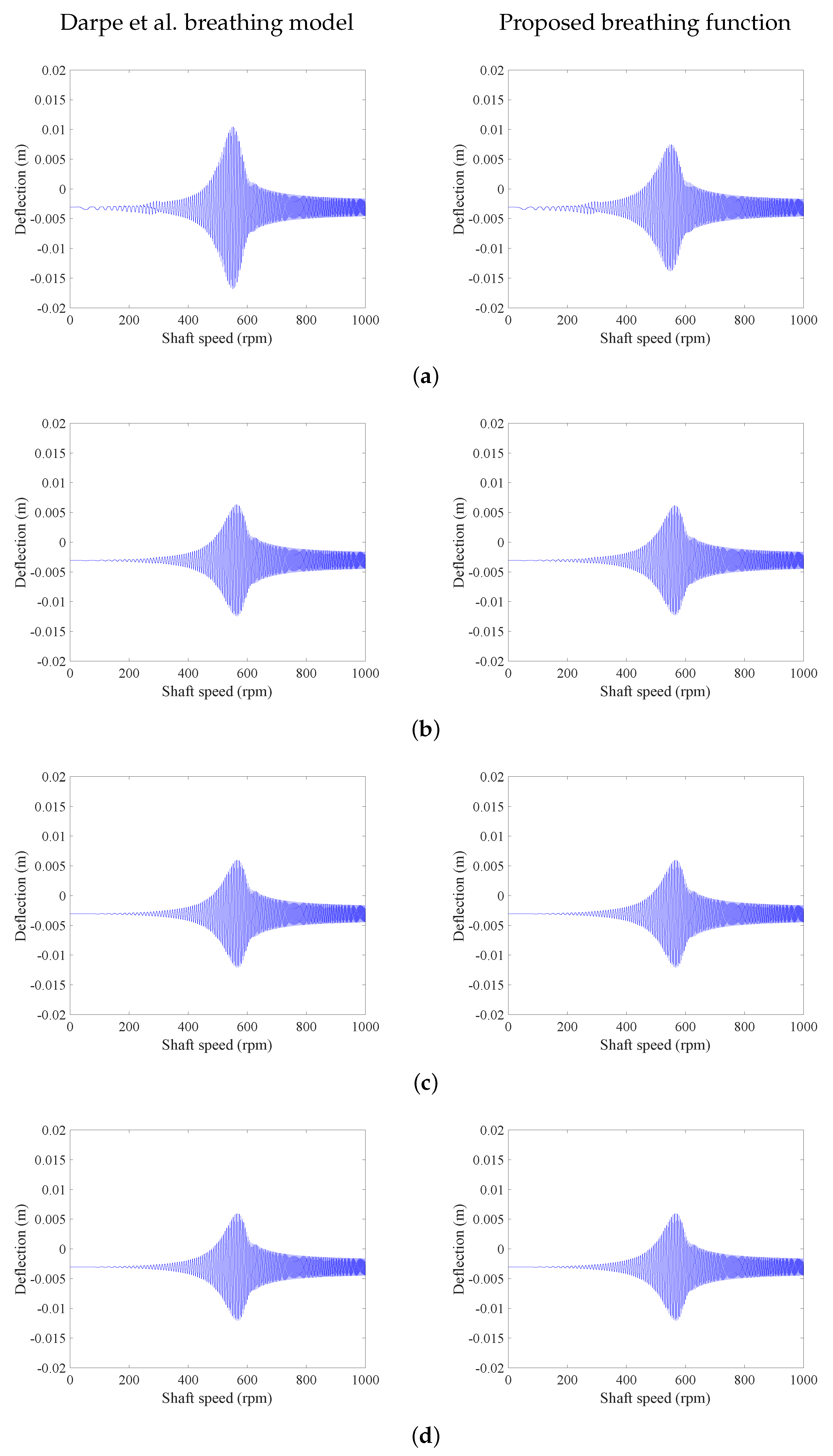
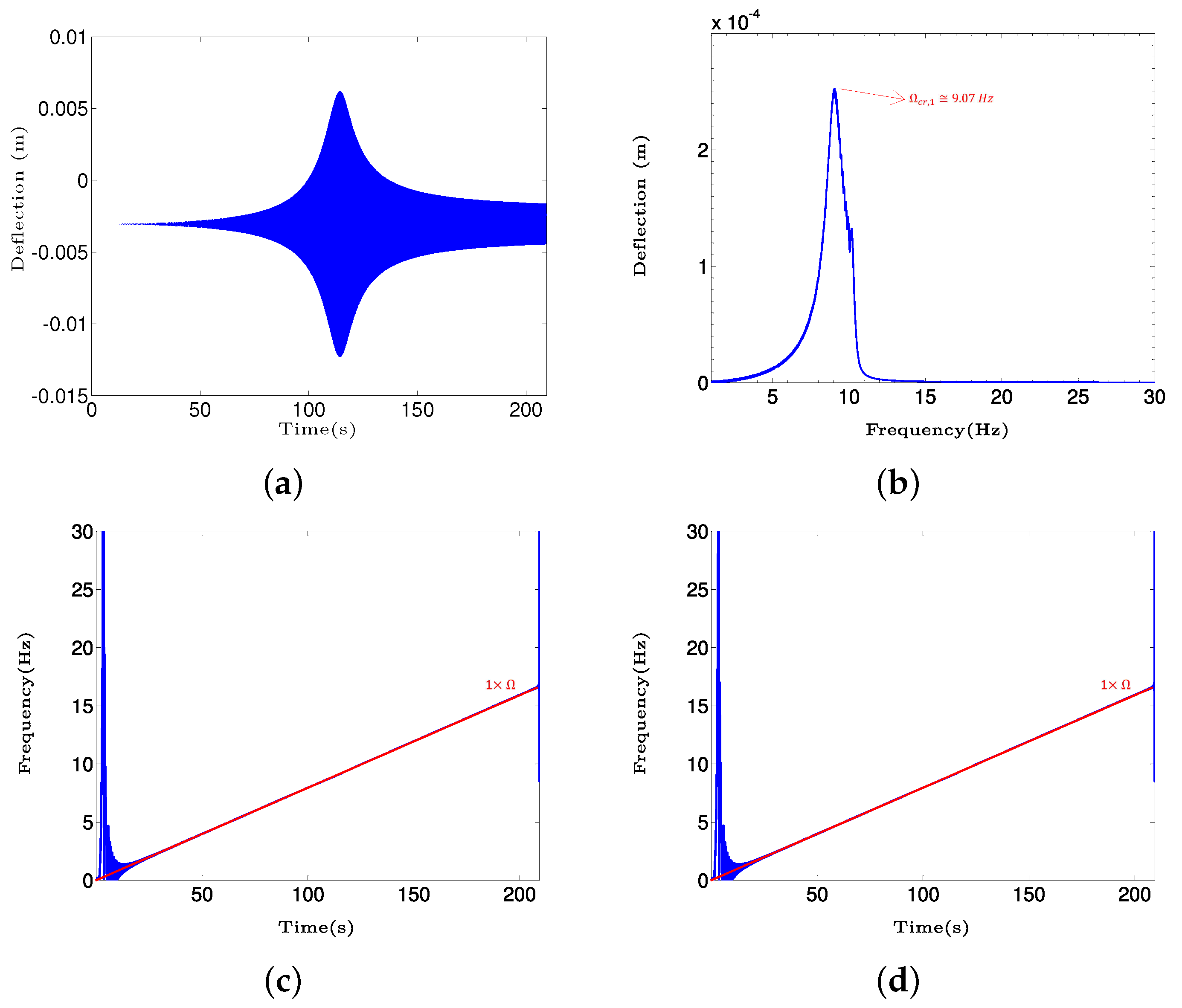
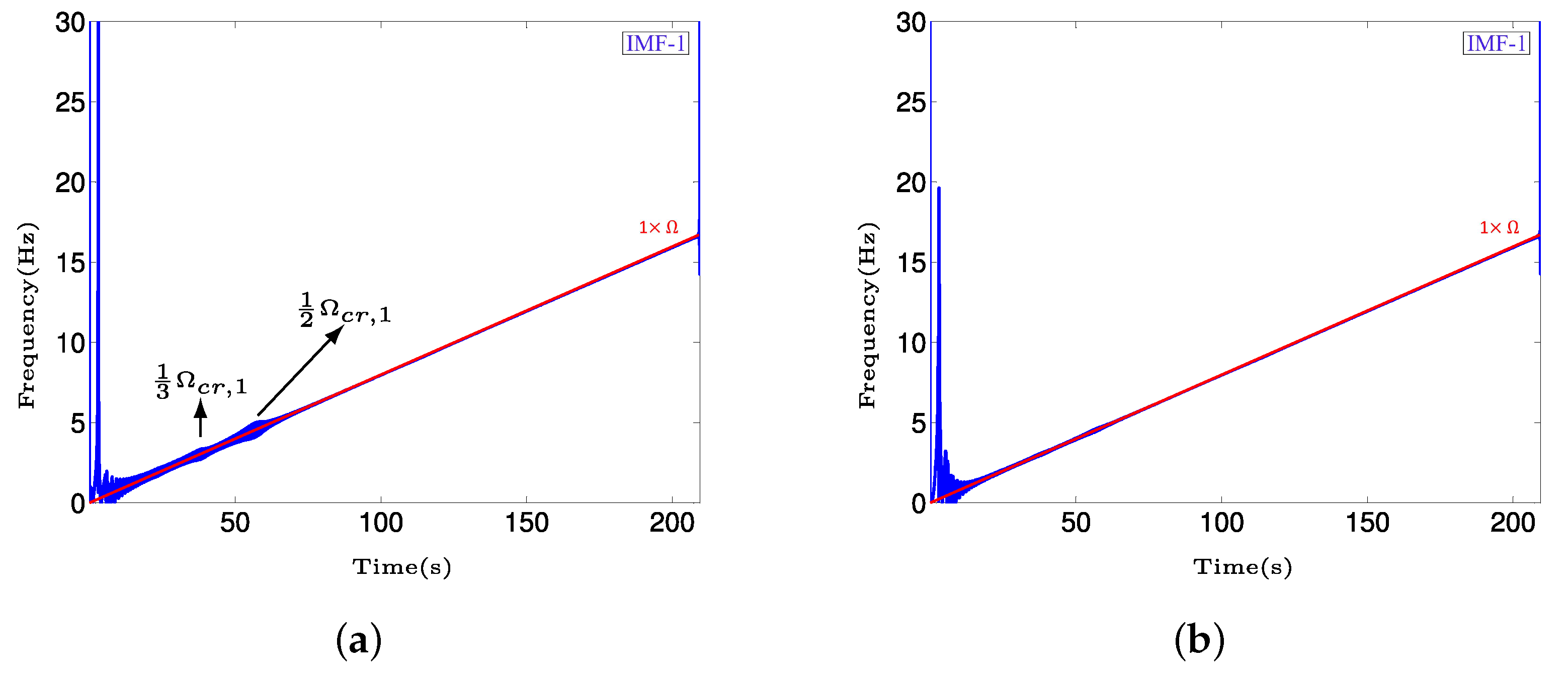
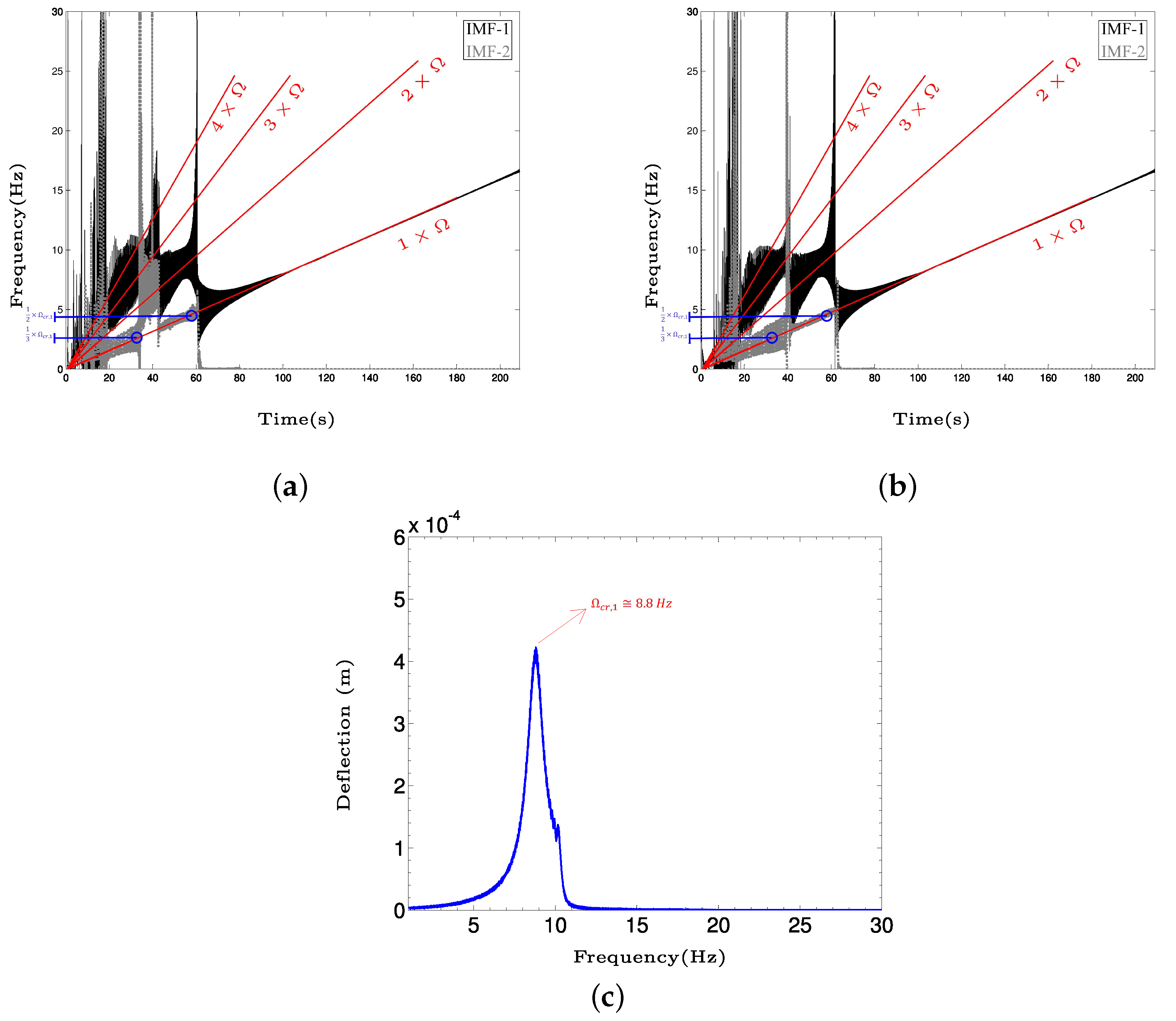
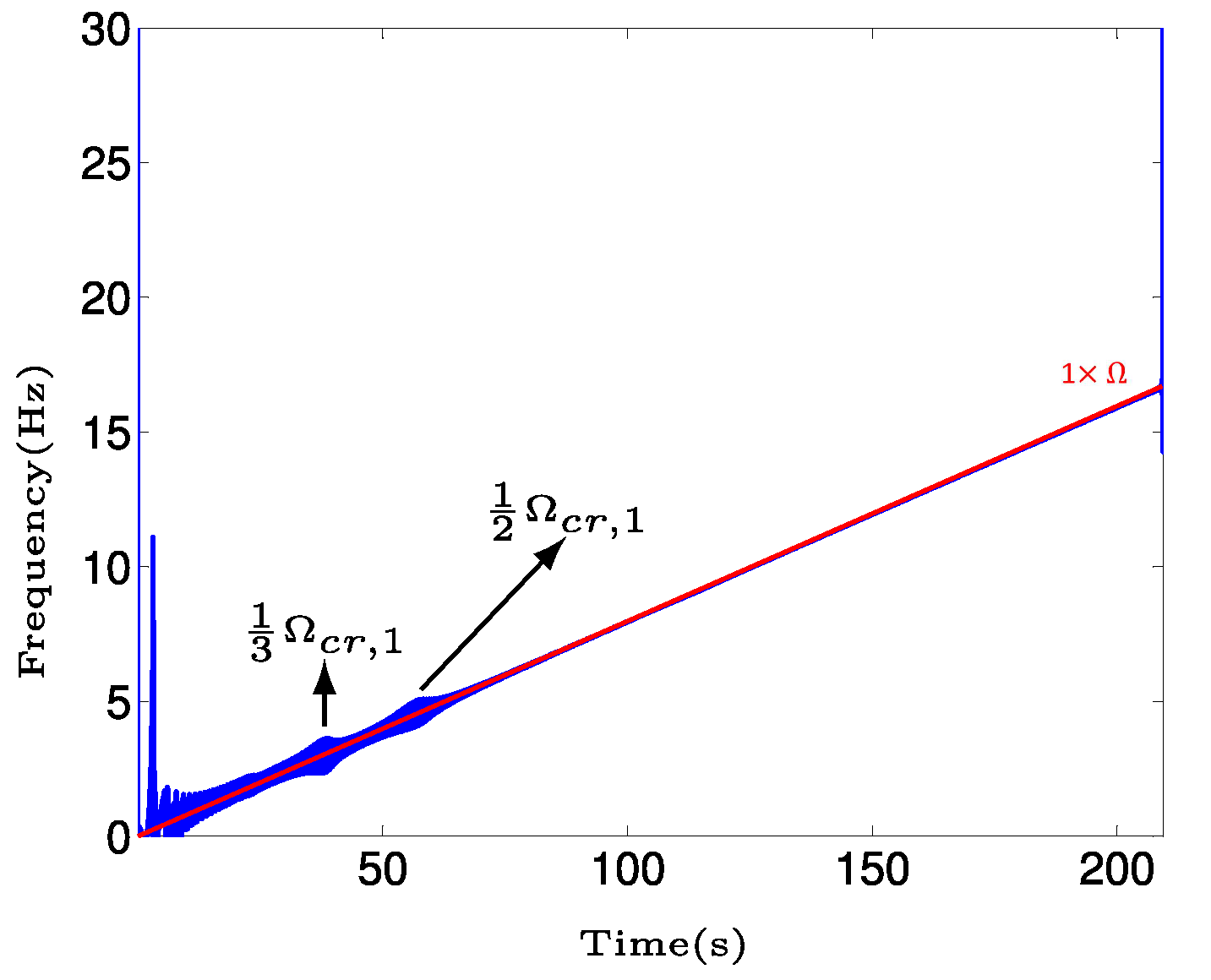
4. Results and Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | crack depth |
| C | external damping coefficient |
| Intrinsic Mode Function, IMF | |
| D | shaft diameter |
| E | shaft modulus of elasticity |
| crack breathing function | |
| shaft compliance matrix in the rotating system | |
| g | acceleration due to gravity |
| compliance elements of the cracked shaft cross-section | |
| in the rotating coordinates | |
| Hilbert transform operation | |
| I | shaft area moment of inertia about x-axis |
| instantaneous frequency of the IMF | |
| strain energy density function due to the crack | |
| stress intensity factors | |
| shaft stiffness matrix in the rotating system | |
| stiffness elements of the cracked shaft cross-section | |
| in the rotating coordinates | |
| lower envelope of the original signal | |
| disc location on the shaft | |
| shaft length | |
| M | disc mass |
| instantaneous mean of the original signal | |
| , | forces acting on the shaft cracked cross-area |
| R | shaft radius |
| upper envelope of the original signal | |
| additional strain energy due to the crack | |
| lateral (vertical and horizontal) response of the shaft, original signal | |
| additional deflections due to the crack () | |
| residual signal | |
| shaft rotational speed | |
| whirling speed of the shaft | |
| shaft acceleration rate | |
| unbalance disc eccentricity | |
| shaft rotational angle | |
| short-time Fourier transform parameter | |
| normalized crack depth |
References
- Zeng, J.; Chen, K.; Ma, H.; Duan, T.; Wen, B. Vibration response analysis of a cracked rotating compressor blade during run-up process. Mech. Syst. Signal Process. 2019, 118, 568–583. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, X.; Li, B. A study on vibration component separation of a rotor system during startup and its application in fault diagnosis. Meas. Sci. Technol. 2019, 30, 095104. [Google Scholar] [CrossRef]
- Sawicki, J.; Wu, X.; Baaklini, G.; Gyekenyesi, A. Vibration-based crack diagnosis in rotating shafts during acceleration through resonance. In Nondestructive Evaluation and Health Monitoring of Aerospace Materials and Composites II; SPIE: Bellingham, WA, USA, 2003; Volume 5046, pp. 1–10. [Google Scholar]
- Darpe, A.; Gupta, K.; Chawla, A. Transient response and breathing behaviour of a cracked Jeffcott rotor. J. Sound Vib. 2004, 272, 207–243. [Google Scholar] [CrossRef]
- Papadopoulos, C.; Dimarogonas, A. Coupled longitudinal and bending vibrations of a rotating shaft with an open crack. J. Sound Vib. 1987, 117, 81–93. [Google Scholar] [CrossRef]
- Darpe, A.; Gupta, K.; Chawala, A. Dynamics of a two-crack rotor. J. Sound Vib. 2003, 259, 649–675. [Google Scholar] [CrossRef][Green Version]
- Eshlemen, R.; Eubanks, R. On the critical speeds of a continuous shaft-disk system. J. Eng. Ind. 1967, 89, 645–652. [Google Scholar] [CrossRef]
- Jun, O.; Kim, J. Free bending vibration of a multi-step rotor. J. Sound Vib. 1999, 224, 625–642. [Google Scholar] [CrossRef]
- Yamamoto, T.; Ishida, Y. Linear and Nonlinear Rotordynamics: A Modern Treatment with Applications, 1st ed.; Wiley and Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Chasalevris, A.; Papadopoulos, C. A continuous model approach for cross-coupled bending vibrations of a rotor-bearing system with a transverse breathing crack. Mech. Mach. Theory 2009, 44, 1176–1191. [Google Scholar] [CrossRef]
- Sinou, J.J.; Denimal, E. Reliable crack detection in a rotor system with uncertainties via advanced simulation models based on kriging and Polynomial Chaos Expansion. Eur. J. Mech. Solids 2022, 92, 104451. [Google Scholar] [CrossRef]
- Fu, C.; Xu, Y.; Yang, Y.; Lu, K.; Gu, F.; Ball, A. Dynamics analysis of a hollow-shaft rotor system with an open crack under model uncertainties. Commun. Nonlinear Sci. Numer. Simulations 2020, 83, 105102. [Google Scholar] [CrossRef]
- Sinou, J.; Lees, A. A non-linear study of a cracked rotor. Eur. J. Mech. A Solids 2007, 26, 152–170. [Google Scholar] [CrossRef]
- AL-Shudeifat, M.; Butcher, E. New breathing functions for the transverse breathing crack of the cracked rotor system: Approach for critical and subcritical harmonic analysis. J. Sound Vib. 2011, 330, 526–544. [Google Scholar] [CrossRef]
- Sekhar, A. Multiple cracks effects and identification. Mech. Syst. Signal Process. 2008, 22, 845–878. [Google Scholar] [CrossRef]
- AL-Shudeifat, M.; Butcher, E.; Stern, C. General harmonic balance solution of a cracked rotor-bearing-disk system for harmonic and sub-harmonic analysis: Analytical and experimental approach. Int. J. Eng. Sci. 2010, 48, 921–935. [Google Scholar] [CrossRef]
- Friswell, M.; Penny, J. Crack modeling for structural health monitoring. Struct. Health Monit. 2002, 1, 139–148. [Google Scholar] [CrossRef]
- Lees, A.; Friswell, M. The vibration signature of chordal cracks in asymmetric rotors. In Proceedings of the 19th International Modal Analysis Conference (IMAC), Kissimmee, FL, USA, 5–8 February 2001; pp. 1–6. [Google Scholar]
- Plaut, R.; Andruet, R.; Suherman, S. Behavior of a cracked rotating shaft during passage through a critical speed. J. Sound Vib. 1994, 173, 577–589. [Google Scholar] [CrossRef]
- Ramesh Babu, T.; Srikanth, S.; Sekhar, A. Hilbert–Huang transform for detection and monitoring of crack in a transient rotor. Mech. Syst. Signal Process. 2008, 22, 905–914. [Google Scholar] [CrossRef]
- Jun, O.; Eun, H.; Earmme, Y.; Lee, C. Modeling and vibration analysis of a simple rotor with a breathing crack. J. Sound Vib. 1992, 155, 273–290. [Google Scholar] [CrossRef]
- Zou, J.; Chen, J.; Niu, J.; Cheng, Z. Application of the Wigner–Ville distribution to identification of a cracked rotor. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2003, 217, 551–556. [Google Scholar] [CrossRef]
- Sawicki, J.; Sen, A.; Litak, G. Multiresolution wavelet analysis of the dynamics of a cracked rotor. Int. J. Rotating Mach. 2009, 2009, 265198. [Google Scholar] [CrossRef]
- Papadopoulos, C. The strain energy release approach for modeling cracks in rotors: A state of the art review. Mech. Syst. Signal Process. 2008, 22, 763–789. [Google Scholar] [CrossRef]
- Darpe, A.; Gupta, K.; Chawla, A. Coupled bending, longitudinal and torsional vibrations of a cracked rotor. J. Sound Vib. 2004, 269, 33–60. [Google Scholar] [CrossRef]
- Sinou, J. Detection of cracks in rotor based on the 2× and 3× super-harmonic frequency components and the crack–unbalance interactions. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 2024–2040. [Google Scholar] [CrossRef]
- Sekhar, A. Vibration characteristics of a cracked rotor with two open cracks. J. Sound Vib. 1999, 223, 497–512. [Google Scholar] [CrossRef]
- Dimarogonas, A.; Papadopoulos, C. Vibration of cracked shafts in bending. J. Sound Vib. 1983, 91, 583–593. [Google Scholar] [CrossRef]
- Mayes, I.; Davies, W. Analysis of the response of a multi-rotor-bearing system containing a transverse crack in a rotor. J. Vib. Acoust. Stress. Reliab. Des. 1984, 106, 139–145. [Google Scholar] [CrossRef]
- Bachschmid, N.; Pennacchi, P.; Vania, A. Identification of multiple faults in rotor systems. J. Sound Vib. 2002, 254, 327–366. [Google Scholar] [CrossRef]
- Sinou, J.; Lees, A. The influence of cracks in rotating shafts. J. Sound Vib. 2005, 285, 1015–1073. [Google Scholar] [CrossRef]
- Gasch, R. A survey of the dynamic behavior of a simple rotating shaft with a transverse crack. J. Sound Vib. 1993, 106, 313–332. [Google Scholar] [CrossRef]
- Sekhar, A. On-line rotor fault identification by combined model and signal based approach. Noise Vib. Worldw. 2004, 35, 16–30. [Google Scholar] [CrossRef]
- Pennacchi, P.; Bachschmid, N.; Vania, A. A model-based identification method of transverse cracks in rotating shafts suitable for industrial machines. Mech. Syst. Signal Process. 2006, 20, 2112–2147. [Google Scholar] [CrossRef][Green Version]
- Papadopoulos, C.; Dimarogonas, A. Stability of cracked rotors in the coupled vibration mode. J. Vib. Acoust. Stress. Reliab. Des. 1988, 110, 356–360. [Google Scholar] [CrossRef]
- Sampaio, D.L.; Nicoletti, R. Detection of cracks in shafts with the Approximated Entropy algorithm. Mech. Syst. Signal Process. 2016, 72, 286–302. [Google Scholar] [CrossRef]
- Nicoletti, R.; Cavalini, A.A.; Steffen, V. Detection of Cracks in Rotating Shafts by Using the Combination Resonances Approach and the Approximated Entropy Algorithm. Shock Vib. 2018, 2018, 4094631. [Google Scholar] [CrossRef]
- Sekhar, A.; Prabhu, B. Condition monitoring of cracked rotors through transient response. Mech. Mach. Theory 1988, 33, 1167–1175. [Google Scholar] [CrossRef]
- Sekhar, A. Detection and monitoring of crack in a coast-down rotor supported on fluid film bearings. Tribol. Int. 2004, 37, 279–287. [Google Scholar] [CrossRef]
- Sekhar, A. Crack detection through wavelet transform for a run-up rotor. J. Sound Vib. 2003, 259, 461–472. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zuo, M. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Huang, N.; Shen, Z.; Long, S.; Wu, M.; Shih, E.; Zheng, Q.; Yen, N.; Tung, C.; Liu, H. The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Guo, D.; Peng, Z. Vibration analysis of a cracked rotor using Hilbert–Huang transform. Mech. Syst. Signal Process. 2007, 21, 3030–3041. [Google Scholar] [CrossRef]
- Harish Chandra, N.; Sekhar, A. Fault detection in rotor bearing systems using time frequency techniques. Mech. Syst. Signal Process. 2016, 72–73, 105–133. [Google Scholar] [CrossRef]
- Teyi, N.; Singh, S. A Decadal Review of Various Modelling and Analysis of Cracked Rotors. Procedia Struct. Integr. 2022, 39, 333–346. [Google Scholar] [CrossRef]
- Chen, G.; Wang, Z. A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components. Mech. Syst. Signal Process. 2012, 28, 258–279. [Google Scholar] [CrossRef]
- Rato, R.; Ortigueira, M.; Batista, A. On the HHT, its problems, and some solutions. Mech. Syst. Signal Process. 2008, 22, 1374–1394. [Google Scholar] [CrossRef]
- He, Z.; Shen, Y.; Wang, Q. Boundary extension for Hilbert–Huang transform inspired by gray prediction model. Signal Process. 2012, 92, 685–697. [Google Scholar] [CrossRef]
- Xun, J.; Yan, S. A revised Hilbert–Huang transformation based on the neural networks and its application in vibration signal analysis of a deployable structure. Mech. Syst. Signal Process. 2008, 22, 1705–1723. [Google Scholar] [CrossRef]
- Zhu, X.; Hu, J.; Lv, S. Comprehensive evaluation study on the methods for restraining the end effect in EMD. Inf. Technol. J. 2013, 12, 3870–3874. [Google Scholar]
- Hawley, S.; Atlas, L.; Chizeck, H. Some properties of an empirical mode type signal decomposition algorithm. IEEE Signal Process. Lett. 2010, 17, 24–27. [Google Scholar] [CrossRef]
- Roy, A.; Doherty, J. Raised cosine filter–based empirical mode decomposition. IET Signal Process. 2011, 5, 121–129. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Zi, Y. A comparative study on the local mean decomposition and empirical mode decomposition and their applications to rotating machinery health diagnosis. J. Vib. Acoust. 2010, 132, 021010. [Google Scholar] [CrossRef]
- Qin, S.; Zhong, Y. A new envelope algorithm of Hilbert–Huang Transform. Mech. Syst. Signal Process. 2006, 20, 1941–1952. [Google Scholar] [CrossRef]
- Shulin, L.; Haifeng, Z.; Hui, W.; Rui, M. Application of improved EMD algorithm for the fault diagnosis of reciprocating pump valves with spring failure. In Proceedings of the 9th International Symposium on ISSPA, Sharjah, United Arab Emirates, 12–15 February 2007; pp. 1–4. [Google Scholar]
- Arlot, S.; Celisse, A. A survey of cross–validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]

| Description | Value |
|---|---|
| Modulus of elasticity (Pa) | 69 × 109 |
| Modulus of rigidity (Pa) | 34 × 109 |
| Shaft diameter (m) | 0.01905 |
| Shaft length (m) | 1.27 |
| Shaft density (kg/m3) | 2700 |
| Disc density (kg/m3) | 2700 |
| Disc diameter (m) | 0.1524 |
| Disc thickness (m) | 0.0254 |
| Normalized disc location | 0.5 |
| Unbalance mass (kg) | 0.01 |
| Unbalance eccentricity (m) | 0.0508 |
| Normalized Crack Depth | Computational Cost (s) | Transient Responses Similarity | |
|---|---|---|---|
| Proposed Breathing Function | Darpe et al. [4] Breathing Model | ||
| 1 | 12.866 | 446.942 | 0.9296 |
| 0.5 | 12.319 | 408.907 | 0.9943 |
| 0.2 | 12.673 | 369.702 | 0.9995 |
| 0.1 | 12.364 | 341.060 | 0.9999 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khorrami, H.; Sedaghati, R.; Rakheja, S. Vertical Transient Response Analysis of a Cracked Jeffcott Rotor Based on Improved Empirical Mode Decomposition. Vibration 2022, 5, 408-428. https://doi.org/10.3390/vibration5030023
Khorrami H, Sedaghati R, Rakheja S. Vertical Transient Response Analysis of a Cracked Jeffcott Rotor Based on Improved Empirical Mode Decomposition. Vibration. 2022; 5(3):408-428. https://doi.org/10.3390/vibration5030023
Chicago/Turabian StyleKhorrami, Hamid, Ramin Sedaghati, and Subhash Rakheja. 2022. "Vertical Transient Response Analysis of a Cracked Jeffcott Rotor Based on Improved Empirical Mode Decomposition" Vibration 5, no. 3: 408-428. https://doi.org/10.3390/vibration5030023
APA StyleKhorrami, H., Sedaghati, R., & Rakheja, S. (2022). Vertical Transient Response Analysis of a Cracked Jeffcott Rotor Based on Improved Empirical Mode Decomposition. Vibration, 5(3), 408-428. https://doi.org/10.3390/vibration5030023







