Post-Breakage Vibration Frequency Analysis of In-Service Pedestrian Laminated Glass Modular Units
Abstract
:1. Introduction
2. State of the Art
2.1. Reference Limit States for Design
- In more complex situations, the minimum performance requirements that the damaged structural must guarantee must be established ad hoc. The structure must, in any case, guarantee “fail safe” behaviour, with specific reference to hierarchy, system redundancy and resilience. The residual load-bearing capacity must include, as a minimum, the characteristic values of the self-weight of the structure;
- the single glass structural element must guarantee section redundancy, never intended as an increase in the sheet thickness, but as an increase in the number of glass layers. For laminated glass, the performance of a package made up of an interlayer and one or more fragmented glass sheets must be properly defined.

2.2. Vibration Frequency of Laminated Glass Elements
2.3. Design of Pedestrian Glass Sytems
3. Preliminary Considerations
3.1. Research Goal
3.2. Literature Approaches for Post-Breakage Performance Assessment
3.3. Post-Breakage Frequency Analysis of Laminated Glass (LG) Elements
4. On-Site Experimental Investigation
4.1. Layout and Geometry
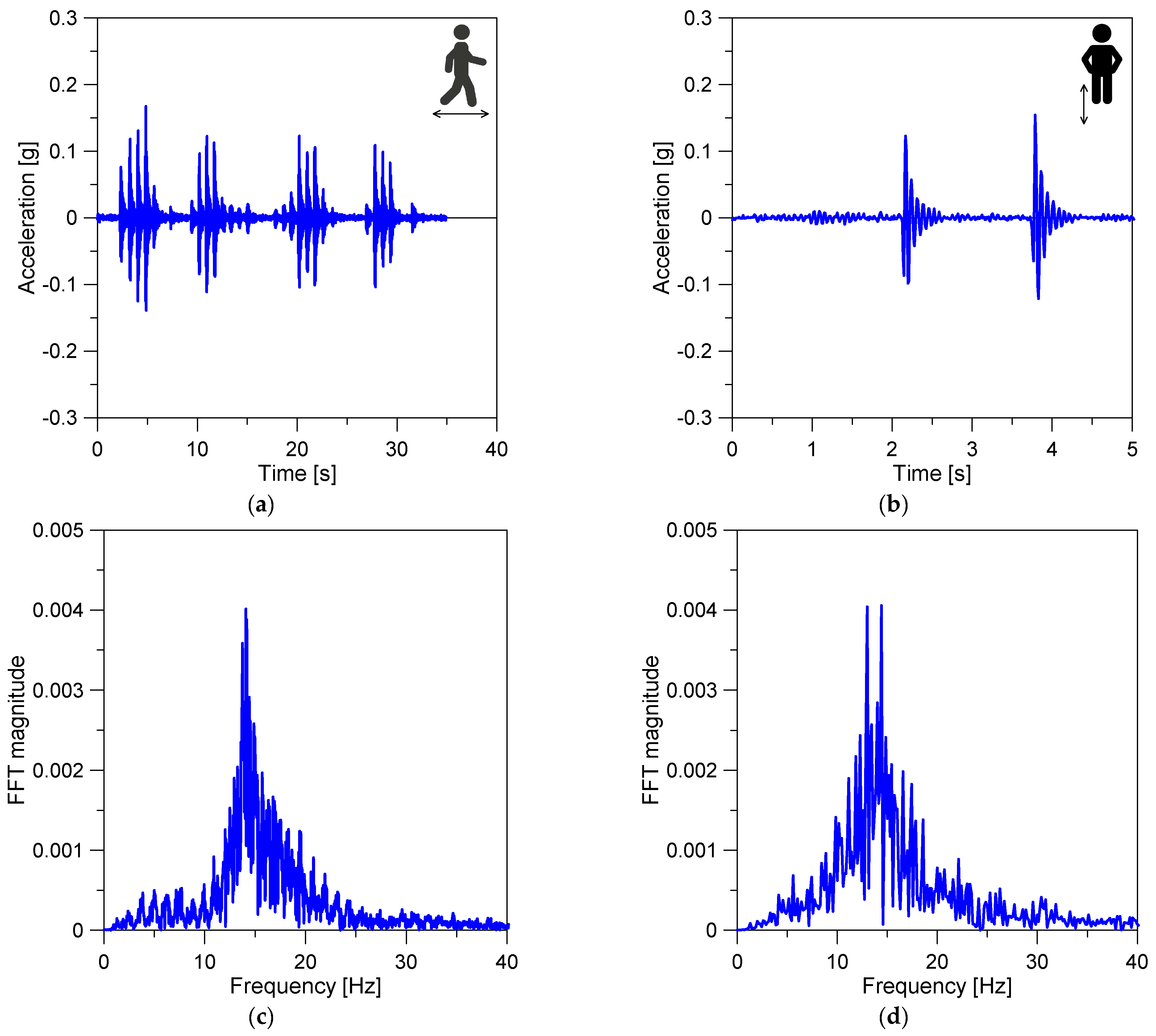
4.2. Test Setup, Instruments and Experimental Records
4.3. Analysis of Experimental Results
5. Frequency Numerical Analysis
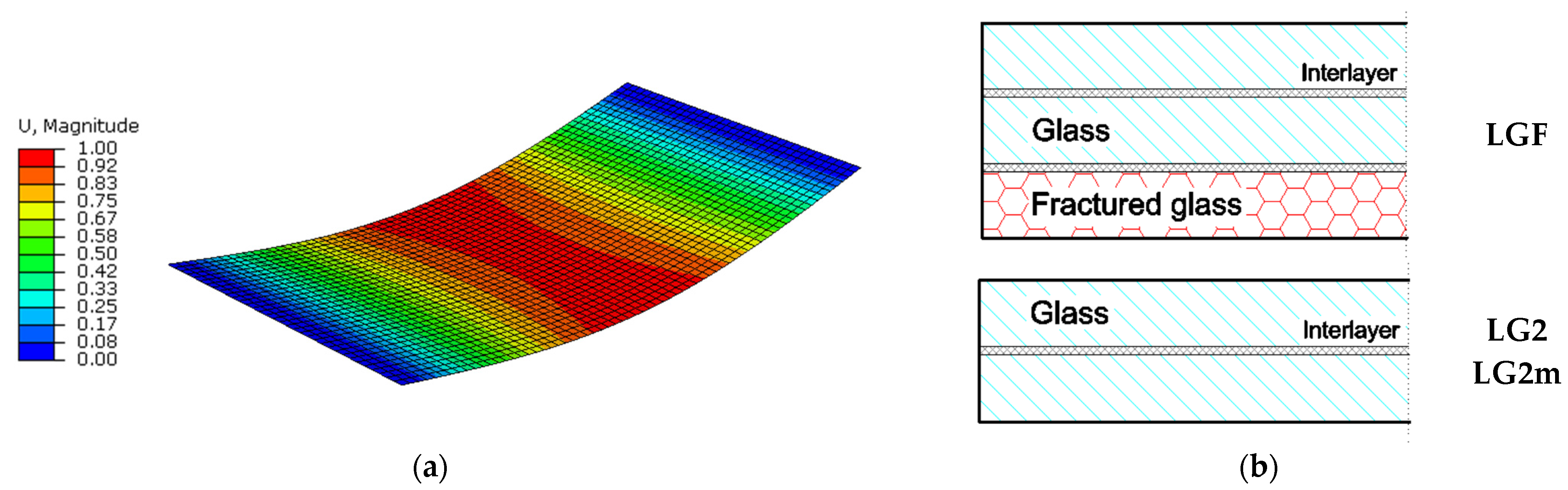
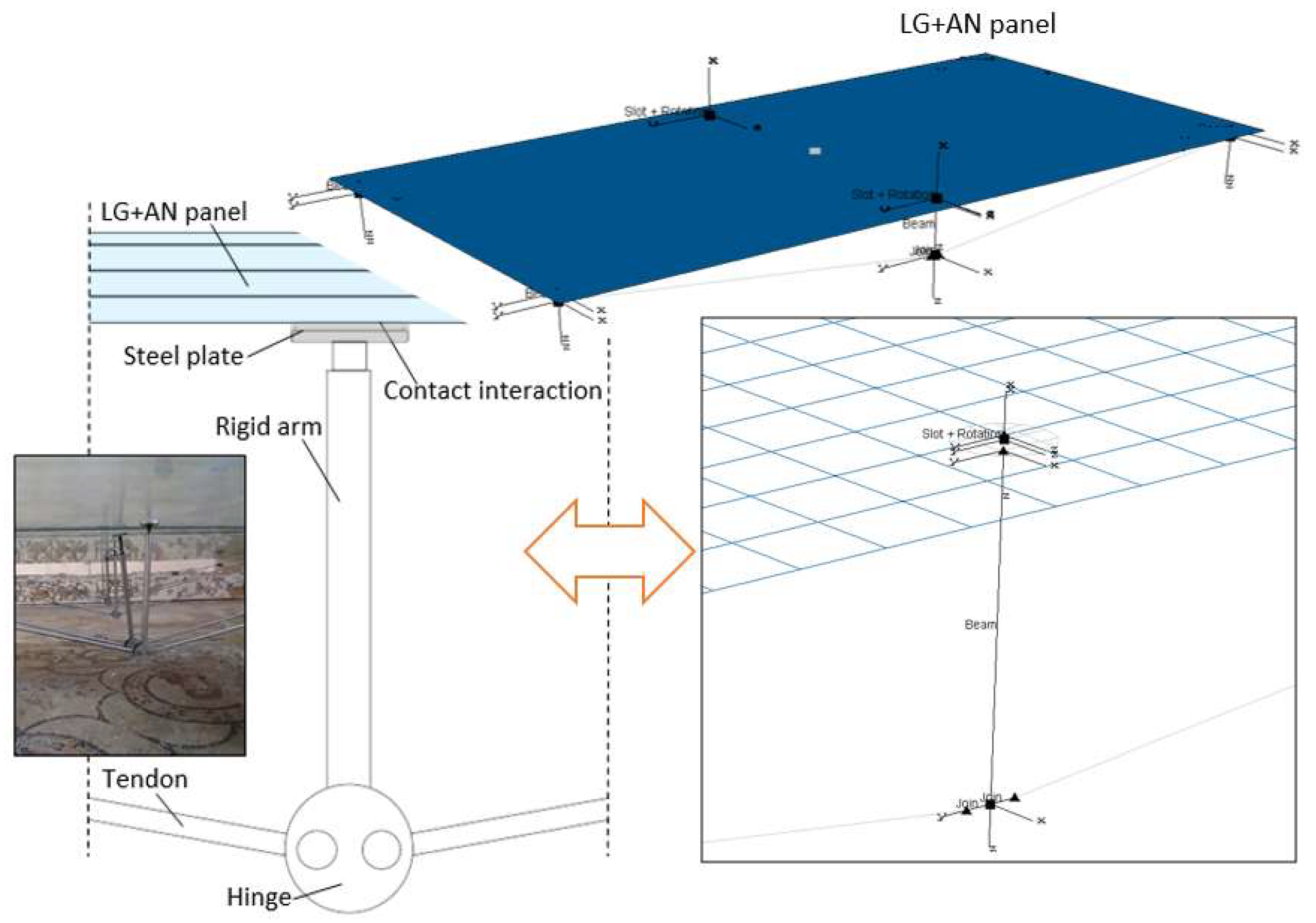
5.1. Modelling
5.2. Boundaries and Mechanical Interactions
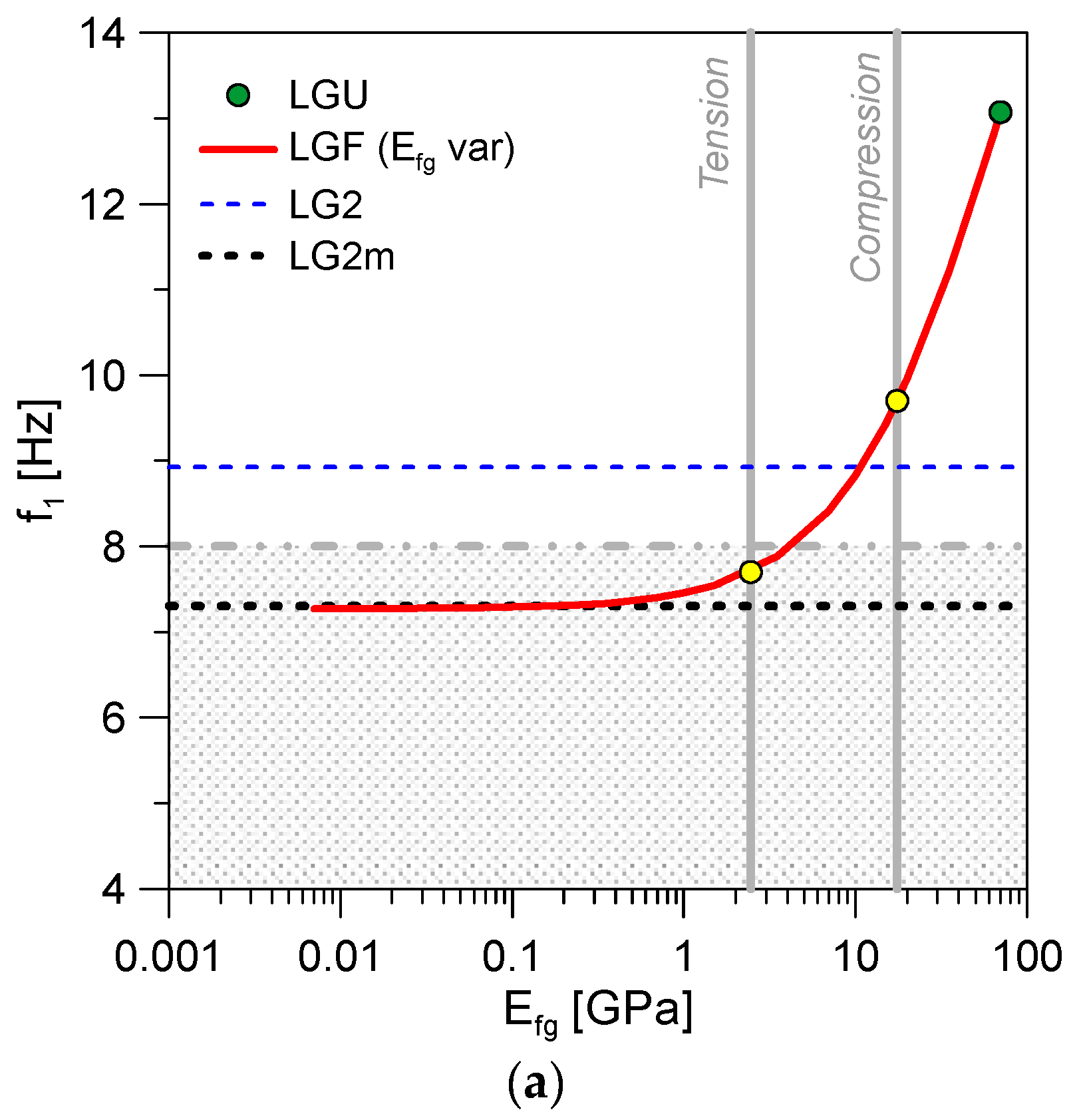
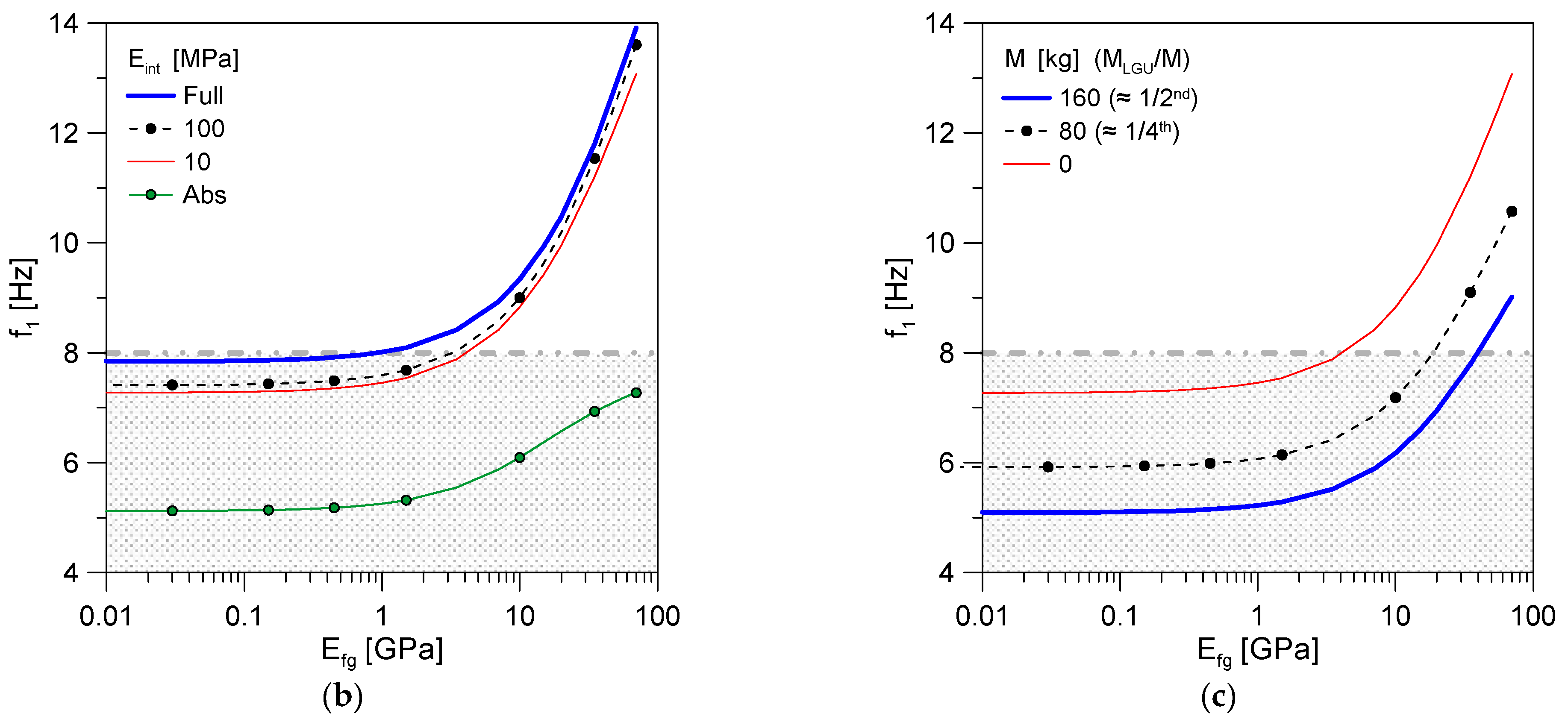
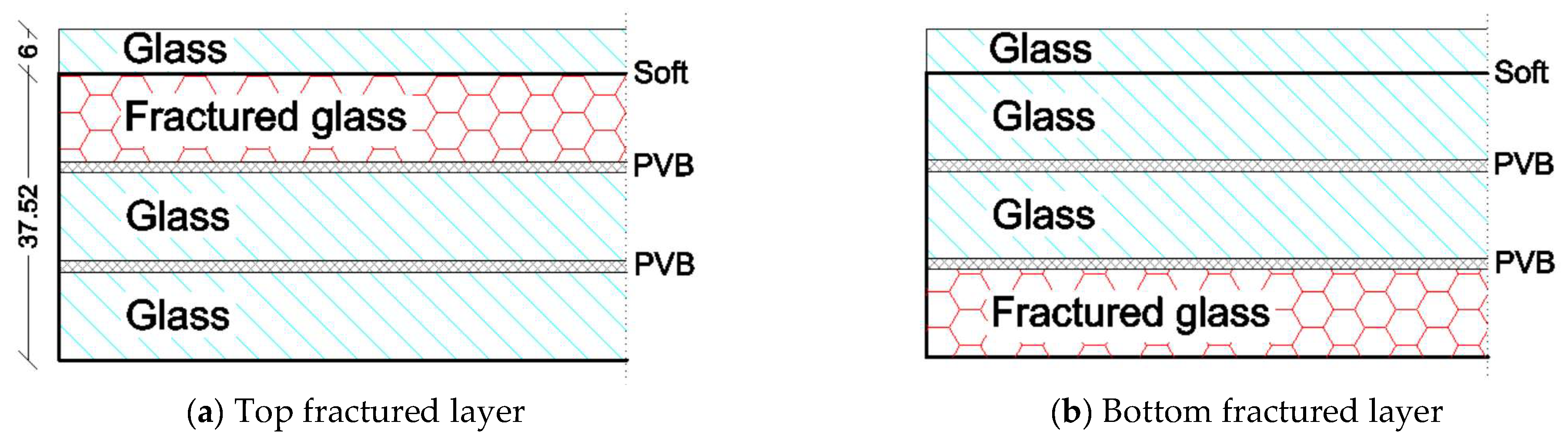
5.3. Material Properties
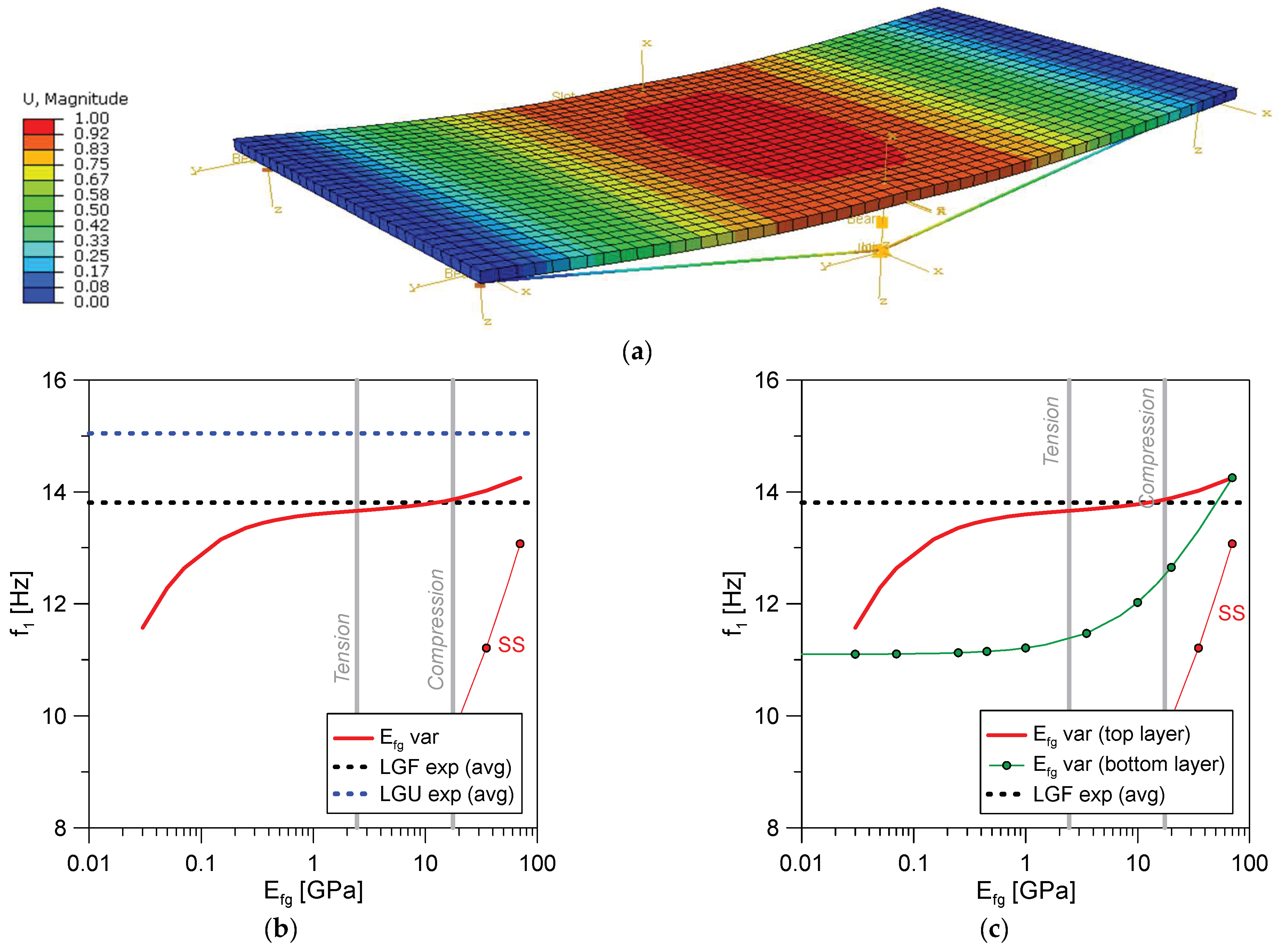
5.4. Discussion of Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bedon, C.; Zhang, X.; Santos, F.; Honfi, D.; Kozłowski, M.; Arrigoni, M.; Figuli, L.; Lange, D. Performance of structural glass facades under extreme loads—Design methods, existing research, current issues and trends. Constr. Build. Mater. 2018, 163, 921–937. [Google Scholar] [CrossRef]
- Kott, A.; Vogel, T. Controlling the post-breakage behavior of laminated safety glass. In Proceedings of the International Symposium on the Application of Architectural Glass, Munich, Germany, 15–16 November 2004. [Google Scholar]
- Zhao, C.; Yang, J.; Wang, X.E.; Azim, I. Experimental investigation into the post-breakage performance of pre-cracked laminated glass plates. Constr. Build. Mater. 2019, 224, 996–1006. [Google Scholar] [CrossRef]
- Galuppi, L.; Royer-Carfagni, G. The post-breakage response of laminated heat-treated glass under in plane and out of plane loading. Compos. Part B Eng. 2018, 147, 227–239. [Google Scholar] [CrossRef]
- Kozłowski, M. Experimental and numerical assessment of structural behaviour of glass balustrade subjected to soft body impact. Compos. Struct. 2019, 229, 111380. [Google Scholar] [CrossRef]
- Bedon, C.; Kalamar, R.; Eliášová, M. Low velocity impact performance investigation on square hollow glass columns via full-scale experiments and Finite Element analyses. Compos. Struct. 2017, 182, 311–325. [Google Scholar] [CrossRef]
- Correia, J.R.; Valarinho, L.; Branco, F.A. Post-cracking strength and ductility of glass-GFRP composite beams. Compos. Struct. 2011, 93, 2299–2309. [Google Scholar] [CrossRef]
- Corradi, M.; Speranzini, E. Post-cracking capacity of glass beams reinforced with steel fibers. Materials 2019, 12, 231. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bedon, C.; Santarsiero, M. Laminated glass beams with thick embedded connections—Numerical analysis of full-scale specimens during cracking regime. Compos. Struct. 2018, 195, 308–324. [Google Scholar] [CrossRef]
- Figuli, L.; Papan, D.; Papanova, Z.; Bedon, C. Experimental mechanical analysis of traditional in-service glass windows subjected to dynamic tests and hard body impact. Smart Struct. Syst. 2021, 27, 365. [Google Scholar]
- Mohagheghian, I.; Wang, Y.; Zhou, J.; Yu, L.; Guo, X.; Yan, Y.; Charalambides, M.; Dear, J. Deformation and damage mechanisms of laminated glass windows subjected to high velocity soft impact. Int. J. Solids Struct. 2017, 109, 46–62. [Google Scholar] [CrossRef]
- Pelferne, J.; van Dam, S.; Kuntsche, J.; van Paepegem, W. Numerical simulation of the EN 12600 Pendulum Test for Structural Glass. In Proceedings of the Challenging Glass Conference Proceedings, Ghent, Belgium, 16 June 2016; Volume 5, pp. 429–438, ISSN 2589-8019. [Google Scholar]
- Salawu, O.S. Detection of structural damage through changes in frequency: A review. Eng. Struct. 1997, 19, 718–723. [Google Scholar] [CrossRef]
- Hearn, G.; Testa, R.B. Modal Analysis for Damage Detection in Structures. J. Struct. Eng. 1991, 117, 3042–3063. [Google Scholar] [CrossRef]
- Limongelli, M.P.; Manoach, E.; Quqa, S.; Giordano, P.F.; Bhowmik, B.; Pakrashi, V.; Cigada, A. Vibration Response-Based Damage Detection. In Structural Health Monitoring Damage Detection Systems for Aerospace; Springer Aerospace Technology; Sause, M.G.R., Jasiūnienė, E., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Dimarogonas, A.D. Vibration of cracked structures: A state of the art review. Eng. Fract. Mech. 1996, 55, 831–857. [Google Scholar] [CrossRef]
- Rainieri, C.; Notarangelo, M.A.; Fabbrocino, G. Experiences of Dynamic Identification and Monitoring of Bridges in Serviceability Conditions and after Hazardous Events. Infrastructures 2020, 5, 86. [Google Scholar] [CrossRef]
- Kawiecki, G. Modal damping measurement for damage detection. Smart Mater. Struct. 2001, 10, 466–471. [Google Scholar] [CrossRef]
- Modena, C.; Sonda, D.; Zonta, D. Damage localization in reinforced concrete structures by using damping measurements. Key Eng. Mater. 1999, 167–168, 132–141. [Google Scholar] [CrossRef]
- Hamey, C.S.; Lestari, W.; Qiao, P.; Song, G. Experimental damage identification of carbon/epoxy composite beams using curvature mode shapes. J. Struct. Health Monit. 2004, 3, 333–353. [Google Scholar] [CrossRef]
- Kim, J.-T.; Ryu, Y.-S.; Cho, H.-M.; Stubbs, N. Damage identification in beam-type structures: Frequency-based method vs mode-shape-based method. Eng. Struct. 2003, 25, 57–67. [Google Scholar] [CrossRef]
- Shahabpoor, E.; Pavic, A.; Racic, V. Interaction between walking humans and structures in vertical direction: A literature review. Shock. Vib. 2016, 2016, 3430285. [Google Scholar] [CrossRef] [Green Version]
- Bedon, C.; Mattei, S. Facial Expression-Based Experimental Analysis of Human Reactions and Psychological Comfort on Glass Structures in Buildings. Buildings 2021, 11, 204. [Google Scholar] [CrossRef]
- CNR-DT 210/2013. Istruzioni Per la Progettazione, L’esecuzione ed il Controllo di Construzioni con Elementi Strutturali di Vetro; National Research Council of Italy (CNR): Roma, Italy, 2013. (In Italian)
- Clough, R.W.; Penzien, J. Dynamics of Structures; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Zemanova, A.; Zeman, J.; Janda, T.; Schmidt, J.; Sejnoha, M. On modal analysis of laminated glass: Usability of simplified methods and Enhanced Effective Thickness. Compos. Part B 2018, 151, 92–105. [Google Scholar] [CrossRef] [Green Version]
- Bedon, C. Issues on the vibration analysis of in-service laminated glass structures: Analytical, experimental and numerical investigations on delaminated beams. Appl. Sci. 2019, 9, 3928. [Google Scholar] [CrossRef] [Green Version]
- Lenci, S.; Consolini, L.; Clementi, F. On the experimental determination of dynamical properties of laminated glass. Ann. Solid Struct. Mech. 2015, 7, 27–43. [Google Scholar] [CrossRef]
- Bedon, C.; Fasan, M.; Amadio, C. Vibration analysis and dynamic characterization of structural glass element with different restraints based on operational modal analysis. Buildings 2019, 9, 13. [Google Scholar] [CrossRef] [Green Version]
- Pelayo, F.; Lopez-Aenlle, M. Natural frequencies and damping ratios of multi-layered laminated glass beams using a dynamic effective thickness. J. Sandw. Struct. Mater. 2017, 21, 439–463. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Xie, M.; Du, J.Z.Y.M.; Song, H.-K. Rapid evaluation of safety-state in hidden-frame supported glass curtain walls using remote vibration measurements. J. Build. Eng. 2018, 19, 91–97. [Google Scholar] [CrossRef]
- Bedon, C.; Fasan, M. Reliability of field experiments, analytical methods and pedestrian’s perception scales for the vibration serviceability assessment of an in-service glass walkway. Appl. Sci. 2019, 9, 1936. [Google Scholar] [CrossRef] [Green Version]
- Bedon, C. Diagnostic analysis and dynamic identification of a glass suspension footbridge via on-site vibration experiments and FE numerical modelling. Compos. Struct. 2019, 216, 366–378. [Google Scholar] [CrossRef]
- Bedon, C. Experimental investigation on vibration sensitivity of an indoor glass footbridge to waling conditions. J. Build. Eng. 2020, 29, 101195. [Google Scholar] [CrossRef]
- Bedon, C.; Bergamo, E.; Izzi, M.; Noè, S. Prototyping and validation of MEMS accelerometers for structural health monitoring—The case study of the Pietratagliata cable-stayed bridge. J. Sens. Actuator Netw. 2018, 7, 18. [Google Scholar] [CrossRef] [Green Version]
- SMIT. Structural Modal Identification Toolsuite. 2021. [Google Scholar]
- Chang, M.; Leonard, R.L.; Pakzad, S.N. SMIT User’s Guide. Available online: http://smit.atlss.lehigh.edu/wp-content/uploads/2012/07/SMIT-Users-Guide.pdf (accessed on 3 October 2021).
- Chang, M.; Pakzad, S.N. Observer Kalman Filter Identification for Output-Only Systems Using Interactive Structural Modal Identification Toolsuite. J. Bridge Eng. 2014, 19, 04014002. [Google Scholar] [CrossRef] [Green Version]
- ABAQUS Computer Software; Simulia: Dassault, RI, USA, 2021.




| Mode Order n | ||
|---|---|---|
| 1 | 2 | 3 |
| π/L | 2π/L | 3π/L |
| Glass | PVB | Steel | Fractured Glass | ||
|---|---|---|---|---|---|
| E | MPa | 70,000 | 4 | 160,000 | Variable (7–70,000) |
| ν | - | 0.23 | 0.49 | 0.3 | 0.23 |
| ρ | Kg/m3 | 2500 | 1100 | 7850 | 2500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedon, C.; Noè, S. Post-Breakage Vibration Frequency Analysis of In-Service Pedestrian Laminated Glass Modular Units. Vibration 2021, 4, 836-852. https://doi.org/10.3390/vibration4040047
Bedon C, Noè S. Post-Breakage Vibration Frequency Analysis of In-Service Pedestrian Laminated Glass Modular Units. Vibration. 2021; 4(4):836-852. https://doi.org/10.3390/vibration4040047
Chicago/Turabian StyleBedon, Chiara, and Salvatore Noè. 2021. "Post-Breakage Vibration Frequency Analysis of In-Service Pedestrian Laminated Glass Modular Units" Vibration 4, no. 4: 836-852. https://doi.org/10.3390/vibration4040047
APA StyleBedon, C., & Noè, S. (2021). Post-Breakage Vibration Frequency Analysis of In-Service Pedestrian Laminated Glass Modular Units. Vibration, 4(4), 836-852. https://doi.org/10.3390/vibration4040047







