Practical Modal Analysis of a Prototyped Hydrogenerator
Abstract
:1. Introduction
2. Materials and Methods
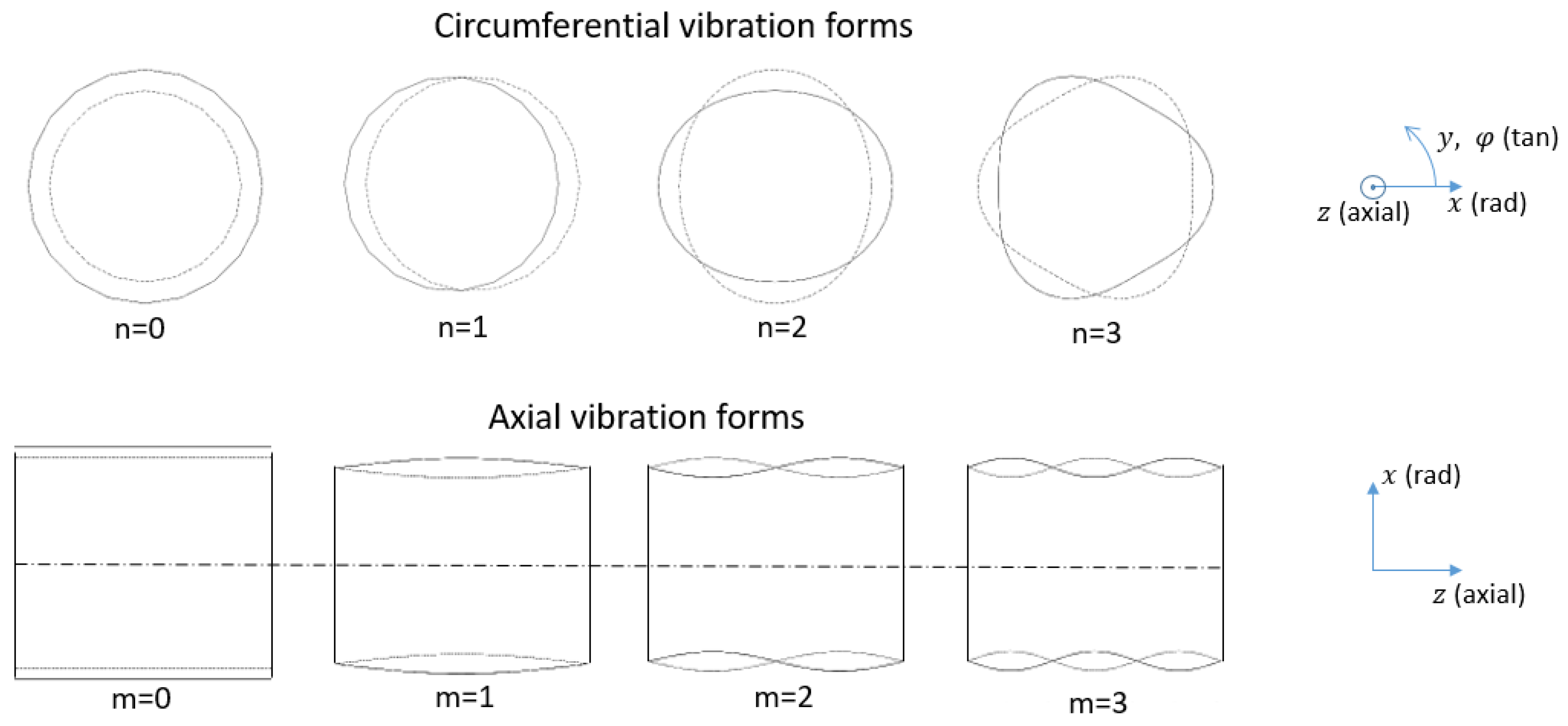
2.1. Analytical Model
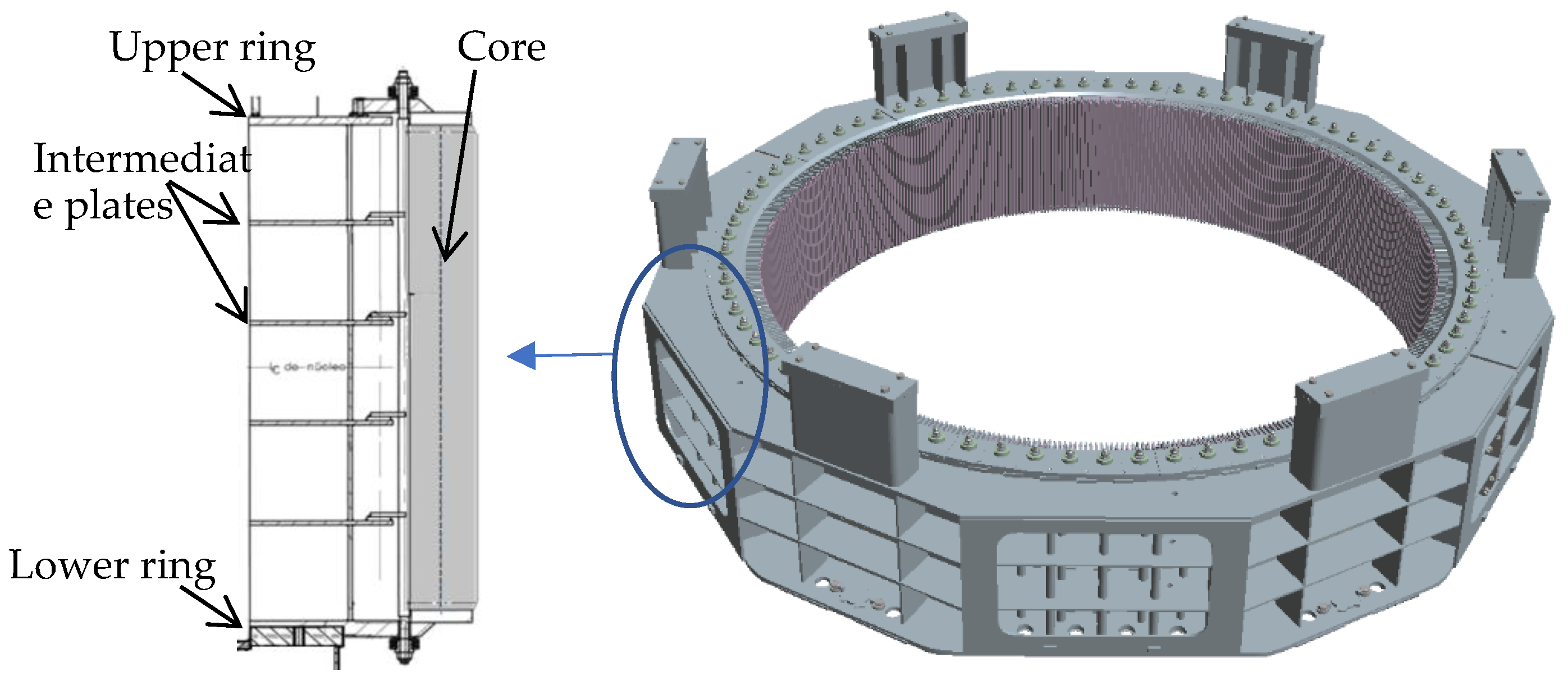
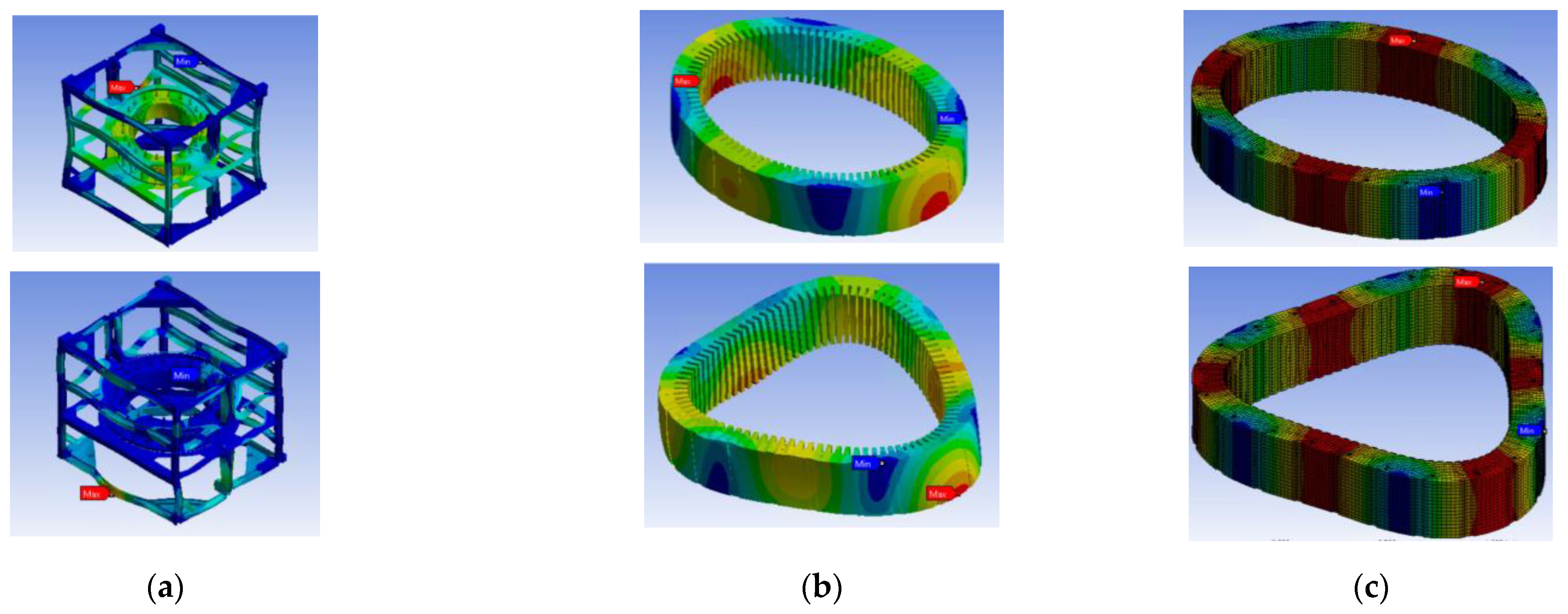
2.2. Finite-Element Model
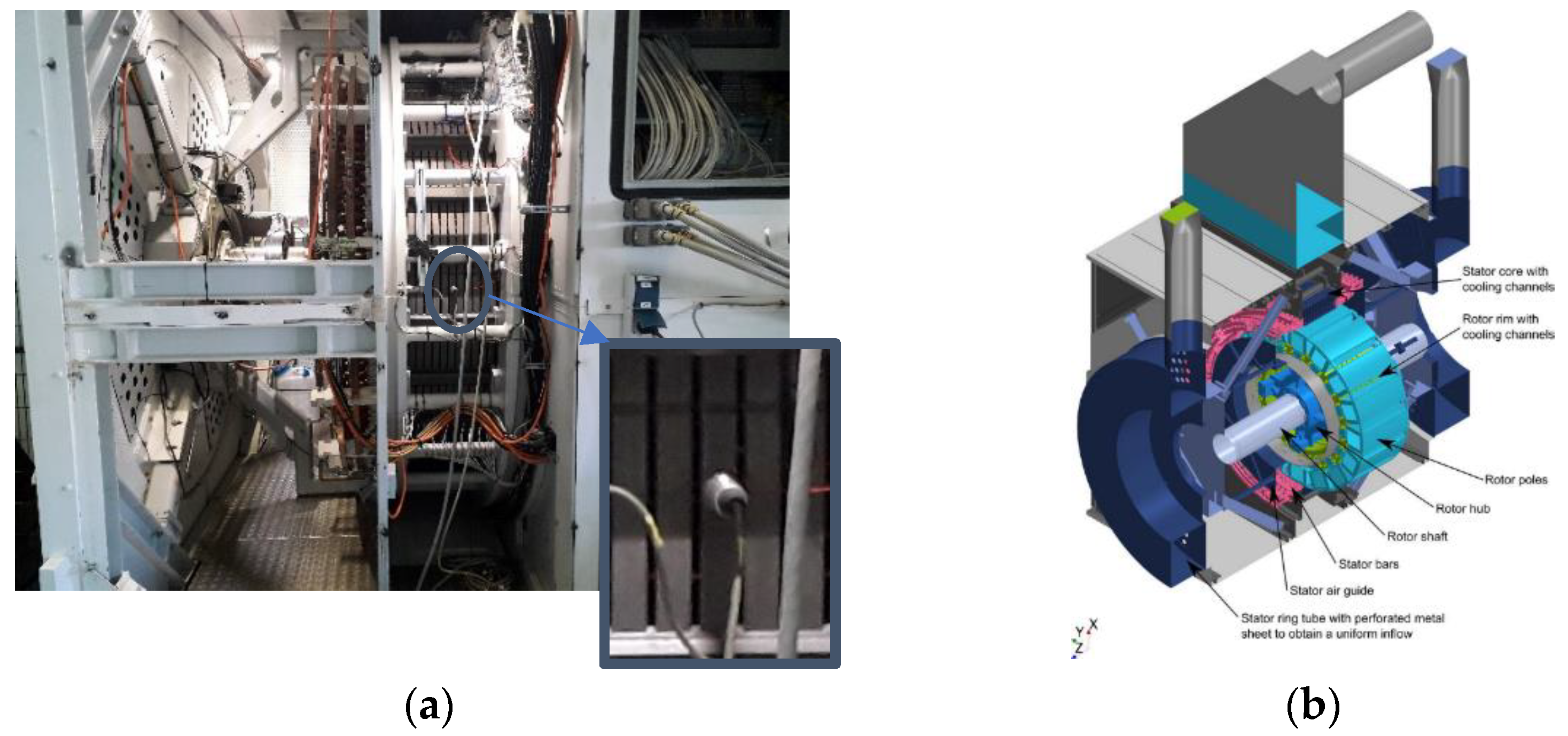
2.3. Validation Measurements on a Prototyped Hydrogenerator
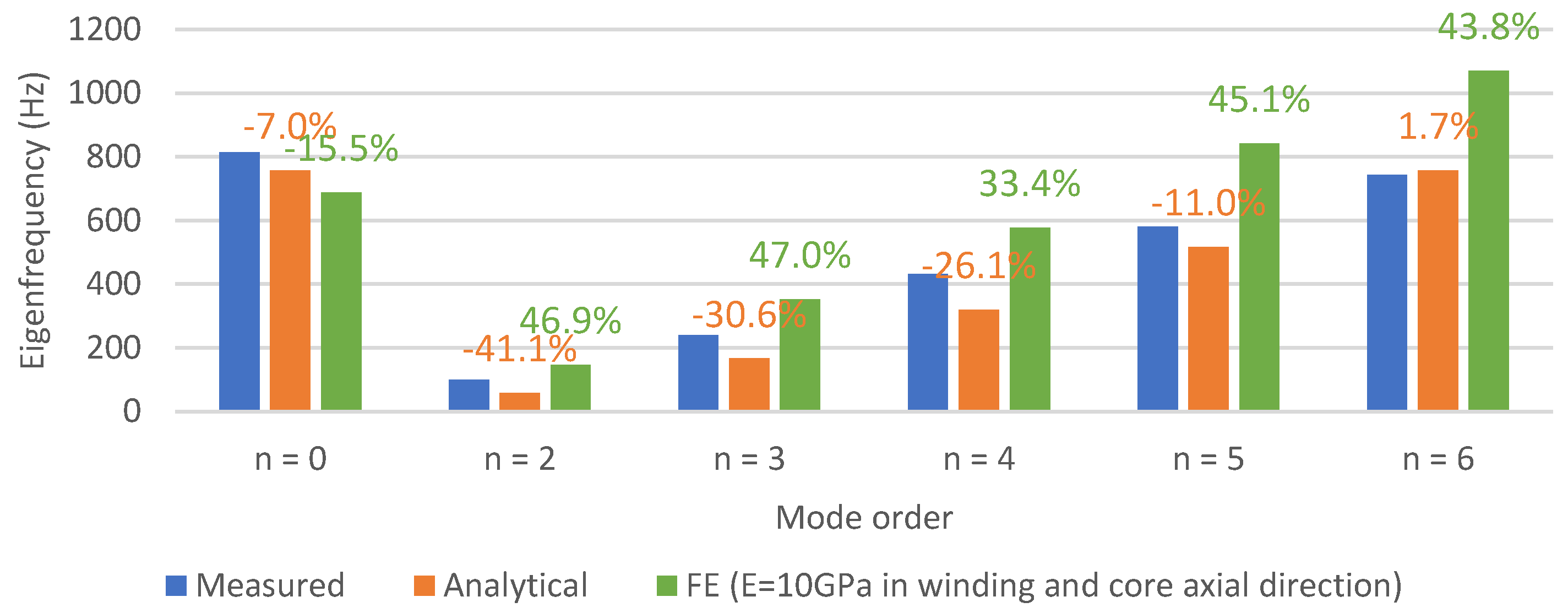
3. Results
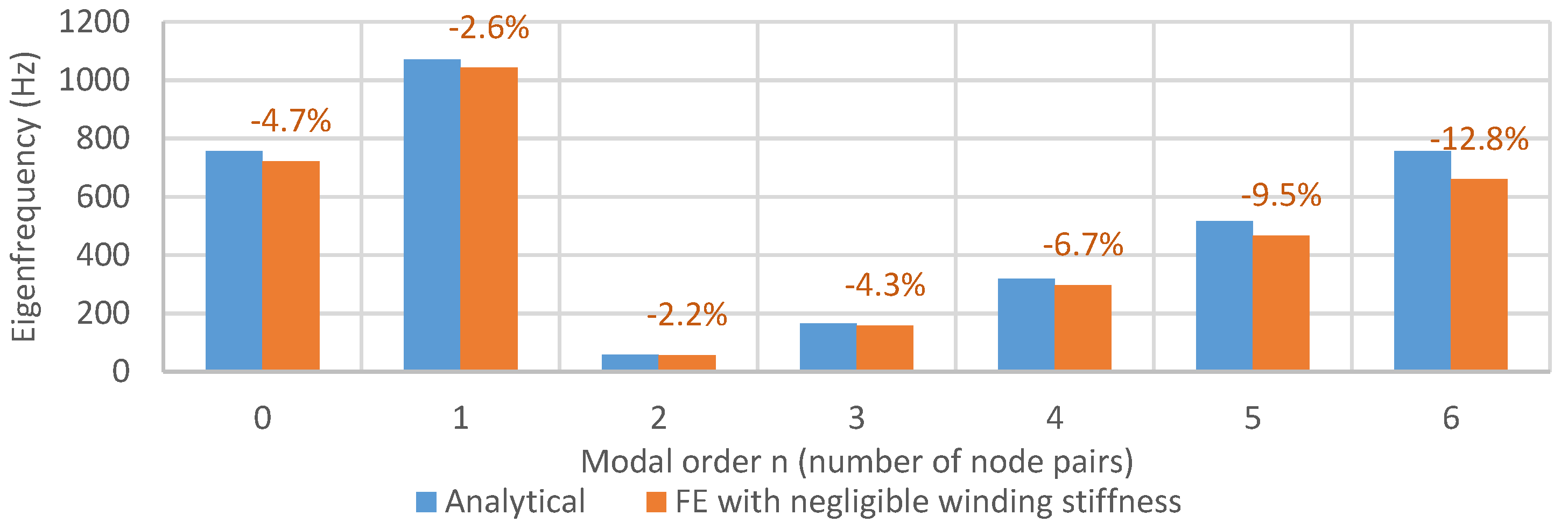
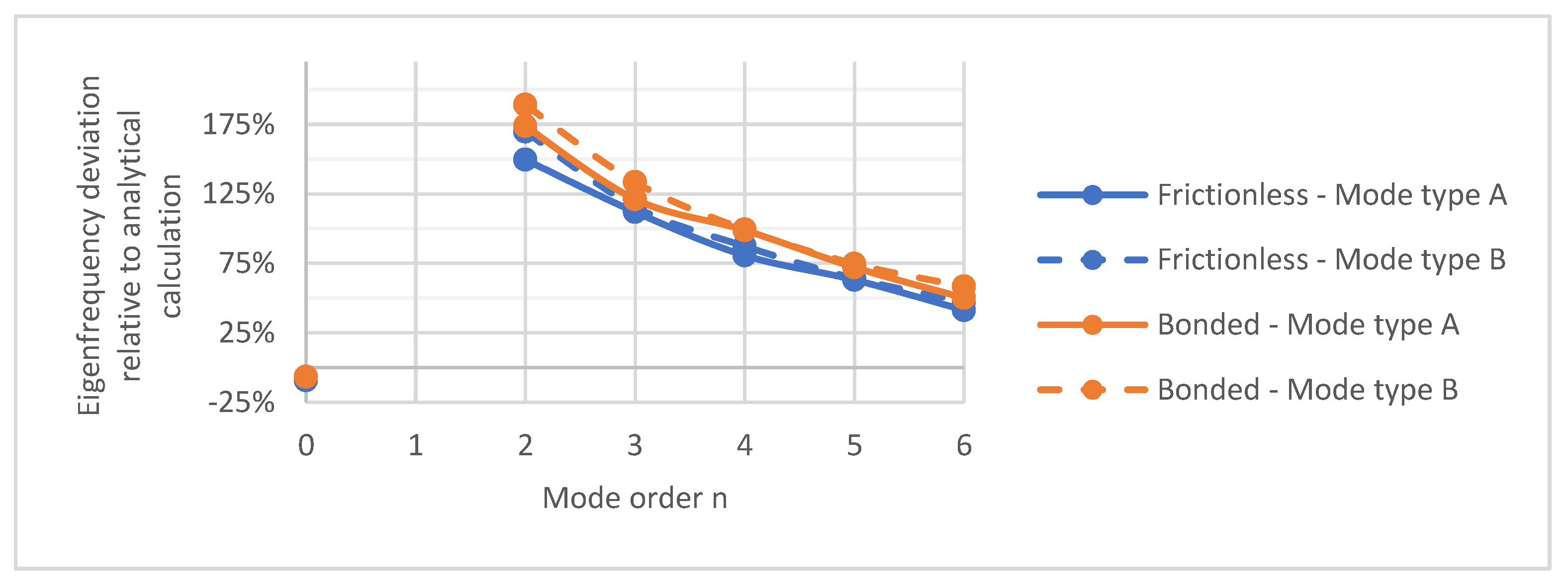
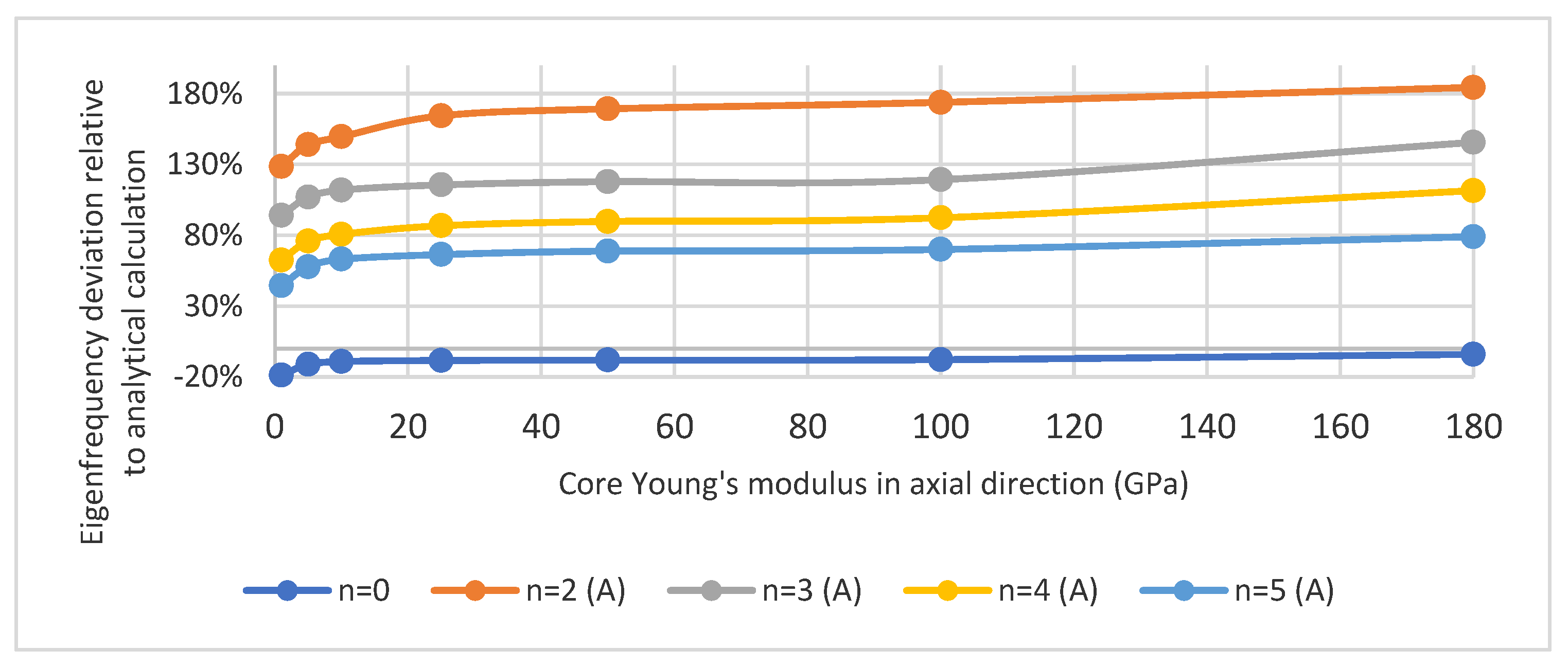
3.1. Comparison between Models Using Different Input Parameters
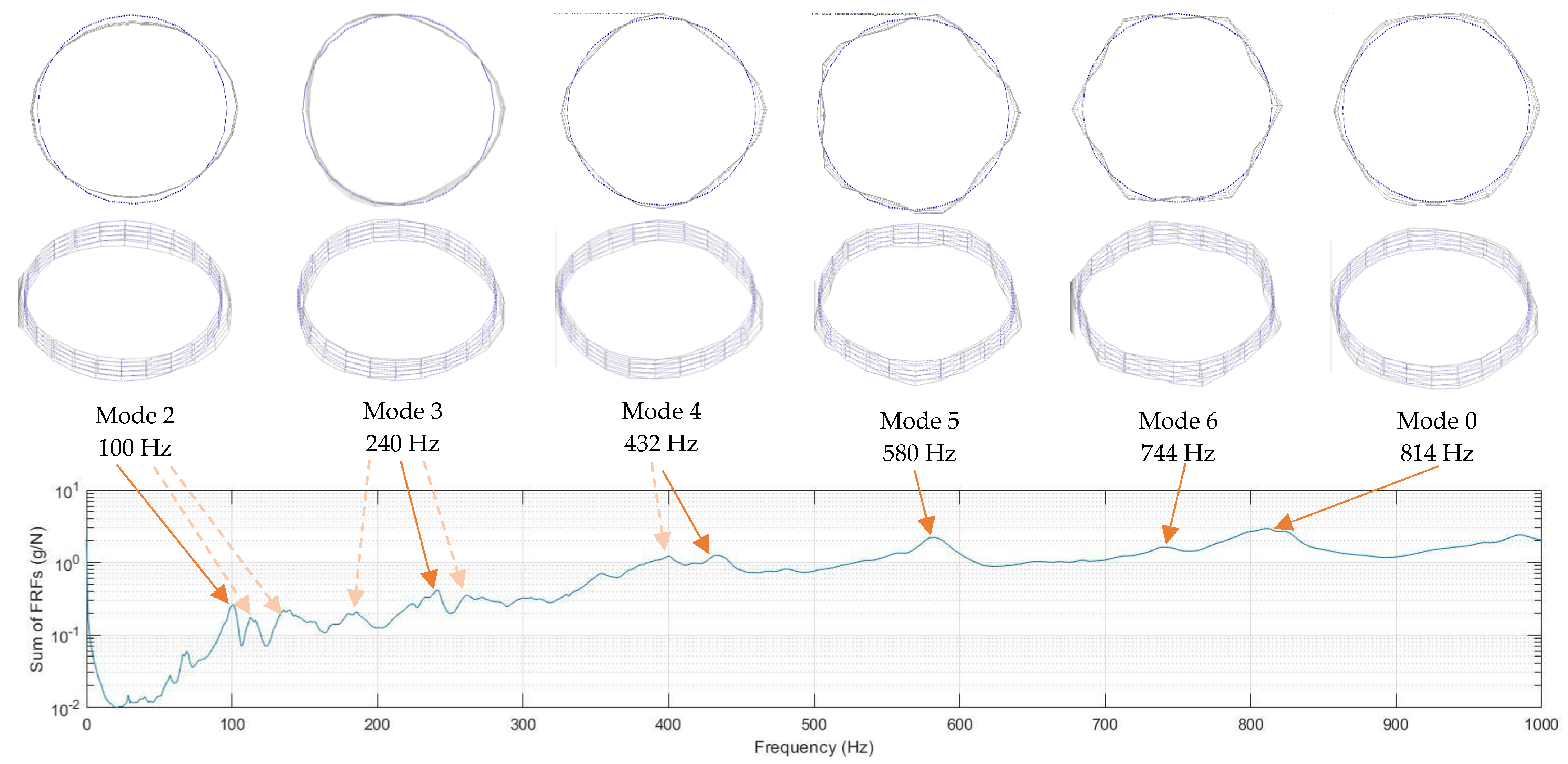
3.2. Experimental Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Barros, A.; Chabu, I.E. Modeling of Airgap Flux Density for the Study of Stator Core Vibration in Low Speed Synchronous Machines. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2020, 39, 839–852. [Google Scholar] [CrossRef]
- Sobra, J.; Byrtus, M. Impact of Electrical Machine Structural Parts on its Modal and Vibration Behavior. Proceedings of IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 1107–1113. [Google Scholar]
- Engevik, E.L. Design and Operation Investigations for Large Converter-Fed Synchronous Machines in Hydropower Applications. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2019. [Google Scholar]
- Jordan, H. Geräuscharme Elektromotoren; W. Girardet: Essen, Germany, 1950. [Google Scholar]
- Arnold, R.N.; Warburton, G.B. Flexural vibrations of the walls of thin cylindrical shells having freely supported ends. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1949, 197, 238–256. [Google Scholar]
- White, J.C. The flexural vibrations of thin laminated cylinders. J. Eng. Ind. 1961, 83, 397–402. [Google Scholar] [CrossRef]
- Girgis, R.S.; Verma, S.P. Method for accurate determination of resonant frequencies and vibration behaviour of stators of electrical machines. IEE Proc. B (Electr. Power Appl.) 1981, 128, 1–11. [Google Scholar] [CrossRef]
- Verma, S.P.; Girgis, R.S. Experimental verification of resonant frequencies and vibration behaviour of stators of electrical machines. Part 1: Models, experimental procedure and apparatus. IEE Proc. B (Electr. Power Appl.) 1981, 128, 12–21. [Google Scholar] [CrossRef]
- Verma, S.P.; Girgis, R.S. Experimental verification of resonant frequencies and vibration behaviour of stators of electrical machines. Part 2: Experimental investigations and results. IEE Proc. B (Electr. Power Appl.) 1981, 128, 22–32. [Google Scholar] [CrossRef]
- Verma, S.P.; Balan, A. Experimental investigations on the stators of electrical machines in relation to vibration and noise problems. In Proceedings of the IEE Proceedings-Electric Power Applications, Cambridge, UK, 1–3 September 1997; Volume 145, pp. 455–461. [Google Scholar]
- Minnier, A.; Gold, B.; Chen, L.; Jahnke, S. Interaction of Generator Rotor/Stator Harmonic Response Under Electromagnetic Forces; Hydrovision: Portland, OR, USA, 2015. [Google Scholar]
- Rau, M. Simulation des mechanischen Schwingungsverhaltens von Generatorständern von Wasserkraftanlagen. Master’s Dissertation, Technische Hochschule Ulm, Ulm, Germany, 2016. [Google Scholar]
- Zhou, J.; Peng, X.; Li, R.; Xu, Y.; Liu, H.; Chen, D. Experimental and finite element analysis to investigate the vibration of Oblique-Stud stator frame in a large hydropower generator unit. Energies 2017, 10, 2175. [Google Scholar] [CrossRef] [Green Version]
- Gerlach, M.E.; Ponick, B. Influence of the Stator Winding and Forming of the End Winding on the Vibration Behavior of Electric Machine’s Stator Core. In Proceedings of the 2020 International Conference on Electrical Machines (ICEM), Gothenburg, Sweden, 23–26 August 2020; pp. 1171–1177. [Google Scholar] [CrossRef]
- Yin, H.; Ma, F.; Zhang, X.; Gu, C.; Gao, H.; Wang, Y. Research on Equivalent Material Properties and Modal Analysis Method of Stator System of Permanent Magnet Motor with Concentrated Winding. IEEE Access 2019, 7, 64592–64602. [Google Scholar] [CrossRef]
- Chauvicourt, F.; Faria, C.; Desmet, W.; Gyselinck, J.J.C. Transversally Asymmetric Stiffness of Laminated Stator Core: A Solution for Noise Mitigation of Electric Machine. IEEE Trans. Energy Convers. 2019, 34, 613–619. [Google Scholar] [CrossRef]
- Garvey, S.D. The vibrational behaviour of laminated components in electrical machines. In Proceedings of the 1989 Fourth International Conference on Electrical Machines and Drives, London, UK, 13–15 September 1989; pp. 226–231. [Google Scholar]
- Van der Giet, M.; Kasper, K.; De Doncker, R.W.; Hameyer, K. Material parameters for the structural dynamic simulation of electrical machines. In the Proceedings of the 2012 XXth International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 2994–3000. [Google Scholar]
- Walker, J.H.; Rogers, G.J.; Jackson, R.L. Pressing and clamping laminated cores. Proc. Inst. Electr. Eng. 1964, 111, 565–577. [Google Scholar] [CrossRef]
- Braunisch, D.; Ponick, B.; Bramerdorfer, G. Combined Analytical–Numerical Noise Calculation of Electrical Machines Considering Nonsinusoidal Mode Shapes. IEEE Trans. Magn. 2013, 49, 1407–1415. [Google Scholar] [CrossRef]
- Cauberghe, B. Applied Frequency-Domain System Identification in the Field of Experimental and Operational Modal Analysis. Ph.D. Thesis, Vrije University Belgium, Brussel, Belgium, 2004. [Google Scholar]


| Parameter | Value |
|---|---|
| Rated output | 732 kVA |
| Rated speed | 375 rpm |
| Number of poles | 16 |
| Number of stator slots | 96 |
| Stator core outer diameter | 1640 mm |
| Stator core total length | 330 mm |
| Ventilation ducts | 11 × 6 mm |
| Parameter | Core | Winding | Frame |
|---|---|---|---|
| (kg/m³) | 7600 | 7965.5 | 7850 |
| (GPa) | 180 | 0.1...67.4 | 200 |
| (GPa) | 1...180 | ||
| (GPa) | 69.23 | 0.04...25.15 1 | 76.92 |
| (GPa) | 0.99...69.23 1 | ||
| 0.3 | 0.34 | 0.3 | |
| 0.0017...0.3 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Barros, A.; Galai, A.; Ebrahimi, A.; Schwarz, B. Practical Modal Analysis of a Prototyped Hydrogenerator. Vibration 2021, 4, 853-864. https://doi.org/10.3390/vibration4040048
de Barros A, Galai A, Ebrahimi A, Schwarz B. Practical Modal Analysis of a Prototyped Hydrogenerator. Vibration. 2021; 4(4):853-864. https://doi.org/10.3390/vibration4040048
Chicago/Turabian Stylede Barros, Allan, Ahmed Galai, Amir Ebrahimi, and Babette Schwarz. 2021. "Practical Modal Analysis of a Prototyped Hydrogenerator" Vibration 4, no. 4: 853-864. https://doi.org/10.3390/vibration4040048
APA Stylede Barros, A., Galai, A., Ebrahimi, A., & Schwarz, B. (2021). Practical Modal Analysis of a Prototyped Hydrogenerator. Vibration, 4(4), 853-864. https://doi.org/10.3390/vibration4040048






