Influence of System and Actuator Nonlinearities on the Dynamics of Ring-Type MEMS Gyroscopes
Abstract
:1. Introduction
2. Governing Equations
3. Development of Nonlinear Electrostatic Force Model for MEMS Ring-Based Gyroscope
4. Results and Discussion
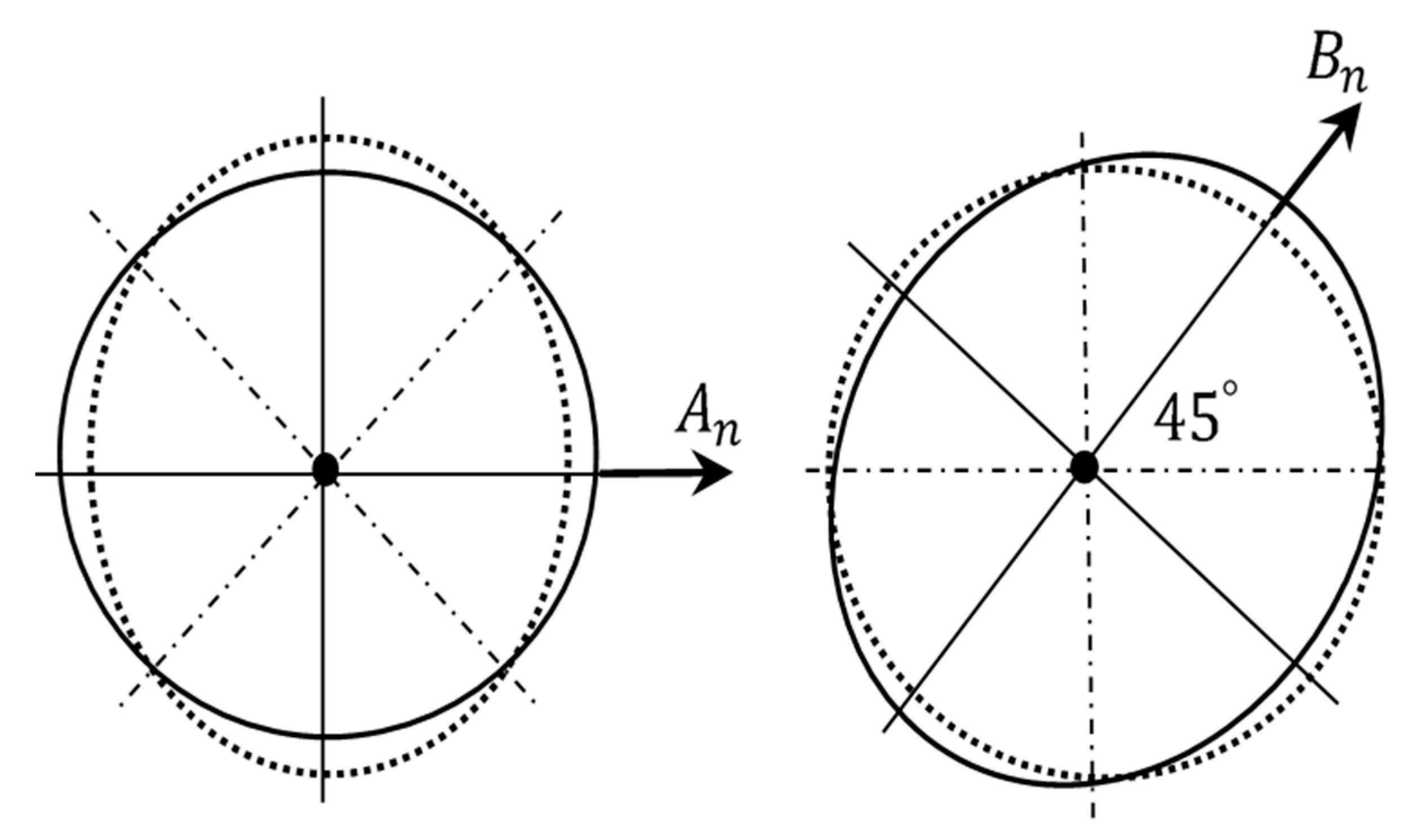
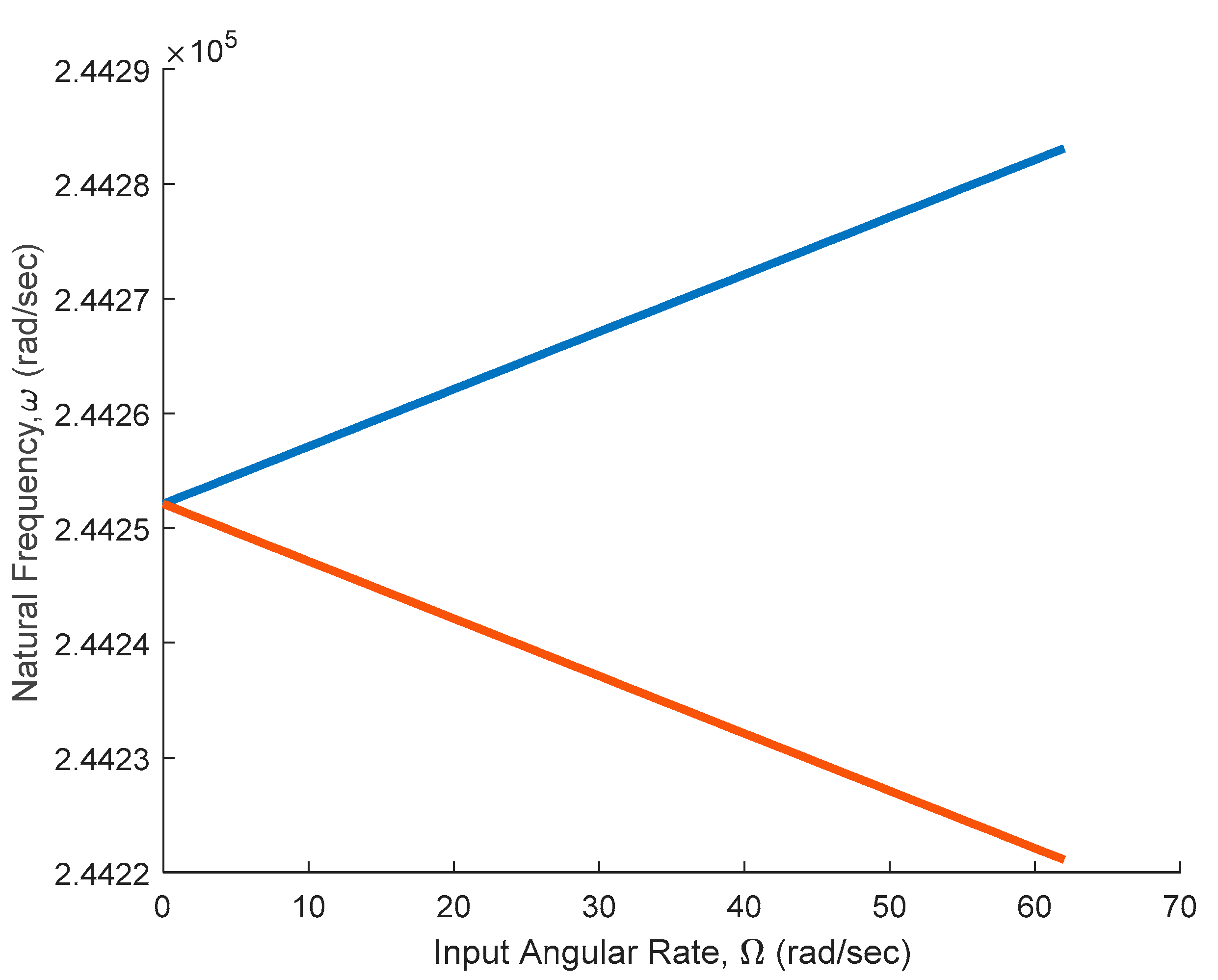
4.1. Natural Frequency Variation
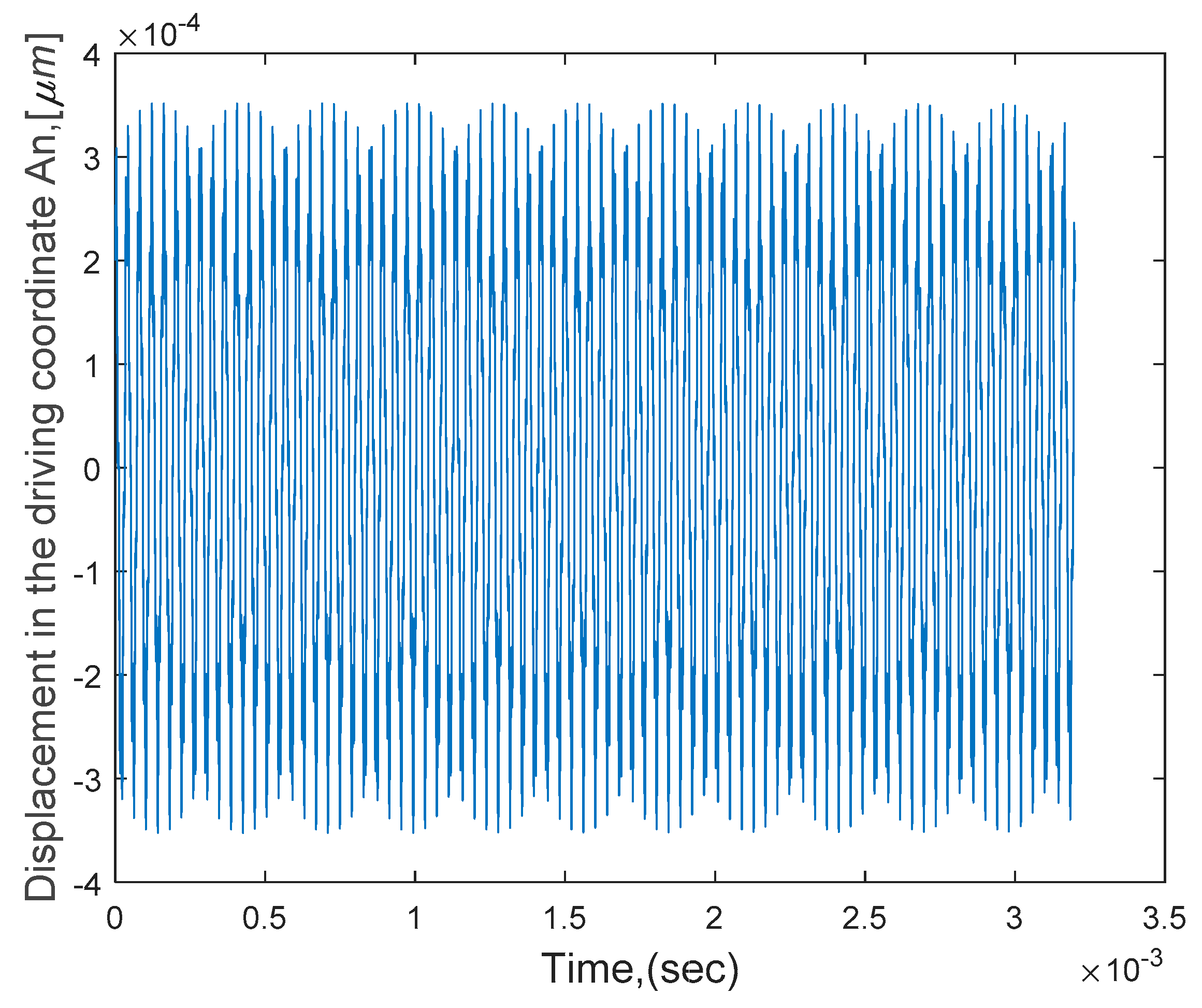
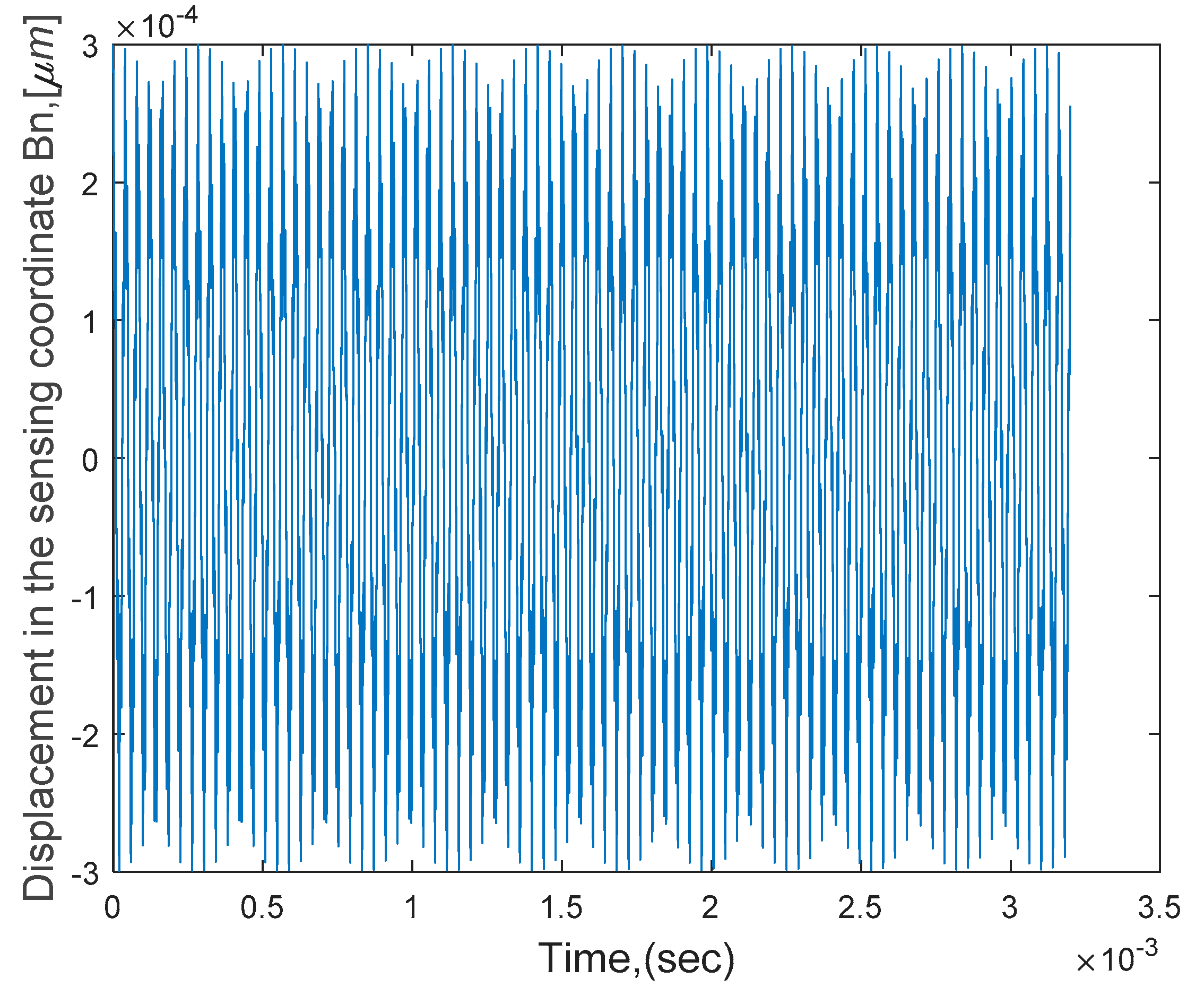
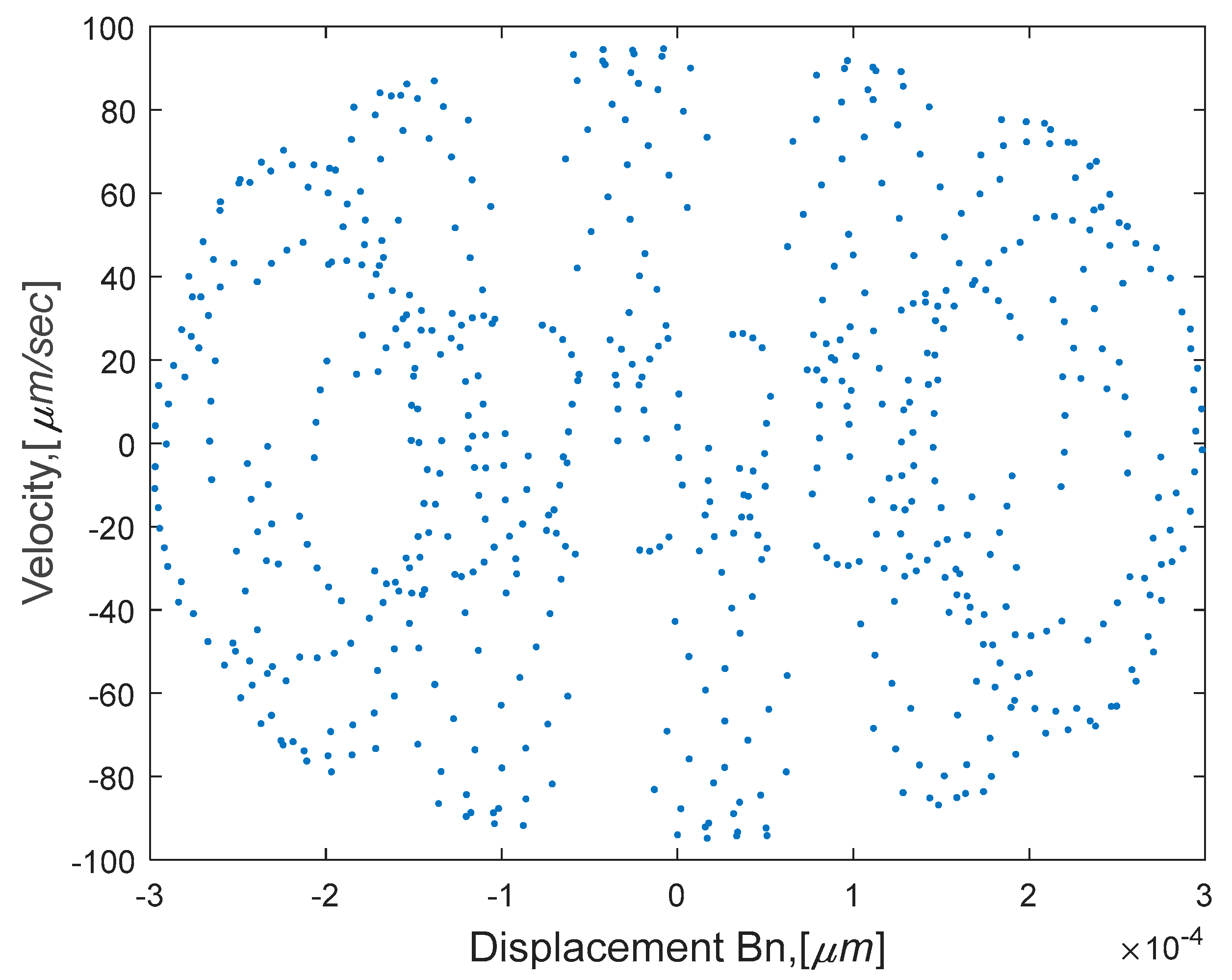
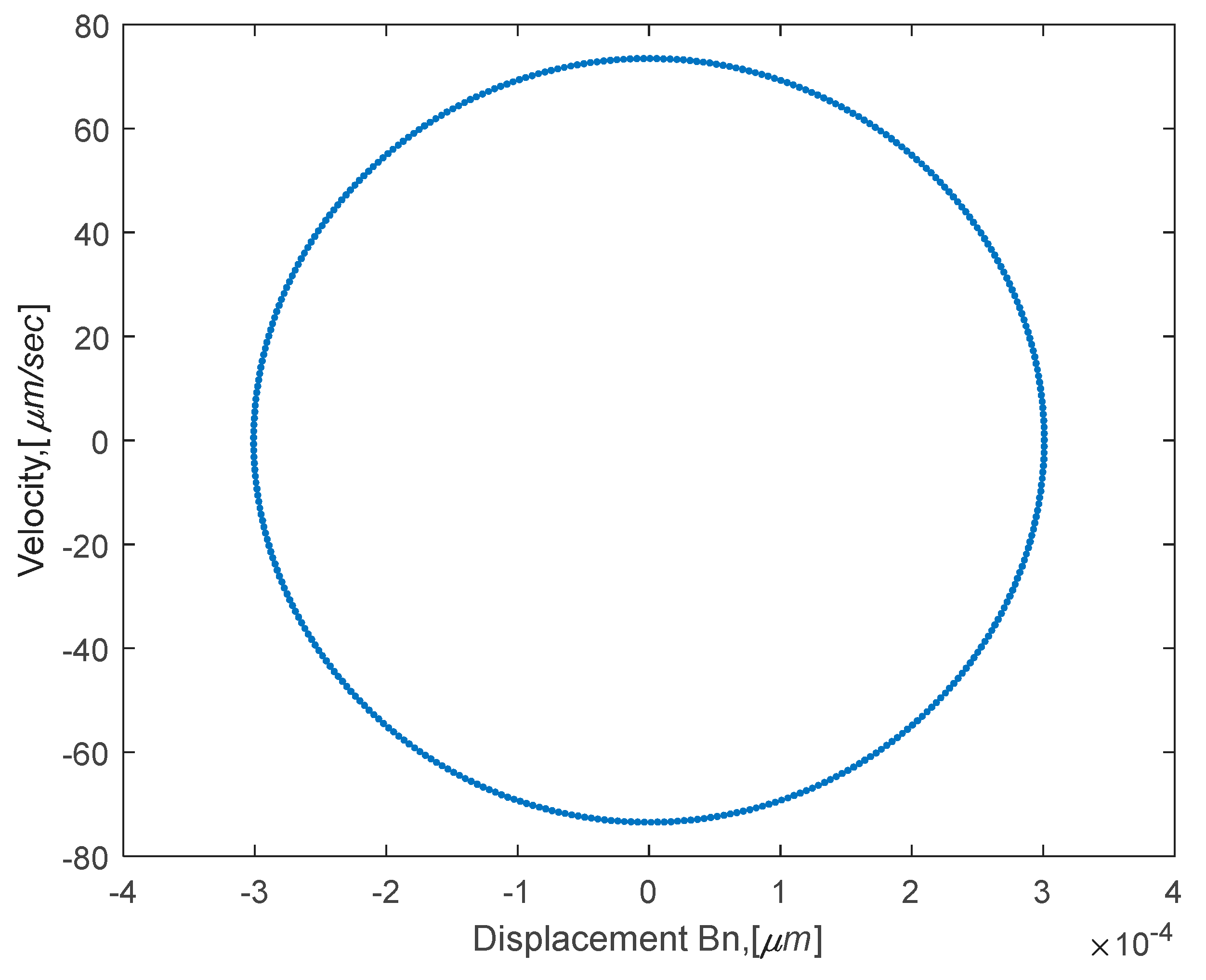
4.2. Time Response
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Putty, M.W.; Najafi, K. A Micro Machined Vibrating Ring Gyroscope. In Solid-State Sensor and Actuator Workshop, Hilton Head, South Carolina; Clarendon: Oxford, UK, 1994; Volume 2, pp. 68–73. [Google Scholar]
- Evensen, D.A. Nonlinear Flexural Vibrations of Thin Circular Rings. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1964. [Google Scholar]
- Evensen, D.A. Nonlinear Flexural Vibrations of Thin Circular Rings. J. Appl. Mech. 1966, 33, 553–560. [Google Scholar] [CrossRef] [Green Version]
- Soedel, W. Vibrations of Shells and Plates; Marcel Dekker, Inc.: New York, NY, USA; Basel, Switzerland, 1981. [Google Scholar]
- Huang, S.; Soedel, W. Effects of coriolis acceleration on the free and forced in-plane vibrations of rotating rings on elastic foundation. J. Sound Vib. 1987, 115, 253–274. [Google Scholar] [CrossRef]
- Eley, R.; Fox, C.; Mcwilliam, S. Coriolis Coupling Effects on the Vibration of Rotating Rings. J. Sound Vib. 2000, 238, 459–480. [Google Scholar] [CrossRef]
- Bickford, W.; Reddy, E. On the in-plane vibrations of rotating rings. J. Sound Vib. 1985, 101, 13–22. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, S.; Liu, J. Analytical Prediction for Free Response of Rotationally Ring-Shaped Periodic Structures. J. Vib. Acoust. 2014, 136, 041016. [Google Scholar] [CrossRef]
- Asokanthan, S.F.; Cho, J. Dynamic stability of ring-based angular rate sensors. J. Sound Vib. 2006, 295, 571–583. [Google Scholar] [CrossRef]
- Cho, J. Nonlinear Instabilities in Ring-Based Vibratory Angular Rate Sensors. Ph.D. Thesis, The University of Western Ontario, London, ON, Canada, 2009. [Google Scholar]
- Asokanthan, S.F.; Arghavan, S.; Bognash, M. Stability of Ring-Type MEMS Gyroscopes Subjected to Stochastic Angular Speed Fluctuation. J. Vib. Acoust. 2017, 139, 040904. [Google Scholar] [CrossRef]
- Gebrel, I.F.; Wang, L.; Asokanthan, S.F. Dynamics of a Ring-Type Macro Gyroscope under Electromagnetic External Actuation Forces. In Proceedings of the the ASME International Design Engineering Technical Conferences, Quebec City, QC, Canada, 26–29 August 2018. [Google Scholar]
- Gebrel, I.F.; Wang, L.; Asokanthan, S.F. Influence of Model Nonlinearities on the Dynamics of Ring-type Gyroscopes. In Proceedings of the Second International Nonlinear Dynamics Conference, NODYCON21, Roma, Italy, 16–19 February 2021. [Google Scholar]
- Gebrel, I.F.; Wang, L.; Asokanthan, S.F. Dynamics of MEMS-based Angular Rate Sensors Excited via External Electrostatic Forces. In Proceedings of the ASME International Mechanical Engineering Congress & Exposition IMECE 2020, Portland, OR, USA, 16–19 November 2020. [Google Scholar]
- Yoon, S.W.; Lee, S.; Najafi, K. Vibration sensitivity analysis of MEMS vibratory ring gyroscopes. Sens. Actuators A Phys. 2011, 171, 163–177. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, Y.-L.; Wu, X.-Z.; Zhang, Y.-M.; Zheng, Y. A novel ring vibrating gyroscope based on side piezo-electrodes. J. Central South Univ. 2016, 23, 555–561. [Google Scholar] [CrossRef]
- Ouakad, H.M. Nonlinear structural behavior of a size-dependent MEMS gyroscope assuming a non-trivial shaped proof mass. Microsyst. Technol. 2019, 26, 573–582. [Google Scholar] [CrossRef]
- Rahmani, M.; Rahman, H.M. A novel Compound Fast Fractional Integral Sliding Mode Control and Adaptive PI Control of a MEMS Gyrscope. Microsyst. Technol. 2019, 25, 3683–3689. [Google Scholar] [CrossRef]
- Di Napoli, V.; McWilliam, S.; Popov, A.A. Frequency Splitting in MEMS Ring-based Coriolis Vibrating Gyroscopes Caused by Support Non-Linearity. Proceedings 2018, 2, 755. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Gebrel, I.; Bognash, M.; Pan, Y.; Liu, F.; Asokanthan, S.; Luo, H.; Qu, T. Time Response of a Cylindrical Fused Silica Resonator Subjected to Varying Input Angular Velocities. IEEE Sens. Council. 2020, 20, 3460–3468. [Google Scholar] [CrossRef]
- Luo, Y.; Gebrel, I.; Bognash, M.; Asokanthan, S.; Luo, H. Dynamic Considerations in the Design of Cylindrical Fused Silica Resonator Based Gyroscopes Subjected to Angular Rate Variations. IEEE Sens. Council. 2020, 1558–1748. [Google Scholar]
- Saghir, S.; Younis, M.I. An investigation of the mechanical behavior of initially curved microplates under electrostatic actuation. Acta Mech. 2018, 229, 2909–2922. [Google Scholar] [CrossRef]
- Ilyas, S.; Alfosail, F.; Bellaredj, M.L.F.; Younis, M.I. On the response of MEMS resonators under generic electrostatic loadings: Experiments and applications. Nonlinear Dyn. 2019, 95, 2263–2274. [Google Scholar] [CrossRef]
- Batra, R.C.; Porfiri, M.; Spinello, D. Review of modeling electrostatically actuated microelectromechanical systems. Smart Mater. Struct. 2007, 16, R23–R31. [Google Scholar] [CrossRef]
- Zhao, C.; Montaseri, M.H.; Wood, G.; Pu, S.H.; Seshia, A.; Kraft, M. A review on coupled MEMS resonators for sensing applications utilizing mode localization. Sens. Actuators A Phys. 2016, 249, 93–111. [Google Scholar] [CrossRef]
- Caruntu, D.I.; Martinez, I. Reduced order model of parametric resonance of electrostatically actuated MEMS cantilever resonators. Int. J. Non-linear Mech. 2014, 66, 28–32. [Google Scholar] [CrossRef]
- Hajjaj, A.; Jaber, N.; Hafiz, M.; Ilyas, S.; Younis, M. Multiple internal resonances in MEMS arch resonators. Phys. Lett. A 2018, 382, 3393–3398. [Google Scholar] [CrossRef]
- Gallacher, B.J.; Burdess, J.S.; Harish, K.M. A control scheme for a MEMS electrostatic resonant gyroscope excited using combined parametric excitation and harmonic forcing. J. Micromech. Microeng. 2006, 16, 320–331. [Google Scholar] [CrossRef]
- Nielson, G.N.; Barbastahis, G. Dynamic Pull-In of Parallel-Plate and Torsional Electrostaic MEMS Actuators. J. Microelectromech. Syst. 2006, 15, 811–821. [Google Scholar] [CrossRef]
- Feng, J.; Liu, C.; Zhang, W.; Han, J.; Hao, S. Mechanical Behaviors Research and the Structural Design of a Bipolar Electrostatic Actuation Microbeam Resonator. Sensors 2019, 19, 1348. [Google Scholar] [CrossRef] [Green Version]
- Rasekh, M.; Khadem, S. Design and performance analysis of a nanogyroscope based on electrostatic actuation and capacitive sensing. J. Sound Vib. 2013, 332, 6155–6168. [Google Scholar] [CrossRef]
- Chuang, W.-C.; Lee, H.-L.; Chang, P.-Z.; Hu, Y.-C. Review on the Modeling of Electrostatic MEMS. Sensors 2010, 10, 6149–6171. [Google Scholar] [CrossRef] [PubMed]
- Gallacher, B.J.; Hedley, J.; Burdess, J.S.; Harris, A.J.; Rickard, A.; King, D.O. Electrostaic correction of structural imperfections present in a microring gyroscope. J. Microelectromech. Syst. 2005, 14, 221–234. [Google Scholar] [CrossRef]
- Gorthi, S.; Mohanty, A.; Chatterjee, A. Cantilever beam electrostatic MEMS actuators beyond pull-in. J. Micromech. Microeng. 2006, 16, 1800–1810. [Google Scholar] [CrossRef] [Green Version]
- El-Sayed, A.M.; Ghoneima, M.; Mahmoud, M.A. Modeling of Nonlinearities in Vibration Ring Gyroscopes. In Proceedings of the Second International Japan-Egypt Conference on Electronics, Communications and Computers (JEC-ECC), Cairo, Egypt, 31 May–2 June 2016; pp. 1–57. [Google Scholar]
- Oropeza-Ramos, L.A.; Burgner, C.B.; Turner, K.L. Robust micro-rate sensor actuated by parametric resonance. Sens. Actuators A Phys. 2009, 152, 80–87. [Google Scholar] [CrossRef]
- Rabenimanana, T.; Walter, V.; Kacem, N.; Le Moal, P.; Bourbon, G.; Lardiès, J. Functionalization of electrostatic nonlinearities to overcome mode aliasing limitations in the sensitivity of mass microsensors based on energy localization. Appl. Phys. Lett. 2020, 117, 033502. [Google Scholar] [CrossRef]
- Kacem, N.; Hentz, S.; Baguet, S.; Dufour, R. Forced large amplitude periodic vibrations of non-linear Mathieu resonators for microgyroscope applications. Int. J. Non-Linear Mech. 2011, 46, 1347–1355. [Google Scholar] [CrossRef] [Green Version]
- Mahboob, I.; Dupuy, R.; Nishiguchi, K.; Fujiwara, A.; Yamaguchi, H. Hopf and period-doubling bifurcations in an electromechanical resonator. Appl. Phys. Lett. 2016, 109, 073101. [Google Scholar] [CrossRef]
- Han, M.; Zhang, Q.; Hao, S.; Li, W. Parametric Characteristics and Bifurcation Analysis of Multi-Degree-of-Freedom Micro Gyroscope with Drive Stiffness Nonlinearity. Micromachines 2019, 10, 578. [Google Scholar] [CrossRef] [Green Version]
- Asokanthan, S.F.; Wang, T. Nonlinear instabilities in a vibratory gyroscope subjected to angular speed fluctuations. Nonlinear Dyn. 2008, 54, 69–78. [Google Scholar] [CrossRef]
- Buono, P.L.; Chan, B.S.; Palacios, A.; In, V. Dynamics and bifurication in a Dn-symmetric Hamiltonian network Applictaion to Coupled Gyroscope. Phys. D 2015, 290, 8–23. [Google Scholar] [CrossRef]
- Karabalin, R.B.; Cross, M.C.; Roukes, M.L. Nonlinear dynamics and chaos in two coupled nanomechanical resonators. Phys. Rev. B 2009, 7, 165309. [Google Scholar] [CrossRef] [Green Version]
- Passaro, V.; Cuccovillo, A.; Vaiani, L.; Carlo, M.; Campanella, C. Gyroscope Technology and Applications: A Review in the Industrial Perspective. Sensors 2017, 7, 2284. [Google Scholar] [CrossRef] [Green Version]
- Bao, M. Analysis and Design Principles of MEMS Devices; Elsevier Inc.: Amsterdam, The Netherlands, 2005; pp. 175–206. ISBN 0-44451-616-6. [Google Scholar]
- Jearl, W.; Halliday, D.; Resnick, R. Fundamentals of Physics, 9th ed.; Cleveland State University: Cleveland, OH, USA, 2011; ISBN 978-0-470-46908-8. [Google Scholar]
- Younis, M.I. MEMS Linear and Nonlinear Statics and Dynamics; Springer: New York, NY, USA, 2011; pp. 1389–2134. ISBN 978-1-4419-6019-1. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gebrel, I.F.; Asokanthan, S.F. Influence of System and Actuator Nonlinearities on the Dynamics of Ring-Type MEMS Gyroscopes. Vibration 2021, 4, 805-821. https://doi.org/10.3390/vibration4040045
Gebrel IF, Asokanthan SF. Influence of System and Actuator Nonlinearities on the Dynamics of Ring-Type MEMS Gyroscopes. Vibration. 2021; 4(4):805-821. https://doi.org/10.3390/vibration4040045
Chicago/Turabian StyleGebrel, Ibrahim F., and Samuel F. Asokanthan. 2021. "Influence of System and Actuator Nonlinearities on the Dynamics of Ring-Type MEMS Gyroscopes" Vibration 4, no. 4: 805-821. https://doi.org/10.3390/vibration4040045




