1. Introduction
Rotating machineries such as pumps, compressors, turbines, etc., play an important role in many different industries. Accurate predictions of rotor system dynamic characteristics are very important in the design of any type of machines. There have been many studies relating to the field of rotor dynamic systems during the recent years. Engineers have developed several new techniques about the dynamics of rotating machines.
The first recorded theory of rotor dynamics was in a classic paper of Jeffcott [
1]. The Jeffcott rotor model has been used to explain the whirling effect. It consists of a simply supported flexible massless shaft with a rigid disc mounted at the mid-span. In the Jeffcott model, the moments of inertia
and
are not considered. This is because there are no gyroscopic moments exerted on the shaft. The disc is assumed to move in a plane that is perpendicular to the shaft spin axis. By developments in the technology of rotating machines, the rotational speed of rotors became higher, and so, the non-conservative forces generated through the bearings of the rotor become considerable. To determine the critical speeds in which resonance has occurred, it is necessary to know the natural frequencies, mode shapes, and forced responses, which are caused by unbalancing in rotor systems. Prohl studied the critical speed evaluation of a turbine shaft, and he suggested the transfer matrix method [
2]. The first application of the finite element method for a rotor system was made by Ruhl and Booker [
3]. In their study, the influences of the rotary inertia, gyroscopic moment, bending, shear deformation, axial load, and internal damping were neglected to simplify the model. The theory has been developed by considering the rotary inertia, gyroscopic moment, and axial forces. Nelson and McVaugh extended this to include gyroscopic effects. They derived the equations of motion for the shaft and the effects of translational and rotary inertia and gyroscopic moments on it [
4]. Erturka et al. presented an analytical method based on Timoshenko beam theory for calculating the frequency response function (FRF) of a spindle–holder–tool combination. They proposed a mathematical model and obtained the point FRF for a tool [
5]. Subbiah et al. showed that a rotor has certain speed ranges in which a large amplitude of vibration could occur. These speed ranges are known as critical speed, which results in excessive rotor deflection [
6]. Phadatare and Barun described a step forward in calculating the nonlinear frequencies and resultant dynamic behavior of a high-speed rotor bearing system with unbalanced mass. In this study, Fast Fourier Transform (FFT) analysis was established for finding the fundamental frequencies of the rotor according to the variation of shaft diameter and location of unbalanced mass [
7]. Metsebo et al. have focused on the influence of the rotating shaft on the dynamic of a rotor ball bearing system. They carried out a mathematical modeling for the system considering the shaft as a Timoshenko beam [
8].
Ball bearings are the essential elements of rotating machineries. So, the influence of bearings on the performance of rotor-bearing systems is very important. El-Sayed derived a set of equations for the stiffness of bearings using the Hertz theory and determined the total deflections of inner and outer races caused by an applied load [
9]. Tamura and Tsuda performed a theoretical study about fluctuations of radial spring characteristics of a ball bearing due to ball revolutions [
10]. Many researchers also estimated bearing stiffness by carrying out some experiments. Stone and Walford developed a rotor-bearing test rig to estimate the bearing’s radial stiffness and damping by measuring the response of the rotor [
11]. Jairo et al. presented an experimental validation for a mathematical modeling of ball bearing. In this model, the bearing was considered as a mass-spring-damper system based on Hertz equations for contact deformation [
12]. Xia sheng et al. proposed a mathematical model for the stiffness of bearings, which is varying by speed. They explained that the speed of a rolling bearing varies the stiffness of the bearing [
13]. Zhang et al. investigated the effect of ring misalignment on the service characteristics of ball bearing and rotor systems [
14]. They improved a quasi-static model of ball bearing considering the misalignment in its ring. Neisi et al. worked on the effect of off-sized balls on contact stresses in a touchdown bearing [
15]. Yi Qin et al. developed a dynamics model for deep groove ball bearings with local faults based on coupled and segmented displacement excitation [
16]. Chandrasekaran et al. used computational fluid dynamic (CFD) methods and mathematical modeling to investigate the impeller design parameters on the effect of fluid follows in the centrifugal pumps [
17].
The objective of this paper is investigation on the effect of impeller diameter on the amplitude of vibration at critical speeds in an overhung centrifugal pump. Modeling of the shaft and impeller is based on Timoshenko theory, and modeling of the bearing is based on the work of Jones and Harris, which is added to the model of shaft simultaneously. Then, numerical analysis for a real centrifugal pomp in the oil refinery has been done based on the proposed model. It has shown that in addition of the effect of the geometrical parameter of the shaft, the effect of the diameter of the impeller on the dynamical behavior of the pump is very important.
The novelty of this research is the development of the mathematical model of the shaft, impeller, and bearing simultaneously. Using this developed model, the effect of impeller size diameter on the dynamic behavior of a centrifugal pump has been investigated, and it has been shown that it is very considerable.
This paper includes four sections. In the first section, the literature has been reviewed and the necessity of research has been recognized. In the second section, the model of the system has been introduced and the equation of motion based on the energy method has been derived by calculating the potential and kinetic energy of the system. In the third section, the model of the bearing has been presented, and the governing equations of motion for the ball bearing have been introduced. Finally, in the last section, the derived equations have been used and solved.
For an actual centrifugal pump, the effect of impeller diameter on the amplitude of vibration has been investigated.
2. System Modeling
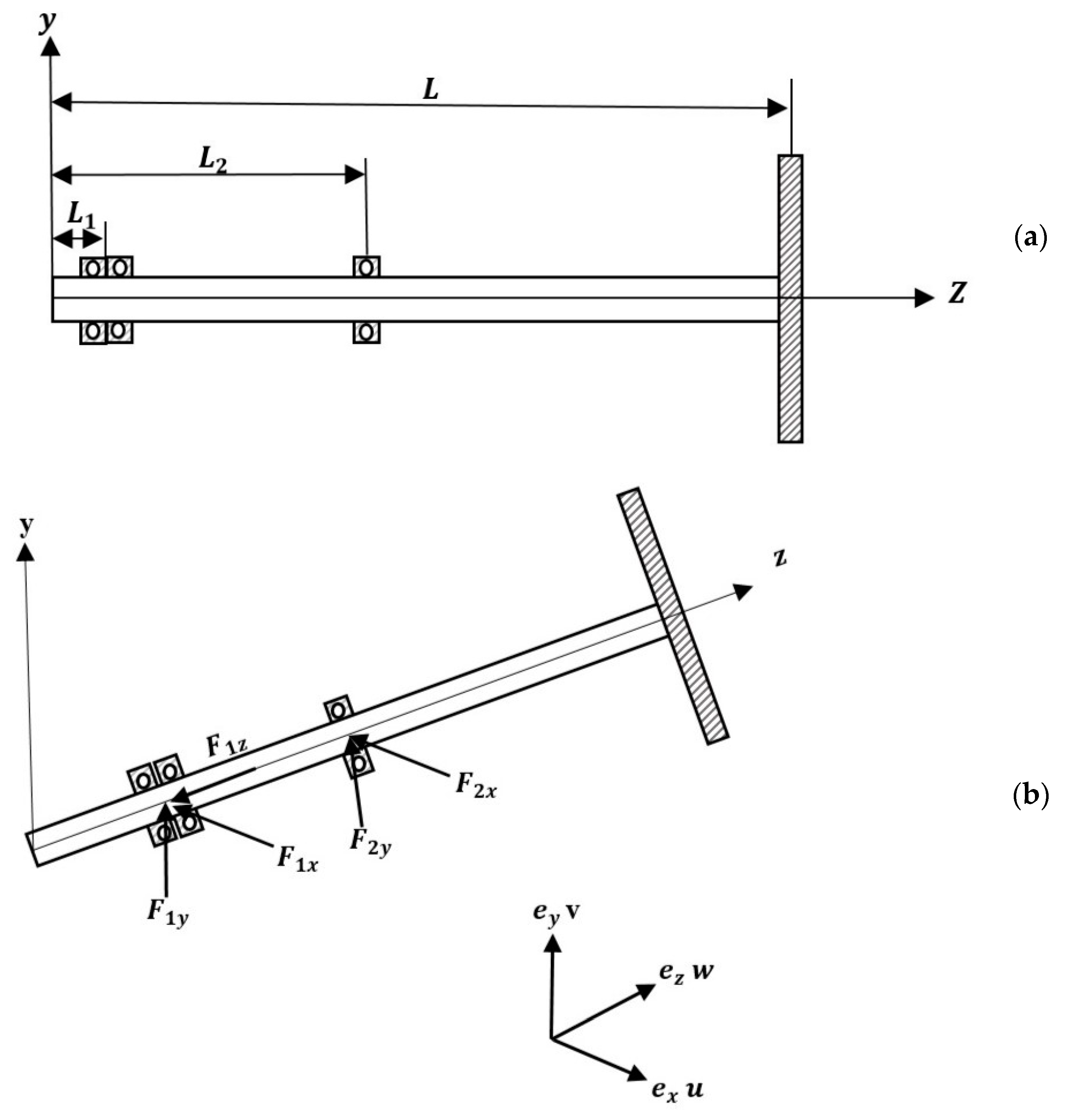
The rotor of a centrifugal pump is approximated by a simple model as shown in
Figure 1a. The model is composed of a shaft of length
L and supported by two bearings located at
and
along the shaft.
u,
v, and
w reflect the displacement in the
,
, and
directions, respectively.
The shaft is modeled as a Timoshenko beam. In this model, first-order shear deformation theory with rotary inertia and gyroscopic effect has been considered. The shaft rotates at a constant speed around its longitudinal axis. In addition, it has a uniform, circular cross-section.
The equations of motion of the system are obtained using the Lagrangian equations as:
where
T is the total kinetic energy of the system,
U is the total potential energy of the system,
qn is the generalized coordinate and
Qnc represents non-conservative forces that are not directly related to the potential energy of the system. So, to derive the governing equations of motion using Equation (1), one must calculate the kinetic and potential energy of the system.
The total kinetic energy of a rotor system is estimated by the dynamic motion of the shaft and disk [
14].
The kinetic energy due to the rotation of the disk is difficult to calculate. Therefore, we assume that the disk is symmetric and rigid and has been fixed at the end of the shaft. The motion of the disk can be defined as two superimposed rotations
,
and two translational deflections
u,
v in directions
,
. So, the kinetic energy of the disk can be expressed as:
where
M is the mass of the rigid disk,
is the diametral mass moment of inertia, and
is the polar mass moment of inertia. The term
represents the gyroscopic effect, and finally, the last term defines the kinetic energy due to the rotation of the disk.
The kinetic energy of the shaft involves the kinetic energy due to bending of the shaft, effect of rotatory inertia, and gyroscopic effect. The kinetic energy of the shaft can be derived as:
where
A is the cross-sectional area,
is the density of the shaft, and
and
are the diametric and polar inertia of the shaft, respectively. So, substituting Equations (3) and (4) in Equation (2), the total kinetic energy of system has been obtained.
The potential energy of the system includes the strain energy due to the deformation of the shaft (
) and the strain potential energy due to the deflection of the bearing installed on the shaft (
) [
12]:
The strain energy of the shaft can be expressed as:
where
E represents the modulus of elasticity,
G is the shear modulus, and
k is the shear coefficient. In addition,
A and
I are the cross-section area and moment of inertia of the shaft receptivity. In the above equation, the first term is related to the shaft bending, and the second term is due to shear deformation. In addition, the potential energy caused by bearing forces can be expressed as:
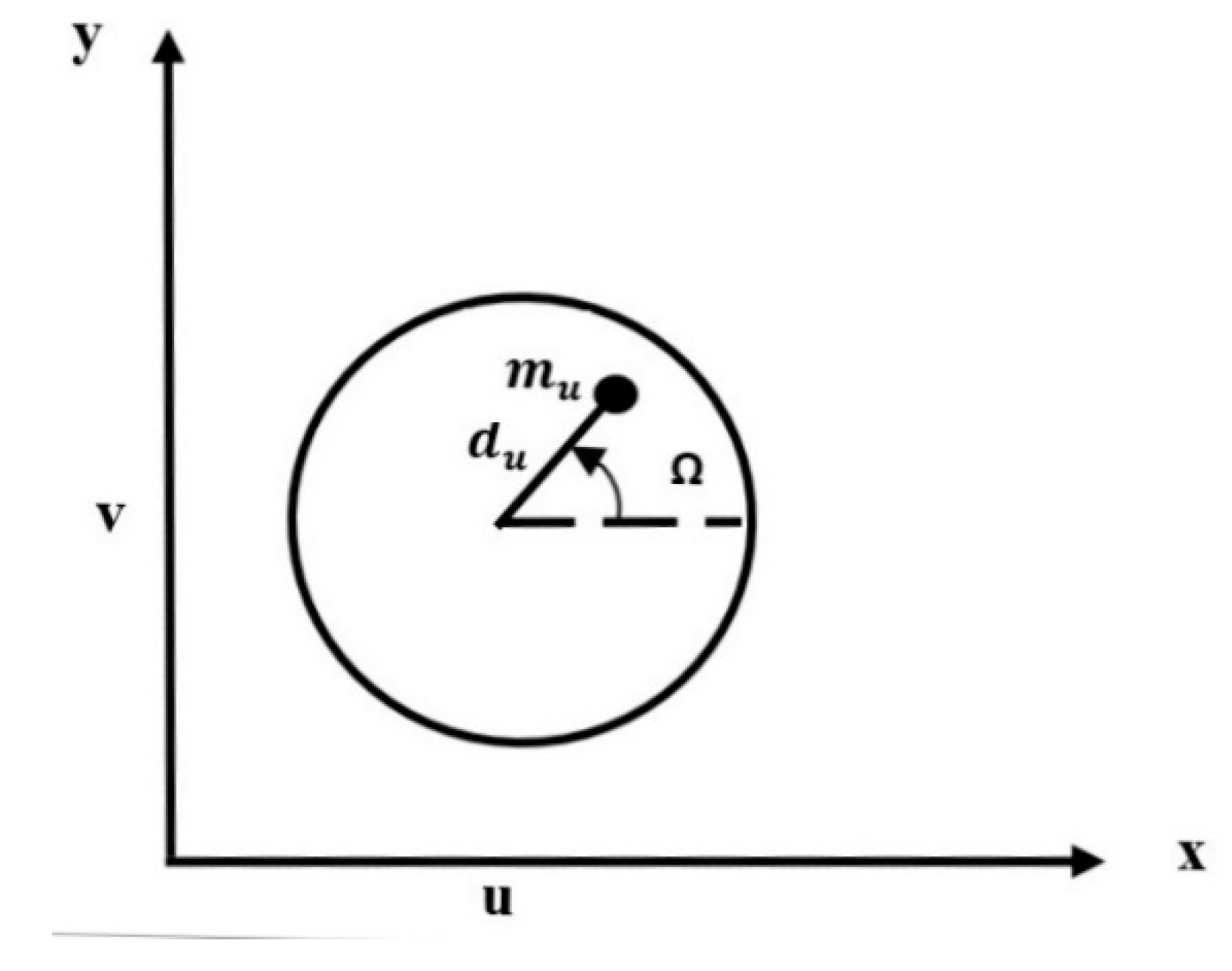
Different forces work on the impeller as a consequence of the fluid. These forces are non-conservative forces and are unknown, and they have been ignored for simplicity. However, mass unbalance generates an additional centrifugal force that makes it possible to calculate this non-conservative force. If the impeller is out of balance, the resulting centrifugal force will induce the rotor to vibrate. When the shaft rotates at a speed equal to the natural frequency, this vibration becomes large. Unbalance is defined by a small mass
situated at a distance
from the geometric center of the impeller, as shown in
Figure 2 [
13].
The out of balance force at the end of the rotor is:
This rotating force can be resolved into two components in the
x and
y direction as:
It is assumed that the unbalance mass is in the
x direction in the initial state. The deflections in the
x and
y directions are expressed as:
where
and
are generalized independent coordinates and
f(
z) is the displacement function that satisfies the boundary conditions of the system. As the rotor of the centrifugal pump has simply supported at both ends,
f(
z) has been selected as [
12]:
The angular displacements
and
are assumed to be small. So, they are approximated by the derivative of
u and
v with respect to the
z-direction. Therefore, using Equations (10) and (11),
and
have been expressed as:
To derive the equations of motion, the kinetic energy and the potential energy are specified by generalized coordinates. So, using Equation (3), the kinetic energy of the disk in generalized coordinates is expressed as:
where
In addition, Equation (4) in the generalized equation becomes:
Likewise, using the generalized coordinates, the potential energy in the generalized coordinate will be:
where
represnts the dirac delta function and
In addition, substituting the displacement function into the kinetic energy of the mass unbalance expression of Equation (11) gives:
Ball Bearing Model
In this section, a mathematical model for calculating bearing stiffness is proposed by analyzing the equations in the bearing dynamic model, which is based on Jones and Harris’s efforts [
14]. This mathematical model aims to give a comprehensive consideration of the nonlinear stiffness of the ball bearing, and it can be seen that the bearing stiffness is critically dependent on the preloading,
g, of the rolling elements. In case of rolling element bearings, the elastic deformation takes place at both the inner raceway and the outer raceway with the rolling element. Based on the Hertzian contact theory, the relation between load
F and deflection is [
15]:
where
is the contact deformation and
is a load–deformation constant for a single point contact (either at the inner or outer raceway). If the ball and raceway are made of steel, then [
16,
17]:
where
is the dimensionless contact deformation and
is the curvature sum [
14]. So, one can write the stiffness of the inner and outer ring contact as:
where
and
In the above equations, subscripts i and o represent inner and outer raceways and is the ball diameter. In addition, is the pitch diameter, and are the inner and outer ring raceway contact diameter, and and are the inner and outer raceway groove radius, respectively.
The total deformation,
, at a single rolling element location is given by:
Equation (19) can be rewritten as:
where
is the load–deformation constant for two point contacts of a ball with raceways.
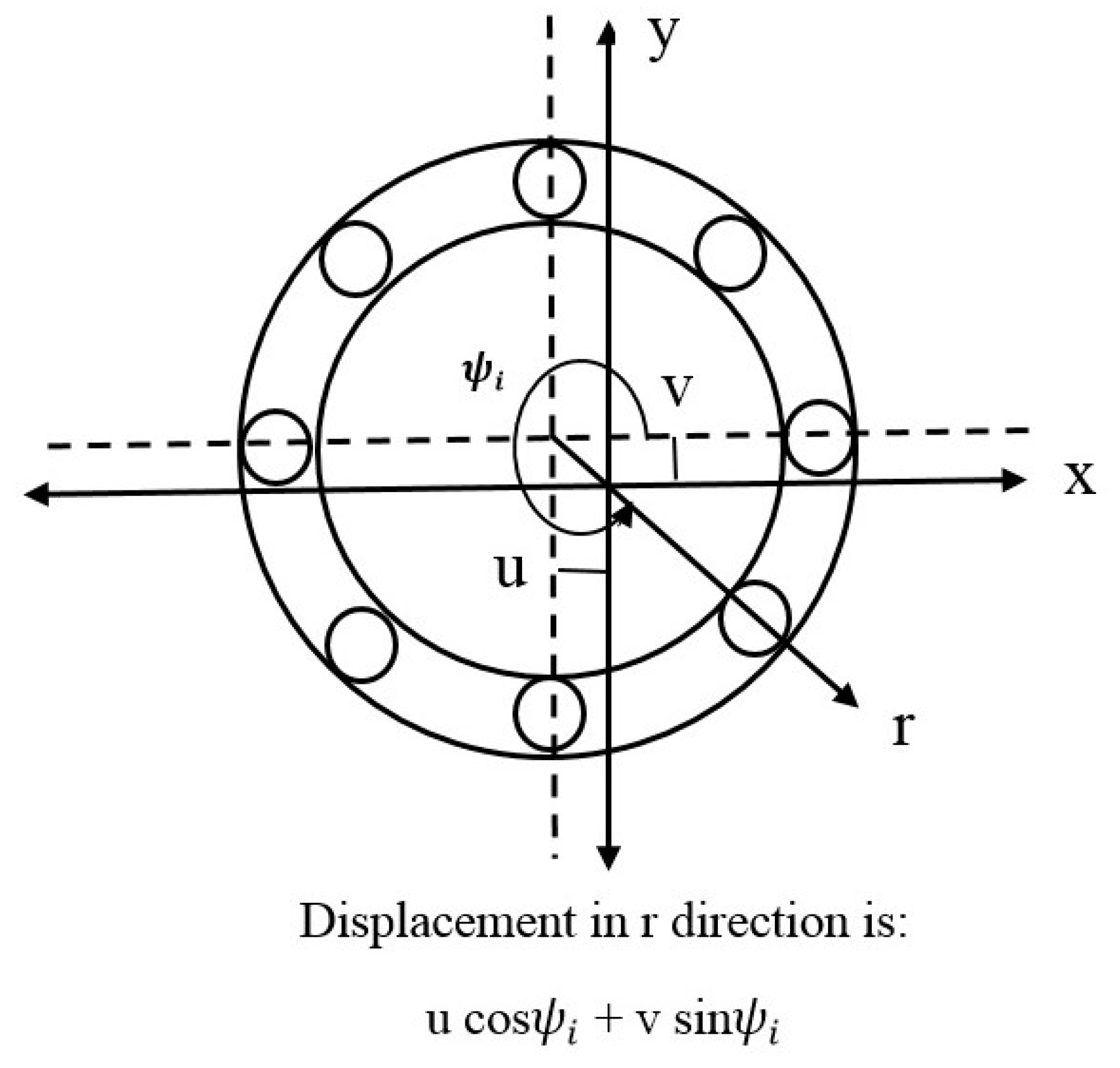
To calculate the deformations, the conventions shown in
Figure 3 are used. Considering the presence of radial clearance, the force produced by every spring in the horizontal and vertical direction can be obtained [
18]:
where
is the radial preload between the ball and races,
u and
v are the displacements of the moving ring in the
x and
y directions, respectively, and
is the angular position of the
i th element.
Finally, the bearing stiffness can be simplified to [
15]:
where
Z is the number of rolling elements.
It can be seen that the bearing stiffness is critically dependent on value of the preloading g of the rolling elements.
4. Conclusions
In this paper, the equations of motion for the shaft of a centrifugal pump have been derived using Lagrangian equations and based on Timoshenko beam theory and Jones and Harris [
20,
21] modeling for bearings based on Hertzian theory for rolling element [
22,
23]. By these equations, it is possible to define a lumped parameter model for the system and determine the amplitude of rotor in critical speeds [
12,
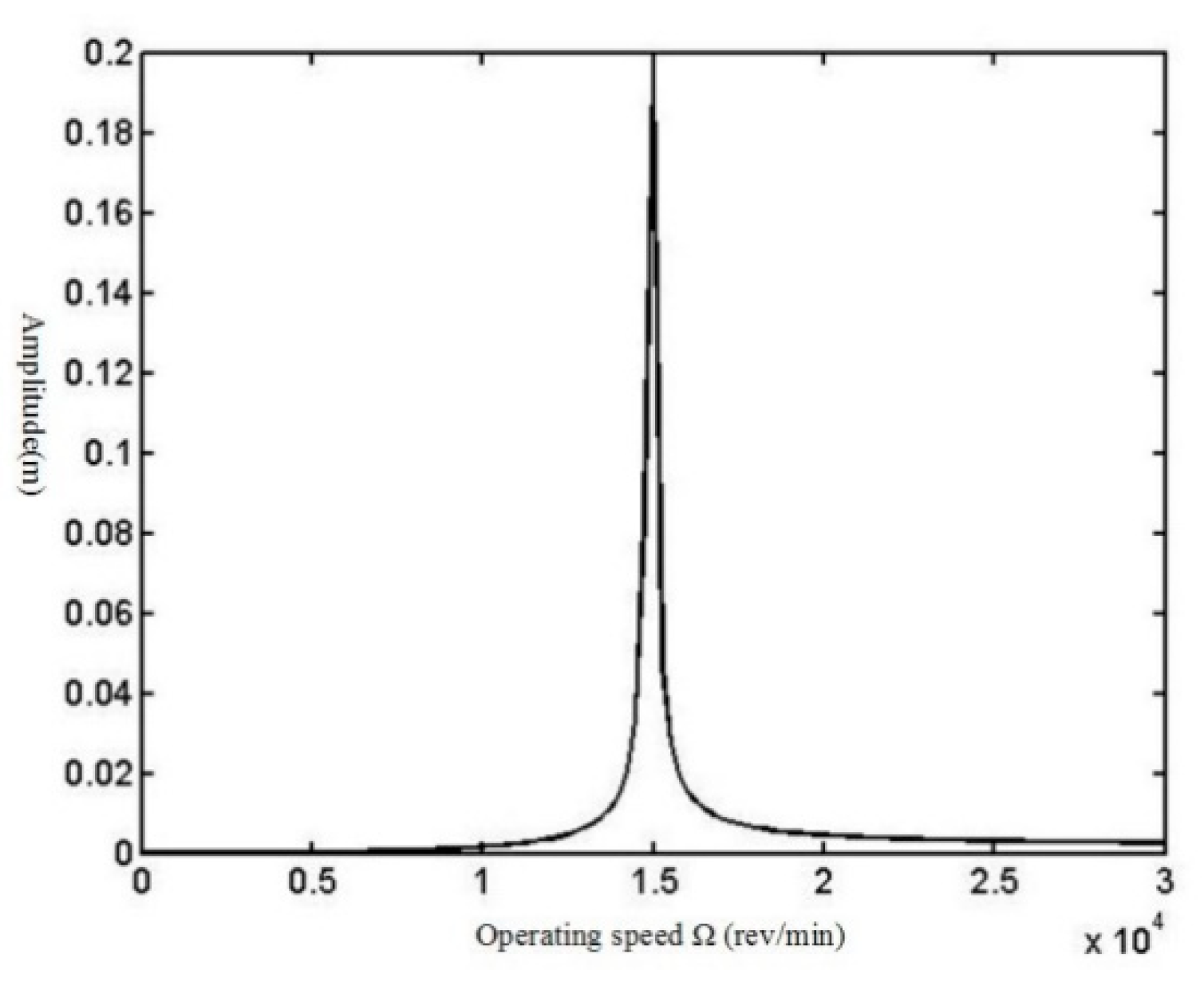
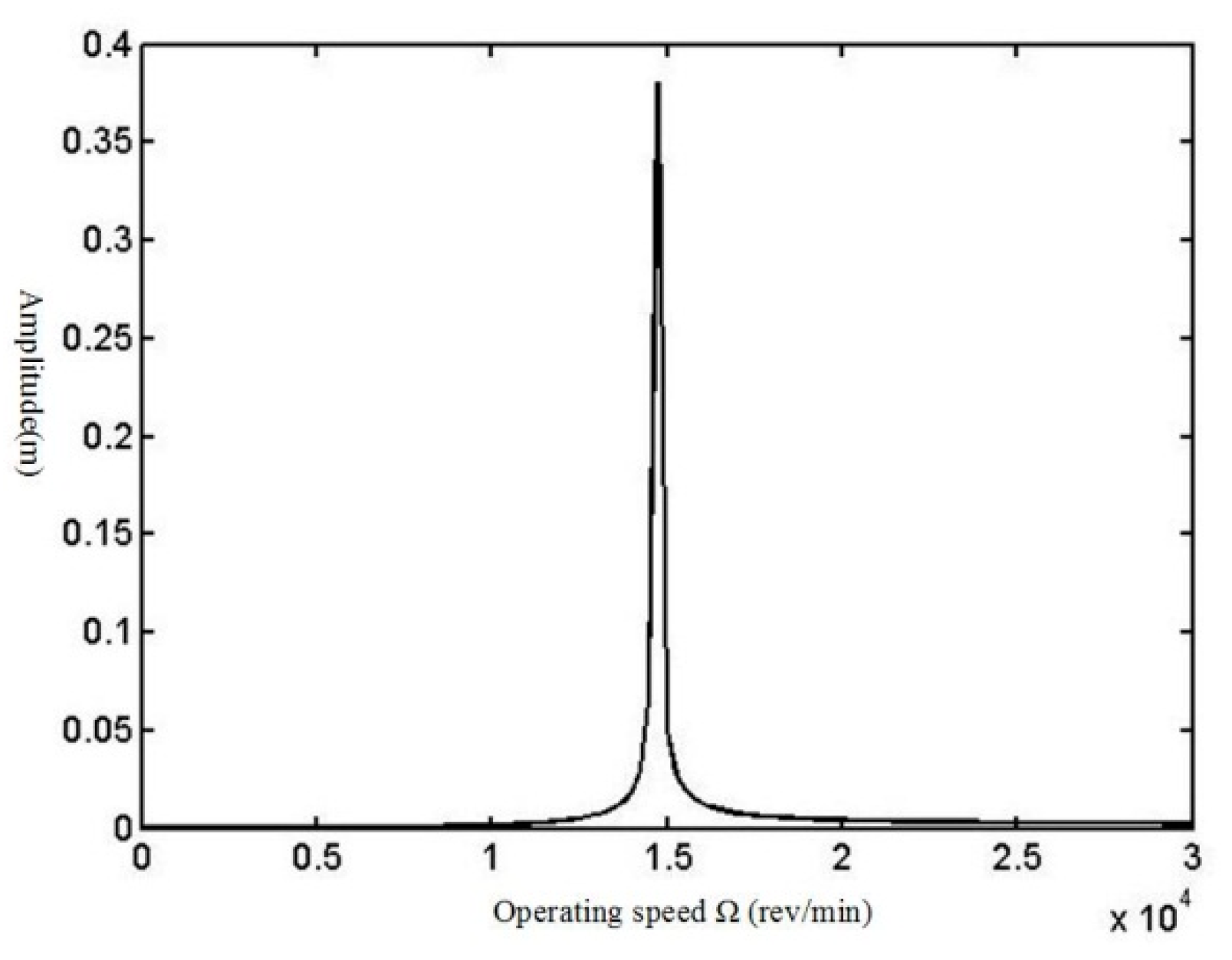
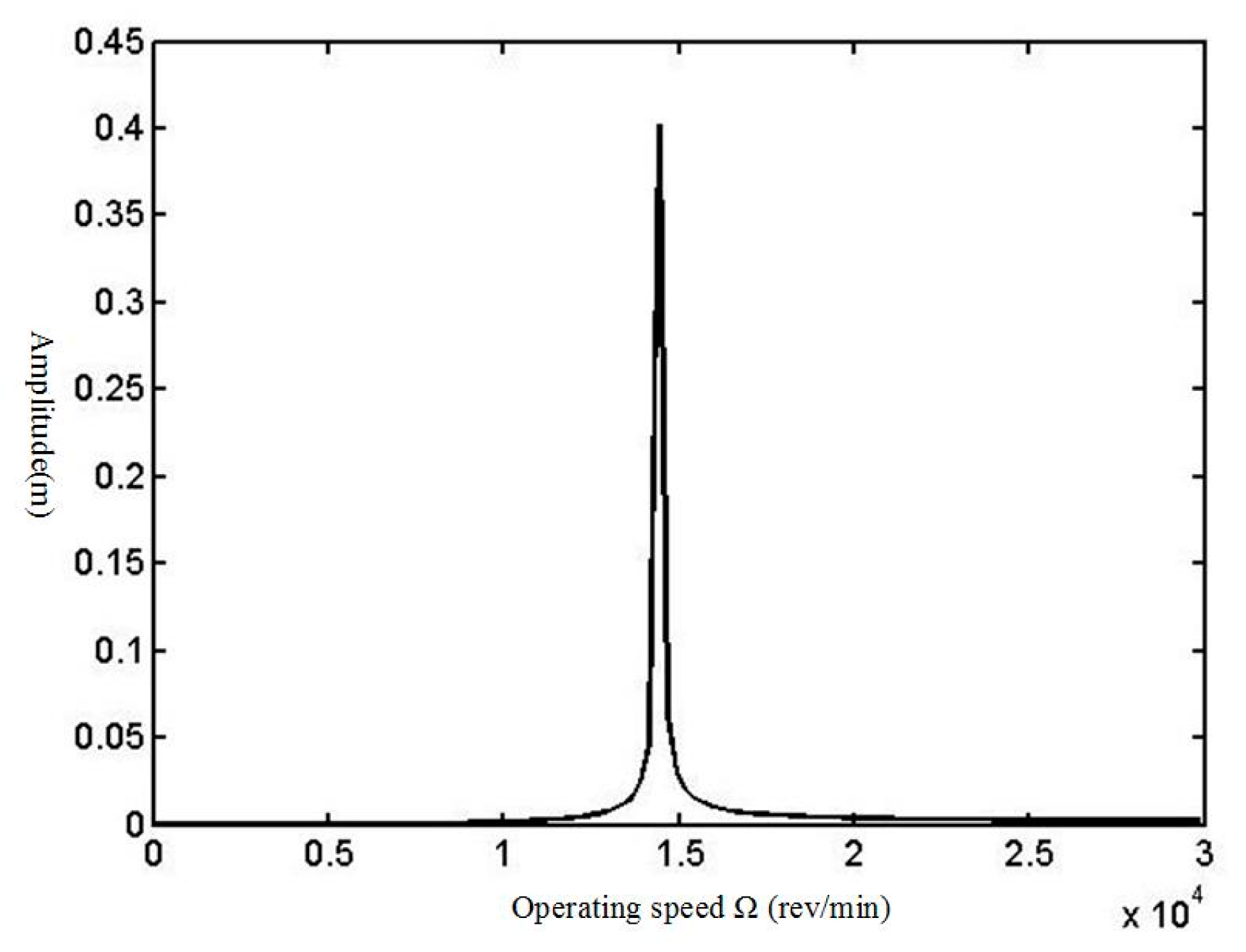
24]. The solutions of these equations for an applied case study show that as the impeller diameter increases, the amplitude of vibration at critical speeds increases, too. In this case study, by replacing the impeller diameter in the equations with a larger size (impeller diameter 0.256 m replaced with 0.32 m), it is shown that the amplitude is approximately increased by 52% in the critical speed. So, as the impeller trimming or impeller exchange is a general method for the maintenance in plants, it must be considered that the bigger diameter will yield more amplitude of vibration at critical speed.
It must be considered that modeling of the shaft, bearings, and impellers with details and assembling them and then conducting finite element analysis is very complex, and as the case study is a process pump in an oil refinery that works 24 h a day, stopping the production line and then measuring, modeling, and conducting FEM analysis is very expensive. On the other hand, the purpose of this manuscript is to introduce an analytical model for all the essential rotary parts of a centrifugal pump in detail and then conduct a sensitive analysis for the effect of impeller diameter on the critical speed of it inversely. For this purpose, the dynamic inverse solution is very suitable when there are practical limitations for FEM analysis, such as it being very complex and expensive.