Comparison of Reduction Methods for Finite Element Geometrically Nonlinear Beam Structures
Abstract
1. Introduction
2. Reduced-Order Models for Finite Element Structures
2.1. Theoretical Framework
2.2. Implicit Condensation and Expansion
2.3. Quadratic Manifold with Modal Derivatives
2.3.1. Definition of Full and Static Modal Derivatives
2.3.2. Reduction with the Quadratic Manifold
2.4. Direct Normal Form Approach
2.5. Analytical Example: A Linear Beam on a Nonlinear Elastic Foundation
2.5.1. Model Equations and Type of Nonlinearity
2.5.2. Results
3. Beam Structures Discretized with Finite Elements
3.1. A Clamped–Clamped Beam with Increasing Curvature
3.2. Clamped Beams with 1:1 Resonance
3.2.1. Backbone Curves
3.2.2. Frequency-Response Curves
3.3. A Cantilever Beam
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Representation of Quadratic and Cubic Nonlinear Terms
Appendix B. Reduced Dynamics for the Clamped Beam with 1:1 Resonance
References
- Steindl, A.; Troger, H. Methods for dimension reduction and their applications in nonlinear dynamics. Int. J. Solids Struct. 2001, 38, 2131–2147. [Google Scholar] [CrossRef]
- Rega, G.; Troger, H. Dimension reduction of dynamical systems: Methods, models, applications. Nonlinear Dyn. 2005, 41, 1–15. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Awrejcewicz, J.; Krysko, V.A.; Narkaitis, G. Bifurcations of a Thin Plate-Strip Excited Transversally and Axially. Nonlinear Dyn. 2003, 32, 187–209. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Balachandran, B. Modal interactions in dynamical and structural systems. ASME Appl. Mech. Rev. 1989, 42, 175–201. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Nonlinear Interactions: Analytical, Computational and Experimental Methods; Wiley Series in Nonlinear Science; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Thomas, O.; Touzé, C.; Luminais, E. Non-linear vibrations of free-edge thin spherical shells: Experiments on a 1:1:2 internal resonance. Nonlinear Dyn. 2007, 49, 259–284. [Google Scholar] [CrossRef]
- Monteil, M.; Touzé, C.; Thomas, O.; Benacchio, S. Nonlinear forced vibrations of thin structures with tuned eigenfrequencies: The cases of 1:2:4 and 1:2:2 internal resonances. Nonlinear Dyn. 2014, 75, 175–200. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Givois, A.; Longobardi, P.; Shen, Y.; Deü, J.F.; Salles, L.; Touzé, C.; Thomas, O. Non-intrusive reduced order modelling for the dynamics of geometrically nonlinear flat structures using three-dimensional finite elements. Comput. Mech. 2020. accepted for publication. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, V.A.; Saveleva, N. Routes to chaos exhibited by closed flexible cylindrical shells. ASME J. Comput. Nonlinear Dyn. 2007, 2, 1–9. [Google Scholar] [CrossRef]
- Touzé, C.; Thomas, O.; Amabili, M. Transition to chaotic vibrations for harmonically forced perfect and imperfect circular plates. Int. J. Non-Linear Mech. 2011, 46, 234–246. [Google Scholar] [CrossRef]
- Cadot, O.; Ducceschi, M.; Humbert, T.; Miquel, B.; Mordant, N.; Josserand, C.; Touzé, C. Wave turbulence in vibrating plates. In Handbook of Applications of Chaos Theory; Skiadas, C., Ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Kapania, R.K.; Byun, C. Reduction methods based on eigenvectors and Ritz vectors for nonlinear transient analysis. Comput. Mech. 1993, 11, 65–82. [Google Scholar] [CrossRef]
- Krysl, P.; Lall, S.; Marsden, J. Dimensional model reduction in non-linear finite element dynamics of solids and structures. Int. J. Numer. Methods Eng. 2001, 51, 479–504. [Google Scholar] [CrossRef]
- Kerschen, G.; Golinval, J. Physical interpretation of the proper orthogonal modes using the singular value decomposition. J. Sound Vib. 2002, 249, 849–865. [Google Scholar] [CrossRef]
- Sampaio, R.; Soize, C. Remarks on the efficiency of POD for model reduction in non-linear dynamics of continuous elastic systems. Int. J. Numer. Methods Eng. 2007, 72, 22–45. [Google Scholar] [CrossRef]
- Amabili, M.; Sarkar, A.; Païdoussis, M.P. Chaotic vibrations of circular cylindrical shells: Galerkin versus reduced-order models via the proper orthogonal decomposition method. J. Sound Vib. 2006, 290, 736–762. [Google Scholar] [CrossRef]
- Amabili, M.; Touzé, C. Reduced-order models for non-linear vibrations of fluid-filled circular cylindrical shells: Comparison of POD and asymptotic non-linear normal modes methods. J. Fluids Struct. 2007, 23, 885–903. [Google Scholar] [CrossRef]
- Shaw, S.W.; Pierre, C. Non-linear normal modes and invariant manifolds. J. Sound Vib. 1991, 150, 170–173. [Google Scholar] [CrossRef]
- Shaw, S.W.; Pierre, C. Normal modes for non-linear vibratory systems. J. Sound Vib. 1993, 164, 85–124. [Google Scholar] [CrossRef]
- Carr, J. Applications of Centre Manifold Theory; Springer: New York, NY, USA, 1981. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Pesheck, E.; Boivin, N.; Pierre, C.; Shaw, S.W. Nonlinear Modal Analysis of Structural Systems Using Multi-Mode Invariant Manifolds. Nonlinear Dyn. 2001, 25, 183–205. [Google Scholar] [CrossRef]
- Jiang, D.; Pierre, C.; Shaw, S. Nonlinear normal modes for vibratory systems under harmonic excitation. J. Sound Vib. 2005, 288, 791–812. [Google Scholar] [CrossRef]
- Apiwattanalunggarn, P.; Pierre, C.; Jiang, D. Finite-Element-based nonlinear modal reduction of a rotating beam with large-amplitude motion. J. Vib. Control 2003, 9, 235–263. [Google Scholar] [CrossRef]
- Touzé, C.; Thomas, O.; Chaigne, A. Hardening/softening behaviour in non-linear oscillations of structural systems using non-linear normal modes. J. Sound Vib. 2004, 273, 77–101. [Google Scholar] [CrossRef]
- Touzé, C.; Amabili, M. Non-linear normal modes for damped geometrically non-linear systems: Application to reduced-order modeling of harmonically forced structures. J. Sound Vib. 2006, 298, 958–981. [Google Scholar] [CrossRef]
- Touzé, C. Normal form theory and nonlinear normal modes: Theoretical settings and applications. In Modal Analysis of Nonlinear Mechanical Systems; Kerschen, G., Ed.; Springer Series CISM Courses and Lectures; Springer: New York, NY, USA, 2014; Volume 555, pp. 75–160. [Google Scholar]
- Touzé, C.; Amabili, M.; Thomas, O. Reduced-order models for large-amplitude vibrations of shells including in-plane inertia. Comput. Methods Appl. Mech. Eng. 2008, 197, 2030–2045. [Google Scholar] [CrossRef][Green Version]
- Haller, G.; Ponsioen, S. Nonlinear normal modes and spectral submanifolds: Existence, uniqueness and use in model reduction. Nonlinear Dyn. 2016, 86, 1493–1534. [Google Scholar] [CrossRef]
- Ponsioen, S.; Pedergnana, T.; Haller, G. Automated computation of autonomous spectral submanifolds for nonlinear modal analysis. J. Sound Vib. 2018, 420, 269–295. [Google Scholar] [CrossRef]
- Breunung, T.; Haller, G. Explicit backbone curves from spectral submanifolds of forced-damped nonlinear mechanical systems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20180083. [Google Scholar] [CrossRef]
- Jain, S.; Tiso, P.; Haller, G. Exact nonlinear model reduction for a von Kármán beam: Slow-fast decomposition and spectral submanifolds. J. Sound Vib. 2018, 423, 195–211. [Google Scholar] [CrossRef]
- Ponsioen, S.; Jain, S.; Haller, G. Model reduction to spectral submanifolds and forced-response calculation in high-dimensional mechanical systems. J. Sound Vib. 2020, 488, 115640. [Google Scholar] [CrossRef]
- Mignolet, M.P.; Przekop, A.; Rizzi, S.A.; Spottswood, S.M. A review of indirect/non-intrusive reduced order modeling of nonlinear geometric structures. J. Sound Vib. 2013, 332, 2437–2460. [Google Scholar] [CrossRef]
- Muravyov, A.; Rizzi, S. Determination of nonlinear stiffness with application to random vibration of geometrically nonlinear structures. Comput. Struct. 2003, 81, 1513–1523. [Google Scholar] [CrossRef]
- Perez, R.; Wang, X.Q.; Mignolet, M.P. Nonintrusive Structural Dynamic Reduced Order Modeling for Large Deformations: Enhancements for Complex Structures. J. Comput. Nonlinear Dyn. 2014, 9, 031008. [Google Scholar] [CrossRef]
- Ewan, M.M.; Wright, J.; Cooper, J.; Leung, A. A finite element/modal technique for nonlinear plate and stiffened panel response prediction. In Proceedings of the 19th AIAA Applied Aerodynamics Conference, Anaheim, CA, USA, 11–14 June 2001. [Google Scholar]
- Ewan, M.I.M. A Combined Modal/Finite Element Technique for the Non-Linear Dynamic Simulation of Aerospace Structures. Ph.D. Thesis, University of Manchester, Manchester, UK, 2001. [Google Scholar]
- Hollkamp, J.J.; Gordon, R.W.; Spottswood, S.M. Non-linear modal models for sonic fatigue response prediction: A comparison of methods. J. Sound Vib. 2005, 284, 1145–1163. [Google Scholar] [CrossRef]
- Hollkamp, J.J.; Gordon, R.W. Reduced-order models for non-linear response prediction: Implicit condensation and expansion. J. Sound Vib. 2008, 318, 1139–1153. [Google Scholar] [CrossRef]
- Frangi, A.; Gobat, G. Reduced order modelling of the non-linear stiffness in MEMS resonators. Int. J. Non-Linear Mech. 2019, 116, 211–218. [Google Scholar] [CrossRef]
- Kuether, R.J.; Deaner, B.J.; Hollkamp, J.J.; Allen, M.S. Evaluation of Geometrically Nonlinear Reduced-Order Models with Nonlinear Normal Modes. AIAA J. 2015, 53, 3273–3285. [Google Scholar] [CrossRef]
- Jain, S.; Tiso, P.; Rutzmoser, J.; Rixen, D. A quadratic manifold for model order reduction of nonlinear structural dynamics. Comput. Struct. 2017, 188, 80–94. [Google Scholar] [CrossRef]
- Rutzmoser, J.B.; Rixen, D.J.; Tiso, P.; Jain, S. Generalization of quadratic manifolds for reduced order modeling of nonlinear structural dynamics. Comput. Struct. 2017, 192, 196–209. [Google Scholar] [CrossRef]
- Veraszto, Z.; Ponsioen, S.; Haller, G. Explicit third-order model reduction formulas for general nonlinear mechanical systems. J. Sound Vib. 2020, 468, 115039. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Shen, Y.; Salles, L.; Blahos, J.; Touzé, C. Direct computation of nonlinear mapping via normal form for reduced-order models of finite element nonlinear structures. Comput. Methods Appl. Mech. Eng. 2020. submitted for publication. [Google Scholar]
- Haller, G.; Ponsioen, S. Exact model reduction by a slow–fast decomposition of nonlinear mechanical systems. Nonlinear Dyn. 2017, 90, 617–647. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Salles, L.; Touzé, C. Comparison of nonlinear mappings for reduced-order modelling of vibrating structures: Normal form theory and quadratic manifold method with modal derivatives. Nonlinear Dyn. 2020. accepted for publication. [Google Scholar] [CrossRef]
- Shen, Y.; Béreux, N.; Frangi, A.; Touzé, C. Reduced order models for geometrically nonlinear structures: Assessment of implicit condensation in comparison with invariant manifold approach. Eur. J. Mech. A/Solids 2021, 86, 104165. [Google Scholar] [CrossRef]
- Fung, Y.C.; Tong, P. Classical and Computational Solid Mechanics; World Scientific: River Edge, NJ, USA, 2001. [Google Scholar]
- Holzapfel, A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering Science; John Wiley and Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Touzé, C.; Vidrascu, M.; Chapelle, D. Direct finite element computation of non-linear modal coupling coefficients for reduced-order shell models. Comput. Mech. 2014, 54, 567–580. [Google Scholar] [CrossRef]
- Givois, A.; Grolet, A.; Thomas, O.; Deü, J.F. On the frequency response computation of geometrically nonlinear flat structures using reduced-order finite element models. Nonlinear Dyn. 2019, 97, 1747–1781. [Google Scholar] [CrossRef]
- Idelsohn, S.; Cardona, A. A reduction method for nonlinear structural dynamic analysis. Comput. Methods Appl. Mech. Eng. 1985, 49, 253–279. [Google Scholar] [CrossRef]
- Weeger, O.; Wever, U.; Simeon, B. On the use of modal derivatives for nonlinear model order reduction. Int. J. Numer. Methods Eng. 2016, 108, 1579–1602. [Google Scholar] [CrossRef]
- Sombroek, C.S.M.; Tiso, P.; Renson, L.; Kerschen, G. Numerical computation of nonlinear normal modes in a modal derivative subspace. Comput. Struct. 2018, 195, 34–46. [Google Scholar] [CrossRef]
- Touzé, C.; Thomas, O. Non-linear behaviour of free-edge shallow spherical shells: Effect of the geometry. Int. J. Non-Linear Mech. 2006, 41, 678–692. [Google Scholar] [CrossRef][Green Version]
- Shen, Y.; Kesmia, N.; Touzé, C.; Vizzaccaro, A.; Salles, L.; Thomas, O. Predicting the type of nonlinearity of shallow spherical shells: Comparison of direct normal form with modal derivatives. In Proceedings of the NODYCON 2021, Second International Nonlinear Dynamics Conference, Rome, Italy, 16–19 February 2021. [Google Scholar]
- Shaw, S.W. An invariant manifold approach to nonlinear normal modes of oscillation. J. Nonlinear Sci. 1994, 4, 419–448. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Lacarbonara, W. On the discretization of distributed-parameter systems with quadratic and cubic non-linearities. Nonlinear Dyn. 1997, 13, 203–220. [Google Scholar] [CrossRef]
- Touzé, C.; Thomas, O.; Huberdeau, A. Asymptotic non-linear normal modes for large amplitude vibrations of continuous structures. Comput. Struct. 2004, 82, 2671–2682. [Google Scholar] [CrossRef]
- Cochelin, B.; Vergez, C. A high order purely frequency-based harmonic balance formulation for continuation of periodic solutions. J. Sound Vib. 2009, 324, 243–262. [Google Scholar] [CrossRef]
- Guillot, L.; Cochelin, B.; Vergez, C. A generic and efficient Taylor series–based continuation method using a quadratic recast of smooth nonlinear systems. Int. J. Numer. Methods Eng. 2019, 119, 261–280. [Google Scholar] [CrossRef]
- Guillot, L.; Lazarus, A.; Thomas, O.; Vergez, C.; Cochelin, B. A purely frequency based Floquet-Hill formulation for the efficient stability computation of periodic solutions of ordinary differential systems. J. Comput. Phys. 2020, 416, 109477. [Google Scholar] [CrossRef]
- Électricité de France. code_aster. Available online: https://www.code-aster.org/ (accessed on 10 February 2020).
- Blahoš, J.; Vizzaccaro, A.; El Haddad, F.; Salles, L. Parallel harmonic balance method for analysis of nonlinear dynamical systems. In Proceedings of the Turbo Expo, ASME 2020, London, UK, 21–25 September 2020; Volume GT2020-15392. [Google Scholar]
- Manevitch, A.I.; Manevitch, L.I. Free oscillations in conservative and dissipative symmetric cubic two-degree-of-freedom systems with closed natural frequencies. Meccanica 2003, 38, 335–348. [Google Scholar] [CrossRef]
- Givois, A.; Tan, J.; Touzé, C.; Thomas, O. Backbone curves of coupled cubic oscillators in one-to-one internal resonance: Bifurcation scenario, measurements and parameter identification. Meccanica 2020, 55, 481–503. [Google Scholar] [CrossRef]
- Crespo da Silva, M.R.M.; Glynn, C.C. Nonlinear flexural-flexural-torsional dynamics of inextensional beams. Part 1: Equations of motion. J. Struct. Mech. 1978, 6, 437–448. [Google Scholar] [CrossRef]
- Pai, P.F.; Nayfeh, A.H. Non-linear non-planar oscillations of a cantilever beam under lateral base excitations. Int. J. Non-Linear Mech. 1990, 25, 455–474. [Google Scholar] [CrossRef]
- Touzé, C.; Thomas, O. Reduced-order modeling for a cantilever beam subjected to harmonic forcing. In Proceedings of the of EUROMECH Colloquium 457: Nonlinear modes of vibrating systems, Frejus, France, 7–9 June 2004; pp. 165–168. [Google Scholar]
- Thomas, O.; Sénéchal, A.; Deü, J.F. Hardening/softening behaviour and reduced order modelling of nonlinear vibrations of rotating cantilever beams. Nonlinear Dyn. 2016, 86, 1293–1318. [Google Scholar] [CrossRef]
- Denis, V.; Jossic, M.; Giraud-Audine, C.; Chomette, B.; Renault, A.; Thomas, O. Identification of nonlinear modes using phase-locked-loop experimental continuation and normal form. Mech. Syst. Signal Process. 2018, 106, 430–452. [Google Scholar] [CrossRef]
- Kim, K.; Khanna, V.; Wang, X.Q.; Mignolet, M.P. Nonlinear reduced order modeling of flat cantilever structures. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2009. [Google Scholar]
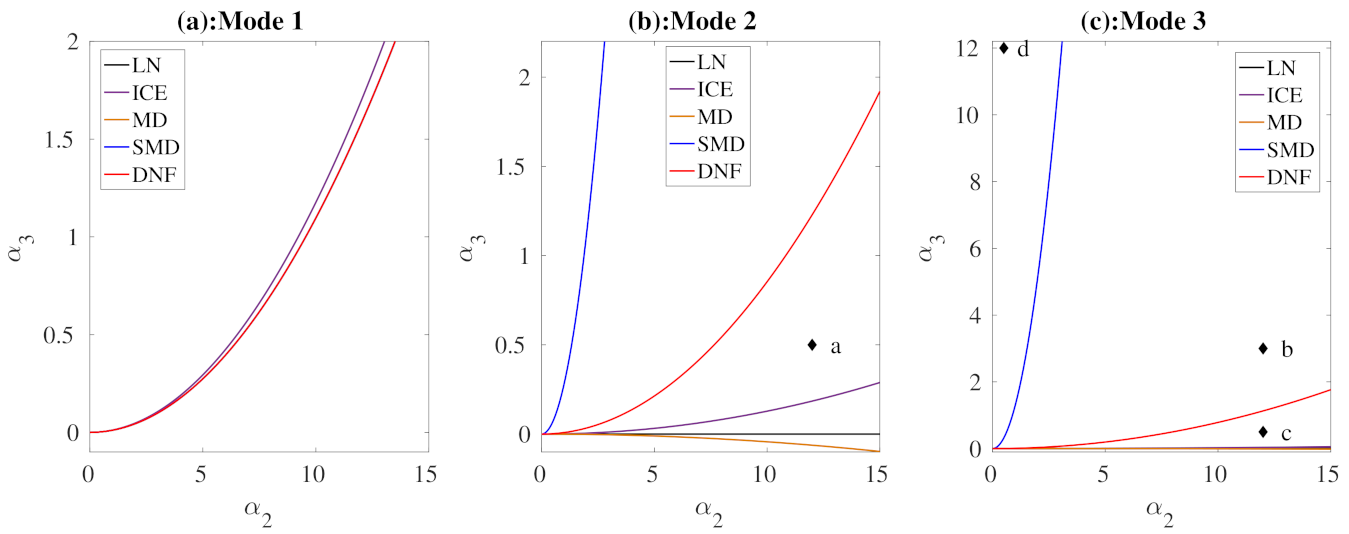
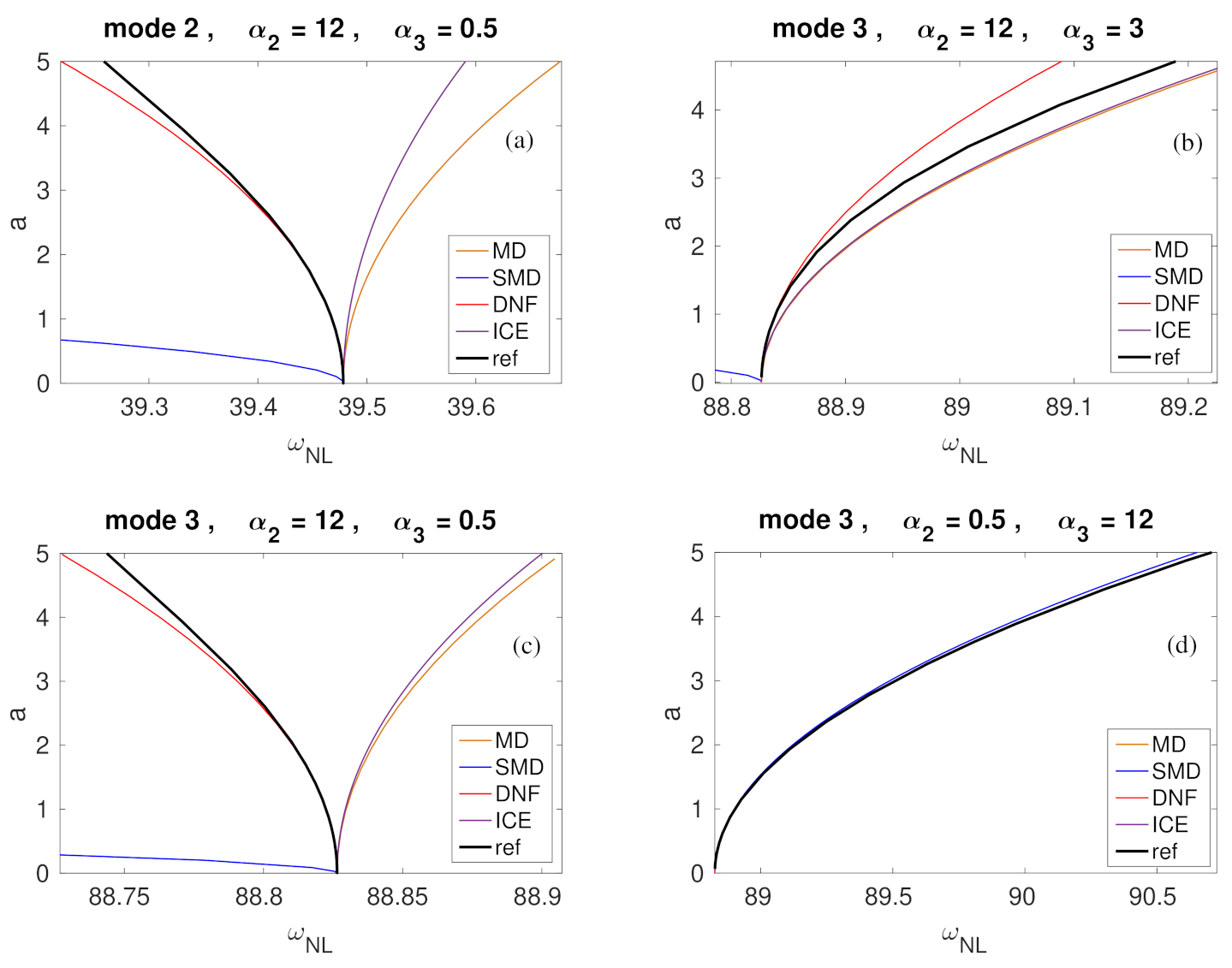

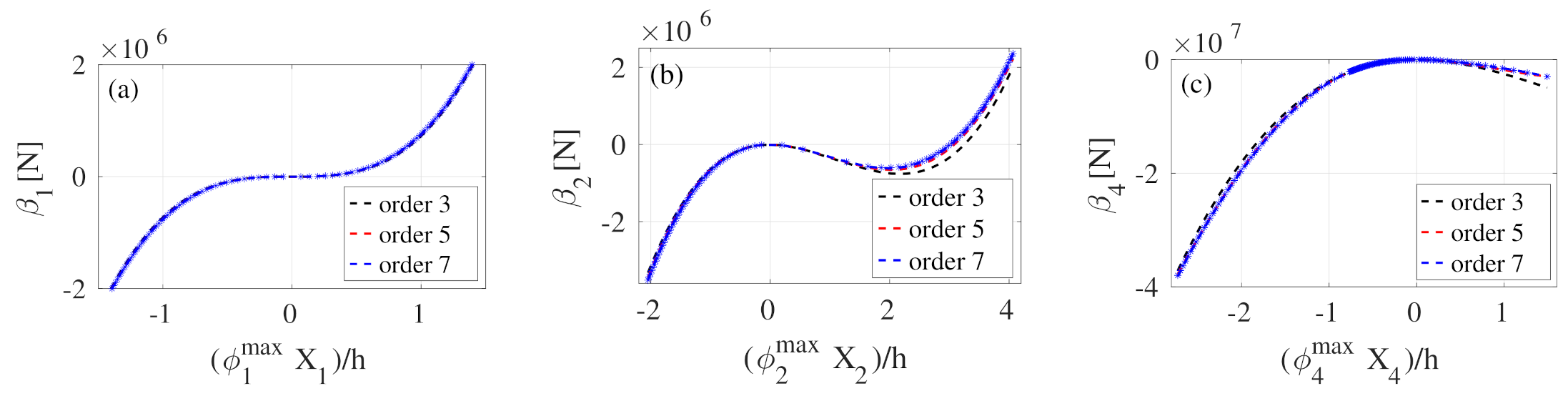

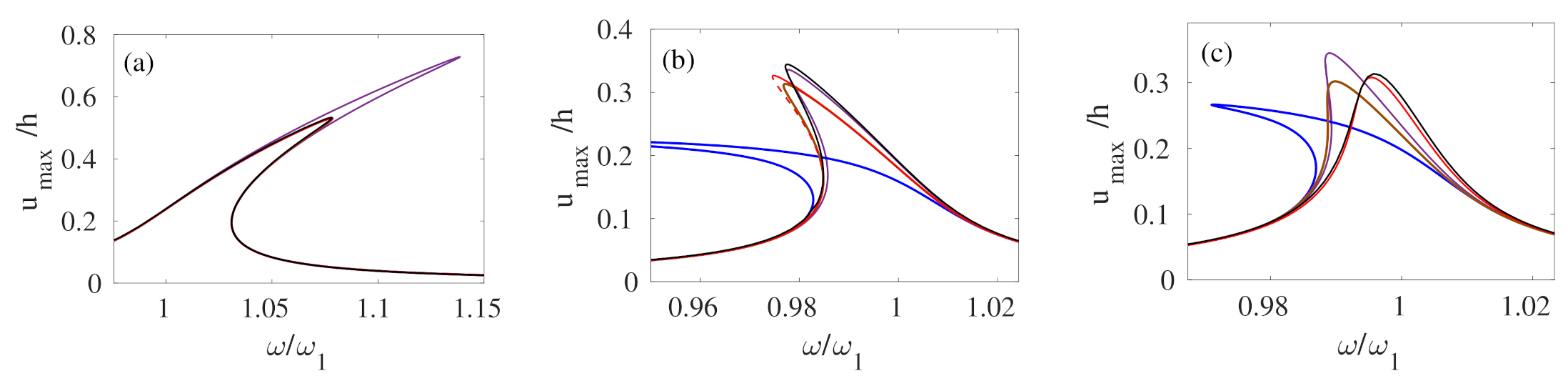

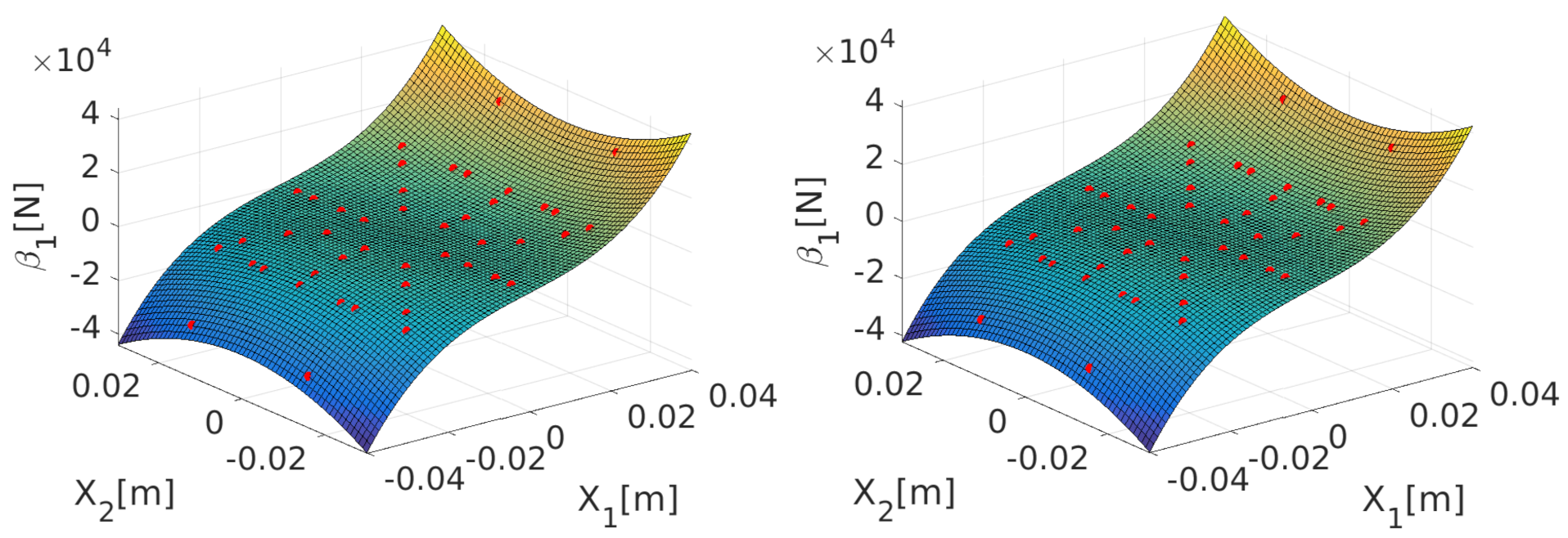
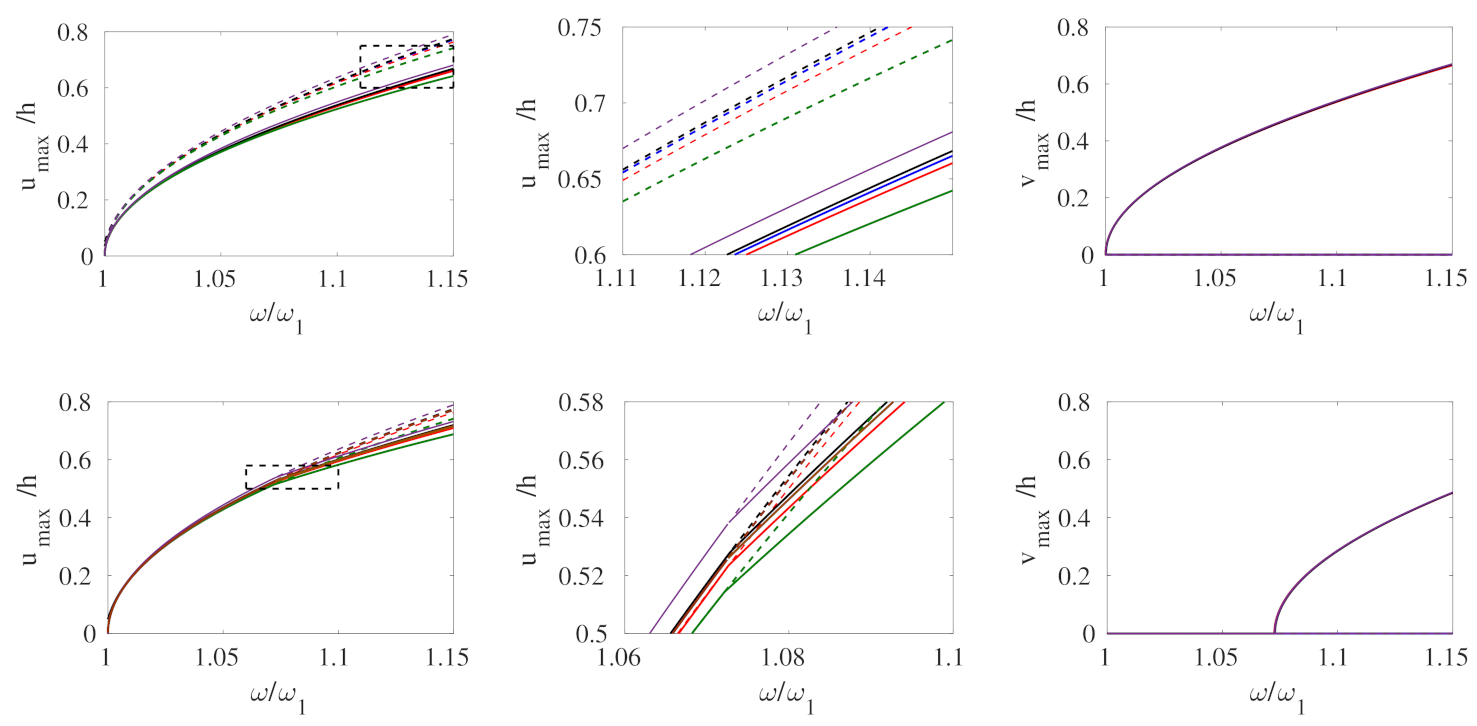

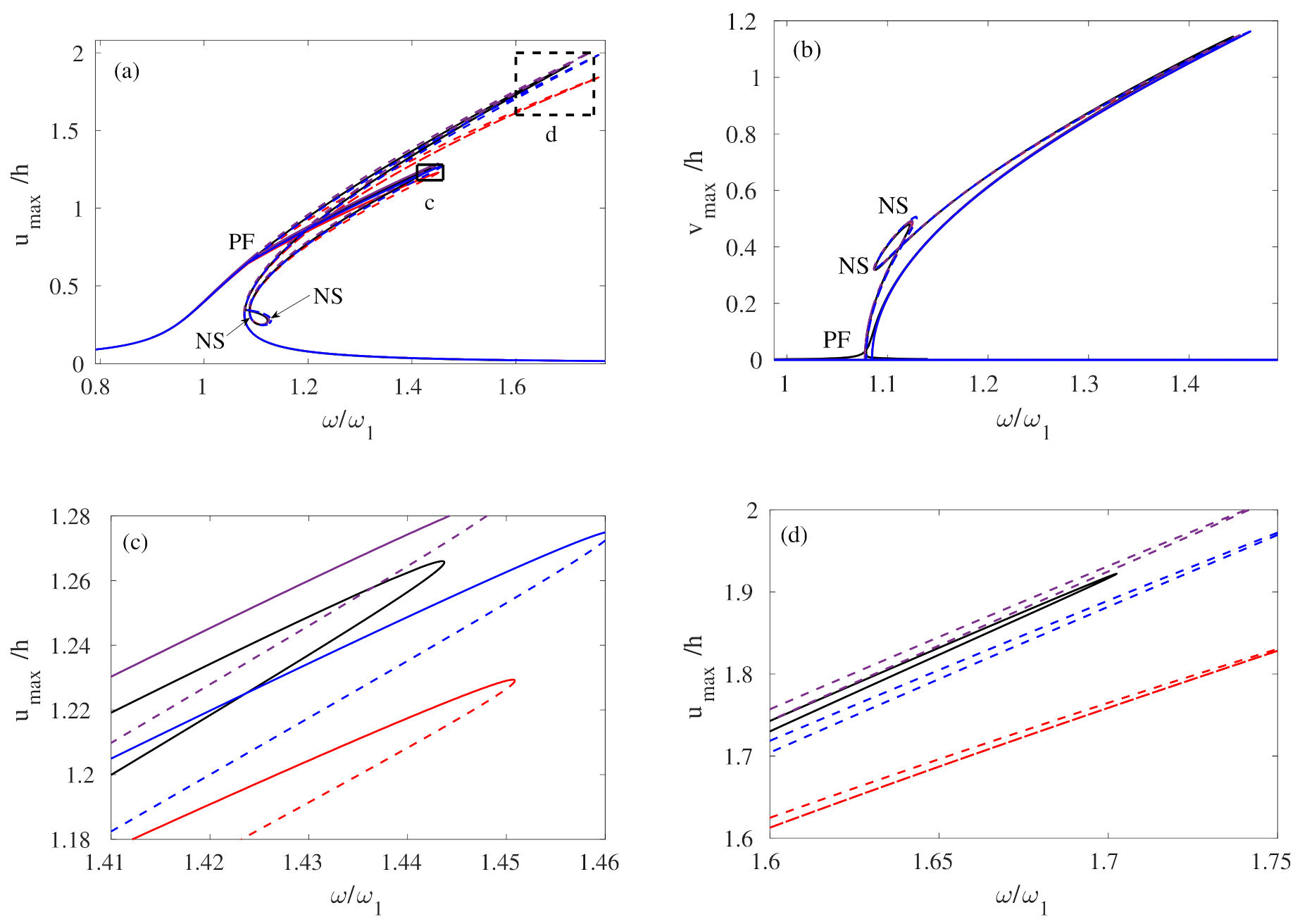
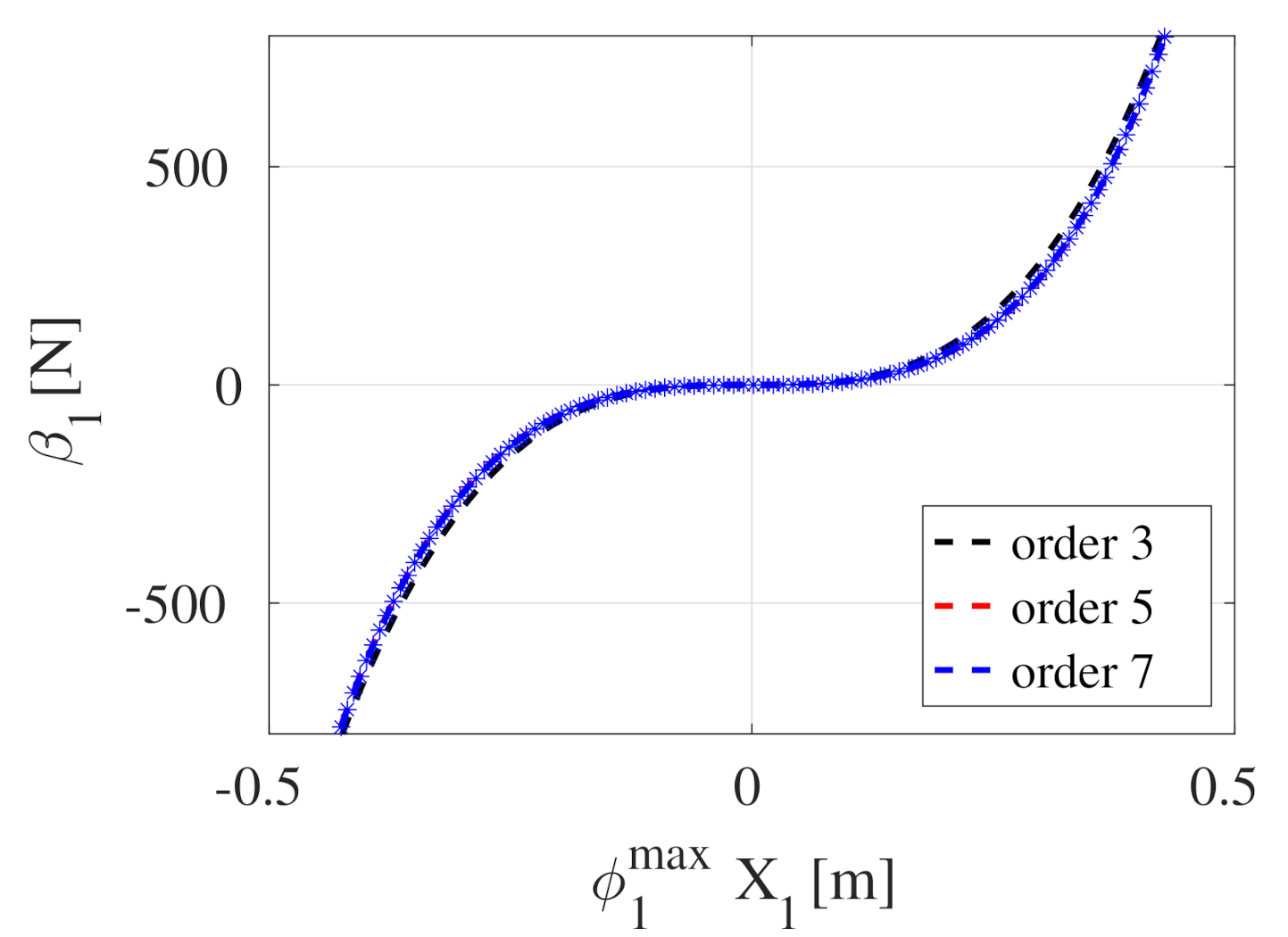
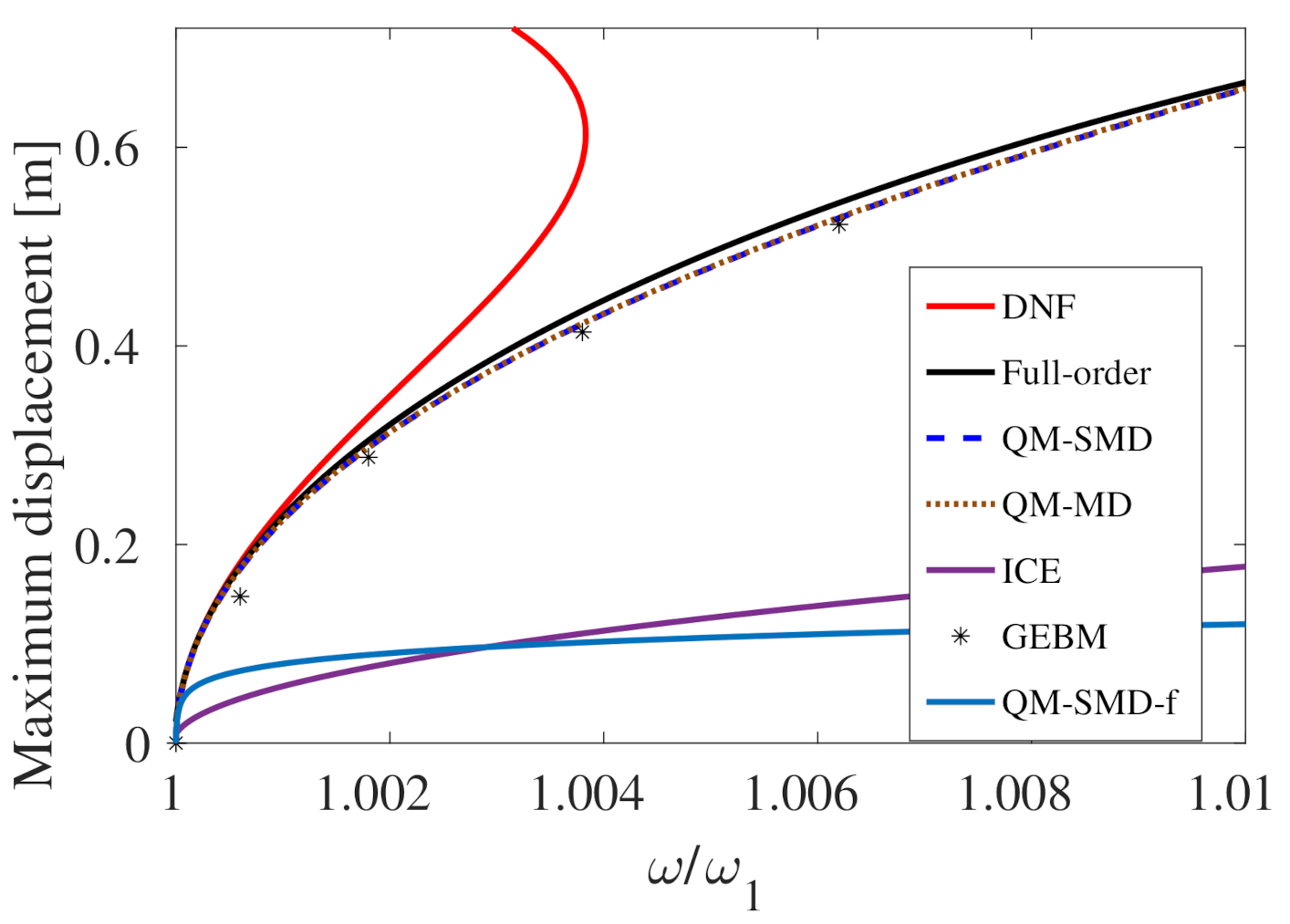
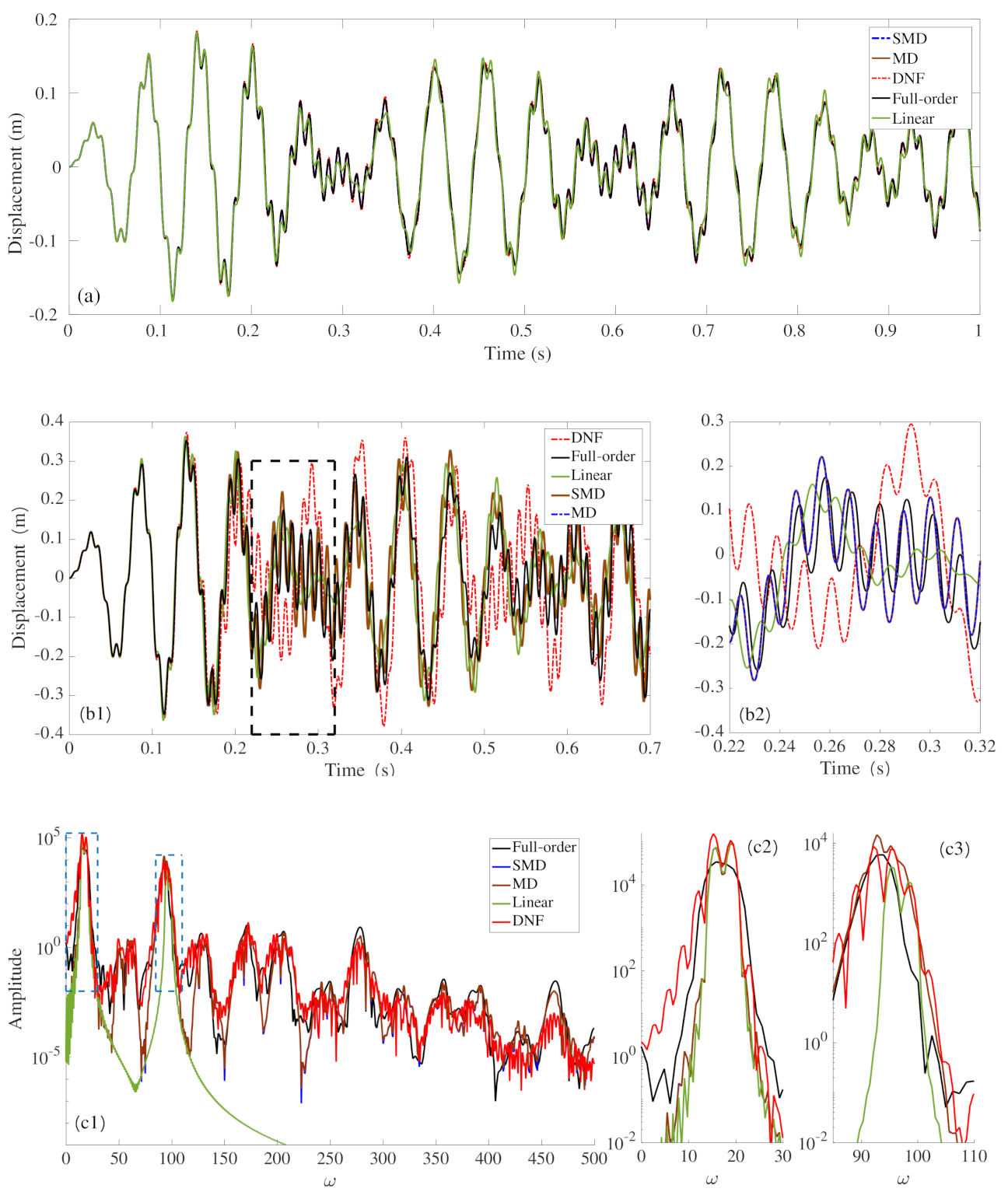

| Case | Length (m) | Thickness (m) | Width (m) | (rad/s) | (rad/s) | Detuning |
|---|---|---|---|---|---|---|
| a | 1 | 0.03 | 0.03 | 941.37 | 941.40 | 0.0 |
| b | 1 | 0.03 | 0.0315 | 941.47 | 987.83 | 4.92% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Vizzaccaro, A.; Kesmia, N.; Yu, T.; Salles, L.; Thomas, O.; Touzé, C. Comparison of Reduction Methods for Finite Element Geometrically Nonlinear Beam Structures. Vibration 2021, 4, 175-204. https://doi.org/10.3390/vibration4010014
Shen Y, Vizzaccaro A, Kesmia N, Yu T, Salles L, Thomas O, Touzé C. Comparison of Reduction Methods for Finite Element Geometrically Nonlinear Beam Structures. Vibration. 2021; 4(1):175-204. https://doi.org/10.3390/vibration4010014
Chicago/Turabian StyleShen, Yichang, Alessandra Vizzaccaro, Nassim Kesmia, Ting Yu, Loïc Salles, Olivier Thomas, and Cyril Touzé. 2021. "Comparison of Reduction Methods for Finite Element Geometrically Nonlinear Beam Structures" Vibration 4, no. 1: 175-204. https://doi.org/10.3390/vibration4010014
APA StyleShen, Y., Vizzaccaro, A., Kesmia, N., Yu, T., Salles, L., Thomas, O., & Touzé, C. (2021). Comparison of Reduction Methods for Finite Element Geometrically Nonlinear Beam Structures. Vibration, 4(1), 175-204. https://doi.org/10.3390/vibration4010014






