Numerical Assessment of Polynomial Nonlinear State-Space and Nonlinear-Mode Models for Near-Resonant Vibrations
Abstract
:1. Introduction
2. Description of the Nonlinear System Identification Methods
2.1. Identification of a Nonlinear-Mode Model
2.2. Identification of a PNLSS Model
3. Overview of Benchmarks and Comparison Strategy
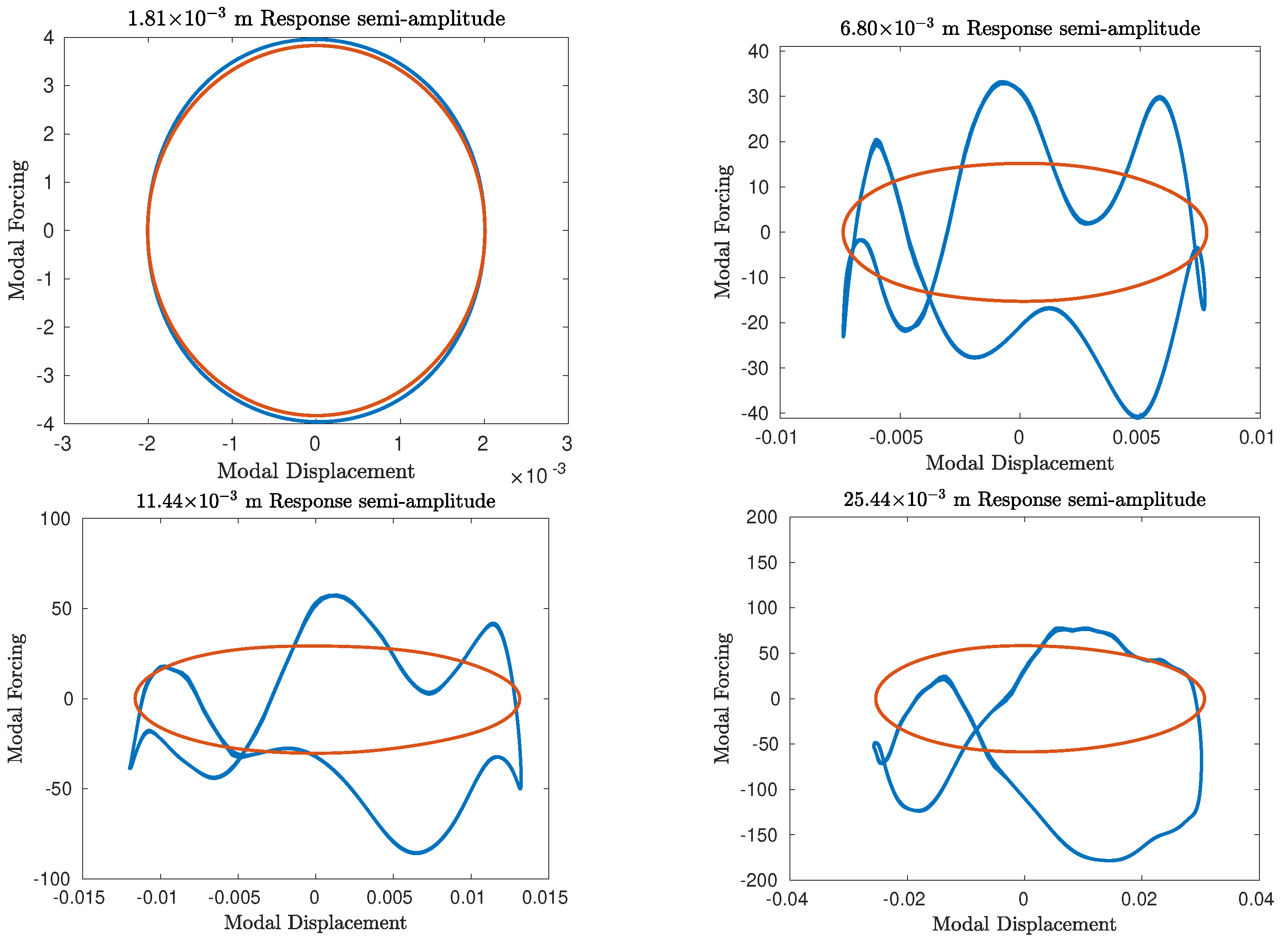
4. Results
4.1. Geometrically Nonlinear Beam/Duffing Oscillator
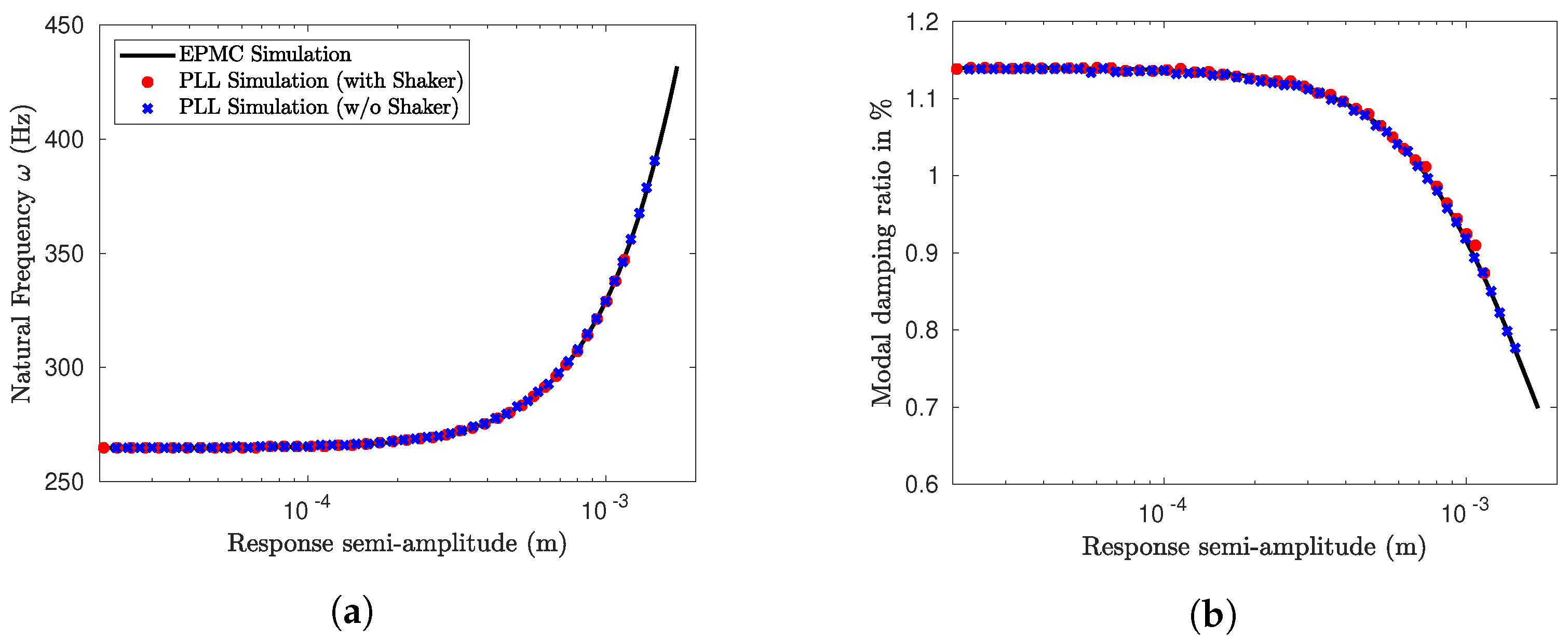
4.1.1. Effect of Excitation Imperfections on the Identified Modal Properties
4.1.2. Effect of Exciter-Structure Interaction on the Training Data for the PNLSS Models
4.1.3. Inability to Identify an Accurate PNLSS Model in the Case of Chaotic Training Data
4.1.4. Assessment of the Prediction Accuracy
4.2. Beam with an Elastic-Dry Friction Contact
4.2.1. Effect of Excitation Imperfections on the Identified Modal Properties
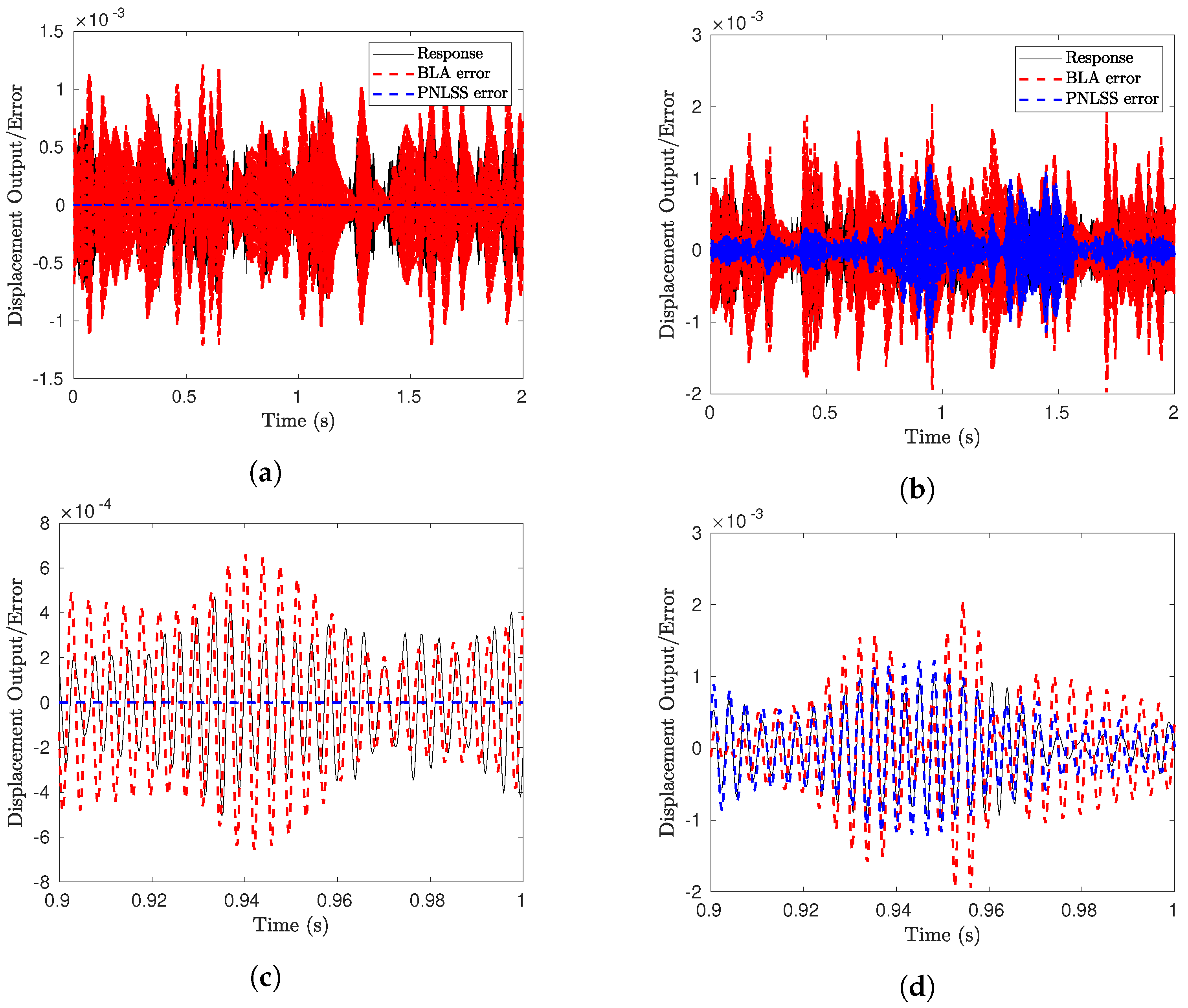
4.2.2. Identification of the PNLSS Models
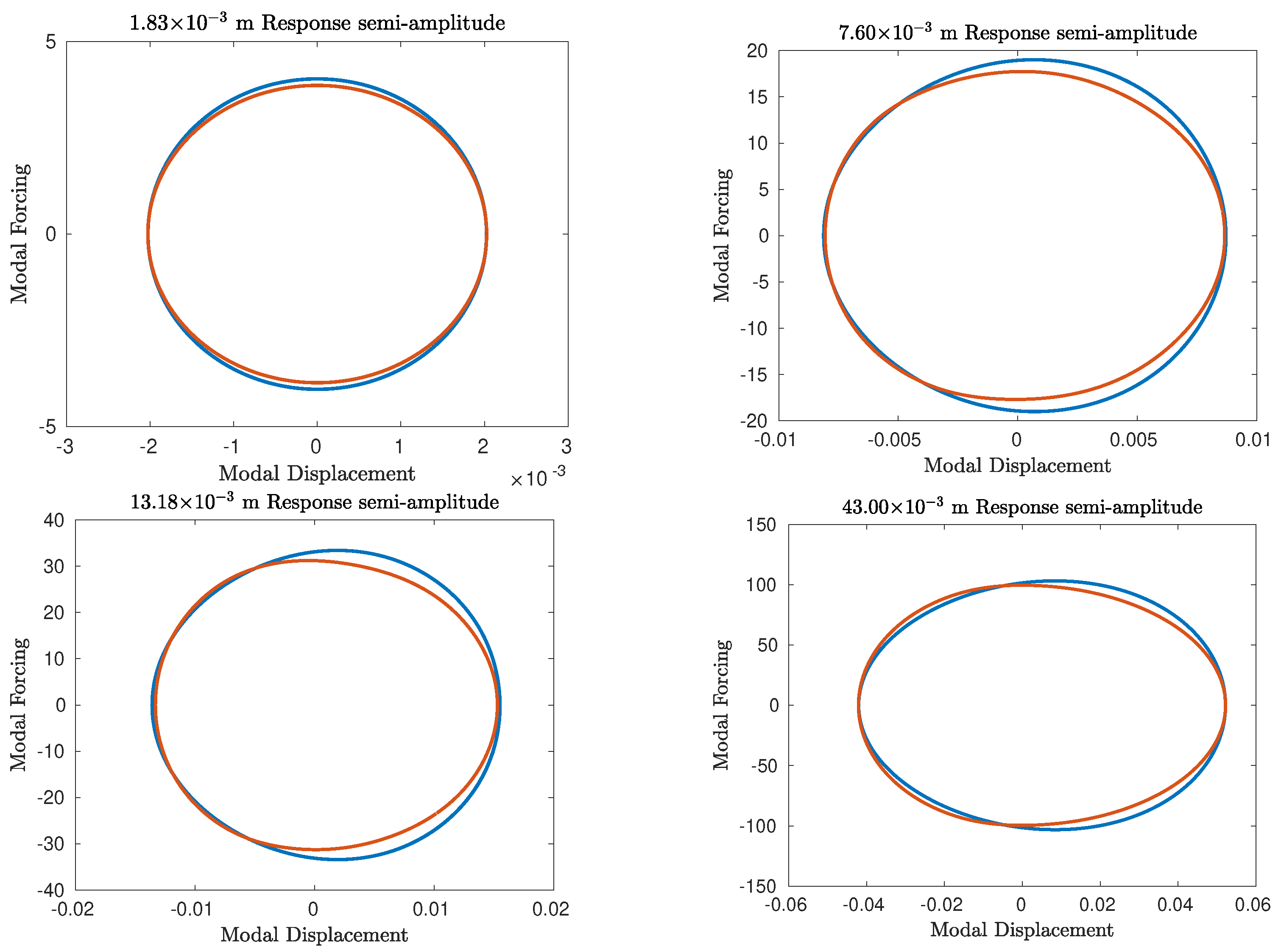
4.2.3. Assessment of the Prediction Accuracy
4.2.4. Training the PNLSS Model with PLL Testing Data and Its Effect on the Prediction Accuracy
4.3. Beam with Unilateral Contact
4.3.1. Occurrence of Uncontrolled Higher Harmonics during PLL Testing with Shaker
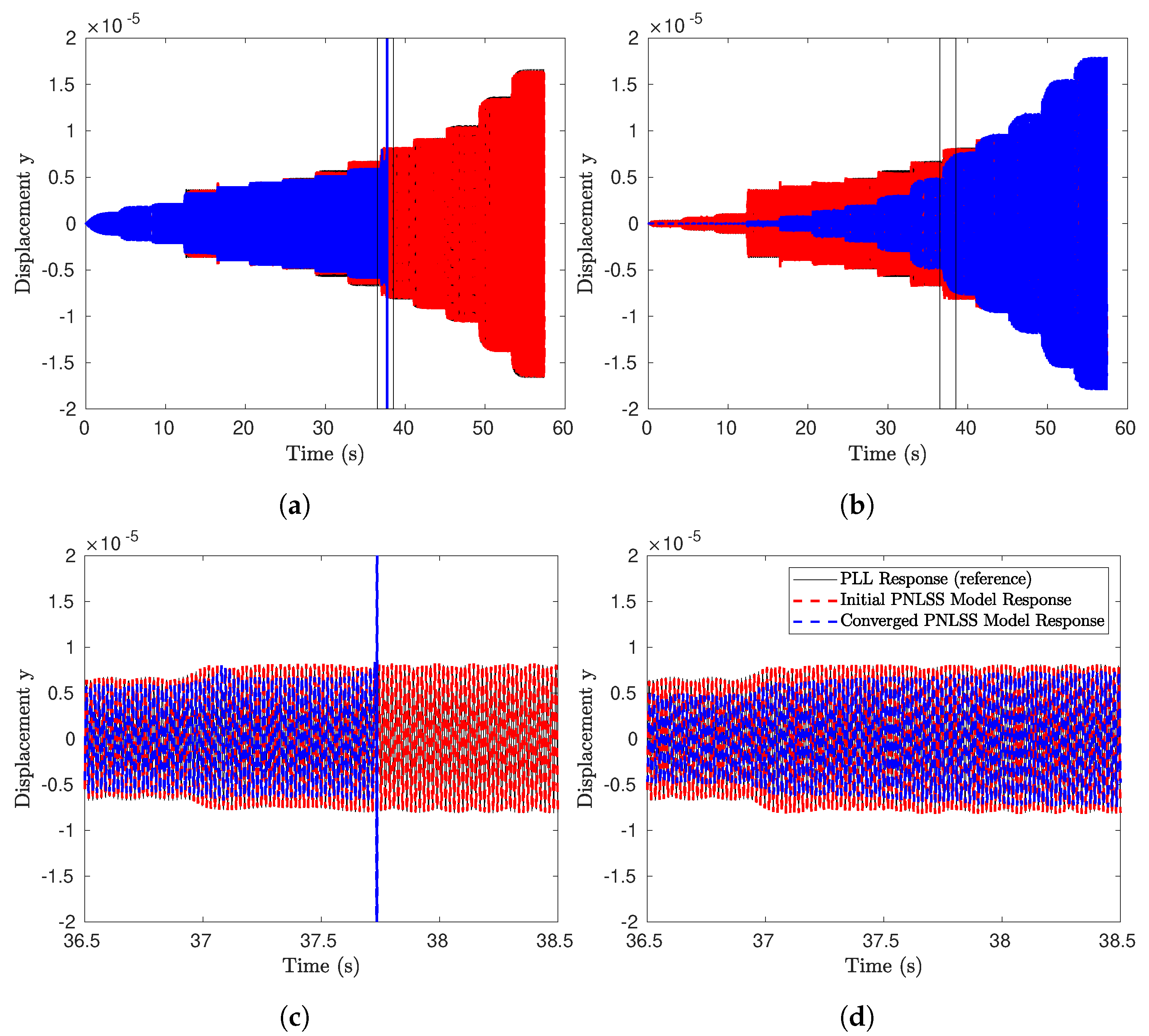
4.3.2. Identification of the PNLSS Models
4.3.3. Assessment of the Prediction Accuracy
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NM-ROM | Nonlinear Modal-Reduced Order Model |
| PNLSS | Polynomial Non-Linear State-Space |
| PLL | Phase-Locked Loop |
| EPMC | Extended Periodic Motion Concept |
References
- Dou, S.; Jensen, J.S. Optimization of nonlinear structural resonance using the incremental harmonic balance method. J. Sound Vib. 2015, 334, 239–254. [Google Scholar] [CrossRef] [Green Version]
- Krack, M.; Salles, L.; Thouverez, F. Vibration prediction of bladed disks coupled by friction joints. Arch. Comput. Methods Eng. 2017, 24, 589–636. [Google Scholar] [CrossRef] [Green Version]
- Schoukens, J.; Ljung, L. Nonlinear system identification: A user-oriented road map. IEEE Control Syst. Mag. 2019, 39, 28–99. [Google Scholar]
- Noël, J.P.; Kerschen, G. Nonlinear system identification in structural dynamics: 10 more years of progress. Mech. Syst. Signal Proces. 2017, 83, 2–35. [Google Scholar] [CrossRef]
- Roache, P.J. Verification and Validation in Computational Science and Engineering; Hermosa: Albuquerque, NM, USA, 1998; Volume 895. [Google Scholar]
- Alijani, F.; Amabili, M. Non-Linear Vibrations of Shells: A Literature Review from 2003 to 2013. Int. J. Non-Linear Mech. 2014, 58, 233–257. [Google Scholar] [CrossRef] [Green Version]
- Brake, M.R.W. The Mechanics of Jointed Structures; Springer Science+Business Media: New York, NY, USA, 2017. [Google Scholar]
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.C. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef] [Green Version]
- Scheel, M.; Kleyman, G.; Tatar, A.; Brake, M.R.W.; Peter, S.; Noël, J.P.; Allen, M.S.; Krack, M. System Identification of Jointed Structures: Nonlinear Modal Testing Vs. State-Space Model Identification. In Nonlinear Dynamics; Kerschen, G., Ed.; Springer International Publishing: Cham, Switzerland, 2019; Volume 1, pp. 159–161. [Google Scholar]
- Scheel, M.; Kleyman, G.; Tatar, A.; Brake, M.R.W.; Peter, S.; Noël, J.P.; Allen, M.S.; Krack, M. Experimental assessment of polynomial nonlinear state-space and nonlinear-mode models for near-resonant vibrations. Mech. Syst. Signal Process. 2020, 143, 106796. [Google Scholar] [CrossRef]
- Rosenberg, R.M. Normal Modes of Nonlinear Dual-Mode Systems. J. Appl. Mech. 1960, 27, 263–268. [Google Scholar] [CrossRef]
- Kerschen, G.; Peeters, M.; Golinval, J.C.; Vakakis, A.F. Nonlinear Normal Modes, Part I: A useful framework for the structural dynamicist: Special Issue: Non-linear Structural Dynamics. Mech. Syst. Signal Proces. 2009, 23, 170–194. [Google Scholar] [CrossRef] [Green Version]
- Szemplinska-Stupnicka, W. The modified single mode method in the investigations of the resonant vibrations of non-linear systems. J. Sound Vib. 1979, 63, 475–489. [Google Scholar] [CrossRef]
- Krack, M.; Panning-von Scheidt, L.; Wallaschek, J. A method for nonlinear modal analysis and synthesis: Application to harmonically forced and self-excited mechanical systems. J. Sound Vib. 2013, 332, 6798–6814. [Google Scholar] [CrossRef]
- Jahn, M.; Stender, M.; Tatzko, S.; Hoffmann, N.; Grolet, A.; Wallaschek, J. The extended periodic motion concept for fast limit cycle detection of self-excited systems. Comput. Struct. 2020, 227, 106139. [Google Scholar] [CrossRef]
- Heinze, T.; Panning-von Scheidt, L.; Wallaschek, J. Global detection of detached periodic solution branches of friction-damped mechanical systems. Nonlinear Dyn. 2019. [Google Scholar] [CrossRef]
- Shaw, S.W.; Pierre, C. Non-Linear Normal Modes and Invariant Manifolds. J. Sound Vib. 1991, 150, 170–173. [Google Scholar] [CrossRef] [Green Version]
- Shaw, S.W.; Pierre, C. Normal Modes for Non-Linear Vibratory Systems. J. Sound Vib. 1993, 164, 85–124. [Google Scholar] [CrossRef] [Green Version]
- Haller, G.; Ponsioen, S. Nonlinear normal modes and spectral submanifolds: Existence, uniqueness and use in model reduction. Nonlinear Dyn. 2016, 86, 1493–1534. [Google Scholar] [CrossRef] [Green Version]
- Krack, M. Nonlinear modal analysis of nonconservative systems: Extension of the periodic motion concept. Comput. Struct. 2015, 154, 59–71. [Google Scholar] [CrossRef]
- Jahn, M.; Tatzko, S.; Panning-von Scheidt, L.; Wallaschek, J. Comparison of different harmonic balance based methodologies for computation of nonlinear modes of non-conservative mechanical systems. Mech. Syst. Signal Proces. 2019, 127, 159–171. [Google Scholar] [CrossRef]
- Scheel, M.; Peter, S.; Leine, R.I.; Krack, M. A phase resonance approach for modal testing of structures with nonlinear dissipation. J. Sound Vib. 2018, 435, 56–73. [Google Scholar] [CrossRef]
- Karaağaçlı, T.; Özgüven, H.N. Experimental modal analysis of nonlinear systems by using response-controlled stepped-sine testing. Mech. Syst. Signal Proces. 2020, 146, 107023. [Google Scholar] [CrossRef]
- Renson, L.; Barton, D.A.W.; Neild, S.S. Experimental Analysis of a Softening-Hardening Nonlinear Oscillator Using Control-Based Continuation. In Nonlinear Dynamics, Volume 1: Proceedings of the 34th IMAC, A Conference and Exposition on Structural Dynamics 2016; Kerschen, G., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 19–27. [Google Scholar] [CrossRef]
- Renson, L.; Barton, D.A.W.; Neild, S.A. Experimental Tracking of Limit-Point Bifurcations and Backbone Curves Using Control-Based Continuation. Int. J. Bifurc. Chaos 2017, 27, 1730002. [Google Scholar] [CrossRef] [Green Version]
- Paduart, J.; Lauwers, L.; Swevers, J.; Smolders, K.; Schoukens, J.; Pintelon, R. Identification of nonlinear systems using Polynomial Nonlinear State Space models. Automatica 2010, 46, 647–656. [Google Scholar] [CrossRef]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach; John Wiley & Sons: Piscataway, NJ, USA, 2012. [Google Scholar]
- Tiels, K. A polynomial nonlinear state-space toolbox for Matlab. In Proceedings of the 21st IMEKO TC4 International Symposium on Understanding the World through Electrical and Electronic Measurement, and 19th International Workshop on ADC Modelling and Testing, Budapest, Hungary, 7–9 September 2016; pp. 28–31. [Google Scholar]
- Schoukens, J.; Pintelon, R.; Rolain, Y.; Dobrowiecki, T. Frequency response function measurements in the presence of nonlinear distortions. Automatica 2001, 37, 939–946. [Google Scholar] [CrossRef]
- Morlock, F. Force Control of an Electrodynamic Shaker for Experimental Testing of Nonlinear Mechanical Structures. Master’s Thesis, Universität Stuttgart, Stuttgart, Germany, 2015. [Google Scholar]
- Dormand, J.R.; Prince, P.J. A family of embedded Runge-Kutta formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef] [Green Version]
- Krack, M.; Gross, J. Harmonic Balance for Nonlinear Vibration Problems; Mathematical Engineering; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Nayfeh, A.; Mook, D. Nonlinear Oscillations; Wiley Classics Library, John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Krack, M.; Panning-von Scheidt, L.; Wallaschek, J. On the computation of the slow dynamics of nonlinear modes of mechanical systems. Mech. Syst. Signal Proces. 2014, 42, 71–87. [Google Scholar] [CrossRef]
- Gaul, L.; Nitsche, R. The Role of Friction in Mechanical Joints. Appl. Mech. Rev. 2001, 54, 93. [Google Scholar] [CrossRef]
- Mathis, A.T.; Balaji, N.N.; Kuether, R.J.; Brink, A.R.; Brake, M.R.W.; Quinn, D.D. A Review of Damping Models for Structures With Mechanical Joints. Appl. Mech. Rev. 2020, 72. [Google Scholar] [CrossRef]
- Noël, J.P.; Esfahani, A.F.; Kerschen, G.; Schoukens, J. A nonlinear state-space approach to hysteresis identification. Mech. Syst. Signal Proces. 2017, 84, 171–184. [Google Scholar] [CrossRef] [Green Version]
- Hurty, W.C. Dynamic analysis of structural systems using component modes. AIAA J. 1965, 3, 678–685. [Google Scholar] [CrossRef]
- Craig, R.R.J.; Bampton, M.C.C. Coupling of substructures using component mode synthesis. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef]














| Description | Parameter | Value |
|---|---|---|
| Electrical resistance | R | 3 |
| Electrical inductivity | L | 140 mH |
| Shaker force generating constant | G | 15.4791 NA |
| Coil mass | 0.019 kg | |
| Coil stiffness | 8.4222 × 10 Nm | |
| Coil damping | 57.1692 Nsm | |
| Table mass | 0.0243 kg | |
| Table stiffness | 20707 Nm | |
| Table damping | 28.3258 Nsm | |
| Stinger stiffness (idealized as a bar) | ||
| Input Level | Lyapunov Exponents (bits/s) | |
|---|---|---|
| A (N) | ||
| 0.01 | −26.7 | −28.0 |
| 0.25 | −22.9 | −31.8 |
| 0.50 | −7.9 | −46.9 |
| 0.75 | 5.7 | −60.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balaji, N.N.; Lian, S.; Scheel, M.; Brake, M.R.W.; Tiso, P.; Noël, J.-P.; Krack, M. Numerical Assessment of Polynomial Nonlinear State-Space and Nonlinear-Mode Models for Near-Resonant Vibrations. Vibration 2020, 3, 320-342. https://doi.org/10.3390/vibration3030022
Balaji NN, Lian S, Scheel M, Brake MRW, Tiso P, Noël J-P, Krack M. Numerical Assessment of Polynomial Nonlinear State-Space and Nonlinear-Mode Models for Near-Resonant Vibrations. Vibration. 2020; 3(3):320-342. https://doi.org/10.3390/vibration3030022
Chicago/Turabian StyleBalaji, Nidish Narayanaa, Shuqing Lian, Maren Scheel, Matthew R. W. Brake, Paolo Tiso, Jean-Philippe Noël, and Malte Krack. 2020. "Numerical Assessment of Polynomial Nonlinear State-Space and Nonlinear-Mode Models for Near-Resonant Vibrations" Vibration 3, no. 3: 320-342. https://doi.org/10.3390/vibration3030022
APA StyleBalaji, N. N., Lian, S., Scheel, M., Brake, M. R. W., Tiso, P., Noël, J.-P., & Krack, M. (2020). Numerical Assessment of Polynomial Nonlinear State-Space and Nonlinear-Mode Models for Near-Resonant Vibrations. Vibration, 3(3), 320-342. https://doi.org/10.3390/vibration3030022






